норматив по ПУЭ, расчет и замеры

Автор Electricity На чтение 3 мин. Опубликовано 12.01.2020

Воздушные линии электропередач – это электроустановка, которая используется для передачи и распределения электрической энергии по проводам различного сечения. Последние закрепляются на изоляторах, которые прикрепляются к траверсам или к специальной арматуре на опорах. При проектировании и монтаже важно соблюдать габариты ВЛ, куда включается длина пролетов, расстояния от объектов, стрела провеса.

Габариты ВЛ

Основным документом, в котором прописываются требования к габаритам, является «Правила устройства электроустановок» (ПУЭ). В этой нормативной документации предоставляется отдельная глава, которая посвящается рассматриваемому вопросу. Разберем основные моменты по заданному направлению.

Определения

Габариты ВЛ – это предельно допустимые расстояния от проводов до поверхности земли и различных объектов, сооружений и устройств. Соблюдение этих требований обеспечивает правильное и безопасное использование электроустановки для передачи и распределения электроэнергии. В понятие включается:

1. Высота подвеса – расстояние от места крепления проводов на изоляторе до земли. Габаритом над землей называется величина от низшей точки пролета до земли.
2. Стрела провеса – это разница от подвеса ЛЭП и проводов в наименьшей точке (посередине пролета) до земли. Величина зависит от температуры воздуха, пролета, марки опор.
3. Существует понятие габарит при пересечении и сближении. Это величины, которые регламентируют длину по вертикали до поверхности дорог, рек, пересекаемых ВЛ, а также наименьшие величины до объектов и строений.

Длина промежуточного пролета – это величина между смежными опорами. Для ВЛ 0,4 кВ этот показатель составляет 30-50 метров в зависимости от сечения, климата, типов опор.

Допустимые величины по ПУЭ

Габариты ВЛ зависят от нескольких факторов, в том числе от напряжения линии, от проходимости в городе или на пересеченной местности, по используемым материала.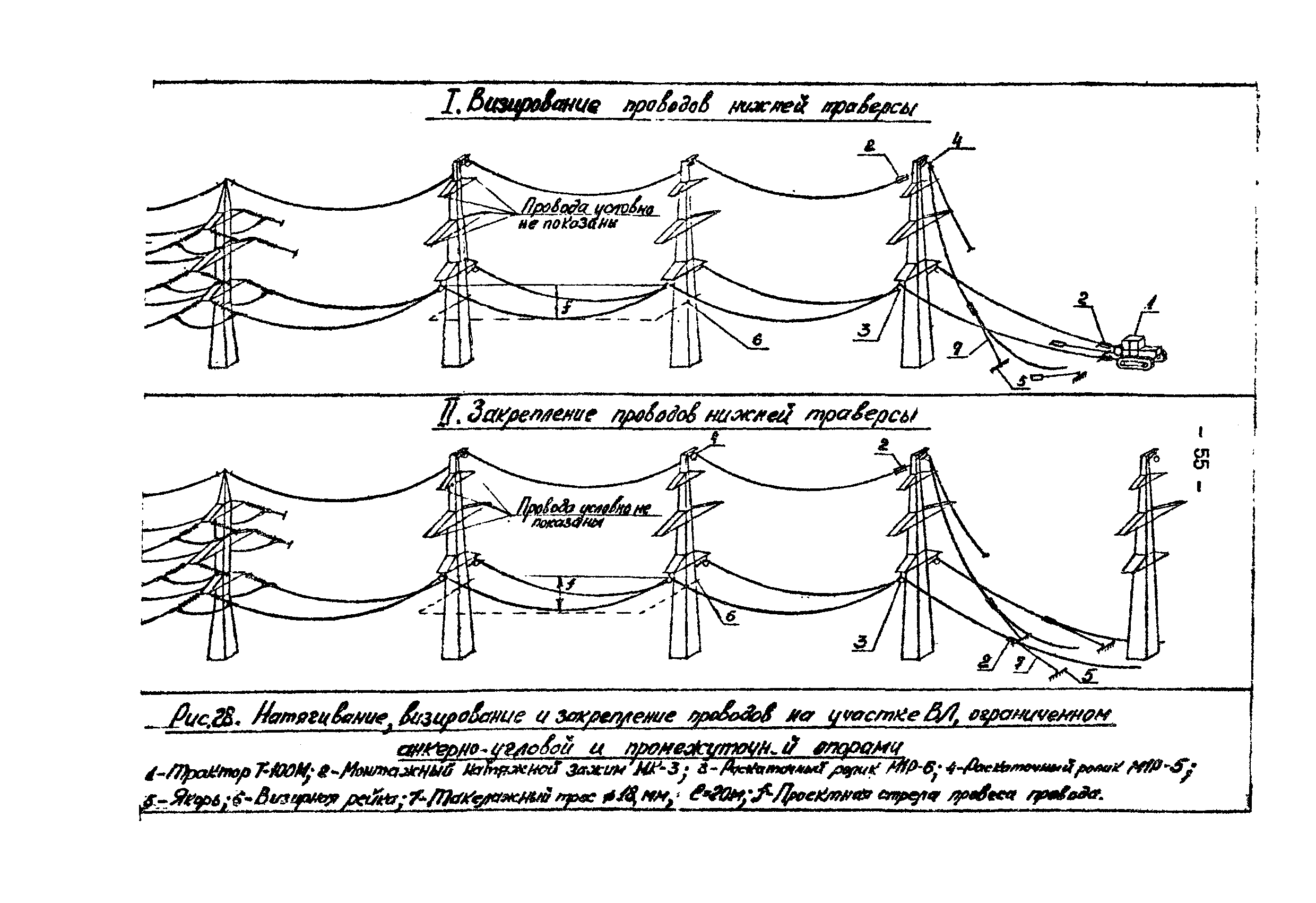 Рассмотрим различные примеры далее:

• Для ВЛ 0,4 кВ согласно ПУЭ следующие – до земли не менее 6 метров. Ответвление ввода через дорогу обязано сопровождаться высотой не менее 3,5 м. От проводов на фронтоне до земли величина составляет не меньше 2,75 метра. При пересечении с железной дорогой, трамвайной или троллейбусной линией не менее 7,5 м, до других проводов не менее 1,5 м. Стрела провеса для линии до 1000 В при пролете 35-45 метров последняя не превышает 1,2 метра.
• Габариты ВЛ 10 кВ регламентируются ПУЭ. Минимальное расстояние до земли составляет не менее 7 м. При пересечении с железной дорогой, трамвайной или троллейбусной линией не менее 9,5 м, до провода не менее 3 метров. Стрела провеса ВЛ 10 киловольт не превышает 1,5 м.

Строительство ВЛ любого напряжения над зданиями не допускается. При совместной подвеске разного напряжения между фазами соблюдается расстояние не менее 1,2 метра.

Расчет габаритов основывается на «Правилах устройства электроснабжения». Этот нормативный документ лег в основу типовых проектов по каждому типу опор ВЛ 0,4-10 кВ. Расчет осуществляется с учетом климатических особенностей. В ПУЭ представлена формула, определяющая стрелу провеса провода для ВЛ от 35 киловольт и выше.

Проведение замеров габаритов

Наиболее точный, безопасный и эффективный способ определения расстояния основан на использовании оптических приборов. Этот вариант позволяет получить информацию без отключения ВЛ электропередач. Для реализации поставленной задачи подходит теодолит, высотомер или другие изделия схожего назначения. Процесс поэтапный, на первой стадии оценивается высота подвеса линии. На второй делается замер до низшей точки провисания провода, а также в местах пересечения с дорогами или объектами.

Стрела провеса провода ВЛ определяется математически. Величина меняется в зависимости от температуры наружного воздуха. Если ЛЭП не введена в эксплуатацию оценка производится с применением штанги или каната с метками.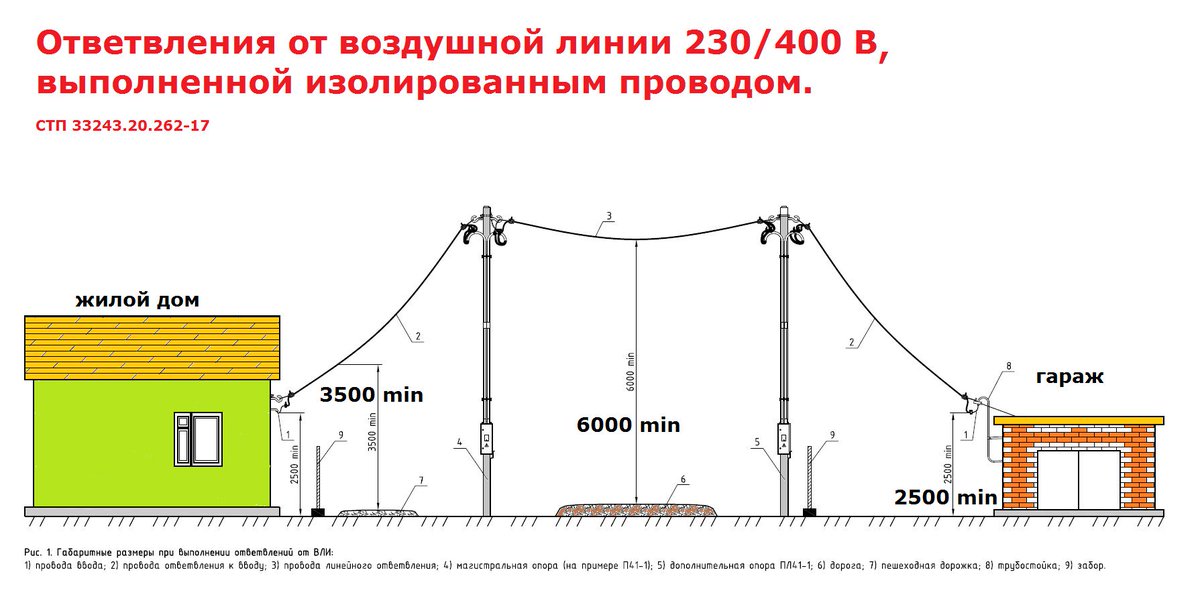 Помните, что неправильно выбранные величины становятся причиной появления несчастных случаев, «схлестов» и обрывов.

Габариты, пересечения и сближения. Правила устройства электроустановок в вопросах и ответах [Пособие для изучения и подготовки к проверке знаний]

Габариты, пересечения и сближения

Вопрос. Каким должно быть расстояние по вертикали от проводов ВЛИ до поверхности земли и проезжей части улиц в населенной и ненаселенной местности?

Ответ. Должно быть не менее 5 м. Оно может быть уменьшено в труднодоступной местности до 2,5 м и в недоступной (склоны гор, скалы, утесы) – до 1 м.

При пересечении непроезжей части улиц ответвлениями от ВЛИ к вводам в здания расстояние от СИП до тротуаров пешеходных дорожек допускается уменьшить до 3,5 м.

Расстояние от СИП и изолированных проводов до поверхности земли на ответвлениях к вводам должно быть не менее 2,5 м.

Расстояние от неизолированных проводов до поверхности земли на ответвлениях к вводам должно быть не менее 2,75 м (2. 4.55).

Вопрос. Каким должно быть расстояние от проводов ВЛ в населенной и ненаселенной местности при наибольшей стреле провеса проводов до земли и проезжей части улиц?

Ответ. Должно быть не менее 6 м. Расстояние от проводов до земли может быть уменьшено в труднодоступной местности до 3,5 м и в недоступной местности (склоны гор, скалы, утесы) – до 1 м (2.4.56).

Вопрос. Каким должно быть расстояние по горизонтали от СИП при наибольшем их отклонении до элементов зданий и сооружений?

Ответ. Должно быть не менее:

1,0 м – до балконов, террас и окон;

0,2 м – до глухих стен зданий, сооружений (2.4.57).

Вопрос. Каким должно быть расстояние по горизонтали от проводов ВЛ при наибольшем их отклонении до зданий и сооружений?

Ответ. Должно быть не менее:

1,5 м – до балконов, террас и окон;

1,0 м – до глухих стен.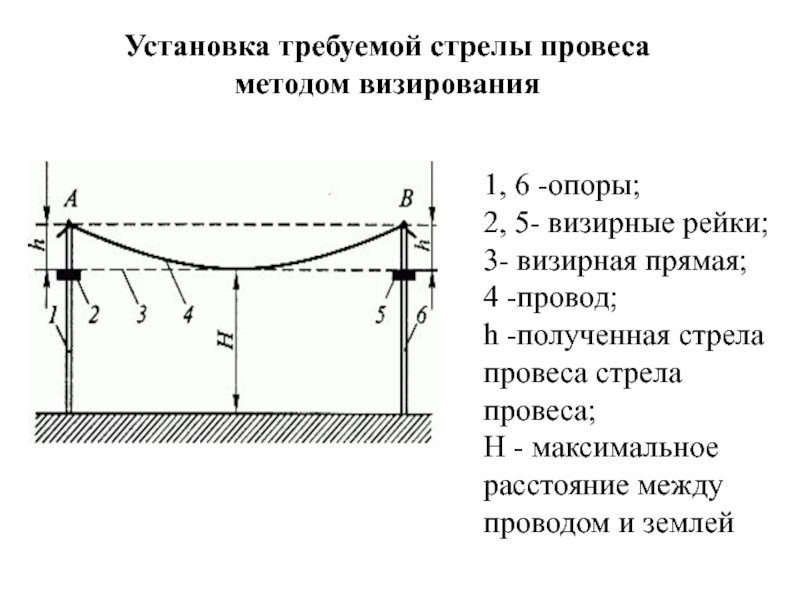

Прохождение ВЛ с неизолированными проводами над зданиями и сооружениями не допускается (2.4.58).

Вопрос. Каким должно быть минимальное расстояние от СИП при прокладке проводов по стенам зданий и сооружениям?

Ответ. Должно быть:

при горизонтальной прокладке:

над окном, входной дверью – 0,3 м;

под балконом, окном, карнизом – 0,5 м;

до земли – 2,5 м;

при вертикальной прокладке:

до окна – 0,5 м;

до балкона, входной двери – 1,0 м.

Расстояние в свету между СИП и стеной здания или сооружением должно быть не менее 0,06 м (2.4.60).

Вопрос. Какими должны быть расстояния по горизонтали от подземных частей опор или заземлителей опор до подземных кабелей, трубопроводов и наземных колонок различного назначения?

Ответ. Должны быть не менее приведенных в табл. 2.4.4 (2.4.61).

Таблица 2.4.4

Наименьшее допустимое расстояние по горизонтали от подземных частей опор или заземляющих устройств опор до подземных кабелей, трубопроводов и наземных колонок

Окончание табл. 2.4.4

Вопрос. Как рекомендуется выполнять пересечение ВЛ (ВЛИ) напряжением до 1 кВ между собой?

Ответ. Рекомендуется выполнять на перекрестных опорах; допускается также их пересечение в пролете. Расстояние по вертикали между проводами пересекающихся ВЛ (ВЛИ) должно быть не менее: 0,1 м на опоре, 1 м в пролете (2.4.65).

Вопрос. При каких условиях допускается совместная подвеска проводов ВЛ напряжением до 1 кВ и неизолированных проводов ВЛ до 20 кВ на общих опорах?

Ответ. Допускается при соблюдении следующих условий:

ВЛ напряжением до 1 кВ должны выполняться по расчетным климатическим условиям ВЛ до 20 кВ;

провода ВЛ напряжением до 20 кВ должны располагаться выше проводов ВЛ напряжением до 1 кВ;

провода ВЛ напряжением до 20 кВ, закрепляемые на штыревых изоляторах, должны иметь двойное крепление (2.4.68).

Вопрос. Какие требования должны соблюдаться при подвеске на общих опорах проводов ВЛ напряжением до 1 кВ и защищенных проводов ВЛЗ напряжением 6-20 кВ?

Ответ. Должны соблюдаться следующие требования:

ВЛ напряжением до 1 кВ должны выполняться по расчетным климатическим условиям ВЛ до 20 кВ;

провода ВЛЗ напряжением 6-20 кВ должны располагаться, как правило, выше проводов ВЛ напряжением до 1 кВ;

крепление проводов ВЛЗ напряжением 6-20 кВ на штыревых изоляторах должно выполняться усиленным (2.4.69).

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Определения, габариты ВЛ | Монтаж электрических установок | Архивы

Страница 70 из 83

Определения.

Промежуточные опоры устанавливаются на прямых участках трассы ВЛ. Эти опоры в нормальных режимах работы не должны воспринимать усилий, направленных вдоль ВЛ.
Анкерные опоры устанавливаются на пересечениях с различными сооружениями, а также в местах изменения количества, марок и сечений проводов. Эти опоры должны воспринимать в нормальных режимах работы усилия от разности тяжения проводов, направленные вдоль ВЛ. Анкерные опоры должны иметь жесткую конструкцию.
Угловые опоры устанавливаются в местах изменения направления трассы ВЛ. Эти опоры при нормальных режимах работы должны воспринимать слагающую тяжения проводов смежных пролетов.
Концевые опоры устанавливаются в начале и конце ВЛ, а также в местах, ограничивающих кабельные вставки. Они являются опорами анкерного типа и должны воспринимать в нормальных режимах работы ВЛ одностороннее тяжение проводов.
Ответвительные опоры устанавливаются в местах ответвления от ВЛ.
Перекрестные опоры устанавливаются в местах пересечения ВЛ двух направлений.
Нормальным режимом BЛ выше 1 кВ называется состояние ВЛ при необорванных проводах и тросах.
Аварийным режимом ВЛ выше 1 кВ называется состояние ВЛ при оборванных одном или нескольких проводах и тросах.
Промежуточный пролет — это расстояние по горизонтали между двумя смежными промежуточными опорами. Эти пролеты на ВЛ до 1 кВ обычно колеблются от 30 до 50 м, а на ВЛ выше 1 кВ составляют 100 — 250 м и больше.
Анкерный пролет — это расстояние по горизонтали между опорами, на которых провода закрепляют жестко На ВЛ 35 кВ и выше с проводами, подвешенными на промежуточных опорах в глухих зажимах с ограниченной прочностью заделки, расстояние между анкерными опорами (длина анкерного пролета) не нормируется и устанавливается в зависимости от условий трассы. На ВЛ 35 кВ и ниже со штыревыми изоляторами длина анкерного пролета не должны превышать 10 км в районах с толщиной стенки гололеда до 10 мм и 5 км в районах с толщиной стенки гололеда 15 мм и более [3].

Габариты.

Воздушные линии характеризуются пролетом (промежуточным и анкерным), стрелой провеса проводов и тросов, допустимыми расстояниями (габаритами) от проводов до земли, до пересекаемых линий дорог и пр.
В [3] определены наименьшие допустимые расстояния по вертикали и горизонтали от проводов ВЛ до поверхности земли, строений и зеленых насаждений, поверхности рек, автомобильных и железных дорог, проводов других линий Расстояние от проводов ВЛ напряжением до 1 кВ до земли и проезжей части улиц при наибольшей стреле провеса должно быть не менее 6 м Расстояние по горизонтали до зданий и строений при наибольшем отклонении проводов должно быть не менее до глухих стен — 1 м, до балконов террас, окон—1,5 м Пересечение ВЛ до 1 кВ между собой рекомендуется выполнять на перекрестных опорах, допускается пересечение в прочетах При этом расстояние го вертикали между ближайшими проводами пересекающихся ВЛ при температуре окружающего воздуха плюс 15°С без ветра должно быть не менее 1 м, место пересечения следует выбирать возможно ближе к опоре верхней пересекающей ВЛ, но при этом расстояние по горизонтали между опорами пересекающей и проводами пересекаемой ВЛ должно быть не менее 2 м

Расстояние от проводов ВЛ выше 1 кВ до 110 кВ до поверхности земли в населенной местности должно быть в нормальном режиме не менее 7 м, в аварийном режиме — не менее 4,5 м Угол пересечения ВЛ выше 1 кВ между собой и с ВЛ до 1 кВ не нормируется Провода ВЛ более высокого напряжения, как правило, должны быть расположены над проводами более низкого напряжения Место пересечения должно выбираться возможно ближе к опоре верхней (пересекающей) ВЛ, при этом, однако, расстояние по горизонтали от этой опоры до проводов нижней (пересекаемой) ВЛ при наибольшем отклонении проводов должно быть не менее 6 м, а от опор нижней (пересекаемой) ВЛ до проводов верхней (пересекающей) ВЛ — не менее

м. Допускается в отдельных случаях выполнение пересечений ВЛ выше 1 кВ на опоре.
Пересечение проводов ВЛ выше 1 кВ с воздушными линиями городской телефонной связи не допускается линии связи в пролете пересечения с проводами ВЛ должны выполняться только подземными кабелями с соблюдением специальных требований, указанных в [3]
На опорах ВЛ до 1 кВ на высоте 2,5—3 м от земли должны быть нанесены порядковый номер и год установки опоры и установлены плакаты, на которых указаны расстояния от опоры ВЛ до кабельной линии связи (на опорах, установленных на расстоянии менее половины высоты опоры ВЛ до кабелей связи).
На опорах ВЛ выше 1 кВ на высоте 2,5—3 м должны быть нанесены следующие постоянные знаки: порядковый номер — на всех опорах; номер ВЛ или ее условное обозначение  на концевых опорах, первых опорах ответвлений от линии, на опорах в месте пересечения линий одного напряжения, на опорах, ограничивающих пролет пересечения с железными дорогами и автомобильными дорогами
V категорий, а также на всех опорах участков трассы с параллельно идущими линиями, если расстояние между их осями менее 200 м. На двухцепных и многоцепных опорах ВЛ, кроме того, должна быть обозначена соответствующая цепь; на ВЛ 35 кВ и выше — расцветка фаз на концевых опорах, опорах, смежных с транспозиционными, и на первых опорах ответвлений от ВЛ; на всех опорах ВЛ в населенной местности должны быть предупреждающие плакаты; на опорах,установленных на расстоянии менее половины высоты опоры от кабелей связи, — плакаты, на которых указаны расстояния от опоры ВЛ до кабельной линии связи.

Проверка габаритов и стрелы провеса проводов и тросов | ПЛ

Стрела провеса — это расстояние по вертикали в промежуточном пролете ВЛ между проводом (тросом) и прямой линией, соединяющей точки его подвеса.
Стрелы провеса проводов и тросов, габариты линии до земли или пересекаемых объектов измеряют при приемке линии в эксплуатацию для проверки правильности монтажа, и в процессе эксплуатации, а в дальнейшем по мере необходимости: при появлении новых пересечений или сооружений, при переустройстве имеющихся переходов или пересекаемых объектов (замена опор, проводов, изоляторов, арматуры), а также при наклонах опор или изменениях их конструкций при ремонтных и реконструктивных работах, вытяжке проводов, проскальзывании проводов в подвесных и натяжных болтовых зажимах, изменения длины гирлянд при замене дефектных изоляторов и перекосе траверс и др.
Габариты линий могут измениться в результате прокладки под проводами дорог, сооружения линий электропередачи.
Если строительство таких сооружений не было согласовано с эксплуатирующей организацией, то габариты могут оказаться недостаточными, возникнет угроза безопасности для посторонних лиц и снизится надёжность работы линии. Строгой периодичности измерения стрел провеса габаритов не установлено и эти измерения должны производиться по мере необходимости, определяемой в результате периодических осмотров.
Измерения, как правило, производят без отключения линии при помощи угломерных приборов или изолирующих штанг и капронового или сухого хлопчатобумажного каната. Для измерений на отключенных линиях могут быть использованы дополнительно обычные рулетки или веревки. В качестве угломерных приборов могут быть использованы теодолиты, нивелиры, а также более простые, но достаточно точные для данных измерений оптические приборы, карманные высотомеры и т.п.
При измерениях следует фиксировать температуру воздуха.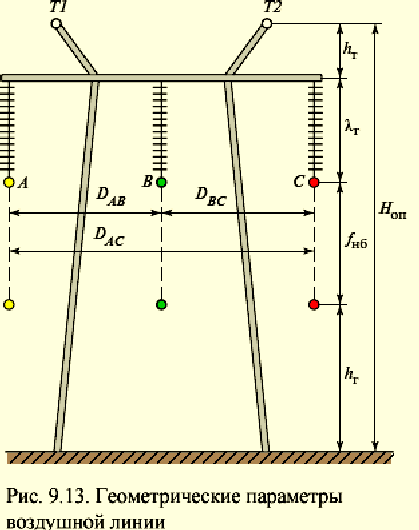 Полученные при измерениях фактические значения путем расчетов или с помощью специальных таблиц приводятся к температуре, при которой получаются наибольшие стрелы провеса, которые сопоставляются с проектными данными и допусками, приведенными в нормативно-технической документации.
Фактическая стрела провеса проводов и тросов не должна отличаться от расчетной более чем на 5%. Разрегулировка проводов любой фазы по отношению к другой, а также разрегулировка тросов допускается не более чем на 10% проектного значения при условии соблюдения необходимого расстояния до земли и пересекаемых объектов. Расстояния от проводов ВЛ до земли и до различных пересекаемых объектов в местах сближения с ним должна быть не менее определённых в  нормативах .
Проверка габаритов в местах пересечения линии с другими сооружениями является обязательной во всех случаях реконструкции и ремонта линии со сменой или переустройством опор, при замене проводов, возвышении каких-либо сооружений под линией и других работах, вызванных изменениями габаритов.
Способы измерения габаритов и стрелы провеса проводов и тросов ВЛ. Измерение габарита линии с помощью капронового каната ведут в такой последовательности. На опору, не доходя 2 м до уровня изолирующих подвесок, поднимается электромонтер и устанавливает блок бесконечного каната. Затем по этому канату он поднимает изолирующую штангу и в специальном чехле ролик с измерительным капроновым канатом. С помощью штанги ролик устанавливают на проводе, второй конец капронового каната держит второй электромонтер, находящийся на земле. После установки ролик с помощью капронового каната вторым электромонтером передвигается до места измерения габарита. По отметкам на канате определяется расстояние от ролика (проводов) до поверхности земли (рис.). После измерения ролик возвращается к опоре и снимается первым электромонтером с помощью изолирующей штанги.

Измерение габарита ВЛ с помощью капронового каната 1 — ролик; 2 — отметки; 3 — капроновый канат

Так как эти работы выполняются под напряжением, к работе допускаются только специально обученные лица. Запрещается производство работ в сырую погоду.
Наиболее точным и простым способом измерения габарита является непосредственное измерение под напряжением с помощью специальной испытанной в соответствии с нормами изолирующей штанги. Один электромонтер в месте измерения одним концом штанги касается провода, другой электромонтер замеряет расстояние от нижнего конца штанги до поверхности земли (дороги, железнодорожного полотна и др.). Сумма длины штанги и измеренного расстояния определяют габарит. Габарит в месте пересечения двух линий определяется разностью габаритов каждой линии.
Для измерения стрелы провеса с помощью штанги определяют габарит линии и расстояние от места крепления провода к изолятору или гирлянд до поверхности земли. Разница между измеренными величинами равна значению стрелы провеса (при прохождении трассы по ровной местности).
Простым и удобным прибором для измерения стрелы провеса или габарита провода до земли (рис. 2. 12.24) является приспособление для определения высоты элементов ПОВЭ (карманный высотомер).
Прибор представляет собой плоскую коробку, имеющую форму равностороннего треугольника. В основание треугольника вставлено стекло, на котором нанесены две риски. В вершине треугольника имеются два отверстия, через которые производится визирование.

 

Карманный высотомер типа ВК-1 ( ПОВЭ)

Для определения высоты измеряемого объекта (высоты дерева под проводами, высоты опоры или подвески провода на опоре) наблюдатель удаляется от него, держа приспособление отверстиями у глаз, на такое расстояние, при котором риски на стекле совпадают: верхняя — с вершиной объекта, нижняя — с его основанием; затем измеряется рулеткой расстояние от объекта до наблюдателя, искомая высота равняется половине этого расстояния.
Для определения высоты провода над землей под проводом в месте измерения забивается колышек. Затем наблюдатель удаляется от линии в направлении, перпендикулярном к ней, держа приспособление отверстиями у глаз на расстояние, при котором риски совпадают, верхняя — с проводом, нижняя — с основание колышка. Измеряется расстояние от наблюдателя до колышка. Габарит провода в месте измерения равен половине этого расстояния.
Для определения стрелы провеса провода измеряется сначала высота подвески провода на опоре, как указано выше, затем наименьший габарит над землей и находят их разность.
Погрешность измерений ПОВЭ при высоте объектов или габаритов до 50 м не превышает 4%, что является допустимым.
Измерение стрелы провеса проводов (тросов) может быть выполнено путем глазомерного визирования (с помощью двух визирующих реек  следующим способом.

Крючок-СпЭ. крепить шурупами

Устройства для визирования стрел провеса проводов
а — на ВЛ со штыревыми изоляторами, б — на ВЛ с подвесными изоляторами, в — на ровном профиле, г — в наклонном пролете
1 — стойка металлической опоры; 2 — окуляр; 3 — рейка с уровнем.
4 — струбцина для крепления; 5 — стрела провеса
На стояках двух смежных опор закрепляют по одной рейке на расстоянии по вертикали от точки крепления провода, равном расчетному значению стрелы провеса провода (определяемому по монтажным таблицам) в проверяемом пролете при данной температуре. Если низшая точка провисания провода находится выше или ниже прямой линии, соединяющей обе визирные рейки, провод смонтирован с отклонением от заданного тяжения (соответственно с перетяжкой или недотяжкой). Для определения фактической стрелы провеса обе рейки перемещают вверх или вниз до положения, когда низшая точка провода совпадет с прямой, соединяющей обе рейки. Значение стрелы провеса определяется как среднее арифметическое расстояние по вертикали от точек подвеса провода до каждой рейки, сравнением полученных данных со значением стрелы провеса по монтажным кривым или таблицам, определяется отклонение от требуемого значения.
Наиболее точно стрелы провеса могут быть измерены с помощью теодолита, однако использование этого метода измерений требует специально обученного персонала. Для измерения габарита теодолит устанавливают на расстоянии 50…60 м от линии, так чтобы расстояния от прибора до вертикальных проекций низшей точки провода и точки подвеса провода на опоре (R1 и R2) были примерно одинаковы (рис. 26). Эти расстояния тщательно измеряют с помощью рулетки или с помощью теодолита и рейки.
Вертикальная визирующая ось теодолита направляется на точку провода на опоре и производится отсчет превышения этой точки над горизонтальной осью прибора (угол р). Аналогично производится отсчет превышения низшей точки провода над горизонтальной осью прибора (угол а). По полученным отсчётам определяется стрела провеса провода как разность подсчитанных значений.
Расстояния от проводов до зданий и сооружений, расположенных вблизи BЛ, должны измеряться от проекции крайнего провода при наибольшем его расчетном отклонении до ближайших выступающих частей этих зданий и сооружений.
Все измерения не разрешается производить при скорости ветра более 10 м/с. Результаты измерений габаритов проводов записывают в специальную ведомость.

2.2. Воздушные линии электропередачи переменного тока

2.2. Воздушные линии электропередачи переменного тока

Технический прогресс конструкций воздушных линий переменного тока на всех этапах их развития заключался в увеличении параметров по напряжению, передаваемой мощности и дальности передачи электроэнергии. Достигнутые соотношения между этими параметрами видны из таблицы 2.1.

Основным фактором, определяющим пропускную способность и дальность передачи воздушной линии, является величина ее линейного напряжения. Эта же величина определяет основные конструктивные решения воздушных линий как сооружений, поскольку с ростом напряжения увеличиваются габариты опор и усложняется их конструкция. Как видно из приведенной таблицы, линии, которые могут выполнять функции межсистемных связей (по мощности и дальности передачи), должны иметь напряжение не ниже 220 кВ. В ОЭС Украины межсистемные ВЛ имеют напряжения 330, 500 (400) и 750 кВ. В ЕЭС России такие линии имеют напряжения 220, 330, 500 и 750 кВ. Наивысшее в мире напряжение воздушных линий переменного тока использовано на линии 1150 кВ на связи Сибирь – Казахстан – Урал.

С учетом высокой ответственности межсистемных линий они в конструктивном отношении выполняются, как правило, на одноцепных опорах с горизонтальным расположением проводов. На высоковольтной линии напряжением выше 220 кВ предпочтение получили портальные опоры П-образного типа (свободностоящие и с тросовыми оттяжками). Портальная конструкция опоры позволила лучше всего обеспечить большие воздушные промежутки между проводами, грозозащитными тросами и телом опоры, требующиеся при напряжениях выше 220 кВ.

 

Таблица 2.1 Параметры высоковольтных линий переменного тока

Напряжение, кВ	Передаваемая мощность, МВт	Дальность передачи, км
110	25 – 50	50 – 150
220	100 – 200	150 – 250
330	300 – 400	200 – 300
500	700 – 900	600 – 1200
750	1800 – 2200	800 – 1500
1150	4000 – 6000	1200 – 2000

Рисунок 2. 1 демонстрирует внушительные габариты конструкции опор, необходимые, например, для ВЛ 750 кВ. Опоры изготавливают из металла (сталь). Для конструкции промежуточных опор также широко используют железобетонные центрофугированные стойки конического типа длиной до 26 м, которые устанавливают в сверленные котлованы (без фундаментов). Двухстоечные железобетонные П-образные промежуточные опоры являются самыми массовыми конструкциями на линиях 330 кВ в Украине и в других странах на воздушных линиях напряжением ниже 380 кВ (рис. 2.2). Применение железобетонных анкерных и угловых опор оказалось неэффективным из-за больших затрат земельных площадей, необходимых для размещения многочисленных тросовых оттяжек, а также из-за низкого уровня внешней эстетичности конструкций.

Протяженность воздушных линий напряжением 330 кВ и выше в ОЭС Украины на конец 2000 года составила: 330 кВ – 12790 км, 500 (400)кВ – 948 км, 750 кВ – 4335 км.

 

Рис. 2.2. Промежуточная железобетонная опора ВЛ 330 кВ (размеры указаны в метрах)

 

Рис. 2.1. Портальные металлические опоры воздушных линий напряжением 750 кВ: а – промежуточная свободностоящая опора; б – промежуточная опора с оттяжками (размеры указаны в метрах)

В конструкции фаз воздушных линий напряжением выше 220 кВ используется принцип расщепления фазы на несколько проводов, расположенных на расстоянии 400–700 мм друг от друга. Это позволяет уменьшить напряженность электрического поля на поверхности проводов до величины, при которой ограничивается развитие коронного разряда (короны) на проводах. В результате уменьшаются потери электроэнергии от короны и снижается уровень радиопомех. Количество проводов в расщепленной фазе линий сверхвысокого напряжения обычно составляет 2 для ВЛ 330 кВ, 3 для ВЛ 500 кВ, 4 или 5 для ВЛ 750 кВ. На более высоких напряжениях фаза линии может составлять 8 проводов и более.

Выдающаяся роль в организации разработки конструкций и строительстве линий сверхвысокого напряжения на территории бывшего СССР принадлежит советскому ученому С. С. Рокотяну (1908–1977). На основе этих линий во второй половине ХХ века были созданы крупнейшие энергообразования – Единая энергосистема России и Объединенная энергосистема Украины.

Конструктивные параметры воздушных линий электропередачи

Основные конструктивные параметры воздушной линии (ВЛ) — это длина пролета, стрела провеса проводов, расстояние от проводов до земли, до покрытия пересекаемых линией дорог и других инженерных сооружений (габарит). Длиной промежуточного пролета называют расстояние вдоль линии, между двумя смежными промежуточными опорами. Длина пролета ВЛ-0,4 кВ колеблется в пределах 30 — 50 м и зависит от типов опор, марки, сечения проводов? а также климатических условий района. Стрелой провеса проводов называют расстояние по вертикали …

Основные конструктивные параметры воздушной линии (ВЛ) — это длина пролета, стрела провеса проводов, расстояние от проводов до земли, до покрытия пересекаемых линией дорог и других инженерных сооружений (габарит).

Длиной промежуточного пролета называют расстояние вдоль линии, между двумя смежными промежуточными опорами. Длина пролета ВЛ-0,4 кВ колеблется в пределах 30 — 50 м и зависит от типов опор, марки, сечения проводов, а также климатических условий района.

Стрелой провеса проводов называют расстояние по вертикали между воображаемой прямой линией, соединяющей точки крепления проводов на двух смежных опорах и низшей точкой их провеса в пролете. Стрела провеса зависит от тех же факторов, что и длина пролета.

Габаритом ВЛ называют наименьшее расстояние по вертикали от проводов до поверхности земли, рек, озер, линий связи, шоссейных и железных дорог и т.п. Габарит ВЛ регламентируется ПУЭ и зависит от напряжения и посещения местности людьми.

Для обеспечения нормальной работы и безопасного обслуживания ВЛ расстояния от них до различных сооружений должны соответствовать нормам, установленным ПУЭ. Так, расстояние от проводов до поверхности земли по вертикали при наибольшей стреле провеса должно быть не менее 6м в населенной местности, расстояние от проводов до земли может быть уменьшено в труднодоступный местности до 3,5 м и в недоступной местности до 1 м. Расстояние 4 по горизонтали от проводов ВЛ до балконов, терасс, окон зданий должно составлять не менее 1,5 м, а до глухих стен не менее 1 м. Прохождение ВЛ над зданиями не допускается.

Трасса ВЛ может проходить по лесным массивам и зеленым насаждениям. Расстояние по горизонтали от проводов до кроны деревьев и кустов при наибольшей стреле провеса должно быть не менее 1 м.

Габариты ВЛ 0,4 — 10 кВ

Опоры ВЛ должны быть расположены от трубопроводов на расстоянии не менее 1 м, от колодцев подземной канализации и водозаборных колонок — не менее 2 м, от бензоколонок не менее 1 м, от силовых кабелей — 0,5-1 м.

Пересечение ВЛ судоходных рек правилами не рекомендуется. При пересечении несудоходных и замерзающих небольших рек и каналов расстояние 4 от проводов ВЛ до наивысшего уровня воды должно быть не менее 2 м, а от поверхности льда не менее 6 м. Расстояние по горизонтали от опоры ВЛ до воды должно быть не менее высоты опоры ЛЭП.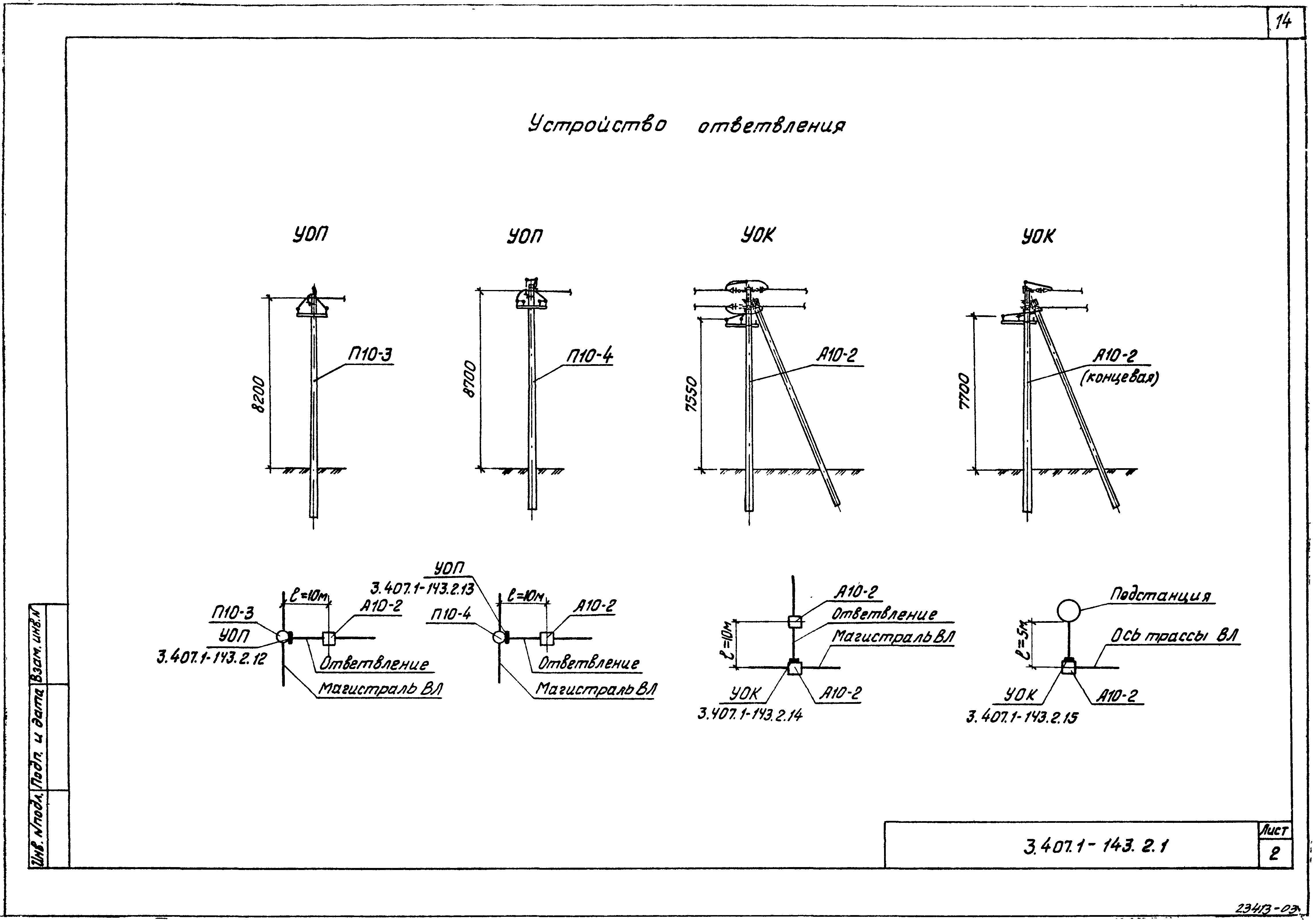

Угол пересечения ВЛ с улицами, площадями, а также с различными сооружениями не нормируется. Пересечения ВЛ до 1 кВ между собой рекомендуется выполнять на перекрестных опорах, а не в пролетах.

Пересечения ВЛ с воздушными линиями связи и сигнализации должны выполняться только в пролете линии, причем провода ВЛ должны располагаться выше.

Расстояние между верхним проводом линии связи и нижним ВЛ должно быть не менее 1,25 м. Особые требования предъявляют к проводам ВЛ в пролете пересечения: они должны быть многопроволочные, сечением не менее 25 мм2 (стальные и сталеалюминиевые) или 35 мм2 (алюминиевые) и закреплены на опорах двойным креплением. Опоры ВЛ, ограничивающие пролет пересечения с линиями связи I и II классов, должны быть анкерными; при пересечении с линиями связи других классов допускаются промежуточные опоры (деревянные должны иметь железобетонные приставки).

При пересечении подземных кабельных линий связи и сигнализации опоры ВЛ должны располагаться на возможно большем расстоянии от кабеля (но не менее 1 м между заземлением опоры и кабелем в стесненных условиях).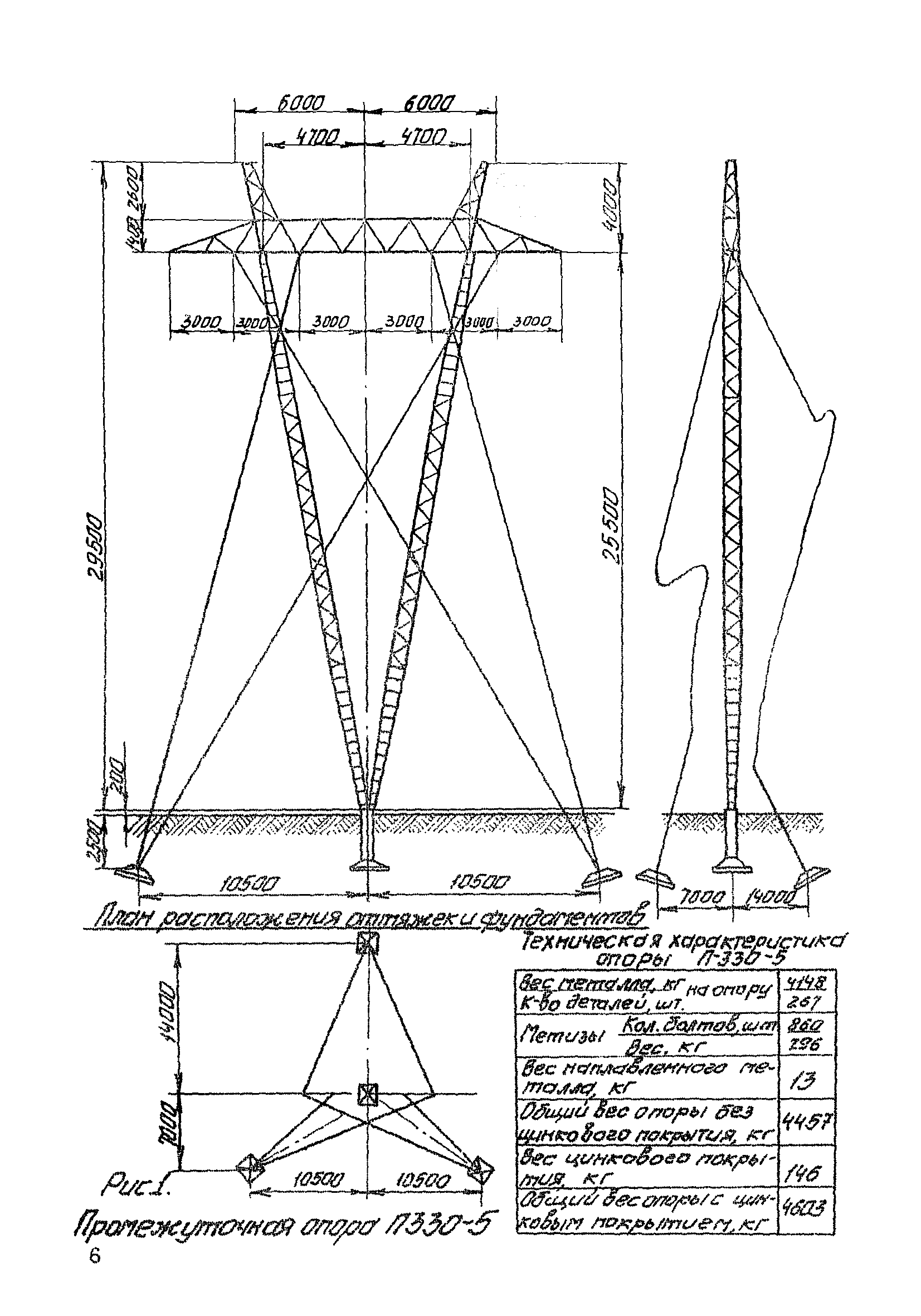

Сближение ВЛ с воздушными линиями связи допускается на расстояние не менее 2 м, а в стесненных условиях — не менее 1,5 м. Во всех остальных случаях это расстояние принимают не менее высоты наибольшей опоры ВЛ или линии связи.

При пересечении не электрофицированных магистральных железных дорог общего пользования, переходные опоры ВЛ должны быть анкерными; подъездные железнодорожные пути допускается пересекать ВЛ на промежуточных (кроме деревянных) под углом не менее 40 град. и по возможности близким к 90 град. Электрифицированные железные дороги должны пересекаться кабельной вставкой в ВЛ.

Пересечение ВЛ автомобильных дорог I категории должно выполняться на анкерных опорах, остальные дороги разрешается пересекать на промежуточных опорах. Сечение проводов ВЛ, проходящих над автомобильными дорогами, должно быть не менее 25 (сталеалюминиевых и стальных) и 35 мм2 (алюминиевых). Наименьшее расстояние от проводов ВЛ до полотна автодороги должно быть не менее 7 м. При переходе через трамвайные и троллейбусные линии наименьшее расстояние от проводов ВЛ до поверхности земли должны быть не менее 8 м.

На рисунке показана схема анкерного пролета ВЛ и пролета пересечения с железной дорогой.

Расстояние по вертикали от проводов линии до поверхности земли в ненаселенной местности при нормальном режиме работы должно быть не менее 6 м для ВЛ до 110 кВ, 6,5; 7; 7,5; 8 м соответственно для ВЛ 150, 220, 330, 500 кВ.

10.12.2016 Без рубрики

Конструктивные параметры лэп | Укрпровод

Как и любое инженерное сооружение, воздушные линии электропередач имеют свои специфические конструктивные характеристики. К ним в первую очередь можно отнести длину пролетов, стрелу провеса, расстояние от провода до поверхности земли или до любых других строений или объектов, над которыми проходит линия, то есть ее габариты.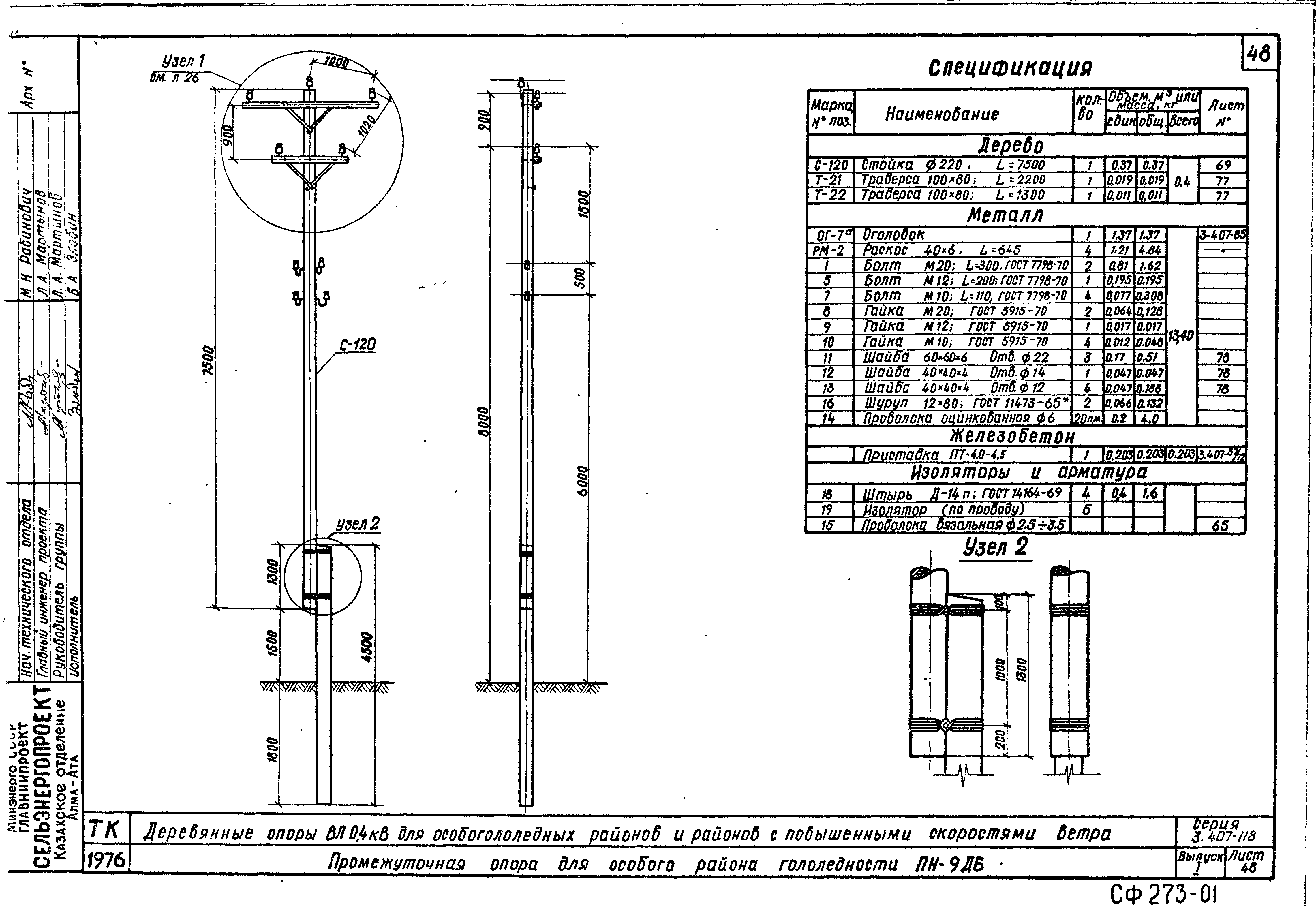 Рассмотрим же более подробно каждый из этих параметров.

Длинна пролета составляет расстояние между двумя соседними промежуточными опорами ЛЭП. Эта характеристика напрямую зависит от напряжения на линии: для ЛЭП с напряжением 0,4 кВ она составляет от 30 до 50 метров. Более точно можно определить эту величину, зная тип используемых опор, марку и сечение провода, а в некоторых случаях и природные условия данной местности.

Стрела провеса — один из конструктивных параметров воздушных линий электропередач, представляющий собой вертикальную прямую, проведенную от воображаемой линии соединения точек крепления проводов на соседних опорах до нижней точки провисания проводов между этими опорами. Фактически, эта величина также зависит от типа опор, марки и сечения провода и климата региона, в котором проведена линия электропередачи.

Габарит воздушной линии элетропередач представляет собой наименьшее существующее расстояние от проводов в каждом пролете до земли или любых других природных объектов, построек или сооружений.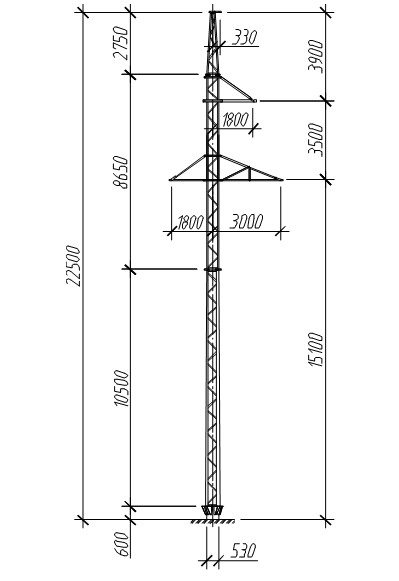 Эти параметры строго регаментируются специальной документацией и напрямую зависят от напряжения на линии и того, насколько часто эту местность посещают люди. В густонаселенной местности минимальное расстояние от проводов до поверхности земли должно составлять 6 м, в труднодоступной и безлюдной местности этот показатель уменьшается до 3,5 м, а в некоторых районах, где нет никакой вероятности, что поблизости

ЛЭП могут оказаться люди, — до 1 м. Следует отметить, что недопустимым является проведение линии электропередач над зданиями. Горизонтальное расстояние до зданий и сооружений должно быть не менее 1,5 м, а если линия проходит параллельно глухой стене объекта, то допускается расстояние в 1 м.

Прохождение линии электропередач по лесистой местности и прочим насаждениям предусматривает расстояние не меньше 1 м то кроны дерева до провода при условии наибольшей стрелы провеса. Расположение опор ЛЭП предусмотрено на расстоянии 1 м от трубопровода, 2 м — от канализационных колодцев, 1 м — от бензоколонок и заправок, от 0,5 до 1 м — от места расположения силовых кабелей. Не рекомендуется пересечение ЛЭП с реками, пригодными для судоплавания.

Если же река не используется для судоходства и замерзает в зимний период, то габарит ЛЭП должен составлять более 2 метров от наивысшего возможного уровня воды и 6 м — от уровня льда. Опоры ЛЭП разрешается располагать относительно реки на расстоянии, соответствующем высоте самой опоры.

Часто воздушные ЛЭП пересекаются с линиями связи. В этом случае провода электропередач всегда располагаются выше, а расстояние между ними и проводом связи должно составлять минимум 1,25 м. Такие пересечения допускаются только в пролетах, при этом на таком участке используются анкерные опоры ЛЭП.

Минимально возможное расстояние при сближении воздушной ЛЭП и линии связи — 1,5 — 2 м. Особое внимание уделяется участкам пересечения ЛЭП и железнодорожных магистралей или автомобильных дорог. Неэлектрофицированные железные дороги требуют использования анкерных переходных опор ЛЭП, а электрифицированные дороги пересекают с использованием кабельной вставки. Угол пересечения в любом случае должен быть максимально близок к 90⁰.

Автомобильные трассы, в зависимости от их категории, можно пересекать с использованием анкерных или промежуточных опор. При этом габарит этого участка ЛЭП должен составлять 7-8 м.

Исходя из вышеизложенного, можно сделать вывод, что конструктивные параметры воздушной линии электропередач определяют не только эффективную ее работу, но и обеспечивают безопасность окружающих объектов и населения данного района. Поэтому при строительстве ЛЭП необходим неукоснительно следовать данным рекомендациям.

Сколько существует измерений?

Попросите кого-нибудь назвать каждое известное ему измерение, и он, вероятно, перечислит следующее: длину, ширину и глубину. Они также могут добавить время, если думают за пределами трехмерной рамки. Но спрашивая теоретика струн: «Сколько существует измерений?» вызовет совсем другой ответ. Согласно этому разделу теоретической физики, существует как минимум 10 измерений пространства, большинство из которых люди не могут воспринять.

Размеры — это метрики, которые физики используют для описания реальности. Звучит широко, правда? Начнем с трех измерений, которые большинство людей изучает в начальной школе. Пространственные размеры — ширина, высота и глубина — легче всего визуализировать. Горизонтальная линия существует в одном измерении, потому что она имеет только длину; квадрат двумерен, потому что он имеет длину и ширину. Добавьте глубины, и мы получим куб или трехмерную форму.

Эти три координаты используются для точного определения местоположения объекта в пространстве.Но космос — не единственный план, на котором мы существуем; мы также существуем во времени, и именно здесь проявляется четвертое измерение. Как только мы узнаем высоту, долготу, широту и положение точки во времени, у нас есть инструменты, необходимые для построения графика ее существования во вселенной, какой мы ее знаем.

Но некоторые физики, придерживающиеся теории струн, утверждают, что реальность — это нечто большее, чем наблюдаемая Вселенная. Теория струн, также известная как «теория суперструн», направлена ​​на объединение двух основных теорий, описывающих, как работает Вселенная: общая теория относительности (которая применяется к очень большим объектам) и квантовая механика (которая применяется к очень маленьким).В четырехмерной Вселенной эта теория была бы невозможна, но как только ученые изменили математику, включив в нее 10 измерений — 11, включая время, — их уравнения заработали.

После создания теории, основанной на существовании 10 пространственных измерений, теоретики струн должны были объяснить, где прячутся эти новые измерения. Их ответ: они так же реальны, как и «большие» измерения, которые мы можем видеть, но дополнительные измерения так сильно скручены, что они слишком малы, чтобы мы могли их заметить.

Наше базовое понимание физики усложняет процесс обработки, но теоретик струн Брайан Грин отлично справляется с формулировкой концепции в терминах, понятных большинству людей. В своем выступлении на TED в 2005 году Грин сравнивает эти невидимые размеры с кабелями, подключенными к телефонным столбам: из окна провод выглядит как одномерная линия. Но если бы мы внимательно изучили его, мы бы увидели, что шнур на самом деле круглый, что делает его трехмерным. Никакая аналогия, сравнивающая ненаблюдаемые измерения с объектами в наблюдаемом мире, никогда не может быть идеальной, но это показывает, как нечто столь фундаментальное для реальности могло скрываться у всех на виду.

Теория струн утверждает, что должно быть как минимум 10 пространственных измерений плюс одно измерение времени, но есть физики, которые утверждают, что их больше. Некоторые считают, что Вселенная состоит из 11 пространственных измерений. Но чтобы по-настоящему поразить кого-то, когда они спрашивают, сколько существует измерений, скажем, 26: это магическое число согласно теории бозонных струн, и оно настолько велико, насколько на данный момент готовы согласиться основные физики.

У вас есть большой вопрос, на который вы хотите, чтобы мы ответили? Если да, сообщите нам об этом по электронной почте на bigquestions @ mentalfloss. com.

Сколько существует измерений и что они делают с реальностью?

Что-то пишет за столом, я протягиваю руку вверх, , чтобы включить лампу, и , вниз, , чтобы открыть ящик и достать ручку. Протягивая руку вперед , я касаюсь пальцами маленькой странной фигурки, подаренной мне моей сестрой в качестве талисмана на удачу, достигнув позади , я могу похлопать черного кота, прижимающегося к моей спине. Справа ведет к аналитическим заметкам для моей статьи, слева к моей стопке «обязательных» пунктов (счета и корреспонденция). Вверх, вниз, вперед, назад, вправо, влево: я пилотирую себя в личном космосе трехмерного пространства, оси этого мира незримо давят на меня прямолинейной структурой моего офиса, определяемой, как и большинство западной архитектуры, три соединяющихся прямых угла.

Наша архитектура, наше образование и наши словари говорят нам, что пространство трехмерно. OED определяет его как «непрерывную область или пространство, которое является свободным, доступным или незанятым… Измерения высоты, глубины и ширины, в которых все существует и движется». В 18 веке Иммануил Кант утверждал, что три: размерное евклидово пространство — это a priori необходимость , и, будучи сейчас насыщенными компьютерными образами и видеоиграми, мы постоянно подвержены представлениям, казалось бы, аксиоматической декартовой сетки. С точки зрения 21 века это кажется почти самоочевидным.

И все же представление о том, что мы живем в пространстве с любой математической структурой , является радикальным нововведением западной культуры, требующим ниспровержения давних представлений о природе реальности. Хотя рождение современной науки часто обсуждается как переход к механистическому объяснению природы, возможно, более важным — и, безусловно, более устойчивым — является преобразование, которое она привнесла в нашу концепцию пространства как геометрической конструкции.

За последнее столетие поиски описания геометрии пространства превратились в крупный проект теоретической физики, в котором эксперты от Альберта Эйнштейна и далее пытались объяснить все фундаментальные силы природы как побочные продукты формы самого пространства.В то время как на локальном уровне нас учат думать о пространстве как о трех измерениях, общая теория относительности рисует картину четырехмерной Вселенной, а теория струн утверждает, что у нее 10 измерений — или 11, если взять расширенную версию, известную как M- Теория. Существуют разновидности теории в 26 измерениях, и недавно чистые математики были наэлектризованы версией, описывающей пространства 24 измерений. Но что это за «размеры»? И что значит говорить о 10-мерном пространстве бытия?

Чтобы прийти к современному математическому образу мышления о пространстве, нужно сначала представить его как некую арену , которую может занимать материя.По крайней мере, «пространство» следует рассматривать как нечто , расширенное . Каким бы очевидным это ни казалось нам, такая идея была анафемой для Аристотеля, представления которого о физическом мире доминировали в западном мышлении в поздней античности и в средние века.

Строго говоря, аристотелевская физика не включала в себя теорию пространства , только концепцию места . Представьте себе чашку, стоящую на столе. Для Аристотеля чаша окружена воздухом, который сам по себе является субстанцией.В его картине мира нет такой вещи, как пустое пространство, есть только границы между одним видом субстанции, чашей, и другим, воздухом. Или стол. Для Аристотеля «пространство» (если вы хотите его так называть) было просто бесконечно тонкой границей между чашей и тем, что ее окружает. Без расширения пространство не было чем-то другим, могло быть в .

За века до того, как Аристотель, Левкипп и Демокрит постулировали теорию реальности, в которой использовался изначально пространственный способ видения — «атомистическое» видение, согласно которому материальный мир состоит из крошечных частиц (или атомов ), движущихся в пустоте. Но Аристотель отверг атомизм, заявив, что само понятие пустоты логически бессвязно. По определению, сказал он, «ничто» не может быть как . Преодоление возражений Аристотеля против пустоты и, следовательно, против концепции расширенного пространства, было бы проектом столетий. Лишь в начале 17 века Галилей и Декарт сделали расширенное пространство одним из краеугольных камней современной физики. Для обоих мыслителей, как выразился американский философ Эдвин Бертт в 1924 году, «физическое пространство считалось тождественным царству геометрии», то есть трехмерной евклидовой геометрии, которой нас сейчас учат в школе.

Задолго до того, как физики приняли евклидово видение, художники были первооткрывателями геометрической концепции пространства, и именно им мы обязаны этим замечательным скачком в нашей концептуальной структуре. В период позднего средневековья, под новым влиянием Платона и Пифагора, главных интеллектуальных соперников Аристотеля, в Европе начало распространяться представление о том, что Бог создал мир в соответствии с законами евклидовой геометрии. Следовательно, если художники хотят изобразить это правильно, они должны подражать Творцу в своих стратегиях изображения.В период с 14 по 16 века такие художники, как Джотто, Паоло Уччелло и Пьеро делла Франческа, разработали методы так называемой перспективы . — стиля, первоначально называвшегося «геометрическое фигурирование». Сознательно исследуя геометрические принципы, эти художники постепенно научился строить изображения предметов в трехмерном пространстве. В процессе они перепрограммировали европейские умы, чтобы видеть пространство евклидовым способом.

Историк Сэмюэл Эдгертон рассказывает об этом замечательном переходе в современную науку в книге «Наследие геометрии Джотто » (1991), отмечая, как ниспровержение аристотелевского мышления о космосе было частично достигнуто как долгий, медленный побочный продукт, когда люди стояли перед перспективой. картины и чувства, интуитивно, как если бы они «просматривали» трехмерные миры по ту сторону стены.Что здесь необычно, так это то, что, в то время как философы и протоученые осторожно оспаривали аристотелевские представления о пространстве, художники радикально сокращали эту интеллектуальную территорию, обращаясь к чувствам. В буквальном смысле перспективное представление было формой виртуальной реальности, которая, как и современные VR-игры, была направлена ​​на создание у зрителей иллюзии того, что они были перенесены в геометрически согласованные и психологически убедительные других миров.

Структура «реального» перешла от философского и теологического вопроса к геометрическому утверждению.

Иллюзорное евклидово пространство перспективной репрезентации, которое постепенно отпечаталось в европейском сознании, было воспринято Декартом и Галилеем как пространство реального мира. Здесь стоит добавить, что сам Галилей обучался перспективе. Его способность изображать глубину была важной особенностью его новаторских рисунков Луны, на которых изображены горы и долины и подразумевается, что Луна была такой же твердой материей, как Земля.

Используя пространство перспективных изображений, Галилей смог показать, как такие объекты, как пушечные ядра, перемещаются в соответствии с математическими законами. Само пространство было абстракцией — безликой, инертной, неприкасаемой, неощутимой пустотой, единственным познаваемым свойством которой была его евклидова форма. К концу 17 века Исаак Ньютон расширил это галилеевское видение, чтобы охватить вселенную в целом, которая теперь стала потенциально бесконечным трехмерным вакуумом — огромной, не имеющей качества пустоты, вечно распространяющейся во всех направлениях.Таким образом, структура «реального» превратилась из философского и теологического вопроса в геометрическое положение.

Там, где художники использовали математические инструменты для разработки новых способов создания изображений, теперь, на заре «научной революции», Декарт открыл способ создавать изображения математических отношений самих по себе. В процессе он формализовал концепцию измерения и внедрил в наше сознание не только новый способ видения мира, но и новый инструмент для занятий наукой.

Почти каждый сегодня признает плоды гения Декарта в образе декартовой плоскости — прямоугольной сетке с осями x и y и системе координат .

По определению, декартова плоскость — это двумерное пространство, потому что нам нужны две координаты , чтобы идентифицировать любую точку в нем. Декарт обнаружил, что с этой структурой он может связывать геометрические формы и уравнения. Таким образом, круг с радиусом 1 можно описать уравнением x ² + y ² = 1.

Огромный массив фигур, которые мы можем нарисовать на этой плоскости, можно описать уравнениями, и такая «аналитическая» или «декартова» геометрия вскоре станет основой для исчисления , разработанного Ньютоном и Г.В. Лейбницем для дальнейшего анализа физиков. движения. Один из способов понять исчисление — это изучение кривых; так, например, он позволяет нам формально определить, где кривая является наиболее крутой или где она достигает локального максимума или минимума. Применительно к изучению движения исчисление дает нам возможность анализировать и предсказывать, где, например, объект, брошенный в воздух, достигнет максимальной высоты или когда мяч, катящийся по изогнутому склону, достигнет определенной скорости. С момента своего изобретения исчисление стало жизненно важным инструментом почти во всех областях науки.

Рассматривая предыдущую диаграмму, легко увидеть, как мы можем добавить третью ось. Таким образом, с помощью осей x, y и z мы можем описать поверхность сферы — как в шкуре пляжного мяча. Здесь уравнение (для сферы с радиусом 1) принимает следующий вид: x ² + y ² + z ² = 1

С помощью трех осей мы можем описывать формы в трехмерном пространстве. И снова каждая точка однозначно идентифицируется тремя координатами: это необходимое условие трехмерности, которое делает пространство тремя -мерными.

Но зачем останавливаться на достигнутом? Что, если я добавлю четвертое измерение? Назовем это «п». Теперь я могу написать уравнение для чего-то, что, как я утверждаю, представляет собой сферу, находящуюся в четырехмерном пространстве: x ² + y ² + z ² + p ² = 1. Я не могу нарисовать этот объект для вы, но математически добавление еще одного измерения — законный ход. «Законное» означает, что в этом нет ничего логически противоречивого — нет причины, я не могу.

«Измерение» становится чисто символическим понятием, не обязательно связанным с материальным миром.

И я могу продолжать, добавляя новые размеры.Итак, я определяю сферу в пятимерном пространстве с пятью осями координат (x, y, z, p, q), что дает нам уравнение: x ² + y ² + z ² + p ² + q ² = 1. И одно из шести измерений: x ² + y ² + z ² + p ² + q ² + r ² = 1 и т. д.

Хотя я, возможно, не смогу визуализировать сферы более высоких измерений, я могу описать их символически, и один из способов понимания истории математики — это осознание того, какие, казалось бы, разумные вещи мы можем превзойти.Именно это имел в виду Чарльз Доджсон, он же Льюис Кэрролл, когда в сериалах «Зазеркалье» и «Что нашла там Алиса » (1871 г. ) он заставил Белую Королеву заявить о своей способности поверить в «шесть невозможных вещей перед завтраком».

Математически я могу описать сферу в любом количестве измерений, которое я выберу. Все, что мне нужно сделать, это добавить новые оси координат, которые математики называют «степенями свободы». Условно их называют x ₁ , x ₂ , x ₃ , x ₄ , x ₅ , x ₆ и так далее . Так же, как любую точку на декартовой плоскости можно описать двумя координатами (x, y), так и любую точку в 17-мерном пространстве можно описать набором из 17 координат (x ₁ , x ₂ , x ₃ , x ₄ , x ₅ , x ₆ … x ₁₅ , x ₁₆ , x ₁₇ ). Поверхности, подобные приведенным выше сферам, в таких многомерных пространствах обычно известны как многообразия и .

С точки зрения математики «измерение» — это не что иное, как другая координатная ось (другая степень свободы), которая в конечном итоге становится чисто символической концепцией, не обязательно связанной с материальным миром. В 1860-х годах логик-первопроходец Август Де Морган, работа которого повлияла на Льюиса Кэрролла, резюмировал все более абстрактный взгляд на эту область, отметив, что математика — это чисто « наука о символах » и как таковая не должна иметь отношения ни к чему. кроме себя. Математика, в некотором смысле, — это логика, выходящая из поля воображения.

В отличие от математиков, которые вольны играть в области идей, физика связана с природой и, по крайней мере, в принципе, связана с материальными вещами.Однако все это открывает возможность освобождения, поскольку, если математика допускает более трех измерений и мы думаем, что математика полезна для описания мира, как мы узнаем, что физическое пространство ограничено тремя? Хотя Галилей, Ньютон и Кант считали длину, ширину и высоту аксиомой, разве в нашем мире не может быть еще измерений?

Опять же, идея вселенной с более чем тремя измерениями была внедрена в общественное сознание через художественную среду, в данном случае литературную спекуляцию, наиболее известную в работе математика Эдвина Эбботта Flatland (1884). Эта очаровательная социальная сатира рассказывает историю скромного Квадрата, живущего на плоскости, которого однажды посетило трехмерное существо, Лорд Сфера, который перенес его в великолепный мир Твердых тел. В этом объемном раю Квадрат созерцает свою трехмерную версию, Куб, и начинает мечтать о продвижении в четвертое, пятое и шестое измерения. Почему не гиперкуб? Интересно, а гипер-гиперкуб?

К сожалению, во Флатландии Квадрат считается сумасшедшим и заперт в психиатрической лечебнице.Одно из достоинств этой истории, в отличие от некоторых более сладких анимаций и адаптаций, которые она вдохновила, — это признание опасностей, связанных с выставлением напоказ социальных условностей. В то время как Квадрат приводит доводы в пользу других измерений пространства, он также приводит аргументы в пользу других измерений бытия — он математический чудак.

В конце 19 — начале 20 веков множество авторов (Герберт Уэллс, математик и писатель-фантаст Чарльз Хинтон, придумавший для четырехмерного куба слово «тессеракт»), художники (Сальвадор Дали) и мыслители-мистики ( Успенский) исследовал идеи о четвертом измерении и о том, что может означать для человека столкновение с ним.

Затем в 1905 году неизвестный физик по имени Альберт Эйнштейн опубликовал статью, в которой реальный мир описывался как четырехмерный сеттинг. В его «специальной теории относительности» к трем классическим измерениям пространства было добавлено время и . В математическом формализме теории относительности все четыре измерения связаны вместе, и термин пространство-время вошел в наш лексикон. Это собрание никоим образом не было произвольным. Эйнштейн обнаружил, что, идя по этому пути, возник мощный математический аппарат, который превзошел физику Ньютона и позволил ему предсказывать поведение электрически заряженных частиц.Только в четырехмерной модели мира можно полностью и точно описать электромагнетизм.

Относительность была намного больше, чем еще одна литературная игра, особенно после того, как Эйнштейн расширил ее от «специальной» до «общей» теории. Теперь многомерное пространство наполнилось глубоким физическим смыслом.

В картине мира Ньютона материя движется в пространстве во времени под действием естественных сил, особенно гравитации. Пространство, время, материя и сила — разные категории реальности.С помощью специальной теории относительности Эйнштейн продемонстрировал, что пространство и время едины, тем самым уменьшив фундаментальные физические категории с четырех до трех: пространство-время, материя и сила. Общая теория относительности делает еще один шаг, включив силу гравитации в структуру самого пространства-времени. Если смотреть с точки зрения 4D, гравитация — это всего лишь артефакт формы пространства.

Чтобы разобраться в этой замечательной ситуации, давайте представим на время ее двумерный аналог. Представьте себе батут и представьте, что мы рисуем на его поверхности декартову сетку.Теперь поместите шар для боулинга на решетку. Вокруг него поверхность будет растягиваться и деформироваться, поэтому некоторые точки удаляются друг от друга. Мы нарушили естественную меру расстояния в пространстве, сделав его неровным. Общая теория относительности утверждает, что это искривление — это то, что тяжелый объект, такой как Солнце, делает с пространством-временем, а отклонение от декартова совершенства самого пространства вызывает явление, которое мы воспринимаем как гравитацию.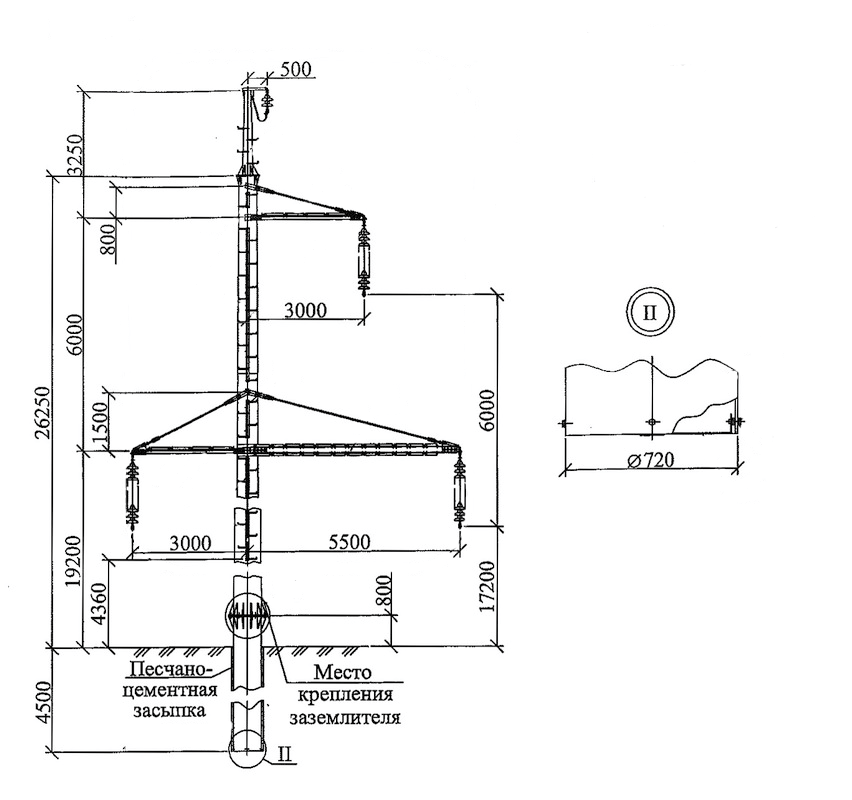

В то время как в физике Ньютона гравитация возникает из ниоткуда, в теории Эйнштейна она возникает естественным образом из внутренней геометрии четырехмерного многообразия; в местах, где многообразие растягивается больше всего или больше всего отклоняется от декартовой регулярности, гравитация ощущается сильнее.Иногда это называют «физикой резинового листа». Здесь огромная космическая сила, удерживающая планеты на орбите вокруг звезд и звезды на орбите вокруг галактик, является не чем иным, как побочным эффектом искривленного пространства. Гравитация — это буквально геометрия в действии.

Если перемещение в четыре измерения помогает объяснить гравитацию, то может ли пятимерное мышление иметь какое-либо научное преимущество? Почему бы не попробовать? — спросил молодой польский математик Теодор Калуца ​​в 1919 году, полагая, что если бы Эйнштейн поглотил гравитацию в пространство-время, то, возможно, другое измерение могло бы аналогичным образом объяснить силу электромагнетизма как артефакт геометрии пространства-времени. Итак, Калуца ​​добавил еще одно измерение к уравнениям Эйнштейна и, к своему удовольствию, обнаружил, что в пяти измерениях обе силы прекрасно складываются как артефакты геометрической модели.

Вы муравей, бегущий по длинному тонкому шлангу, даже не подозревая о крошечном размере круга под ногами.

Математика подходит как по волшебству, но проблема в этом случае заключалась в том, что дополнительное измерение, казалось, не коррелировало с каким-либо конкретным физическим качеством. В общей теории относительности четвертое измерение было раз ; Согласно теории Калуцы, это не было на что-то , на что можно было указать, увидеть или почувствовать: это было просто в математике.Даже Эйнштейн отказался от такой неземной инновации. Что это? он спросил. Где это ?

В 1926 году шведский физик Оскар Кляйн ответил на этот вопрос в манере, которая звучит как что-то прямо из страны чудес. Представьте, сказал он, что вы муравей, живущий на длинном и очень тонком шланге. Вы можете бегать по шлангу взад и вперед, даже не осознавая крошечный размер круга под ногами. Только ваши муравьиные физики с их мощными муравьиными микроскопами могут увидеть это крошечное измерение.Согласно Кляйну, каждая точка в нашем четырехмерном пространстве-времени имеет небольшой дополнительный круг пространства, подобный этому, который слишком мал, чтобы мы могли его увидеть. Поскольку он на много порядков меньше атома, неудивительно, что мы до сих пор его упустили. Только физики со сверхмощными ускорителями элементарных частиц могут надеяться увидеть все в таком крошечном масштабе.

Когда физики преодолели первоначальный шок, они были очарованы идеей Кляйна, и в 1940-х годах теория была разработана с мельчайшими математическими подробностями и помещена в квантовый контекст.К сожалению, бесконечно малый масштаб нового измерения не позволил представить, как это можно проверить экспериментально. Кляйн подсчитал, что диаметр крошечного круга составлял всего 10 ^-30 см. Для сравнения: диаметр атома водорода составляет 10 ^-8 см, так что мы говорим о чем-то более чем на 20 порядков меньше, чем самый маленький атом. Даже сегодня мы и близко не видим такой минутной шкалы. Так идея вышла из моды.

Калуцу, однако, было нелегко удержать. Он верил в свое пятое измерение, и он верил в силу математической теории, поэтому он решил провести собственный эксперимент. Он остановился на плавании. Калуца ​​не умел плавать, поэтому он прочитал все, что мог о теории плавания, и когда он почувствовал, что увлекся водными упражнениями в принципе, он сопровождал свою семью к морю и бросился в волны, где о чудо он умел плавать.По мнению Калуцы, плавательный эксперимент подтвердил справедливость теории, и, хотя он не дожил до триумфа своего любимого пятого измерения, в 1960-х теоретики струн возродили идею многомерного пространства.

К 1960-м годам физики открыли две дополнительные силы природы, действующие на субатомном уровне. Названные слабой ядерной силой и сильной ядерной силой , они ответственны за некоторые типы радиоактивности и за удерживание кварков вместе, чтобы сформировать протоны и нейтроны, составляющие атомные ядра. В конце 1960-х годов, когда физики начали исследовать новый предмет теории струн (который утверждает, что частицы подобны крохотным резиновым полоскам, колеблющимся в пространстве), идеи Калуцы и Кляйна снова стали осознаваться, и теоретики постепенно начали задаваться вопросом, есть ли эти два субатомных элемента. силы могли бы также быть описаны в терминах геометрии пространства-времени.

Оказывается, чтобы охватить обе эти две силы, мы должны добавить еще пяти измерений к нашему математическому описанию.Нет a priori , почему должно быть пять; и, опять же, ни одно из этих дополнительных измерений не имеет прямого отношения к нашему сенсорному опыту. Они просто есть в математике. Итак, это подводит нас к 10 измерениям теории струн. Здесь четыре крупномасштабных измерений пространства-времени (описываемых общей теорией относительности) плюс шесть дополнительных «компактных» измерений (одно для электромагнетизма и пять для ядерных сил), все они свернуты в некоторые дьявольски сложные, сжатые- вверх, геометрическая структура.

Физики и математики прилагают огромные усилия, чтобы понять все возможные формы, которые может принимать это миниатюрное пространство, и какая из множества альтернатив, если таковая имеется, реализуется в реальном мире. Технически эти формы известны как многообразия Калаби-Яу, и они могут существовать в любом количестве , даже более высоких измерений. Экзотические, сложные создания, эти необычные формы составляют абстрактную таксономию в многомерном пространстве; их двухмерный разрез (лучшее, что мы можем сделать для визуализации того, как они выглядят) напоминает кристаллические структуры вирусов; они почти выглядят вживую .

Двумерный разрез многообразия Калаби-Яу. Предоставлено Википедией

Существует множество версий уравнений теории струн, описывающих 10-мерное пространство, но в 1990-х математик Эдвард Виттен из Института перспективных исследований в Принстоне (давнее увлечение Эйнштейна) показал, что все можно несколько упростить. если взять 11-мерную перспективу. Он назвал свою новую теорию M-теорией и загадочно отказался сказать, что означает буква «M». Обычно говорят, что это «мембрана», но также предлагались «матрица», «хозяин», «тайна» и «монстр».

Наша могла бы быть лишь одной из многих сосуществующих вселенных, каждая из которых представляет собой отдельный 4-мерный пузырь на более широкой арене 5-мерного пространства

До сих пор у нас нет доказательств существования каких-либо из этих дополнительных измерений — мы все еще находимся в стране плавающих физиков, мечтающих о миниатюрном ландшафте, к которому мы еще не можем получить доступ, — но теория струн, как оказалось, имеет важные последствия для самой математики. Недавно разработка версии теории, имеющей 24 измерения, показала неожиданные взаимосвязи между несколькими основными разделами математики, а это означает, что, даже если теория струн не удастся найти в физике, она окажется очень полезным источником чисто теоретических знаний. теоретическое понимание.В математике 24-мерное пространство — это нечто особенное — в нем происходят волшебные вещи, такие как способность упаковывать сферы вместе особенно элегантным образом — хотя маловероятно, что реальный мир имеет 24 измерения. Большинство струнных теоретиков считают, что для мира, который мы любим и в котором мы живем, достаточно 10 или 11 измерений.

В теории струн есть еще одно последнее изменение, заслуживающее внимания. В 1999 году Лиза Рэндалл (первая женщина, получившая должность физика-теоретика в Гарварде) и Раман Сундрам (индийско-американский теоретик частиц) предположили, что может быть дополнительное измерение в космологической шкале, которая описывается общей теорией относительности.Согласно их теории «брана» — «брана» — это сокращение от «мембрана» — то, что мы обычно называем нашей Вселенной , может быть встроено в гораздо большее пятимерное пространство, своего рода сверхвселенную. В этом суперпространстве наша могла бы быть лишь одной из целого ряда сосуществующих вселенных, каждая из которых представляет собой отдельный 4-мерный пузырь в более широкой арене 5-мерного пространства.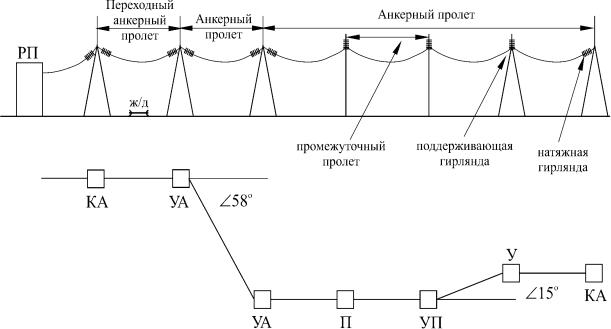

Трудно сказать, сможем ли мы когда-нибудь подтвердить теорию Рэндалла и Сандрама. Однако между этой идеей и зарождением современной астрономии были проведены аналогии.500 лет назад европейцы сочли невозможным представить себе другие физические «миры», помимо нашего собственного, однако теперь мы знаем, что Вселенная населена миллиардами других планет, вращающихся вокруг миллиардов других звезд. Кто знает, однажды наши потомки смогут найти доказательства существования миллиардов других вселенных, каждая со своими уникальными уравнениями пространства-времени.

Проект понимания геометрической структуры пространства — одно из знаковых достижений науки, но, возможно, физики достигли конца этого пути.Ведь оказывается, что в некотором смысле Аристотель был прав — действительно, есть логические проблемы с понятием расширенного пространства. Несмотря на все экстраординарные успехи теории относительности, мы знаем, что ее описание пространства не может быть окончательным, потому что на квантовом уровне оно не работает. В течение последних полувека физики безуспешно пытались объединить свое понимание пространства в космологическом масштабе с тем, что они наблюдают в квантовом масштабе, и все больше кажется, что такой синтез может потребовать радикально новой физики.

После того, как Эйнштейн разработал общую теорию относительности, он провел большую часть своей жизни, пытаясь «построить все законы природы из динамики пространства и времени, сведя физику к чистой геометрии», как сказал Робберт Дейкграаф, директор Института для продвинутого исследования в Принстоне, поставил недавно. «Для [Эйнштейна] пространство-время было естественным« базовым уровнем »в бесконечной иерархии научных объектов». Подобно картине мира Ньютона, Эйнштейн делает пространство первичной основой бытия, ареной, на которой все вещи происходят.Однако в очень крошечных масштабах, где преобладают квантовые свойства, законы физики показывают, что пространство, как мы привыкли думать о нем, может не существовать.

Среди некоторых физиков-теоретиков возникает мнение, что космос на самом деле может быть возникающим явлением, созданным чем-то более фундаментальным, во многом таким же образом, как температура проявляется как макроскопическое свойство, возникающее в результате движения молекул. Как выразился Дейкграаф: «Современная точка зрения рассматривает пространство-время не как отправную точку, а как конечную точку, как естественную структуру, которая возникает из сложности квантовой информации.’

Ведущим сторонником новых взглядов на пространство является космолог Шон Кэрролл из Калифорнийского технологического института, который недавно сказал, что классическое пространство не является «фундаментальной частью архитектуры реальности», и утверждал, что мы ошибаемся, придавая ему такой особый статус. четыре или 10 или 11 измерений. Там, где Дейкграаф проводит аналогию с температурой, Кэрролл предлагает нам рассмотреть «влажность», возникающий феномен соединения множества молекул воды. Никакая отдельная молекула воды не является влажной, только когда вы собираете их вместе, влажность становится качеством.100) измерения »- это 10, за которыми следует гугол нулей, или 10 000 триллионов триллионов триллионов триллионов триллионов триллионов триллионов триллионов нулей. Трудно представить себе такое невероятно огромное количество, которое сводит на нет количество частиц в известной Вселенной. Тем не менее, каждый из них представляет собой отдельное измерение в математическом пространстве, описываемом квантовыми уравнениями; каждому — новая «степень свободы», которой располагает Вселенная.

Даже Декарт мог бы быть ошеломлен тем, куда нас привело его видение, и какая ослепительная сложность заключена в простом слове «измерение».

Это эссе стало возможным благодаря поддержке гранта журнала Aeon от Templeton Religion Trust. Мнения, выраженные в данной публикации, принадлежат автору (авторам) и не обязательно отражают точку зрения Templeton Religion Trust.

Спонсоры журнала Aeon Magazine не участвуют в принятии редакционных решений, включая ввод в эксплуатацию или утверждение содержания.

Как у Вселенной могло быть больше измерений

Теория струн — это предполагаемая теория всего, что, как надеются физики, однажды объяснит… все.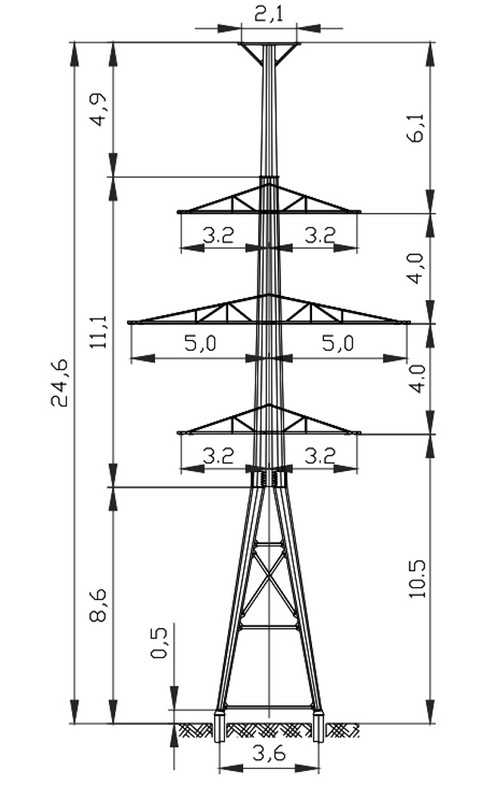

Все силы, все частицы, все константы, все вещи под одной теоретической крышей, где все, что мы видим, является результатом крошечных вибрирующих струн. Теоретики работали над этой идеей с 1960-х годов, и первое, что они поняли, — это то, что для того, чтобы теория работала, должно быть на измерений больше, чем четыре, к которым мы привыкли, .

Но эта идея не так безумна, как кажется.

Связано: Объяснение альтернатив теории большого взрыва (инфографика)

Пространственная катастрофа

В теории струн маленькие петли вибрирующей струнности (в теории они являются фундаментальным объектом реальности) проявляются как различные частицы (электроны, кварки, нейтрино и т. д.) и как носители сил природы (фотоны, глюоны, гравитоны и т. д.). Они делают это через свои вибрации. Каждая струна настолько крошечная, что кажется нам не более чем точечной частицей, но каждая струна может колебаться в разных режимах, точно так же, как вы можете получить разные ноты из гитарной струны.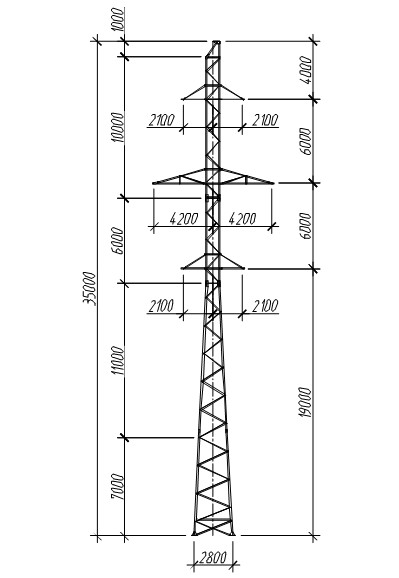

Считается, что каждый режим вибрации относится к разному типу частиц. Итак, все струны, вибрирующие в одну сторону, выглядят как электроны, все струны, вибрирующие в другую сторону, выглядят как фотоны и так далее.То, что мы видим как столкновение частиц, с точки зрения теории струн, представляет собой связку струн, сливающихся вместе и разделяющихся на части.

Но для того, чтобы математика работала, в нашей Вселенной должно быть более четырех измерений. Это потому, что наше обычное пространство-время не дает струнам достаточно «места» для вибрации всеми способами, которые им необходимы для того, чтобы полностью выразить себя как все разновидности частиц в мире. Они слишком стеснены.

Другими словами, струны не просто качаются, они качаются в гиперпространстве.

Текущие версии теории струн требуют всего 10 измерений, в то время как еще более гипотетическая теория сверхструн, известная как M-теория, требует 11.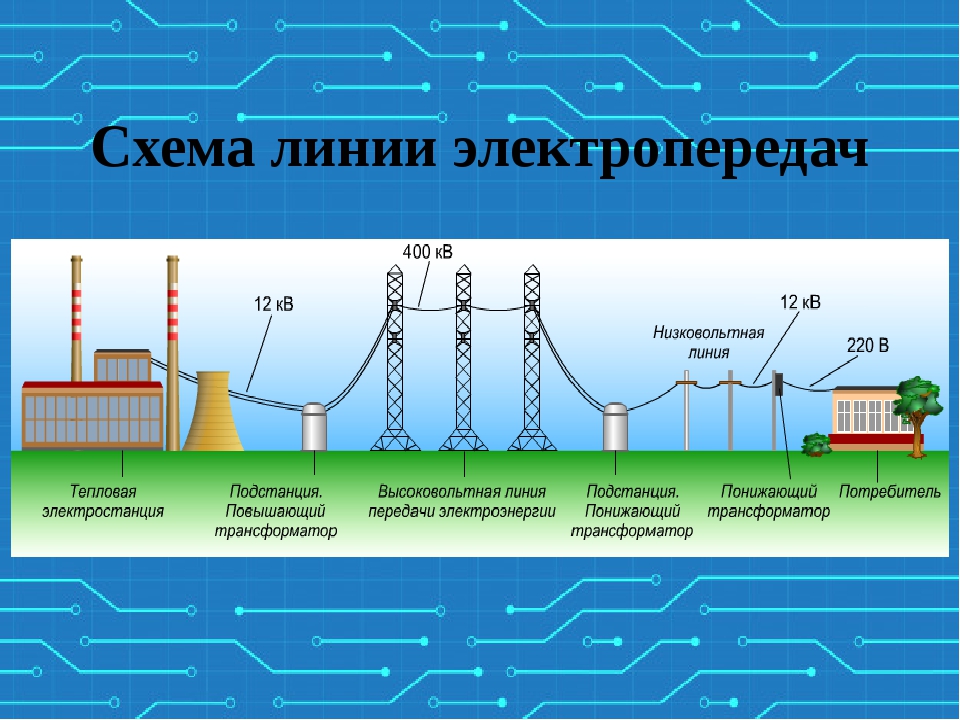 Но когда мы смотрим вокруг Вселенной, мы всегда видим только три обычных пространственных измерения плюс измерение время. Мы почти уверены, что если бы у Вселенной было более четырех измерений, мы бы уже заметили это.

Каким образом требование теории струн о дополнительных измерениях может быть согласовано с нашим повседневным опытом во Вселенной?

Свернувшись калачиком и компактно

К счастью, теоретики струн смогли указать на исторический антецедент этой, казалось бы, радикальной идеи.

Еще в 1919 году, вскоре после того, как Альберт Эйнштейн опубликовал свою общую теорию относительности, математик и физик Теодор Калуца ​​просто забавлялся с уравнениями. И он обнаружил кое-что особенно интересное, когда добавил к уравнениям пятое измерение — ничего не произошло. Уравнения относительности на самом деле не заботятся о количестве измерений; это то, что вы должны добавить, чтобы применить теорию к нашей Вселенной.

Но затем Калуца ​​добавил особый поворот к этому пятому измерению, заставив его обернуться вокруг себя в том, что он назвал «цилиндрическим состоянием». «Это требование привело к появлению чего-то нового: Калуца ​​восстановил обычные уравнения общей теории относительности в обычных четырех измерениях, а также новое уравнение, которое имитировало выражения электромагнетизма.

Похоже, добавление измерений могло потенциально объединить физику.

В ретроспективе это было немного отвлекающим маневром

Тем не менее, пару десятилетий спустя другой физик, Оскар Кляйн, попытался интерпретировать идею Калуцы в терминах квантовой механики.-35 метров.

Множество многообразий теории струн

Если бы дополнительное измерение (или измерения) действительно было таким маленьким , мы бы сейчас не заметили. Он настолько мал, что мы не могли надеяться напрямую исследовать его с помощью наших экспериментов с высокими энергиями. И если эти измерения обернуты сами по себе, то каждый раз, когда вы перемещаетесь в четырехмерном пространстве, вы действительно путешествуете по этим дополнительным измерениям миллиарды и миллиарды раз.

И это измерения, в которых живут струны теории струн.200000.

Оказывается, когда вам нужно шесть измерений свернуться калачиком и дать им почти любой возможный способ сделать это, это… складывается.

Есть много разных способов обернуть эти дополнительные измерения в себя. И каждая возможная конфигурация будет влиять на то, как струны внутри них вибрируют. Поскольку способы, которыми вибрируют струны, определяют их поведение здесь, в макроскопическом мире, каждый выбор многообразия приводит к отдельной вселенной со своим собственным набором физики.

Таким образом, только один коллектор может дать начало миру в том виде, в каком мы его видим . Но какой?

К сожалению, теория струн не может дать нам ответа, по крайней мере, пока. Проблема в том, что теория струн еще не закончена — у нас есть только различные методы приближения, которые, как мы надеемся, приблизятся к реальным, но прямо сейчас мы понятия не имеем, насколько мы правы. Таким образом, у нас нет математической технологии для отслеживания цепочки, от определенного многообразия до конкретной вибрации струны и физики Вселенной.

Ответ теоретиков струн — это нечто, называемое Пейзаж, мультивселенная всех возможных вселенных, предсказываемых различными многообразиями, причем наша Вселенная является лишь одной точкой среди многих.

И вот где теория струн находится сегодня где-то на Ландшафте.

Пол М. Саттер , астрофизик в SUNY Стоуни-Брук и Институт Флэтайрон, ведущий Спросите космонавта и Космическое радио и автор Your Place во Вселенной .

Узнайте больше, послушав серию «Стоит ли того теория струн? (Часть 3: Измерение — это судьба)» в подкасте «Спросите космонавта», доступном в iTunes и в Интернете по адресу http://www.askaspaceman .com. Спасибо John C., Zachary H., @edit_room, Matthew Y., Christopher L., Krizna W., Sayan P., Neha S., Zachary H., Joyce S., Mauricio M., @shrenicshah, Panos T. ., Dhruv R., Maria A., Ter B., oiSnowy, Evan T., Dan M., Jon T., @twblanchard, Aurie, Christopher M.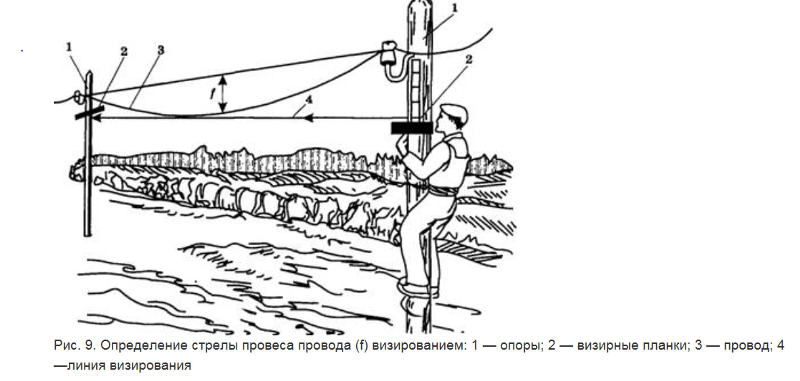 , @unplugged_wire, Giacomo S., Gully F. за вопросы, которые привели к этому материалу! Задайте свой вопрос в Twitter, используя #AskASpaceman, или подписавшись на Paul @PaulMattSutter и facebook.com/PaulMattSutter.

Следуйте за нами в Twitter @Spacedotcom и на Facebook .

Как найти нужный размер

Мы включаем продукты, которые, по нашему мнению, будут полезны нашим читателям. Если вы покупаете по ссылкам на этой странице, мы можем получить небольшую комиссию.Вот наш процесс.

Презервативы бывают разных форм и размеров. Подобрать подходящую одежду может быть непросто, но это поможет людям вести более лучшую и безопасную половую жизнь.

Размер презерватива важен для обеспечения его эффективности в предотвращении инфекций, передаваемых половым путем (ИППП), и беременности.

Слишком маленькие презервативы могут сломаться, а слишком большие — соскользнуть с полового члена. Плохо подогнанные презервативы также могут вызывать дискомфорт во время секса.

В этой статье мы рассмотрим, как правильно выбрать презерватив в зависимости от длины и обхвата полового члена, как измерить половой член и других факторов, которые следует учитывать при использовании презервативов.

Первый шаг к подбору презерватива наилучшего размера — это измерить половой член. Для этого человек может использовать линейку, рулетку или кусок веревки. Для получения наиболее точных результатов измерения следует проводить при эрегированном половом члене.

Чтобы точно измерить половой член и найти наиболее подходящий презерватив, выполните следующие действия:

1. Измерьте длину от основания полового члена, где половой член встречается с тазом, до конца.
2. Используйте веревку или гибкую измерительную ленту.Оберните им самую толстую часть полового члена, которая обычно находится около середины стержня. При использовании веревки отметьте место ее пересечения и измерьте расстояние линейкой.

Существует множество презервативов на выбор, и у большинства людей не должно возникнуть проблем с поиском подходящего презерватива. Производители основывают размеры презервативов как по длине, так и по ширине.

Большинство презервативов длиннее, чем они должны быть. Если человек обнаружит, что у основания слишком много переката, ему может потребоваться более плотная посадка.Если рулона не осталось, им потребуется презерватив большего размера.

Обхват для презерватива важнее длины, так как обхват является самой толстой частью эрегированного полового члена.

Не существует абсолютного правила для того, кому следует использовать презервативы разных размеров, но следующие рекомендации в дюймах могут помочь:

• обхват менее 4,7 дюйма требует плотного прилегания
• обхват 4,7– 5,1 дюйма требует стандартной подгонки
• обхват 5,1–6 дюймов требует большой посадки

Компании, выпускающие презервативы, не всегда предоставляют свои размеры в готовом виде, а размеры брендов варьируются в зависимости от источника.

В следующих таблицах представлена ​​некоторая информация о размерах и характеристиках презервативов распространенных в США марок в дюймах (“) и миллиметрах (мм), а также ссылки на то, где их можно купить:

Плотная посадка

Стандартная посадка

Большой размер

Презервативы бывают не только разных форм и размеров, но и из разных материалов, включая латекс, полиуретан и овечью шкуру.

В то время как производители используют латекс для изготовления подавляющего большинства презервативов, некоторые бренды предлагают альтернативы без латекса людям, которые не любят латекс или страдают аллергией.

Латексные

Латексные презервативы имеют очень гибкую тонкую оболочку. Латекс — эффективный барьер против спермы, бактерий и вирусов. Однако латекс не передает тепло, что может уменьшить приятные ощущения.

Человек должен избегать использования масла или смазок на масляной основе с латексным презервативом.

Масла разрушают латекс, что может привести к разрыву презерватива. Лубриканты на водной или силиконовой основе — лучший вариант при использовании латексного презерватива.

Полиуретан

Полиуретан — это пластик, используемый во многих сферах, от изоляции до мебели и презервативов.Презервативы из полиуретана обычно тоньше, чем презервативы из латекса, и они лучше переносят тепло.

Полиуретановые презервативы обеспечивают эффективную защиту от ВИЧ и бактериальных ИППП. Однако полиуретан менее гибкий, чем латекс, что делает их немного более хрупкими, чем латексные презервативы.

Полиизопрен

Полиизопрен очень похож на латекс, но в нем отсутствуют белки, которые иногда могут вызывать аллергические реакции. Эти презервативы немного толще полиуретана, но они мягче и кажутся более естественными, чем латекс.

Овчина

Презервативы из овечьей шкуры не содержат кожи ягненка. Вместо этого слепая кишка ягненка, часть кишечника, является основным компонентом. Слепая кишка тонкая, прочная и хорошо переносит тепло. К сожалению, презервативы из овчины не могут защитить от ИППП или ВИЧ.

Поделиться на Pinterest Человек должен быть осторожен, чтобы не повредить презерватив при открытии упаковки.

Презервативы наиболее эффективны при правильном использовании. Воспользуйтесь следующими советами о том, как правильно пользоваться презервативом:

1. Проверьте срок годности на упаковке.Презерватив с истекшим сроком годности менее эффективен и с большей вероятностью порвется.
2. Убедитесь, что презерватив не поврежден. Презервативы, которые люди могут хранить в кошельках или кошельках, могут быть повреждены. Убедитесь, что обертка не повреждена. Если презерватив порван или имеет признаки повреждения, не используйте его и немедленно выбросьте.
3. Осторожно откройте обертку. Избегайте использования зубов и сильных разрывов упаковки, так как это может порвать презерватив.
4. Убедитесь, что ободок обращен наружу, чтобы можно было катить презерватив по половому члену.
5. Сожмите кончик презерватива и поместите его на головку эрегированного полового члена. Сжатие наконечника удаляет лишний воздух и дает дополнительное пространство вверху для сбора спермы.
6. Прокатите презерватив по стержню к основанию полового члена.
7. Если презерватив не имеет смазки, нанесите небольшое количество смазки на водной или силиконовой основе на внешнюю сторону презерватива.
8. После эякуляции возьмитесь за основу презерватива при вытягивании. Это предотвратит его падение.
9. Осторожно снимите презерватив, завяжите узел на открытом конце и выбросьте его в мусор.

Выбор подходящего презерватива может оказаться сложной и даже сложной задачей. Как только люди узнают, какой для них размер, они могут провести небольшое исследование и найти предпочтительный материал и стиль.

Презервативы — неотъемлемая часть хорошего сексуального здоровья. Они защищают от распространения ИППП и вирусных инфекций, таких как Эбола и Зика. Они также могут предотвратить незапланированную беременность.

Выбор подходящего презерватива поможет предотвратить беременность и защитить от ИППП. Кроме того, правильно подобранные презервативы также могут улучшить опыт полового акта, делая секс более комфортным и приятным.

Департамент транспорта штата Орегон: негабаритные операции: Отдел торговли и соблюдения нормативных требований: штат Орегон

Доступен ТОЛЬКО в Oregon Trucking Online или в штаб-квартире отдела торговли и соблюдения требований Салема
C04 — Дырявый груз
C50 — Превышение высоты соломы семян травы

COVP Годовой Разрешения

Вы можете добавить округа и / или город Портленда авторизации.

Годовое разрешение на увеличение веса

13 — Удлиненный вес

Годовые разрешения на грузовые тягачи / полуприцепы
01 — Превышение ширины и допустимый вес
03 — Превышение ширины и веса для тяжелых грузовых автомобилей 98000 фунтов
30 — Задний свес грузового тягача / полуприцепа

Годовые разрешения на комбинированные перевозки тяжелых грузов
39 — Тягач / полуприцеп с джипом и / или бустером без груза для перевозки тяжелых грузов
12 — Контейнер для перевозки тяжелых грузов за рубежом

Ежегодные разрешения на грузовики и прицепы
32 — Превышение ширины грузовика и прицепа и допустимый вес 80 000 фунтов
34 — Превышение ширины грузовика и прицепа и тяжелая тяговая масса 80000 фунтов
36 — Превышение ширины грузовика и прицепа и масса тяжеловесного груза 98 000 фунтов

Другие комбинации
06 — Длинные бревна, столбы, сваи и структурные элементы
09 — Передвижной дом / модульный блок

43 — Индивидуальный автомобиль

Другие годовые разрешения — только государственные автомагистрали

Разрешения на превышение ширины полосы
C45 — Превышение ширины пикапа и прицепа
C29 — Оборудование для животноводства
C55 — Пиломатериалы / фанера / шпон в нескольких партиях
C05 — Тюки сена в нескольких партиях
C11 — Пакеты с семенами травы / листьями мяты в нескольких пакетах

Разрешение на превышение длины
C14 — Разрешение на тройную комбинацию
C07 — Грузовой автомобиль общего назначения и прицеп-шест

Разрешения на превышение высоты
C23 — Превышение высоты — Неделимое
C24 — Превышение высоты — Мобильное / модульное
C50 — Солома из семян травы

Разрешение на превышение габаритов эвакуатора
C18 — Разрешение на буксировку грузовика
C19 — Буксирование бревенчатого грузовика и прицепа
C31 — Автобуксирование индивидуального автомобиля

Разрешения на самоходное транспортное средство
C37 — Самоходное транспортное средство — Таблица веса 3
C38 — Самоходное транспортное средство — Таблица веса 4
C35 — Самоходное транспортное средство с ускорителем / тележками — Таблица веса 3

Другие годовые разрешения
C04 — Утечка нагрузки
C16 — Самозагружающийся бревенчатый грузовик

Как измеряется сток

• Школа водных наук ГЛАВНАЯ • Темы, связанные с поверхностными водами •

Введение в USGS Streamgaging

The U.Геологическая служба S. Geological Survey (USGS) начала свое первое водное хозяйство в 1889 году на реке Рио-Гранде в Нью-Мексико, чтобы помочь определить, достаточно ли воды для орошения, чтобы стимулировать новое развитие и расширение на запад. Геологическая служба США управляет более чем 8 200 системами непрерывной записи водотоков, которые предоставляют информацию о речных потоках для самых разных целей, включая прогнозирование наводнений, управление и распределение водных ресурсов, инженерное проектирование, исследования, эксплуатацию шлюзов и плотин, а также безопасность и развлечения для отдыха.

Как измеряется сток

Наслаждаясь отдыхом на тихом берегу местной реки, вы можете задать себе один вопрос: «Сколько воды течет в этой реке?» Вы пришли в нужное место, чтобы получить ответ. Геологическая служба США на протяжении многих десятилетий измеряет сток на тысячах рек и ручьев, и, прочитав этот набор веб-страниц, вы сможете узнать, как работает весь процесс измерения стока.

Часто во время сильного ливня по радио можно услышать объявление вроде: «Пичтри-Крик, как ожидается, поднимется сегодня в 14 часов».5 футов ». 14,5 футов, о которых говорит диктор, — это этап потока. Этап потока важен тем, что его можно использовать (после сложного процесса, описанного ниже) для вычисления потока или количества воды, протекающего в потоке в любой момент. мгновенный.

Ступень потока (также называемая ступенью или измерительной высотой) — это высота поверхности воды в футах над установленной высотой, на которой ступень равна нулю. Нулевой уровень является произвольным, но часто близок к руслу реки. Вы можете получить представление о том, что такое этап потока, посмотрев на изображение обычного штатного датчика , который используется для визуального считывания этапа потока.Датчик маркируется с шагом 1/100 и 1/10 фута.

Потоковая передача обычно включает 3 этапа:

1. Ступень измерения расхода — получение непрерывной записи ступени — высоты поверхности воды в месте вдоль ручья или реки
2. Измерение расхода — получение периодических измерений расхода (количества проходящей воды местоположение вдоль ручья)
3. Связь ступень-выпуск — определение естественного, но часто меняющегося отношения между ступенью и выпуском; с использованием соотношения стадия-расход для преобразования непрерывно измеряемой ступени в оценки расхода или расхода

Ступень измерительного потока

Мост-У.S. Геологическая служба (USGS) измеряет этап потока и состоит из структуры, в которой размещены инструменты, используемые для измерения, хранения и передачи информации этапа потока. Этап, иногда называемый измерительной высотой, может быть измерен с помощью различных методов. Один из распространенных подходов — это успокоительный колодец на берегу реки или примыкание к мостовой опоре. Вода из реки поступает в успокоительный колодец и выходит из него по подводным трубам, позволяя водной поверхности в успокоительном колодце находиться на той же высоте, что и поверхность воды в реке.Затем ступень измеряется внутри успокоительного колодца с помощью поплавка или датчика давления, оптического или акустического датчика. Измеренное значение ступени регулярно сохраняется в электронном регистраторе данных, обычно каждые 15 минут.

На некоторых участках водозабора установка успокаивающего колодца невозможна или неэффективна по стоимости. В качестве альтернативы, стадия может быть определена путем измерения давления, необходимого для поддержания небольшого потока газа через трубку и барботаж в фиксированном месте под водой в потоке.Измеренное давление напрямую связано с высотой воды над выпускным отверстием трубы в потоке. По мере того, как глубина воды над выпускным отверстием трубки увеличивается, требуется большее давление, чтобы протолкнуть пузырьки газа через трубку.

Streamgages, эксплуатируемые Геологической службой США, обеспечивают измерения ступеней с точностью до 0,01 фута или 0,2 процента ступени, в зависимости от того, что больше. Этап на ручье должен измеряться относительно постоянной исходной отметки, известной как точка отсчета. Иногда водоточные конструкции повреждаются наводнениями или со временем оседают.Для поддержания точности, и чтобы гарантировать, что стадия измеряется выше постоянной эталонной высоты, высотные отметки streamgage структур, а также измерения, связанных стадии, обычно обследоваться относительно постоянных ориентиров высот вблизи streamgage.

Хотя стадия представляет собой ценную информацию для некоторых целей, большинство пользователей данных о водотоке интересуются стоком или расходом — количеством воды, текущей в ручье или реке, обычно выражаемое в кубических футах в секунду или галлонах в день.Однако для ручья непрактично постоянно измерять расход. К счастью, существует сильная связь между уровнем воды в реке и расходом, и в результате непрерывная запись расхода воды в реке может быть определена из непрерывной записи уровня. Для определения расхода со ступени необходимо определить взаимосвязь между ступенью и расходом путем измерения расхода на широком диапазоне ступеней реки.

Расходомер

Расход — это объем воды, движущейся вниз по ручью или реке за единицу времени, обычно выражаемый в кубических футах в секунду или галлонах в день.Как правило, сток реки рассчитывается путем умножения площади воды в поперечном сечении канала на среднюю скорость воды в этом поперечном сечении:

расход = площадь x скорость

Геологическая служба США использует множество методов и типов оборудования для измерения скорости и площади поперечного сечения, включая следующий измеритель тока и акустический доплеровский профилограф.

Схема поперечного сечения канала с подсечками.

Наиболее распространенный метод, используемый Геологической службой США для измерения скорости, — это измеритель тока. Однако для определения уровня и измерения расхода воды также можно использовать разнообразное современное оборудование. В самом простом методе счетчик тока вращается вместе с течением реки или ручья. Измеритель течения используется для измерения скорости воды в заранее определенных точках (подсекциях) вдоль размеченной линии, подвесной канатной дороги или моста через реку или ручей. В каждой точке также измеряется глубина воды.Эти измерения скорости и глубины используются для вычисления общего объема воды, протекающей мимо линии в течение определенного интервала времени. Обычно река или ручей измеряются в 25–30 точках, расположенных на регулярной основе через реку или ручей.

Общественное достояние

Измеритель тока

Одним из методов, который на протяжении десятилетий использовался Геологической службой США для измерения разряда, является метод механического измерителя тока. В этом методе поперечное сечение русла потока делится на множество вертикальных подсекций.В каждом подразделе площадь определяется путем измерения ширины и глубины подсекции, а скорость воды определяется с помощью измерителя тока. Расход в каждой подсекции рассчитывается путем умножения площади подсекции на измеренную скорость. Затем рассчитывается общий расход путем суммирования расхода по каждому подразделу.

Персонал USGS использует множество типов оборудования и методов для проведения измерений с помощью измерителя тока из-за широкого диапазона условий потока на всей территории Соединенных Штатов.Ширина подсекции обычно измеряется с помощью троса, стальной ленты или подобного оборудования. Глубина участка измеряется с помощью забродной удочки, если позволяют условия, или путем подвешивания измерительного груза к откалиброванному кабелю и системе катушек на мосту, канатной дороге или лодке или через отверстие, пробуренное во льду.

Разработан в начале 1900-х годов и много раз модифицирован до 1930 года. Приобретен в компании W. & L.E. Gurley Company, Трой, Нью-Йорк.
ID объекта: USGS-000458

Кредит: Джастин Бонгард, У.С. Геологическая служба. Всеобщее достояние.

Скорость водотока можно измерить с помощью измерителя тока. Наиболее распространенным измерителем тока, используемым USGS, является измеритель тока Price AA. Измеритель тока Price AA имеет колесо из шести металлических чашек, которые вращаются вокруг вертикальной оси. Электронный сигнал передается измерителем на каждом обороте, позволяя подсчитывать обороты и рассчитывать время. Поскольку скорость вращения чашек напрямую связана со скоростью воды, рассчитанные по времени обороты используются для определения скорости воды.Измеритель Price AA предназначен для крепления к водяной штанге для измерения на мелководье или для установки непосредственно над грузом, подвешенным на тросе и катушечной системе для измерения на быстрой или глубокой воде. На мелководье можно использовать измеритель тока Pygmy Price. Это версия измерителя Price AA в масштабе двух пятых, предназначенная для крепления на удилище для болота. Третий механический измеритель тока, также разновидность измерителя тока Price AA, используется для измерения скорости воды подо льдом.Его размеры позволяют ему легко проходить через небольшую дырочку во льду, а роторное колесо из полимера препятствует налипанию льда и слякоти.

Акустический доплеровский профилограф тока

Гидрологические специалисты Геологической службы США используют акустический доплеровский профилограф для измерения стока реки Бойсе в Мемориальном парке ветеранов Бойсе в рамках исследования баланса массы фосфора.

Предоставлено: Тим Меррик, Геологическая служба США. Общественное достояние

В последние годы технологические достижения позволили Геологической службе США проводить измерения разряда с использованием акустического доплеровского профилометра тока (ADCP).ADCP использует принципы эффекта Доплера для измерения скорости воды. Эффект Доплера — это явление, которое мы испытываем, когда проезжаем мимо автомобиля или поезда, который звучит в свой гудок. По мере того, как проезжает машина или поезд, кажется, что звуковой сигнал падает.

ADCP использует эффект Доплера для определения скорости воды, посылая звуковой импульс в воду и измеряя изменение частоты этого звукового импульса, отраженного обратно в ADCP отложениями или другими частицами, переносимыми в воде.Изменение частоты или доплеровский сдвиг, которое измеряется ADCP, переводится в скорость воды. Звук передается в воду от преобразователя на дно реки и принимает ответные сигналы на всей глубине. ADCP также использует акустику для измерения глубины воды, измеряя время прохождения звукового импульса до дна реки позади ADCP.

Для измерения расхода ADCP устанавливается на лодке или в небольшом плавсредстве (рисунок выше), его акустические лучи направляются в воду с поверхности воды.Затем ADCP направляется по поверхности реки для измерения скорости и глубины в русле. Функция отслеживания дна реки с помощью акустических лучей ADCP или глобальной системы позиционирования (GPS) используется для отслеживания продвижения ADCP по каналу и обеспечения измерений ширины канала. Используя измерения глубины и ширины для вычисления площади и измерений скорости, расход рассчитывается ADCP с использованием выражения разряд = площадь x скорость, аналогично традиционному методу измерителя тока.Акустические измерители скорости также были разработаны для проведения измерений вброд (рисунок слева).

ADCP оказался полезным для потокового управления несколькими способами. Использование ADCP сократило время, необходимое для измерения расхода. ADCP позволяет проводить измерения расхода в некоторых условиях затопления, которые ранее были невозможны. Наконец, ADCP обеспечивает подробный профиль скорости и направления воды для большей части поперечного сечения, а не только в точках с механическим измерителем тока; это улучшает точность измерения разряда.

Связь ступени и разряда

Водомеры непрерывно измеряют стадию, как указано в разделе «Стадия измерения». Эта непрерывная запись стадии преобразуется в речной сток путем применения соотношения стадия-расход (также называемого рейтингом). Соотношения стадия-расход разрабатываются для водомеров физически измерение расхода реки с помощью механического измерителя тока или ADCP на широком диапазоне этапов; для каждого измерения расхода существует соответствующее измерение этапа.Геологическая служба США проводит измерения расхода на большинстве участков реки каждые 6-8 недель, обеспечивая регулярное измерение диапазона ступеней и потоков на водотоках. Особые усилия прилагаются для измерения чрезвычайно высоких и низких ступеней и потоков, поскольку эти измерения происходят реже. Отношение ступени к расходу зависит от формы, размера, наклона и шероховатости канала у ручья и различно для каждого ручья.

USGS Пример связи ступенчатый разряд.

Непрерывная запись стадии преобразуется в поток путем применения математической кривой оценки. Кривая рейтинга (рис. 3) — это графическое представление отношения между уровнем и стоком для данной реки или ручья. Компьютеры USGS используют эти рейтинговые кривые для конкретных участков для преобразования данных об уровне воды в информацию о течении реки.

Создание точного соотношения ступени и расхода требует многочисленных измерений расхода во всех диапазонах ступени и расхода.Кроме того, эти соотношения необходимо постоянно проверять по текущим измерениям расхода, поскольку каналы потока постоянно меняются. Изменения в руслах ручьев часто вызваны эрозией или отложением материала русла, сезонным ростом растительности, обломками или льдом. Новые измерения расхода, нанесенные на существующий график зависимости уровня разряда от расхода, покажут это, и рейтинг может быть скорректирован, чтобы позволить правильно оценить расход для измеряемого этапа.

Преобразование информации стадии в информацию потока

Большинство водотоков USGS передают данные об этапах через спутник на компьютеры USGS, где эти данные используются для оценки стока с использованием разработанного соотношения (рейтинга) «уровень-расход».Информация о стадии регулярно просматривается и проверяется, чтобы гарантировать точность рассчитанного расхода. Кроме того, Геологическая служба США имеет процессы контроля качества, чтобы гарантировать, что информация о речных потоках, сообщаемая по всей стране, имеет сопоставимое качество, а также ее получение и анализ с использованием последовательных методов.

Большая часть информации о стадиях и речных потоках, производимой Геологической службой США, доступна в режиме онлайн почти в реальном времени через Национальную информационную систему по водным ресурсам (NWIS) Web .В дополнение к данным о потоках в реальном времени, веб-сайт NWIS также предоставляет доступ к дневным расходам и годовым максимальным расходам за период записи для всех активных и прекращенных потоков, управляемых Геологической службой США.

Сводка по потоку

Управление потоком включает в себя получение непрерывной записи стадии, выполнение периодических измерений разряда, установление и поддержание связи между стадией и разгрузкой, а также применение отношения разряда стадии к записи стадии для получения непрерывной записи разряда.Геологическая служба США более 115 лет предоставляет нации последовательную и надежную информацию о речных стоках. Информация о речных потоках USGS имеет решающее значение для поддержки управления водными ресурсами, управления опасностями, экологических исследований и проектирования инфраструктуры.

Источники и дополнительная информация :

Деконструкция третьего измерения — как микросреда трехмерной культуры изменяет клеточные сигналы

Резюме

Большая часть нашего понимания биологических механизмов, лежащих в основе клеточных функций, таких как миграция, дифференциация и восприятие силы, была получена в результате изучения клеток, культивированных на двумерных (2D) стеклянных или пластиковых поверхностях.Однако в последнее время в области клеточной биологии стало понятно различие между этими плоскими поверхностями и топографически сложной трехмерной (3D) внеклеточной средой, в которой клетки обычно функционируют in vivo. Это стимулировало значительные усилия по разработке трехмерных биомиметических сред in vitro и стимулировало большую междисциплинарную работу среди биологов, материаловедов и тканевых инженеров. По мере того, как мы движемся к более физиологичным системам культивирования для изучения фундаментальных клеточных процессов, крайне важно точно определить, какие факторы действуют в трехмерных микросредах.Таким образом, в центре внимания данного комментария будет выявление и описание фундаментальных особенностей систем трехмерных культур клеток, которые влияют на структуру клеток, адгезию, механотрансдукцию и передачу сигналов в ответ на растворимые факторы, которые, в свою очередь, регулируют общую клеточную функцию таким образом, чтобы резко отличается от традиционных форматов 2D-культуры. Кроме того, мы опишем экспериментальные сценарии, в которых трехмерное культивирование особенно актуально, выделим последние достижения в области материаловедения для изучения клеточной биологии и обсудим примеры, когда изучение клеток в трехмерном контексте дало понимание, которое невозможно было бы наблюдать в традиционных 2D-системах.

Введение

Наше нынешнее понимание многих биологических процессов основано в основном на исследованиях гомогенных популяций клеток, культивируемых на плоских, двумерных (2D) пластиковых или стеклянных субстратах. Однако in vivo клетки в основном существуют в сложной и богатой информацией среде, которая содержит множество компонентов внеклеточного матрикса (ЕСМ), смешанные популяции клеток, которые взаимодействуют гетеротипно, и смесь секретируемых клетками факторов. Поразительное несоответствие между традиционной однослойной культурой и сценарием in vivo было обоюдоострым мечом: простота 2D-культуры позволила редукционистские подходы к пониманию отдельных клеточных явлений, но эти открытия были сделаны с оговоркой, что 2D-модель может не точно отражать физиологическое поведение клеток in vivo.

В самом деле, многие типы клеток, когда изолированы от тканей и помещены в культуру планарных клеток, становятся все более плоскими, аберрантно делятся и теряют свой дифференцированный фенотип (von der Mark et al., 1977; Petersen et al., 1992). Интересно, что некоторые из этих типов клеток могут восстанавливать свою физиологическую форму и функции, будучи встроенными в трехмерную (3D) среду культивирования. Например, инкапсуляция дедифференцированных хондроцитов восстанавливает их физиологический фенотип, включая форму клеток и экспрессию хрящевых маркеров (Benya and Shaffer, 1982).Сходным образом, эпителиальные клетки молочных желез, встроенные в трехмерную среду, останавливают неконтролируемое деление, собираются в ацинарные структуры и создают базальную мембрану de novo (Emerman and Pitelka, 1977; Lee et al., 1984; Petersen et al., 1992).

Эти наблюдения привели к мнению, что размер, в котором культивируются клетки, является решающим фактором, определяющим судьбу, и к смутному впечатлению, что культивирование клеток в монослое вызывает аномальную функцию клеток или дедифференцировку, тогда как 3D-культура вызывает более физиологическое состояние.Однако мы должны опасаться чрезмерного упрощения этих сравнений до единственного различия между двумя состояниями, то есть трехмерности в сравнении с двумерностью. В настоящее время размерность стала общим заявлением о том, что влечет за собой множество потенциальных различий между традиционной культурой в двухмерном монослое, трехмерными системами культивирования и физиологической обстановкой. Вместо общей размерной формы клетки или культуры, функциональные последствия возникают из более тонких особенностей, присущих каждому из этих контекстов.Таким образом, вместо того, чтобы просто заключать, что фактор размерности играет роль, мы должны идентифицировать и понимать характерные особенности каждой экспериментальной установки и стремиться демистифицировать то, что именно 3D-культура предоставляет клеткам, что отличается от более традиционных 2D-настроек.

Имея в виду эту цель, в этом комментарии будут рассмотрены основные пути, с помощью которых сигналы микросреды, как известно, влияют на функцию клеток — клеточные адгезии, механические силы и диффузионные факторы — и как такие сигналы могут быть представлены в трехмерной культуре по сравнению с двумерной.Помимо предоставления соответствующих физиологических сигналов, 3D-культура также способствует биологическим ответам, которые могут не наблюдаться на 2D-субстратах. Например, коллективная миграция клеток, генерация сил и сворачивание ткани, происходящие во время гаструляции, ангиогенное разрастание кровеносных сосудов и миграция раковых клеток через строму в лимфатические сосуды во время метастазирования — все это случаи клеточных процессов более высокого порядка, которые по своей сути 3D (Рис. 1). Разделение этих трехмерных микросред и связанных процессов на адгезионные, механические и химические компоненты поможет нам понять основные механизмы, которые направляют эти процессы.Более того, поскольку технологии конструирования клеточной среды быстро развиваются, мы также исследуем некоторые методы, которые можно использовать для изучения этих различных сигналов in vitro (см. Вставки 1 и 2). Этот комментарий не является исчерпывающим сборником литературы по клеточной биологии в трехмерном пространстве, а скорее направлен на выявление некоторых характерных особенностей трехмерных экспериментальных систем, которые следует учитывать в задаваемых нами вопросах и проводимых нами исследованиях.

Рисунок 1.

Трехмерные клеточные явления в развитии, гомеостазе тканей и заболеваниях управляются адгезивными, механическими и химическими сигналами, исходящими от других клеток и внеклеточной среды. ( A ) Хондроциты (синие) находятся внутри специализированного перицеллюлярного внеклеточного матрикса, где они подвергаются действию сжимающих сил, потока интерстициальной жидкости, адгезивных сигналов и растворимых сигналов в виде цитокинов, которые позволяют клеткам формировать и поддерживать окружающую среду. хрящ. ( B ) В ответ на растворимые и связанные с матрицей факторы роста и индуцированные потоком механические силы на стенку кровеносных сосудов, эндотелиальные клетки (розовые) изменяют свою полярность и межклеточные контакты, а также разрушают окружающую базальную мембрану (коричневый) и стромальный ECM (оранжевый), чтобы коллективно вторгаться в окружающие ткани и формировать трубчатые отростки.( C ) Для формирования нормальных эпителиальных структур (розовый) требуются адгезивные и механические сигналы от соседних клеток и базальной мембраны (коричневый), чтобы жестко регулировать пролиферацию и апоптоз. Неправильная регуляция пролиферации через генетические или внеклеточные изменения инициирует каскад растворимых сигналов, которые активируют фибробласты (синий цвет) в окружающей строме. Последующие механические и структурные изменения в стромальном ECM позволяют трансформированным эпителиальным клеткам (зеленые) мигрировать в соседнюю сосудистую сеть (светло-голубые) и, в конечном итоге, метастазировать.Рисунки не в масштабе.

Вставка 1. Материалы и системы для 3D-культуры

Подавляющее количество биоматериалов было разработано для изучения, а также управления клеточными взаимодействиями в 3D (Langer and Tirrell, 2004; Lutolf and Hubbell, 2005). Чтобы эксперименты были осуществимы с технической точки зрения, эти системы обычно начинаются с жидкого предшественника, содержащего суспендированные клетки, которые гелеобразуются или затвердевают цито-совместимым и гидратированным образом. Полученные гели являются пористыми, чтобы обеспечить обмен питательными веществами и отходами, и обладают достаточными механическими свойствами, чтобы быть самоподдерживающимися.Основная биологическая функциональность достигается добавлением клеточно-адгезионных лигандов, обычно в форме пептидов Arg-Gly-Asp. В экспериментах, где представляет интерес миграция клеток, ремоделирование матрикса или многоклеточная организация, встроенные клетки должны преодолевать стерические ограничения своего окружения. Чтобы это произошло, 3D ECM должен содержать структурные единицы, которые подвержены деградации либо посредством протеолитического расщепления, либо гидролиза. Наконец, специфическая биологическая активность и взаимодействия могут быть облегчены путем добавления растворимых или нерастворимых факторов и биологических доменов.Такие материалы могут быть природного или синтетического происхождения, но большая часть инженерных разработок синтетических материалов основана на нашем понимании того, как функционируют естественные ECM.

В течение нескольких десятилетий внеклеточные маты из природных источников служили важным инструментом для биологов. Эти материалы включают очищенный коллаген типа I (A на рисунке) (Grinnell, 2003), фибриновые гели, образованные тромбиновым расщеплением фибриногена, восстановленную базальную мембрану (например, Matrigel) (Kleinman and Martin, 2005) и стромальный ECM, синтезируемый фибробластами (C in Рисунок) (Бичем и др., 2007). В результате своего клеточного происхождения эти материалы по своей природе обладают адгезивными лигандами и другой биологической активностью и могут легко перестраиваться клетками. По этой же причине эти системы могут оказаться невыгодными при изоляции определенных клеточных ответов. Например, Матригель содержит коллагены, ламинин и энтактин, но также обладает не охарактеризованной популяцией факторов роста, которые существенно различаются между партиями (Hughes et al., 2010). Дополнительные ограничения природных систем включают проблему модификации этих систем для включения дополнительных функциональных фрагментов и сложность независимой настройки различных характеристик микросреды.Например, в коллагеновом геле невозможно регулировать жесткость без изменения плотности адгезивного лиганда, размера пор и пористости.

Разработка синтетических гелей быстро продвигалась в течение последнего десятилетия и была мотивирована желанием обеспечить больший контроль над материалами и биологическими свойствами, чем может быть достигнуто с помощью их естественных аналогов (Lutolf and Hubbell, 2005). Эти материалы обычно обладают структурным каркасом, лигандами, связывающими клетки, и «дружественным для клеток» механизмом сшивания.Наиболее распространенными из них являются гидрогели на основе полиэтиленгликоля (PEG) (D на рисунке) (Mann et al., 2001; Burdick and Anseth, 2002; Raeber et al., 2005; Miller et al., 2010) и самогидрогели. сборка пептидов (Kisiday et al., 2002; Zhang, 2003; Mata et al., 2009). Эти гели легко настраиваются и часто имеют модульную структуру с включением дополнительных функций, таких как домены, расщепляемые матриксной металлопротеазой, или сайты связывания факторов роста. О преимуществах синтетических материалов лучше всего свидетельствует постоянно расширяющаяся гибкость и разнообразие этих систем.Например, недавно были разработаны гели, в которых динамические изменения жесткости могут быть вызваны в ответ на свет (Kloxin et al., 2009).

Изображения на рисунке были адаптированы с разрешения Grinnell et al., 2003 (A), Doyle et al., 2009 (C) и Legant et al., 2010 (D) (Grinnell et al., 2003; Doyle et al., ., 2009; Легант и др., 2010). Масштабные линейки: 20 мкм.

Вставка 2. Как разработать микросреду для отражения особенностей 3D-культуры

Растет интерес к выделению и использованию конкретных сигналов микросреды, которые может предоставить 3D-культура.С этими инструментами можно было бы воссоздать определенный клеточный фенотип без необходимости 3D-культуры и связанных с ней экспериментальных недостатков (например, неоптимальная визуализация и взаимозависимые факторы микросреды). Примеры включают методы контроля адгезии и формы клеток, механики и топографии матрикса, а также доставки растворимых факторов.

Адгезия

Субстраты с микрорельефом содержат определенное расположение областей, адгезивных к клеткам и устойчивых к адсорбции белка, которые расположены на плоской поверхности.Эти субстраты могут точно контролировать адгезию и распространение клеток без изменения физических или химических свойств микросреды (Whitesides et al., 2001; Théry, 2010). В зависимости от геометрии паттернов такие субстраты использовались для определения размера и распределения адгезий, опосредованных интегрином, формы клеток и архитектуры цитоскелета (A на рисунке), а также многоклеточной организации (B на рисунке), и сыграли важную роль. в демонстрации важности этих факторов в регулировании тесной связи между клеточной структурой, передачей сигналов и функцией.Нанотопографические материалы (E – F на рисунке) обычно представляют собой жесткие подложки с наноразмерными топологическими особенностями, которые предназначены для ограничения размера и геометрии адгезии клетка-матрица. Эти материалы могут быть изготовлены с использованием нескольких методов, включая литографию, химическое и физическое придание шероховатости, электропрядение или электрораспыление (Dalby et al., 2004; Anselme et al., 2010). По мере приближения к масштабам нанометров локальная кривизна и шероховатость могут влиять на расположение плазматической мембраны, поверхностных рецепторов и связанных с ними структур.Например, Салаита и его коллеги использовали решетки в нанометровом масштабе, чтобы ограничить движение и кластеризацию рецепторов EPH рецептора A2 (EPHA2) и, таким образом, изменить передачу сигналов от этих рецепторов (Salaita et al., 2010).

Механика

Элементы в нанометровом масштабе также можно использовать для изменения механических свойств клеточного микросреды, когда она формируется в более мягких материалах. Например, мы создали массивы силиконовых штифтов субмикрометрового диаметра и различной длины, чтобы изучить влияние жесткости ECM на клетки (C на рисунке, Fu et al., 2010). Силиконы также могут быть получены с различной плотностью сшивки, чтобы регулировать жесткость получаемого субстрата (Prager-Khoutorsky et al., 2011). Точно так же многочисленные гидрогели, такие как и все большее количество дизайнерских систем, могут быть поперечно сшиты по-разному для изменения жесткости субстрата (D на рисунке). Важной особенностью, присущей всем этим системам, является ортогональный контроль жесткости и плотности лигандов.

Растворимые факторы

Высокопроизводительные методы работы с жидкостями и микрофлюидные обеспечивают два средства, с помощью которых можно строго определить растворимую среду.Подходы высокопроизводительного скрининга могут использоваться для воздействия на клетки библиотек растворимых факторов и изучения результирующего биологического ответа. Хуанг с соавторами использовали высокопроизводительный подход для оптимизации растворимых факторов, которые способствуют хондрогенезу мезенхимальных стволовых клеток (Huang et al., 2008). Микрожидкостные устройства (G, H на рисунке), основанные на мягкой литографии, могут использоваться для управления более тонкими характеристиками растворимого микросреда, включая временное и пространственное представление биологических факторов (Quake and Scherer, 2000), или могут просто уменьшить эффективный объем культуры и, таким образом, усиление аутокринных сигналов (Yu et al., 2007). Эти устройства различаются по конструкции от простых систем свободной диффузии до более сложных генераторов градиента на основе потоков, которые обеспечивают больший контроль и гибкость при создании динамических профилей во времени и пространстве. В настоящее время микрофлюидика обычно используется для обеспечения градиентов растворимых факторов роста в клетках, в первую очередь для изучения поляризации и хемотаксиса (Kim et al., 2010).

Изображения на рисунке были адаптированы с разрешения Kilian et al., 2010 (A), Desai et al., 2009 (B), Fu et al., 2010 (C), Bettinger et al., 2009 (E), Teixeira et al., 2003 (F), Gomz-Sjöberg et al., 2007 (G) (Kilian et al., 2010; Desai et al., 2009; Fu et al., 2010; Bettinger et al., 2009; Teixeira et al., 2003; G�mez-Sjöberg et al., 2007). Изображения в D любезно предоставлены Колином Чоем и Кристофером Ченом. Изображение H, Кортси Альберта Фолча (Вашингтонский университет, Сиэтл, Вашингтон).

Клеточная адгезия и структура

Для клеток, зависящих от закрепления, адгезивные взаимодействия с окружающими ECM и соседними клетками определяют форму и организацию клеток.Организация, состав и количество адгезий являются одними из наиболее понятных сигналов, которые интегрируются клеткой, чтобы регулировать многие фундаментальные клеточные поведения, включая выживание, дифференцировку, пролиферацию и миграцию (Wozniak et al., 2004; Weber et al., 2011; Орр и др., 2006; Гейгер и др., 2009). Неизбежно, изучение клеточной биологии in vitro требует удаления из клеток этих естественных взаимодействий клетка-клетка и клетка-ECM, и введения их в чужеродную адгезивную среду, которая определяется системой культивирования.

Одно из наиболее ярких различий, наблюдаемых при сравнении клеток в 2D и 3D, — это различие в морфологии (Fig. 2). Клетки, выращенные в монослое, являются плоскими, могут прилипать и свободно распространяться в горизонтальной плоскости, но не имеют поддержки для распространения в вертикальном измерении. Одним из следствий этого является то, что клетки, которые культивируются на 2D-поверхностях, обладают принудительной апикально-базальной полярностью. Эта полярность, возможно, актуальна для некоторых типов клеток, таких как эпителиальные клетки, но неестественна для большинства мезенхимальных клеток, которые, будучи встроенными в 3D ECM, принимают звездчатую морфологию и поляризуются только спереди назад во время миграции (Mseka et al., 2007). Эти изменения в геометрии и организации клеток могут напрямую влиять на функцию клеток. Напр., Апикально-базальная полярность, как было показано, модулирует чувствительность клеток к апоптозу (Weaver et al., 2002). Также было высказано предположение, что уплощение клеток может изменить эффективное соотношение поверхности к объему (то есть мембраны к цитоплазме), так что сигнал от поверхности клетки лучше распространяется в клетку (Meyers et al., 2006). . Используя адгезивные островки с микрорельефом на 2D-субстратах, мы и другие продемонстрировали, что изменение степени распространения клеток может влиять на пролиферацию, апоптоз и дифференцировку клеток (Singhvi et al., 1994; Чен и др., 1997; Thomas et al., 2002; McBeath et al., 2004). В дополнение к общей площади распространения, геометрическая форма (например, круглая или звездчатая, кубовидная или удлиненная), которую принимает клетка, может влиять на ее функцию (Brock et al., 2003; Théry et al., 2006; Théry et al., 2007; Mahmud et al., 2009; Kilian et al., 2010). Несмотря на очевидную роль формы и площади в функционировании клеток в 2D-культуре, остается неясным, как эти идеи соотносятся с настройками 3D. Методы контроля клеточной адгезии в 3D только начинают разрабатываться (Lee et al., 2008; ДеФорест и др., 2009; Хетан и Бурдик, 2010; Klein et al., 2011). В самом деле, процесс расширения или расширения в трехмерную матрицу может сильно отличаться от процессов, происходящих на плоской поверхности. Например, на 2D-субстратах опосредованная интегрином адгезия сопровождается ламеллиподным расширением, опосредованным миозином напряжением цитоскелета и усилением фокальных спаек (Hynes, 1987; Burridge et al., 1988; Lauffenburger and Horwitz, 1996; Reinhart-King et al. др., 2005). В целом этот процесс занимает короткое время на этих безудержных основаниях.В 3D-настройках, однако, клетки часто должны преодолевать или протеолитически расщеплять физический каркас, чтобы расширяться. Таким образом, распространение клеток происходит в течение часов, а в некоторых случаях — дней, а не минут (Khetan and Burdick, 2010).

Рис 2.

Клейкие, топографические, механические и растворимые подсказки в 2D и 3D. Сигналы, с которыми сталкивается клетка, разительно отличаются между стеклянной или пластиковой поверхностью, покрытой ECM (2D), и типичным 3D ECM, таким как коллаген.

Клетки принимают двумерную или трехмерную геометрию в основном в зависимости от того, формируются ли опосредованные интегрином адгезии с внеклеточным матриксом на одной стороне клетки или по всей поверхности клетки (рис.2). Различные клеточные ответы в 2D и 3D культуре могут возникать из-за этих вариаций пространственного распределения спаек. Например, Beningo et al. «Зажатые» фибробласты между двумя полиакриламидными гелями, покрытыми ЕСМ, для одновременного взаимодействия как дорсальных, так и вентральных интегринов (Beningo et al., 2004). Теперь, когда связывание интегрина происходит в двух противоположных плоскостях, образование ламеллиподов уменьшилось в пользу звездчатой ​​морфологии с длинными, богатыми актином расширениями, сродни морфологии фибробластов, наблюдаемой in vivo (Langevin et al., 2005). Было показано, что подобные «сэндвич-культуры» поддерживают дифференцированную функцию гепатоцитов (Dunn et al., 1989). Как пространственное распределение адгезии в 3D может влиять на передачу сигналов и функцию клеток, остается в значительной степени спекулятивным, но, учитывая совокупность знаний, которые мы приобрели при контроле распределения адгезии в 2D, такие исследования хорошо мотивированы.

Достижения в нашей способности контролировать представление ВКМ на 2D-поверхностях облегчили исследования, которые начинают объяснять, как пространственное распределение лиганда влияет на адгезию и функцию, опосредованную интегрином (Théry, 2010; Geiger et al., 2009). Напр., Распределение адгезий, лежащих в основе клетки, может смещать ось планарной полярности и митотическое веретено (Théry et al., 2006; Théry et al., 2007). Используя 8-нм золотые частицы, покрытые пептидами Arg-Gly-Asp (RGD), которые позволяют связывать только один интегрин, Арнольд и его коллеги определили минимальное расстояние между лигандами, необходимое для возникновения индуцированной интегриновой кластеризацией передачи сигналов (Arnold et al. , 2004). Технология пространственного моделирования адгезионных лигандов в 3D все еще находится в зачаточном состоянии, усилия по разработке подходов, аналогичных этим 2D-технологиям, будут иметь решающее значение для перевода нашего понимания клеточной адгезии в 3D-контекст.Тем не менее, эти результаты предполагают, что архитектура ECM в нанометровом масштабе влияет на структуру, функцию и, возможно, состав адгезий, опосредованных интегрином. Этот вопрос архитектуры особенно важен с учетом большого разнообразия фибриллярных структур нативного внеклеточного матрикса нанометрового масштаба, которые могут динамически изменяться в процессе прогрессирования заболевания (Levental et al., 2009; Amatangelo et al., 2005; Provenzano et al., 2006). ; Räsänen, Vaheri, 2010; Beacham, Cukierman, 2005).

Учитывая структурное разнообразие внеклеточной среды, неудивительно, что спайки в 3D сильно изменчивы. Такие факторы, как жесткость матрикса и топография, вероятно, будут способствовать привлечению белков к сайтам адгезии и могут объяснить некоторые вариации, наблюдаемые в различных трехмерных контекстах (Harunaga and Yamada, 2011; Fraley et al., 2010; Kubow and Horwitz, 2011). ). Подходы к количественному описанию этих вариаций еще не появились из-за дополнительных препятствий, связанных с тем, что визуализация фокальных спаек в трехмерном контексте затруднена из-за уменьшенного размера или интенсивности спаек или неоптимальной оптики в неплоских образцах.Несмотря на эти проблемы, были описаны 3D-матричные адгезии на матрицах, происходящих из клеток, и было высказано предположение, что тип интегрина, используемого клеткой, по-разному определяется в 3D и в 2D микро средах (Cukierman et al., 2001). Интересно, что последующие исследования подтвердили, что эти трехмерные адгезии могут быть воспроизведены путем культивирования клеток на плоских поверхностях, которые представляют собой узкие полоски ECM с микрорельефом (Doyle et al., 2009). Другими словами, фибриллярная природа ECM может быть ответственной за модуляцию структуры адгезии и передачи сигналов, и один важный механизм, с помощью которого 3D-культура может влиять на функцию клеток, заключается в таких наноразмерных особенностях.Заглядывая вперед, в то время как несколько естественных ECM уже доступны в качестве моделей для изучения этих топографических эффектов (например, коллагена I и фибрина), недавний прогресс в синтетических матрицах может позволить более настраиваемый контроль над структурными и механическими характеристиками трехмерной среды.

Механотрансдукция

Стало широко признано, что механические силы всегда присутствуют между клетками и их окружением, и что эти силы обеспечивают решающий набор сигналов, которые могут контролировать структуру и функцию клетки (Eyckmans et al., 2011; Hoffman et al., 2011). Механические стрессы, генерируемые или испытываемые клетками, когда они прикрепляются к ЕСМ и к своим соседям, представляют собой центральный компонент того, как клетки передают опосредованные адгезией передачу сигналов и процессов (Orr et al., 2006). Однако, в отличие от адгезий, где большая часть нашего понимания была получена из исследований на 2D-поверхностях, некоторые из самых ранних свидетельств, указывающих на роль механики внеклеточного матрикса, возникли при сравнении клеток, культивированных в гелях, которые оставались связанными с чашкой (прикреплены), с клетками культивировали в гелях, которые отделялись и, следовательно, позволяли сокращаться (плавать).Напр., Образование ацинусов эпителиальных клеток молочных желез и образование канальцев происходит только в плавающих гелях (Emerman and Pitelka, 1977; Parry et al., 1985; Keely et al., 1995). Здесь мы рассматриваем возможность того, что 3D-культура воздействует на механические силы и их трансдукцию в клетках.

Традиционная 2D культура на стеклянных или пластиковых подложках помещает клетки в статическую механическую среду, которая является супрафизиологической с точки зрения жесткости (рис. 2). Признавая несоответствие между этими искусственными условиями и заметно более податливым микроокружением большинства тканей, недавняя работа с использованием мягких 2D-гелей подтвердила, что жесткость ВКМ может влиять на спайки, морфогенез, дифференцировку и поддержание стволовых клеток (Engler et al., 2006; Paszek et al., 2005; Гилберт и др., 2010). Низкая жесткость не обязательно является неотъемлемым свойством трехмерной среды; однако это общая черта для большинства 3D-систем и фактор, который следует принимать во внимание при обнаружении различий между поведением ячеек в 2D и 3D. Наше понимание того, как клетки ощущают жесткость или жесткость, все еще развивается, и большая часть текущих усилий направлена ​​на выявление механизмов с помощью 2D-гелей. Однако возможно, что механизмы, которые клетки используют для определения жесткости, различаются между 2D-поверхностями и 3D-микросредами.Напр., Huebsch и соавторы исследовали влияние жесткости геля на дифференцировку мезенхимальных стволовых клеток (MSC) в трехмерных RGD-модифицированных альгинатных гелях (Huebsch et al., 2010). Интересно, что дифференцировка МСК продемонстрировала бимодальный ответ, при котором остеогенез происходил максимально при промежуточной жесткости, тогда как 2D исследования предполагали ответ на плато, при котором как стеклянные, так и пластиковые субстраты эффективно индуцируют остеогенез. Изучая взаимодействия клетка-ECM с помощью FRET-визуализации, авт. Также обнаружили, что остеогенез в трехмерном контексте требует кластеризации интегрина за счет вызываемых клетками сил тяги, и что это кластеризация отменяется в чрезмерно жесткой трехмерной матрице.По неизвестным причинам эта зависимость от кластеризации интегринов не наблюдалась на 2D субстратах (Huebsch et al., 2010).

Помимо восприятия пассивных механических сигналов, таких как податливость окружающей матрицы, ткани обычно испытывают множество активных нагрузок, которые приводят к трансдукции силы и деформации на клеточном уровне (Hoffman et al., 2011). Хотя остается неясным, воспринимаются ли экзогенные и внутренне генерируемые силы посредством общих механизмов механотрансдукции (Chen, 2008), существуют четкие различия в том, как силы воспринимаются клетками в 2D и в 3D контекстах.Например, в типичных 2D-экспериментах эффект деформаций растяжения исследуется путем растяжения клеток, которые прилипают к плоским силиконовым мембранам, покрытым ECM. Результирующие поля деформации являются гладкими и однородными, а деформация ячеек происходит предсказуемым, аффинным образом. Напротив, большинство трехмерных тканей являются волокнистыми и, следовательно, структурно гетерогенными и анизотропными (Pathak and Kumar, 2011). Способ, которым сила передается на клетку, зависит от масштаба и организации волокон матрицы по сравнению с клеткой, а также от того, связана ли клетка напрямую и / или физически ограничена материалом.Напр., Соседние клетки, расположенные внутри фиброзного хряща, испытывают значительно разную степень растяжения в зависимости от их близости и адгезии к фибриллам коллагена (Upton et al., 2008). Помимо сложности, морфология и ориентация клеток по отношению к направлению приложенных сил и матричной архитектуре могут иметь глубокое влияние на клеточный ответ (Kurpinski et al., 2006; Nathan et al., 2011). Хео и его коллеги заметили, что расхождение между ориентацией приложенных сил и структурной анизотропией в волокнистом материале изменяет клеточную деформацию и по-разному влияет на экспрессию генов (Heo et al., 2011). Учитывая эти многочисленные сложности, понимание эффектов экзогенных нагрузок на клетки, встроенные в структурно сложные материалы в 3D, потребует комбинации экспериментального и вычислительного подходов к моделированию (Niklason et al., 2010), что порождает потребность в междисциплинарном сотрудничестве. между биологами и инженерами.

Даже если отбросить сложность гетерогенных, анизотропных волокнистых материалов, 3D-культура приводит к важным различиям в отношении механического состояния.В 2D-культуре клетке позволяют деформироваться вне плоскости оси и без механических или физических ограничений. В 3D-культуре это не так. Например, несоответствие между тем, как ячейка и окружающая матрица сужаются, когда они удлиняются при растяжении, могут создавать напряжения в поперечной плоскости ячейки. Точно так же ориентация напряжения по отношению к фокальным адгезиям является касательной к поверхности клетки на 2D-подложке (то есть вызывает сдвиг в адгезиях) и приводит к передаче силы вдоль базально расположенных стрессовых волокон (Dembo and Wang, 1999 ; Tan et al., 2003) (рис.2). Напротив, растяжение встроенной ячейки приведет к напряжениям, которые лежат перпендикулярно мембране, и приведут к силам, которые проходят через среднюю линию ячеек. То, как клетки и адгезии преобразовывают механические силы, вполне может меняться в зависимости от ориентации этих сил. Хотя мы использовали приложенные силы, чтобы проиллюстрировать различия между напряжениями, испытываемыми в 2D- и 3D-средах, силы, генерируемые ячейками, также могут ощущаться совершенно по-разному в 2D и в 3D контекстах.Недавние разработки в измерении сил клеточной тяги в 2D и 3D настройках позволили начальную характеристику этих различий и будут способствовать лучшему пониманию передачи силы клетка-ECM (Maskarinec et al., 2009; Legant et al., 2010).

Эффекторный транспорт

Помимо адгезивной и механической поддержки клеток, ECM также играет важную роль в регулировании пространственного распределения питательных веществ, газов (таких как кислород и оксид азота) и растворимых эффекторных молекул (включая морфогены, факторы роста, гормоны и цитокины. ).Эти градиенты важны для регуляции фундаментальных клеточных процессов, таких как миграция и хоуминг клеток (Kay et al., 2008), ангиогенное прорастание (Adams и Alitalo, 2007; Otrock et al., 2007) и формирование паттерна ткани на раннем этапе развития ( Gurdon, Bourillot, 2001; Saha, Schaffer, 2006; Manjón et al., 2007; Bollenbach et al., 2008) (рис.1). Пространственное представление диффундирующих факторов в тканях сложное и продиктовано структурой и пористостью окружающего внеклеточного матрикса, а также наличием и распределением сосудистой сети и окружающих клеток (оба из которых могут служить источниками или поглотителями этих факторов).Последующая компартментализация наших тканей во время развития является результатом, а также последующим фактором формирования сигнальных градиентов, и эта петля обратной связи между структурой ECM и эффекторным транспортом важна для поддержания дифференцированных структур у взрослых.

В традиционных условиях двумерного монослоя культивирования секретируемые клетками или добавленные экзогенно растворимые факторы конвективно перемешиваются и свободно диффундируют по среде, тем самым быстро уравновешиваясь.Временные градиенты могут быть созданы в этих контекстах для изучения короткоживущих хемотаксических событий, таких как поляризация клеток и миграция на 2D-поверхностях (см. Вставку 2), но более долгосрочные морфогенетические события требуют градиентов, которые поддерживаются на протяжении от часов до дней. Простое присутствие ECM, созданного с помощью 3D-культуры или простого наложения матриц на 2D-культуру, замедляет перенос и уравновешивание растворимых факторов и может поддерживать такие устойчивые градиенты. Гранулированный кластер клеток, в котором отсутствует экзогенный ECM, представляет собой относительно простую трехмерную модель, которая также может улавливать радиальные градиенты, опосредованные диффузией.Например, сфероиды опухолевых клеток достаточного размера обладают гипоксически-некротическим ядром, напоминающим настоящие опухоли, и оказались полезными для изучения роли гипоксии в производстве онкогенных факторов и устойчивости к лекарствам (Hirschhaeuser et al., 2010; Mueller -Klieser, 1997).

Когда клетки инкапсулированы в 3D ECM, структурные особенности ECM, такие как размер пор, взаимосвязь и размеры геля — в дополнение к плотности клеток, размеру растворенного вещества и заряду — все это модулирует диффузию растворимых факторов (Ramanujan et al., 2002). Фактически, поскольку клетки обычно встраиваются в гели миллиметрового размера с ограничением диффузии, часто бывает трудно отличить прямые эффекты инкапсуляции в 3D-ECM от различий во времени распространения растворимых сигналов через материал. Чтобы решить эту проблему, мы создали трехмерные гели микронного размера, которые из-за своего небольшого размера лишены диффузионных барьеров. Сравнивая реакцию клеток MDCK на растворимый фактор роста гепатоцитов (HGF) в микронном и традиционном миллиметровых гелях, мы подтвердили, что время и уровень передачи сигналов были очень чувствительны к скорости диффузии HGF, а не к размерности.Поразительно, что HGF-индуцированное фосфорилирование ERK значительно повышается в гелях микронного размера, но почти отсутствует в гелях большего размера даже в течение нескольких часов (Raghavan et al., 2010). Таким образом, хотя эффекты диффузии через трехмерные ткани in vitro часто игнорируются, ограничения диффузии растворимых факторов могут объяснить некоторые различия, часто наблюдаемые между 2D и 3D настройками. Эти эффекты диффузии могут приводить к неожиданно локальным ответам. Например, Нельсон с соавторами определили роль ингибирующих морфогенов, которые действуют аутокринным образом, чтобы определять точное пространственное расположение прорастания в эпителиальных трубках микронного размера с трехмерным рисунком (Nelson et al., 2006). Точно так же градиенты кислорода в трехмерных тканях — из-за низкой растворимости кислорода в водных средах — могут четко определять границы метаболически активных клеток и области гипоксии или гибели клеток (Volkmer et al., 2008).

Контроль над пространственным представлением растворимых факторов в 3D ECM регулируется не только законами диффузии. Градиенты давления и макромасштабные деформации тканей приводят к направленному внутриклеточному потоку жидкости и конвективному переносу. В самом деле, связь между механическими силами и транспортом растворенных веществ может быть другим важным средством, с помощью которого механические сигналы могут быть преобразованы в передачу клеточных сигналов в трех измерениях (Griffith and Swartz, 2006).Кроме того, ЕСМ не только ограничивает диффузионный и конвективный перенос растворимых факторов, но также может активно изолировать растворимые факторы. Например, давно известно, что протеогликаны сульфата гепарина активно связывают факторы роста в ЕСМ, а трансформирующий фактор роста β (TGF-β), как было показано, имеет сродство к коллагену IV типа (Влодавский и др., 1987; Парк и др. ., 1993; Паралкар и др., 1991). Хранение факторов в ECM, вероятно, является важным механизмом, с помощью которого строго регулируется временное и пространственное представление факторов клеткам.Такие факторы затем могут высвобождаться с помощью различных механизмов, таких как протеолитическая деградация матрикса (Башкин и др., 1989) или активное высвобождение посредством механического притяжения клетками (Wipff et al., 2007), что иллюстрирует не только способ: какие клетки могут контролировать потребление факторов, связанных с ЕСМ, но другой механизм, в котором механическая и химическая передача сигналов тесно переплетаются.

Заключительные замечания

Область клеточной биологии постоянно приближается к измерению, стремясь подтвердить результаты 2D в более физиологических условиях, разработать более надежные скрининги лекарств и органотипические модели, а также не забывать о тканевой инженерии или регенеративных целях.Во всех этих начинаниях критическое изучение микросреды, вместо того, чтобы приписывать наблюдаемые расхождения неспецифическим эффектам размерности, будет иметь важное значение для выявления конкретных сигналов и механизмов, лежащих в основе желаемого эффекта. Мы узнали, что в зависимости от обстоятельств могут быть совершенно разные и часто множественные причины, по которым поведение ячеек различается между 2D и 3D контекстами. Плодотворные темы для изучения в будущем включают в себя то, как структура, состав и трехмерное распределение адгезивных доменов изменяют форму клеток и организацию цитоскелета и, в свою очередь, влияют на передачу сигналов и функцию клеток, как пассивная и активная механическая трансдукция силы в трехмерных внеклеточных матрицах сильно отличается от статическая и жесткая или линейно-эластичная механика пластиковых или плоских гелей тканевых культур, соответственно, и то, как химическая и физическая структура матрицы изменяет перенос и доступность растворимых и связанных эффекторов.Хотя вовлеченные факторы могут быть многочисленными, сложными и взаимозависимыми, как ученые, наша природа и наша задача — выявить скрытые механизмы, управляющие поведением клеток.

Применяя этот пристальный взгляд к примерам культур хондроцитов и эпителиальных клеток молочных желез, упомянутых выше, мы видим, что существуют существенные различия в системах трехмерных культур, которые используются для поддержания дифференцированного фенотипа хондроцитов по сравнению с эпителиальными клетками молочных желез, что позволяет предположить, что лежащие в основе задействованы механизмы.Хондроциты сохраняют свою функциональность, когда они встроены в биологически инертные агарозные гели (Benya and Shaffer, 1982), тогда как инкапсуляция в геле коллагена 3D типа I ускоряет дедифференцировку в направлении фибробластного фенотипа (van Susante et al., 1995). Оперативная особенность инкапсуляции в 3D не была, как первоначально предполагалось, фактором, который оказывал эти эффекты на форму клеток (Benya and Shaffer, 1982). Вместо этого именно удаление адгезивных лигандов привело к поддержанию фенотипа (Mallein-Gerin et al., 1991; Langelier et al., 2000; Woods et al., 2005; Коннелли и др., 2007). Таким образом, однослойная культура нефизиологична для хондроцитов, поскольку способствует избыточной адгезии. Более того, снижения уровня адгезии (будь то на 2D- или 3D-подложке) достаточно для восстановления морфологии и функции хондроцитов (Glowacki et al., 1983; Woods and Beier, 2006; Gao et al., 2010). Напротив, образование ацинусов молочной железы сильно зависит от количества ламинина и коллагена IV в матриксе (Weaver et al., 1997), присутствие субстрата с низкой жесткостью (Paszek et al., 2005) и апоптотические сигналы, которые запускают образование просвета (Debnath et al., 2002). Фактически, инкапсуляция эпителиальных клеток молочных желез в 3D не является существенной для этого ответа, т.к. посев клеток поверх базальной мембраны приводит к сходным морфогенетическим событиям (Debnath et al., 2003). Таким образом, жизненно важные изменения, необходимые для восстановления нормальной функции клеток, возникают не непосредственно из трехмерной культуры, а из важных основных особенностей избранных микросредов, которые, возможно, изначально были обнаружены случайно в конкретной трехмерной среде.

В дополнение к модуляции симфонии адгезионных, механических и химических сигналов, которые регулируют функцию клетки, трехмерный контекст также позволяет возникать явлениям более высокого порядка, когда сами клеточные реакции имеют структурную природу. Морфогенез, ремоделирование тканей и миграция раковых клеток изменяют трехмерную организацию самого микроокружения, и трудно, если не невозможно, воспроизвести эти процессы в двумерных культуральных системах (Рис. 1). Даже простые процессы могут принимать совершенно разные формы в 2D и 3D настройках.Например, миграция на двумерных поверхностях итеративно проходит через несколько этапов: удлинение передней кромки, образование адгезии, создание тяги и последующее втягивание задней кромки (Lauffenburger and Horwitz, 1996; Ridley et al., 2003). В отличие от этой довольно определенной последовательности, способ, которым клетки мигрируют в трехмерном пространстве, зависит от топографии, стерических препятствий и анизотропной механики, специфичных для волокнистого внеклеточного матрикса, в который встроены клетки, а также от активации протеолитического аппарата для проникновения в матрицу. или активация механизмов, необходимых для проталкивания через поры (Doyle et al., 2009; Заман и др., 2006; Raeber et al., 2005; Вольф и др., 2003). Поэтому неудивительно, что большое количество режимов и механизмов миграции было описано для клеток в различных трехмерных средах.

В заключение, существует большой риск чрезмерного упрощения различий между культурой клеток и окружающей средой нативных тканей как просто вопрос размерности. Вместо этого более продуктивно думать о классических сигналах микросреды, которые управляют функцией клеток — клеточных адгезиях, механических силах и диффузионных факторах — и о том, как они модулируются различными 2D- и 3D-культурами по сравнению с in vivo.Благодаря такому пониманию мы будем лучше приспособлены для разработки микросреды (вставка 2), которая более точно отражает сценарий in vivo, или даже тех, которые могут определять функцию клетки и использовать ее для регенеративных целей. Наконец, обсуждение клеточного микроокружения и его регуляции клеточного поведения было бы неполным, если бы не пройти полный круг и не признать, что источником ECM является сама клетка. Это двустороннее взаимодействие между матрицей и клетками, называемое «динамической взаимностью» (Bissell et al., 1982), оставляет нам скромное напоминание о том, что наши культуры, будь то 2D или 3D, контролируются только с точки зрения начального состояния. Остальное предоставлено самим клеткам.

Благодарности

Авторы благодарят Сару Стэплтон, Бритту Траппманн и Мишель Возняк (Университет Пенсильвании, Пенсильвания) за содержательные обсуждения и предложения.

Footnotes

• Финансирование

  Эта работа была частично поддержана грантами NIH [номера грантов EB00262, EB08396, HL73305, GM74048] и Центра инженерных ячеек и регенерации Университета Пенсильвании.B.M.B. выражает признательность за финансовую поддержку Национальной исследовательской премии имени Рут Л. Киршштейн. Депонируется в ЧВК для выпуска через 12 месяцев.

• Эта статья является частью минифокуса по механотрансдукции. Для дальнейшего чтения см.

  No related posts.