Разбивка на местности. Обноска.[Razbivka-na-mestnosti-Obnoska] | Мой загородный дом

Поскольку здания и сооружения на местности имеют прямые углы, попробуем построить такой угол на местности. Нам понадобится: три штыря из проволоки, диаметром 6-8 мм и длиной 40 см, а так же полипропиленовый шпагат- около 15 метров.

Отрежем два куска шпагата – 4м и 5 м.Выберем исходную точку на участке, где у нас планируется один из углов будущего сооружения. Возьмём один штырь, привяжем к нему оба куска шпагата и воткнём штырь в нашу исходную точку. Это и будет вершина первого прямого угла.

Затем рулеткой отмеряем на длинном куске шпагата ровно 4 м.На этом месте привязываем ещё один штырь.

Теперь на коротком куске шпагата отмеряем ровно 3 м и, точно так же, привязываем третий штырь.

У нас получилось, что один штырь воткнут в исходной точке, и к нему привязаны 2 отрезка шпагата- 3 и 4 м со штырями на концах. Берём третий отрезок шпагата и привязываем его к одному из не воткнутых в землю штырей.

От штыря по этому отрезку отмеряем ровно 5 м и завязываем на этой отметке узелок.

Получился простейший, но довольно точный инструмент для построения прямых углов на местности.

Как им пользоваться? Воткнём в землю второй штырь. Обычно это штырь с четырёхметровым отрезком шпагата. Ориентируем его так, как пойдет длинная стена нашего будущего сооружения. Далее, совмещаем место 5и метровой отметки и место третьего штыря, как показано на рисунке 1.

Получился прямой угол на местности.

Таким же образом строим весь прямоугольник будущего сооружения. Теперь правим его диагональю.

Допустим, наше сооружение имеет размер по осям 6м на 8 м.Рассчитаем размер диагонали Д.

Д=6*6+8*8=36+64=100

Извлекаем корень квадратный из 100, получим 10 м

Берём отрезок шпагата чуть более 10м и двумя узелками отметим 10 м. Проверим диагонали, как показано на рисунке 2.

Если диагонали не попадают в углы, переставим штыри. Таким образом, мы вынесли план будущего сооружения в осях.

Выполнение обноски

Простейшие измерения на местности (стр. 2 из 3)

Рисунок 6.

Поле зрения отсчетного микроскопа теодолита Т30.

Отсчет по горизонтальному кругу 70° 0,5¢; отсчет по вертикальному кругу 358° 48¢.

Измерение и построение горизонтальных углов

 Построение углов на местности при помощи ленты

Произведя соответствующие расчеты, можно при помощи ленты решать и обратную задачу – строить на местности углы заданной величины. Пусть требуется построить угол, равный 37°30¢. Так этому углу соответствует хорда 6,43м, тем самым построим данный угол. Он будет заключен между десяти метровыми сторонами. Точно также вместо десятиметровых сторон можно откладывать другие, например 5 или 20м, но в этом случае в соответствующее число раз надлежит уменьшать или увеличивать значение хорды (в данном случае в 2 раза).

Изложенный прием, основанный на использовании таблицы хорд, может быть с успехом применен и при построении (измерении) углов на плане.

При выполнении топографических работ все чаще встречается необходимость в построении прямого угла 90° и угла 45°. Построение этих углов можно выполнять и без таблицы хорд.

На (рис. 7, стр. 11) показано построение прямого угла в точке С к стороне АС. Это построение основано на том, что в треугольнике со сторонами 3; 4 и 5 м угол, лежащий против пятиметровой стороны, — прямой угол (90°).[2] Для получения большей точности, стороны этого треугольника могут быть увеличены в любое число раз.

Аналогичным образом может быть построен прямой угол при помощи треугольника со сторонами 5,00; 7,07; и 5м. на этот раз углы против 5,00м сторон будут равны 45°, а против 7,07м — 90°.

Кроме того для построения угла в 45° можно использовать треугольник со сторонами 7,00; 4,00; и 5,04м или 7,00; 6,00; и 5,06м, в которых угол в 45° будет лежать опять против пятиметровой стороны.

Рисунок 7. Использование длин сторон треугольника: построение треугольника.

С большей точностью угол в 45° может быть построен по треугольнику 17; 17; и 13м, здесь он будет лежать против стороны 13м[3].

 Построение углов с помощью экера

Экер – специальный прибор для построения прямых углов. Простейший экер крестообразный; состоит из кола и двух планок, на каждой из которых вбито отвесно по две иголки. Иголки расположены таким образом, что соединяющие их линии пересекаются под прямым углом.

Для построения прямого угла в точке С к линии АВ нужно установить кол экера отвесно в точке С, расположив одну пару иголок в стороне АВ

(точка С лежит на линии АВ). Тогда вторая пара иголок будет перпендикулярна к этой линии. Остается в створе с ними выставить веху D(рис. 8).

Рисунок 8. Построение перпендикуляров с помощью экера.

 Построение угла с помощью мензулы

Мензула – это переносной столик для черчения плана непосредственно на местности. Состоит из планшета – квадратной доски, которая скрепляется при помощи подставки со штативом. Перед работой планшет оклеивается сверху бумагой так, чтобы после составления плана можно было легко снять чертеж, с планшета не повредив его. При мензуле имеется специальный прибор – кипрегель, служащий для наведения на окружающие предметы и прочерчивания на планшете соответствующих направлений

(рис. 9а). Кипрегель имеет вертикальный круг для измерения углов наклона и дальномерной нити в трубе, позволяющие определять расстояния. Прототипом кипрегеля является алидада – простейший прибор, состоящий из линейки и приспособления для наведения, например двух вертикально воткнутых иголок или двух стоек с визирами (рис. 9б).

При помощи кипрегеля можно построить угол с точностью до 3 — 5¢, а при помощи линейки, снабженной двумя иголками, эта точность снижается в десять раз (1¤2 — 1°).

Для построения на планшете угла ВАС местности мензулу устанавливают над точкой А, при помощи уровня (или на глаз) планшет приводят в горизонтальное положение и на бумаге намечают точку а, соответствующую точке А местности: они должны лежать на одной отвесной линии. К точке а плана прикладывают линейку и, направив ее в точку В местности, по краю чертят направление ab, которое будет лежать в стороне точек А и В. После чего точно так же чертят направление ас. Изображенный на бумаге угол bacбудет равен горизонтальному положению угла ВАС на местности.

Рисунок 9. а – кипрегель, б – алидада.

а б

 Измерение горизонтальных углов

В производстве для определения величины горизонтального угла применяют приборы двух типов: мензулу и теодолит. Мензулой угол строят на бумаге (как сказано на странице 12), а теодолитом измеряют его градусную величину. Кроме этого для определения величины горизонтального угла может послужить компас имени » Андрианова » (рис. 11, стр. 16).

Для измерения величины угла нужно иметь лимб [4], расположен в горизонтальном положении над точкой А местности так, что его центр лежит на одной отвесной линии с этой точкой.

Допустим далее, что около центра круга вращается линейка – алидада. Алидада имеет приспособление для наводки и отсчета называемый индекс штрих. Сделать отсчет – это значит определить, против какого деления лимба остановился штрих алидады.

Техника измерения угла ВАС сводится к следующему (рис. 10, стр. 14). Алидаду сначала наводят на точку В и делают отсчет, допустим 16°, далее ее направляют на точку С и снова производят отсчет, допустим 63°. Вычитая из правого отсчета левый, получаем величину угла: 63° — 16° = 47°. Может случиться что правы отсчет (23°) меньше левого (336°), тогда перед вычитанием к нему следует прибавить 360°. Величина угла будет найдена так: 23° + 360° — 336° = 47°. Этот случай соответствует положению нулевого штриха лимба внутри измеряемого угла.

Называя точки и стороны угла » правая » и » левая «, считается, что наблюдатель расположен лицом внутрь измеряемого угла. Наконец учитываем, что на лимбе подписи делений возрастают от 0 до 360°. Таким образом, отсчет следует рассматривать как периодическую функцию, с периодом 360°.

Рисунок 10. Измерение горизонтального угла теодолитом.

а – отсчет направлений по лимбу, б – принцип измерения горизонтального угла теодолитом.

Если с данной точки А необходимо определить значения углов между направлениями на точки числом больше двух, например между направлениями на точки В, С, Dи Е (рис 10), то можно измерять не каждый угол ВАС, CADи т. д в отдельности, а все совместно: производя отсчеты последовательно, по ходу часовой стрелки, на каждую из точек В, С, Dи т.д. Такие отсчеты называют направлениями, а совокупность измеренных совместно направлений – рядом направлений.

Обозначив направления на точки В, С, D,…соответственно (В), (С), (D) и т.д, применительно как на рисунке. 10, а будем иметь (В) = 16°, (С) = 63°, (D) = 139° и (Е) = 221°. Ряд направлений обладает тем свойством, что ко всем направлениям ряда можно прибавить (вычитать) произвольное число, не изменяя значения углов, определяемых этим рядом. Ряд направлений записывают так, что первое направление равно нулю: (В) = 0°, (С) = 47°, (D) = 123° и (Е) = 205°.

Теодолиты – имеют сложный вид (рисунки. 1, 3 и 4), но измерение ими углов производят по изложенному выше принципу.

 Измерение горизонтального угла с помощью компаса Андрианова

Крышка компаса » Андрианова » может свободно вращаться, она имеет приспособление – прицел для визирования. Компас позволяет измерить магнитный азимут направления (линии) местности, т.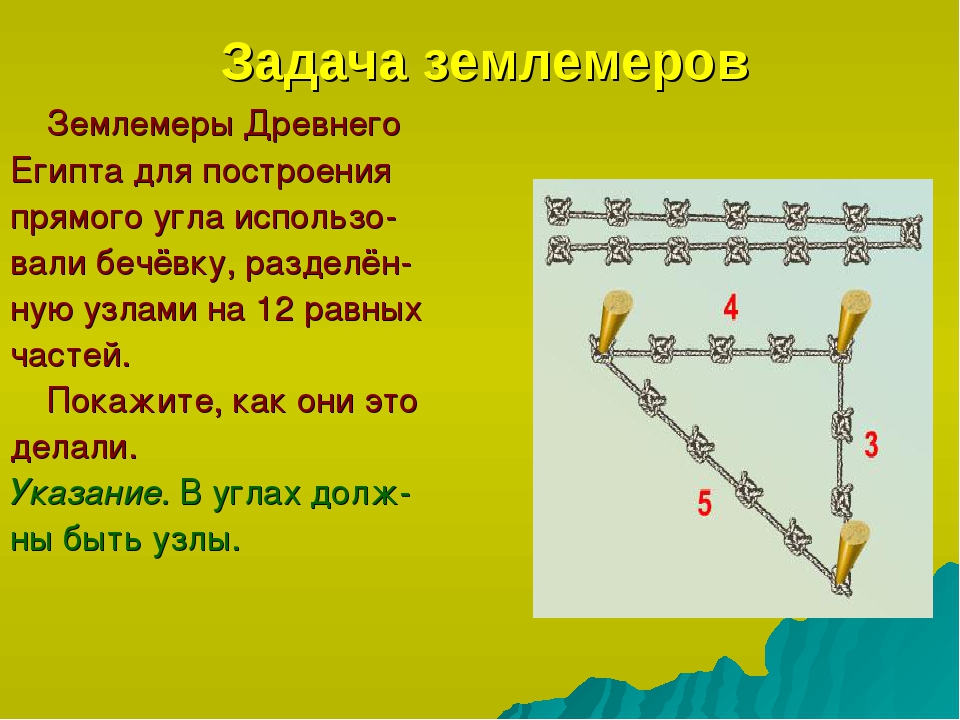 е. горизонтальный угол, который образует это направление с северным концом магнитной стрелки. Азимут отсчитывается от направления на север, через восток, юг и запад от 0 до 360° (по ходу часовой стрелки).

Для измерения магнитного азимута съемщик держит компас так, чтобы северный конец освобожденной стрелки указывал точно на деление 0°. Далее, вращая крышку, он наводит прицел на предмет, азимут направления на который определяется, после чего остается сделать отсчет по специальному указателю, расположенному под прицелом в плоскости кольца с делениями (рис. 11, стр. 16).

Рисунок 11. Определение магнитного азимута по компасу.

Если измерить азимуты двух сторон угла, то их разность даст его величину. При аккуратных измерениях ошибка угла будет порядка 5° (цена одного деления компаса Андрианова 3°).

Большие компасы называются буссолям, они позволяют измерять углы с точностью до 0,5°.

Зональные технологии

Рост производства продуктов растениеводства находится в прямой зависимости от освоения зональных систем земледелия.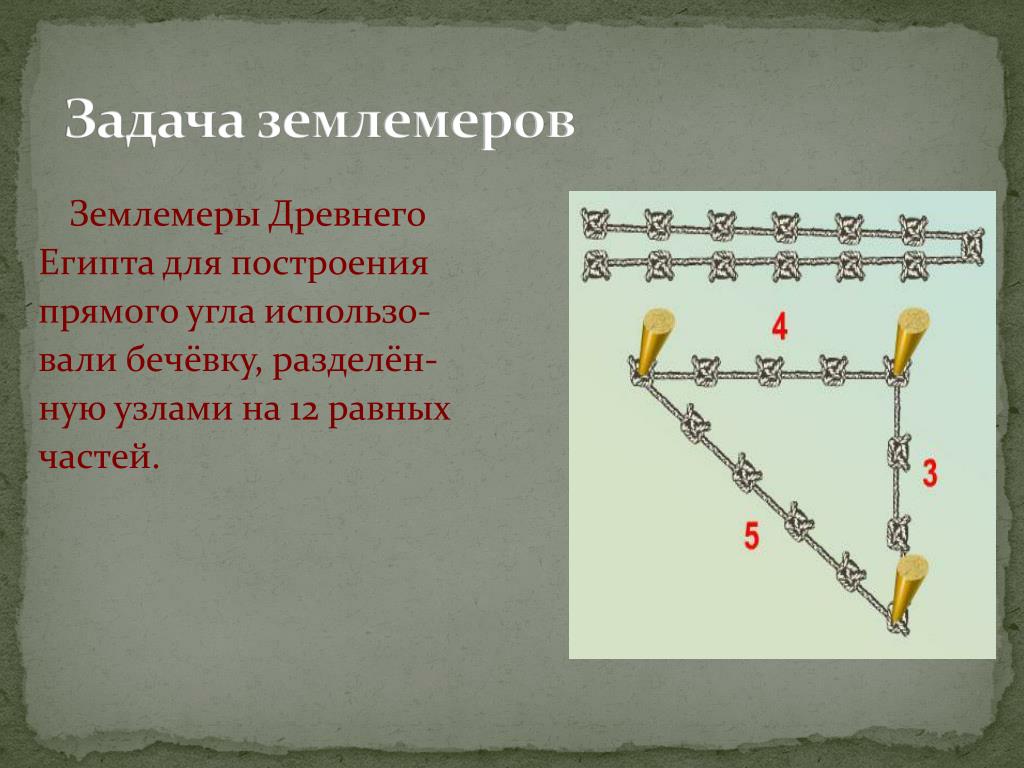

Системы земледелия по зонам разрабатываются многие годы, накоплен богатый материал по общим и частным вопросам (методы защиты почв от эрозии, севооборотам, обработке почвы, срокам посева и т.д.). На данном этапе с учетом этих достижений необходимо дать производству научно обоснованные зональные технологии возделывания культур, обеспечивающих планируемое производство сельскохозяйственной продукции.

Характер природно – климатических условий, размещение городов и промышленных предприятий определили специализацию сельскохозяйственного производства по зонам. В степной и южной части лесостепной зоны (Омской области) развивается зерновое хозяйство, особенно производство сильных и ценных пшениц. Эта отрасль дополняется скотоводством, а также овощеводством в ряде хозяйств. В северной лесостепи и северных зонах, где нет условий для производства ценного произвольного зерна, развивается производство озимой ржи, овса, ячменя, гороха. Эти культуры сочетаются с интенсивным скотоводством. В южной лесостепи, где расположен ряд городов, концентрируется производство овощей, картофеля, молока, яиц.

Мария Синянская: о принципе «вертикаль – горизонталь» и значении прямого угла в геодезии

Мария Синянская – исследователь, защитивший кандидатскую диссертацию по истории и циклам развития геодезии, популяризатор наук о Земле, сооснователь и редактор проекта «История геодезии», автор многочисленных научных и научно-популярных статей – представила статью с тонкими наблюдениями об условиях параллельности и перпендикулярности.

---

О принципе «вертикаль – горизонталь»

В человека природой изначально заложены прямой угол, условия параллельности и перпендикулярности. Этих знаний на первых этапах жизнедеятельности было достаточно для построения на земле прямоугольных фигур и выполнения различных измерений на местности, в том числе при разбивке земельных угодий.

В применяемых системах измерений, в конструировании всех геодезических инструментов раннего времени изначально был заложен

принцип «вертикаль – горизонталь». Вследствие данного обстоятельства все приборы и устройства (ватерпасы, хоробаты, землемерные кресты, позднее – теодолиты, нивелиры и др. приборы) должны были иметь устройства для приведения их в рабочее положение, где одна ось была бы расположена вертикально, а другая горизонтально. Принцип четырех направлений являлся также основой таких геодезических понятий, как азимут, дирекционный угол, румб и т.д.

Геодезические системы измерения развивались на основе этих принципов, в том числе и для решения задач, связанных с

геометризацией и координатизацией пространства, с практикой и теорией обработки результатов измерений. В основу структуры систем измерения был заложен, как правило, прямой угол, и поэтому, по существу, эти системы измерений представляли инструменты прямого угла. Конструирование геодезических инструментов начиная с ватерпаса, хоробата и землемерных крестов, а в дальнейшем – астролябии, теодолита, нивелира и других осуществлялось с жестким соблюдением условий прямоугольности основных частей приборов. Во всех геодезических инструментах такими составными частями являлись различные оси и плоскости: вертикальная ось вращения инструмента, ось вращения зрительной трубы, зрительная ось, ось уровня, плоскости лимба, алидады горизонтального и вертикального кругов. 

О методах построения прямого угла

Во взаимном положении рассматриваемых плоскостей и осей закладывалось условие прямого угла, условие перпендикулярности. Соответственно основными поверками во всех геодезических инструментах закладывались соблюдения условий перпендикулярности взаимного положения плоскостей и осей. Например, зрительная ось должна быть перпендикулярна оси вращения трубы; ось уровня перпендикулярна или параллельна оси вращения инструмента; плоскости горизонтальных и вертикальных кругов перпендикулярны соответствующим осям и т.д.

Поверки перпендикулярности (поверки прямого угла) осуществлялись во все времена, начиная с использования ватерпаса. Поэтому конструктивной особенностью геодезических инструментов не только Древнего мира, но и Нового времени являлось жесткое условие взаимного расположения в инструменте рассматриваемых частей и обязательное выполнение соответствующих поверок и юстировок.

Угловых измерений как таковых, в нынешнем их понимании, в Древнем мире не существовало. Все измерения сводились в основном к построению прямого угла и разделялись (по тому времени) на приближенные и точные. В первом случае измерения осуществлялись с помощью всевозможных землемерных крестов, угольников и различных способов с использованием человеческой фигуры.

Во втором случае применялся египетский треугольник, в вещественном варианте представлявший собой веревочный шаблон из мерной веревки с метками на расстоянии в 3, 4, 5 единиц длины, в вершинах которых устанавливались колышки. Далее по ним натягивалась веревка, которая образовывала прямоугольный треугольник, у которого при вершине двух катетов получался прямой угол, как показано на рис.

1 (египетский треугольник со сторонами 3, 4, 5).

Данный вариант имел наибольшую точность построения прямого угла, которая в большей степени зависела от точности изготовления (нанесения меток) мерной веревки.

Другой вариант точного построения прямого угла (циркульный) был в большей степени теоретическим способом построений и основывался на получении вписанного в окружность прямого угла, стороны которого опирались на концы диаметра (см. рисунок ниже). Для получения прямого угла нужно было провести полуокружность, на которой взять любую точку и соединить ее с концами диаметра. При вершине, противолежащей диаметру получившегося треугольника, образовывался прямой угол.

Проложение хода. При проложении ходов требовалось построение прямого угла. Например, на какой-либо выбранной стороне хода АВ в намеченной точке требуется построить прямой угол. Первоначально на основании отрезка АВ строился равнобедренный треугольник с боковыми сторонами, равными радиусу окружности, а затем в эту окружность вписывался прямой угол. Третьей точкой (вершиной) для этого треугольника являлась точка О, как центр окружности. Далее на продолжении в направлении

АО откладывался отрезок ОС, равный радиусу R. В этом случае отрезок АС является диаметром этой окружности, в которую вписан прямой угол АВС. Сторона ВС, естественно, является перпендикуляром к линии АВ. Если точки В или С являются крайними точками хода, то в них всегда имеется возможность построить прямоугольный треугольник, необходимый для решения той или иной инженерной задачи.

Способы, связанные с египетским треугольником и циркульным методом, послужили средством для получения образцовых мер построения прямого угла. Именно на их основе получали рабочие меры, в частности, различные землемерные кресты и т.п.

В решении различных землеустроительных задач и задач по созданию различных сооружений, в том числе инженерно-технических, в системе геодезических построений использовалось всего несколько главных фигур: прямой угол, прямоугольный треугольник, прямоугольный четырехугольник и квадрат.

Прямой угол. Прямой угол является универсальным мировым стандартом, заложенным в человека, в природу и взаимодействие различных физических сил.

Для реализации прямого угла в геодезических работах использовался угольник. Нивелирование с применением вертикальных реек или ватерпасов широко применялось с древнейших времен и вплоть до XX века. В различных системах координат, использовавшихся с древнейших времен, их основу составляли две взаимно перпендикулярные (координатные) линии (рис. 3): начальный меридиан и экватор (декуманус максимум и кардо максимум). На рисунке ниже изображён маркировочный центурийный камень (СМ – кардо максимум, ориентация с юга на север, DM – декуманус максимум, ориентация с востока на запад):

Построение прямого угла на местности было возможным начиная с глубокой древности с помощью ранее описанных различных вариантов. В Средневековье и в более позднее время применялись землемерные кресты различных видов и формы, в том числе экеры. В построении прямых углов использовались героновские диоптры, а также астрономические методы и устройства. Во всех видах построений их точность была невысокой (около ¼ градуса), но в особых случаях (как при сооружении египетских пирамид) достигала величины порядка 3 минут.

Человек в вершине угла

Следует отметить, что в глубокой древности, ещё до использования инструментов, люди могли проводить межевание с помощью фигуры человека. Так, например, человек вставал в вершине первого угла. По направлению створа плеч строилось одно направление, а по прямому взгляду – перпендикулярное ему направление. В одном из этих направлений человек шагами измерял нужное расстояние. Затем в другой точке операция повторялась. Такая реальность, возможно, предшествовала появлению первых геодезических инструментов. Точность построения прямого угла подобным способом находилась в пределах от 10^-1 до 10^-2.

Прямоугольный треугольник. Прямоугольный треугольник представляется структурным продолжением прямого угла. Эта фигура и ее материальные реализации, в том числе в веревочном варианте, находили самое разнообразное применение. Так, с помощью подобного построения треугольника Фалес определял расстояние до корабля. Иногда это построение считают открытием триангуляции. Фалес Милетский, находясь в Египте, использовал условие подобия прямоугольных треугольников для решения задач по определению высоты Гизехских пирамид. Он утверждал, что, как только его тень станет равной длине (высоте) его фигуры, в это время нужно измерить длину тени пирамиды, которая будет равна её высоте, что показано на рисунке ниже:

  

Реализация семнадцати героновских задач в большинстве случаев была возможна с применением прямоугольного треугольника. С помощью прямоугольного треугольника простейшим способом определялись длины катетов, гипотенуза и площадь треугольника. Египтяне еще в III тысячелетии до н.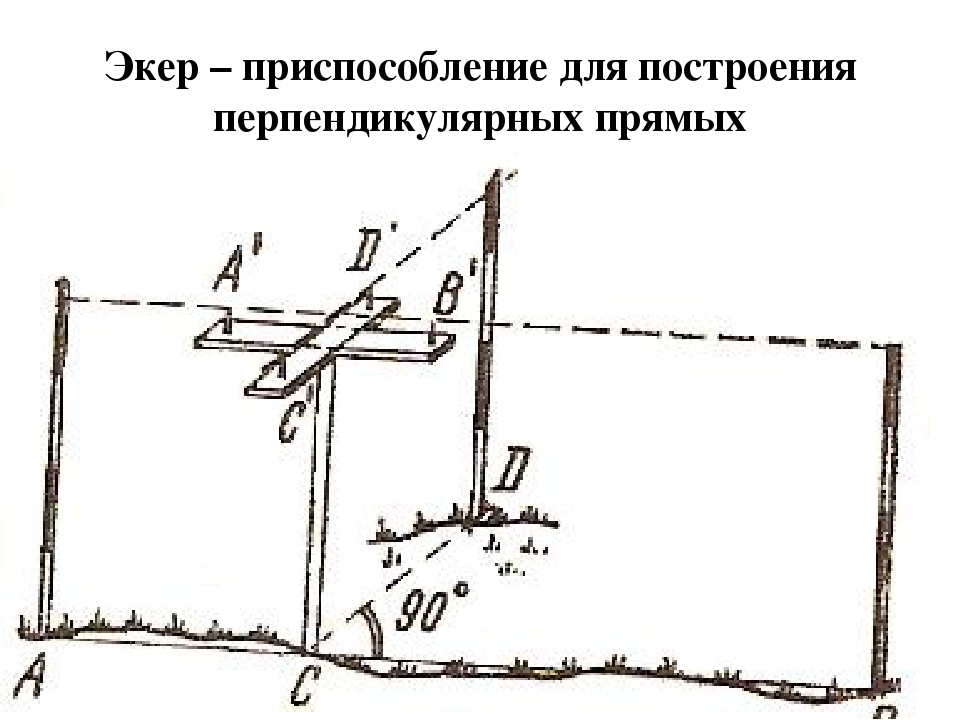 э. определяли эту площадь по известной формуле половины произведения двух катетов. Открытие Пифагором доказательства теоремы было значительным событием для теоретической и практической геометрии, а также для хозяйственной действительности. Формула Пифагора по существу определяет и характеризует метрику окружающего (евклидова) пространства. А такие фигуры, как прямоугольный четырехугольник и квадрат, получили свое раннее применение при планировке отдельных сооружений, особенно в землеустройстве, межевании, земельном кадастре. Прямоугольный треугольник использовался в Древнем Риме и других странах при проектировании водопроводов, каналов и городской канализации. Вместе с тем для подсчета площади прямоугольного треугольника использовалась формула: 

где S – площадь; a, b – соответствующие прямоугольные катеты.

Возможно, данное выражение было известно еще с тех времен, когда люди изобрели формулы для подсчета площади квадрата и прямоугольного четырехугольника (как их половину).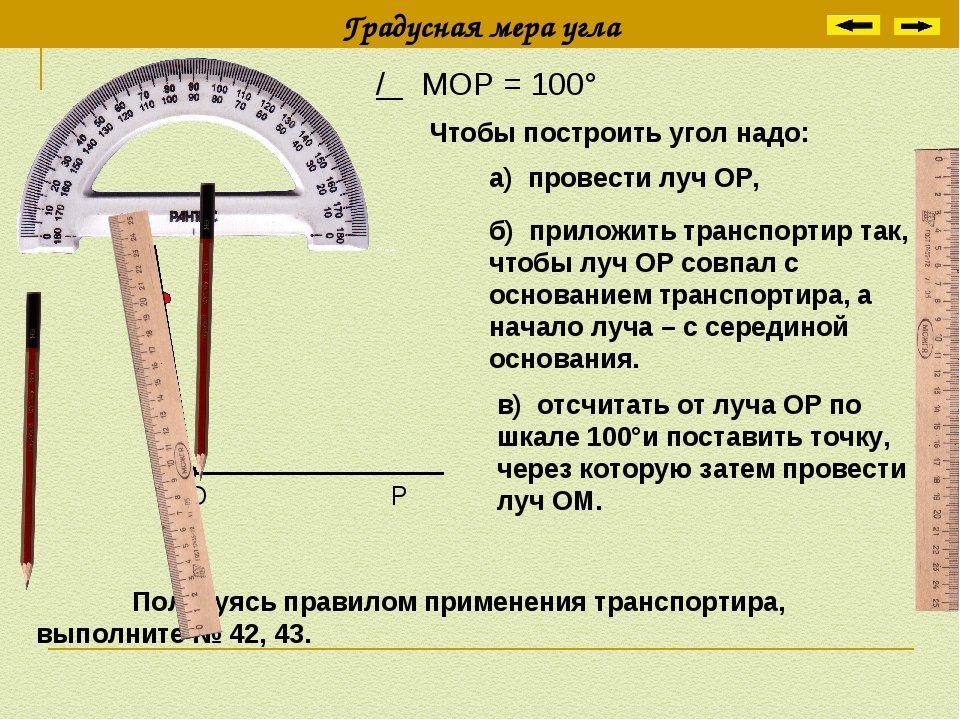 В плане исторического времени это уже совпадает со временем деления земельных угодий и их оценки (не позднее третьего тысячелетия до н.э.).

Важнейшим фактором для широкого использования прямоугольного четырёхугольника является его универсальность и оптимальность, а также его преимущество перед другими формами при разбивке, планировке сооружений, городов, земельных угодий и т.д. Необходимо заметить, что данная фигура в большей степени отвечает использовавшимся тогда формам координатизации пространства.

Около 10 тысячелетий назад в строительстве жилищ человек перешел от круглой формы к прямоугольной. Примерно в это же время (или чуть позднее) начали делить земельные угодья прямыми линиями с прямым углом между ними. Намного раньше прямой угол стали использовать в организации окружающего пространства и ориентировке в нем. Объяснение феномена раннего появления и использования прямого угла в деятельности людей лежит в сфере влияния внешней среды. Это влияние выражено и сформировано в виде принципов влияния: принцип «вертикаль – горизонталь» и принцип четырех направлений. Они оказывали фундаментальное влияние на развитие геодезии в течение всей истории ее развития. Главной характеристикой и составной частью этих принципов является прямой угол. Он стал важнейшей характеристикой окружающей среды и всего пространства, как и два других геометрических свойства – перпендикулярность и параллельность. Наиболее наглядно эти геометрические свойства выражены в фигуре человека. В геометрии фигуры человека вполне четко и очевидно заложено шесть главных направлений. Ими в человека заложена пространственная система координат. Эта «система координат», заложенная в человека внешней средой («принципы влияния»), и вся встроенная в нее система прямых углов (условий перпендикулярности и параллельности) позволяют человеку не только отлично выстраивать систему ориентации в пространстве, но и строить простейшие геометрические фигуры на земле. Вся геометрия человека подчинена условиям перпендикулярности и параллельности – основному геометрическому свойству окружающего пространства.

Важнейшей функцией прямого угла в геодезии являлись системы координат, которые во все времена были прямоугольными. В измерении и моделировании пространства необходимым условием является ориентировка в нем. Поэтому, как правило, определяется главная ориентирующая линия в пространстве (на местности или модели), которая затем становится одной из осей координат («Принцип четырех направлений»). К ней под прямым углом проводится вторая ось. Этим обеспечивается возможность координатизации окружающего пространства (в плоскости). Для трехмерного пространства ориентируется уже две оси (или плоскости), на базе которых строится пространственная система координат. В координатизации окружающего пространства и угловых измерениях роль прямого угла как важнейшей составной части сохраняется. Столь же велика роль прямого угла в моделировании, контроле объектов и явлений окружающего пространства. В инженерной геодезии при возведении сооружений и контроле их геометрии важнейшее значение имеют условия перпендикулярности и параллельности.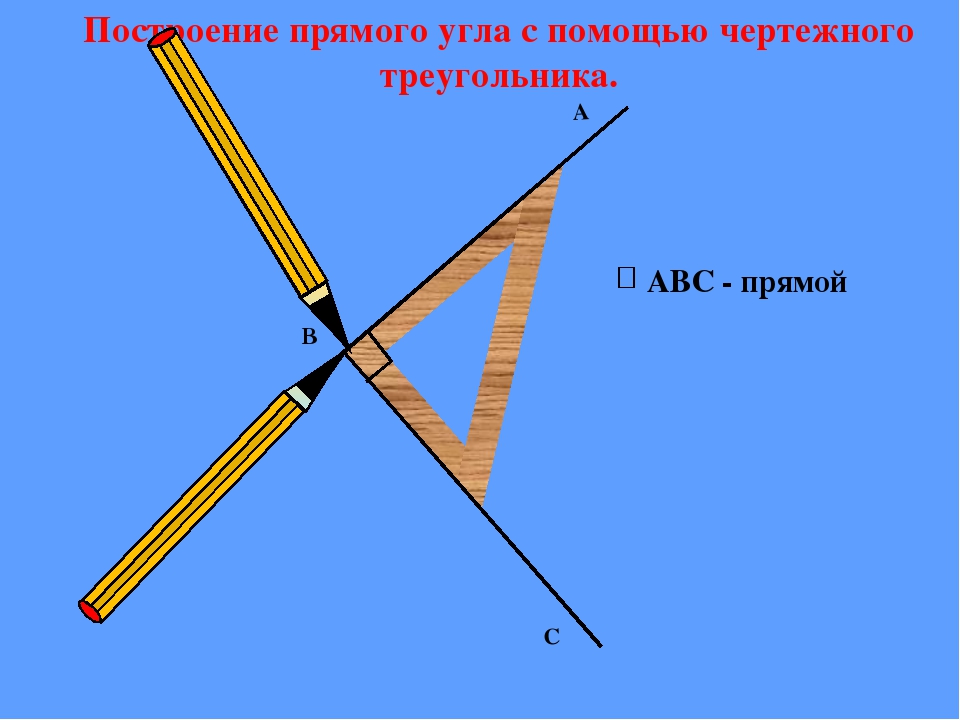 Эти два важнейших свойства окружающего пространства есть свойство прямого угла (или двух прямых). Сформировавшаяся или формируемая геодезическая технология в существенной части предопределяла возможность реализации этих геометрических требований. Пока прямой угол остается некой нормой окружающей среды, пока сохраняется «геометрия» человека, до тех пор рассмотренное значение прямого угла в геодезии будет сохраняться.

Египетский треугольник

О египетском треугольнике и его свойствах хорошо известно ещё с древних времён. Эта фигура широко применялась в строительстве для разметки и построения правильных углов.

История египетского треугольника

Создателем этой геометрической конструкции является один из величайших математиков древности Пифагор. Именно благодаря его математическим изысканиям мы можем в полной мере использовать все свойства данного геометрического построения в строительстве.

Важно! Принято считать, что толчком к открытию этой геометрической фигуры послужило путешествие Пифагора в Африку, где он увидел египетские пирамиды.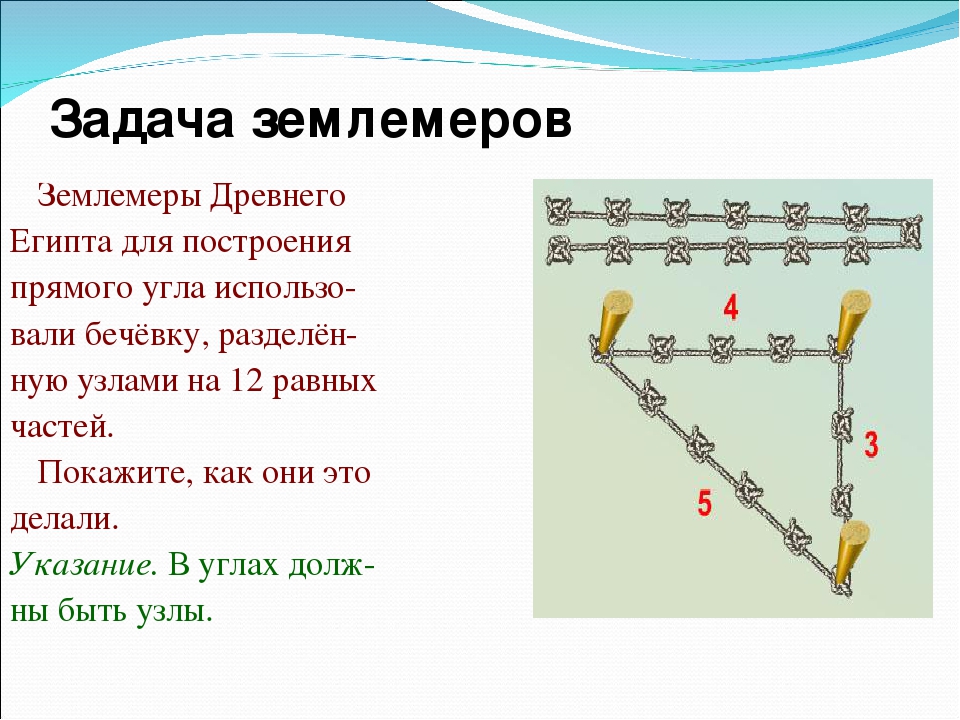 Возможно, именно они стали прообразом данной конструкции.

Можно предположить, что математические навыки позволили Пифагору заметить закономерность в формах строения. Дальнейшее развитие событий можно легко представить. Базовый анализ и построение выводов создали одну из самых значимых фигур в истории. Скорее всего, в качестве прообраза была выбрана именно пирамида Хеопса из-за своих практически совершенных пропорций.

Египетский треугольник в строительстве

Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.

Важно! Конечно, в идеале лучшим вариантом будет использование транспортира или угольника.

Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:

1. 5,
2. 4,
3. 3.

Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.

Внимание! Свойства египетского треугольника таковы, что квадрат гипотенузы равен квадратам двух катетов.

Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.

Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.

Внимание! Длина каждого отрезка составит 4 и 3 см (при минимальных значениях). Пересечение этих прямых образует прямой угол, равняющийся 90 градусам.

Альтернативные способы построить прямой угол на 90 градусов

Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций.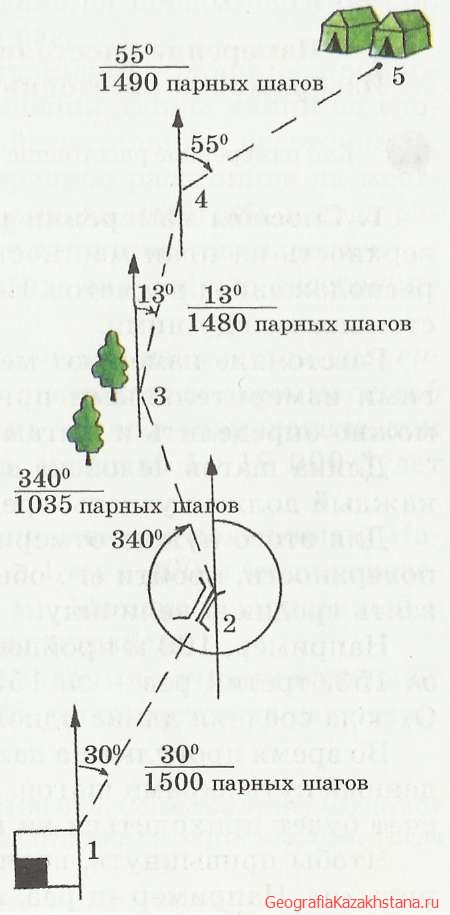 Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.

Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.

Как получить египетский треугольник при помощи верёвки

Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.

Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.

Как построить угол в 45, 30 и 60 градусов

Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.

Важно! Для получения нужного наклона вырвите лист бумаги из журнала и согните его. При этом линии изгиба будут проходить через угол. Края должны совпасть.

Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.

Внимание! Соотношение сторон на 30º нужно, чтобы сделать шестиугольники. Их свойства востребованы в столярных заготовках.

Итоги

Свойства египетского треугольника широко использовались в строительстве на протяжении почти, что двух с половиной веков. Даже сейчас при недостатке инструментов строители применяют эту открытую ещё Пифагором методику, чтобы добиться ровных прямых углов.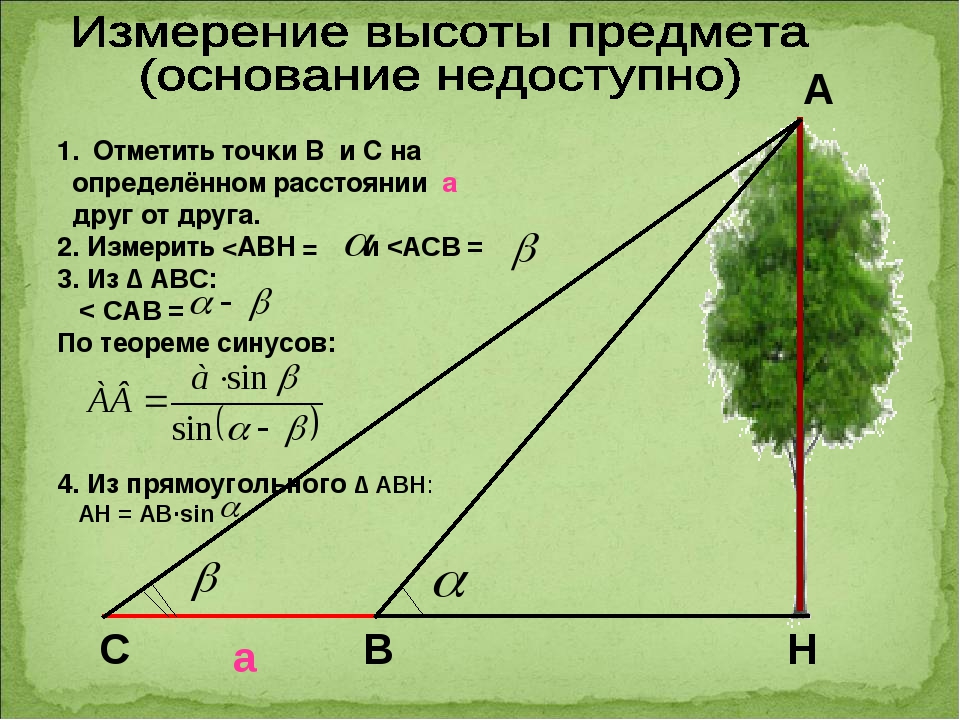

Как начертить прямой угол

Начертить прямой угол кажется простым, если под рукой есть технические приспособления. А если нет? Или вам необходимо построить прямой угол на большой площади, например, участке земли.И сколько существует способов построить прямой угол?Вам понадобится

Способ первый – с помощью линейки, карандаша и транспортира. Начертите с помощью линейки прямую. Отметьте на ней точку. Совместите точку с серединой транспортира. Найдите на шкале транспортира отметку 90о и обозначьте ее точкой. Проведите линию через две точки. Две прямые линии пересекаютсядруг с другом под прямым углом.

Способ второй – с помощью линейки-треугольника и карандаша. Один угол у треугольника прямой.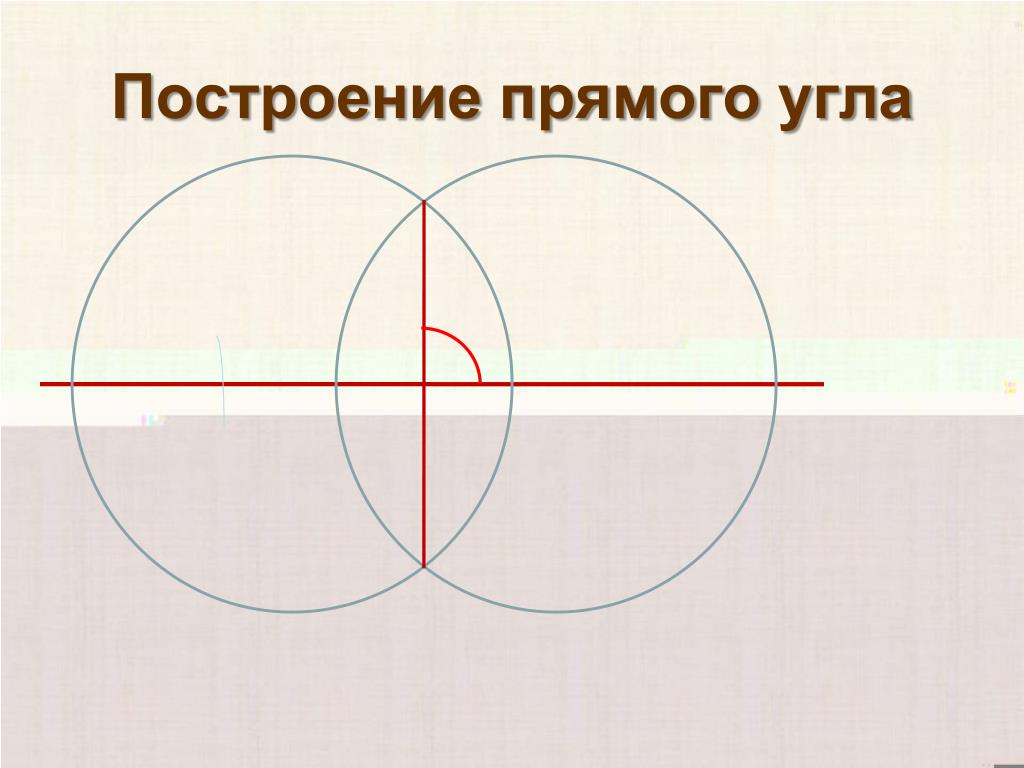 Приложите его одной стороной к линии, от которой необходимо построить прямой угол. По перпендикулярной стороне треугольника от линии начертите отрезок. Угол между отрезком и линией будет прямым. Или просто обведите прямой угол треугольника карандашом на бумаге.

Способ третий – с помощью прямоугольного предмета. Так же, как и чертежный треугольник, вы можете использовать любой предмет, углы которого прямые. Например,книгу, папку, коробку.

Способ четвертый – с помощью линейки и карандаша. Из точки А отложите два отрезка АВ и АС одной длины под острым углом друг к другу. Соедините их концы – у вас получится равнобедренный треугольник. Найдите середину его основания D и соедините с вершиной A. Отрезок АD является медианой, биссектрисой, высотой, т.е. перпендикулярен основанию ВС.

Способ пятый – с помощью линейки, карандаша и циркуля. В геометрии вписанный угол, опирающийся на диаметр – прямой. Начертите циркулем окружность. Проведите диаметр через ее центр. Отметьте произвольную точку на окружности и соедините ее сконцами диаметра отрезками. Угол, образованный отрезками – прямой.

Способ шестой — другой вариант построения прямого угла с помощью циркуля и линейки. Начертите две произвольных окружности так, чтобы они пересекались друг с другом в двух точках. Соедините эти точки отрезком RR’. Затем проведите через центры окружностей прямую. Отрезок и прямая пересекаются под углом 90о.

Способ седьмой – если вам надо построить перпендикуляр на вертикальной поверхности, например стене, воспользуйтесь отвесом. К одному концу веревки привяжите груз. Теперь, если вы держите за другой конец, веревка будет натянута под углом 90о к горизонтали. Приблизив отвес к стене, начертите вдоль веревки прямую линию. Угол между линией и полом будет прямым, если пол у вас горизонтален.

Способ восьмой – с помощью веревки с завязанными через 12 равных промежутков узелками и теоремы Пифагора. Этот способ использовали древние египтяне. Если натянуть эту веревку так, чтобы она образовала треугольник со сторонами в 3, 4 и 5 промежутков, угол напротив длинной стороны будет прямым.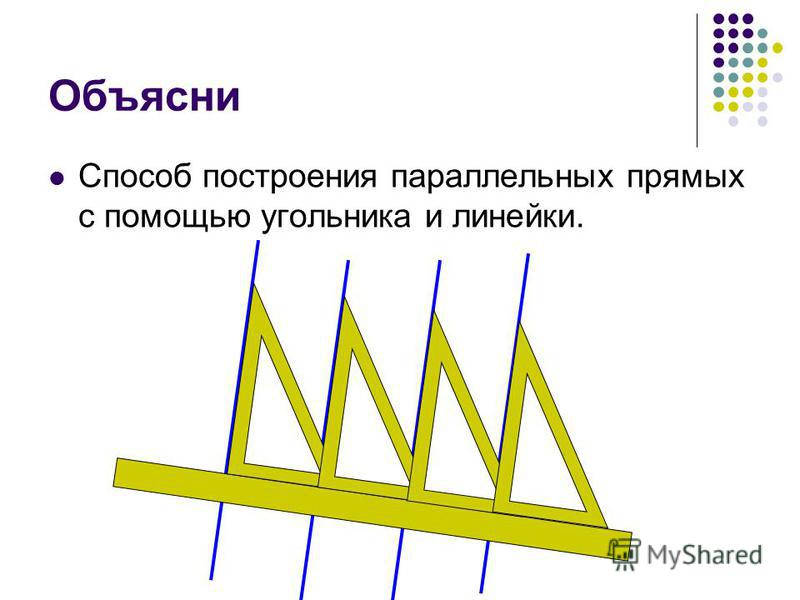 2. Значит, треугольник – прямоугольный.

«Строим углы без транспортира» (5 класс)

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа № 4

г.Нелидово Тверской области

Выполнила: ученица 5а класса

Генченкова Елизавета

Руководитель работы: Орлова Ольга Геннадьевна

2017 г.

Объект исследования:
углы с различными градусными мерами; инструменты для измерения углов.

Предмет исследования:
процесс построения углов без использования транспортира.
Гипотеза:
можно предположить, что существуют углы разных градусных мер, которые

можно построить без применения транспортира, а только пользуясь линейкой без мерных делений, клетчатой бумагой.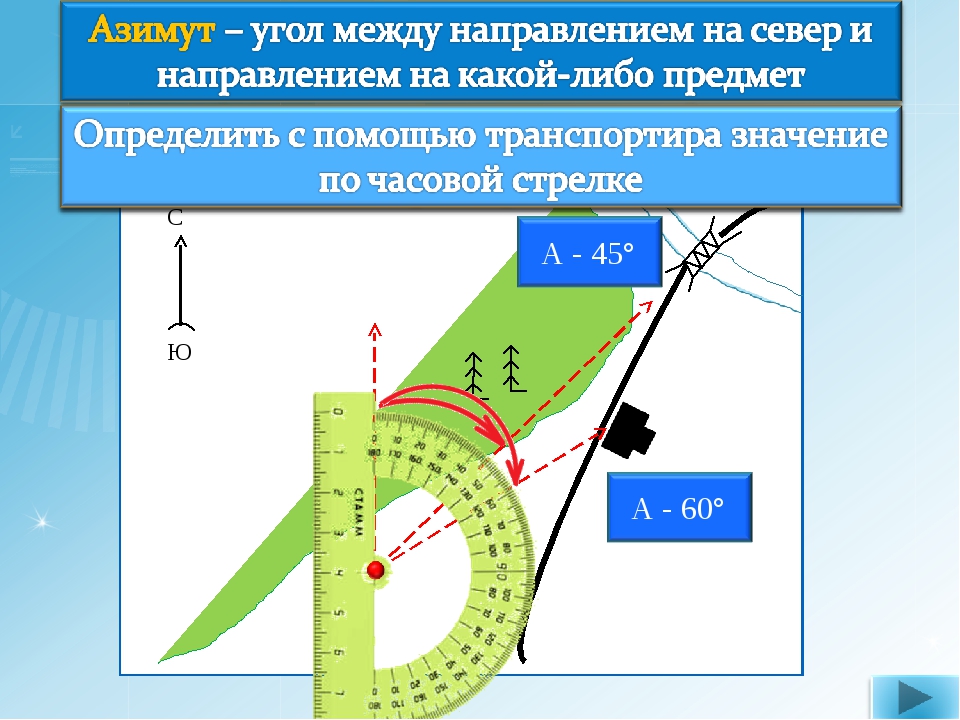

Методы исследования:
— поисковый метод с использованием научной и учебной литературы, а также поиск необходимой информации в сети Интернет;
— графическое моделирование, анализ и классификация полученных результатов.

Целью работы:
является знакомство с инструментами для измерения углов, исследование метода построения углов заданной градусной меры без использования транспортира.

Задачи:

1. Провести практическую работу по построению острых углов заданной градусной меры (от 10° до 80°, кратных 10) и выявлению «контрольных» точек – узлов для лучей каждого угла.

2. Проанализировать полученные результаты и систематизировать их

3. Определить группы задач, которые можно решить с помощью исследованного метода построения углов.

4. Сделать вывод о подтверждении или опровержении выдвинутой гипотезы.

Актуальность:

 в курсе геометрии при решении задач часто приходится строить иллюстративные чертежи различных фигур по заданному условию. Владение методом построения углов на клетчатой бумаге позволяет чертить заданные углы с достаточной точностью, не требует наличия транспортира и экономит время на выполнение чертежа.

Содержание:

1. Введение.

2. Построение углов: история и современность.

3. Практическая часть. Построение углов без помощи транспортира.

1) Построение угла 45° без помощи транспортира.

2) Построение острых углов с градусной мерой, кратной 10° без помощи транспортира.

3) Построение тупых углов с градусной мерой, кратной 10°, от 100° до 170°

без помощи транспортира.

4) Построение углов с помощью угольников.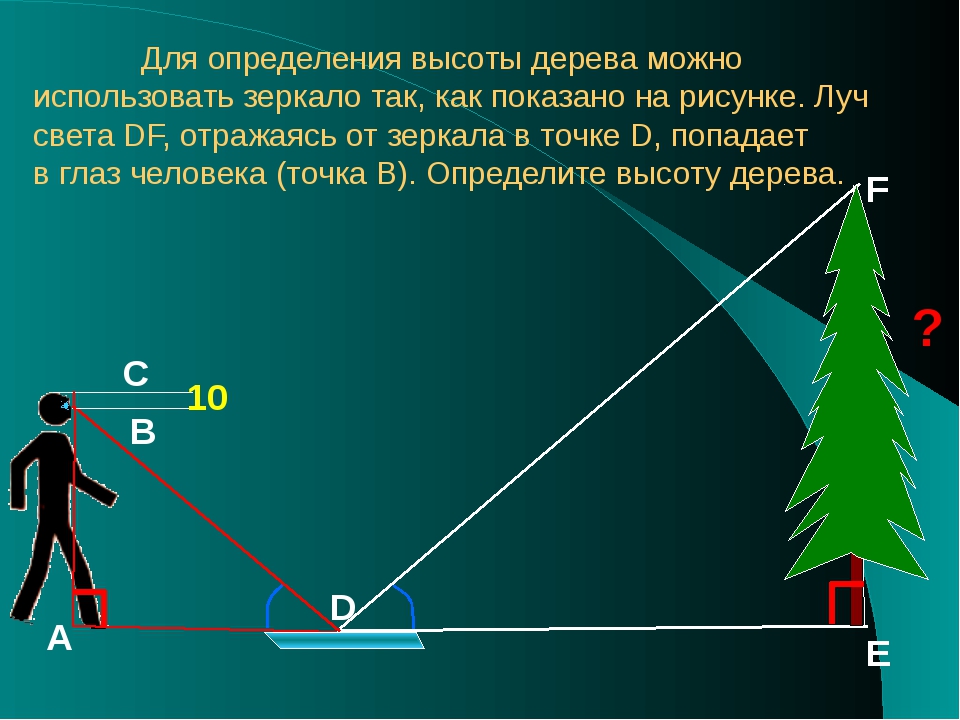

5) Построение углов 30°, 45°, 60°, 90° в практической жизни.

6) Измерение углов по пальцам рук.

4. Выводы и заключение.

5. Литература.

1.ВВЕДЕНИЕ

Увлечение отдельной областью математики часто начинается с размышления над какой-то особенно понравившейся задачей. При изучении в 5 классе на уроках математики темы «Построение угла заданной величины», мы научились строить углы с помощью транспортира.

И сразу обнаружили, что некоторые углы гораздо быстрее и более точно можно начертить в тетрадке с помощью одной только линейки.

Углы с градусными мерами 90° и 180° можно построить, проведя луч по горизонтальным или вертикальным линиям тетради, а углы в 135° и 45° — по диагоналям клеток.

Именно тогда я и заинтересовалась вопросом, а можно ли построить и другие углы, используя только клетчатую бумагу и линейку?

Так появилась моя исследовательская работа «Строим углов без транспортира».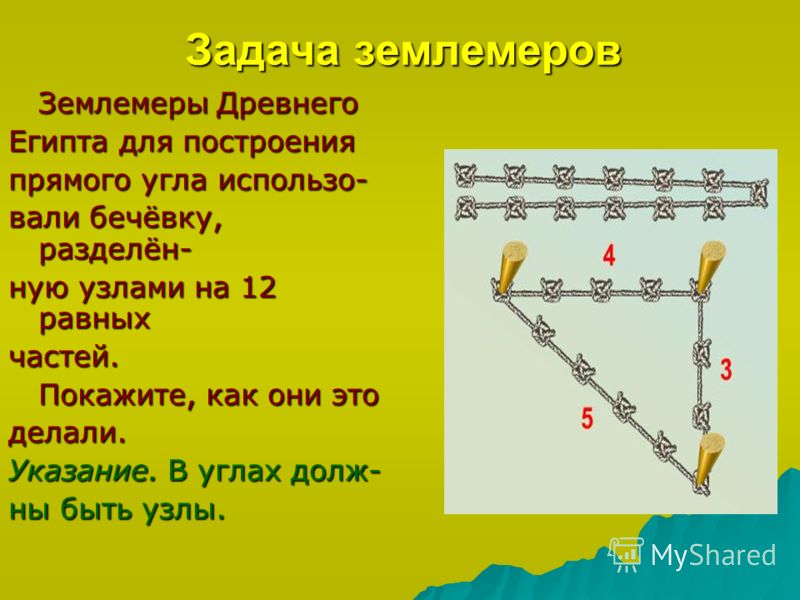

Казалось бы, что увлекательного можно найти на клетчатой плоскости, то есть, на листке бумаги, расчерченном на одинаковые квадратики?

Оказывается, задачи, связанные с бумагой в клеточку, достаточно разнообразны.

Своё исследование я решила начать с изучения ответа на вопрос, как решались задачи на построение углов, начиная с древних времен и до сегодняшнего времени.

2. ПОСТРОЕНИЕ УГЛОВ: ИСТОРИЯ И СОВРЕМЕННОСТЬ

Понятие градуса и появление первых инструментов для измерения углов связывают с развитием цивилизации в древнем Вавилоне, хотя само слово градус имеет латинское происхождение (градус–от лат. gradus- “шаг, ступень”). Градус получится, если, разделить окружность на 360 частей.

Возникает вопрос – а почему древние вавилоняне делили именно на 360 частей.

Дело в то, что в Вавилоне была принята шестидесятиричная система счисления. Более того, число 60 считалось священным. Поэтому все вычисления были связаны с числом 60.

История не сохранила имя ученого, который изобрел транспортир – возможно в древности этот инструмент имел совсем другое название.

Современное название происходит от французского слова ”ТRANSPORTER”, что означает “переносить”.

Первые задачи на построение углов возникли в глубокой древности. Возникли они из хозяйственных потребностей человека. Уже древними архитекторами и землемерами приходилось решать простейшие задачи на построение, связанные с их профессией.

Первые греческие ученые, которые занимались решением геометрических задач на

построение, были: Фалес Милетский (624 – 547 гг. до н.э.), Пифагор (ок. 580 – 500 гг. до н.э.), Платон (427 – 347 гг. до н.э.).

Самые первые задачи на построение, по-видимому, решались непосредственно на

местности и заключались в проведении прямых линий и построения прямого угла.

К задачам на построение прибегали древние инженеры, когда составляли рабочий чертеж того или иного сооружения и решали вопросы, связанные с отысканием красивых геометрических форм сооружения и его наибольшей вместимости.

Задачи на построение помогали людям в их хозяйственной жизни, их решения формулировались в виде ‘практических правил», исходя из наглядных соображений.

Именно эти задачи и были основой возникновения наглядной геометрии, нашедшей довольно широкое развитие у древних народов Египта, Вавилона, Индии и др.

Платон и его ученики считали построение геометрическим, если оно выполнилось при помощи циркуля и линейки, то есть путем проведения окружностей и прямых линий. Если же в процессе построения использовались другие чертежные инструменты, например транспортир, то построение не считалось геометрическим.

Древние греки вслед за Платоном стремились к геометрическим построениям и считали их идеалом в геометрии.

Но древние ученые производили измерения не только транспортиром – ведь этот

инструмент был неудобен для измерений на местности и решения задач прикладного

характера. А именно прикладные задачи и являлись главным предметом интереса древних геометров.

Изобретение первого инструмента, позволяющего измерять углы на местности,

связывают с именем древнегреческого ученого Герона Александрийского (I в. до н.э). Он описал инструмент “диоптр”, позволяющий измерять углы на местности и решать множество прикладных задач.

Но прогресс не стоит на месте и в ХVII веке был изобретен прибор нивелир, а в следующем веке английским механиком Джессе Рамсденом был изобретен другой прибор – теодолит.

теодолит

Сегодня теодолит – сложный прибор. Многие работы (в том числе и строительство) требуют предварительной консультации геодезистов измерений с помощью теодолита.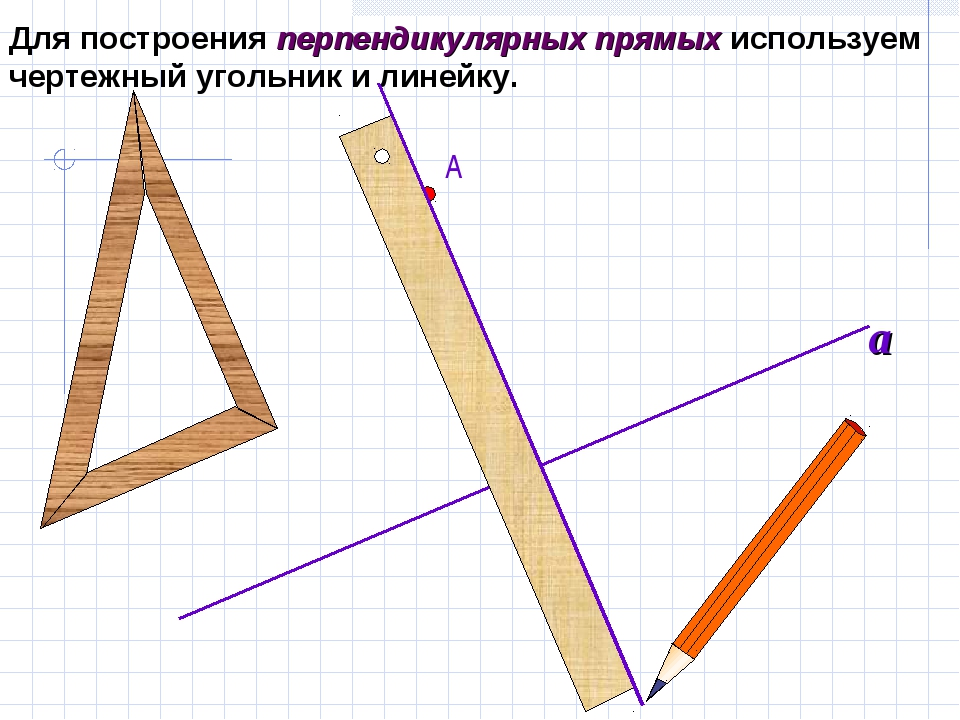

Однако усовершенствование инструментов для измерения углов связано не только с

проведением строительных работ. С древнейших времен люди путешествовали, познавая окружающий мир. Путешественниками необходимо было уметь ориентироваться в пространстве. На долгие века основным ориентиром путешественников стали звезды.

Появился первый инструмент путешественников – астролябия. Астролябия(греч. astrolabion, от astron — «звезда» и labe – “схватывание»; лат. astrolabium) — угломерный прибор, служивший до начала XVIII в. для определения положений светил на небе.

Секстант — это наиболее совершенный прибор для измерения угловых координат небесных тел того времени. Его изобретение приписывается Исааку Ньютону. Секстант позволял измерять как широту, так и долготу точки наблюдения, причем с довольно высокой точностью.

В настоящее время широко используются современные приборы для измерения углов на местности.

Геодезический инструмент для измерения углов при съёмках на местности, специальный вид компаса- буссоль.

Простейший геодезический инструмент, служащий для измерения углов наклона местности с точностью до десятых долей градуса- эклиметр.

Необычный объект, который мы можем наблюдать на фото, был найден в гробнице древнеегипетского архитектора Ха (Kha). Без малого столетие прошло с тех пор, как историки впервые задались вопросом о предназначении странного артефакта.

Недавно предположение о возможном способе использования объекта выдвинула ученая-физик. Гипотеза, предложенная Амелией Спаравигной (Amelia Sparavigna) из Туринского политехнического университета (Turin Polytechnic), базируется на числовых отметках, якобы присутствующих на поверхности артефакта.

Архитектор Ха известен тем, что во времена 18-той династии (приблизительно 1400 год до нашей эры) он был задействован в строительстве гробницы фараона. Собственную же усыпальницу Ха нашли 1906 году неподалеку от Долины Царей — это открытие принадлежит археологу Эрнесто Скьяпарелли (Ernesto Schiaparelli). Среди вещей, когда-то принадлежащих архитектору, удалось идентифицировать измерительные пруты длиной в локоть (45 см), инструмент, напоминающий современный угольник, а также неизвестное полое деревянное орудие. По мнению Скьяпарелли, это был инструмент для выставления уровня.

Детально осмотрев старую находку, Амелия Спаравигна пришла к выводу, что на самом деле этот последний объект служил в качестве транспортира — в пользу такой версии свидетельствуют 16 лепестков, расположенных по окружности и находящихся на равном расстоянии друг от друга. Эти лепестки окружены круглым узором, имеющим 36 углов. Очевидно, продолговатая ровная часть инструмента устанавливалась на поверхность, после чего, с помощью уровня, можно было определить угол наклона того или иного объекта.

Числа, присутствующие на находке, якобы соответствовали двум измерительным системам, применявшимся в древнем Египте. Первая, внутренняя часть узора, соответствует шестнадцатичной счетной системе (соответствует современной десятичной). Вторая отображает 36 созвездий, известных египтянам.

Современные угломеры

Транспорти́р (фр. transporteur, от лат. transporto «переношу») — инструмент для построения и измерения углов. Транспортир состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы), разделённого на градусы от 0 до 180°. В некоторых моделях — от 0 до 360°.

Разновидности транспортиров

• Полукруговые (180 градусов) — наиболее простые и древние транспортиры.

• Круговые (360 градусов).

• Геодезические, которые бывают двух типов: ТГ-А — для построения и измерения углов на планах и картах; ТГ-Б — для нанесения точек на чертежной основе по известным углам и расстояниям. Цена деления угломерной шкалы — 0,5°, прямолинейной — 1 миллиметр.

• Улучшенные типы транспортиров, которые необходимы для более точных построений и измерений. Например, существуют специальные транспортиры с прозрачной линейкой с угломерным нониусом, которая вращается вокруг центра.

Транспортиры изготавливаются из стали, пластмассы, дерева и других материалов. Точность транспортира прямо пропорциональна его размеру (чем больше транспортир, тем меньше цена одного деления).

Полукруговой транспортир Круговой транспортир Геодезический транспортир

Угломер электронный Угломер строительный

Угломер Чижевского представлял собой треногу, на которой крепился круг с делениями, на его оси — подвижная алидада с указателем и визирная трубка на ней. Был еще и компас для ориентирования прибора. Измерив угловые расстояния между своей батареей и целью, командир производит геометрические расчеты и передает необходимые данные по телефону или через связных на свою батарею. Используя их, обученные наводчики направляют орудия на цель. Во время стрельбы командир батареи с помощью бинокля корректирует точность попадания снарядов в цель. Новый способ стрельбы с закрытых позиций давал возможность нанести удар по врагу не одним выстрелом из одного орудия, а со всех орудий разом широким фронтом огня – веером, сохранив при этом людей и технику.

Вот такая история возникновения различных приборов для измерения углов не только на чертежах, но и на любой местности, включая даже небесное пространство!

Таким образом, я выяснила, что на современном этапе существует множество приборов, позволяющих измерять и строить углы с различной степенью точности, которые применяются людьми самых разнообразных профессий, а при изучении курса геометрии в школе для построения углов заданной градусной меры в основном используется циркуль, линейка и транспортир.

3.ПРАКТИЧЕСКАЯ ЧАСТЬ.

1)Построение угла 45° без помощи транспортира.

Угол 45 градусов в геометрии встречается часто.

Рассмотрим, как легко можно построить угол 45 градусов без транспортира, пользуясь только линейкой, карандашом и клеточками тетради.

Легче всего строить прямой угол.

 

Для этого из одной точки по клеточкам строим горизонтальный и вертикальный лучи. 

Градусная мера прямого угла — 90 градусов. 45 градусов — половина от 90º. Значит, чтобы построить угол 45 градусов, нужно взять половину прямого угла.

Сделать это очень легко. Выбираем вершину угла на пересечении клеточек. Одну сторону угла, например, горизонтальный луч, проводим с помощью линейки по клеточкам. Для построения второй стороны угла 45º каждую клеточку делим по диагонали (отмечаем несколько точек):

Затем с помощью линейки и карандаша через эти точки проводим второй луч. Получили угол 45 градусов:

2)Построение острых углов с градусной мерой, кратной 10° без помощи транспортира.

Для проведения исследования я на листке клетчатой бумаги построила острые углы,

начиная от 10° до 80°, с интервалом в 10°. Центр угла был расположен в узле клеток. Один из лучей, образующих угол, провела горизонтально слева направо.

Далее с помощью транспортира начертила лучи для всех исследуемых углов.

Если второй луч проходил точно через узел клеток, то информацию об этом угле заносила в таблицу.

Положение «контрольного» узла относительно вершины данного угла отмечалось следующим образом: сначала указывалось количество целых клеток вверх, затем вправо.

В результате получилась такая таблица:

Проанализировав данные таблицы для построения углов, можно заметить, что для углов

от 20° до 70° количество клеток вверх на единицу превышает количество десятков в

градусной мере угла. Причем сумма клеток вверх и вправо для всех этих углов равна 11.

Если прибавить к числу десятков искомого угла единицу, то получим количество клеток по вертикали. Если это число отнять от 11, то получим количество клеток по горизонтали от вершины угла.»

Например, для построения угла в 70° нужно отступить 8 (7+1) клеток по вертикали и 3(11-8) клетки по горизонтали в сторону первого луча.

Анализ данных в полученной таблице еще раз убеждает нас в существовании красоты, закона симметрии и порядка в науке математике.

3)Построение тупых углов с градусной мерой, кратной 10°, от 100° до 170° без помощи транспортира.

Исследованный метод построения углов позволяет решать следующую геометрическую задачу: построение тупых углов от 100° до 170° с шагом в 10°.

Смежные углы имеют общий луч. Поэтому для построения тупых углов можно

пользоваться «контрольной» точкой смежного ему острого угла из таблицы. Только

отсчет клеток по горизонтали выбирается в противоположном горизонтальному лучу

направлении (в нашем случае влево).

4)Построение углов с помощью угольников.

Я исследовала чертёжные инструменты – угольники.

Угольник — линейка в форме прямоугольного треугольника, как правило, с миллиметровой шкалой и с пустотой в форме уменьшенного подобного треугольника внутри.

Наиболее распространены угольники двух видов: с острыми углами по 30 и 60 градусов и равнобедренными с одинаковыми острыми углами по 45 градусов. Угольники используются в черчении для построения некоторых углов без помощи транспортира.

При использовании двух угольников можно построить больший набор углов, прикладывая их друг к другу, например, угол в 75 градусов (30+45), 120 градусов (90+30) и т.д. Покажу, как это сделать…

Понадобятся два вида угольников: первый с углами по 45 градусов, а второй — по 30 и 60.
1)75 градусов можно построить следующим образом: сначала построить угол в 30, а затем от него отложить 45 градусов.

2) 135 градусов: построить прямой угол, затем от него отложить 45 градусов.
3) 25 градусов: построить угол в 60 градусов,  затем от луча внутри угла отложить 45 градусов.

С помощью угольников можно построить углы 105◦, 15◦ и другие.

105= 60+45, 15=60-45 и так далее.

5)Построение углов 30°, 45°, 60°, 90° в практической жизни.

Часто домашнему мастеру необходимо срочно произвести какое либо измерение или сделать разметку под определенным углом, а под рукой нет либо угольника, либо транспортира. В этом случае его выручат несколько простых правил.

Угол 90 градусов.

Если нужно срочно построить прямой угол, а угольника нет, можно воспользоваться любым печатным изданием. Угол бумажного листа — очень точный прямой угол (90 град. ). Резательные (вырубочные) машины в типографиях настроены очень точно. Иначе исходный рулон бумаги начнет резаться вкривь и вкось. Поэтому вы можете быть уверены, что этот угол — именно прямой.

А если нет даже печатного издания или необходимо построить угол на местности, например при разметке фундамента или листа фанеры с неровными краями? В этом случае нам поможет правило золотого (или египетского) треугольника.

Золотым (или египетским, или Пифагоровым) треугольником называется треугольник со сторонами, которые соотносятся друг с другом как 5:4:3. По теореме Пифагора, у прямоугольного треугольника квадрат гипотенузы равен сумме квадратов катетов. Т.е. 5х5 = 4х4 + 3х3. 25=16+9 и это неоспоримо.

Поэтому для построения прямого угла достаточно на заготовке провести прямую линию длиной 5 (10,15,20 и т.д. кратной 5 см). А затем, из краев этой линии начать отмерять с одной стороны 4 (8,12,16 и т.д кратно 4 см), а с другой — 3 (6,9,12,15 и т.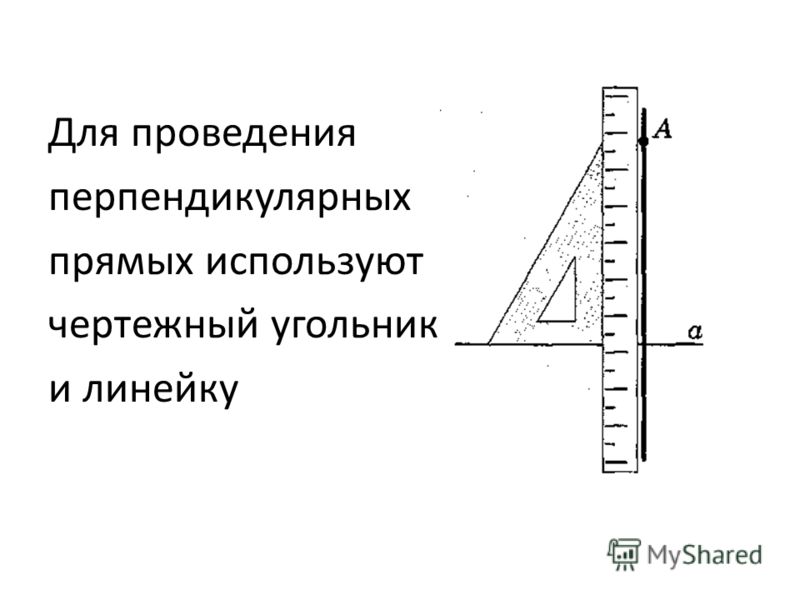 д. кратно 3 см) расстояния. Должны получиться дуги с радиусом 4 и 3 см. Где эти дуги пересекутся между собой и будет прямой (90 градусов) угол.

Угол 45 градусов.

Такие углы обычно применяют при изготовлении прямоугольных рамок. Материал из которого делается рамка (багет) пилится под углом 45 градусов и стыкуется. Если под рукой нет стусла или транспортира, получить шаблон угла в 45 градусов можно следующим образом. Необходимо взять лист писчей бумаги или любого печатного издания и согнуть его так, что бы линия сгиба проходила точно через угол, а края загнутого листа совпадали. Получившийся угол и будет равен 45 градусам.

Угол 30 и 60 градусов.

Угол в 60 градусов требуется для построения равносторонних треугольников. Например, вам надо напилить такие треугольники для декоративных работ или точно установить силовой укос. Угол в 30 градусов редко применяется в чистом виде. Однако с его помощью (и с помощью угла в 90 градусов) строится угол 120 градусов. А это угол, необходимый для построения равносторонних шестиугольников, фигуры весьма популярной у столяров.

Для построения весьма точного шаблона этих углов в любой момент необходимо запомнить константу (число) 173. Они вытекает из соотношений синусов и косинусов этих углов.

Возьмите лист бумаги из любого печатного издания. Его угол равен точно 90 градусам. От угла по одной стороне отмерьте 100 мм (10 см.), а по другой — 173 мм (17,3 см). Соедините эти точки. Таким образом мы и получили шаблон, у которого один угол 90 градусов, один 30 градусов и один 60 градусов. Можете проверить на транспортире — все точно!

Запомните это число — 173, и вы всегда сможете построить углы в 30 и 60 градусов.

6)Измерение углов по пальцам рук.

Итак, смотрим на свою руку, которая есть у каждого человека. Уточнение! — левша должен снимать показания углов с правой руки, а правша с левой. Причина проста — приоритет действующей руки со временем деформирует кости, суставы и сильнее растягивает мышцы. Поэтому у правшей левая рука менее деформирована и разработана, а у левшей наоборот.

Теперь растопыриваем в стороны пальцы, как только можете за счет усилия только руки, ничем их раздвигать не нужно — только максимальное мышечное усилие. Богом так заложено у человека и это правда, что у здорового человека с нормальной рукой растопыренные пальцы — это полноценно действующий и относительно точный транспортир.

Угол между большим и безымянным пальцами равен 90 гр.

Угол между большим и указательным пальцами равен 45 гр.

Угол между безымянным и средним пальцами равен 22.5 гр.

Угол между безымянным и мизинцем равен 15 гр. — солнечному часу.

4.ВЫВОДЫ И ЗАКЛЮЧЕНИЕ.

Своей исследовательской работой мне хотелось бы доказать, что построение углов очень интересное и познавательное занятие, совсем не сложное и трудоемкое, как может показаться на первый взгляд.

Поработав с материалом и подготовив его к применению на практике, я сделала

следующие выводы:

1. Обычный лист бумаги в клетку может выполнять функцию своеобразного инструмента для построения углов.

2. Угольники можно использовать для построения некоторых углов без использования транспортира.

Таким образом, методы построения углов без помощи транспортира актуальны для школьников, так как большинство задач оформляется на листке тетради в клетку и большинство задач в учебнике геометрии связано с построением фигур с углами, градусная мера которых кратна10°.

5 ЛИТЕРАТУРА.

1. В.В. Вавилов, А.В. Устинов. Задачи на клетчатой бумаге. – М.: Школа им. А.Н.

Колмогорова, 2006. – 183 с

2. Ганьшин В.Н. Простейшие измерения на местности. 3-е изд., перераб. и доп., М.,

Недра, 1983, 108 с., ил.

3.Смирнов В.А, Смирнова И.М. Геометрия на клетчатой бумаге. М., МЦНМО, 2009

4. Большая советская энциклопедия

5. ГОСТ 13494-80. Транспортиры геодезические. Технические условия (с Изменениями N 1-4).

6. Большой энциклопедический политехнический словарь 2004

Список интернет-ресурсов:

http://allencyclopedia.ru/17254 Большая Советская энциклопедия/ Геодезические

инструменты

http://journal.kuzspa.ru/articles/95/ -Электронный научный журнал «Информационно-

коммуникационные технологии в педагогическом образовании»

http://sm-shihova.ucoz.ru/Komu_interesno/Komuinteresno_6.pdf — Математика, 5-6: книга для учителя Автор/создатель: Суворова С.Б., Кузнецова Л.В., Минаева С.С., Рослова Л.О.

http://enc-dic.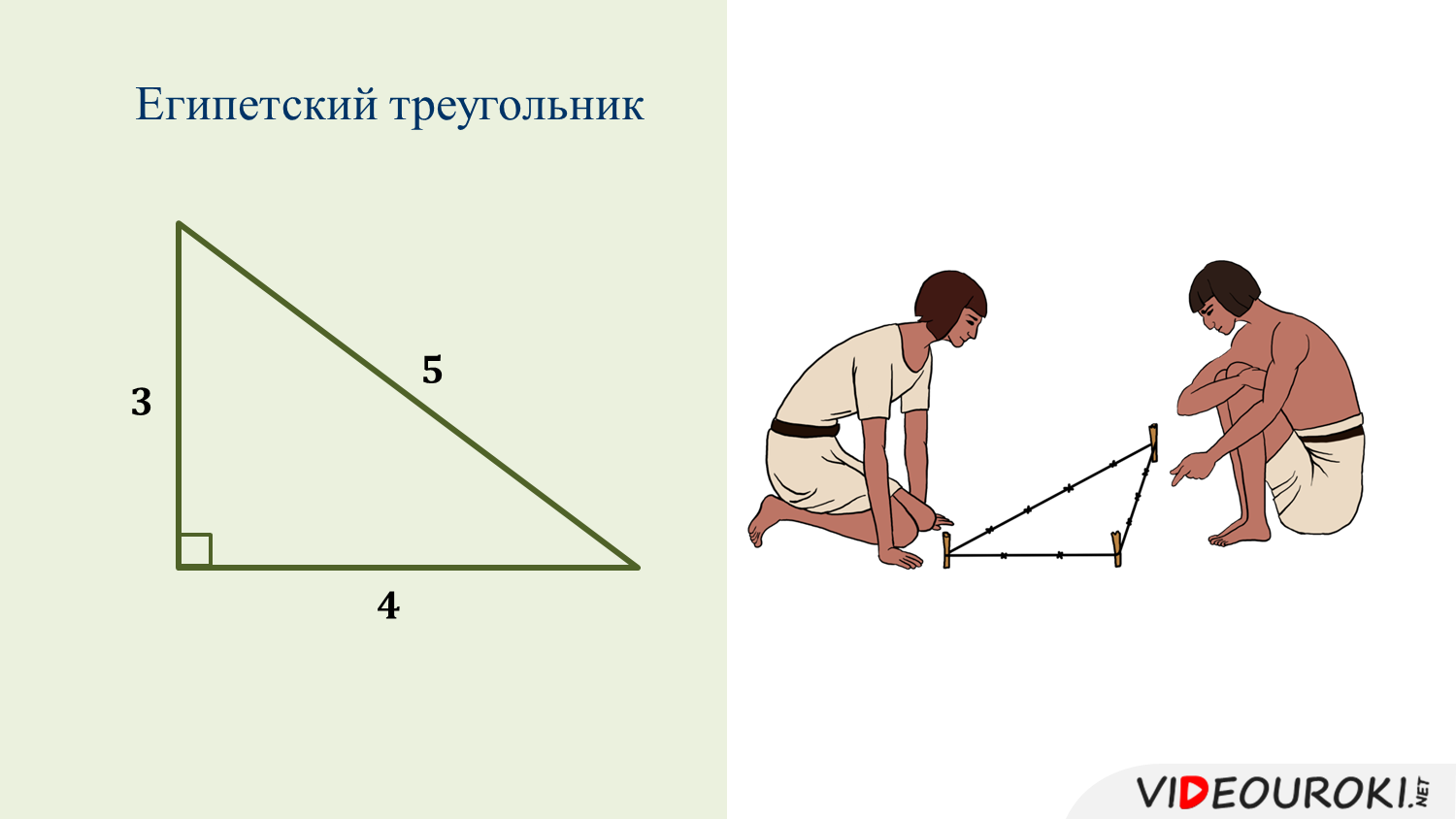 com/word/t/Transportir-4655.html [энциклопедии и словари]

http://www.gs-market.ru/index.php?show_aux_page=70 [угломеры электронный, строительный]

http://znaika.ru/catalog/5-klass/matematika/Izmerenie-uglov.-Transportir. [история возникновения приборов измерения углов]

http://virtoo.ru/almanach/nepoznannoe/pervyj-v-mire-transportir-izobreli-eg.html [первый в мире транспортир изобрели египтяне]

http://www.vest-news.ru/article.php?id=18508 [угломер Чижевского Л.В.]
http://astro.uni-altai.ru/picture/src/0+1066279852/ [средневековые угломерные инструменты]

.

Феномен прямого угла и прямоугольности в геодезии Текст научной статьи по специальности «Биологические науки»

УДК 528 (091)

528 (092)

Г. Н. Тетерин, М.Л. Синянская СГГ А, Новосибирск

ФЕНОМЕН ПРЯМОГО УГЛА И ПРЯМОУГОЛЬНОСТИ В ГЕОДЕЗИИ

В статье рассматриваются роль и значение прямого угла и свойства прямоугольности в теории и практике геодезии, формирование и развитие геодезической технологии. Отмечается их историческая значимость.

G.N. Teterin, M.L. Sinyanskaya SSGA, Novosibirsk

THE PHENOMENON OF RIGHT ANGLE AND SQUARENESS IN GEODESY

The role and the significance of the right angle, the properties of the squareness in the theory and practice of geodesy as well as the formation and development of the geodetic technology are considered. Their historic significance is stated.

Около 10 тысячелетий назад человек перешел в строительстве жилищ от круглой формы к прямоугольной.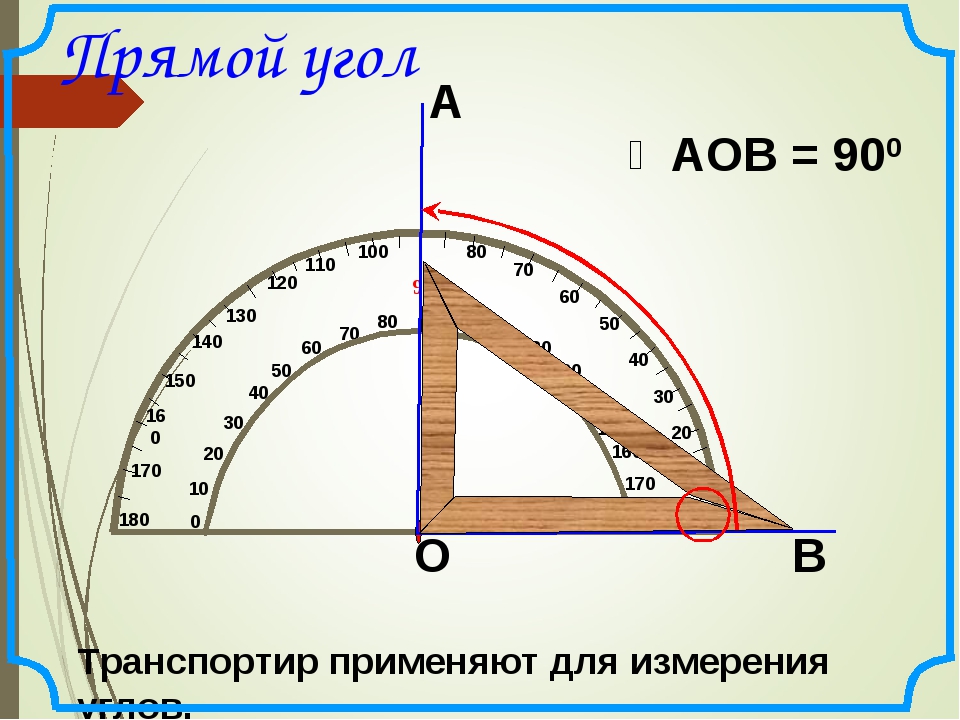 Примерно в это же время (или чуть позднее) начали делить земельные угодья прямыми линиями с прямым углом между ними. Много ранее прямой угол люди стали использовать в организации окружающего пространства и ориентировке в нем. Все это возможно предопределило некую заданность развития геометрического и геодезического знания.

По крайней мере, это правомерно поскольку геодезия характеризуется как система знаний о геометрических построениях на земной поверхности.

Объяснение феномена раннего появления и использования прямого угла в деятельности людей лежит в сфере влияния внешней среды.

Это влияние в работе [1] выражено и сформировано в виде принципов влияния: принцип «Вертикаль-горизонталь» (ПВГ) и «Принцип четырех направлений» (П4Н). Они оказывали фундаментальное влияние на развитие геодезии в течение всей ее истории. Главной характеристикой и составной частью этих принципов является прямой угол.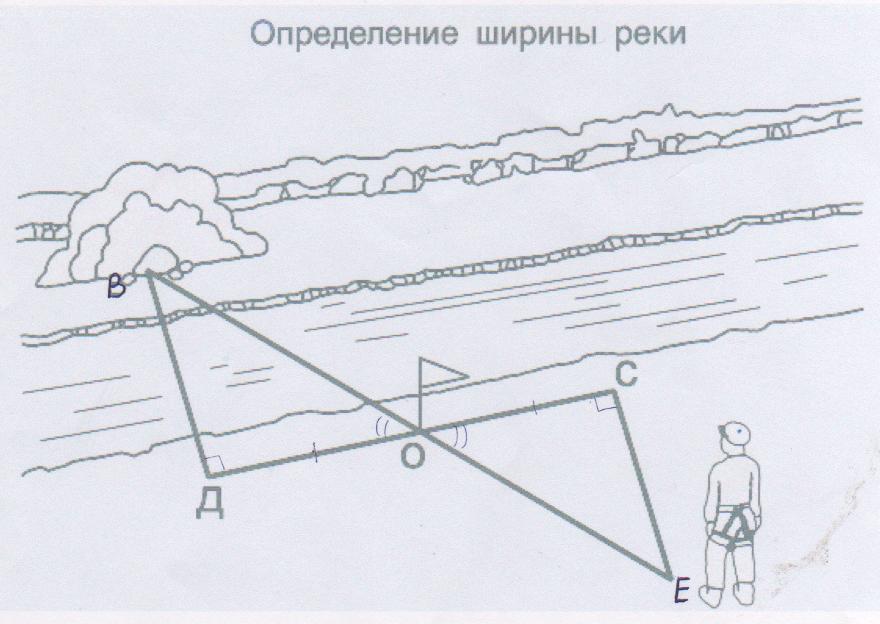

Этот угол стал важнейшей характеристикой всей окружающей среды и всего пространства, как и два геометрических свойства —

перпендикулярность и параллельность. Но наиболее наглядно эти геометрические свойства выражены в фигуре человека.

В геометрии фигуры человека вполне четко и очевидно заложено шесть главных направлений, представленных стрелками на рис. 1. Ими в человека заложена пространственная система координат. Эта «система координат», заложенная в человека внешней средой («принципы влияния») и вся встроенная в него система прямых углов (условий перпендикулярности и параллельности) позволяет человеку не только отлично «строить» систему

ориентации в пространстве, но и «строить» простейшие геометрические фигуры на земле.

▲

Рис.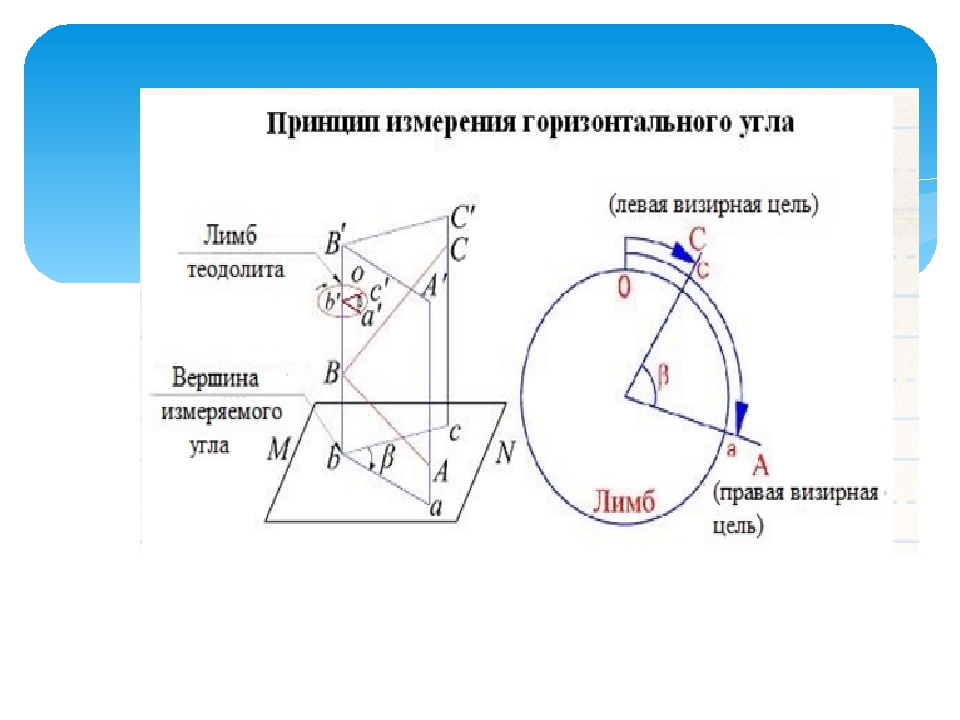 1. Геометрия фигуры человека

Роль прямого угла в жизни человека, общества, цивилизации огромна. Это предопределено всей физиологией человека, которая подчинена и устроена с учетом прямого угла. Все подвижные части человека в суставах имеют пределы движений в диапазоне одного или двух прямых углов. Вертикаль человека перпендикулярна разрезу глаз и линии плеч. Вся «геометрия» человека подчинена условиям перпендикулярности и параллельности — основному геометрическому свойству окружающего пространства. Эти соответствующие геометрические свойства человека определялись как основа гармонии, красоты, как основной закон и фундамент мироздания.

Как только человек начал создавать сложные механические системы (охотничий лук) и организовывать окружающее пространство, так прямой угол стал в некотором роде их сердцевиной. Первые отрасли (строительство и земледелие) в хозяйственной деятельности людей формировались изначально на использовании прямого угла.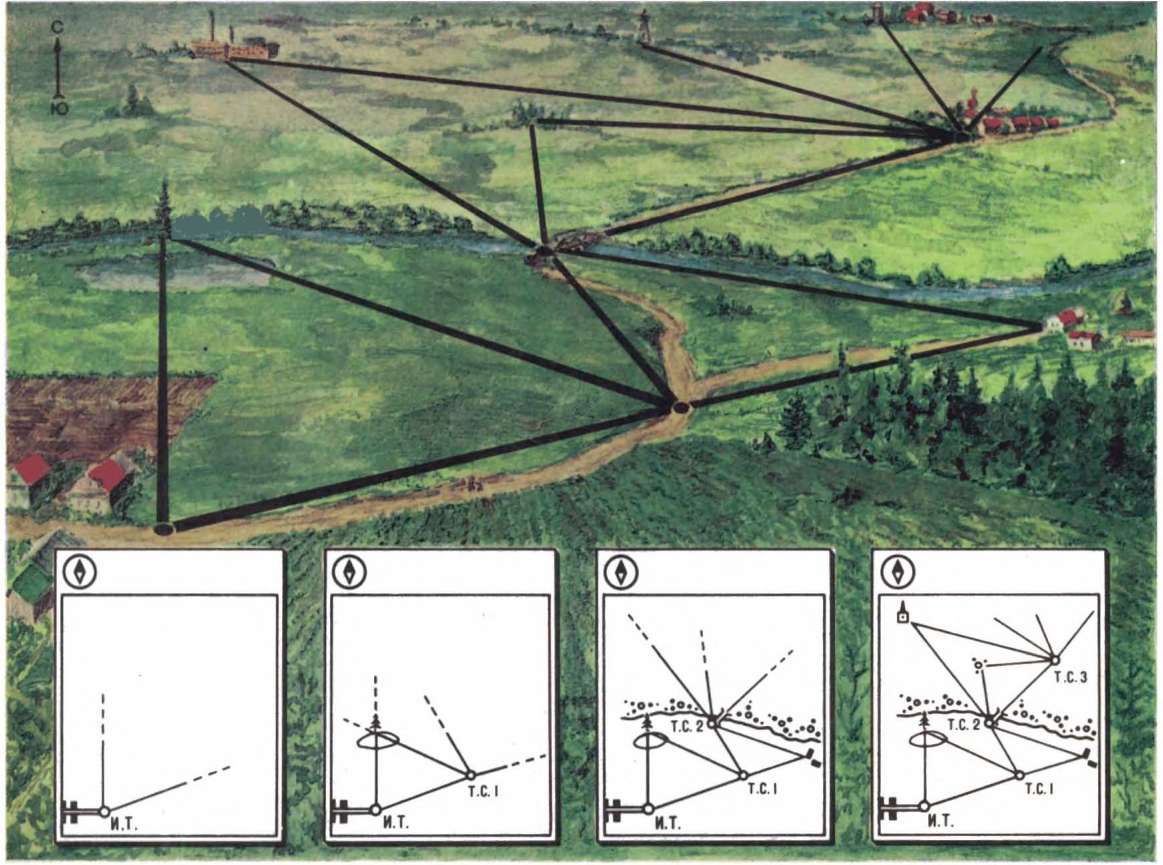 Вся искусственная, вторичная среда, созданная человеком, прямоугольна — прямолинейна, с соблюдением в ней условий параллельности и перпендикулярности. Реализация этих геометрических условий была возложена на человека.

В земледелии, в его организации (землеустройстве) геометрическую основу составляет межевание. В этой основе геометрический каркас создают прямые линии, прямые углы, соответствующие фигуры в виде квадрата и прямоугольника [1]. Правильная (геометрическая) система межевания земельных угодий берет свое начало в 3-ем тысячелетии до н.э. Но попытки деления угодий прямыми линиями на прямоугольные четырехугольники были много ранее- возможно в 5-6 тысячелетиях до н.э. Еще до изобретения специальных средств измерений (мерной веревки, землемерного креста)

человек мог построить на местности простейший квадрат, обходясь тем, «чем бог послал» ему в его фигуре [3].

В первых геометрических построениях на земле, которые необходимы были человеку и в которых прямой угол был важнейшей составляющей, реализация их происходила исходя из принципа «самодостаточности».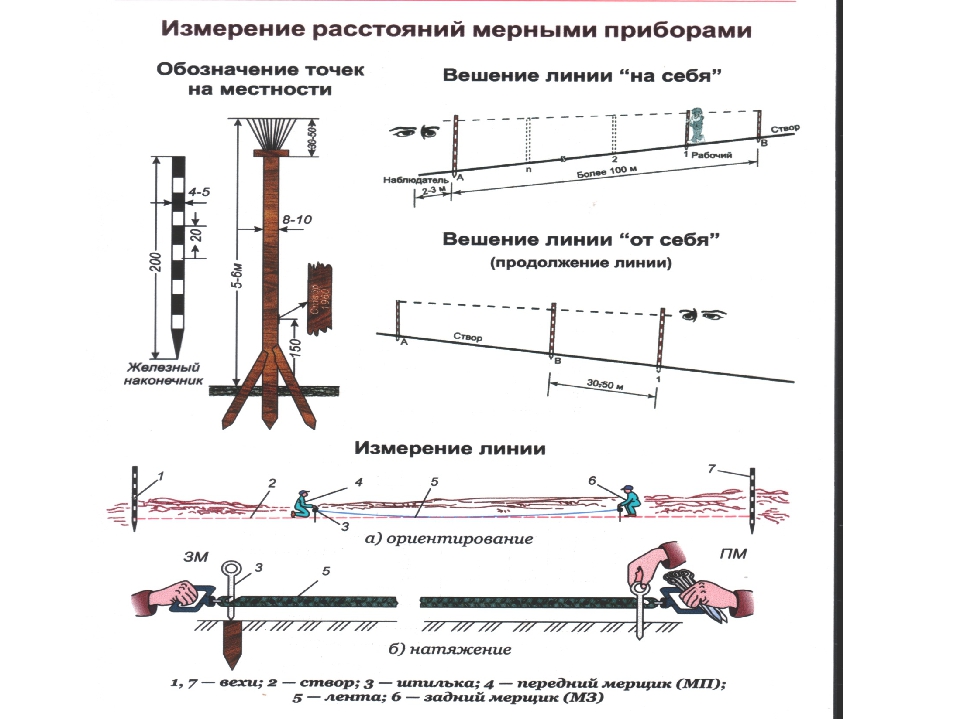 Действительно, «выстроив» свое тело, его «геометрию» в нужном варианте (прямой взгляд, вытянутые в сторону руки) и продолжив линии рук и взгляда в пространстве и отметив эти линии на земле вешками (колышками), получали прямой угол в пространстве [3]. Естественно, его вершина находилась в точке стояния человека.

Далее нетрудно перейти к построению простейших фигур: квадрата, прямоугольного четырехугольника и треугольника путем отложения по полученным направлениям заданных отрезков с использованием пошаговой меры. Построение таких фигур при размежевании земель показано в работах [1,2,3]. Реализацию «геометрии» в строительстве и межевании осуществляли геодезисты, землемеры. Потребовалось создание соответствующих геометрических геодезических инструментов: мерной веревки, землемерного креста, ватерпаса, хорабаты и т.д. Геометрия в жизни человека есть условие его существования и процветания. Реализацию этого «геометрического» миропорядка осуществлял, в какой-то мере, только геодезист, в разные исторические времена носивший разные наименования, в том числе и геометра. В результате и была создана соответствующая технология. С глубокой древности в геодезии сформировалась прямоугольно-

прямолинейная технология [2], использовавшаяся в земледелии, строительстве и военном деле в течение почти пяти тысячелетий. В основе этой технологии было построение на местности прямых углов и прямых линий.

Геодезия в своей деятельности, связанной с геометрией объектов и явлений окружающего пространства, реализует указанные два «принципа влияния»- ПВГ и П4Н [1].

В геодезических инструментах и системах, с помощью которых осуществляется измерение и построение линий и поверхностей в

пространстве, в качестве их частей имеются линии (оси) и плоскости, во взаимном положении которых заложено важнейшее требование перпендикулярности и параллельности. Выполнение этого условия осуществляется с помощью поверок. Основные поверки представляют собою поверки прямого угла: поверки уровня, поверки перпендикулярности осей и плоскостей. Эти поверки характерны не только для современных

геодезических приборов, но еще в большей степени для инструментов

древнего и нового времени. Качество и точность приборов определялась степенью соблюдения при их создании основных геометрических требований. Точность измерений, по крайней мере, в древние времена зависела от точности построения и измерения прямых углов и линий на местности.

Второй важнейшей функцией прямого угла в геодезии, были системы координат, которые во все времена были прямоугольными. В измерении и моделировании пространства необходимым условием является ориентировка в нем. Поэтому, как правило, определяется главная ориентирующая линия в пространстве (на местности или модели), которая затем определяется как одна из осей координат (см. П4Н). К ней под прямым углом проводится вторая ось. Этим обеспечивается возможность координатизации окружающего пространства (в плоскости). Для трехмерного пространства ориентируется уже две оси (или плоскости), на базе которых строится пространственная система координат.

В координатизации окружающего пространства и угловых измерениях роль прямого угла, как важнейшая составная часть сохраняется, поскольку эти измерения выполняются в пределах одного, двух — четырех прямых углов (для широт, долгот с добавлением соответственно северная или южная, восточная или западная).

На протяжении многих столетий использовалось понятие румба -угловая величина, определявшаяся в пределах прямого угла (какой-либо четверти круга). Столь же велика роль прямого угла в моделировании, контроле объектов и явлений окружающего пространства.

В инженерной геодезии при возведении сооружений и контроле их геометрии важнейшее значение имеют условия перпендикулярности и параллельности. Эти два важнейших свойства окружающего пространства есть свойство прямого угла (или двух прямых). Формировавшаяся или формируемая геодезическая технология в существенной части предопределяла возможность реализации этих геометрических требований.

Пока прямой угол остается некой «нормой» окружающей среды, пока сохраняется «геометрия» человека, до тех пор рассмотренное значение прямого угла в геодезии будет сохраняться.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Тетерин, Г.Н. Феномен и проблемы геодезии. — Новосибирск: СГГА, 2009. — 95

с.

2. Тетерин, Г.Н. История геодезии (до ХХВ.). — Новосибирск: Альянс-Регион, 2008. — 300 с.

3. Тетерин, Г.Н. Древние измерительные системы и два принципа влияния (ПВГ и П4Н) [Текст] / Тетерин Г. Н., Тетерина М.Л. // «ГЕ0-Сибирь-2009» V Междунар. выставка и науч. конгр. Т. 1, ч. 1. Геодезия, геоинформатика, картография, маркшейдерия. -Новосибирск: СГГА, 2009. — С. 123-124.

© Г.Н. Тетерин, М.Л. Синянская, 2010

Поворачивая путь майя под прямым углом

Великая пирамида майя Кукулькан «Эль Кастильо», вид с платформы Орлов и Ягуаров, Чичен-Ица, Мексика.

Как построить прямой угол, если у вас нет способа измерения углов? Один очень хитрый способ исходит от народа майя. Классический период майя длился примерно с 250 по 900 год нашей эры. За это время майя построили сотни городов на территории, простирающейся от нынешней южной Мексики через полуостров Юкатан до западного Гондураса и Сальвадора, включая то, что сейчас является Гватемалой и Белизом.Мы узнали о трюке с прямым углом от Кристофера Пауэлла из Исследовательского центра майя.

На лекции во время ознакомительной поездки MAA 2011 Пауэлл объяснил, что слышал об этой технике от мастера-строителя, который изучил ее, будучи учеником шамана. Вы начинаете со шнура, на котором есть восемь узлов, и делите его на семь равных отрезков с узлом на каждом конце. На каждом узле есть петли для привязки к земле.

Поскольку узлы расположены равномерно, когда узлы 1 и 4 удерживаются вместе, а шнур натянут, образуется равносторонний треугольник с внутренними углами 60 °.Затем узел 6 соединяется с узлом 3, и шнур натягивается туго, в результате получается еще один равносторонний треугольник, образованный узлами 4, 5 и 6. Наконец, узел 8 соединяется с узлом 5, образуя третий равносторонний треугольник (и все вместе половину шестиугольника) . Если провести луч (или веревку) от узла 1 до узла 2, а другой луч — от узла 1 до узла 7, полученный угол будет прямым (60 ° + 30 °). На анимации ниже (созданной Джоном К. Д. Диамантопулосом) показано, как образуется прямой угол.

Джон К.Д. Диамантопулос также создал следующее видео с участием студентов-добровольцев, чтобы продемонстрировать способ майя формировать прямой угол.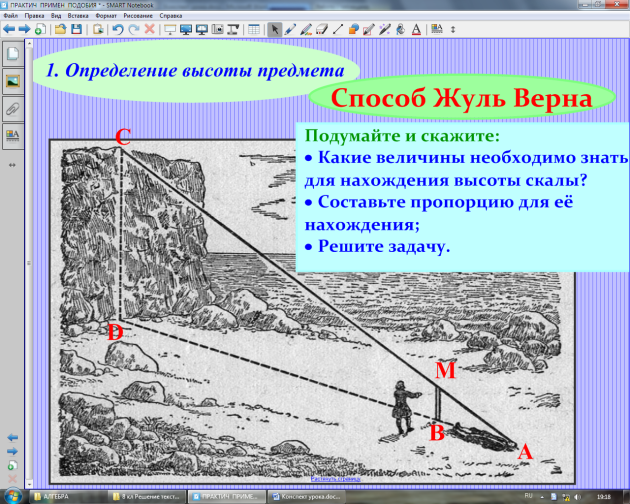 См. Здесь подробные инструкции о том, как воссоздать упражнение со своими учениками.

---

Об этой статье

Эта статья впервые появилась в книге Convergence , опубликованной Математической ассоциацией Америки, чтобы помочь учителям преподавать математику с использованием истории математики. Щелкните здесь, чтобы увидеть все ресурсы по геометрии майя, опубликованные на Convergence .

Джон К. Д. Диамантопулос — профессор кафедры математики и компьютерных наук Северо-Восточного государственного университета в Талекуа, штат Оклахома. Он был очень активен в MAA, как на уровне секции, так и на национальном уровне. Его математические интересы включают обыкновенные дифференциальные уравнения, математическое образование и историю математики. Диамантопулос также очень активен в своей церкви, работая волонтером в компьютерной продукции / презентациях и в любой другой области, требующей внимания.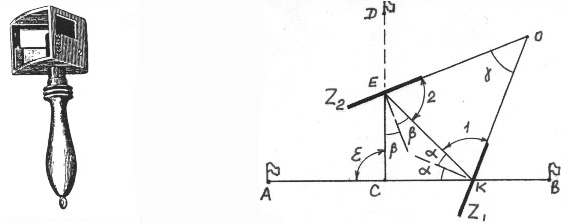

Синтия Дж. Хаффман — профессор факультета математики Питтсбургского государственного университета в Питтсбурге, штат Канзас. С 2009 года она участвовала во всех обучающих турах MAA. Ее области исследований включают вычислительную коммутативную алгебру и историю математики. Хаффман — солистка с колокольчиками, имеет черный пояс по китайскому Кенпо карате.

Вы измеряете угол подъема от земли до верха здания как 32 °. При приближении к зданию на 50 м угол подъема составит 53 °.Насколько высоко здание?

Привет Макина-

Вот как можно решить эту проблему. Начнем с чертежа:

|

|

|

|

|

|

(32 ^o ) (53 ^o ) |

X- (50м) -Y (Зм) |

Первое, что нужно признать, это то, что это создает два прямоугольных треугольника.Когда у нас есть прямоугольные треугольники, мы можем использовать тригонометрические функции для определения недостающих сторон.

Сначала мы пытаемся найти высоту, и нам известна только длина другого основания. Это говорит нам о том, что мы, скорее всего, будем использовать функцию tan. Во-первых, можно сказать следующее:

высота

загар (32) = ———

50 + я

Это проблематично, потому что нам нужно решить две переменные.Прежде чем приступить к рассмотрению приведенного выше уравнения, отметим, что мы также можем создать второе уравнение:

высота

загар (53) = ———

z

Вы должны заметить, что теперь вы можете использовать замену, чтобы ответить на этот вопрос. Например, если вы выделите z во втором уравнении, вы получите:

высота

г = ———

коричневый (53)

Затем подставьте это в первое уравнение:

высота
загар (32) = ————————
50 + рост / загар (53)

высота

. 625 = ——————-

50 + высота / 1,327

31,25 + 0,625 (высота) / 1,327 = высота

31,25 + 0,471 (высота) = высота

31,25 = 0,529 (высота)

высота = 59,07 метра

примеров тригонометрии, используемых в строительстве | Работа

Стефани Дьюб Дуилсон

Тригонометрия — это один из основных уроков математики, которые вы обычно посещаете в старших классах, и он также необходим вам в качестве основного курса практически для любой степени бакалавра.Он включает в себя изучение и расчет углов в трех измерениях. Строители широко используют тригонометрию, чтобы рассчитать лучший способ построить стабильные и безопасные проекты.

Фундаменты для дома

Когда строители закладывают фундамент дома, они в значительной степени полагаются на тригонометрию, чтобы убедиться, что фундамент ровный и устойчивый. Поскольку земля обычно наклонная и неровная, подрядчики должны использовать тригонометрию для определения углов и объемов, необходимых для вырезания и засыпки участков земли, чтобы выровнять ее.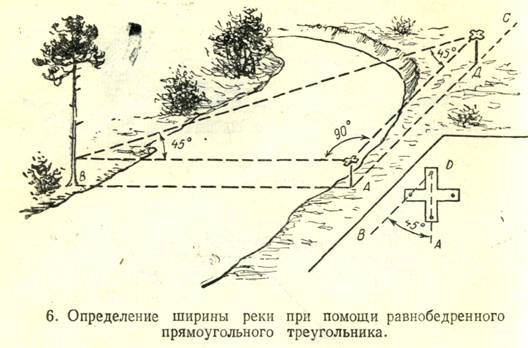 Все усложняется, если для дома требуется фундамент неправильной формы для изогнутых коридоров или стен.

Расчет длины моста

В проекте строительства моста тригонометрия важна для определения того, какой длины должен быть мост. Подрядчик может использовать свойства прямого угла и касательные, чтобы определить ширину реки, что напрямую определяет длину моста. Например, если он стоит на берегу реки, в 10 футах от того места, где будет мост, то все, что ему нужно, — это измерить угол от того места, где он стоит, до места остановки моста на другой стороне реки.Затем он может использовать свойства прямоугольного треугольника для вычисления остальных.

Определение конструкций крыши

Угол ферм, которые обеспечивают опору для поддержки крыш, и длина стропил в крыше определяются с помощью тригонометрии. Например, для крыши треугольной формы, если вы уже знаете длину стропил и горизонтальную длину крыши, вы можете использовать закон косинусов, чтобы определить, под каким углом фермы должны быть обрезаны для максимальной поддержки.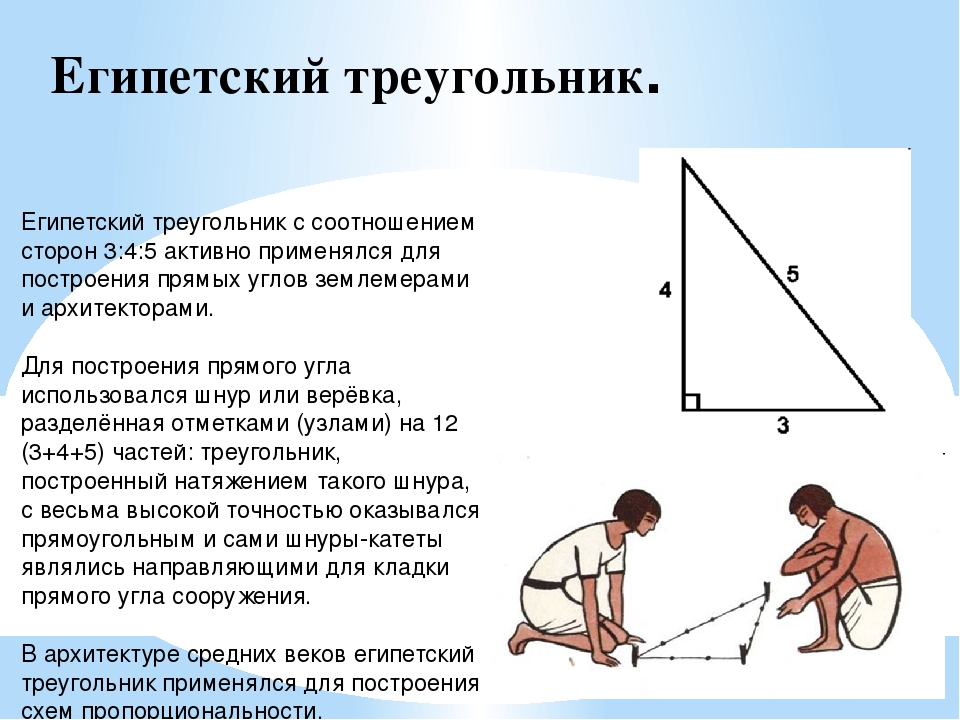 Если вы знаете высоту крыши и ее горизонтальную длину, вы также можете использовать тригонометрию, чтобы определить, какой длины должны быть стропила.

Пандусы для инвалидных колясок

Простой пример использования тригонометрии в строительстве — строительство пандусов для инвалидных колясок. Например, если пандус должен располагаться под углом в шесть градусов для максимальной безопасности, и вы знаете, насколько высоко находится выход от земли, вы можете рассчитать необходимую длину пандуса для инвалидных колясок, используя простое отношение касательных для прямоугольного треугольника.

Ссылки

Писатель Биография

Стефани Дьюб Дуилсон — опытный писатель со степенью юриста и магистром в области научно-технической журналистики, благодаря функциям, опубликованным такими СМИ, как Business Week и Fox News. Она писала для юридических фирм, агентств по связям с общественностью и маркетинга, веб-сайтов, посвященных науке и технологиям, и деловых журналов.

Что такое прямоугольная тригонометрия в деревообработке

Для плотника умение «решать» прямоугольные треугольники — чрезвычайно важный навык.Сложные митры, многосторонние конструкции и множество других сложных строительных проектов можно понять и рассчитать с помощью тригонометрии прямоугольного треугольника. Если термин «тригонометрия» вызывает у вас внезапное «математическое беспокойство», вы будете рады узнать, что тригонометрия, необходимая для работы с деревом, не так уж и сложна.

Базовые знания — это все, что необходимо для решения практически любой угловой проблемы, которая когда-либо возникнет при обработке дерева. Ниже мы воспроизведем несколько хорошо известных формул и соотношений из тригонометрии прямоугольного треугольника, которые действительно могут пригодиться в деревообработке.

Теорема Пифагора

Теорема Пифагора — это геометрическое соотношение между длиной трех сторон прямоугольного треугольника:

Для любого прямоугольного треугольника ABC, A² + B² = C² , где A и B — стороны треугольника, которые пересекаются под углом 90 градусов. Пример: использование теоремы Пифагора для определения длины (L) диагональной распорки, которая выступает на 8 дюймов от поверхности стены, чтобы поддерживать полку, и на 12 дюймов вниз от нижней поверхности полки:

L² = 8² + 12²

=> L² = 208

=> sqrt (L²) = sqrt (208)

=> L = 14.4222 »

=> L = (приблизительно) 14-27 / 64 »

Тригонометрические функции Синус, косинус и тангенс

Теорема Пифагора пригодится для вычисления размеров сторон прямоугольных треугольников, но для вычисления углов необходимо использовать тригонометрические функции. Тригонометрические функции описывают отношения между сторонами прямоугольного треугольника: Sin (x) = O / H Cos (x) = A / H Tan (x) = O / A

Отношения применяются ко всем прямоугольным треугольникам независимо от размера или пропорций треугольника.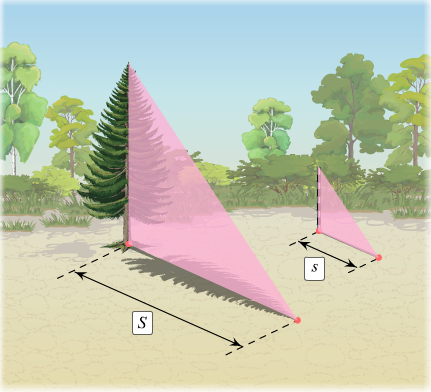

Пример: Выше мы использовали теорему Пифагора для расчета длины диагональной распорки полки на основе 8-дюймовой проекции распорки от стены и 12-дюймовой проекции распорки вниз от нижней части полки. . На этот раз вместо того, чтобы распорка касалась стены ровно на 12 дюймов ниже полки, мы хотим, чтобы диагональная распорка отклонялась от стены под углом 30 градусов, но все же выступала от стены ровно на 8 дюймов.

Поскольку мы знаем угол w (где стена и распорка пересекаются) и длину стороны прямоугольного треугольника, образованного распоркой, стенкой и нижней частью полки, противоположный угол w , мы можем использовать функцию синуса, чтобы определить длину (L) скобки:

sin ( w ) = 8 / л

=> грех (30) * L = 8

=>.5 * L = 8

=> L = 8 / 0,5

=> L = 16 дюймов

Если нам также необходимо знать расстояние ( D ) вниз от нижней поверхности полки до нижнего конца распорки, мы могли бы использовать любую теорему Пифагора: D = sqrt (16² — 8²) = 13,8564 или тангенциальная функция: D = 8 / tan (30) = 13,8564 = приблизительно 13-57 / 64 »

Угол s разреза в месте соединения скобы с полкой является просто дополнением угла w: 90-30 = 60 градусов

Расчет значений тригонометрической функции

Чтобы вычислить значение тригонометрической функции, вам необходимо использовать научный калькулятор или таблицу значений тригонометрической функции. Научный калькулятор — это удобный инструмент, который стоит иметь в магазине и который стоит затрат на добавление в вашу коллекцию инструментов. Вы также найдете таблицы тригонометрических значений на веб-сайте Rockler по адресу Woodworking Math Formulas, Tables and Calculators.

Обратные тригонометрические функции

В некоторых случаях значение тригонометрической функции является известной величиной, и угол, которому она соответствует, необходимо определить. В этих случаях необходимо использовать обратные тригонометрические функции.Обратные тригонометрические функции, проще говоря, тригонометрические функции наоборот. Другими словами, они вычисляют угол, соответствующий заданному значению тригонометрической функции.

Обратные тригонометрические функции часто называют функцией «дуги» — «арксинус», например, относится к функции, обратной функции синуса. Для целей деревообработки можно определить обратные тригонометрические функции: x = arcsin [sin (x)] x = arccos [cos (x)] x = arctan [tan (x)] Например, sin (30) знак равно5 arcsin (. 5) = 30 arcsin [sin (30)] = 30 sin [arcsin (.5)] = 0,5

Пример: Выше мы использовали теорему Пифагора для расчета длины диагональной распорки, которая выступает на 8 дюймов из стены, чтобы поддерживать полку, и на 12 дюймов вниз от нижней части полки. Теорема Пифагора сообщила нам длину распорки (14,4222 дюйма), но ничего не сказала об углах, которые нам нужно вырезать, чтобы прижать скобу к нижней части полки и к стене. Мы будем использовать обратные тригонометрические функции, чтобы найти угол s надреза на конце полки распорки и угол w надреза в месте соприкосновения распорки со стеной.

загар (ш) = 8/12

=> арктангенс [загар (ш)] = арктангенс (8/12)

=> ш = арктангенс (0,0667)

=> ш = 33,69 градуса

В качестве альтернативы мы могли бы использовать либо функции арксинуса и синуса с длиной диагональной распорки 14,4222 дюйма и выступом распорки от стены 8 дюймов, либо аналогично функции арккосинуса и косинуса с длиной распорки и 12 » выступ распорки вниз с полки.

Угол s для разреза на конце распорки, которая встречается с полкой, также можно рассчитать с помощью обратных тригонометрических функций, но проще просто вычесть угол w из 90 градусов, чтобы найти его дополнение: 90 градусов — 33,69 градусов = 56,31 градусов = угол с

ПРАВЫЙ УГОЛ — диагональность

Как феномен диагональности изменил облик современной архитектуры

ДИАГОНАЛЬНАЯ ИНФОРМАЦИЯ

ГЛАВА ВТОРАЯ

ПРАВЫЙ УГОЛ

«Очень рано площадь стала символом истины, справедливости и праведности, и так остается по сей день, хотя прошло бесчисленное количество веков.”

Сэр Айзек Ньютон

БЕДРОК ОРИЕНТАЦИЯ ПРИРОДЫ

Что оправдало непоколебимую веру в правильный угол на протяжении последних семидесяти веков строительства зданий? Что такого особенного в правильном угле, что способствовало его распространению и почитанию при строительстве зданий и планировке площадок, и почему он стал использоваться до использования диагоналей? Как ни странно, ответ на эти вопросы — серьезность.

Рис. 2.1 Гравитационные силовые линии расходятся веером из центра каждого космического тела

Гравитация — это фундаментальная сила природы, само существование которой восходит к неясным истокам Вселенной. Гравитация не только контролирует движение космических объектов, таких как звезды, галактики и планеты, но также влияет на все неорганические структуры, такие как горы, вода и тектонические плиты. [Рис. 2.1] Гравитация удерживает океан на морском дне, связывает нашу атмосферу с земной корой, уносит дождевую воду с горных вершин и уносит рыхлые породы с возвышенностей в долины.На обитаемых планетах, таких как наша, гравитация также влияет на рост растений и передвижение животных. Он заставляет большинство растений и деревьев подниматься преимущественно вертикально к свету, а не под углом. [Рисунок 2.2]

Рис. 2.2 Обычные деревья в Нормандии, Франция.

В мире микроорганизмов и клеток гравитация удивительным образом влияет даже на их размер относительно силы окружающего гравитационного поля. У более крупных существ гравитация формирует структуру скелета, чтобы обеспечить упорядоченное и эффективное движение в воздухе, на море и на суше.Что еще более неожиданно, прямой угол заложен в электромагнитных явлениях. Например, сила магнетизма проходит перпендикулярно электрическому току. Даже фотон, движущийся в пространстве со скоростью света, состоит из дополнительных волн, бегущих под прямым углом друг к другу. [Рис. 2.3] Некоторые материалы, отталкиваемые магнитным полем, мгновенно выстраиваются под прямым углом к ​​полю: процесс, известный как диамагнетизм.

Рис. 2.3. Схема дополнительных сил, действующих в движущемся фотоне света.

Не будет преувеличением сказать, что гравитация — одна из самых фундаментальных сил, формирующих форму, влияющих на все органические и неорганические структуры на Земле.

ЧЕЛОВЕК И ТЯЖЕСТЬ

Мы, люди, не можем видеть саму силу гравитации, но мы реагируем на ее прохождение через наши тела и видим ее эффекты во всем на поверхности земли. Если мы стоим, наклонившись в одном направлении, а затем наклоняемся еще дальше, мы опрокидываемся. Можно сказать, что наша реакция на гравитацию запечатлена в самом сердце нашего существа.У нас есть укоренившееся чувство того, что является прямым, когда мы встаем, и бессознательно ощущаем, что действительно вертикально или действительно горизонтально. Новорожденный смотрит в лицо своего родителя и видит, как глаза, уши и рот расположены перпендикулярно оси носа. [Рисунок 2.4]

Рис. 2.4 Перпендикулярные взаимоотношения в структурах человеческого лица.

То же самое с осями плеч и бедер, поскольку они относятся к центральной оси позвоночника.[Рис. 2.5] Все эти переживания и телесные отношения способствуют нашему чувству перпендикулярности и нашему пониманию правильного угла.

Рис. 2.5 Перпендикулярные взаимоотношения в человеческом теле, показанные на этом рисунке Леонардо да Винчи.

Следствием этой повсеместной перпендикулярности является то, что на пути от глаза к мозгу существуют клетки, которые реагируют только на импульсы энергии от вертикальных линий. Другие клетки реагируют только на горизонтальные линии, а третьи распознают только линии с наклонной ориентацией.Более того, у амбулаторных существ не только глаза определяют вертикальное и горизонтальное положение; внутреннее ухо также посылает предупреждающие сигналы, когда животное теряет равновесие и / или не стоит в вертикальном положении. Эта вестибулярная система в ушах людей и других животных обеспечивает общее ощущение пространственной ориентации. Также интересно то, что пространство кажется изображенным в уме с его собственной причудливой, врожденной системой координат. Например, в наших снах то, что мы знаем как вертикальную и горизонтальную ориентацию с открытыми глазами, изображается как таковое, даже когда мы лежим на боку.Это говорит о том, что наши мысленные образы вертикальности преобладают над нашим телесным ощущением того, что является вертикальным … по крайней мере, во время сна. Можно предположить, что это может быть так, потому что, хотя тело склонно, внутреннее ухо (вестибулярная система) все еще реагирует на гравитационные силы.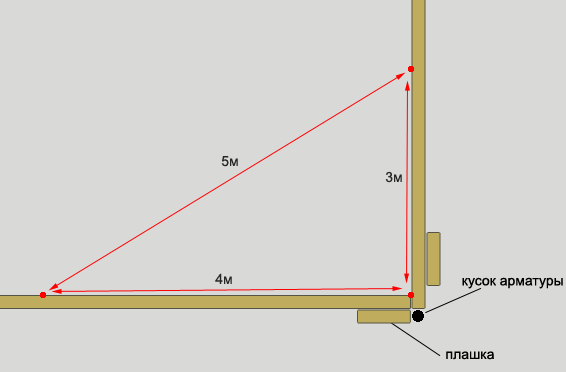 Эти примеры призваны указать на примат силы гравитации и на то, что наше глубоко укоренившееся чувство горизонтали и вертикали является составными компонентами нашего сознания.

Во внешних частях человеческого тела перпендикулярность и соответствующий прямой угол очевидны.Это симметричное и перпендикулярное расположение частей тела по отношению к позвоночнику очевидно для почти всех организмов, которые свободно перемещаются в своей среде, будь то в воздухе, воде или на суше. Симметрия и движение неразрывно связаны. То же самое чувство симметрии всегда выражалось в дизайне зданий, независимо от того, имела ли симметрия смысл или нет.

Симметрия в плане этажа и фасада является неотъемлемой характеристикой и побочным продуктом перпендикулярных отношений и обеспечивает качество, которое обычно считается прекрасным.Однако симметрия часто достигается за счет программной функции. В симметричном здании потребности в пространстве в крыле справа от центральной оси обычно не совпадают с потребностями в пространстве в крыле слева. Тем не менее, стремление к красоте и покою часто преобладает над функциональными проблемами. Стремление к симметрии усиливает склонность к построению под прямым углом.

КОНСТРУКЦИЯ ПРЯМОУГОЛЬНАЯ И ЧЕТЫРЕХ КВАДРАТА

Хотя временные сооружения, такие как палатки, вигвамы и юрты, были круглыми, именно прямой угол доминировал в геометрии постоянных зданий на протяжении большей части зарегистрированной истории.Поскольку прямые углы формировали бесчисленное количество отдельных комнат, они также превращали след целых зданий в простые объемы в форме обувных коробок или их комбинации. [Рисунок 2.6]

Рисунок 2.6 Коттедж в стиле Кейп-Код

Если посмотреть на план этажа большинства зданий, построенных до двадцатого века, особенно величественных зданий, таких как трехэтажная усадьба елизаветинской эпохи под названием Лонглит, и наложить на план прозрачную пленку, помеченную линиями сетки, подобными миллиметровой бумаге, он уверен, что стены здания будут параллельны линиям сетки.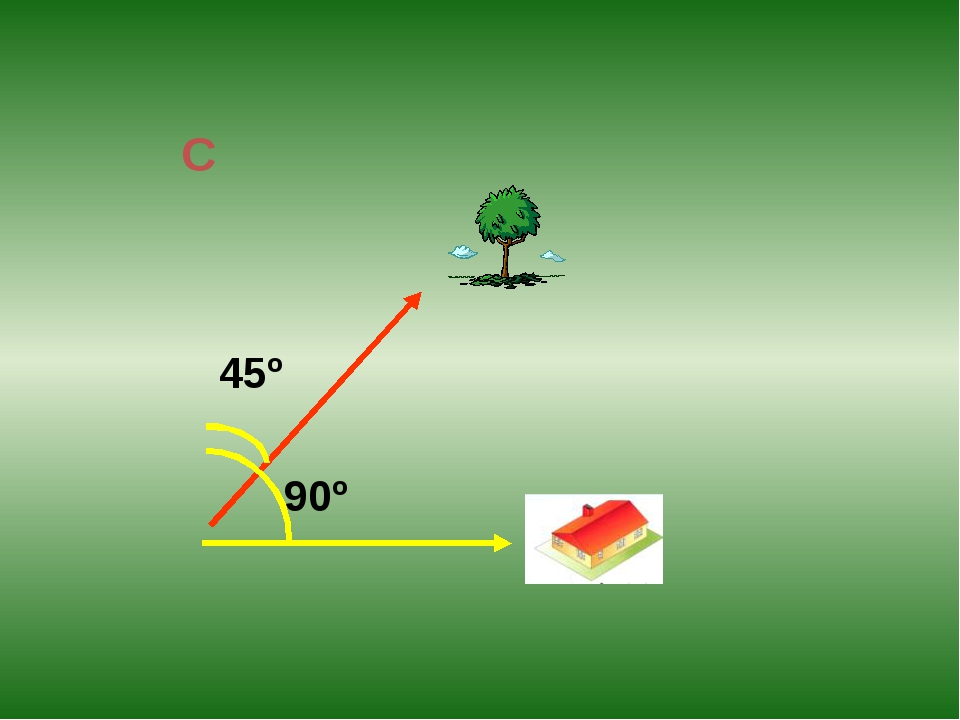 [Рисунок 2.7] Эта геометрия прямых углов называется ортогональностью.

Рис. 2.7 Лонглит, особняк елизаветинской эпохи.

Кроме того, на протяжении всей истории несколько зданий, составляющих единый комплекс, часто располагались перпендикулярно друг другу, как белые плитки в домино для настольной игры. Запретный город в Пекине, Китай, является прекрасным примером такого расположения, где не только площадь отдельных зданий основана на квадратных углах, но и ортогональный формат также распространяется на общий план территории комплекса; все здания расположены параллельно и / или под прямым углом друг к другу.[Рисунок 2.8] Это как если бы использование квадратных углов было предопределено неизменным биологическим императивом, заложенным в мозгах людей, которые обрабатывали камни, рубили бревна или рисовали планы.

Рисунок 2.8 План участка Запретного города в Пекине, Китай

Чтобы добиться стабильности и безопасности в строительстве, люди давно обнаружили, что стены должны строиться как можно ближе к отвесу (вертикальному).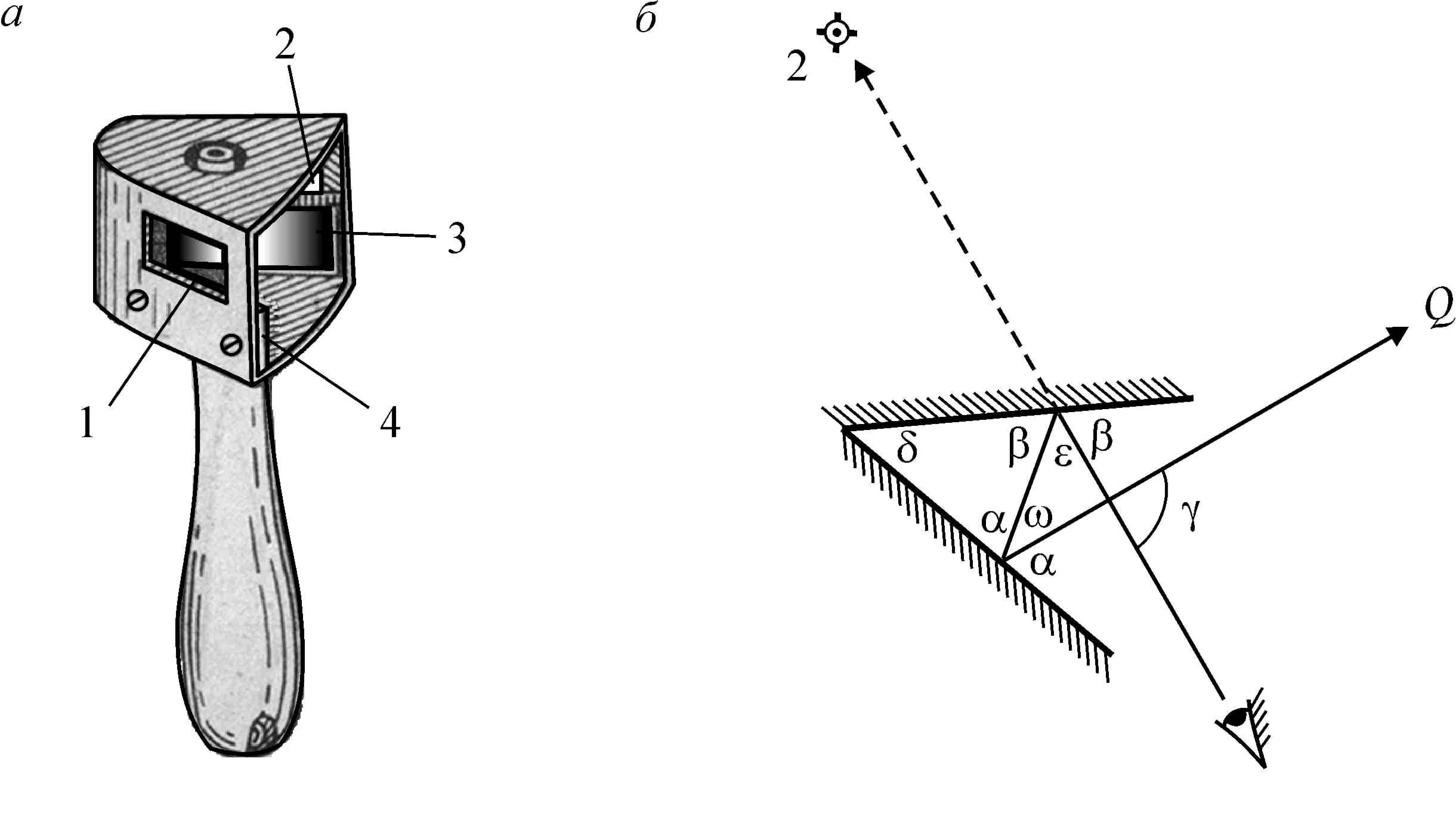 [Рис. 2.9] Сигналы, посылаемые внутренним ухом, датчиками в мышцах и суставах, а также функционирование глаз указывали строителю, что находится в вертикальном положении и, следовательно, перпендикулярно среднему уровню земли, на которой он стоял.Строитель мог одним глазком увидеть, «выглядит» ли стена вертикальной. Но этот метод не был абсолютно надежным, поэтому строители обнаружили, что подвешивание тяжелого объекта в форме стрелы острием вниз на веревке может точно установить вертикальную линию: сила тяжести в действии Этот объект в форме стрелы стал известен как отвес и до сих пор используется, чтобы определить, является ли стена идеально вертикальной. [Рисунок 2.9A] [Рисунок 2.9B] [Рисунок 2.9C]

Рисунок 2.9 Отвес.

Рисунок 2.9B Перпендикулярная конструкция

Рис. 2.9C Стена обычно считается небезопасной, если она наклоняется до такой степени, что отвес, проходящий через ее центр тяжести, не попадает внутрь средней трети ее основания (так называемое правило V-3)

.

В течение эонов четырехугольная конструкция находила отклик глубоко внутри строителей на бессознательном уровне. Было оценено, но не понято, что существует сила, которая удерживает вертикально расположенные объекты стабильно на поверхности земли и заставляет наклоненные объекты падать на землю.Это внутреннее чувство перпендикулярности стало мощным символом скрытого порядка вещей. [Рисунки 2.10]

Рисунки 2.10 Плантации деревьев в Нормандии во Франции.

Хотя это и загадочно, здесь был порядок вещей, которые в буквальном, переносном и структурном смысле оказались полезными и долговечными. [Рисунки 2.11]

Рисунки 2.11 Колоннада в Париже, Франция.

Архитекторы и строители также пришли к выводу, что стены, поддерживающие балки, следует возводить параллельно друг другу, потому что более эффективно резать брус и куски камня для балок до одинаковой длины.Это относилось также к торцевым стенам комнаты, поскольку, если они находились не под прямым углом к ​​опорным стенам, бревна в конце комнаты должны были быть индивидуально измерены и отрезаны на разную длину.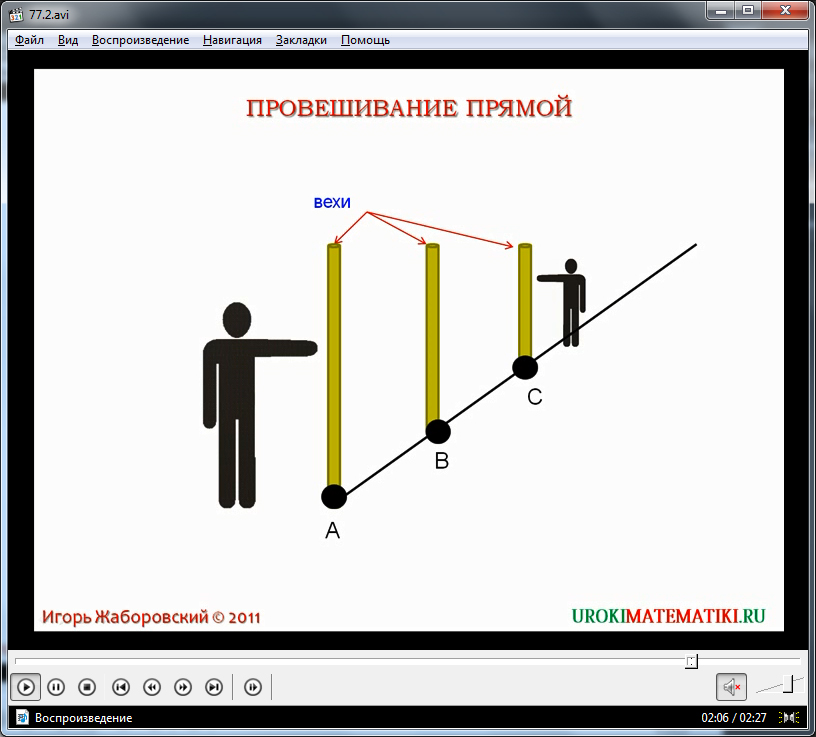 Следовательно, четырехугольная конструкция стала базовой геометрией строительства. [Рисунки 2.12]

[Рис. 2.12] Несущий отсек с однородными элементами каркаса, образующими пространство с прямыми углами.

Еще один фактор в пользу прямоугольных помещений — резка камня под острыми углами рискованна и непредсказуема.Чтобы разрезать конец каменной балки под углом 45 °, требуется гораздо больше времени, энергии и осторожности, чем для резки под углом 90 °, потому что при угловом пропиле необходимо пропилить гораздо больше материала, и возможна поломка в остром углу . Эти острые углы также уязвимы для разрушения из-за внешнего воздействия или внутренних структурных сил. Следовательно, строители научились избегать обрезки концов балок под углом, когда это возможно.

Существует только один способ пересечения одной линии с другой в двухмерной плоскости, в результате чего все четыре угла будут равны.То есть две линии должны быть перпендикулярны, и это дает четыре прямых угла 90 °.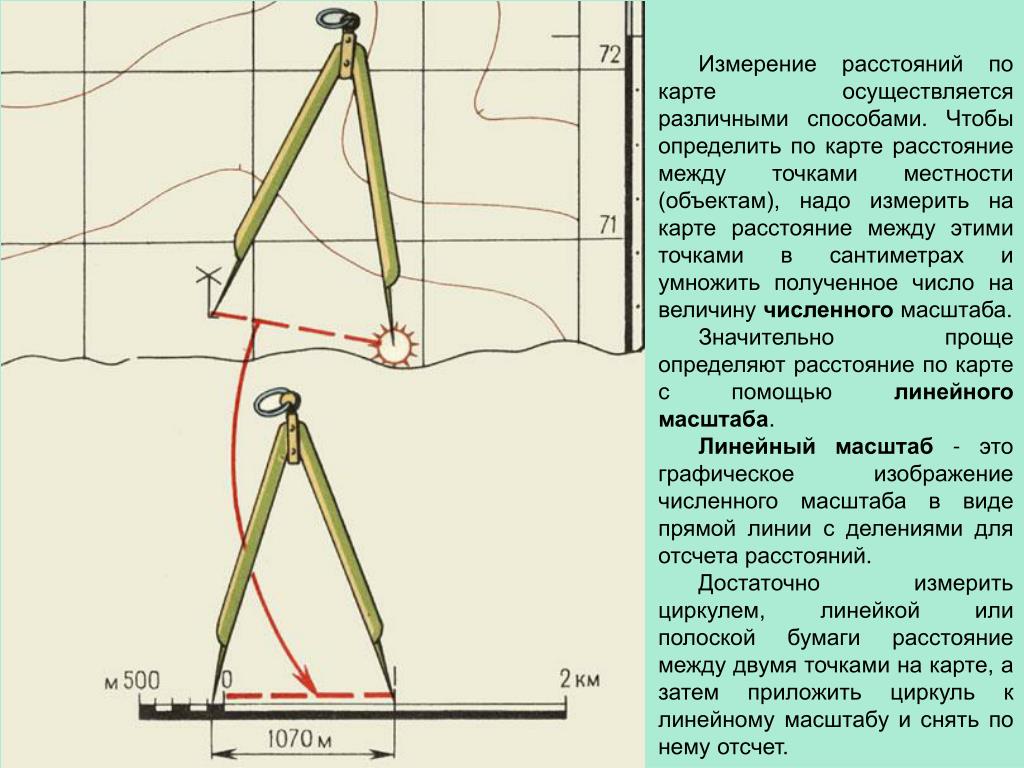 До 20-го века физические и абстрактные элементы прямого угла делали его геометрией по умолчанию при строительстве зданий, примером чего является, например, конструкция из колонн и балок таких структур, как Храм Хефрена в Гизе. [Рисунок 2.13]

Рисунок 2.13 Гиза, Храм Хефрена в долине.

Использование прямого угла дает также преимущества в экономии места.Если посмотреть на прямоугольную комнату сверху, можно увидеть, что площадь закрытого пола имеет решающее значение для общей длины четырех ограждающих стен. За счет самой короткой общей длины четырех стен создается наибольшее полезное пространство. Однако, если бы можно было сжать прямоугольник, сделав угол любых двух противоположных углов тупым (что сделает два других противоположных угла острыми, что приведет к образованию ромбовидного следа или параллелограмма), площадь замкнутого пространства уменьшится пропорционально серьезности задействованных углов.[Рис. 2.14]

Рис.

2.14. План квадратного, ромбовидного и восьмиугольного помещения с расчетами, показывающими квадратные метры при одинаковой длине стен.

Потребовалось немного геометрического интеллекта, чтобы оценить тот факт, что если бы ограждающие стены сходились равномерно под прямым углом, наибольшая полезная площадь была бы ограждена при минимальных конструктивных усилиях. Тем не менее, те, кто изучал геометрию, знают, что многоугольные формы, имеющие более четырех сторон, были бы более эффективными, чем прямоугольники, с точки зрения максимизации внутреннего пространства по отношению к длине ограждающих стен.Однако многие древние культуры были недостаточно развиты в геометрическом плане, чтобы использовать эти более сложные многоугольники в строительстве.

Использование прямого угла имело также символические преимущества. Впечатление постоянства и стабильности было главной заботой в древних культурах, таких как Египет. Вечное путешествие души, пока она не воссоединилась с телом, требовало могилы, которая, казалось, могла длиться вечно.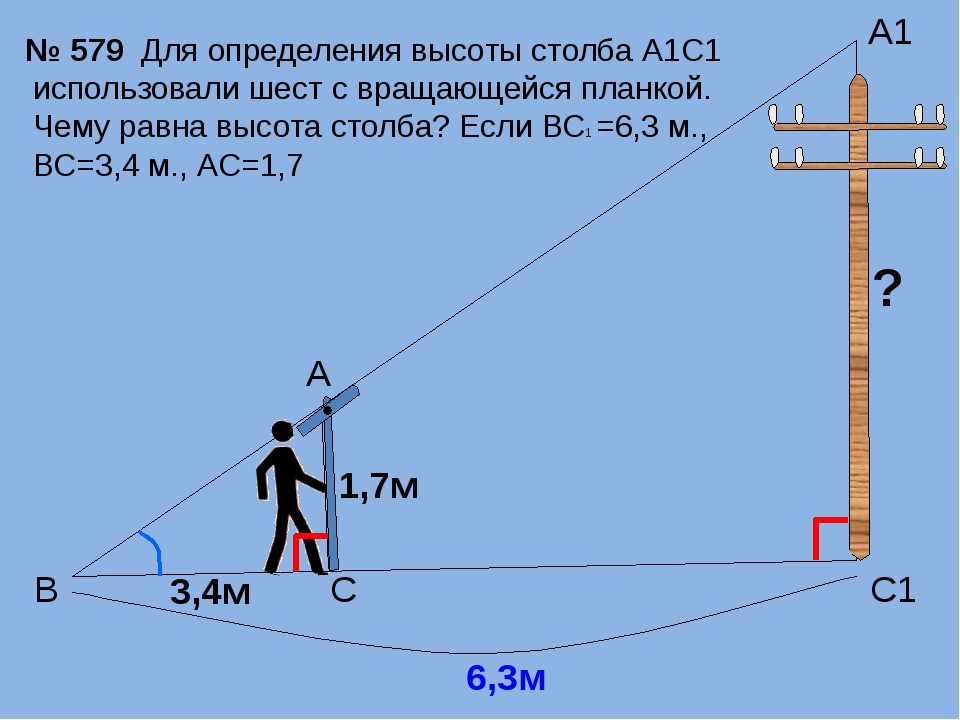 Кроме того, королевская власть требовала храмов, которые выглядели так, будто они будут стоять вечно и никогда не поддадутся силам природы (таким как землетрясения и ураганы) или атакам врагов, намеревающихся доминировать или революционизировать.По этим причинам прямоугольная конструкция с ее стабильным и долговечным внешним видом имела большое символическое значение. Тем не менее, египтяне поняли, что пирамида была окончательной формой, связанной со строительством, которое могло сохраняться бесконечно, и для этого требовалось слияние крыши и стены в наклонную плоскость. След пирамиды квадратный, но ее обращенные к небу плоскости — треугольники. Две диагонали пересекают квадрат, образуя треугольные внешние поверхности.

Наконец, мы обратимся к экономическим преимуществам использования прямого угла.В Древнем Египте был нужен способ передать землю фермерам, а затем, после того, как поднявшиеся воды Нила стерли границы владений, пересмотреть границы земельных участков. Великий греческий историк Геродот видел это наводнение еще до того, как египтяне научились укрощать реку дамбами, каналами и водосборными бассейнами. Он писал: «Когда Нил затопляет землю, весь Египет становится морем, и только города остаются над водой, выглядя скорее как острова Эгейского моря».

Рис.2.15 Разделение земель вдоль Нила в Египте.

После каждого сезонного наводнения земля делилась на огромное лоскутное одеяло из идеальных квадратов и прямоугольников с точностью, которая остается поразительной даже сегодня. [Рис. 2.15]. Геродот сообщил об использовании этих квадратов и прямоугольников для расчета налога: «Этот царь разделил землю… так, чтобы дать каждому по четырехугольнику равного размера и… на каждого, обложив налогом. Но [к] каждому, с какой стороны река что-то оторвала… он послал надзирателей, чтобы они измерили, насколько уменьшилась земля, чтобы владелец мог заплатить за то, что осталось.Таким образом, мне кажется, возникла геометрия, которая перешла оттуда в Грецию ».

Пол Калтер в своей книге «В квадрате круга: геометрия в искусстве и архитектуре» предполагает, что «Если разлив Нила символизировал ежегодное возвращение водянистого хаоса, то геометрия, используемая для восстановления границ, возможно, рассматривалась как восстанавливающая закон и порядок на земле. Мы снова увидим это понятие о геометрии как сакральной, потому что она представляет порядок, особенно в средние века ». (Calter 2004)

ОРТОГОНАЛЬНАЯ СЕТКА

Среди самых ранних примеров прямоугольного строительства — «укрепления и частично раскопанные прямоугольные дома в Иерихоне, которые могут быть датированы докерамической эпохой, а согласно исследованию углерода 14 — серединой шестого и средним веками. седьмого тысячелетия [до нашей эры].”[Gideon, 1964] P. 183. Еще одним свидетельством доисторической конструкции под прямым углом являются ямы и траншеи длинных деревянных домов около 5000 г. до н.э. в районе Ситтарда в Нидерландах.

Примерами комплексов, расположенных в соответствии с ортогональной сеткой, являются Цитадель Саргона, возведенная в 742 году до нашей эры [рис. 2.16], и Персеполис, построенный в 518 году до нашей эры, на территории современного Ирана.

Рисунок 2.16 План дворца Саргона (он же

Дур-Шаррукин ), Хорсабад (реконструкция 1905 года)

Другой пример одиночного здания, в котором используется ортогональная сетка, — это типичный дом, построенный в Индии в соответствии с традицией Ватсу Шастра .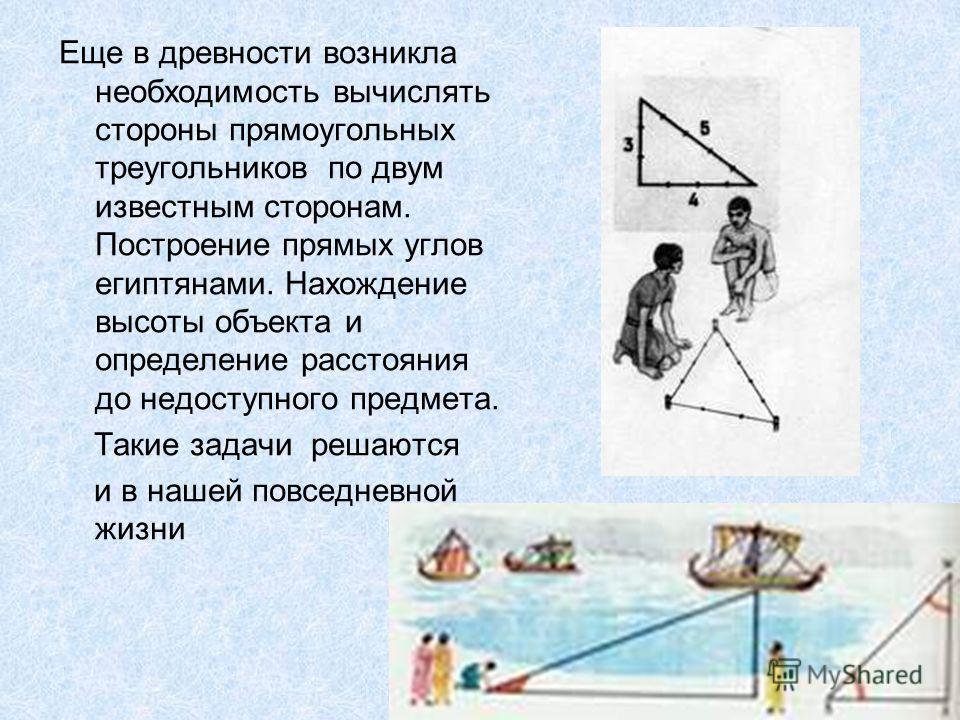 [Рис. 2.17] Требуемый квадратный план жилища состоит из 81 квадрата, по девять в сторону. Центр дома, внутренний двор, состоящий из девяти квадратов, подобен человеческим легким и поэтому оставлен открытым для неба. [Рис. 2.18] Во дворе не происходит обычных повседневных дел; он предназначен для религиозных и культурных мероприятий.

Рис. 2.17 Индийский план дома на основе традиции

Ватасу Шастра .

Рисунок 2.18 Мандала

Ватасу Пурша .

УСЛОВИЯ НЕСОВМЕСТИМЫЕ С ЧЕТЫРЕХ КВАДРАТНОЙ КОНСТРУКЦИЕЙ

Хотя подавляющее большинство зданий, построенных на протяжении всей истории, имеют ортогональные планы, следует отметить, что угловые стены часто появлялись при строительстве — но не по собственному желанию, не намеренно. Строители были вынуждены иногда искажать форму прямоугольного здания, чтобы приспособиться к уже существующим условиям участка, таким как извилистая дорога или прилегающая стена, идущая под углом к ​​ортогональной геометрии здания или многоквартирного комплекса.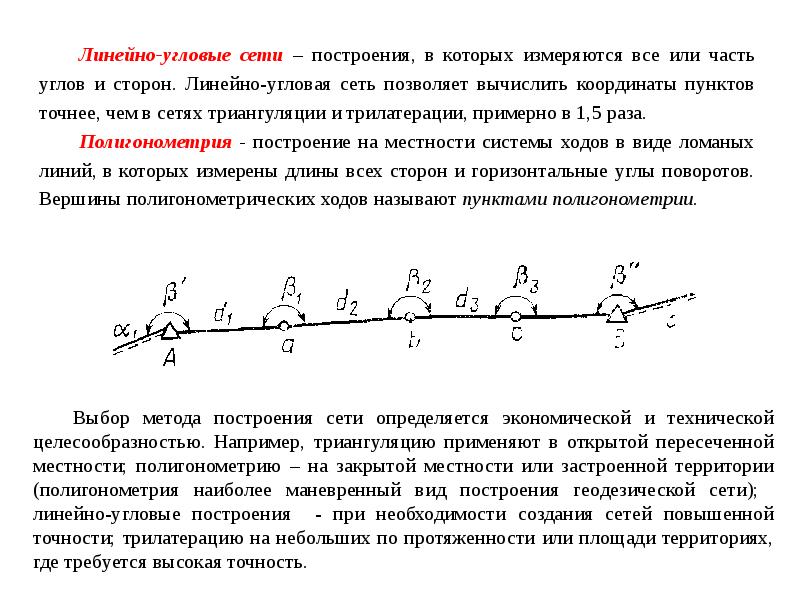

Крепость Уронарти , [рис. 2.19 A и B], построенная около 2000 г. до н.э., иллюстрирует, как преобладающая ортогональная геометрия комплекса может, без дизайнерского намерения, включать треугольные комнаты. Но эти треугольные комнаты возникают как обязательный ответ на уже существующие условия. Эта крепость длиной 500 футов, которая «стала прототипом большинства крепостей, построенных в Европе и Азии в течение следующих 3000 лет, демонстрирует ортогональную геометрию, которую просто нужно было« срезать »под углом вдоль массивной северной стены.Геометрия получаемых в результате угловых комнат никак не влияет на геометрию прямоугольных пространств; они остаются верными ортогональной сетке. Следует понимать, что диагональность, рассматриваемая в этом трактате, не существует, когда требуемое приспособление к уже существующему состоянию приводит к угловым усеченным пространствам.

Рисунок 2.19 Древнеегипетская крепость

Уронати , расположенная на острове на реке Нил. 19 век до н.э. г.

Рисунок 2.19A Вид с воздуха на настоящую крепость Уронати.

Строительство здания отличается от создания городского поселения. Органические городские поселения развивались не по заранее составленному плану, а за счет наращивания отдельных построек. Процесс аккреции происходит в порядке, который иногда называют случайным или органическим, но только потому, что так он выглядит. Типичный средневековый город мог возникнуть в месте на берегу реки с плоскими берегами, или на холме с прекрасным видом, или с защищаемой местностью, или в определенном доме, где продавались или обменивались продукты или товары.Людей привлекало это место, и они приезжали по живописным или легко управляемым маршрутам. Пешеходные дорожки превратились в проторенные тропы, которые огибали валуны и гостеприимно и эффективно следовали контурам. Вдоль этих извилистых троп возводились сооружения, и со временем из них образовалась деревня. Вдоль этих извилистых маршрутов возводились здания, которые для эффективности и / или порядка были составлены из комбинации прямоугольников. Однако их ортогональная геометрия часто уступала существовавшим ранее условиям, которые чаще всего были нерегулярными, то есть не ортогональными.Это примеры размещения, а не дизайн. Архитектор или строитель не намеревался проектировать комнаты со скошенными стенами, но пассивно реагировал на внешние условия, как показано на фото углового угла в Париже. [Рис. 20]. Нередки случаи, когда наклонная стена была утолщена в форму клина, так что внутри сохранились квадратные углы комнат. [Рис. 21] Исключение составляли храм, святыня или отдельное специальное здание, в котором, вне зависимости от формы и ориентации соседних построек и природных ландшафтов, можно было свободно использовать прямой угол.

Рис. 20 Тупой угол улицы в Париже, Франция, иллюстрирующий неортогональное «столкновение» соседних зданий.

Рис. 21 Вилла Франезе в Капароле, Италия.

ПРАВИЛЬНЫЙ ЯЗЫК

В английском языке слова right и square относятся как к прямому углу, так и к тому, что считалось правильным, хорошим или правильным. Таким образом, прямой угол в строительстве считался хорошим и считался правильным.Рассмотрим такие фразы, как «, пожалуйста, сравните это со мной, », или «, он на правильном пути, », или «она, , не может быть более правильной, ».

И наоборот, слово наклонное, в дополнение к отношениям, которые не были ортогональными, стало относиться к вещам, которые были « неправильный », « плохой, сомнительный или коварный ». Обратите внимание на эти цитаты на английском языке.

1713 Стил Гвардии. № 20 с.2 Косой взгляд, которым всегда видит ненависть .

1770 Jortin Serm. (1771) I. vii. 128 Есть люди… которые становятся богатыми и великими… различными косвенными и скандальными путями.

В масонской традиции есть три определения квадрата: «(1) концепция прямого угла — наш ритуал говорит нам, что квадрат — это угол в девяносто градусов, или четвертая часть круга; (2) Инструмент строителя, один из наших рабочих инструментов, собственное недвижимое украшение Мастера; (3) То качество характера, которое сделало «квадратного человека» синонимом не только члена нашего Братства, но и порядочности, честности и надежности. Масоны считают квадрат символом добродетели ».

Видно, что язык усиливал обоснованность и полезность прямого угла и препятствовал рассмотрению того, что было наклонным или наклонным. Рассмотрим слово вертикальное . Слово может происходить от ветхозаветного еврейского слова, транслитерированного как yashar . Это означает прямой, прямой и ровный. Это также означает приятный, правильный, праведный и справедливый. Происхождение нашего английского слова upright — германское, с последующими вариациями на староанглийском, голландском, немецком и английском языках.В качестве прилагательного это слово означает вертикальный, прямой, перпендикулярный и отвесный. Но применительно к человеку или его поведению это слово также означает «честный, благородный, порядочный, законопослушный, этичный, добродетельный, принципиальный и благородный».

На более абстрактном уровне качества порядка, рациональности, единообразия и надежности, связанные с прямым углом, казались почти данными богами.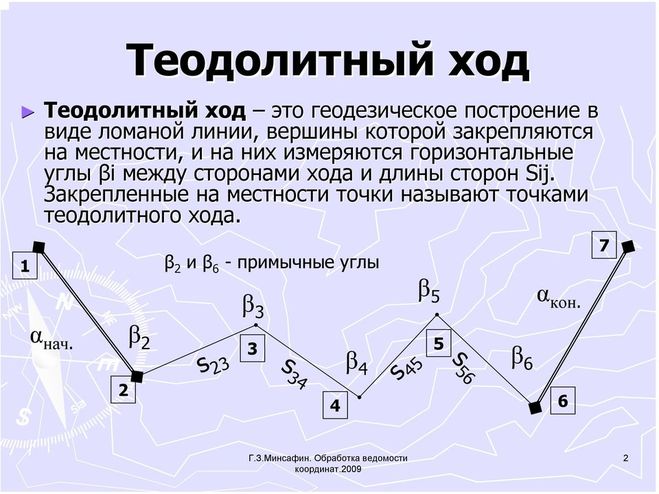 Язык отражал предпочтение слова right и, как указано выше, наполнял его трансцендентным значением, включая такие качества, как надежность, честный, надежный, лояльный, устойчивый, равноправный, существенный и прямой.Подумайте о квадратной сделке или квадратных обедах .

На этом фоне становится понятно, что на протяжении веков неквадратные конструкции избегались и избегались. Точно так же избегалось того, что было наклонным и неквадратным, и слова, связанные с вещами , а не квадратом , имели уничижительный оттенок.

Что интересно с культурной точки зрения, так это то, что по мере того, как современный мир развивался в конце 19-го и 20-го веков, использование слова квадрат теперь приобрело новое, не очень благоприятное значение, и это соответствовало изменению дух времени современной эпохи.По мере того как жесткая ортодоксальность прошлых веков начала разрушаться, честность, ясность и добродетель, связанные со словом right , стали олицетворять вещи, которые были жесткими, устаревшими, оторванными от реальности, ограничивающими, условными и нежелательными. Появились такие фразы, как «будь там или будь честным». Другие подобные фразы и значения включали: неклассный, не свойственный, душный, старомодный и строго условный. На протяжении двадцатого века, по целому ряду причин, которые будут изложены далее в этой книге, архитектура уходила корнями в правильный угол, а ортогональная сетка постепенно теряла популярность в определенных обстоятельствах, и более смелые дизайнеры обращались к смелым геометрическим мотивам диагональный и косой.

Таким образом, очевидно, что на протяжении всей истории прямой угол с энтузиазмом применялся при строительстве зданий по нескольким причинам: (1) он создавал устойчивые конструкции; (2) Это было легко и эффективно при резке и соединении элементов конструкции; (3) Это также было полезно для разбивки земельных участков, расчета налогов на эти участки и восстановления границ после наводнения; (4) Созданные архитектурные пространства были простыми, открытыми и функциональными.

Как построить фундамент беседки или сарая — Cedarshed USA

3 / Определить тип фундамента
1. PATIO STONE FOUNDATION
Если почва устойчивая и имеет достаточный дренаж, вы можете установить камни для террасы прямо на твердую уплотненную почву. В противном случае положите его на гравий или щебень, как описано выше.

САДОВЫЕ НАБИВКИ: Начиная с одной секции пола, расположите камни по ее периметру и определенным балкам. (Для получения дополнительной информации см. Специальное руководство по эксплуатации) Для правильной установки используйте прямой кусок пиломатериала 2х4 по краю и плотницкий уровень. Добавьте или удалите грунт / песок под каждым камнем до уровня.Таким же образом завершите оставшиеся секции пола. Когда все панели пола будут выровнены друг с другом, переверните, привинтите их и снова установите на ровный фундамент.

ГАЗЕБО: Поместите камни террасы на контур беседки, как описано выше. Подробнее о том, как и куда уходят камни, см. В специальном руководстве по эксплуатации. Для правильной установки используйте прямой брус размером 2х4 по краю и плотницкий уровень.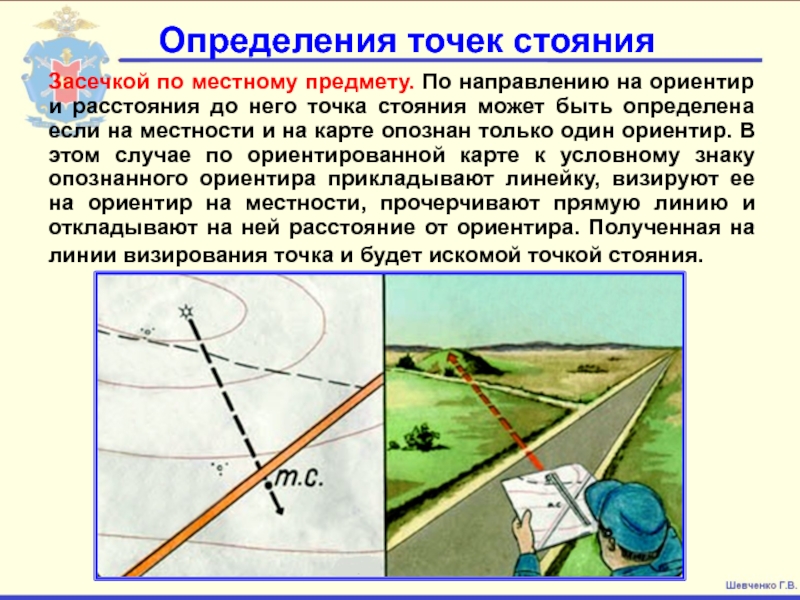 Добавьте или удалите грунт / песок под каждым камнем до уровня. Когда камни выровнены, поместите готовую подконструкцию (обод, длинную и короткую балку и основной блок) сверху.Еще раз используйте уровень, чтобы подтвердить положение и внести необходимые корректировки.

2. ФУНДАМЕНТ ДЛЯ БАЛКИ, ОБРАБОТАННОЙ ДАВЛЕНИЕМ 4×4
Вы можете строить прямо на балках, обработанных давлением, или железнодорожных шпалах, уложенных на правильно подготовленной строительной площадке. Прокладывайте балки перпендикулярно балкам перекрытия. Для правильной установки используйте прямой брус размером 2х4 по краю и плотницкий уровень.

Чтобы предотвратить смещение балок, закрепите их арматурным стержнем диаметром 1/2 дюйма, вставленным в отверстия, просверленные в балках, и вбитым на 3–4 фута в землю.Оставьте каждую сторону или конец фундамента открытыми, чтобы обеспечить дренаж и циркуляцию воздуха под полом.

ФУНДАМЕНТ, ОБРАБОТАННЫЙ ДАВЛЕНИЕМ 4×4
Этот простой фундамент состоит из балок, обработанных давлением, уложенных непосредственно на уплотненное гравийное основание. Используйте арматурный стержень 1/2 дюйма, чтобы предотвратить смещение балок. Балки крепятся к балкам с помощью оцинкованных гвоздей 16d.

3. ФУНДАМЕНТ БЕТОННОЙ ПЛИТЫ
Обычно плита толщиной 3-4 дюйма уложена на основание из 4 дюймов гравия или щебня достаточно, но он может варьироваться в зависимости от вашего географического положения.

Использование либо собственного бетона, либо его доставки грузовиком, готового к заливке, зависит от того, сколько времени и усилий вы должны посвятить проекту. Плита для нашего ранчо 8×10 футов или 10-футовая беседка на глубину 4 дюйма потребует приблизительно 1 кубический ярд предварительно смешанного бетона.

Используйте следующую процедуру:
1. Выкопайте зону перекрытия и траншею для фундамента.

2. Выкопайте участок плиты на глубину 6 дюймов. Это поместит поверхность готовой плиты на 2 дюйма над землей (4 дюйма гравия)

3.Установите струны тестовой доски так, чтобы они представляли внешнюю поверхность плиты. В каждом углу проведите отвес от пересекающихся струн до дна траншеи, затем вбейте в эту точку кол 2×4. Снова используя отвес, вбейте гвоздь в верхнюю часть стойки в том месте, где его касается отвес. Между столбами привяжите нитки. Используя струны в качестве направляющих, вбейте колья формы 2×4 по периметру траншеи, расположенные на расстоянии 2 футов между центрами.

4. Прикрепите опалубочные доски к кольям двуглавыми гвоздями.Убедитесь, что стойки находятся на внешней стороне досок и на одном уровне с ними или под ними.

5. Используйте колья 2х4, чтобы закрепить углы форм.

6. Засыпьте котлован гравием толщиной 4 дюйма, затем установите пластиковую пароизоляцию.

7. Разложите или залейте бетон граблями или мотыгой, аккуратно утрамбовывая его в местах основания. Используйте лопату, чтобы переместить бетон в траншею для фундамента. Сделайте заливку примерно на 1 дюйм выше форм, чтобы дать возможность осесть. Используйте длинный 2×4, чтобы выровнять бетон. Перемещайте доску из стороны в сторону, подтягивая ее к себе.

8. Используйте чистовые инструменты, такие как гладильная терка и шпатель, чтобы выровнять бетонную поверхность. Дайте бетону полностью высохнуть (от семи до десяти дней).

ФУНДАМЕНТ ИЗ БЕТОННЫХ ПЛИТ
1. Отсыпка грунта гравием; установить пароизоляцию.

2. Залить бетон в формы и разложить граблями или лопатой. Для стяжки бетонного уровня используйте длинную стяжку 2х4.

3. С помощью чистовых инструментов, таких как утка и шпатель, выровняйте бетонную поверхность до желаемой отделки.

Как вы должны запустить мяч, чтобы достичь наибольшего расстояния?

В эпизоде ​​«Движение снаряда» телеканала NBC Learn «Наука о футболе НФЛ» вы видите, что мячи с иглами движутся по дуге, известной математикам как парабола.

В любом футбольном матче обе команды сражаются друг с другом, а также с общим противником — гравитацией. Гравитационное притяжение Земли делает передачу на дальние дистанции сложной задачей и сбивает даже самые сильные удары ногами и метками.

Поскольку сила тяжести постоянна, опытные квотербэки и кикеры могут учитывать ее эффекты, чтобы максимально эффективно перемещать мяч вниз по полю. Как и все снаряды, футбольный мяч, будучи выпущенным, следует по траектории, известной в математических терминах как парабола — симметричная дуга, которая в конечном итоге возвращает мяч обратно на землю. (В реальной жизни на полет снаряда влияет не только сила тяжести, но и ветер, и сопротивление воздуха, поэтому парабола не будет идеальной.)

Параболы изучались тысячелетиями, и их свойства хорошо изучены. Для любого снаряда, находящегося под действием силы тяжести, расстояние, достигаемое во время его полета, равно sin (2θ) X v² / g, где v — начальная скорость снаряда, g, — ускорение к Земле под действием силы тяжести и θ — угол, под которым запускается снаряд.

Это может выглядеть как сложное уравнение, но пару переменных можно игнорировать.Во-первых, поскольку сила тяжести постоянна, г и будут одинаковыми независимо от того, как игрок бьет по мячу. Во-вторых, для игрока, пытающегося как можно глубже забить мяч, вы можете предположить, что он бьет так сильно, как может физически, поэтому против зависит просто от того, насколько сильно он может ударить, а не от какого-либо стратегического решения для данного конкретного случая. плоскодонка.

Единственный выбор, который он должен сделать, чтобы максимизировать расстояние, — это угол, под которым он бьет по мячу. Из приведенного выше уравнения видно, что расстояние, пройденное мячом, будет наибольшим, когда sin (2θ) наибольший.Синусоидальная функция достигает своего наибольшего выходного значения, 1, с входным углом 90 градусов, поэтому мы можем видеть, что для пантов с наибольшим радиусом действия 2θ = 90 градусов и, следовательно, θ = 45 градусов. Другими словами, снаряд летит дальше всего, когда он запущен под углом 45 градусов.

Но как насчет попытки увеличить высоту снаряда для увеличения времени зависания? В параболе максимальная высота, достигаемая снарядом, равна (sin (θ)) ² X v² / 2g. Еще раз, мы можем игнорировать v и g, по тем же причинам, что и выше.(Любой, кто хочет поднять снаряд как можно выше, просто запустит его как можно быстрее, а гравитация будет постоянной.)

Итак, чтобы отправить снаряд так высоко, как он может лететь, вы можете увидеть, что вы хотите сделать ( sin (θ)) ² как можно больше, что означает просто сделать sin (θ) как можно большим. Как упоминалось выше, синусоидальная функция достигает своего наибольшего выходного значения, 1, с входным углом 90 градусов, поэтому мы можем видеть, что для заоблачной высоты θ = 90. Это означает, что лучший способ запустить высотный Снаряд должен отправить его под углом 90 градусов к земле — прямо вверх.

Конечно, вертикальная плоскодонка не очень помогает с положением на поле, так что вряд ли в ближайшее время вы увидите на футбольном поле плоскодонку под углом 90 градусов.

No related posts.