штукатурим по маякам и выравниваем плоскости и углы
Штукатурка внутренних углов: допустимые отклонения.
Углы – один из самых сложных элементов в отделке стен. В отличии от штукатурки стен по маякам, трудность заключается в том, что даже самое минимальное отклонение, незаметное не стене, в углу хорошо видно.
Требования к оштукатуриванию довольно строгие:
- Линия должна быть идеально ровной с отклонением не более 1мм.
Нарушение требования ведет к искривлению угла, затруднению крепежа навесной мебели, внешней эстетической непривлекательности такой отделки.
- Отсутствие уклонов: стены строго вертикальны, потолки – горизонтальны.
Значительный уклон стены затрудняет фиксацию навесной мебели, декоративных элементов, не позволяет приставлять предметы вплотную к стене (сверху или снизу обязательно будет косой просвет).
- Строго 90 градусов.

Усложняет монтаж поворотных элементов коммуникаций. Например, при проведении отопления, сложнее проложить трубу, ведь стандартные «повороты» бывают только 90 и 45 градусов.
Сложнее стыковать пластиковые плинтусы.
Небольшие отклонения, искажения допустимы, но лишь в 1-2мм. При значительной исходной кривизне добиться качественных результатов сложнее. Поэтому штукатурка углов стен своими руками считается непростой задачей.
Как сделать прямой угол.
Незначительный уклон стены, который можно выровнять раствором – 15-20 мм. Работу можно сделать и своими руками, необходимо лишь соблюдать правила:
- Штукатурка стен по маякам. Без правильно расставленных ориентиров выполнить работу качественно затруднительно. Маяки устанавливают по отвесу или уровню на расстоянии 10-15 см от угла.
- Соблюсти последовательность.
 Штукатурка внутренних и внешних углов не укладывается сразу. Вначале набрасывают жидковатый раствор, дают ему схватиться, только потом наносят основную часть.
Штукатурка внутренних и внешних углов не укладывается сразу. Вначале набрасывают жидковатый раствор, дают ему схватиться, только потом наносят основную часть.
Если выравнивание предполагает наличие толстого слоя раствора, то работу выполняют в два приема: набрасывают один слой, дают ему затвердеть, затем второй. Штукатурка стен по маякам, нанесенная сразу толстым слоем, отваливается, отрывается от стены под собственным весом, связь слоя с основанием будет слабой.
- Не торопиться. Не стоит сразу сделать все сразу. Сначала выравнивают правилом стену по маякам, не доходя до угла 1-2см. Затем, используя правило, ровняют уже сам угол.
Простой способ сделать штукатурку ровной – поэтапная работа. Сначала обрабатывают одну стену, дают ей просохнуть. Затем выравнивают вторую, сопряженную с ней. Так работать легче, ведь одна стена уже ровная и твердая.
Еще проще
 Его используют как правило, направляя движение снизу-вверх. Инструмент опирается и скользит по маякам, укрепленных вблизи углов.
Его используют как правило, направляя движение снизу-вверх. Инструмент опирается и скользит по маякам, укрепленных вблизи углов.Как выровнять угол при значительной кривизне стены.
При уклоне стен более, чем на 1-2 см, необходимы дополнительные операции, нельзя выровнять искажение стены в 5-7 см!
«Отвешивание».
Степень деформации стен нужно достоверно оценить. Для этого поверхность изучают с помощью отвеса – тяжелого металлического грузика на веревке или строительного уровня, закрепленного на правиле.
Слишком глубокие впадины лучше подготовить до установки маяков, чтобы последние не мешали работе. На небольших по площади, но глубоких искажениях, можно делать штукатурку стен по маякам сразу.
Армирование.
Слишком толстая штукатурка плохо держится на стене. Поэтому места, где с помощью раствора выравнивают кривизну стены, армируют.
Для этого в стене высверливают отверстия для дюбелей через каждые 40-50см. В них укрепляют арматуру – армирующую сетку. Можно использовать куски проволоки, которые оплетаются вокруг шурупов.
В них укрепляют арматуру – армирующую сетку. Можно использовать куски проволоки, которые оплетаются вокруг шурупов.
Арматура должна находиться в толще будущего выравнивающего слоя. Поэтому ее располагают не ближе 1-2см к поверхности будущей штукатурки.
В деревянных домах штукатурка стен по маякам с глиняной основой, в качестве арматуры используют дранку, отходы пиломатериалов. Сечение реек не должно превышать 4-5см кв.
Дранку просто прибивают к стене гвоздями, располагая под наклоном (45 град. к полу) с расстоянием 3-5см.
Перед тем, как вывести угол, армированным выравнивающим вставкам дают полностью просохнуть.
Оштукатуривание.
Выравнивающая штукатурка не отличается по составу от обыкновенной, поэтому ее наносят по стандартным правилам:
- Грунтовка. Чтобы раствор имел прочное сцепление со стеной, последнюю покрывают слоем грунтовки.
- Обрызг – нанесение жидкого, сметанообразного раствора на стену и арматуру.
 Для более надежного контакта раствора со стеной, он набрасывается с ударом, своеобразными «шлепками».
Для более надежного контакта раствора со стеной, он набрасывается с ударом, своеобразными «шлепками». - Грунт – основной слой штукатурки. Для очень кривых стен грунт лучше наносить в несколько (2-3) этапов с просушкой каждого слоя.
Как сделать ровные углы при минимальной штукатурке.
При небольших деформациях стен (1-2 см) можно не выравнивать всю поверхность. Если возникает необходимость обойтись минимальным по времени и затратам ремонт, выравнивают только непосредственно углы комнат, стыки стен с полом и потолком.
Штукатурка в комнате остается кривой, но из-за идеально ровных углов, этого не заметно.
Вот как сделать ровный угол стены:
- Стены. Штукатурку наносят в углы и здесь выравнивают. Но далее, по протяженности стены, слой раствора сводят на нет. Чтобы вставка была незаметной, необходимо избегать создания резких перепадов. Для вставки толщ. 1-2см ширина должна быть ок.15-20см.
- Полы.
 Здесь выравнивание необходимо для монтажа плинтуса.
Здесь выравнивание необходимо для монтажа плинтуса. - Потолки.
Однако поверхность потолка необходимо также сделать ровной в области примыкания к стене, но с минимальной толщиной.
Такой экономичный способ выравнивания применим только при необходимости небольших вставок в 1-2см. На более глубоких деформациях вставки будут слишком заметны.
Штукатурка закругленных углов стен своими руками.
Углы с закруглением штукатурить не сложнее, чем обыкновенные:
- Выравнивание стен. Стены штукатурят и выравнивают по стандартной технологии.
- Армирование. Эллипс незначительного диаметра не требует арматуры. Но при создании значительных закруглений (при диам. более 10см), их укрепляют армирующей сеткой, проволокой. Можно обойтись вкручиванием шурупов (шаг не менее 20 см).

- Обрызг.
- Применение шаблона. Набрасывают раствор и снимают его излишки правилом. В случае с закруглениями роль маяков выполняет поверхность обеих стен, а правила – специально изготовленный шаблон.
Такое искривленное правило делают так: прикладывают к скруглению легко гнущуюся, но прочную проволоку, вдавливают ее в эллипс. Так получают точный рисунок будущего шаблона.
Проволоку прикладывают к фанере (не менее 6мм толщ.) или листовой стали, жести. Обводят карандашом. По этой линии обрезают излишки. Шаблон готов!
Когда штукатурка углов полностью высохнет, наносят последний, накрывочный слой с применением мелкого песка (фракция не более 1мм). Этот слой затирают войлоком, чтобы сделать стену максимально гладкой.
Стоит помнить, что закругленные углы затирают только горизонтальными движениями.
Необходимые инструменты и приспособления.
Штукатурка внутренних углов требует наличия стандартного набора инструментов и расходных материалов. Некоторые из них могут быть заменены, другие – нет.
Некоторые из них могут быть заменены, другие – нет.
Маяки.
Стальной профиль – лучший вариант: металлические элементы не «боятся» воды, легко укрепляются, идеально ровные. Но не подходят для проведения экономичного, минимального ремонта.
Деревянные маяки – рейки небольшого сечения (2.5х3см и тоньше). Трудность их применения заключается в целом наборе недостатков:
- Искривления. Трудно подобрать достоверно ровные рейки, ведь древесина постоянно деформируется, напитываясь влагой из воздуха и отдавая ее.
- Разбухание. Древесина увеличивается в размере, разбухает. Применительно к маякам этот недостаток наиболее актуален, ведь штукатурка – это «мокрая» работа.
- Демонтаж оцинкованных стальных маяков считается необязательным. Деревянные же рейки необходимо обязательно извлекать перед тем, как ровнять углы штукатуркой. Образовавшиеся пустоты, борозды восполняют раствором, выравнивают.
 Это требует дополнительных усилий и времени.
Это требует дополнительных усилий и времени.
Однако дощатые направляющие значительно дешевле металлических и иногда используются при жестком бюджете, выделенном на ремонт помещения.
Маяки из раствора – фрагменты смеси, нанесенные на стену с удобным для работы правилом шагом. Такие ориентиры имеют преимущества: их не нужно удалять, да и обходятся они бесплатно. Но работать с ними не удобно, выравнивать довольно сложно. Такой способ приемлем для небольших стен и применяется большей частью опытными специалистами.
Проверка углов лазерным построителем плоскостей.
Лазерный нивелир – наиболее удобный и точный контрольный инструмент. Для проверки угла его достаточно установить по линии биссектрисы (приблизительно) и совместить вертикальную плоскость света с обследуемой вертикальной линией.
Инструмент.
Штукатурка стен по маякам потребует наличия основных инструментов, которые сложно заменить:
- Правило.
 Широкая (10-12см) жесткая алюминиевая «рейка» не менее 130-150см длиной. Позволяет точно оценить состояние штукатурного слоя, его искривления, впадины и выпирания.
Широкая (10-12см) жесткая алюминиевая «рейка» не менее 130-150см длиной. Позволяет точно оценить состояние штукатурного слоя, его искривления, впадины и выпирания. - Полутерок. Деревянная, пластиковая или стальная «доска» с рукояткой. Длина полутерка ок. 50-70см. Используется для разравнивания раствора на стене.
- Терка. То же, что и полутерок, но небольшого размер (20см). Удобна в плохо доступных местах, а также для выравнивания, накрывки и затирки.
- Уголок – металлическое или деревянное приспособление в форме прямого треугольника. Используется для контроля ровности, а также как шаблон для оштукатуривания, протяжки штукатурного раствора. Используется как правило.
Чем больше размер инструмента, тем достовернее результат измерений. Для штукатурных работ наиболее удобен угольник с длиной катета 100 см, так как сделать угол 90 градусов штукатуркой легче, используя максимальную площадь сопряженных стен для ориентира.
- Кельма, шпатель. Мастерок необходим для набрасывания раствора на стену. Если объем работ небольшой, он может быть заменен шпателем.
- Отвес, строительный уровень. Отвесом работу по изучению уклона стен и установке маяков можно провести быстрее (если работать вдвоем), поскольку веревку можно натянуть на всю высоту помещения.
Уровень (ватерпас) удобнее, но он короткий, что затрудняет работу. Однако без него трудно обойтись.
Кроме этого, могут понадобиться приспособления и инструменты для приготовления строительного раствора – корыто, совковая лопата для песка, ведра. Если вставки штукатурки связаны не с устройством углов, а лишь с их выравниванием, раствор приготавливают в ведре, перемешивая миксером (насадкой для эл. дрели) или шпателем – на пол ведра раствора.
Возможна ли штукатурка углов стен своими руками.
Для новичка штукатурка стен по маякам – занятие сложное. Но выравнивание углов принято считать наиболее трудным занятием, требующим высокого профессионализма.
Однако, при соответствующем кропотливом и добросовестном подходе, создание ровных углов возможно и для воплощения своими руками. Разница с работой профессионалов будет заключаться лишь во времени, затраченном на выполнение задачи.
data-matched-content-ui-type=»image_stacked» data-matched-content-rows-num=»2″ data-matched-content-columns-num=»3″ data-ad-format=»autorelaxed»>Строительный угольник — назначение и применение измерительного прибора
Любые строительные и ремонтные работы связаны с использованием различных измерительных инструментов. К таковым инструментам относятся рулетки, уровни, правила и угольники. Именно с последним прибором следует ознакомиться подробно, чтобы узнать его возможности и особенности правильного применения. Угольник предназначен для определения точности перпендикуляра двух поверхностей. Если возникла необходимость приобретения инструмента, то первоначально рекомендуем разобраться с устройством, видами и особенностями выбора угольников.
Угольник — его назначение и устройство
Угольником именуется измерительный прибор, основывающийся на двух линейках, которые расположены друг к другу под прямым углом 90 градусов. Простая конструкция прибора положительно отражается на его стоимости, поэтому купить строительный угольник можно по цене от 25 гривен в интернет магазине «Цилиндр».
Свое применение инструмент нашел в различных сферах — строительство, слесарное и столярное дело, а также производство. В силу своего устройства можно сказать, что предназначен инструмент для получения прямых углов. С его помощью не только удается получить прямой угол для построения двух перпендикулярных поверхностей, но еще и произвести поверку с целью определения конструкции на наличие брака.Простота конструкции угольника позволяет изготавливать инструмент самостоятельно из подручных средств. Для изготовления угольника понадобится взять две линейки, и расположить их перпендикулярно друг к другу, обеспечив надежное соединение. Однако пользоваться самодельным инструментом можно только по хозяйству, а в случае необходимости выполнения точных работ, следует воспользоваться инструментом заводского производства.
Однако пользоваться самодельным инструментом можно только по хозяйству, а в случае необходимости выполнения точных работ, следует воспользоваться инструментом заводского производства.
Какие материалы используются для производства угольников
Для производства современных угольников используются такие материалы, как древесины, сталь и пластик. Одними из самых прочных являются инструменты из стали. Пластиковые угольники являются самыми дешевыми, а деревянные применяются при работе с хрупкими материалами, например, керамическая плитка, стекло и т.п.
На одной или двух направляющих рассматриваемых инструментов нанесены шкалы, которые позволяют применять прибор не только для выравнивания углов, но еще и проведения измерительных манипуляций. Длина линеек может достигать отметки в 1600 мм, а самыми короткими являются модели от 60 мм.
Другое название инструмента — уголок, а аналогом этого прибора является раскладной угольник, именуемый малкой. Отличается малка от обычного угольника тем, что направляющие имеют не жесткое соединение, а подвижное (шарнирное). Для изготовления металлических угольников используются следующие разновидности стали:
Для изготовления металлических угольников используются следующие разновидности стали:
- Х
- У8А
- 9Х
- ШХ15
Стальные угольники являются самыми востребованными. Однако они бывают разными, и подвергаются обработке высокими температурами с целью закаливания до определенной степени твердости. Максимальная твердость угольников составляет 50-58 HRC. Высокая степень твердости нужна для того, чтобы обеспечить высокую точность измерительных работ. По точности угольники бывают с 0, 1 и 2 классом. Самым точным прибором считается инструмент, который имеет нулевой класс точности. Используются такие инструменты преимущество в специальных метрологических службах и поверочных станциях.
Угольники с первым классом точности применяются специалистами — каменщиками, сварщиками, строителями и т.п. Самыми низкоточными являются приборы второго класса точности, нашедшие свое применение среди домашних мастеров. Самодельные инструменты не имеют никакого класса точности, поэтому применяться для выполнения высокоточных работ они не могут.
Поверочные угольники — типы и где они применяются
Существует пять видов поверочных угольников, которые нашли свое применение для контроля прямых углов в различных сферах. Рассмотрим более подробно, какие виды поверочных угольников бывают, и чем они отличаются между собой.
- Лекальный — обозначается в виде букв УЛ. Используется для нанесения разметочных линий. Прибором осуществляется контроль перпендикулярности соответствующих элементов различных конструкций. Главное преимущество прибора заключается в его высокой точности. Достигается это за счет наличия острых измерительных поверхностей. Отличительная особенность инструмента заключается в том, что одна сторона представлена в виде короткой части с утолщенным размером, а вторая длинная с утонченным профилем
- Лекальные плоские — для обозначения применяется аббревиатура УЛП. Отличительная особенность этого типа инструмента от предыдущего в том, что обе части оснований представлены в виде утолщенного профиля.
 Служат лекальные плоские угольники для нанесения разметки на плоской поверхности
Служат лекальные плоские угольники для нанесения разметки на плоской поверхности - Лекальный цилиндрический или УЛЦ — кардинально отличается по конструкции от предыдущих двух вариантов. Представлен прибор в виде цилиндра с фасками. Основание цилиндра с боковой поверхностью создают высокоточный прямой угол. Приборы представляют собой эталонные или образцовые изделия, которые нашли свое применения в метрологических станциях и в сфере машиностроения. Лекальные цилиндрические угольники имеют не только нулевой, но и первый класс точности, и бывают разной длины
- Плоские — для их обозначения используется аббревиатура УП. Состоит инструмент из двух плоских оснований. Это самый распространенный вариант угольников, которые выпускаются с разными классами точности от 0 до 2
- Широкие — свое название они получили по причине того, что одна сторона основания имеет увеличенную конструкцию профиля. Широкое основание предназначается для того, чтобы иметь возможность расположения инструмента на плоской поверхности без его удержания.
 Широкие угольники маркируются в виде двух букв УШ
Широкие угольники маркируются в виде двух букв УШ
В домашнем хозяйстве применяются обычные плоские угольники. Они в свою очередь классифицируются на три вида, с которыми следует ознакомиться более подробно. Зная, какие виды плоских угольников бывают, не составит большого труда осуществить их правильный выбор в зависимости от поставленной задачи.
Разновидности плоских угольников и сфера их применения
Рассматриваемые виды инструментов классифицируются на виды по способу их применения. Угольники бывают следующих видов:
- Столярные — изготавливаются из стали и древесины. Свое применение они нашли в столярном деле при проведении деревообрабатывающих работ. По длине такие угольники бывают от 10 см до 10 метров
- Разметочные — приборы, которые служат специально для нанесения разметки карандашом. Для этого в конструкции профильных оснований имеются отверстия, посредством которых наносится разметка
- Комбинированные — отличительная их особенность в наличии подвижного соединения, посредством чего прибор можно использоваться для настройки необходимого угла.
 На рукоятки инструмента имеется камера, заполненная водой с пузырьком воздуха. Посредством которого удается определить ровность поверхностей, углы которых проверяются угольником
На рукоятки инструмента имеется камера, заполненная водой с пузырьком воздуха. Посредством которого удается определить ровность поверхностей, углы которых проверяются угольником - Магнитные — особый вид инструментов, которые нашли свое применение среди сварщиков. Магниты, которые крепятся к основанию прибора предназначены для временного соединения металлических заготовок под прямым углом. После временного соединения заготовок специалист осуществляет соединение заготовок посредством сварочного оборудования
Немаловажно также отметить, что угольники могут быть представлены в виде равнобедренного прямоугольного треугольника (угольник Свенсона). Две стороны такого инструмента расположены под прямым углом. Такая конструкция прибора способствует достижению высокой прочности, что положительно отражается на точности угольника. Стоят они дороже обычных профильных приборов, но при этом они имеют высокий класс точности.
Выбор инструмента или что надо учитывать при покупке угольников
Выбор инструмента требует особого подхода.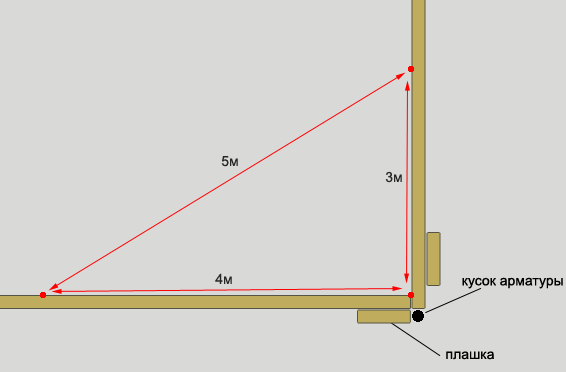 И не имеет значения, какой тип этого прибора — ручной или электрический, измерительный или пневматический. Первоначально надо определиться с фронтом работ, которые планируется выполнять инструментом. На основании работ, которые планируется выполнять прибором, можно сделать вывод о необходимости приобретения угольника соответствующего класса точности. Если прибор нужен для высокоточных манипуляций, тогда выбираются изделия с 0 и 1 классом точности. Для работы с металлическими заготовками, древесиной и прочими материалами используются изделия со вторым классом точности.
И не имеет значения, какой тип этого прибора — ручной или электрический, измерительный или пневматический. Первоначально надо определиться с фронтом работ, которые планируется выполнять инструментом. На основании работ, которые планируется выполнять прибором, можно сделать вывод о необходимости приобретения угольника соответствующего класса точности. Если прибор нужен для высокоточных манипуляций, тогда выбираются изделия с 0 и 1 классом точности. Для работы с металлическими заготовками, древесиной и прочими материалами используются изделия со вторым классом точности.
При выборе угольника в интернет магазине «Цилиндр» следует учитывать ряд следующих особенностей:
- Размер — здесь подразумевается длина сторон угольника. Чем длиннее профильные части, тем соответственно выше точность проводимых измерений. Однако покупать угольник с длинными основаниями не стоит, если прибор планируется использовать для работы с мелкими деталями.
 Для работы с керамической плиткой и прочими мелкими деталями достаточно инструментов, длина которых не превышает 30 см
Для работы с керамической плиткой и прочими мелкими деталями достаточно инструментов, длина которых не превышает 30 см - Углы измерений — для разметки и проверки прямых углов, необходимо выбирать модели классического типа, которые оснащены неподвижными соединителями
- Наличие разметки на основании — позволяет использовать инструмент не только для нанесения разметки прямых углов, но и осуществления соответствующих измерений
- Качество фиксации — здесь важно проследить одну особенность, которая проявляется не только в длине профильных оснований, но и в толщине оснований. Чем длиннее основание, тем толще оно должно быть. Если длина линейки будет большой, но при этом основания тонкими, то здесь будут присутствовать большие значения погрешностей
- Материал производства — самыми популярными являются металлические угольники, отличающиеся не только прочностью, но еще и высоким эксплуатационным ресурсом. Кроме того, металлическим угольником удобно работать, но далеко не во всех случаях.
 Именно поэтому в некоторых случаях рационально рассмотреть варианты пластиковых и деревянных угольников
Именно поэтому в некоторых случаях рационально рассмотреть варианты пластиковых и деревянных угольников
На основании вышеперечисленных особенностей следует выбирать угольники для выполнения соответствующих манипуляций. Большой выбор угольников представлен в интернет магазине «Цилиндр». В каталоге сайта представлено большое разнообразие различных моделей, поэтому каждый найдет для себя подходящий вариант.
Как пользоваться угольником правильно
Рассматриваемый инструмент является незаменимым помощником для каждого строителя и ремонтника. Если мастера знают, как правильно пользоваться инструментом, то новички не в курсе особенностей правильного использования угольника.
Рассмотрим, как правильно пользоваться угольником, и что при этом надо знать.
- Как наносить перпендикуляр. При помощи уголка можно нанести маркером или карандашом линии под прямым углом. Линии рисуются со стороны расположения квадратной части прибора
- Проверка соединения заготовок под прямым углом — достигается за счет прикладывания прибора к элементам, чтобы проверить правильность углов.
 Особенно часто для проверки правильности прямых углов применяются инструменты в сфере сборки и производства мебели
Особенно часто для проверки правильности прямых углов применяются инструменты в сфере сборки и производства мебели - Прочерчивание линий под углов 45 градусов. Мало кто знает, что при помощи уголька можно прочертить не только прямой угол, но еще и разделенный пополам на 45 градусов. Делается это очень просто — для этого изначально проводится прямой угол в виде двух линий, а затем следует поставить точку с внутренней стороны прибора (где основания соединяются друг с другом). После этого остается только прочертить линию, разбив прямой угол пополам
- Рисование параллельных линий — для этого прибор следует приложить к краю заготовки, и измерить необходимое расстояние. После этого угольник перемещается до соответствующей отметки, нанося при этом параллельную линию, соответствующую краю заготовки
- Чтение и нанесение различных углов — опорной точкой является прямой угол, а на необходимом значении разметки делается соответствующая отметка при помощи карандаша.
 После этого проводится соответствующая прямая линия
После этого проводится соответствующая прямая линия - Направление для резки циркульной пилой — для этого прибор располагается на заготовку, и фиксируется струбциной. После этого осуществляется резка инструментом в параллельном направлении катету прибора
- Использование в качестве обычной линейки — позволяет определить нужные размеры
Этот специфический инструмент нашел свое широкое распространение в различных сферах. Получить прямой угол можно без угольника, но с применением специального инструмента сделать это не только проще, но еще и с максимальной точностью.
В завершении следует отметить, что угольником называется специализированный инструмент, главным предназначением которого является получение прямого угла с целью последующего соединения деталей, а также для их правильности проверки при соединении.
Научно-исследовательская работа «Измеряем углы без транспортира»
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА с. РУССКИЙ КАМЕШКИР
РУССКИЙ КАМЕШКИР
(МБОУ СОШ с. Русский Камешкир)
Измерение углов без транспортира
Исследовательско — практическая работа
Работу выполнила ученица 6 Б класса
Прасулова Кристина
Научный руководитель: Скосырева Лилия Васильевна
Предмет: математика
2019 г
Содержание
1. Введение
2. Цели и задачи
3. Обзор литературы по данной теме
4. Методика работы
5. Описание работы
6. Выводы
7. Используемые ресурсы
8. Приложения
Объект исследования:
углы с различными градусными мерами; инструменты для измерения углов.
Предмет исследования:
процесс измерения углов без использования транспортира.
Гипотеза:
можно предположить, что существуют углы разных градусных мер, которые
можно измерить без применения транспортира, а только пользуясь линейкой без мерных делений, клетчатой бумагой и другими подручными материалами
Методы исследования:
— поисковый метод с использованием научной и учебной литературы, а также поиск необходимой информации в сети Интернет;
— графическое моделирование, анализ и классификация полученных результатов.
Целью работы:
является знакомство с инструментами для измерения углов, исследование метода измерения углов заданной градусной меры без использования транспортира.
Задачи:
1. Провести практическую работу по построению острых углов заданной градусной меры (от 10° до 80°, кратных 10) и выявлению «контрольных» точек – узлов для лучей каждого угла.
2. Проанализировать полученные результаты и систематизировать их
Проанализировать полученные результаты и систематизировать их
3. Определить группы задач, которые можно решить с помощью исследованного метода построения углов.
4. Сделать вывод о подтверждении или опровержении выдвинутой гипотезы.
Актуальность:
в курсе геометрии при решении задач часто приходится строить иллюстративные чертежи различных фигур по заданному условию. Владение методом построения углов на клетчатой бумаге позволяет чертить заданные углы с достаточной точностью, не требует наличия транспортира и экономит время на выполнение чертежа.
Содержание:
Введение.
2. Построение углов: история и современность.
3. Практическая часть. Построение углов без помощи транспортира.
1) Построение угла 45° без помощи транспортира.
2) Построение острых углов с градусной мерой, кратной 10° без помощи транспортира.
3) Построение тупых углов с градусной мерой, кратной 10°, от 100° до 170°
без помощи транспортира.
4) Построение углов с помощью угольников.
5) Построение углов 30°, 45°, 60°, 90° в практической жизни.
6) Измерение углов по пальцам рук.
4. Выводы и заключение.
5. Литература.
1.ВВЕДЕНИЕ
Увлечение отдельной областью математики часто начинается с размышления над какой-то особенно понравившейся задачей. При изучении в 5 классе на уроках математики темы «Построение угла заданной величины», мы научились строить углы с помощью транспортира.
И сразу обнаружили, что некоторые углы гораздо быстрее и более точно можно начертить в тетрадке с помощью одной только линейки.
Углы с градусными мерами 90° и 180° можно построить, проведя луч по горизонтальным или вертикальным линиям тетради, а углы в 135° и 45° — по диагоналям клеток.
Именно тогда я и заинтересовалась вопросом, а можно ли построить и другие углы, используя только клетчатую бумагу и линейку?
Так появилась моя исследовательская работа «Строим углов без транспортира».
Казалось бы, что увлекательного можно найти на клетчатой плоскости, то есть, на листке бумаги, расчерченном на одинаковые квадратики?
Оказывается, задачи, связанные с бумагой в клеточку, достаточно разнообразны.
Своё исследование я решила начать с изучения ответа на вопрос, как решались задачи на построение углов, начиная с древних времен и до сегодняшнего времени.
2. ПОСТРОЕНИЕ УГЛОВ: ИСТОРИЯ И СОВРЕМЕННОСТЬ
Понятие градуса и появление первых инструментов для измерения углов связывают с развитием цивилизации в древнем Вавилоне, хотя само слово градус имеет латинское происхождение (градус–от лат.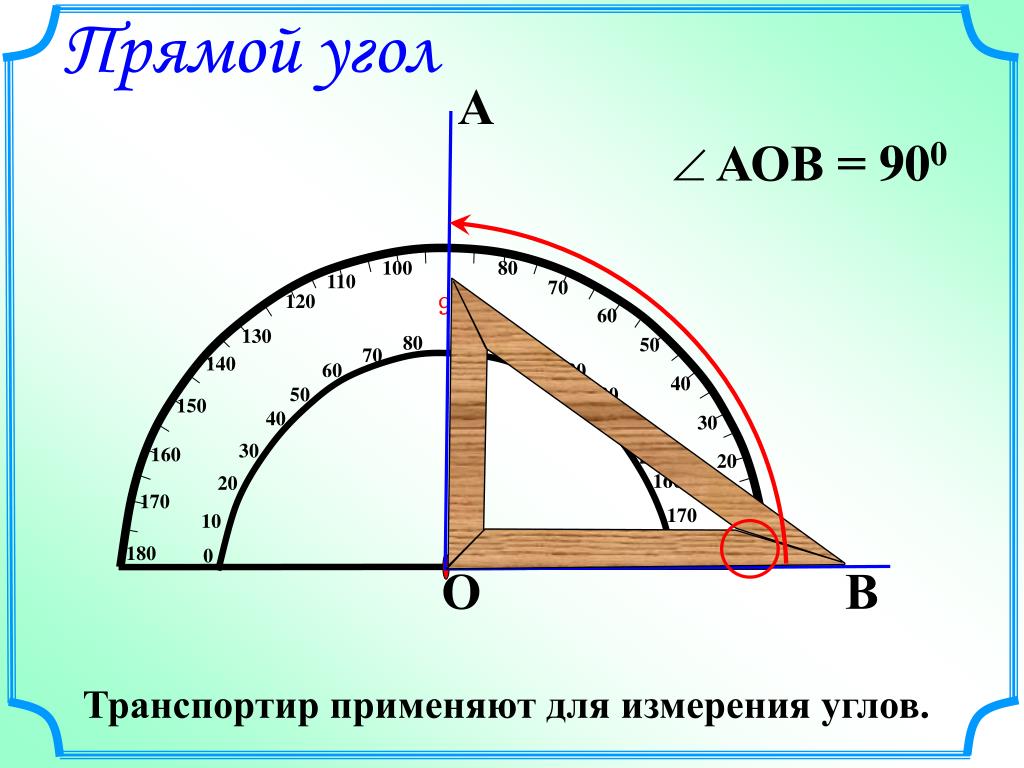 gradus- “шаг, ступень”). Градус получится, если, разделить окружность на 360 частей.
gradus- “шаг, ступень”). Градус получится, если, разделить окружность на 360 частей.
Возникает вопрос – а почему древние вавилоняне делили именно на 360 частей.
Дело в то, что в Вавилоне была принята шестидесятиричная система счисления. Более того, число 60 считалось священным. Поэтому все вычисления были связаны с числом 60.
История не сохранила имя ученого, который изобрел транспортир – возможно в древности этот инструмент имел совсем другое название.
Современное название происходит от французского слова ”ТRANSPORTER”, что означает “переносить”.
Первые задачи на построение углов возникли в глубокой древности. Возникли они из хозяйственных потребностей человека. Уже древними архитекторами и землемерами приходилось решать простейшие задачи на построение, связанные с их профессией.
Первые греческие ученые, которые занимались решением геометрических задач на
построение, были: Фалес Милетский (624 – 547 гг.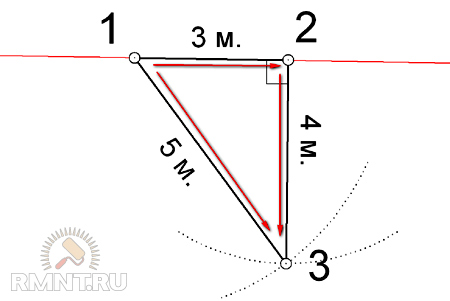 до н.э.), Пифагор (ок. 580 – 500 гг. до н.э.), Платон (427 – 347 гг. до н.э.).
до н.э.), Пифагор (ок. 580 – 500 гг. до н.э.), Платон (427 – 347 гг. до н.э.).
Самые первые задачи на построение, по-видимому, решались непосредственно на
местности и заключались в проведении прямых линий и построения прямого угла.
К задачам на построение прибегали древние инженеры, когда составляли рабочий чертеж того или иного сооружения и решали вопросы, связанные с отысканием красивых геометрических форм сооружения и его наибольшей вместимости.
Задачи на построение помогали людям в их хозяйственной жизни, их решения формулировались в виде ‘практических правил», исходя из наглядных соображений.
Именно эти задачи и были основой возникновения наглядной геометрии, нашедшей довольно широкое развитие у древних народов Египта, Вавилона, Индии и др.
Платон и его ученики считали построение геометрическим, если оно выполнилось при помощи циркуля и линейки, то есть путем проведения окружностей и прямых линий. Если же в процессе построения использовались другие чертежные инструменты, например транспортир, то построение не считалось геометрическим.
Если же в процессе построения использовались другие чертежные инструменты, например транспортир, то построение не считалось геометрическим.
Древние греки вслед за Платоном стремились к геометрическим построениям и считали их идеалом в геометрии.
Но древние ученые производили измерения не только транспортиром – ведь этот
инструмент был неудобен для измерений на местности и решения задач прикладного
характера. А именно прикладные задачи и являлись главным предметом интереса древних геометров.
Изобретение первого инструмента, позволяющего измерять углы на местности,
связывают с именем древнегреческого ученого Герона Александрийского (I в. до н.э). Он описал инструмент “диоптр”, позволяющий измерять углы на местности и решать множество прикладных задач.
Но прогресс не стоит на месте и в ХVII веке был изобретен прибор нивелир, а в следующем веке английским механиком Джессе Рамсденом был изобретен другой прибор – теодолит.
теодолит
Сегодня теодолит – сложный прибор. Многие работы (в том числе и строительство) требуют предварительной консультации геодезистов измерений с помощью теодолита.
Однако усовершенствование инструментов для измерения углов связано не только с
проведением строительных работ. С древнейших времен люди путешествовали, познавая окружающий мир. Путешественниками необходимо было уметь ориентироваться в пространстве. На долгие века основным ориентиром путешественников стали звезды.
Появился первый инструмент путешественников – астролябия. Астролябия(греч. astrolabion, от astron — «звезда» и labe – “схватывание»; лат. astrolabium) — угломерный прибор, служивший до начала XVIII в. для определения положений светил на небе.
Секстант — это наиболее совершенный прибор для измерения угловых координат небесных тел того времени. Его изобретение приписывается Исааку Ньютону. Секстант позволял измерять как широту, так и долготу точки наблюдения, причем с довольно высокой точностью.
Его изобретение приписывается Исааку Ньютону. Секстант позволял измерять как широту, так и долготу точки наблюдения, причем с довольно высокой точностью.
В настоящее время широко используются современные приборы для измерения углов на местности.
Геодезический инструмент для измерения углов при съёмках на местности, специальный вид компаса- буссоль.
Простейший геодезический инструмент, служащий для измерения углов наклона местности с точностью до десятых долей градуса- эклиметр.
Первый в мире транспортирНеобычный объект, который мы можем наблюдать на фото, был найден в гробнице древнеегипетского архитектора Ха (Kha). Без малого столетие прошло с тех пор, как историки впервые задались вопросом о предназначении странного артефакта.
Недавно предположение о возможном способе использования объекта выдвинула ученая-физик. Гипотеза, предложенная Амелией Спаравигной (Amelia Sparavigna) из Туринского политехнического университета (Turin Polytechnic), базируется на числовых отметках, якобы присутствующих на поверхности артефакта.
Архитектор Ха известен тем, что во времена 18-той династии (приблизительно 1400 год до нашей эры) он был задействован в строительстве гробницы фараона. Собственную же усыпальницу Ха нашли 1906 году неподалеку от Долины Царей — это открытие принадлежит археологу Эрнесто Скьяпарелли (Ernesto Schiaparelli). Среди вещей, когда-то принадлежащих архитектору, удалось идентифицировать измерительные пруты длиной в локоть (45 см), инструмент, напоминающий современный угольник, а также неизвестное полое деревянное орудие. По мнению Скьяпарелли, это был инструмент для выставления уровня.
Детально осмотрев старую находку, Амелия Спаравигна пришла к выводу, что на самом деле этот последний объект служил в качестве транспортира — в пользу такой версии свидетельствуют 16 лепестков, расположенных по окружности и находящихся на равном расстоянии друг от друга. Эти лепестки окружены круглым узором, имеющим 36 углов. Очевидно, продолговатая ровная часть инструмента устанавливалась на поверхность, после чего, с помощью уровня, можно было определить угол наклона того или иного объекта.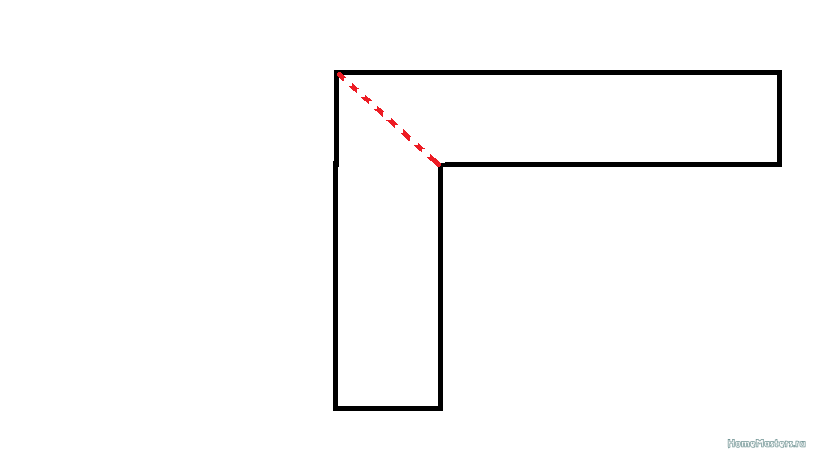
Числа, присутствующие на находке, якобы соответствовали двум измерительным системам, применявшимся в древнем Египте. Первая, внутренняя часть узора, соответствует шестнадцатичной счетной системе (соответствует современной десятичной). Вторая отображает 36 созвездий, известных египтянам.
Современные угломеры
Транспорти́р (фр. transporteur, от лат. transporto «переношу») — инструмент для построения и измерения углов. Транспортир состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы), разделённого на градусы от 0 до 180°. В некоторых моделях — от 0 до 360°.
Разновидности транспортиров
Полукруговые (180 градусов) — наиболее простые и древние транспортиры.
Круговые (360 градусов).
Геодезические, которые бывают двух типов: ТГ-А — для построения и измерения углов на планах и картах; ТГ-Б — для нанесения точек на чертежной основе по известным углам и расстояниям.
 Цена деления угломерной шкалы — 0,5°, прямолинейной — 1 миллиметр.
Цена деления угломерной шкалы — 0,5°, прямолинейной — 1 миллиметр.Улучшенные типы транспортиров, которые необходимы для более точных построений и измерений. Например, существуют специальные транспортиры с прозрачной линейкой с угломерным нониусом, которая вращается вокруг центра.
Транспортиры изготавливаются из стали, пластмассы, дерева и других материалов. Точность транспортира прямо пропорциональна его размеру (чем больше транспортир, тем меньше цена одного деления).
Полукруговой транспортир Круговой транспортир Геодезический транспортир
Угломер электронный Угломер строительный
Изобретение Леонида Чижевского — командирский угломер Угломер Чижевского представлял собой треногу, на которой крепился круг с делениями, на его оси — подвижная алидада с указателем и визирная трубка на ней. Был еще и компас для ориентирования прибора. Измерив угловые расстояния между своей батареей и целью, командир производит геометрические расчеты и передает необходимые данные по телефону или через связных на свою батарею. Используя их, обученные наводчики направляют орудия на цель. Во время стрельбы командир батареи с помощью бинокля корректирует точность попадания снарядов в цель. Новый способ стрельбы с закрытых позиций давал возможность нанести удар по врагу не одним выстрелом из одного орудия, а со всех орудий разом широким фронтом огня – веером, сохранив при этом людей и технику.
Был еще и компас для ориентирования прибора. Измерив угловые расстояния между своей батареей и целью, командир производит геометрические расчеты и передает необходимые данные по телефону или через связных на свою батарею. Используя их, обученные наводчики направляют орудия на цель. Во время стрельбы командир батареи с помощью бинокля корректирует точность попадания снарядов в цель. Новый способ стрельбы с закрытых позиций давал возможность нанести удар по врагу не одним выстрелом из одного орудия, а со всех орудий разом широким фронтом огня – веером, сохранив при этом людей и технику.
Вот такая история возникновения различных приборов для измерения углов не только на чертежах, но и на любой местности, включая даже небесное пространство!
Таким образом, я выяснила, что на современном этапе существует множество приборов, позволяющих измерять и строить углы с различной степенью точности, которые применяются людьми самых разнообразных профессий, а при изучении курса геометрии в школе для построения углов заданной градусной меры в основном используется циркуль, линейка и транспортир.
3.ПРАКТИЧЕСКАЯ ЧАСТЬ.
1)Построение угла 45° без помощи транспортира.
Угол 45 градусов в геометрии встречается часто.
Рассмотрим, как легко можно построить угол 45 градусов без транспортира, пользуясь только линейкой, карандашом и клеточками тетради.
Легче всего строить прямой угол.
Для этого из одной точки по клеточкам строим горизонтальный и вертикальный лучи.
Градусная мера прямого угла — 90 градусов. 45 градусов — половина от 90º. Значит, чтобы построить угол 45 градусов, нужно взять половину прямого угла.
Сделать это очень легко. Выбираем вершину угла на пересечении клеточек. Одну сторону угла, например, горизонтальный луч, проводим с помощью линейки по клеточкам. Для построения второй стороны угла 45º каждую клеточку делим по диагонали (отмечаем несколько точек):
Затем с помощью линейки и карандаша через эти точки проводим второй луч. Получили угол 45 градусов:
Получили угол 45 градусов:
2)Построение острых углов с градусной мерой, кратной 10° без помощи транспортира.
Для проведения исследования я на листке клетчатой бумаги построила острые углы,
начиная от 10° до 80°, с интервалом в 10°. Центр угла был расположен в узле клеток. Один из лучей, образующих угол, провела горизонтально слева направо.
Далее с помощью транспортира начертила лучи для всех исследуемых углов.
Если второй луч проходил точно через узел клеток, то информацию об этом угле заносила в таблицу.
Положение «контрольного» узла относительно вершины данного угла отмечалось следующим образом: сначала указывалось количество целых клеток вверх, затем вправо.
В результате получилась такая таблица:
Проанализировав данные таблицы для построения углов, можно заметить, что для углов
от 20° до 70° количество клеток вверх на единицу превышает количество десятков в
градусной мере угла.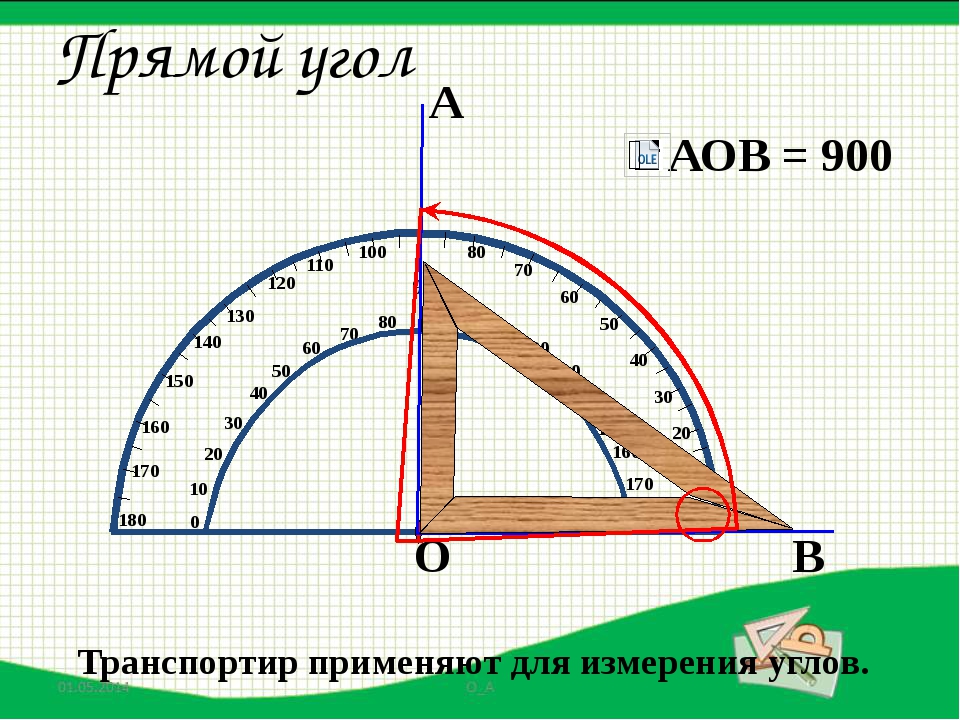 Причем сумма клеток вверх и вправо для всех этих углов равна 11.
Причем сумма клеток вверх и вправо для всех этих углов равна 11.
Величина острого угла | Количество клеток вверх от вершины угла | Количество клеток вправо от вершины угла |
10° | 1 | 6 |
20° | 3 | 8 |
30° | 4 | 7 |
40° | 5 | 6 |
50° | 6 | 5 |
60° | 7 | 4 |
70° | 8 | 3 |
80° | 6 | 1 |
То есть, чтобы знать все «контрольные» узлы, полученные в таблице достаточно
запомнить только точку для угла в 10° –(1;6), и для угла 80°- ей служит противоположная(6;1).
А все остальные «контрольные» точки лучей (для углов от 20° до 70°, кратных 10)
подчиняются несложному правилу: «Если прибавить к числу десятков искомого угла единицу, то получим количество клеток по вертикали. Если это число отнять от 11, то получим количество клеток по горизонтали от вершины угла.»
Например, для построения угла в 70° нужно отступить 8 (7+1) клеток по вертикали и 3(11-8) клетки по горизонтали в сторону первого луча.
Анализ данных в полученной таблице еще раз убеждает нас в существовании красоты, закона симметрии и порядка в науке математике.
3)Построение тупых углов с градусной мерой, кратной 10°, от 100° до 170° без помощи транспортира.
Исследованный метод построения углов позволяет решать следующую геометрическую задачу: построение тупых углов от 100° до 170° с шагом в 10°.
Смежные углы имеют общий луч. Поэтому для построения тупых углов можно
Поэтому для построения тупых углов можно
пользоваться «контрольной» точкой смежного ему острого угла из таблицы. Только
отсчет клеток по горизонтали выбирается в противоположном горизонтальному лучу
направлении (в нашем случае влево).
4)Построение углов с помощью угольников.
Я исследовала чертёжные инструменты – угольники.
Угольник — линейка в форме прямоугольного треугольника, как правило, с миллиметровой шкалой и с пустотой в форме уменьшенного подобного треугольника внутри.
Наиболее распространены угольники двух видов: с острыми углами по 30 и 60 градусов и равнобедренными с одинаковыми острыми углами по 45 градусов. Угольники используются в черчении для построения некоторых углов без помощи транспортира.
При использовании двух угольников можно построить больший набор углов, прикладывая их друг к другу, например, угол в 75 градусов (30+45), 120 градусов (90+30) и т. д. Покажу, как это сделать…
д. Покажу, как это сделать…
Понадобятся два вида угольников: первый с углами по 45 градусов, а второй — по 30 и 60.
1)75 градусов можно построить следующим образом: сначала построить угол в 30, а затем от него отложить 45 градусов.
2) 135 градусов: построить прямой угол, затем от него отложить 45 градусов.
3) 25 градусов: построить угол в 60 градусов, затем от луча внутри угла отложить 45 градусов.
С помощью угольников можно построить углы 105◦, 15◦ и другие.
105= 60+45, 15=60-45 и так далее.
5)Построение углов 30°, 45°, 60°, 90° в практической жизни.
Часто домашнему мастеру необходимо срочно произвести какое либо измерение или сделать разметку под определенным углом, а под рукой нет либо угольника, либо транспортира. В этом случае его выручат несколько простых правил.
Угол 90 градусов.
Если нужно срочно построить прямой угол, а угольника нет, можно воспользоваться любым печатным изданием. Угол бумажного листа — очень точный прямой угол (90 град.). Резательные (вырубочные) машины в типографиях настроены очень точно. Иначе исходный рулон бумаги начнет резаться вкривь и вкось. Поэтому вы можете быть уверены, что этот угол — именно прямой.
Угол бумажного листа — очень точный прямой угол (90 град.). Резательные (вырубочные) машины в типографиях настроены очень точно. Иначе исходный рулон бумаги начнет резаться вкривь и вкось. Поэтому вы можете быть уверены, что этот угол — именно прямой.
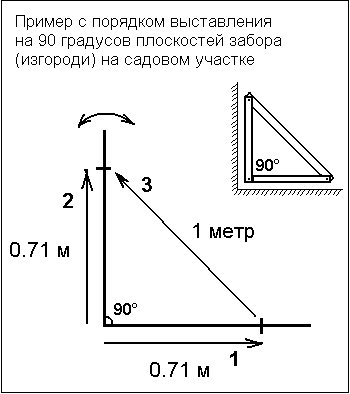
А если нет даже печатного издания или необходимо построить угол на местности, например при разметке фундамента или листа фанеры с неровными краями? В этом случае нам поможет правило золотого (или египетского) треугольника.
Золотым (или египетским, или Пифагоровым) треугольником называется треугольник со сторонами, которые соотносятся друг с другом как 5:4:3. По теореме Пифагора, у прямоугольного треугольника квадрат гипотенузы равен сумме квадратов катетов. Т.е. 5х5 = 4х4 + 3х3. 25=16+9 и это неоспоримо.
Поэтому для построения прямого угла достаточно на заготовке провести прямую линию длиной 5 (10,15,20 и т.д. кратной 5 см). А затем, из краев этой линии начать отмерять с одной стороны 4 (8,12,16 и т. д кратно 4 см), а с другой — 3 (6,9,12,15 и т.д. кратно 3 см) расстояния. Должны получиться дуги с радиусом 4 и 3 см. Где эти дуги пересекутся между собой и будет прямой (90 градусов) угол.
д кратно 4 см), а с другой — 3 (6,9,12,15 и т.д. кратно 3 см) расстояния. Должны получиться дуги с радиусом 4 и 3 см. Где эти дуги пересекутся между собой и будет прямой (90 градусов) угол.
Угол 45 градусов.
Такие углы обычно применяют при изготовлении прямоугольных рамок. Материал из которого делается рамка (багет) пилится под углом 45 градусов и стыкуется. Если под рукой нет стусла или транспортира, получить шаблон угла в 45 градусов можно следующим образом. Необходимо взять лист писчей бумаги или любого печатного издания и согнуть его так, что бы линия сгиба проходила точно через угол, а края загнутого листа совпадали. Получившийся угол и будет равен 45 градусам.
Угол 30 и 60 градусов.
Угол в 60 градусов требуется для построения равносторонних треугольников. Например, вам надо напилить такие треугольники для декоративных работ или точно установить силовой укос. Угол в 30 градусов редко применяется в чистом виде. Однако с его помощью (и с помощью угла в 90 градусов) строится угол 120 градусов. А это угол, необходимый для построения равносторонних шестиугольников, фигуры весьма популярной у столяров.
Однако с его помощью (и с помощью угла в 90 градусов) строится угол 120 градусов. А это угол, необходимый для построения равносторонних шестиугольников, фигуры весьма популярной у столяров.
Для построения весьма точного шаблона этих углов в любой момент необходимо запомнить константу (число) 173. Они вытекает из соотношений синусов и косинусов этих углов.
Возьмите лист бумаги из любого печатного издания. Его угол равен точно 90 градусам. От угла по одной стороне отмерьте 100 мм (10 см.), а по другой — 173 мм (17,3 см). Соедините эти точки. Таким образом мы и получили шаблон, у которого один угол 90 градусов, один 30 градусов и один 60 градусов. Можете проверить на транспортире — все точно!
Запомните это число — 173, и вы всегда сможете построить углы в 30 и 60 градусов.
6)Измерение углов по пальцам рук.
Итак, смотрим на свою руку, которая есть у каждого человека. Уточнение! — левша должен снимать показания углов с правой руки, а правша с левой. Причина проста — приоритет действующей руки со временем деформирует кости, суставы и сильнее растягивает мышцы. Поэтому у правшей левая рука менее деформирована и разработана, а у левшей наоборот.
Уточнение! — левша должен снимать показания углов с правой руки, а правша с левой. Причина проста — приоритет действующей руки со временем деформирует кости, суставы и сильнее растягивает мышцы. Поэтому у правшей левая рука менее деформирована и разработана, а у левшей наоборот.
Теперь растопыриваем в стороны пальцы, как только можете за счет усилия только руки, ничем их раздвигать не нужно — только максимальное мышечное усилие. Богом так заложено у человека и это правда, что у здорового человека с нормальной рукой растопыренные пальцы — это полноценно действующий и относительно точный транспортир.
Угол между большим и безымянным пальцами равен 90 гр.
Угол между большим и указательным пальцами равен 45 гр.
Угол между безымянным и средним пальцами равен 22.5 гр.
Угол между безымянным и мизинцем равен 15 гр. — солнечному часу.
4. ВЫВОДЫ И ЗАКЛЮЧЕНИЕ.
ВЫВОДЫ И ЗАКЛЮЧЕНИЕ.
Своей исследовательской работой мне хотелось бы доказать, что построение углов очень интересное и познавательное занятие, совсем не сложное и трудоемкое, как может показаться на первый взгляд.
Поработав с материалом и подготовив его к применению на практике, я сделала
следующие выводы:
1. Обычный лист бумаги в клетку может выполнять функцию своеобразного инструмента для построения углов.
2. Угольники можно использовать для построения некоторых углов без использования транспортира.
Таким образом, методы построения углов без помощи транспортира актуальны для школьников, так как большинство задач оформляется на листке тетради в клетку и большинство задач в учебнике геометрии связано с построением фигур с углами, градусная мера которых кратна10°.
5 ЛИТЕРАТУРА.
1. В.В. Вавилов, А.В. Устинов. Задачи на клетчатой бумаге. – М.: Школа им. А.Н.
В.В. Вавилов, А.В. Устинов. Задачи на клетчатой бумаге. – М.: Школа им. А.Н.
Колмогорова, 2006. – 183 с
2. Ганьшин В.Н. Простейшие измерения на местности. 3-е изд., перераб. и доп., М.,
Недра, 1983, 108 с., ил.
3.Смирнов В.А, Смирнова И.М. Геометрия на клетчатой бумаге. М., МЦНМО, 2009
4. Большая советская энциклопедия
5. ГОСТ 13494-80. Транспортиры геодезические. Технические условия (с Изменениями N 1-4).
6. Большой энциклопедический политехнический словарь 2004
Список интернет-ресурсов:
http://allencyclopedia.ru/17254 Большая Советская энциклопедия/ Геодезические
инструменты
http://journal.kuzspa.ru/articles/95/ -Электронный научный журнал «Информационно-
коммуникационные технологии в педагогическом образовании»
http://sm-shihova. ucoz.ru/Komu_interesno/Komuinteresno_6.pdf — Математика, 5-6: книга для учителя Автор/создатель: Суворова С.Б., Кузнецова Л.В., Минаева С.С., Рослова Л.О.
ucoz.ru/Komu_interesno/Komuinteresno_6.pdf — Математика, 5-6: книга для учителя Автор/создатель: Суворова С.Б., Кузнецова Л.В., Минаева С.С., Рослова Л.О.
http://enc-dic.com/word/t/Transportir-4655.html [энциклопедии и словари]
http://www.gs-market.ru/index.php?show_aux_page=70 [угломеры электронный, строительный]
http://znaika.ru/catalog/5-klass/matematika/Izmerenie-uglov.-Transportir. [история возникновения приборов измерения углов]
http://virtoo.ru/almanach/nepoznannoe/pervyj-v-mire-transportir-izobreli-eg.html [первый в мире транспортир изобрели египтяне]
http://www.vest-news.ru/article.php?id=18508 [угломер Чижевского Л.В.]
http://astro.uni-altai.ru/picture/src/0+1066279852/ [средневековые угломерные инструменты]
.
Как сделать разбивку в 5 градусов
Как найти угол 90 градусов
Как правильно сделать разбивку фундамента самостоятельно . ..
..
Как правильно сделать разбивку фундамента самостоятельно …
Разбивка под фундамент своими руками
Как правильно сделать разбивку фундамента самостоятельно …
Как построить прямой угол на местности \u2013 линейка без прямых …
Разбивка под фундамент своими руками
Как сделать разбивку под фундамент своими руками …
Как найти прямой угол 90 градусов. Сделать и построить …
Разбивка под фундамент своими руками
Как правильно сделать разбивку фундамента самостоятельно . ..
..
Разметка для фундамента своими руками
8. Как легко разметить фундамент
Разбивка осей фундамента своими руками |
Как сделать разбивку под фундамент своими руками …
Разметка под фундамент своими руками | Инструкции по …
Разбивка фундамента по осям своими руками
Разбивка осей фундамента
Как правильно сделать разбивку фундамента самостоятельно …
90°60°30° Как определить прямой угол?
Разметка под фундамент своими руками | Инструкции по . ..
..
Разбивка фундамента по осям своими руками
Разбивка под фундамент своими руками
Разбивка осей фундамента. КАК СДЕЛАТЬ РАЗБИВКУ (РАЗМЕТКУ …
Как правильно сделать разбивку фундамента самостоятельно …
Разбивка фундамента по осям своими руками
Разбивка осей фундамента
Разбивка осей фундамента. КАК СДЕЛАТЬ РАЗБИВКУ (РАЗМЕТКУ …
Как найти прямой угол 90 градусов. Сделать и построить …
Как сделать прямой угол между стенами | Советы Хозяевам.РФ
Как применять правило 3 4 5 при строительстве прямых углов
Акт разбивки осей на местности объекта капитального . ..
..
Как применять правило 3 4 5 при строительстве прямых углов
Универсальная шкала на планшайбу токарного станка
Модель: «ДВОЙНАЯ РИМСКАЯ» Поверхность: гладкая Размеры …
Как сделать разбивку под фундамент своими руками
Разбивка фундамента своими руками \u2014 что нужно знать?
Разметка под фундамент своими руками | Инструкции по …
Разбивка осей фундамента. КАК СДЕЛАТЬ РАЗБИВКУ (РАЗМЕТКУ …
Как сделать прямой угол между стенами | Советы Хозяевам.РФ
Разбивка осей фундамента
Разметка фундамента: как разметить под дом своими руками . ..
..
Как построить прямой угол на местности \u2013 линейка без прямых …
Как сделать разбивку под фундамент своими руками …
Диагональ фундамента: чертежи, схема разметки и проекты (77 …
Угол 90 градусов с помощью рулетки
Разметка под фундамент своими руками | Инструкции по …
Как применять правило 3 4 5 при строительстве прямых углов
Как сделать прямой угол между стенами | Советы Хозяевам.РФ
Разбивка под фундамент своими руками
Разметка фундамента: как разметить под дом своими руками . ..
..
Как отмерять угол 90 градусов без угольника
Разметка под фундамент своими руками | Инструкции по …
7 правил проектирования печатных плат / Хабр
Разбивка осей фундамента. КАК СДЕЛАТЬ РАЗБИВКУ (РАЗМЕТКУ …
Как сделать прямой угол между стенами | Советы Хозяевам.РФ
Разметка фундамента \u2013 как разметить под дом своими руками …
Разбивка под фундамент своими руками
Акт разбивки осей на местности объекта капитального …
Разбивка осей фундамента
Разметка фундамента: как разметить под дом своими руками . ..
..
Разметка фундаментов: разбивка и вынос осей фундамента в …
Как сделать прямой угол между стенами | Советы Хозяевам.РФ
Разметка фундаментов: разбивка и вынос осей фундамента в …
Самый маленький компьютер / Хабр
Как рассчитать и вывести диагональ фундамента
Лазерный нивелир 360 градусов
Разбивка фундамента своими руками: интересные моменты …
Как построить прямой угол на местности \u2013 линейка без прямых …
Деление окружности на 3; 6; 12 равных частей
Как правильно сделать разбивку фундамента самостоятельно . ..
..
Как найти прямой угол 90 градусов. Сделать и построить …
Диагональ фундамента: чертежи, схема разметки и проекты (77 …
Разбивка осей фундамента своими руками |
Как применять правило 3 4 5 при строительстве прямых углов
Приложение Sports.ru для Android и iOS получило обновление …
ИК паяльная станция на Arduino Mega 2560. Доработка скетча …
Как начертить угол без транспортира заданной величины.
Разбивка фундамента. Разбивка фундамента: как правильно …
Разбивка фундамента по осям своими руками
Разбивка осей фундамента
Как правильно сделать разбивку фундамента самостоятельно . ..
..
Прогноз погоды в Иркутске: 8 января днем -9 градусов
Как сделать распашные ворота с электроприводом на дачном …
Акт разбивки осей на местности объекта капитального …
Конкурс «Клиника года — 2019»: Клиника косметологии «Алтика»
Разметка фундамента \u2013 как разметить под дом своими руками …
Как разбить фундамент своими руками? — Капитальное …
Разбивка под фундамент своими руками
Разбивка осей здания теодолитом |
Жара в Петербурге: как законно прогулять работу
Универсальная шкала на планшайбу токарного станка
Чертежи шестигранной беседки с размерами (8 Фото + скачать .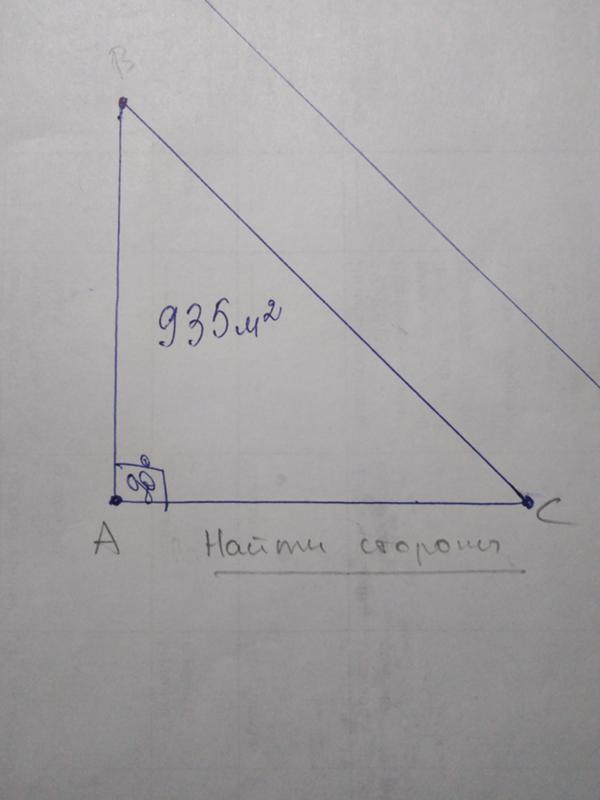 ..
..
Обзор моноблока Lenovo IdeaCentre 520S-23IKU
Оценка 360 градусов (оценка 360 онлайн)
Чем накрыть крышу гаража
Угольник 90 градусов
Расширенный поиск
Название:
Артикул:
Текст:
Выберите категорию:
Все Оборудование для бассейнов » Фильтр для бассейна »» Фильтровальные установки с насосом »» Фильтр без насоса »» Фильтрующие материалы » Закладные из нержавеющей стали » Закладные из пластика » Химия для бассейнов от Маркопул Кемиклс » Химстанции для бассейна »» КРИСТАЛЛ — Российский производитель »» УФ обработка воды бассейна »» Станции дезинфекции из Германии »» Станции дезинфекции из Италии »» Бесхлорные системы »» Станции контроля Hayward »» Хлоргенераторы » Химия для бассейнов BAYROL Германия » Подогрев воды в бассейне »» Электронагреватели »» Теплообменники »» Тепловые насосы »»» Fairland »»» Hayward » Лестницы для бассейна » Противоток — устройство искуственного течения » Подводное освещение » Роботы пылесосы для бассейна » Водопады-фонтаны » Аэромассаж (гейзер) » Гидромассаж » Насосы »» KRIPSOL Испания »» HAYWARD »» AquaViva » Блоки управления оборудованием бассейна »» Блоки управления бассейном ДАРИН-ПРО РОССИЯ »» Блоки управления бассейном на основе комплектующих АВВ »» Блоки управления бассейном DIAL РОССИЯ » Трубы и фитинги ПВХ »» Тройники »» Угольник 90 градусов »» Угольник 45 градусов »» Фланцевое соединение »» Трубы »» Краны »» Муфты переходные »» Муфты с внутренней резьбой »» Муфты с наружней резьбой »» Муфты соеденительные »» Обратные клапана »» Муфты разъемные, разборное соединение »» Клей и прочее » Оборудование общественных бассейнов »» Подъемники для инвалидов »» Фитнес »» Разделительные дорожки и стартовые тумбы » Осушители воздуха » Плавающее покрытие » Пленка ПВХ для бассейнов » Переливная решетка Оборудование для прудов и водоемов » Фильтрация для прудов и водоемов » Насосы для водоемов, прудов, фонтанов » Скиммеры — очистка зеркала воды прудов и водоемов. » УФ установки для водоемов, борьба с сине-зелеными водорослями
» Фонтанные насадки, изливы и каменные фонтаны
» Освещение прудов водоемов фонтанов
» Аэраторы — обогащение пруда кислородом
» Пленка ПВХ, EPDM (бутилкаучук) для гидроизоляции водоема, готовые чаши декоративных водоемов
» Аксессуары и принадлежности для водоемов
» Фитинги и шланги для прудового оборудования
» Биологические препараты для прудов и фонтанов
Оборудование для фонтанов
» Светильники для фонтанов
»» Серия UL(V) RGB PWM
»» Серия ULR RGBW
»» cерия XL
»» серия PL
»» серия Light Fixture
»» серия Tube Light Fixture
»» Safe Rain
» Фонтанные насадки
»» Одноструйные
»» Пенные
»» Многоструйные
»» Веерные
»» Полусферы
»» Сферы
»» Пленочные
»» Кольцевые
»» Линейные
»» Ротационные
»» Распыляющие
»» Плавающие шары
»» Водопады
» Фонтанные насосы
»» FP 6 SERIES
»» FPH SERIES
»» Кожухи FP SERIES
»» Кожухи USP SERIES
» Плавающие фонтаны
»» Display Aerator
»» Fountain
»» Titan
»» Titan Salt Water
»» Комплектующие
» Фонтанные комплекты
»» Серия FK.
» УФ установки для водоемов, борьба с сине-зелеными водорослями
» Фонтанные насадки, изливы и каменные фонтаны
» Освещение прудов водоемов фонтанов
» Аэраторы — обогащение пруда кислородом
» Пленка ПВХ, EPDM (бутилкаучук) для гидроизоляции водоема, готовые чаши декоративных водоемов
» Аксессуары и принадлежности для водоемов
» Фитинги и шланги для прудового оборудования
» Биологические препараты для прудов и фонтанов
Оборудование для фонтанов
» Светильники для фонтанов
»» Серия UL(V) RGB PWM
»» Серия ULR RGBW
»» cерия XL
»» серия PL
»» серия Light Fixture
»» серия Tube Light Fixture
»» Safe Rain
» Фонтанные насадки
»» Одноструйные
»» Пенные
»» Многоструйные
»» Веерные
»» Полусферы
»» Сферы
»» Пленочные
»» Кольцевые
»» Линейные
»» Ротационные
»» Распыляющие
»» Плавающие шары
»» Водопады
» Фонтанные насосы
»» FP 6 SERIES
»» FPH SERIES
»» Кожухи FP SERIES
»» Кожухи USP SERIES
» Плавающие фонтаны
»» Display Aerator
»» Fountain
»» Titan
»» Titan Salt Water
»» Комплектующие
» Фонтанные комплекты
»» Серия FK. VL
»» Шкафы управления комплектами FK
»» Серия MINI Blueline
»» Серия B
»» Серия C
»» Серия D
» Водные пушки
»» Jumping Jet
»» Laminar Jet
»» Rainbow Jet
» Пешеходный модуль
» Водный экран
» Крепеж и фитинги
»» Крепление
»» Шаровые соединения
»» Хомуты из нержавеющей стали
»» Фитинги
» Закладные детали и фильтрующие сетки
»» Overflow Drain Adjustable
»» Cable Inlets with Junction Box
»» Cable inlet/ Stub ups
»» Wall Flush Mounted Adjustable Overflow
»» Floor Drain
»» Floor/Wall Fittings
»» Серия YH
»» Серия YF
»» Серия YFM
» Кабель и системы управления
»» Wind Control Panel
»» Water Level Control
»» Контролеры
»» Шкафы управления
»» Кабель подводный
»» Кабель экранированный
»» Подводные кабельные муфты и коробки
»» Клапаны соленоидные
Каркасные бассейны для дачи
» Каркасный бассейн (сборный бассейн для дачи) из Канады
» Монтаж бассейнов Atlantic Pool
» Аксессуары для каркасных бассейнов
Распродажа оборудования
Насосы Pedrollo
» Вихревые насосы
»» Pedrollo PK
»» Pedrollo PKS
»» Pedrollo PQ
»» Pedrollo PQA
»» Pedrollo PV
» Самовсасывающие насосы для воды
»» Pedrollo CK
»» Pedrollo CKR
»» Pedrollo JCR1
»» Pedrollo JDW
»» Pedrollo JSW1
»» Pedrollo JSW2
»» Pedrollo JSW3
»» Pedrollo PLURIJET 90-130-200
»» Самовсасывающие насосы для воды
» Центробежные насосы
»» Pedrollo 2-4CP
»» Pedrollo 2CP
»» Pedrollo AL-RED
»» Pedrollo CP 0
»» Pedrollo 2-5 CR
»» Pedrollo CP 1.
VL
»» Шкафы управления комплектами FK
»» Серия MINI Blueline
»» Серия B
»» Серия C
»» Серия D
» Водные пушки
»» Jumping Jet
»» Laminar Jet
»» Rainbow Jet
» Пешеходный модуль
» Водный экран
» Крепеж и фитинги
»» Крепление
»» Шаровые соединения
»» Хомуты из нержавеющей стали
»» Фитинги
» Закладные детали и фильтрующие сетки
»» Overflow Drain Adjustable
»» Cable Inlets with Junction Box
»» Cable inlet/ Stub ups
»» Wall Flush Mounted Adjustable Overflow
»» Floor Drain
»» Floor/Wall Fittings
»» Серия YH
»» Серия YF
»» Серия YFM
» Кабель и системы управления
»» Wind Control Panel
»» Water Level Control
»» Контролеры
»» Шкафы управления
»» Кабель подводный
»» Кабель экранированный
»» Подводные кабельные муфты и коробки
»» Клапаны соленоидные
Каркасные бассейны для дачи
» Каркасный бассейн (сборный бассейн для дачи) из Канады
» Монтаж бассейнов Atlantic Pool
» Аксессуары для каркасных бассейнов
Распродажа оборудования
Насосы Pedrollo
» Вихревые насосы
»» Pedrollo PK
»» Pedrollo PKS
»» Pedrollo PQ
»» Pedrollo PQA
»» Pedrollo PV
» Самовсасывающие насосы для воды
»» Pedrollo CK
»» Pedrollo CKR
»» Pedrollo JCR1
»» Pedrollo JDW
»» Pedrollo JSW1
»» Pedrollo JSW2
»» Pedrollo JSW3
»» Pedrollo PLURIJET 90-130-200
»» Самовсасывающие насосы для воды
» Центробежные насосы
»» Pedrollo 2-4CP
»» Pedrollo 2CP
»» Pedrollo AL-RED
»» Pedrollo CP 0
»» Pedrollo 2-5 CR
»» Pedrollo CP 1. 1-11 кВт
»» 25 2
»» 2 кВт
»» Центробежные насосы
»» Pedrollo F без фланца
»» Pedrollo HF высокой производительности
»» Pedrollo HF средней производительности
»» Pedrollo NGA
»» Pedrollo NGA PRO
» Насосные станции
» Дренажные насосы
»» Pedrollo RX VORTEX
»» Pedrollo TOP VORTEX
»» Pedrollo D
»» Pedrollo DC
»» Pedrollo RX
»» Pedrollo TOP
»» Pedrollo TOP FLOOR
» Фекальные насосы
»» Pedrollo MC-F (PMC)
»» Погружные фекальные насосы
»» Pedrollo TRITUS
»» Pedrollo ZX2
»» Pedrollo BC 50
»» Pedrollo VX-ST
»» Pedrollo MC 45
»» Pedrollo MC 50-70
»» Pedrollo MC-INOX
»» Pedrollo VX
»» Pedrollo VXC 35 45
»» Pedrollo VXC 50-70
»» Pedrollo VXC-F
»» Pedrollo ZX
»» Pedrollo BC-ST
» Насосы для колодцев
»» Pedrollo NK2
»» Pedrollo TOP MULTI
»» Pedrollo TOP MULTI TECH
» Насосы для скважин
»» Pedrollo DAVIS
»» Pedrollo 4SR
»» Двигатели к скважинным насосам 4SR/6SR
»» 4FK/6FK
»» Pedrollo SALI
»» Скважинный насос 3 дюйма Pedrollo 3SR
»» Pedrollo 4BLOCK
»» Pedrollo 6SR
»» Гидравлика 4SR-HYD
» Многоступенчатые вертикальные насосы
» Канализационные станции
»» Канализационные накопительные станции Pedrollo SAR 100 литров
»» Канализационные накопительные станции Pedrollo SAR 250 литров
»» Канализационные накопительные станции Pedrollo SAR 550 литров
» Агрегаты для поддержания давления
» Пульты управления и аксессуары для насосов Pedrollo
»» Пульты управления для скважинных насосов Pedrollo QEM 220В
»» Пульт управления для фекальных насосов Pedrollo QED1
»» Пульт управления для фекальных насосов Pedrollo QED2
»» Пульт управления для фекальных насосов Pedrollo QES
»» Пульты управления для скважинных насосов Pedrollo QET 380В
»» Пульты управления для скважинных 4″ насосов Pedrollo QSM с датчиком уровня 220В
»» Пульты управления для скважинных насосов Pedrollo QST с датчиком уровня 380В
»» Муфты изоляционные
»» Реле давления
»» Поплавки
»» Комплектующие к регуляторам давления
»» Трос и зажимы
»» Клапаны
»» Гибкие шланги
»» Аксесуары для канализационных накопительных станций SAR
»» Гидроаккумуляторы
»» EASY PRESS
»» EASY SMALL
»» Станция управления для погружных насосов EVOLUTION
1-11 кВт
»» 25 2
»» 2 кВт
»» Центробежные насосы
»» Pedrollo F без фланца
»» Pedrollo HF высокой производительности
»» Pedrollo HF средней производительности
»» Pedrollo NGA
»» Pedrollo NGA PRO
» Насосные станции
» Дренажные насосы
»» Pedrollo RX VORTEX
»» Pedrollo TOP VORTEX
»» Pedrollo D
»» Pedrollo DC
»» Pedrollo RX
»» Pedrollo TOP
»» Pedrollo TOP FLOOR
» Фекальные насосы
»» Pedrollo MC-F (PMC)
»» Погружные фекальные насосы
»» Pedrollo TRITUS
»» Pedrollo ZX2
»» Pedrollo BC 50
»» Pedrollo VX-ST
»» Pedrollo MC 45
»» Pedrollo MC 50-70
»» Pedrollo MC-INOX
»» Pedrollo VX
»» Pedrollo VXC 35 45
»» Pedrollo VXC 50-70
»» Pedrollo VXC-F
»» Pedrollo ZX
»» Pedrollo BC-ST
» Насосы для колодцев
»» Pedrollo NK2
»» Pedrollo TOP MULTI
»» Pedrollo TOP MULTI TECH
» Насосы для скважин
»» Pedrollo DAVIS
»» Pedrollo 4SR
»» Двигатели к скважинным насосам 4SR/6SR
»» 4FK/6FK
»» Pedrollo SALI
»» Скважинный насос 3 дюйма Pedrollo 3SR
»» Pedrollo 4BLOCK
»» Pedrollo 6SR
»» Гидравлика 4SR-HYD
» Многоступенчатые вертикальные насосы
» Канализационные станции
»» Канализационные накопительные станции Pedrollo SAR 100 литров
»» Канализационные накопительные станции Pedrollo SAR 250 литров
»» Канализационные накопительные станции Pedrollo SAR 550 литров
» Агрегаты для поддержания давления
» Пульты управления и аксессуары для насосов Pedrollo
»» Пульты управления для скважинных насосов Pedrollo QEM 220В
»» Пульт управления для фекальных насосов Pedrollo QED1
»» Пульт управления для фекальных насосов Pedrollo QED2
»» Пульт управления для фекальных насосов Pedrollo QES
»» Пульты управления для скважинных насосов Pedrollo QET 380В
»» Пульты управления для скважинных 4″ насосов Pedrollo QSM с датчиком уровня 220В
»» Пульты управления для скважинных насосов Pedrollo QST с датчиком уровня 380В
»» Муфты изоляционные
»» Реле давления
»» Поплавки
»» Комплектующие к регуляторам давления
»» Трос и зажимы
»» Клапаны
»» Гибкие шланги
»» Аксесуары для канализационных накопительных станций SAR
»» Гидроаккумуляторы
»» EASY PRESS
»» EASY SMALL
»» Станция управления для погружных насосов EVOLUTIONПроизводитель:
ВсеASAHI- Asahi Chemical Industry Co. , LTD — ЯпонияAtlantic Pool (Атлантик Пул Канада)Bayrol (Байрол Германия)Behncke (Бенке Германия)DIALEmaux — Opus (Гонконг, КНР)EMEC (ЭМЕК Италия)ERGIS eurofilmsFirestoneFlexinox (Флексинокс Испания)Hidro Ten — ИспанияKripsol (Крипсол Испания)MESSNERMountfield (Маунтфилд Чехия)Pahlen (Пален Швеция)PedrolloSELIGER waterpowerSoll (Золь Германия)VAN ERP Int. (Нидерланды)VELDAАкватехника РоссияДАРИН-ПРО (Дарин Россия)Маркопул КемиклсНПО ЛИТ, Россия
, LTD — ЯпонияAtlantic Pool (Атлантик Пул Канада)Bayrol (Байрол Германия)Behncke (Бенке Германия)DIALEmaux — Opus (Гонконг, КНР)EMEC (ЭМЕК Италия)ERGIS eurofilmsFirestoneFlexinox (Флексинокс Испания)Hidro Ten — ИспанияKripsol (Крипсол Испания)MESSNERMountfield (Маунтфилд Чехия)Pahlen (Пален Швеция)PedrolloSELIGER waterpowerSoll (Золь Германия)VAN ERP Int. (Нидерланды)VELDAАкватехника РоссияДАРИН-ПРО (Дарин Россия)Маркопул КемиклсНПО ЛИТ, РоссияНовинка:
ВседанетСпецпредложение:
ВседанетРезультатов на странице:
5203550658095Найти
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Виды углов: острый, прямой, тупой, развёрнутый, выпуклый и полный
Каждый угол, в зависимости от его величины, имеет своё название:
- Острый угол — это угол, который меньше прямого угла (<90°).

- Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол обозначается буквой d и равен 90°.
Если два смежных угла равны между собой, то каждый из них называется прямым углом. Прямой угол обычно обозначается не дугой, а уголком:
∠AOC и ∠COB — прямые углы. Общая сторона прямых углов OC называется перпендикуляром к прямой AB, а точка O — основанием перпендикуляра.Сумма двух прямых углов равна развёрнутому углу, значит, прямой угол равен половине развёрнутого угла.
- Тупой угол — это угол, который больше прямого угла, но меньше развёрнутого:
90° < тупой угол < 180°.
- Развёрнутый угол — это угол, образованный двумя дополнительными лучами.
Развёрнутый угол равен сумме двух прямых углов или, короче, двум прямым углам. Следовательно, развёрнутый угол равен 180° или 2d.

Все развёрнутые углы равны между собой.
- Выпуклый угол — это угол, который больше развёрнутого угла, но меньше полного:
180° < выпуклый угол < 360°.
- Полный угол — это угол, обе стороны которого совпадают с одним лучом.
Полный угол равен сумме четырёх прямых углов, то есть 4d (360°).
Прилежащие углы
Прилежащие углы — это пара углов, имеющих общую вершину и общую сторону, другие стороны которых лежат по разные стороны от общей стороны.
∠AOB и ∠BOC — прилежащие углы, O — общая вершина, OB — общая сторона.
Если из вершины любого угла провести луч, разделяющий угол на два угла, то образованные углы будут прилежащими.
Угол, разделённый лучом, будет называться суммой полученных углов, например угол AOB является суммой углов AOC и COB:
∠AOB = ∠AOC + ∠COB.
Каждый из прилежащих углов, ∠AOC и ∠COB, называется разностью углов AOB и другого прилежащего, то есть:
∠AOC = ∠AOB — ∠COB,
∠COB = ∠AOB — ∠AOC.
ручных инструментов — Как сделать квадрат без квадрата?
Я только начинаю заниматься деревообработкой, и, поскольку у меня еще нет проекта, который я хотел бы завершить, я заинтересован в создании многих инструментов, которые я бы использовал в процессе обучения (молотки, квадраты , маркер и т. д.).
Так я учусь работать с деревом, а потом и с металлом. Это хороший способ. Строительство квадратов — это красивый маленький проект.
Так как же сделать квадрат без квадрата?
Вы правы, что на первый взгляд здесь возникает проблема курицы и яйца.
Можно сделать точный квадрат, не имея точного квадрата для его проверки, но вам нужны вещи, которые должны быть прямым .
Предположим, вы можете получить два куска дерева, у которых есть хотя бы одна плоская прямая сторона. Это будут внешние стороны вашего квадрата. Одним из кусочков нарисуйте прямую горизонтальную линию на чем-нибудь плоском.
Временно соедините две части вместе так, чтобы они все еще могли вращаться относительно друг друга — например, проденьте в них один винт, один дюбель или что-то еще.Сделайте их как можно более квадратными. Затем поместите одну сторону вдоль линии, которую вы только что нарисовали, с квадратом, расположенным как буква L, и используйте новый квадрат, чтобы нарисовать перпендикулярную линию. Теперь переверните все это на так, чтобы теперь это была обратная L, и попытайтесь провести точно такую же перпендикулярную линию. Если квадрат точный, перпендикуляры совпадут. Если это не так, вы можете оценить, насколько далеко от квадрата находится ваш квадрат, отрегулируйте его и попробуйте снова.
Продолжайте делать это, пока не получите что-то настолько близкое к квадрату, насколько вы хотите, и вставьте еще один фиксатор в квадрат, чтобы он больше не мог вращаться, и эй, у вас есть точный квадрат, построенный только из точного прямая линия.
Теперь, конечно, возникает вопрос: «Как мне построить точную прямую линию?» Но это другой вопрос.
Как они были первоначально изготовлены, если точность должна быть правильной, но современные методы измерения и производства недоступны.
Вы не говорите, как далеко в истории хотите уйти. Способы, которыми древние египтяне добивались квадратной формы строительных блоков, довольно сильно отличаются от способов, которыми средневековые плотники строили квадратные здания, и они сильно отличаются от методов, используемых для создания квадратных точных станков во время промышленной революции.Уточните свой вопрос, если вас интересует история создания инструмента.
Я смотрел много видео Пола Селлерса на YouTube, и они меня подстегнули.
woodgears.ca — тоже хороший сайт для такого рода вещей; там есть видео о том, как сделать свои собственные пробные квадраты, обрамлять квадраты и так далее.
В поисках правильного угла | ЭТО Столярные
В соавторстве с Майком Слоггаттом
Около 2500 лет назад греческий философ, которого мы все встретили в средней школе, по имени Пифагор открыл теорему, которая может облегчить жизнь плотникам и подрядчикам — если бы мы просто знали, как ее использовать, и как найти прямые углы !
Большинство из нас помнят азбуку из средней школы, и мы также помним теорему Пифагора, которая применима к любому треугольнику с углом 90 градусов.
| Но мы так и не научились использовать и применять необычное правило Пифагора с классной доски! Прогрессивные плотники знают, что учиться никогда не поздно; Фактически, изучение чего-то нового — это клей, который связывает нас с плотницкими работами, а рабочее место — идеальный класс. | (Примечание: щелкните любое изображение, чтобы увеличить) |
Строительные калькуляторы позволяют плотникам легко использовать теорему Пифагора на строительной площадке в дюймах и футах! Калькулятор переводит a, b и c в Rise, Run и Diagonal.
Он также включает кнопку «PITCH», которая позволяет вводить или вычислять углы треугольника с помощью тригонометрических функций. Главное, что нужно помнить о шаге в строительном калькуляторе, — это то, что это всегда угол, противоположный подъему.
Возможно, мы называем это «прямоугольным треугольником» не только потому, что у него прямой угол, но и потому, что это прямоугольный треугольник для решения почти всех геометрических задач… особенно на строительной площадке. Использовать прямоугольный треугольник легко: если мы знаем по крайней мере два измерения или одно измерение и угол прямоугольного треугольника, мы можем найти остальные размеры или углы.Иногда самая большая проблема — найти правильные треугольники и знать, как их использовать.
Поиск прямых углов в фундаменте
Раньше закладывание фундамента было медленным и утомительным процессом. Я помню, как бригадир моего отца, Лорен, носил в кошельке потрепанный сложенный листок со списком из 3-4-5 переменных, которые мой дядя записал для него. Этот список начинался с 3 ′ x 4 ′ x 5 ′, и он продолжался до 30 ′ x 40 ′ x 50 ′ с шагом 2 фута! Лорен гордился этой бумагой и показал ее мне, когда мне было десять или двенадцать, когда я впервые увидел, как он закладывает фундамент.Многие плотники до сих пор используют тот же метод.
Этот список начинался с 3 ′ x 4 ′ x 5 ′, и он продолжался до 30 ′ x 40 ′ x 50 ′ с шагом 2 фута! Лорен гордился этой бумагой и показал ее мне, когда мне было десять или двенадцать, когда я впервые увидел, как он закладывает фундамент.Многие плотники до сих пор используют тот же метод.
Треугольник 3 ‘x 4’ x 5 ‘часто слишком мал, чтобы обеспечить точность для фундамента любого размера, поэтому плотники обычно выбирают самый большой из возможных треугольников для данного прямоугольного дополнения. Затем они дважды проверяют квадратность макета, измеряя диагонали и тщательно перемещая угловые точки, пока диагонали не станут равными. Но все эти усилия не нужны. С помощью строительного калькулятора вы режете прямо до прямого угла .
Создание основы — один из примеров того, почему старые техники не всегда являются лучшими. Сегодня плотники часто на собственном опыте обнаруживают, что многие старые методы работают медленнее и менее точны. С помощью строительного калькулятора кладка фундамента выполняется быстро и точно.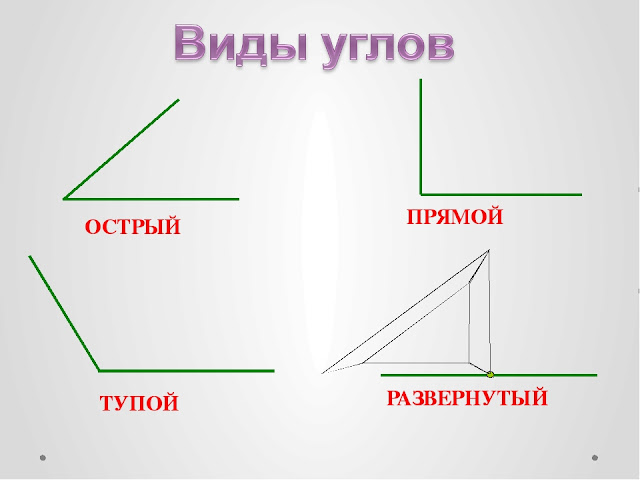 Просто введите RISE и RUN, затем нажмите кнопку DIAGONAL. Плотник, работающий в одиночку и держащий в руках две рулетки — одну, протянутую по высоте 20 футов, а другую — по диагонали 37 футов — 8 13/16 дюймов, — может одновременно найти точные угловые точки и , лежащие в квадрате фундамента.
Просто введите RISE и RUN, затем нажмите кнопку DIAGONAL. Плотник, работающий в одиночку и держащий в руках две рулетки — одну, протянутую по высоте 20 футов, а другую — по диагонали 37 футов — 8 13/16 дюймов, — может одновременно найти точные угловые точки и , лежащие в квадрате фундамента.
Поиск прямых углов в обрамлении
Обрамление — еще одна рутинная работа, которую строительный калькулятор может упростить и улучшить. Независимо от того, обрамляете ли вы выдвижной отсек в полу или в конце фронтона, зная вашу точную планировку — как по горизонтали, так и по наклонным пластинам — и зная точную длину ваших шпилек или балок, сокращается время монтажа более чем вдвое. , и обеспечивает точность.
Большинство строителей спроектировали бы свои балки поперек угла выдвижной секции или измерили бы каждую отдельно, и они бы измерили компоновку перпендикулярно каждой предыдущей балке.Но намного быстрее , чтобы увидеть и использовать правильный угол.
| Прямой угол образует балка обода и первая балка. Даже если вы еще не установили его, вы знаете, что он будет там. В 30-градусном отсеке введите 30 на вашем калькуляторе, затем нажмите клавишу PITCH. Если угол наклона составляет 45 градусов, введите 45 и нажмите клавишу PITCH. |
| Если балки или стойки на 16 дюймов. центров, вы будете знать две вещи о правильном угле: шаг и бег.Введите 16 дюймов и нажмите кнопку RUN. |
| Нажмите кнопку RISE, чтобы найти длину первой балки или стойки. Помните, RISE всегда противоположен Pitch (и наоборот!). |
Вот где действительно сияет калькулятор . Оставьте на дисплее 9 1/4 дюйма. Чтобы определить длину следующей балки или стойки , нажмите клавишу «+» один раз , а затем нажмите клавишу «=». Калькулятор прибавит 9 1/4 дюйма. на себя при нажатии клавиши «+». Чтобы узнать длину всех оставшихся балок или стоек, не нажимайте кнопку «+» снова! Если вы сделаете это, вы добавите новое число на дисплее к самому себе и потеряете десятичную дробь в памяти калькулятора. Вместо этого нажимайте только клавишу «=» для каждой последующей балки или стойки!
на себя при нажатии клавиши «+». Чтобы узнать длину всех оставшихся балок или стоек, не нажимайте кнопку «+» снова! Если вы сделаете это, вы добавите новое число на дисплее к самому себе и потеряете десятичную дробь в памяти калькулятора. Вместо этого нажимайте только клавишу «=» для каждой последующей балки или стойки!
Помните, что калькулятор округляет фактическое десятичное значение до 9 1/4 дюйма. Если результат не равен точно 1/4 дюйма.или даже 1/16 дюйма, калькулятор всегда будет округлять до ближайшего дробного значения, исключая любую кумулятивную ошибку (предпочтение дробного разрешения на калькуляторе может быть установлено от 1/2 дюйма до 1/64 дюйма .). Примечание. Большинство строительных калькуляторов также включают функцию «Rake Wall», которую можно использовать для этих расчетов, но это выходит за рамки данной статьи.
Используйте ту же последовательность для размещения «диагональной» балки обода или верхней пластины.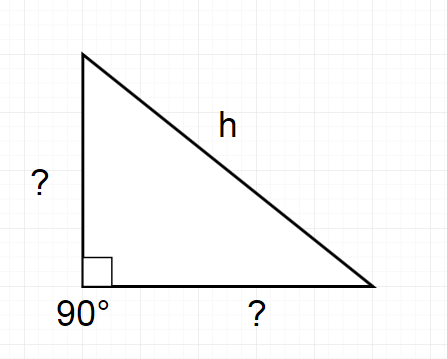 Введите 30 и нажмите PITCH, затем введите 16 дюймов.и нажмите RUN, а затем нажмите DIAGONAL, чтобы найти расстояние вдоль обода до первой балки. Введите 30 и нажмите PITCH, затем введите 16 дюймов.и нажмите RUN, а затем нажмите DIAGONAL, чтобы найти расстояние вдоль обода до первой балки. |
Чтобы найти точное расположение последующих балок или стоек, используйте ту же процедуру, что и для длины балок / стоек — нажмите клавишу «+», а затем клавишу «=» для второй метки компоновки, и только клавиша «=» для каждой последующей отметки макета!
Поиск прямых углов в отделке: Cabinet Crown
Фундаменты и обрамления — не единственные места, где встречаются прямые углы.
У меня не было проблем с отрезанием всех частей короны для этих прямоугольных шкафов — я просто добавил 1 дюйм для каждой выступающей стороны. Но вырезка карниза для углового шкафа — это совсем другое дело. Я отрезал все части по длине, решив, что отмечу их по точной длине на шкафу. Конечно, Майк заранее собрал детали, думая, что все они были обрезаны до нужной длины!
«Что с этим?» Майк стоял на лестнице с пистолетом для гвоздей в руке, недоумевая, почему сборка не подошла.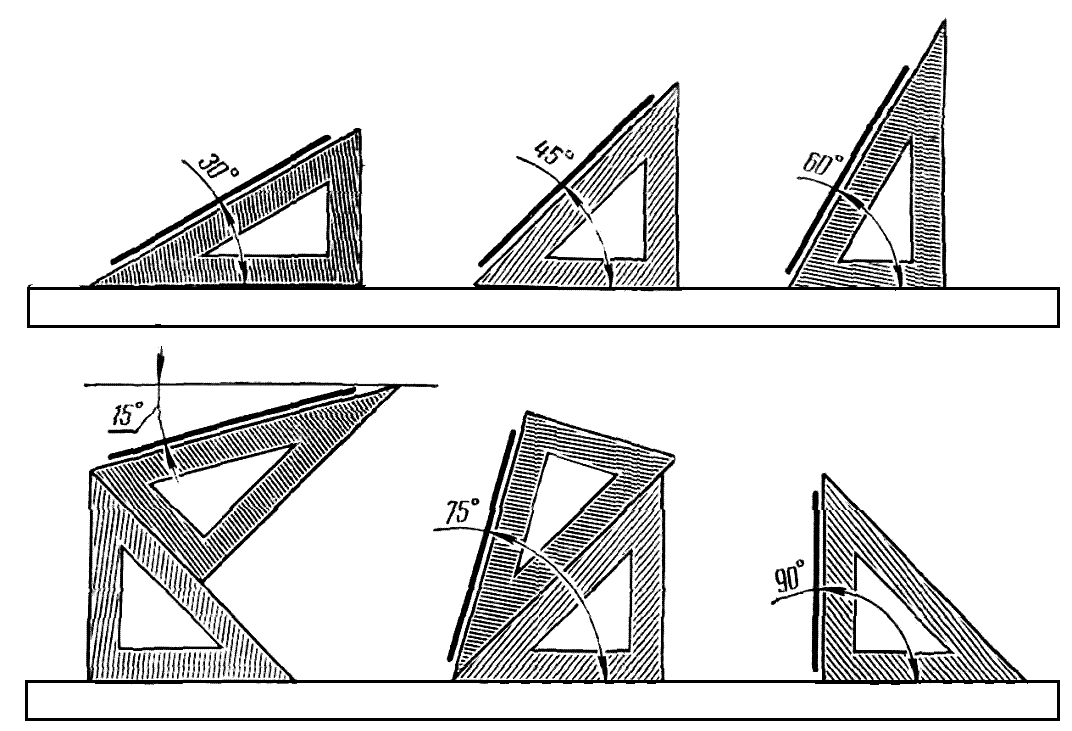 «Я не мог определить длину», — сказал я. «Я хотел отметить их на месте!» Майк ответил: «Но разве вы не видели прямой угол и ?!»
«Я не мог определить длину», — сказал я. «Я хотел отметить их на месте!» Майк ответил: «Но разве вы не видели прямой угол и ?!»
Карниз состоит из трех частей: бусинка служит основанием для лицевой панели и короны. Бортик выступает ровно на 1 дюйм за край корпуса. Расчет длинных точек на прямоугольных шкафах был легким — я добавил 1 дюйм к боковым размерам шкафа для боковых частей, и я добавил 2 дюйма (по одному дюйму для каждого внешнего угла) к переднему размеру шкафа.
Но вычислить размер длинной точки углового шкафа оказалось не так-то просто. Вместо того, чтобы переносить линии обратно на внутреннюю часть шкафа и вырезать из коротких точек измерения, гораздо проще и точнее найти прямой угол .
Прямой угол в этом примере является воображаемым — он образован не каркасом или фундаментом, а скорее углом скоса, требуемым для углового шкафа (22 1/2 градуса), и выступом бортика.
| Введите 22 1/2 для PITCH (помните, PITCH всегда противоположен RISE). Введите 1 дюйм для RUN, а затем нажмите клавишу RISE. |
Для левой и правой сторон добавьте 7/16 дюйма к глубине шкафа; для бортика передней части шкафа добавьте 7/8 дюйма к переднему размеру шкафа (7/16 дюйма для каждого внешнего угла).
В поисках прямого угла… и эллипс
Если присмотреться, можно найти скрытые прямоугольные треугольники в местах, о которых вы даже не догадывались.
Вентиляционная труба или круглый дымоход, проходящий через крышу или наклонный потолок, являются прекрасным примером.
| Если вы читаете «Элегантный эллипс», то вы знаете, что цилиндр или труба, разрезанные (или пересекающиеся) под углом, образуют эллиптическую форму, и эта форма определяется Большой и Малой осями. |
Малая ось — это просто диаметр цилиндра и не изменяется, но размер главной оси изменяется в зависимости от угла (или шага) пересечения. |
Чтобы найти длину Большой оси:
| Введите диаметр цилиндра как РАБОЧИЙ. Введите уклон крыши (дюймы подъема на 12 дюймов пробега) как НАСОС. Решите для ДИАГОНАЛА. При использовании соотношения подъема / спуска крыши не забудьте нажать кнопку «Inch» при вводе PITCH. |
После определения Большой и Малой Осей можно использовать струнный метод для определения необходимой формы.Очевидно, что этот метод не будет часто использоваться при черновом обрамлении, но это полезный трюк, чтобы знать, когда вырез должен быть качественным!
Для получения дополнительной информации о строительных калькуляторах и мобильных приложениях для строительных калькуляторов (удобно для работы!), Ознакомьтесь с Construction Master Pro от Calculated Industries, мобильными версиями Construction Master Pro от Calculated Industries и BuildCalc.
(рисунки SketchUp, созданные Уильямом Тоддом Мердоком; эта статья изначально была опубликована на сайте GaryMKatz. com)
com)
Что такое угол 45 градусов? — Определение, факты и пример
Угол 45 градусовКогда два луча пересекаются в одной конечной точке, они образуют угол. Общая конечная точка называется вершиной, а лучи — плечами угла.
Угол измеряется в ° или радианах. Если два плеча угла проходят в противоположных направлениях, это прямой угол. Прямой угол составляет 180 °. Угол можно измерить с помощью транспортира, а угол измерения 90 градусов называется прямым углом.Под прямым углом две руки перпендикулярны друг другу.
Если прямой угол разделен на две равные части, каждый угол составляет 45 °.
Построение угла с помощью транспортира
Шаг 1 : Нарисуйте луч и назовите его AB.
Шаг 2 : Держите центральную точку транспортира на уровне A. Поскольку угол открывается вправо, выберите 45 ° в списке, который начинается справа и перемещается против часовой стрелки. Отметьте точку C.
Отметьте точку C.
Шаг 3 : Соедините A и C. Здесь меры.
Углы 45 градусов в реальной жизни:
Дополнительные знания:
Построение угла с помощью компаса
Шаг 1 : Нарисуйте отрезок прямой и серединный перпендикуляр, пересекая дуги с радиусом больше половины длины MN. Пусть серединный перпендикуляр пересекает отрезок прямой в точке O.
Шаг 2 : Нарисуйте дугу с центром в точке O и радиусом OM, разрезая серединный перпендикуляр в точке P.
Шаг 3 : Соедините M и P прямой линией. меры.
Градус измерения также можно построить, построив биссектрису прямого угла.
Интересные факты
|
30 60 90 Правые треугольники
Треугольник особого вида
Прямоугольный треугольник 30-60-90 (буквально произносится как «тридцать шестьдесят девяносто») — это особый тип прямоугольного треугольника, в котором три угла составляют 30 градусов, 60 градусов и 90 градусов. Треугольник важен, потому что стороны существуют в легко запоминающемся соотношении: 1: \ (\ sqrt {3} \): 2.Другими словами, гипотенуза в два раза длиннее более короткого отрезка, а более длинное отрезок представляет собой квадратный корень из 3-кратного более короткого отрезка. Вы также можете помнить это как «корни X, 2X и X из 3», как я его помню, но тогда вы должны помнить, что на самом деле самая длинная сторона — это 2X, а не корни X из 3.
Какая сторона какая? Сторона, противоположная углу 30 градусов, будет иметь наименьшую длину. Сторона, противоположная углу 60 градусов, будет в \ (\ sqrt {3} \) раз длиннее, а сторона, противоположная углу 90 градусов, будет вдвое длиннее.Треугольник ниже показывает эту взаимосвязь. Помните, что самая длинная сторона будет противоположна наибольшему углу, а самая короткая — противоположному наименьшему углу.
Сторона, противоположная углу 60 градусов, будет в \ (\ sqrt {3} \) раз длиннее, а сторона, противоположная углу 90 градусов, будет вдвое длиннее.Треугольник ниже показывает эту взаимосвязь. Помните, что самая длинная сторона будет противоположна наибольшему углу, а самая короткая — противоположному наименьшему углу.
Мы можем использовать соотношение между углами и сторонами треугольника 30-60-90, чтобы найти недостающие углы или длины сторон. Взгляните на этот пример:
Пример 1
Для треугольника 30-60-90 ниже найдите длины недостающих сторон:
Поскольку это прямоугольный треугольник 30-60-90, мы знаем, что стороны существуют в соотношении 1: \ (\ sqrt {3} \): 2.Самая короткая сторона, 1, находится напротив угла 30 градусов. Поскольку сторона X противоположна углу в 60 градусов, мы знаем, что он равен \ (1 * \ sqrt {3} \), или примерно 1,73. Наконец, сторона Y противоположна прямому углу, и это в два раза короче сторона, или 2.
Откуда взялась формула?
Это еще одна выдуманная математическая формула? Нет! Это просто приложение базовой тригонометрии. В приведенном выше примере мы могли бы взять синус крайнего левого угла: sin (30) = 1/2.Поскольку синус дает нам отношение противоположности к гипотенузе, мы бы знали, что гипотенуза должна быть 2. По сути, вся причина, по которой треугольник 30-60-90 легко решить, заключается в том, что синус и косинус этих углов равны тоже очень просто.
Пример 2
Используйте те же принципы для поиска неизвестных переменных X и Y.
Известная сторона — 4, и это самая длинная сторона. Помните, как самая длинная сторона в два раза больше самой короткой стороны для треугольника 30-60-90? Значит, Y должно быть 2!
Теперь мы можем найти оставшуюся сторону.Так как сторона , противоположная углу в 60 градусов, равна кратной стороне, умноженной на квадратный корень из 3 , мы можем вычислить, что X равно \ (2 * \ sqrt {3} \).
Резюме
Для прямоугольного треугольника с углами 30, 60 и 90 градусов, стороны будут иметь длину в соотношении 1: \ (\ sqrt {3} \): 2, как показано на этой диаграмме:
Дополнительная справка
Как всегда, вы можете задать свои конкретные вопросы на нашей доске сообщений справки по математике, выполнить поиск в Google или пройти этот урок по 30-60-90 треугольникам или этот.Или, чтобы вычислить стороны и углы треугольника, воспользуйтесь интерактивным инструментом ниже:
Специальные значения углов: 30-60-90 и 45-45-90 треугольников
Purplemath
Есть несколько ( очень несколько) углов, которые имеют относительно «аккуратные» тригонометрические значения, включая, в худшем случае, один квадратный корень.Из-за их относительно простых значений, это углы, которые обычно используются в математических задачах (особенно в расчетах), и вы будете ожидаемо, что запомнят значения этих углов.
Ожидается, что вы будете использовать эти значения для получения «точных» ответов при решении прямоугольных треугольников и для нахождения значений различных тригонометрических соотношений.
Обычно в учебниках эти значения представлены в виде таблицы, которую вы должны запомнить.Но картинки часто легче вспомнить на тестах и т.д., по крайней мере, для некоторых из нас. Если эти таблицы не работают для вас, то этот урок покажет, как многие люди (включая меня!) на самом деле отслеживают эти значения.
MathHelp.com
Далее я использую градусы для измерения углов.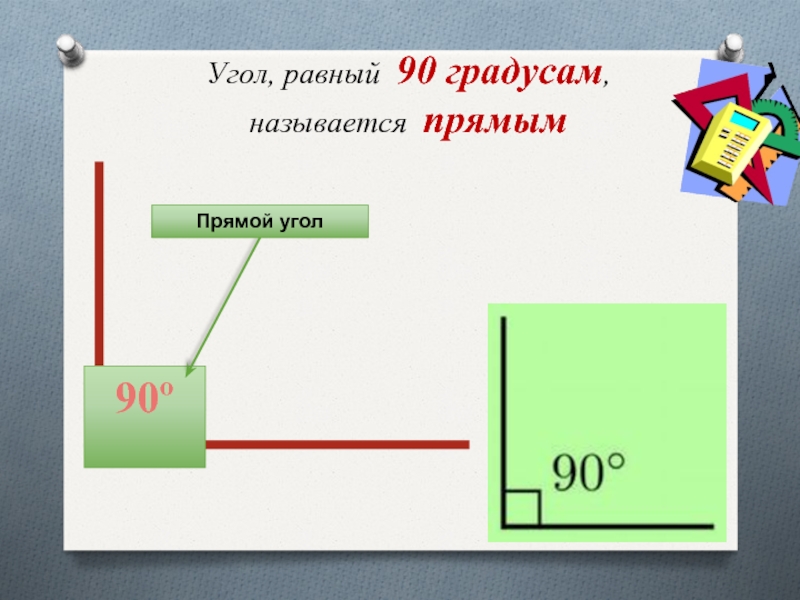 Обычно так студентов знакомят с угловыми мерами. Однако, если вы работаете с радианами, я также отмечу эквиваленты радианов для измерения угла.
Обычно так студентов знакомят с угловыми мерами. Однако, если вы работаете с радианами, я также отмечу эквиваленты радианов для измерения угла.
Значения угла 45 ° (из треугольника 45-45-90)
Все треугольники 45-45-90 похожи; то есть все они имеют соотношения сторон. (Угол в 45 ° равен в радианах
π / 4.) Итак, давайте посмотрим на очень простой 45-45-90:Гипотенуза этого треугольника, обозначенного выше как 2, находится путем применения теоремы Пифагора к прямоугольному треугольнику со сторонами, имеющими длину
sqrt [2] .Базовый угол в левом нижнем углу обозначен символом «тета» (θ, THAY-tuh) и равен 45 °. Так как же нам помогает знание этого треугольника? Это помогает нам, потому что все треугольники 45-45-90 похожи. Следовательно, любой вопрос «оценки» или «решение треугольника», включающий треугольник 45-45-90 или просто угол 45 °, может быть выполнен с использованием этого треугольника. Эта картинка — все, что вам нужно.
Эта картинка — все, что вам нужно.
Значения углов 30 ° и 60 ° (из треугольника 30-60-90)
Когда нам нужно работать под углом 30 или 60 градусов, процесс аналогичен описанному выше, но настройка немного дольше.(Угол 30 ° эквивалентен углу
π / 6 радиан; угол 60 ° эквивалентен углу π / 3 радиан.)Для любого из углов это треугольник, с которого мы начинаем:
Это треугольник 60-60-60 (то есть равносторонний треугольник), длина сторон которого равна двум единицам.
Опускаем вертикальную биссектрису с верхнего угла вниз на нижнюю сторону:
Обратите внимание, что эта биссектриса также является высотой (высотой) треугольника.
Используя теорему Пифагора, мы получаем, что длина биссектрисы равна
sqrt [3].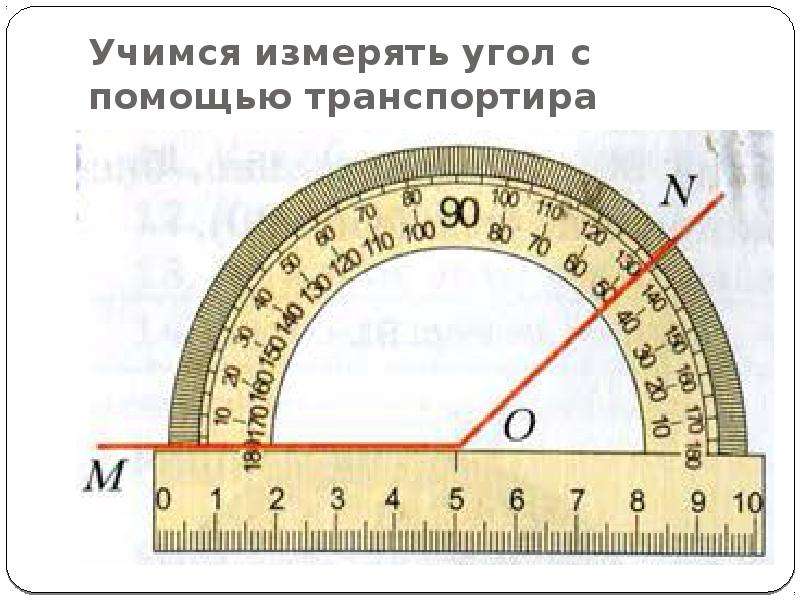 И эта биссектриса образовала два треугольника 30-60-90.
И эта биссектриса образовала два треугольника 30-60-90.Когда мы работаем с углом 60 градусов, мы используем левый треугольник наверху, он стоит, с основным углом (слева), обозначенным «α» (AL-phuh, забавно выглядящим «a»). «):
Когда мы работаем с углом 30 градусов, мы используем правый треугольник, перевернутый влево, базовый угол (слева) обозначен «β» (BAY-tuh, забавно выглядящее «b» ):
Мы можем найти тригонометрические значения и соотношения для треугольников с 30 и 60 градусами точно так же, как и с треугольниками с 45 градусами.Все, что вам нужно, — это изображения выше.
Вы можете найти одного из тех учителей, которые не хотят, чтобы вы рисовали эти картинки (потому что к этому моменту вы должны все запомнить). Вот почему у твоего карандаша есть ластик. Мой инструктор по исчислению II сказал, что если мы нарисуем картинки в наших тестах, вся задача будет засчитана неправильно.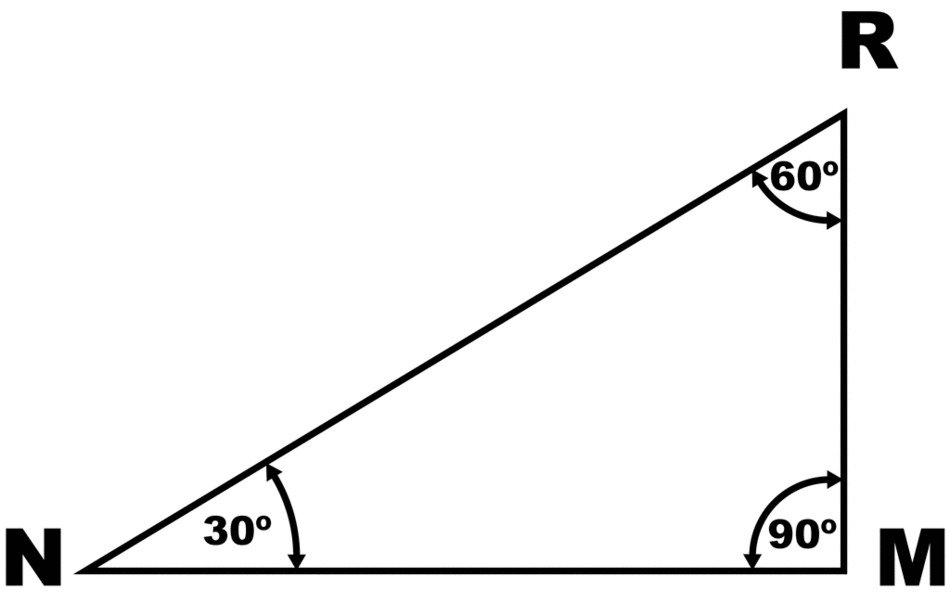 Я все равно рисовал картинки, но очень легко, и стер их все, прежде чем сдать тесты. Он так и не узнал, и я прошел курс.Делай то, что должен.
Я все равно рисовал картинки, но очень легко, и стер их все, прежде чем сдать тесты. Он так и не узнал, и я прошел курс.Делай то, что должен.
Использование стола
Рисунки выше — это то, что я всегда использовал, и многие находят их полезными. С другой стороны, некоторые люди предпочитают таблицы или другие методы. Если вам больше подходят столы, то настоятельно рекомендуется использовать этот стол, который прошел «полевые испытания» работающим инструктором:
Чтобы найти, скажем, синус угла в сорок пять градусов, вы должны провести поперек в строке «грех» и вниз по столбцу «45 °», взяв с собой символ квадратного корня и не забывая включите «деленное на 2» снизу, чтобы получить
sin (45 °) = sqrt (2) / 2.Аккуратный узор «1, 2, 3» в верхней строке и «3, 2, 1» в средней строке призван помочь вам запомнить значения таблицы. Имейте в виду, что квадратный корень из 1 равен 1, поэтому, например, cos (60 °) = sqrt (1) / 2 = 1/2. Чтобы найти тангенс, нужно разделить значение синуса на значение косинуса.
Имейте в виду, что квадратный корень из 1 равен 1, поэтому, например, cos (60 °) = sqrt (1) / 2 = 1/2. Чтобы найти тангенс, нужно разделить значение синуса на значение косинуса.Использование пальцев
Другой метод использует вашу левую руку, чтобы сделать то же самое. Повернув ладонь к себе, отсчитайте основные исходные углы, начиная с большого пальца: 0 °, 30 °, 45 °, 60 ° и 90 °.
Чтобы найти значение триггера, вы опустите палец, соответствующий этому углу, держа ладонь к себе. В качестве значения синуса возьмите квадратный корень из числа пальцев слева от опущенного пальца и разделите на 2; для значения косинуса возьмите квадратный корень из числа пальцев справа от опущенного пальца и разделите его на 2; для касательной разделите квадратный корень из числа пальцев слева на квадратный корень из числа справа (и при необходимости рационализируйте).
Например, если вы хотите работать под углом в тридцать градусов, вы должны сориентировать руку следующим образом:
Синус — это квадратный корень из большого пальца (то есть квадратный корень из «единицы») над двумя, что дает:
Косинус — это квадратный корень из трех ваших пальцев (то есть квадратный корень из трех) над двумя, что дает:
Филиал
С другой стороны, если вы хотите оценить sin (0 °), cos (0 °) и cot (0 °), вы должны сориентировать левую руку следующим образом:
Поскольку ваш большой палец сложен, 0 пальцев слева и 4 пальца справа.Тогда значения синуса и косинуса находятся как:
sin (0 °) = sqrt [0] / 2 = 0
cos (0 °) = sqrt [4] / 2 = 1
Котангенс — это величина, обратная касательной. Каково значение тангенса?
Каково значение тангенса?
загар (0 °) = sqrt [0] / sqrt [4] = 0
Переворачивание вышеуказанного приведет к делению на ноль, что недопустимо.Таким образом, cot (0 °) не определено.
(Угол в 0 ° эквивалентен углу в 0 радиан. Угол в 90 ° эквивалентен углу в
π / 2 радиан.)URL: https://www.purplemath.com/modules/specang.htm
Как использовать скоростной квадратик (Руководство DIYer’s)
Фото: istockphoto.com
Планируете столярный проект? Быстро, хватай квадрат скорости! Этот простой инструмент, изобретенный Альбертом Свансоном, также известный как стропильный квадрат или треугольный квадрат, с 1925 года облегчает жизнь плотникам благодаря своей универсальности и доступности. Спустя более 80 лет вы все еще можете использовать это чудо-многозадачность в качестве инструмента для разметки, транспортира, квадратного квадрата, пробного квадрата или даже направляющей для пилы. Он упрощает работу во всем: от строительства лестниц и шкафов до измерения уклона крыши до изготовления рам для картин и скворечников.
Он упрощает работу во всем: от строительства лестниц и шкафов до измерения уклона крыши до изготовления рам для картин и скворечников.
Прежде чем мы начнем, вот несколько терминов, которые вам необходимо знать:
- Кромка — также известная как забор — проходит вдоль одной из сторон квадрата скорости под углом 90 градусов. и позволяет прикрепить инструмент к доске или поверхности, с которой вы работаете. Часто на нем будет хотя бы одна линейка; чем больше, тем лучше.
- Поворот — это точка на одном конце выступа, вокруг которой вы можете вращать квадратик скорости для определения углов.(Часто она отмечается прямо на инструменте; в противном случае отметка 0 градусов должна находиться на конце линейки с выступом, противоположном оси вращения.)
- Гипотенуза — самая длинная сторона квадрата скорости. Здесь вы увидите отметки от 0 до 90 градусов.
Как только вы научитесь работать с квадратом скорости, вы найдете несколько столь же удобных инструментов.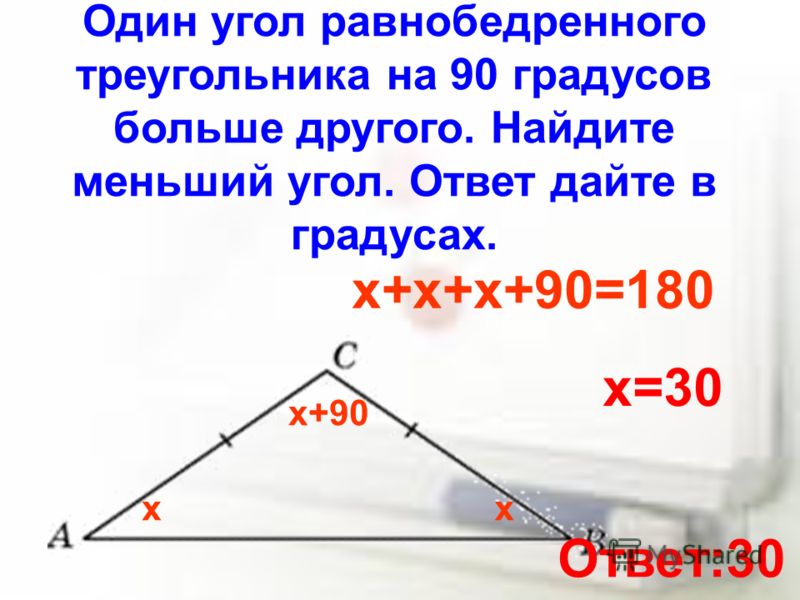 Ниже вы узнаете, как использовать квадратик скорости в полной мере!
Ниже вы узнаете, как использовать квадратик скорости в полной мере!
Фото: amazon.com
Разметка линий с помощью Speed SquareКогда вы строите шкафы, строите навесы или работаете над другими проектами, требующими большого количества длинных прямых разрезов, разметка линий облегчает вашу работу, позволяя вам быстро отметить, где именно пилить.Когда я был ребенком, мой отец так быстро делал линии разреза на фанере своим квадратом скорости, что я был бы поражен.
Не на каждом квадрате скорости есть маркировка и выемки, необходимые для разметки. Найдите один или два ряда выемок, каждый на четверть дюйма друг от друга, в открытой середине квадрата скорости. Вставьте кончик карандаша в желаемую выемку (если, например, вы хотите вырезать два дюйма из фанерной доски, выберите выемку на двухдюймовой отметке), затем проведите квадратом и карандашом вдоль край доски.За несколько секунд вы наметите прямую линию, полностью параллельную краю, и столько, сколько вам нужно, возможно, столько же, сколько и сама доска.
Квадрат можно перевернуть для стыковки с любой стороны доски, что позволяет выполнять перпендикулярные разметки, пока эта линия находится в пределах ширины вашего квадрата. Для линий, проходящих дальше по центру доски, прижмите кромку квадрата к доске, чтобы инструмент мог действовать как твердый перпендикулярный край, чтобы упираться в линейку или мерило.
Поиск углов с помощью квадрата скорости Если вы хотите сделать красивую скатную крышу для своего детского домика на дереве или вам нужен пандус для входа в сарай, получение правильного угла со всех сторон — сложная работа, которая может быть упрощено с вашим квадратом скорости. Во-первых, прижмите кромку квадрата скорости к той стороне доски, с которой вы работаете. Другая рука под прямым углом будет направлена от вас. Посмотрите на отметки градусов вдоль гипотенузы, и вы увидите, что это плечо обозначает угол в 90 градусов.Удерживая точку поворота на месте, отведите квадратный выступ скорости от доски. Найдите желаемый угол вдоль гипотенузы — например, если вы хотите отметить 30-градусный угол, точно совместите 30-градусную отметку с краем доски — затем удерживайте квадрат на месте и нарисуйте 30-градусный угол. линия градусов вдоль края квадрата скорости, противоположного показаниям угла, а также перпендикулярного выступу инструмента. Всегда используйте этот край для обозначения углов; используйте гипотенузу для маркировки разрезов только под углом 45 градусов.(См. Следующий раздел об использовании инструмента в качестве квадрата под углом, чтобы узнать, как это сделать.)
Найдите желаемый угол вдоль гипотенузы — например, если вы хотите отметить 30-градусный угол, точно совместите 30-градусную отметку с краем доски — затем удерживайте квадрат на месте и нарисуйте 30-градусный угол. линия градусов вдоль края квадрата скорости, противоположного показаниям угла, а также перпендикулярного выступу инструмента. Всегда используйте этот край для обозначения углов; используйте гипотенузу для маркировки разрезов только под углом 45 градусов.(См. Следующий раздел об использовании инструмента в качестве квадрата под углом, чтобы узнать, как это сделать.)
Резка молдингов короны в гостиной или рамы для стены галереи становится ветерок со скоростью квадрат! Просто прижмите кромку квадрата скорости к краю доски, начертите карандашом линию гипотенузы квадрата скорости и — вуаля! У вас есть идеальный угол в 45 градусов для легких поворотов. Нужен в обратном направлении? Просто переверните квадрат скорости и используйте обратную сторону инструмента.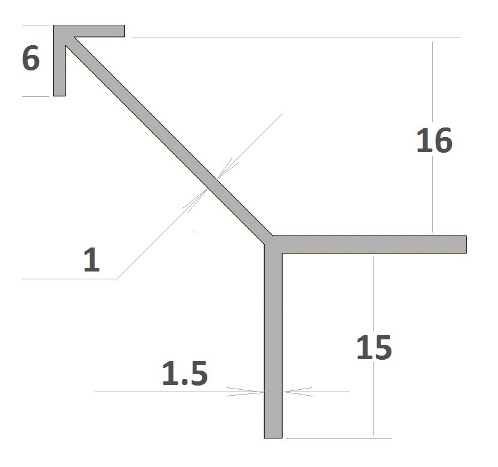 Приобретите угольник большего размера, и вы даже сможете использовать его для более длинных резов.
Приобретите угольник большего размера, и вы даже сможете использовать его для более длинных резов.
Прямой угол в 90 градусов, выходящий из точки поворота и выступа, позволяет легко и быстро находить прямые углы. Это особенно полезно, когда вы сталкиваетесь с повторяющимися сокращениями в таких проектах, как сборка колод. Просто прижмите губу к краю доски, проведите карандашом прямо под прямым углом, и получится линия под углом 90 градусов для резки!
Использование скоростного угольника в качестве направляющей для пилы Если вы хотите сэкономить время на распиливании бесконечных досок, необходимых для новой деки, качественный металлический скоростной угольник может стать настоящим активом в качестве направляющей для пилы.Пропуская карандашные линии и устанавливая инструмент прямо на режущую доску, вы избавляетесь от ступенек и получаете прочную кромку для более прямых и быстрых резов.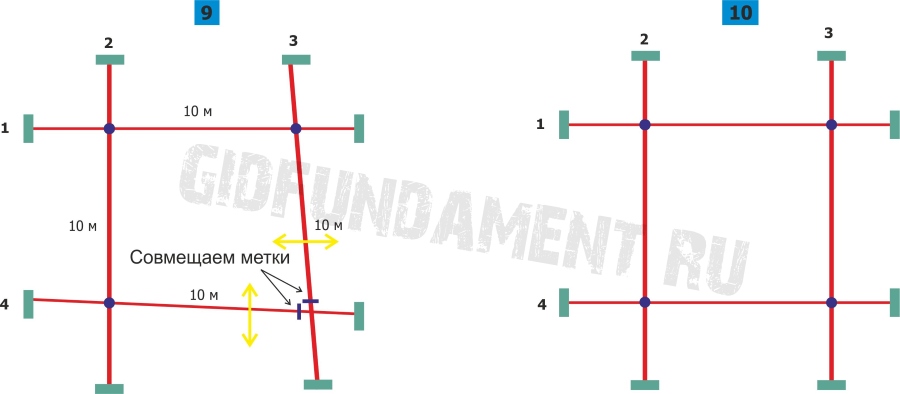 Совет по безопасности: закрепите кромку квадрата на стороне пиломатериала, которая находится от вас, так, чтобы, удерживая квадрат на месте, вы практически тянули скрепленный квадрат и пиломатериал к себе. Затем, когда вы водите циркулярной пилой по краю квадрата и отталкиваете пилу от себя, вы сможете лучше контролировать пиломатериал.Противоборствующие силы нейтрализуют друг друга, делая доску более устойчивой.
Совет по безопасности: закрепите кромку квадрата на стороне пиломатериала, которая находится от вас, так, чтобы, удерживая квадрат на месте, вы практически тянули скрепленный квадрат и пиломатериал к себе. Затем, когда вы водите циркулярной пилой по краю квадрата и отталкиваете пилу от себя, вы сможете лучше контролировать пиломатериал.Противоборствующие силы нейтрализуют друг друга, делая доску более устойчивой.
Ищите прочный большой скоростной квадрат с максимально возможным количеством функций — возможно, даже со встроенным уровнем — и вы никогда не начнете новую работу своими руками без него.
Решения практических задач (Триггер без слез)
Решения практических задач (Триггер без слез)Триггер без слез:
Авторские права 19972020 Стэн Браун, BrownMath.com
Решения для части 1: Введение
1 Найдите эти углы в градусах: (а) π / 6; (б) 2π; (c) 1 (это верно, радианные углы не обязательно дроби или кратные π).Решения :
(а) (π / 6) × (180 / π) = 30
(б) 2π × (180 / π) = 360
(в) 1 × (180 / π) = (180 / π) ≈ 57,3
2 Какое правильное определение острого угла в интервале обозначения?(а) (0, 90) (б) [0, 90]
Ответ : (0, 90) от 0 до 90 градусов за исключением 0 и 90; [0, 90] от 0 до
90 градусов включая 0 и 90. Острые углы
от 0 до 90 исключая , поэтому ответ
(а) (0, 90).
Острые углы
от 0 до 90 исключая , поэтому ответ
(а) (0, 90).
Решение : внутренние углы треугольник всегда должен составлять 180. 80 + 40 = 120, поэтому, чтобы сделать полные 180, третий угол должен быть 60.
4 Треугольник имеет угол 90. Две короткие стороны (рядом с угол) равны 5 и 12. Найдите третью сторону.Решение : Воспользуйтесь теоремой Пифагора!
c = a + b
с = 5 + 12
c = 25 + 144 = 169
c = √169 = 13
5 Найдите эти углы в радианах: (а) 60 (б) 126; (в) 45.По возможности, дайте точный ответ, а не десятичный приближение.
Решения :
(а) 60 + (π / 180) = π / 3.
(б) 126 × (π / 180) ≈ 2.20
(в) 45 × (π / 180) = π / 4
Обратите внимание, что вам не нужно говорить радианы, когда
давая угол в радианах, хотя это было бы неправильно. В этой книге углы в градусах помечены знаком градуса (), поэтому
Я скажу радианы только тогда, когда это необходимо
Во избежание путаницы.
В этой книге углы в градусах помечены знаком градуса (), поэтому
Я скажу радианы только тогда, когда это необходимо
Во избежание путаницы.
Ответ : Это было Чучело в фильме Волшебник Оз (1939).И нет, это звучит глупо, но это чушь. Это не может быть верным для любого треугольника , равнобедренного или не. (Вы понимаете, почему?)
7 На круглом циферблате, числа которого являются границами каждого квадрант?Ответы : Квадрант I: 12 и 3; Квадрант II: 9 и 12; Квадрант III: 6 и 9; Квадрант IV: 3 и 6.
Решения для части 2: Шесть функций
1 Найдите все шесть функций угла 30. Найдите синус, косинус, и тангенс 60. Решение : Во-первых, вам нужна длина горизонтального
сторона.Вы помните теорему Пифагора:
1 + b = 2, откуда вы
получаем b = √3. После этого это просто
вопрос запоминания определений. Если вам нужно освежиться,
вы найдете синус и косинус в уравнении 1, касательную в
уравнение 4, а остальные в уравнении 5.
После этого это просто
вопрос запоминания определений. Если вам нужно освежиться,
вы найдете синус и косинус в уравнении 1, касательную в
уравнение 4, а остальные в уравнении 5.
грех 30 = 1/2
cos 30 = √3 / 2
tan 30 = 1 / √3 или √3 / 3
детская кроватка 30 = 1 / (1 / √3) = √3
сек 30 = 1 / (√3 / 2) = 2 / √3 или (2 √3) / 3
csc 30 = 1 / (1/2) = 2
грех 60 = √3 / 2
cos 60 = 1/2
загар 60 = √3 / 1 = √3
Поскольку 60 = 90–30, обратите внимание, что грех 60 = соз 30, соз 60 = грех 30 и загар 60 = детская кроватка 30.
2 Найдите sin A , sin B , tan A и tan B .Решение :
sin A = 3/5 или 0,6
sin B = 4/5 или 0,8
коричневый A = 3/4 или 0,75
загар B = 4/3 ≈ 1,33
Между прочим, A ≈ 36,87, а B ≈ 53,13.
3 A ≈ 53,13. Найдите примерную площадь треугольник.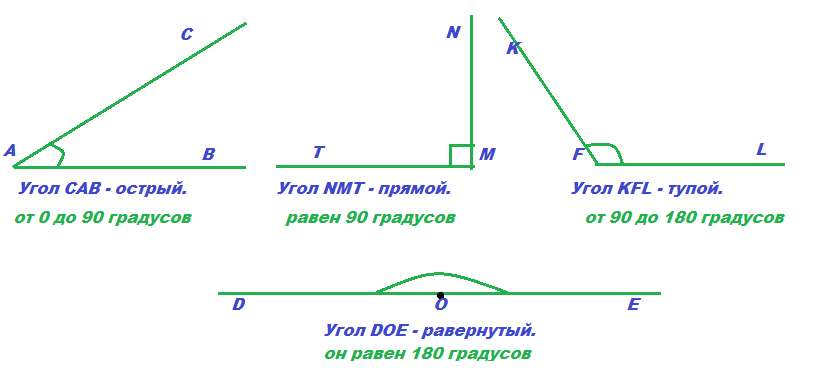 Подсказка: площадь треугольника равна основание × высота /2.
Подсказка: площадь треугольника равна основание × высота /2.Решение : У вас есть основание (5), поэтому вам просто нужна высота. Но sin A = h /3, поэтому h = 3 × sin A . Таким образом, площадь (5 × 3 × sin A ) / 2 ≈ 5,99999.
Решения для части 3: Функции специальных углов
1 (a) Нарисуйте треугольник 45-45-90 с гипотенузой 1. Обозначьте размер каждого угла и точную длину каждой стороны, а не калькулятор аппроксимации. (Подсказка: поскольку два острых угла равны, две короткие стороны должны быть равны.Это и теорема Пифагора достаточно, чтобы вы могли их найти.) (b) Нарисуйте треугольник, все стороны которого равны 1. Если все стороны
равны, все углы должны быть равны. Зная, что они добавляют к
180, введите значение каждого угла. Теперь опустите перпендикуляр
от вершины треугольника до середины противоположной стороны. Ты
теперь есть два треугольника 30-60-90 с гипотенузой 1. Заполните
точные длины коротких сторон этих двух треугольников.
Для решения остальных проблем обратитесь к этим эскизам. Если вам нужно. Дайте точные ответы, а не десятичные дроби.
Решение : Сравните свои наброски с теми, что в глава.
2 Найдите tan 45, cos 45, sin 90, cos 30, грех 30, cos 90.Ответы : загар 45 = 1; cos 45 = 1 / √2 или √2 / 2; грех 90 = 1; cos 30 = √3 / 2; грех 30 = 1/2; cos 90 = 0.
3 Найдите sin (π / 4), cos (π / 6), tan (π / 3).Ответы : sin (π / 4) = √2 / 2 или 1 / √2; cos (π / 6) = √3 / 2; загар (π / 3) = √3
4 Найдите каждый из следующих углов от ключей, предполагая, что все углы составляют от 0 до π / 2 (от 0 до 90) включительно.Дать каждый ответ в градусах и радианах. sin A = 0; cos B = √3 / 2; sin C = 1/2; sin D = 1; tan E = 1; cos F = 1/2; tan G = 0; загар H = √3; cos I = 1; cos Дж = 0.Ответы :
sin A = 0 ⇒ A = 0 или 0 [радиан]
cos B = √3 / 2 ⇒ B = 30 или π / 6
sin C = 1/2 ⇒ C = 30 или π / 6
sin D = 1 ⇒ D = 90 или π / 2
загар E = 1 ⇒ E = 45 или π / 4
cos F = 1/2 ⇒ F = 60 или π / 3
загар G = 0 ⇒ G = 0 или 0 [радиан]
загар H = √3 ⇒ H = 60 или π / 3
cos I = 1 ⇒ I = 0 или 0 [радиан]
cos Дж = 0 ⇒ Дж = 90 или π / 2
5 Найдите сек 60 и детскую кроватку 30. Подсказка: помните, как
секанс и котангенс определяются в терминах
большие три функции: синус, косинус и тангенс.
Подсказка: помните, как
секанс и котангенс определяются в терминах
большие три функции: синус, косинус и тангенс.Решения : сек 60 = 1 / (cos 60) = 1 / (1/2) ⇒ сек 60 = 2
детская кроватка 30 = 1 / (загар 30) = 1 / (√3 / 3) = 3 / √3 = √3 ⇒ детская кроватка 30 = √3
Вы также можете сделать второй, используя уравнение 6:
детская кроватка 30 = загар (90-30) = загар 60 = √3
6 Найдите sin 120, cos 120 и tan 120.Решение:
грех 120 = грех (180 — 120) = √3 / 2.
cos 120 = −cos (180 — 120) = −1/2.
А как насчет касательной? У вас нет правила о добавках для него, но у вас есть другой способ найти ответ:
загар 120 = грех 120 / соз 120 = (√3 / 2) / (−1/2) = −√3
7 Несмотря на то, что вы всегда можете получить дополнительный угол от синуса и косинуса, это экономит время, чтобы иметь правило для дополнения касательной. Решение последних проблем предположил, что это за правило.
Доказательство: загар (180 — A ) = −tan А .
Проба:
желто-коричневый (180- A ) = sin (180 — A ) / cos (180 — A )
желто-коричневый (180- A ) = sin A / (−cos A )
желто-коричневый (180- A ) = −sin A / cos A
желто-коричневый (180- A ) = −tan A QED
8 Найдите загар 150.Решение: загар 150 = −tan (180 — 150) = −tan 30 = −√3 / 3
Решения для части 4: Решение треугольников
1 У вас есть прямоугольный треугольник ( C = 90) с короткие стороны a = 88 и b = 37.Решите треугольник.Всегда начинайте с эскиза. На скетче справа видно прочь, что это случай с SAS, или сторона-угол-сторона. Чтобы получить третью сторону, вам нужен закон косинусов, уравнение 31.
c = a + b — 2 a b × cos C
с = 37 + 88 — 2 × 37 × 88 × cos 90
Обратите внимание, что когда включенный угол C равен 90,
cos C = 0, и вы только что получили пифагорейский
Теорема.
c = 37 + 88
с = √37 + 88
c ≈ 95,5
Чтобы найти два угла, вы можете использовать Закон синуса, но почему бы не взять Преимущество прямого угла и использования тангенса?
желто-коричневый A = 37/88 ⇒ A ≈ 22,8
Конечно загар B = 88/37, но вы также знаете, что
A + B = 90 ⇒ B = 90 — A ⇒ B ≈ 67.2
2 (Нарисуйте эту проблему по мере ее чтения.) В государственном парке река течет практически прямо к 1800 м. Вы хотите построить монорельс из A , один конец этот участок до точки C на дальнем берегу. Вы также хотите построить пешеходный мост от B , на другом конце этого участка реки, до той же точки C на дальнем берегу. При A угол между линиями обзора к B и C — 67.У B угол между вашим прицелом линии на A и C — 38.Какой длины должны быть монорельс и пешеходный мост?
Бонусный вопрос: если река имеет одинаковую ширину на всем протяжении протянуть от A до B , насколько он широкий?
На эскизе b — монорельс, a — подножка. мост, а w ширина реки. Поскольку вы знаете двух
углы и включенная сторона, это случай ASA.Хотя ты
не особо заботьтесь об угле C , вы должны его найти
так что вы можете использовать закон синусов, чтобы получить стороны a и b :
мост, а w ширина реки. Поскольку вы знаете двух
углы и включенная сторона, это случай ASA.Хотя ты
не особо заботьтесь об угле C , вы должны его найти
так что вы можете использовать закон синусов, чтобы получить стороны a и b :
С = 180 — 67 — 38 = 75
Очевидно, когда я смотрел на углы A и B Я не очень их оценил! Но это хорошо, набросок достаточно близок, чтобы быть полезным.
Какова длина пешеходного моста? От Закон синуса,
a / sin A = c / sin C ⇒ a = c sin A / sin C
= 1800 × грех 67 / грех 75
Пешеходный мост: a ≈ 1715 м
Какова длина монорельса? От Закон синуса,
b / sin B = c / sin C ⇒ b = c sin B / sin C
б = 1800 × грех 38 / грех 75
Монорельс: b ≈ 1147 м
Насколько широка река?
w = b sin A
w ≈ 1147 sin 67
Ширина реки: w ≈ 1056 м
3 Найдите другие элементы треугольника с B = 117, a = 16 см и b = 25 см.
Это случай SSA (или ASS); обратитесь к таблица возможностей для SSA. Эта проблема принадлежит строке 1, столбцу 2: противоположная сторона длиннее, чем соседняя сторона, и известный угол> 90. Итак, есть одно и только одно решение.
Вы можете использовать закон синусов, чтобы найти угол A :
(sin A ) / a = (sin B ) / b
sin A = ( a / b ) sin B
sin A = (16/25) sin 117 ≈ 0.57024
A ≈ 34,8
Найдите третий угол, вычтя:
С = 180- А — В
C ≈ 180 — 34,8 — 117
C ≈ 28,2
Наконец, используйте Закон синуса, чтобы найти сторону с :
c / sin C = b / sin B
c = b sin C / sin B
c ≈ 25 sin 28.2 / грех 117
c ≈ 13,3 см
4 Очень современно выглядящая подставка представляет собой треугольную форму со сторонами 6 дюймов, 9 дюймов и 12 дюймов. Какие
три угла?
Какие
три угла?Это случай SSS. Сначала используйте Закон косинусов для определения угла A:
cos A = ( b + c — a ) / 2 b c
cos A = (9 + 12-6) / (2 × 9 × 12) = 0,875
A ≈ 29,0
Затем используйте закон синусов, чтобы найти угол B :
(sin B ) / b = (sin A ) / a ⇒ sin B = ( b / a ) sin A
sin B ≈ (9/6) sin 29.0 ≈ 0,72618
B ≈ 46,6
Наконец, вычтите два угла из 180, чтобы найти третий угол:
C = 180- A — B
C ≈ 180 — 29,0 — 46,6
C ≈ 104,5
Кстати, это не опечатка. A и B оба оказались округленными, но я использовал неокругленные значения, чтобы найти С . Вы никогда не должны использовать округленные числа в дальнейшем расчеты.
5После того, как вы покрасили спальню, у вас достаточно краской осталось покрыть 25 футов. Вы решаете нарисовать треугольник
на стене другой комнаты, как акцент. Два угла должны быть
30 и 40. Найдите третий угол и длины
с трех сторон.
Вы решаете нарисовать треугольник
на стене другой комнаты, как акцент. Два угла должны быть
30 и 40. Найдите третий угол и длины
с трех сторон.Третий угол 180-30-40, поэтому С = 110. Сделайте свой набросок, используя эти три угла. (Я сделал это без Измерение углов, так что это не идеально. Но зарисовки не обязательно быть идеальным, просто достаточно близким.)
Найдите сторону c по уравнению 32:
с = √2 площадь × sin C / (sin A sin B )
с = √2 × 25 × sin 110 / (sin 30 sin 40)
c ≈ 12,1 футов
Тогда закон синуса дает вам другое с двух сторон:
a = c sin A / sin C
a ≈ 12,1 sin 30 / sin 110
a ≈ 6.4 фута
и
b = c sin B / sin C
b ≈ 12,1 sin 40 / sin 110
b ≈ 8,3 фут
6 Вы проезжаете 6,0 миль по прямому шоссе, затем съезжаете.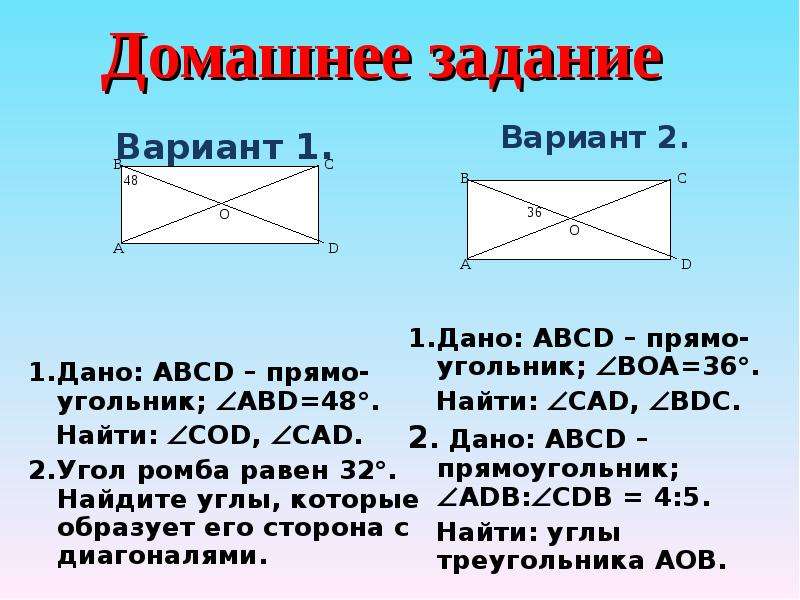 Поворот направо, но угла не замечаешь.
Поворот направо, но угла не замечаешь.Вы едете по прямой проселочной дороге. Пройдя 9,8 миль по проселочной дороге, вы повернете 135 на правильно, на третьей дороге. (Если вы визуализируете это сверху, изменение направления на 135 соответствует углу 180 — 135 = 45 в треугольнике.)
Если предположить, что дорога идет в том же направлении, как далеко? нужно ехать, чтобы добраться до отправной точки?
Это сложный набросок, потому что вы не знаете угол первого поворота. Но описание дает вам две стороны и невключенный угол; это проблемный случай SSA. Вы не знаете, где именно сторона c будет соответствовать стороне a . Если быть более точным, вы даже не знаю , встретятся ли .
Можно ли им встретиться? Ссылаясь на таблица возможностей в SSA, мы видим, что были в третьем ряду, первом столбце: соседние сторона (9.8) длиннее противоположной стороны (6.0), и известный угол (45) <90. Вычислить
h = b sin A
h = 9,8 sin 45 ≈
6. 9 миль
9 миль
Что это значит? Кратчайшее расстояние от точки C к стороне c — это отрезок, который соответствует сторона c под прямым углом. Другими словами, чтобы получить от точки C к стороне c , кратчайшее возможное расстояние 6.9 миль. Но сторона и всего 6,0 миль в длину, так что она может никогда не встречал стороны c .
Эта проблема не имеет решения.
Вы выкладываете треугольную грядку для своего сада. Две стороны 40 м и 60 м, а угол между ними равен 22. Какова длина третьей стороны и какие две другие? углы?Вы знаете две стороны и угол между ними. Вы можете использовать Закон косинусов для получения третьей стороны:
a = b + c — 2 b c × cos A
= 60 + 40 — 2 × 60 × 40 × cos 22
c ≈ √749.52 ⇒ c ≈ 27,4 м
Далее для угла B можно использовать Закон синуса:
(sin B ) / b = (sin A ) / a ⇒ sin B = (б / а) sin A
sin B ≈ (60 / 27,4) sin 22 ≈ 0,82099
Ваш калькулятор дает около 55,2 как угол, синус которого равен
0. 82099, но это выглядит не так
с эскиза. Очевидно, что угол B должен быть тупым углом, так что помните
что грех (180 — х ) = грех х ,
и вы вычитаете 180 — 55.2, чтобы получить
82099, но это выглядит не так
с эскиза. Очевидно, что угол B должен быть тупым углом, так что помните
что грех (180 — х ) = грех х ,
и вы вычитаете 180 — 55.2, чтобы получить
B ≈ 124,8
Видите, насколько важен эскиз? Конечно твой скетч наверное не совсем точен, поэтому вы относитесь к нему как к способу указать что-то может быть неправильным, но тогда вы ищете способ подтвердить это. В этом случае у вас есть два способа подтвердить it:
- Вы можете использовать Закон косинусов, который автоматически
учитывает тупые углы:
cos B = ( a + c — b ) / (2 a c )
cos B ≈ (27.4 + 40-60) / (2 × 27,4 × 40)
cos B ≈ −0,57095 ⇒ B ≈ 124,8
- Или вы можете вычислить угол C (ниже), а затем вспомнить этот угол C должен быть < B , потому что сторона c — < b . Если вы сделали C тупой, 180 — 33,2 = 146,8, было бы
> B независимо от того, является ли B острым или тупым.
 Так C должен быть <90 и B должен быть
> 90.
Так C должен быть <90 и B должен быть
> 90.
Теперь поверните на угол C:
(sin C ) / c = (sin A ) / a ⇒ sin C = (c / a) sin A
sin C ≈ (40 / 27,4) sin 22 ≈ 0,54732
C ≈ 33,2
Решения для Части 5: Функции под любым углом
1 В каком квадранте находится угол -868? Что о 42 радиана? Каковы знаки их синусов, косинусов и касательных?Решение: Ваша задача всегда — изгнать кратные 360 или 2π, чтобы вы оставались с положительным углом от 0 до 360 (от 0 до 2π).
−868 = −1080 + 212. И 212 находится между 180 и 270, так что −868 встречается в Q III.
42 радиана составляет около 13,37π, или 12π + 1,37π. 1,37π, очевидно, находится между π и 3π / 2 (1.5π), поэтому 42 (радианы) находится в III квартале.
В Q III значения x и y отрицательны. Следовательно
В Q III синус и косинус отрицательны, а тангенс положительна.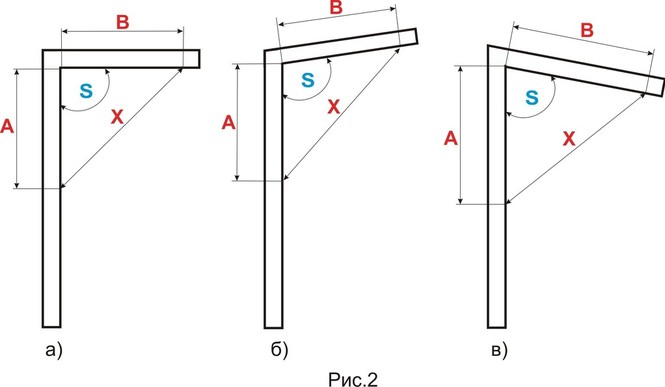
Решение: (a) 700 = 360 + 340, поэтому грех 700 = грех 340. 340 в Q IV, где y отрицательно; следовательно, синус отрицательный. Базовый угол равен 20, поэтому грех 700 = −sin 20.
(б) 780 = 720 + 60, поэтому загар 780 = загар 60.
(в) −390,5 ≈ −124,3π, или −126π + 1,7π; следовательно cos (-390,5) ≈ cos 1,7π. Угол 1,7π радиан находится между 1,5π и 2π, поэтому Q IV, где x положительно и, следовательно, косинус равен положительный.Базовый угол составляет около 2π — 1,7π ≈ 0,3π или 0,94, поэтому cos (-390,5) ≈ cos 0,94.
3 Запишите как функцию всего A : (а) cos (720 — А ) (б) грех (43π + A ) Решение: (a) 720 делится на 360, поэтому
cos (720 — A ) = cos (- A ).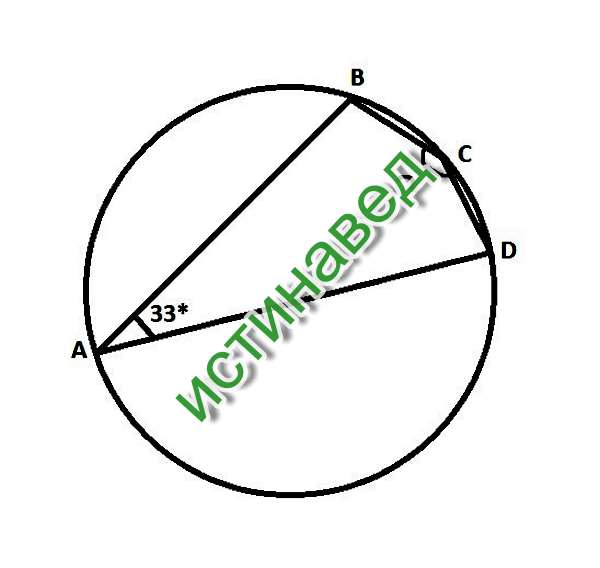 Но cos (- A ) = cos A , и поэтому
cos (720 — A ) = cos A .
Но cos (- A ) = cos A , и поэтому
cos (720 — A ) = cos A .
(б) sin (43π + A ) = грех (42π + π + A ) = sin (π + A ).sin (π + A ) = −sin A , поэтому sin (43π + A ) = −sin A .
Решения для части 6: Квадратные идентичности
1 Если sin A = 3/4, найдите cos A .Решение :
sin² A + cos² A = 1
cos² A = 1 — sin² A = 1 — (3/4) = 1 — 9/16
cos² A = 7/16
cos A = √7 / 16 ⇒ cos A = √7 / 4 или −√7 / 4
Вы помните знак? Как только x = 9 имеет два решения, 3 и −3, поэтому любое уравнение в cos² A имеет два решения.
Это имеет смысл с точки зрения функций. Есть два
углы в интервале [0, 2π) или [0, 360)
где sin A = 3/4, один острый и один тупой. В
острый имеет положительный косинус, а тупой — отрицательный
косинус.
Решение : Поскольку эта глава посвящена в квадрате личности, вы можете быть уверены, что она существует который соединяет загар x и sec x .Но предположим, вы встретили это проблема в другом контексте?
Ну, вы знаете два тождества с касательной функцией. Определение tan B = (sin B ) / cos B , не много ли вам добра, потому что в нем смешаны синус и косинус все вместе. Вы плохо помните квадратную идентичность (если вы как и я, он тусклый), но вы также знаете, что можете воссоздать его легко, с одного личность в квадрате, которую невозможно забыть:
sin² B + cos² B = 1
У вас есть sin² B , который станет tan² B , если вы разделите обе стороны на cos² B .
(sin² B ) / cos² B + (cos² B ) / cos² B = 1 / cos² B
tan² B + 1 = sec² B
Успех! У вас есть личность, которая связывает касательную и
секущие функции. Теперь можно переходить к решению проблемы.
Теперь можно переходить к решению проблемы.
(−2√2) + 1 = сек² B
сек² B = (4 × 2) + 1 = 9
сек B = 3
Знак вам нужен, потому что оба ( x ) и (- x ) составляют x .Но делает это имеет смысл с точки зрения триггера? Да, потому что касательная отрицательна в Q II и Q IV, а секущая, имеющая то же знак как косинус, 1 по косинусу положителен в Q IV, но отрицательный в Q II.
3 загар C = √15. Найдите cos C .Решение : Подождите, что? У тебя нет тождество, соединяющее тангенс и косинус. Но у вас до есть соединяя касательную и секанс, и вы знаете, что секанс на 1 больше косинус, так что вы тоже можете сделать это.
Начните с квадрата идентичности из предыдущей задачи:
tan² C + 1 = sec² C
(√15) + 1 = 15 + 1 = 16 ⇒ сек² C = 16
сек C = 4 ⇒ cos C = 1/4
4 tan D = √15, Найти sin D .
Решение : Хорошо, в предыдущей задаче вы получили касательная к косинусу. Но вы уже знаете, как перейти от косинуса к sine, так что у вас есть еще одно звено в цепочке.
tan² D + 1 = sec² D
сек² D = (√15) + 1 = 16
сек D = 4 ⇒ cos D = 1/4
sin² D + cos² D = 1
sin² D = 1 — cos² D = 1 — (1/4) = 1 — 1/16 = 15/16
sin D = √15 / 4
5 Докажите: sin² x = tan² x / (tan² x + 1)Предполагается, что x ≠ π / 2 + k π, для целого числа к или 90 + 180 к , если вы предпочитаю, потому что тангенс для этих углов не определен.
Доказательство :
желто-коричневый x = коричневый x
загар x cos x = загар x cos x
sin x = коричневый x / сек x
sin² x = tan² x / сек² x
But tan² x + 1 = sec² x , поэтому замена у вас
sin² x = tan² x / (tan² x + 1) QED
Возможны многие другие доказательства. Например, вы можете заменить
tan² x с sin² x / cos² x в
личность вас попросили подтвердить, а затем упростить дробь.
Пока каждый шаг вашего доказательства действителен как в обратном, так и в обратном направлении.
вперед, ваше доказательство в порядке.
Например, вы можете заменить
tan² x с sin² x / cos² x в
личность вас попросили подтвердить, а затем упростить дробь.
Пока каждый шаг вашего доказательства действителен как в обратном, так и в обратном направлении.
вперед, ваше доказательство в порядке.
Если ваше доказательство начинается с очевидной личности, а затем работает вперед к личности, которую мы попросили подтвердить, как и вышеприведенное доказательство, тогда имеет значение только то, что все шаги действительны в этом форварде направление.
Решения для части 7: формулы суммы и разности
1 Точно найдите sin (−15).Решение: Начать с −15 = 30-45
грех (-15) = грех (30-45)
грех (-15) = грех 30 cos 45 — соз 30 грех 45
грех (-15) = (1/2) (√2 / 2) — (√3 / 2) (√2 / 2) = √2 / 4 — √6 / 4
грех (-15) = (√2 — √6) / 4
Альтернативное решение: Вы также можете сделать это, используя 45-60:
грех (-15) = грех (45−60)
грех (-15) = грех 45 cos 60 — соз 45 грех 60
грех (-15) = (√2 / 2) (1/2) — (√2 / 2) (√3 / 2) = √2 / 4 — √6 / 4 = (√2 — √6) / 4
2 Найдите загар 105 точно.
Решение: 105 = 60 + 45
загар 105 = загар (60 + 45)
загар 105 = (загар 60 + загар 45) / (1 — загар 60 загар 45)
загар 105 = (√3 + 1) / (1 — (√3) (1)) = (√3 + 1) / (1 — √3)
Умножить верхнюю и нижнюю на 1 + √3, чтобы получить рационализировать знаменатель:
загар 105 = (√3 + 1) / ((1 — √3) (1 + √3))
загар 105 = (3 + 2√3 + 1) / (1-3) = (4 + 2√3) / (- 2) = −2 — √3
3 Докажите: cos 2 A = 2 cos² A — 1. (Подсказка: 2 A = A + A .)Проба:
cos 2 А = cos ( A + A )
cos 2 А = cos A cos A — sin A sin A
cos 2 А = cos² A — sin² A
Но sin² A = 1 — cos² A
cos 2 А = cos² A — (1 — cos² A ) = cos² A — 1 + cos² A
cos 2 А = 2 cos² A — 1 QED
4 Докажите эти формулы из уравнения 22, используя формулы для функций суммы и разности.
(а) cos (- A ) = cos A (Я сделал за вас первый шаг.)
cos (- А ) = cos (0 — А )
cos (- А ) = cos 0 cos A + sin 0 sin A
cos (- А ) = 1 cos A + 0 sin A
cos (- А ) = cos A QED
(б) tan (π + A ) = tan A
загар (π + A ) = (tan π + tan A ) / (1 — tan π tan A )
загар (π + A ) = (0 + загар A ) / (1-0 загар A )
загар (π + A ) = (загар A ) / 1
загар (π + A ) = желто-коричневый A QED
(c) sin (π — A ) = sin A
sin (π — A ) = sin π cos A — cos π sin A
грех (π — A ) = 0 cos A — (−1) sin A
грех (π — A ) = грех A QED
Решения для Части 8: Формулы двойного и половинного угла
1 Используйте формулы половинного угла, чтобы найти sin 90 и cos 90. Конечно, вы их уже знаете; эта проблема
просто для практики в работе с формулами и легкими числами.
Конечно, вы их уже знаете; эта проблема
просто для практики в работе с формулами и легкими числами.Решение: : 90 — это половина 180. Синус и косинус равны положительный или ноль на 90, поэтому знаки в формулах можно рассматривать как положительный.
грех (180/2) = √ (1 — cos 180) / 2 = √ (1 — (−1)) / 2 = √2 / 2
грех 90 = 1
cos (180/2) = √ (1 + соз 180) / 2 = √ (1 + (−1)) / 2 = √0 / 2
cos 90 = 0
Почему я не просил вас сделать то же самое для загар 90?
2 Воспользуйтесь формулами двойного угла, чтобы найти sin 120, cos 120, а tan 120 точно.Опять же ты уже знать это; Вы только начинаете знакомиться с формулами.Решение: 120 — это двойное 60. sin 60 = √3 / 2, cos 60 = 1/2 и загар 60 = √3.
грех (260) = 2 sin 60 cos 60 = 2 (√3 / 2) (1/2)
грех 120 = (√3) / 2
cos (260) = 2 cos² 60 — 1 = 2 × (1/2) — 1 = (1/2) — 1
cos 120 = -1/2
загар (260) = 2 загар 60 / (1 — загар² 60) = 2 √3 / (1 — (√3)) = 2 √3 / (1-3) = 2 √3 / (−2)
загар 120 = −√3
Альтернативное решение: Вы также можете разделить:
загар 120 = грех 120 / соз 120 = (√3 / 2) / (−1/2) = −√3
3 3 A = 2 A + A . Используйте формулы двойного угла вместе с
формулы для синуса или косинуса суммы, чтобы найти
формулы для sin 3 A только в терминах sin A ,
и cos 3 A только с точки зрения cos A .
Используйте формулы двойного угла вместе с
формулы для синуса или косинуса суммы, чтобы найти
формулы для sin 3 A только в терминах sin A ,
и cos 3 A только с точки зрения cos A .(На самом деле это было сделано позже раздел, используя другой метод.)
Решение: Сначала синус:
sin (2 A + A ) = sin 2 A cos A + cos 2 A sin A
sin 3 A = (2 sin A cos A ) cos A + (1-2 sin² A ) sin A
sin 3 A = 2 sin A cos² A + sin A — 2 sin³ A
sin 3 A = 2 sin A (1 — sin² A ) + sin A — 2 sin³ A
sin 3 A = 2 sin A — 2 sin³ A + sin A — 2 sin³ A
sin 3 A = 3 sin A — 4 sin³ A , или (3 — 4 sin² A ) sin A
Теперь косинус:
cos (2 A + A ) = cos 2 A cos A — sin 2 A sin A
cos 3 А = (2 cos² A — 1) cos A — (2 sin A cos A ) sin A
cos 3 А = 2 cos³ A — cos A — 2 sin² A cos A
cos 3 А = 2 cos³ A — cos A — 2 (1 — cos² A ) cos A
cos 3 А = 2 cos³ A — cos A — 2 cos A + 2 cos³ A
cos 3 А = 4 cos³ A — 3 cos A , или (4 cos² A — 3) cos A
4 Учитывая грех 3 А = (3 — 4 sin² A ) sin A и cos 3 A = (4 cos² A — 3) cos A , найти tan 3 A только для желтовато-коричневого A . Проверьте себя, вычислив загар (2 A + A ).
Проверьте себя, вычислив загар (2 A + A ).Решение:
загар 3 A = sin 3 A / cos 3 A
загар 3 A = ((3 — 4 sin² A ) sin A ) / ((4 cos² A — 3) cos A )
загар 3 A = (sin A / cos A ) (3 — 4 sin² A ) / (4 cos² A — 3)
загар 3 A = tan A (3 — 4 sin² A ) / (4 cos² A — 3)
Разделите верх и низ на cos² A .Это по крайней мере избавляет sin² A и cos² A , несмотря на то, что он вводит секущие функции. (Вы помните, что 1 / cos A = сек A , верно?)
загар 3 A = желто-коричневый A (3 сек² A — 4 tan² A ) / (4 — 3 сек² A )
Возможно, это выглядит не лучше, но раньше вам пришлось
избавиться от двух нежелательных функций; теперь у вас есть только один нежелательный
функция, даже если это происходит дважды. И его sec² A .
Разве нет какого-то
Пифагорейская идентичность с участием
сек² A ? Да, есть! sin² A +
cos² A = 1 ⇒ tan² A +1 =
сек² A .
И его sec² A .
Разве нет какого-то
Пифагорейская идентичность с участием
сек² A ? Да, есть! sin² A +
cos² A = 1 ⇒ tan² A +1 =
сек² A .
загар 3 A = желто-коричневый A (3 (tan² A + 1) — 4 tan² A ) / (4 — 3 (tan² A + 1))
загар 3 A = желто-коричневый A (3 tan² A + 3-4 tan² A ) / (4–3 tan² A -3)
загар 3 A = желто-коричневый A (3 — tan² A ) / (1 — 3 tan² A )
Чек:
желто-коричневый (2 A + A ) = (желто-коричневый 2 A + коричневый A ) / (1 — коричневый 2 A желто-коричневый A )
Из уравнения 60, tan 2 A = 2 желто-коричневый A / (1 — коричневый² A ).
загар 3 A = (2 желто-коричневый A / (1 — коричневый² A ) + коричневый A ) / (1 — (2 желто-коричневый A / (1 — коричневый² A )) коричневый A )
Ну вот и бардак! Очистите это, умножив вершину и
снизу по (1 — tan² A ).
загар 3 A = (2 желто-коричневый A + (1 — коричневый² A ) коричневый A ) / ((1 — коричневый² A ) — 2 желто-коричневый A коричневый A )
загар 3 A = (3 желтых A — желто-коричневых³ A ) / (1 — 3 желтых² A )
Вынести за скобки tan A из верхней части фракции, и он такой же, как и в первом методе:
загар 3 A = желто-коричневый A (3 — tan² A ) / (1 — 3 tan² A )
5 Точно найдите синус, косинус и тангенс числа π / 8.Решение: π / 8 (22) составляет половину от π / 4 (45), поэтому вам нужны формулы половинного угла. А π / 8 находится в квадранте I, поэтому все значения функции будут положительными.
грех π / 8 = √ (1 — cos π / 4) / 2
грех π / 8 = √ (1 — √2 / 2) / 2 = √ (2 — √2) / 4 = () √2 — √2
Это выражение содержит вложенных радикала .
Хотя некоторые вложенные радикалы могут быть денестированы, следуя
техника в Denesting Radicals (или Unnesting Radicals), эта
к сожалению, нет.
cos π / 8 = √ (1 + cos π / 4) / 2
cos π / 8 = √ (1 + √2 / 2) / 2 = √ (2 + √2) / 4 = () √2 + √2
Теперь перейдем к касательной.Вы можете использовать формула полуугла, или просто разделите синус на косинус.
тангенса π / 8 = (грех π / 8) / (соз π / 8)
тангенса π / 8 = √2 — √2 / √2 + √2
Этот можно денестировать , если умножить вершину и снизу на √2 — √2. Ты обычно делаешь это так или иначе, чтобы рационализировать знаменатель, но это хороший бонус, который происходит, чтобы очистить числитель.
тангенса π / 8 = √ (2 — √2) (2 — √2) / √ (2 + √2) (2 — √2)
тангенса π / 8 = (2 — √2) / √ (4 — 2) = (2 — √2) / √2 = √2 — 1
Решения для Части 9: Обратные функции
1 Возможные выходные значения Arcsin x включают π / 2, но возможные выходные значения Arctan x делают не.Почему Arctan x никогда не может равняться −π / 2 или π / 2? Решение :
Arctan x — это угол, тангенс которого равен x , поэтому
возможные значения Arctan x — это углы в Q IV и
Q I, касательные к которым можно брать.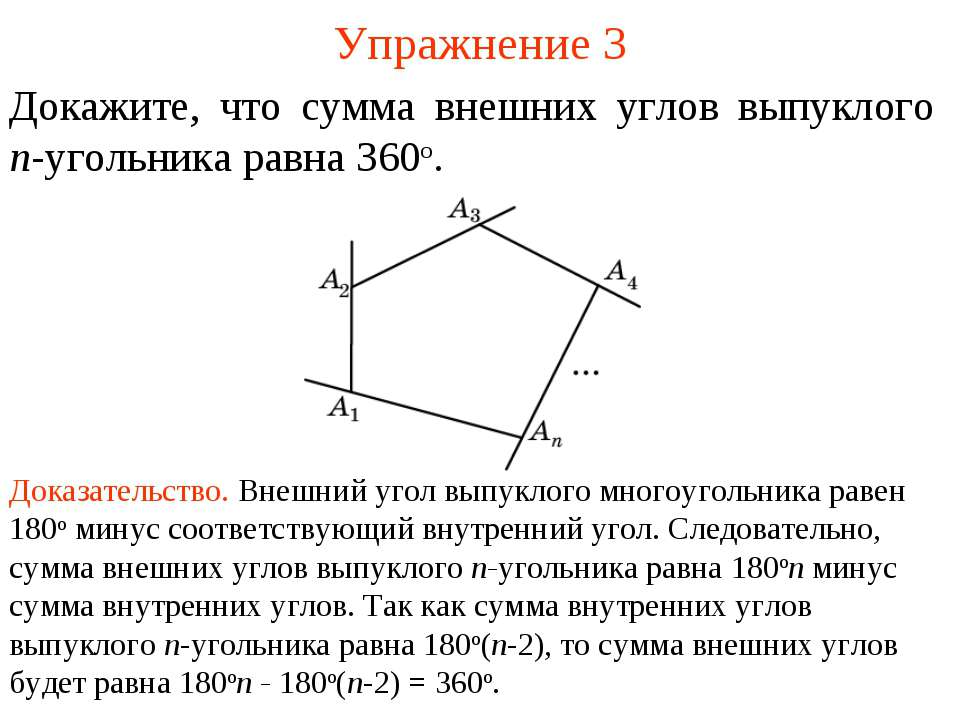 Но tan −π / 2
и tan π / 2 не существует,
поэтому они не являются возможными значениями
Arctan x .
Но tan −π / 2
и tan π / 2 не существует,
поэтому они не являются возможными значениями
Arctan x .
Решение : Если угол A равен Arcsin x , то мы можем сделайте x противоположную сторону и 1 гипотенузу. Посредством теорема Пифагора, которая делает смежную сторону √1 — х . sec A поэтому сек (Arcsin x ) = 1 / √1 — x .
В ответе нет нечетных степеней x , поэтому мы не нужно беспокоиться о знаке x .
Давайте проверим это с помощью х = -0.7: Arcsin −0,7 ≈ −44,43, а с -44,3 = 1 / cos −44,3 ≈ 1,40. 1 / √ (1 — 0,7) ≈ 1,40 также, так что формула верна, по крайней мере, для этого теста.
3 Найдите грех (Arccos 1/ x ). Не забудьте сделать набросок, чтобы помочь вам. Выберите значение, например x = 1,3, в качестве тестового примера для
Проверьте свой ответ.
Выберите значение, например x = 1,3, в качестве тестового примера для
Проверьте свой ответ.Решение : Если угол A равен Arccos 1/ x , мы можем установить гипотенузу на x , а прилегающую сторону на 1, поэтому что cos A = 1/ x , как требуется.Третья сторона равно √ x — 1.
Что грешит А ? Это должно быть √ x — 1/ x . Но это выражение имеет нечетную степень x , поэтому нам нужно проверьте знаки. Если x отрицательно, то Arccos x будет во втором квартале. Функция синуса имеет все положительные значения в Q II, значит, у нас должен быть положительный ответ. Но как написано, дробь отрицательна, если x отрицательна, поэтому требуется знак абсолютного значения, как в примере 3.Наш окончательный ответ —
sin (Arccos 1/ x ) = √ ( x — 1) / | x |
Давайте проверим это с помощью х = -1,3:
Arccos (1 / −1,3) ≈ 140,28, дюйм
Q II, как ожидалось, и
sin 140,28 ≈ 0,64, положительное число вроде
синусы всех углов в Q II. √ ((- 1,3) — 1) / | −1,3 | ≈
0,64 тоже.
Итак, формула верна, по крайней мере, для этого теста
даже с отрицательным x, положив угол в Q II, формула
при необходимости возвращает положительное число.
√ ((- 1,3) — 1) / | −1,3 | ≈
0,64 тоже.
Итак, формула верна, по крайней мере, для этого теста
даже с отрицательным x, положив угол в Q II, формула
при необходимости возвращает положительное число.
Решения для части 10: развлечения с комплексными числами
1 Выразите в форме a + b i: (а) 62∠240 (б) 100e 1.17iРешения : (а) 62 (cos (240) + i sin (240)) ≈ −31−53,69i
(b) очевидно в радианах, так как градусы отсутствуют. отметка. 100 (cos (1,17) + i sin (1,17)) ≈ 39.02 + 92.08i
2 Выразите в полярной форме в градусах и радианах: (а) −42 + 17i (б) 100i (в) −14,7Решения : (а) r = √ (-42) + 17 ≈ 45,31. θ = 2 Арктан (17 / (- 42 + 45,31)) ≈ 2,76; умножьте на 180 / π, чтобы получить 157,96. Ответы: 45,31 цис 157.96 или 45,31 цис 2,76. Конечно, вы могли бы использовать любые другие формы, показанные в главе.
(b) и (c) — пустяки, так как у вас нет
для вычисления радиуса или угла.
(б) 100i = 100∠90 или
100e iπ / 2
(в) −14,7 = 14,7∠180 или
14,7 e iπ
Решение : Сначала положите −i в полярную форму, что достаточно просто, поскольку −i на отрицательной оси y : −i = 1 цис 3π / 2.Затем примените формулу, уравнение 83:
(1 цис 3π / 2) 1/3 = 1 1/3 цис (π / 2 + 2π k /3) для k = 0, 1, 2
Три угла равны π / 2, π / 2 + 2π / 3 = 7π / 6 и π / 2 + 4π / 3 = 11π / 6 = 3π / 2.
(1 цис 3π / 2) 1/3 = 1 цис π / 2, 1 цис 7π / 6, 1 цис 11π / 6.
Вы знаете точные синусы и косинусы для любого числа, кратного π / 6, так что вам не нужен ваш калькулятор, чтобы конвертировать обратно в a + b i форма:
Кубические корни из −i:
я, — (√3 / 2) — (1/2) я, (√3 / 2) — (1/2) я.
Между прочим, я не только кубический корень из −i, но −i — кубический корень из я. Я позволю тебе найти два других кубических корня я себя.
4 Найдите (1.04−0.10i) 16 .Решение : Сначала представьте это число в полярной форме: r = √1,04 + 0,10 ≈ 1.044796631. Затем найти θ = 2 Арктан (-0,10 / (1,04 + 1,044796631)) ≈ −0,09585. (Мой калькулятор работает в радианах, но это не имеет значения, потому что я буду конвертировать обратно в в любом случае прямоугольный формат.) Так
(1.04−0.10i) ≈ 1,04796631 цис -0,09585
И поэтому
(1.04−0.10i) 16 ≈ 1,04796631 16 цис (-16; 0,09585)
≈ 2,016082111 цис (-1,533746354)
≈ 0,0746787−2,01469853i
Что нового
- 6 ноября 2020 г. : страница преобразована из HTML 4.01 в HTML5, и улучшено форматирование радикалов.
- 20 декабря 2016 : в проблеме, которая создает вложенные радикалы,
добавлена ссылка на методику на этом сайте
за их разрушение.

- 11 декабря 2016 : Добавлены решения практических задач для Часть 5; добавлены три новых доказательства в части 7.
- 29 ноября 2016 г. : добавлены три новые задачи в части 3.
- 26/27 ноя 2016 : Добавлены решения для проблем Части 7 и Части 8.
- 19/20 ноября 2017 г. : добавлены решения для части 1, части 3 и Часть 6 проблемы.
- 13 ноя 2016 : Добавлены решения для проблем Части 5. (Часть 5 был перенумерован в Часть 4 29 ноября 2016 г.)
- 30 октября 2016 г. : Добавлены решения для проблем Части 9 и Части 10.
- 27 октября 2016 г. : Новый документ (только задачи части 2).


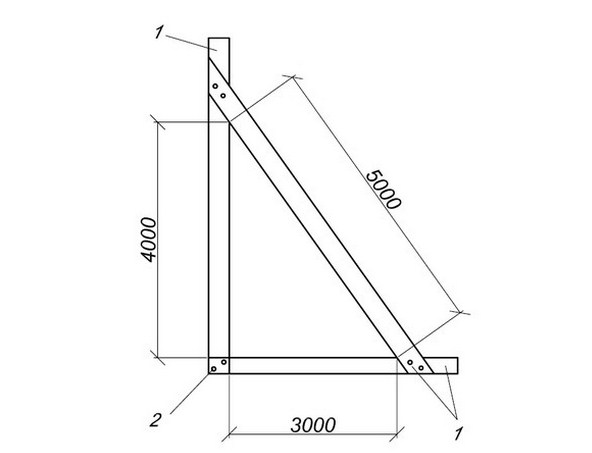 Штукатурка внутренних и внешних углов не укладывается сразу. Вначале набрасывают жидковатый раствор, дают ему схватиться, только потом наносят основную часть.
Штукатурка внутренних и внешних углов не укладывается сразу. Вначале набрасывают жидковатый раствор, дают ему схватиться, только потом наносят основную часть.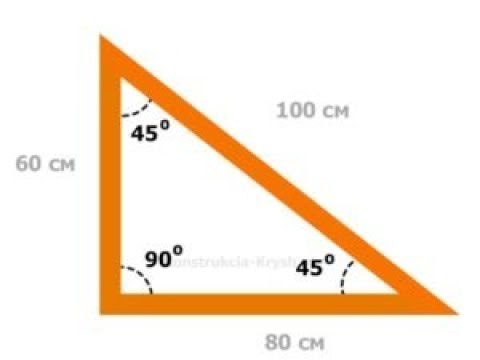 Для более надежного контакта раствора со стеной, он набрасывается с ударом, своеобразными «шлепками».
Для более надежного контакта раствора со стеной, он набрасывается с ударом, своеобразными «шлепками». Здесь выравнивание необходимо для монтажа плинтуса.
Здесь выравнивание необходимо для монтажа плинтуса. Это требует дополнительных усилий и времени.
Это требует дополнительных усилий и времени.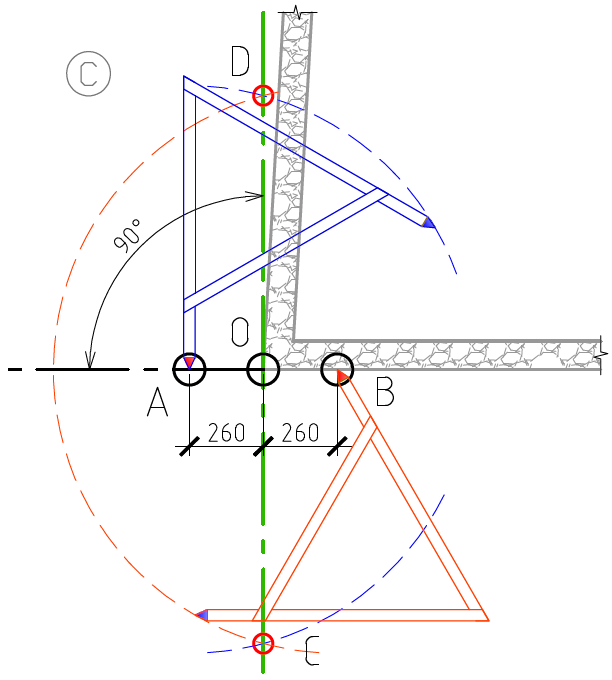 Широкие угольники маркируются в виде двух букв УШ
Широкие угольники маркируются в виде двух букв УШ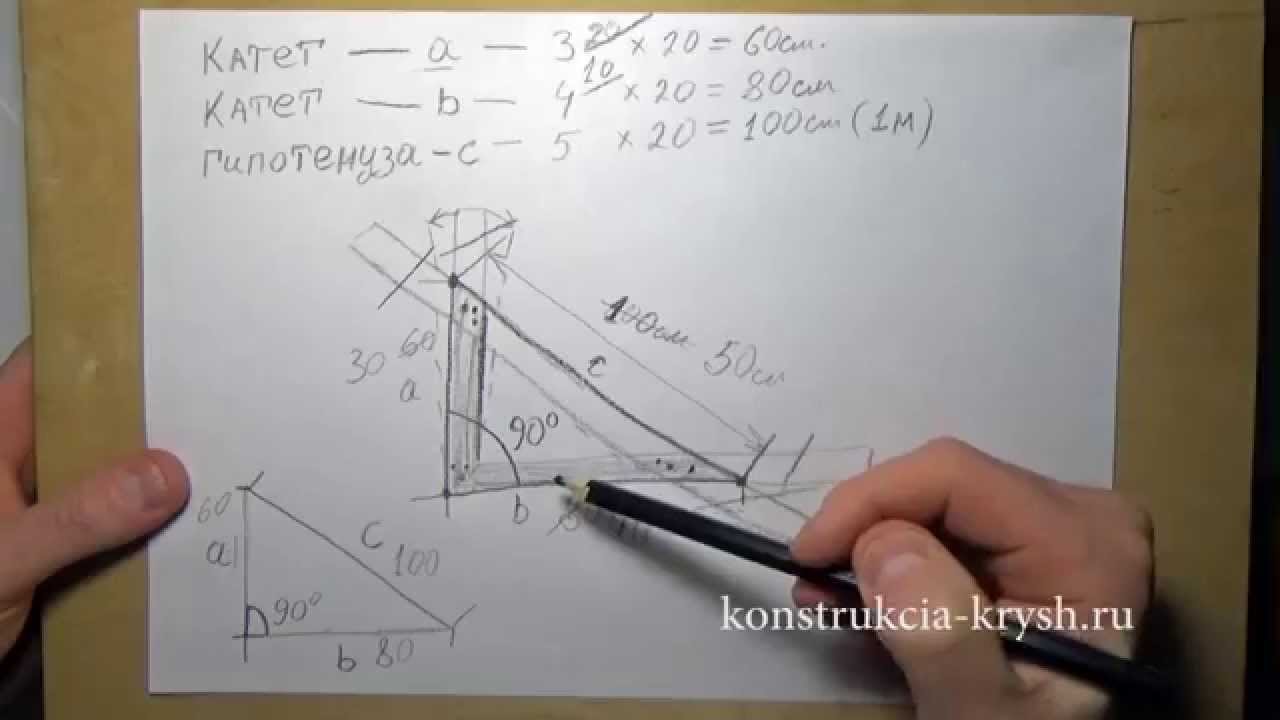 На рукоятки инструмента имеется камера, заполненная водой с пузырьком воздуха. Посредством которого удается определить ровность поверхностей, углы которых проверяются угольником
На рукоятки инструмента имеется камера, заполненная водой с пузырьком воздуха. Посредством которого удается определить ровность поверхностей, углы которых проверяются угольником Для работы с керамической плиткой и прочими мелкими деталями достаточно инструментов, длина которых не превышает 30 см
Для работы с керамической плиткой и прочими мелкими деталями достаточно инструментов, длина которых не превышает 30 см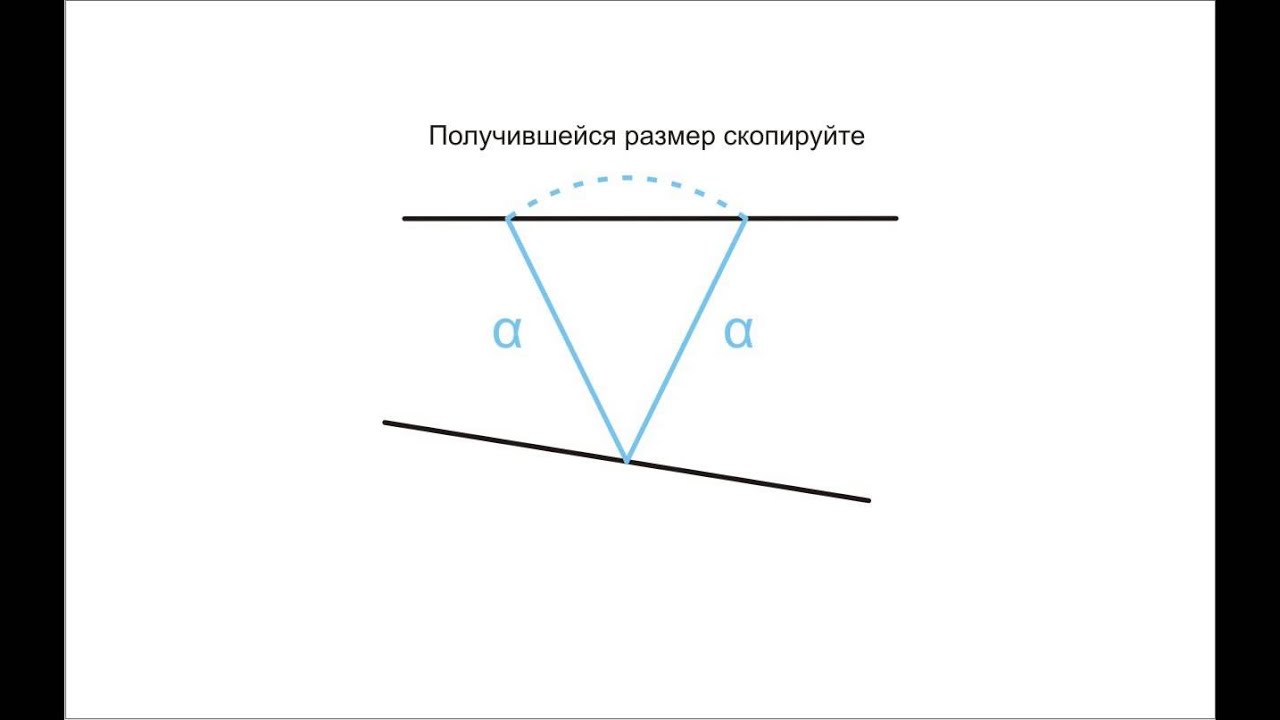 Именно поэтому в некоторых случаях рационально рассмотреть варианты пластиковых и деревянных угольников
Именно поэтому в некоторых случаях рационально рассмотреть варианты пластиковых и деревянных угольников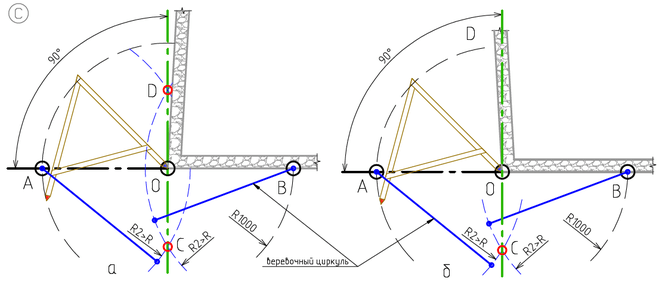 Особенно часто для проверки правильности прямых углов применяются инструменты в сфере сборки и производства мебели
Особенно часто для проверки правильности прямых углов применяются инструменты в сфере сборки и производства мебели После этого проводится соответствующая прямая линия
После этого проводится соответствующая прямая линия Цена деления угломерной шкалы — 0,5°, прямолинейной — 1 миллиметр.
Цена деления угломерной шкалы — 0,5°, прямолинейной — 1 миллиметр. Самым распространенным является угольник с рабочим углом 90°, так же встречаются угольники на 45, 60, и 120°. Общие технические условия на поверочные угольники 90° регламентированы ГОСТ 3749-77. Поверка угольников регламентирована методикой МИ 1799-87. Периодичность поверки – 1 раз в год. При необходимости на угольник может быть выдан сертификат о калибровке собственной метрологической службы. Образец протокола поверки угольника можно скачать здесь. Подробная информация о угольников здесь.
Самым распространенным является угольник с рабочим углом 90°, так же встречаются угольники на 45, 60, и 120°. Общие технические условия на поверочные угольники 90° регламентированы ГОСТ 3749-77. Поверка угольников регламентирована методикой МИ 1799-87. Периодичность поверки – 1 раз в год. При необходимости на угольник может быть выдан сертификат о калибровке собственной метрологической службы. Образец протокола поверки угольника можно скачать здесь. Подробная информация о угольников здесь. В стандартный комплект поставки входят: угольник, паспорт, свидетельство о поверке (по запросу). Ниже приводится описание инструментов различного типа.
В стандартный комплект поставки входят: угольник, паспорт, свидетельство о поверке (по запросу). Ниже приводится описание инструментов различного типа.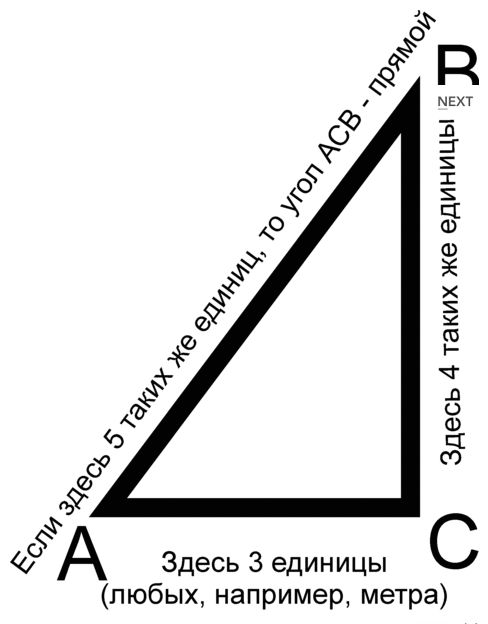 Лекальный угольник имеет острые измерительные и плоские опорные поверхности. Разновидностями плоского лекального угольника являются – угольник лекальный УЛ (все грани острые) и угольник лекальный цилиндрический УЛЦ . Основные характеристики слесарного угольника УЛП приведены в таблице.
Лекальный угольник имеет острые измерительные и плоские опорные поверхности. Разновидностями плоского лекального угольника являются – угольник лекальный УЛ (все грани острые) и угольник лекальный цилиндрический УЛЦ . Основные характеристики слесарного угольника УЛП приведены в таблице.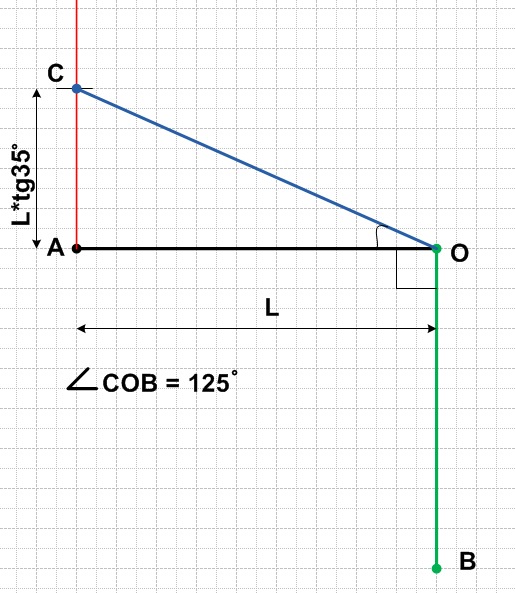 Основное отличие угольников данного типа – наличие широкого основания позволяющее устанавливать угольник без дополнительных приспособлений. Основные характеристики поверочных слесарных угольников УШ приведены в таблице.
Основное отличие угольников данного типа – наличие широкого основания позволяющее устанавливать угольник без дополнительных приспособлений. Основные характеристики поверочных слесарных угольников УШ приведены в таблице. Амурск, Ангарск, Архангельск, Астрахань, Барнаул, Белгород, Бийск, Брянск, Воронеж, Великий Новгород, Владивосток, Владикавказ, Владимир, Волгоград, Волгодонск, Вологда, Иваново, Ижевск, Йошкар-Ола, Казань, Калининград, Калуга, Кемерово, Киров, Кострома, Краснодар, Красноярск, Курск, Липецк, Магадан, Магнитогорск, Мурманск, Муром, Набережные Челны, Нальчик, Новокузнецк, Нарьян-Мар, Новороссийск, Новосибирск, Нефтекамск, Нефтеюганск, Новочеркасск, Нижнекамск, Норильск, Нижний Новгород, Обнинск, Омск, Орёл, Оренбург, Оха, Пенза, Пермь, Петрозаводск, Петропавловск-Камчатский, Псков, Ржев, Ростов, Рязань, Самара, Саранск, Смоленск, Сочи, Сыктывкар, Таганрог, Тамбов, Тверь, Тобольск, Тольятти, Томск, Тула, Тюмень, Ульяновск, Уфа, Ханты-Мансийск, Чебоксары, Челябинск, Череповец, Элиста, Ярославль и другие города, кроме того, в Республике Крым. А также Республики Казахстан, Белоруссия и другие страны СНГ.
Амурск, Ангарск, Архангельск, Астрахань, Барнаул, Белгород, Бийск, Брянск, Воронеж, Великий Новгород, Владивосток, Владикавказ, Владимир, Волгоград, Волгодонск, Вологда, Иваново, Ижевск, Йошкар-Ола, Казань, Калининград, Калуга, Кемерово, Киров, Кострома, Краснодар, Красноярск, Курск, Липецк, Магадан, Магнитогорск, Мурманск, Муром, Набережные Челны, Нальчик, Новокузнецк, Нарьян-Мар, Новороссийск, Новосибирск, Нефтекамск, Нефтеюганск, Новочеркасск, Нижнекамск, Норильск, Нижний Новгород, Обнинск, Омск, Орёл, Оренбург, Оха, Пенза, Пермь, Петрозаводск, Петропавловск-Камчатский, Псков, Ржев, Ростов, Рязань, Самара, Саранск, Смоленск, Сочи, Сыктывкар, Таганрог, Тамбов, Тверь, Тобольск, Тольятти, Томск, Тула, Тюмень, Ульяновск, Уфа, Ханты-Мансийск, Чебоксары, Челябинск, Череповец, Элиста, Ярославль и другие города, кроме того, в Республике Крым. А также Республики Казахстан, Белоруссия и другие страны СНГ.
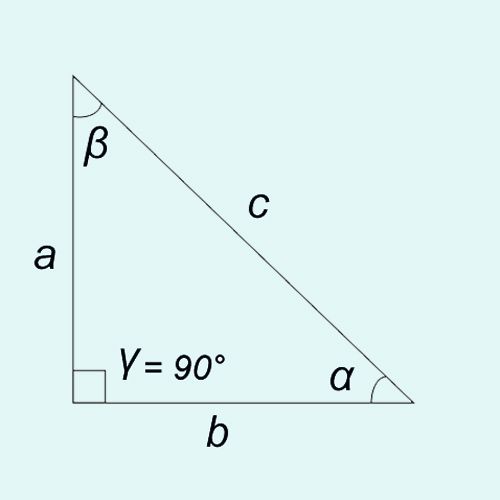
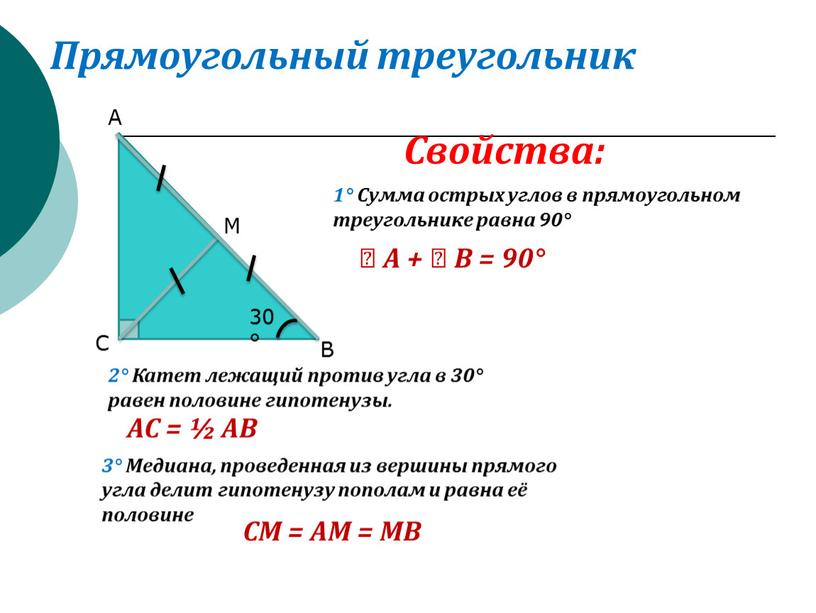
 Так C должен быть <90 и B должен быть
> 90.
Так C должен быть <90 и B должен быть
> 90.