Разметка фундамента: углы и диагонали
Разметка фундамента: углы и диагонали. Разметка фундамента – это процесс перенесения размеров будущей конструкции с плана на участок. Разметку фундамента следует проводить грамотно и точно, так как от качественного выполнения данной работы зависит ровность будущего фундамента и соответственно сооружения возводимого на нём. Так же изначальная точная и ровная разметка поможет избежать ошибок в последующих строительных работах.
Для разметки фундамента используют колья, шпагат и рулетку.
При проведении работ по разметки фундамента следует соблюдать определённые правила:
- Установку первого колышка угла фундамента следует проводить, согласно плану застройки, учитывая СНиП. От первого колышка откладывается расстояние равное расстоянию стен фундамента в одну сторону и в другую, желательно с небольшим запасом.
- Две выставленные стороны должны образовать прямой угол.

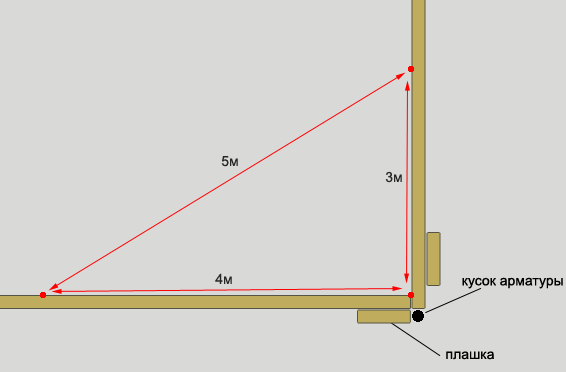
- Когда все углы выровнены, начинаем проверять диагонали фундамента. Для начала, их следует высчитать математическим способом по уравнению корень квадратный из а2 + в2. Например, если стороны фундамента 8 и 10, диагональ будет равна 64 (8х8) + 100 (10х10) =»164, вычисляем корень из 164, получаем 12,8. Наша диагональ равна 12,8. У прямоугольников и квадратов диагонали равны.
- При выставлении опалубки все углы и диагонали ещё раз внимательно перепроверяются.

- Часто встречаются фундаменты не правильной формы, с различными выступами и нишами. В этом случае, для грамотной разметки фундамента, необходимо разделить его на прямоугольники или квадраты. Если стены образуют не прямой угол, то обозначают контур, а затем вычитаем или прибавляем прямоугольный треугольник.
Информацию о строительстве фундамента можно узнать по телефону +7 (812) 918-82-93 или отправить нам заявку на расчет
Предлагаем услуги по строительству монолитных фундаментов для загородного дома в Санкт-Петербурге и Ленинградской области с высоким качеством проводимых работ и по разумным ценам.
Решение прямоугольного треугольника | Формулы и расчеты онлайн
Решение прямоугольного треугольника по двум сторонам
Если даны две стороны прямоугольного треугольника, то третья сторона может быть вычислена по теореме Пифагора. Острые углы определяются по формулам тригонометрических функций острого угла — Синус угла — sin(A),
Косинус угла — cos(A),
Тангенс угла — tg(A),
Котангенс угла — ctg(A),
Секанс угла — sec(A),
Косеканс угла — cosec(A).
Угол A определится по формуле тангенса:
\[ \tg(A) = \frac{a}{b} \]
Поскольку сумма всех углов треугольника равна 180° то второй острый угол определится так:
\[ B = 180° — 90° — A \]
Вычислить, найти решение прямоугольного треугольника по двум сторонам (катет и катет)
Решение прямоугольного треугольника по стороне и острому углу
Если дан острый угол A, то B найдется по формуле:
\[ B = 90° — A \]
Стороны можно найти по следующим формулам:
\[ a = c · \sin(A) \] | \[ b = c · \cos(A) \] | \[ a = b · \tg(A) \] |
\[ b = c · \sin(B) \] | \[ a = c · \cos(B) \] | \[ b = a · \tg(B) \] |
\[ c = \frac{a}{\sin(A)} \] | \[ c = \frac{b}{\cos(A)} \] | \[ b = \frac{a}{\tg(A)} \] |
Вычислить, найти решение прямоугольного треугольника если известны катет a и противолежащий угол A
Здесь все углы мы найдем по формуле (7).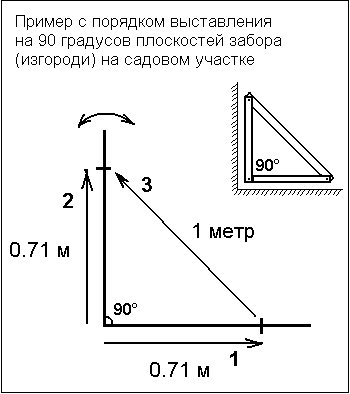 Гипотенузу по формуле (14) и второй катет по формуле (16).
Гипотенузу по формуле (14) и второй катет по формуле (16).
Решение прямоугольного треугольника | стр. 237 |
|---|
Угол между векторами, формулы и онлайн калькуляторы
Определение
Углом между векторами $\overline{a}$ и $\overline{b}$ называется угол $\phi=\angle A O B=(\bar{a}, \bar{b})$.
Угол между сонаправленными векторами равен 0°, а между противоположно направленными — 180°.
Определение
Два вектора называются перпендикулярными или ортогональными, если угол между ними равен 90°.
Угол между двумя векторами $\overline{a}=\left(a_{1} ; a_{2} ; a_{3}\right)$, $\overline{b}=\left(b_{1} ; b_{2} ; b_{3}\right)$ заданными своими координатами, вычисляется по формуле:
Пример
Задание. Читать дальше: разложение вектора по ортам координатных осей. Данный материал посвящен такому понятию, как угол между двумя пересекающимися прямыми. В первом пункте мы поясним, что он из себя представляет, и покажем его на иллюстрациях. Потом разберем, какими способами можно найти синус, косинус этого угла и сам угол (отдельно рассмотрим случаи с плоскостью и трехмерным пространством), приведем нужные формулы и покажем на примерах, как именно они применяются на практике. Для того чтобы понять, что такое угол, образующийся при пересечении двух прямых, нам потребуется вспомнить само определение угла, перпендикулярности и точки пересечения. Мы называем две прямые пересекающимися, если у них есть одна общая точка. Эта точка называется точкой пересечения двух прямых. Каждая прямая разделяется точкой пересечения на лучи. Обе прямые при этом образуют 4 угла, из которых два – вертикальные, а два – смежные. Если мы знаем меру одного из них, то можем определить и другие оставшиеся. Допустим, нам известно, что один из углов равен α. В таком случае угол, который является вертикальным по отношению к нему, тоже будет равен α. Чтобы найти оставшиеся углы, нам надо вычислить разность 180°-α. Если α будет равно 90 градусам, то все углы будут прямыми. Пересекающиеся под прямым углом линии называются перпендикулярными (понятию перпендикулярности посвящена отдельная статья). Взгляните на рисунок: Перейдем к формулированию основного определения. Угол, образованный двумя пересекающимися прямыми – это мера меньшего из 4-х углов, которые образуют две эти прямые. Из определения нужно сделать важный вывод: размер угла в этом случае будет выражен любым действительным числом в интервале (0, 90]. Если прямые являются перпендикулярными, то угол между ними в любом случае будет равен 90 градусам. Умение находить меру угла между двумя пересекающимися прямыми полезно для решения многих практических задач. Метод решения можно выбрать из нескольких вариантов. Для начала мы можем взять геометрические методы. Если нам известно что-то о дополнительных углах, то можно связать их с нужным нам углом, используя свойства равных или подобных фигур. Например, если мы знаем стороны треугольника и нужно вычислить угол между прямыми, на которых эти стороны расположены, то для решения нам подойдет теорема косинусов. Если у нас в условии есть прямоугольный треугольник, то для подсчетов нам также пригодится знание синуса, косинуса и тангенса угла. Координатный метод тоже весьма удобен для решения задач такого типа. Поясним, как правильно его использовать. У нас есть прямоугольная (декартова) система координат Oxy, в которой заданы две прямые. Обозначим их буквами a и b. Прямые при этом можно описать с помощью каких-либо уравнений. Начнем с формулировки основного принципа нахождения угла в заданных условиях. Нам известно, что с понятием прямой линии тесно связаны такие понятия, как направляющий и нормальный вектор. Если у нас есть уравнение некоторой прямой, из него можно взять координаты этих векторов. Мы можем сделать это сразу для двух пересекающихся прямых. Угол, образуемый двумя пересекающимися прямыми, можно найти с помощью: Теперь рассмотрим каждый способ отдельно. 1. Допустим, что у нас есть прямая a с направляющим вектором a→=(ax, ay) и прямая b с направляющим вектором b→(bx, by). Теперь отложим два вектора a→ и b→ от точки пересечения. После этого мы увидим, что они будут располагаться каждый на своей прямой. Из нее мы можем вывести формулу косинуса угла между двумя заданными прямыми: cos α=ax·bx+ay·byax2+ay2·bx2+by2=ax·bx+ay·byax2+ay2·bx2+by2 Тогда сам угол можно найти по следующей формуле: α=arccosax·bx+ay+byax2+ay2·bx2+by2 Здесь a→=(ax, ay) и b→=(bx, by) – это направляющие векторы заданных прямых. Приведем пример решения задачи. В прямоугольной системе координат на плоскости заданы две пересекающиеся прямые a и b. Их можно описать параметрическими уравнениями x=1+4·λy=2+λλ∈R и x5=y-6-3. Вычислите угол между этими прямыми. Решение У нас в условии есть параметрическое уравнение, значит, для этой прямой мы сразу можем записать координаты ее направляющего вектора. Для этого нам нужно взять значения коэффициентов при параметре, т.е. прямая x=1+4·λy=2+λλ∈R будет иметь направляющий вектор a→=(4, 1). Вторая прямая описана с помощью канонического уравнения x5=y-6-3. Нахождение самого угла: α=arcsin=ax·nbx+ay·nbyax2+ay2·nbx2+nby2 Здесь a→ является направляющим вектором первой прямой, а nb→ – нормальным вектором второй. Две пересекающиеся прямые заданы уравнениями x-5=y-63 и x+4y-17=0. Найдите угол пересечения. Решение Берем координаты направляющего и нормального вектора из заданных уравнений. Получается a→=(-5, 3) и n→b=(1, 4). Берем формулу α=arcsin=ax·nbx+ay·nbyax2+ay2·nbx2+nby2 и считаем: α=arcsin=-5·1+3·4(-5)2+32·12+42=arcsin7234 Обратите внимание, что мы взяли уравнения из предыдущей задачи и получили точно такой же результат, но другим способом. Ответ: α=arcsin 7234 Приведем еще один способ нахождения нужного угла с помощью угловых коэффициентов заданных прямых. У нас есть прямая a, которая задана в прямоугольной системе координат с помощью уравнения y=k1·x+b1, и прямая b, заданная как y=k2·x+b2. α=arccosk1·k2+1k12+1·k22+1, гдеk1 и k2 являются угловыми коэффициентами заданных прямых. Для получения этой записи были использованы формулы определения угла через координаты нормальных векторов. Есть две пересекающиеся на плоскости прямые, заданные уравнениями y=-35x+6 и y=-14x+174. Вычислите величину угла пересечения. Решение Угловые коэффициенты наших прямых равны k1=-35 и k2=-14. Добавим их в формулу α=arccosk1·k2+1k12+1·k22+1 и подсчитаем: α=arccos-35·-14+1-352+1·-142+1=arccos23203424·1716=arccos23234 Ответ: α=arccos23234 В выводах этого пункта следует отметить, что приведенные здесь формулы нахождения угла не обязательно учить наизусть. Для этого достаточно знать координаты направляющих и/или нормальных векторов заданных прямых и уметь определять их по разным типам уравнений. А вот формулы для вычисления косинуса угла лучше запомнить или записать. {\circ}$$
{\circ}$$Угол между пересекающимися прямыми: определение, примеры нахождения
Что такое угол между пересекающимися прямыми

Как найти угол между пересекающимися прямыми на плоскости
 Исходные прямые имеют точку пересечения M. Как определить искомый угол (обозначим его α) между этими прямыми?
Исходные прямые имеют точку пересечения M. Как определить искомый угол (обозначим его α) между этими прямыми? a→·b→=ax·bx+ay·byax2+ay2·bx2+by2
a→·b→=ax·bx+ay·byax2+ay2·bx2+by2 =ax·nbx+ay·nbyax2+ay2·nbx2+nby2
=ax·nbx+ay·nbyax2+ay2·nbx2+nby2 Это уравнения прямых с угловым коэффициентом. Чтобы найти угол пересечения, используем формулу:
Это уравнения прямых с угловым коэффициентом. Чтобы найти угол пересечения, используем формулу:
В итоге мы получили, что нужный нам угол будет равен arccos12=45°.
Ответ: cos α=12, α=45°.
Урок 63. виды треугольников по видам углов. закрепление изученного материала — Математика — 3 класс
Математика
3 класс
Урок № 63
Виды треугольников по видам углов. Закрепление изученного материала
Перечень вопросов, рассматриваемых в теме:
Какие виды треугольников различают по видам углов?
Как различать треугольники: прямоугольный, тупоугольный, остроугольный?
Тезаурус:
Геометрия – это раздел математики, изучающий геометрические фигуры и их свойства.
Виды треугольников по величине углов
Остроугольный треугольник – это треугольник, в котором все три угла острые, т.е. меньше 90°.
Прямоугольный треугольник – это треугольник, в котором один угол прямой, т.е. 90º.
Тупоугольный треугольник
Основная и дополнительная литература:
1. Моро М. И. Учебник для 3 класса четырехлетней начальной школы. М. «Просвещение» — 2017. С. 85-87.
2. Волкова С. И. математика. Тесты. 3 кл. – М.: Просвещение, 2018. С. 60-67.
3. Рудницкая В. Н. Математика. Дидактические материалы. ч.1 3 кл. – М. «Вентана- Граф», 2016, с. 47-53.
Теоретический материал для самостоятельного изучения
Давайте вспомним, что вы уже знаете о видах треугольников.
По длине сторон различают: разносторонние, равнобедренные и равносторонние треугольники.
Но было бы несправедливо разделить все треугольники на 3 вида по длине сторон.
У вас уже появились идеи?
Углы бывают:
Острые – меньше прямого
Прямые – угол 90 градусов
Тупые – больше прямого
Оказывается, по величине углов все треугольники тоже можно разделить на 3 вида:
те, у которых все углы острые, – остроугольные,
те, у которых есть прямой угол, – прямоугольные,
те, у которых есть тупой угол, – тупоугольные.
Для того чтобы безошибочно определить вид треугольника по величине углов, необходимо измерить все три угла при помощи транспортира.
Попробуйте определить виды треугольников по величине углов без измерений.
Проверим.
Прямоугольный –1, 3
Остроугольный – 6
тупоугольный– 2, 4, 7, 5
Сделаем вывод:
По величине углов различают 3 вида треугольников:
Остроугольные, прямоугольные и тупоугольные
Определить вид треугольника можно тремя способами:
с помощью измерений, на глаз и по условным обозначениям.
Теперь вы можете различать виды треугольников по сторонам и по углам. Эти знания необходимы в геометрии.
Задания тренировочного модуля
Закончите предложения:
Остроугольный треугольник – это треугольник, у которого ……………………
Прямоугольный треугольник – это треугольник, у которого есть ……………………
Тупоугольный треугольник – треугольник, все стороны которого есть ……………………
Правильные варианты ответов:
Остроугольный треугольник — это треугольник, у которого все углы острые.
Прямоугольный треугольник — это треугольник, у которого есть прямой угол.
Тупоугольный треугольник — треугольник, все стороны которого есть тупой угол.
Определите вид треугольника по величине углов и выпишите номера треугольников по порядку:
Правильный ответ:
Остроугольные: 1, 2, 10
Прямоугольные: 4, 6, 8, 12
Тупоугольные: 3, 5, 7, 9, 11
Как понять смежные углы.
 Как найти смежный угол угол до развернутого, то есть равного 180°, поэтому для их нахождения вычтите из этого известную величину основного угла α₁ = α₂ = 180°-α.
Как найти смежный угол угол до развернутого, то есть равного 180°, поэтому для их нахождения вычтите из этого известную величину основного угла α₁ = α₂ = 180°-α.Из этого имеются . Если два угла одновременно являются и смежными, и равными, то они прямые. Если один из смежных углов является прямым, то есть составляет 90 градусов, то другой угол тоже прямой. Если один из смежных углов острый, то другой будет тупым. Аналогично, если один из углов тупой, то второй, соответственно, будет острым.
Острый угол – это такой, градусная мера которого меньше 90 градусов, но больше 0. Тупой угол имеет градусную меру больше 90 градусов, но меньше 180.
Другое свойство смежных углов формулируется так: если два угла равны, то углы, смежные с ними, также равны. Это , что если есть два угла, градусная мера для которых совпадает (например, она составляет 50 градусов) и при этом из них имеет смежный угол, то значения этих смежных углов тоже совпадают (в примере их градусная мера будет равна 130 градусам).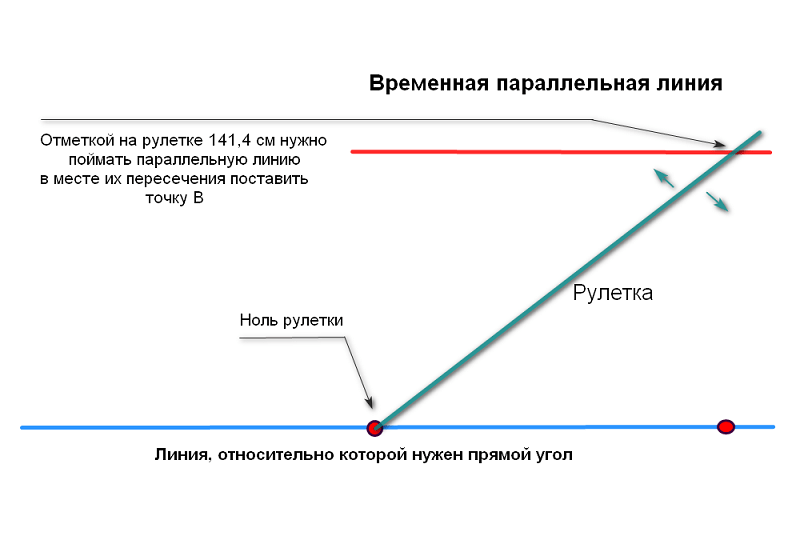
Источники:
- Большой Энциклопедический Словарь — Смежные углы
- угол 180 градусов
Слово « » имеет различные толкования. В геометрии угол – это часть плоскости, ограниченная двумя лучами, выходящими из одной точки – вершины. Когда речь идет о прямых, острых, развернутых углах, то подразумеваются именно геометрические углы.
Как и любые фигуры в геометрии, углы можно сравнивать. Равенство углов определяется с помощью движения. Угол нетрудно разделить на две равные части. Разделить на три части немного сложнее, но все же это можно сделать с помощью линейки и циркуля. Кстати, эта задача казалась довольно трудной. Описать, что один угол больше или меньше другого, геометрически несложно.
В качестве единицы измерения углов принят – 1/180
Начальные сведения об углах
Пусть нам даны два произвольных луча. Наложим их начала друг на друга. Тогда
Определение 1
Углом будем называть два луча, которые имеют одно и тоже начало.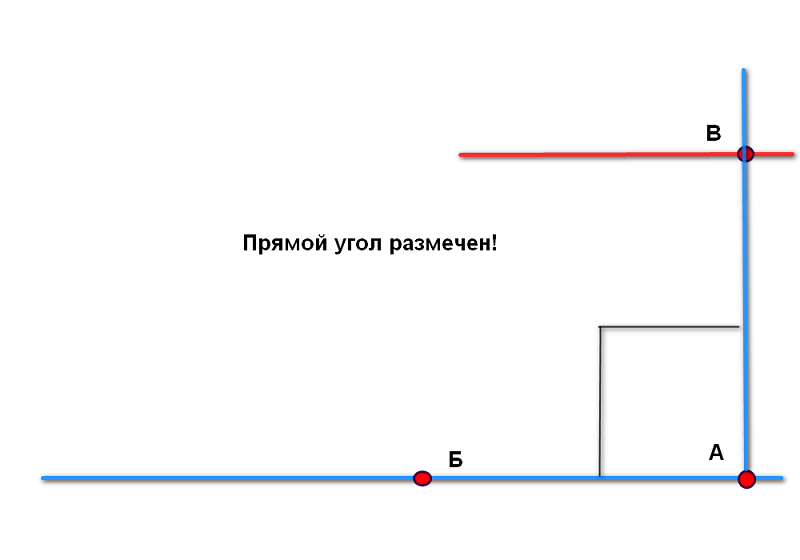 0$.
0$.
Вертикальные углы
Рассмотрим развернутые углы $AOB$ и $MOC$. Совместим их вершины между собой (то есть наложим точку $O»$ на точку $O$) так, чтобы никакие стороны этих углов не совпали. Тогда
Определение 8
Два угла будем называть вертикальными, если пары их сторон являются развернутыми углами, а их величины совпадают (рис. 3).
В данном случае углы $MOA$ и $BOC$ являются вертикальными и углы $MOB$ и $AOC$ также вертикальные.
Теорема 2
Вертикальные углы равняются между собой.
Доказательство.
Рассмотрим рисунок 3. Докажем, к примеру, что угол $MOA$ равняется углу $BOC$.
Г Л А В А I.
ОСНОВНЫЕ ПОНЯТИЯ.
§11. СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ.
1. Смежные углы.
Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (черт. 72): / А ВС и / СВD, у которых одна сторона ВС общая, а две другие АВи ВD составляют прямую линию.
Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.
Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.
Например, / АDF и / FDВ — углы смежные (черт. 73).
Смежные углы могут иметь самые разнообразные положения (черт. 74).
Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 2d.
Отсюда прямой угол можно определить как угол, равный своему смежному углу.
Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.
Например, если один из смежных углов равен 3 / 5 d , то второй угол будет равен:
2d — 3 / 5 d = l 2 / 5 d .
2. Вертикальные углы.
Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На чертеже 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.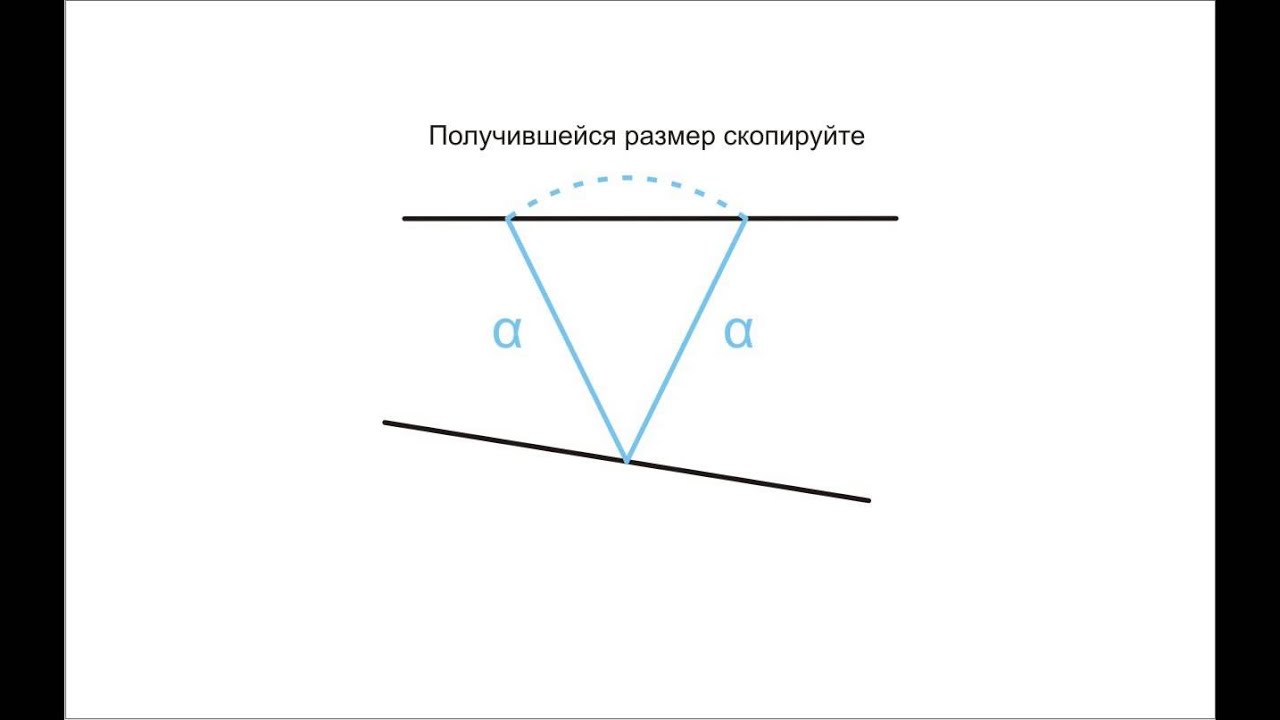
Пусть / 1 = 7 / 8 d (черт. 76). Смежный с ним / 2 будет равен 2d — 7 / 8 d , т. е. 1 1 / 8 d .
Таким же образом можно вычислить, чему равны / 3 и / 4.
/ 3 = 2d — 1 1 / 8 d = 7 / 8 d ; / 4 = 2d — 7 / 8 d = 1 1 / 8 d (черт. 77).
Мы видим, что / 1 = / 3 и / 2 = / 4.
Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.
Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.
Убедиться в справедливости свойства вертикальных углов необходимо путём рассуждения, путём доказательства.
Доказательство можно провести следующим образом (черт.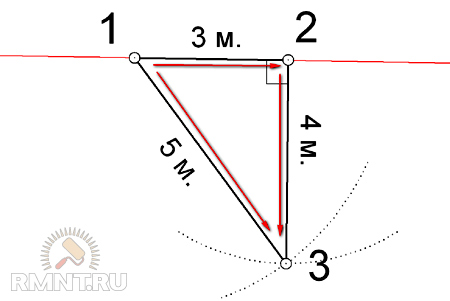 78):
78):
/ a + / c = 2d ;
/ b + / c = 2d ;
(так как сумма смежных углов равна 2d ).
/ a + / c = / b + / c
(так как и левая часть этого равенства равна 2d , и правая его часть тоже равна 2d ).
В это равенство входит один и тот же угол с .
Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: / a = / b , т. е. вертикальные углы равны между собой.
При рассмотрении вопроса о вертикальных углах мы сначала объяснили, какие углы называются вертикальными, т. е. дали определение вертикальных углов.
Затем мы высказали суждение (утверждение) о равенстве вертикальных углов и в справедливости этого суждения убедились путём доказательства. Такие суждения, справедливость которых надо доказывать, называются теоремами . Таким образом, в данном параграфе мы дали определение вертикальных углов, а также высказали и доказали теорему об их свойстве.
Таким образом, в данном параграфе мы дали определение вертикальных углов, а также высказали и доказали теорему об их свойстве.
В дальнейшем при изучении геометрии нам постоянно придётся встречаться с определениями и доказательствами теорем.
3. Сумма углов, имеющих общую вершину.
На чертеже 79 / 1, / 2, / 3 и / 4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.
/ 1+ / 2+/ 3+ / 4 = 2d .
На чертеже 80 / 1, / 2, / 3, / 4 и / 5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. / 1 + / 2 + / 3 + / 4 + / 5 = 4d .
Упражнения.
1. Один из смежных углов равен 0,72 d. Вычислить угол, составленный биссектрисами этих смежных углов.
2. Доказать, что биссектрисы двух смежных углов образуют прямой угол.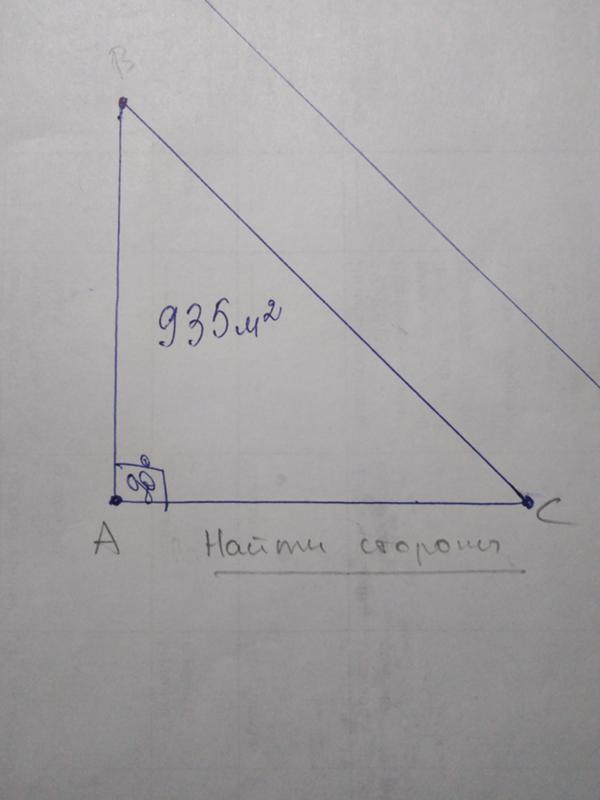
3. Доказать, что если два угла равны, то равны и их смежные углы.
4. Сколько пар смежных углов на чертеже 81?
5. Может ли пара смежных углов состоять из двух острых углов? из двух тупых углов? из прямого и тупого угла? из прямого и острого угла?
6. Если один из смежных углов прямой, то что можно сказать о величине смежного с ним угла?
7. Если при пересечении двух прямых линий один угол прямой, то что можно сказать о величине остальных трёх углов?
Геометрия — это весьма многогранная наука. Она развивает логику, воображение и интеллект. Конечно, из-за своей сложности и огромного количества теорем и аксиом, она не всегда нравится школьникам. Кроме этого, существует необходимость постоянно доказывать свои выводы, используя общепринятые стандарты и правила.
Смежные и вертикальные углы — это неотъемлемая составляющая геометрии. Наверняка многие школьники просто обожают их по той причине, что их свойства понятны и просты в доказательстве.
Образование углов
Любой угол образуется путем пересечения двух прямых или проведения двух лучей из одной точки. Они могут называться либо одной буквой, либо тремя, которые последовательно обозначают точки построения угла.
Углы измеряются в градусах и могут (в зависимости от их значения) по-разному называться. Так, существует прямой угол, острый, тупой и развернутый. Каждому из названий соответствует определенная градусная мера или ее промежуток.
Острым называется угол, мера которого не превышает 90 градусов.
Тупым является угол, превышающий 90 градусов.
Угол называется прямым в том случае, когда его градусная мера равна 90.
В том случае, когда он образован одной сплошной прямой, и его градусная мера равна 180, его называют развернутым.
Углы, имеющие общую сторону, вторая сторона которых продолжает друг друга, называются смежными. Они могут быть как острыми, так и тупыми. Пересечение линией образует смежные углы. Свойства их следующие:
- Сумма таких углов будет равна 180 градусам (существует теорема, доказывающая это).
 Поэтому можно легко вычислить один из них, если известен другой.
Поэтому можно легко вычислить один из них, если известен другой. - Из первого пункта следует, что смежные углы не могут быть образованы двумя тупыми или двумя острыми углами.
Благодаря этим свойствам, можно всегда вычислить градусную меру угла, имея значение другого угла или, по крайней мере, отношение между ними.
Вертикальные углы
Углы, стороны которых являются продолжением друг друга, называются вертикальными. В качестве такой пары могут выступать любые их разновидности. Вертикальные углы всегда равны между собой.
Они образуются при пересечении прямых. Совместно с ними всегда присутствуют и смежные углы. Угол может быть одновременно смежным для одного и вертикальным для другого.
При пересечении произвольной линией также рассматривают еще несколько видов углов. Такая линия называется секущей, она и образует соответственные, односторонние и накрест лежащие углы. Они равны между собой. Их можно рассматривать в свете свойств, которые имеют вертикальные и смежные углы.
Таким образом, тема углов представляется довольно простой и понятной. Все их свойства легко запомнить и доказать. Решение задач не представляется сложным до тех пор, пока углам соответствует числовое значение. Уже дальше, когда начнется изучение sin и cos, придется запоминать множество сложных формул, их выводов и следствий. А до того времени можно просто наслаждаться легкими задачками, в которых необходимо найти смежные углы.
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.
Сумма смежных углов равна 180°
Теорема 1. Сумма смежных углов равна 180°.
Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .
Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.
Вертикальные углы равны
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).
Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).
Теорема 2. Вертикальные углы равны.
Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1 ∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.
Отсюда заключаем, что ∠ АОВ = ∠ COD.
Следствие 1. Угол, смежный с прямым углом, есть прямой угол.
Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.
АН — перпендикуляр к прямой
Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
Чертежный угольник
Справедлива следующая теорема.
Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).
Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».
Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».
Пример 1. Один из смежных углов равен 44°. Чему равен другой?
Решение. Обозначим градусную меру другого угла через x , тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.
Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?
Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.
∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.
Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.
Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.
Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.
Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол
АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° — 50° = 130°.
Microsoft Word — геометрия-1.doc
%PDF-1.6 % 955 0 obj > endobj 952 0 obj >stream 2009-08-03T12:57:02ZMicrosoft Word — геометрия-1.doc2009-08-12T12:51:21+04:002009-08-12T12:51:21+04:00application/pdf
Как найти угол в прямоугольном треугольнике
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы вуза предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы вуза предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как так как ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Выполните следующие действия, чтобы отправить уведомление:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного расположения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или агентом такого владельца; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или агентом такого владельца; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Как найти меру угла
Два луча с одинаковой конечной точкой создают угол. Точка, в которой они пересекаются, называется вершиной. Угол образует часть воображаемого круга.А поскольку круги измеряют 360 градусов, вы можете найти угол, образованный лучами. Вот несколько вещей, которые вы должны знать о том, как найти величину угла.
Угол образует часть воображаемого круга.А поскольку круги измеряют 360 градусов, вы можете найти угол, образованный лучами. Вот несколько вещей, которые вы должны знать о том, как найти величину угла.
Четыре типа углов
Есть четыре типа углов. Знание разницы поможет вам оценить размер угла. Вот четыре типа углов и размеров, которые помогут вам классифицировать каждый из них.
Использование транспортира
Лучший способ измерить угол — использовать транспортир.Для этого вы начнете с выстраивания одного луча вдоль линии под углом 0 градусов на транспортире. Затем совместите вершину с серединой транспортира. Следуйте по второму лучу, чтобы определить угол с точностью до градуса.
Углы в треугольниках
Треугольники получили свое название от трех углов, которыми они обладают. Эти три угла в сумме должны составлять 180 градусов. Часто у вас есть измерения двух углов. Однако вам нужно вычислить размер третьего угла.Используемое уравнение:
Эти три угла в сумме должны составлять 180 градусов. Часто у вас есть измерения двух углов. Однако вам нужно вычислить размер третьего угла.Используемое уравнение:
угол A + угол B + угол C = 180 градусов.
Например, у вас есть следующий треугольник. Что такое измерение угла C?
Если вы подставите эти числа в уравнение, вы получите следующее уравнение:
Углы в четырехугольнике
Квадраты и прямоугольники имеют четыре прямых угла. Если сложить углы, получится 90 + 90 + 90 + 90 = 360. Четырехугольник также имеет четыре угла.Следовательно, углы формы составляют в сумме 360 градусов, даже если нет прямых углов. Чтобы определить недостающий угол четырехугольника, вы можете использовать следующее уравнение:
угол A + угол B + угол C + угол D = 360 градусов.
Посмотрите следующий пример. Можете ли вы определить недостающий угол в этом четырехугольнике?
Чтобы найти недостающий угол, подставьте значения угла в уравнение:
Работаете ли вы с лучом, треугольником или четырехугольником, существуют методы, которые можно использовать для обнаружения недостающего измерения угла. Если вам интересно, как найти величину угла на луче, треугольнике или четырехугольнике, попробуйте использовать транспортир или уравнения, которые мы обсуждали. Они должны работать и помочь вам немного облегчить жизнь!
Если вам интересно, как найти величину угла на луче, треугольнике или четырехугольнике, попробуйте использовать транспортир или уравнения, которые мы обсуждали. Они должны работать и помочь вам немного облегчить жизнь!
О Джейми Гудвине
Джейми окончил Университет Бригама Янга в Айдахо со степенью в области английского образования. Она провела несколько лет, обучая учеников начальной, средней школы и колледжа. В настоящее время она работает по контракту и разработчиком учебных программ для онлайн-курсов.В свободное время она любит бегать и проводить время со своими мальчиками!прямоугольных треугольников | GMAT бесплатно
Прямые треугольники — это треугольники, в которых один из внутренних углов равен 90 градусам, то есть прямым углом. Поскольку три внутренних угла треугольника в сумме составляют 180 градусов, в прямоугольном треугольнике, поскольку один угол всегда равен 90 градусам, два других всегда должны составлять 90 градусов (они дополняют друг друга).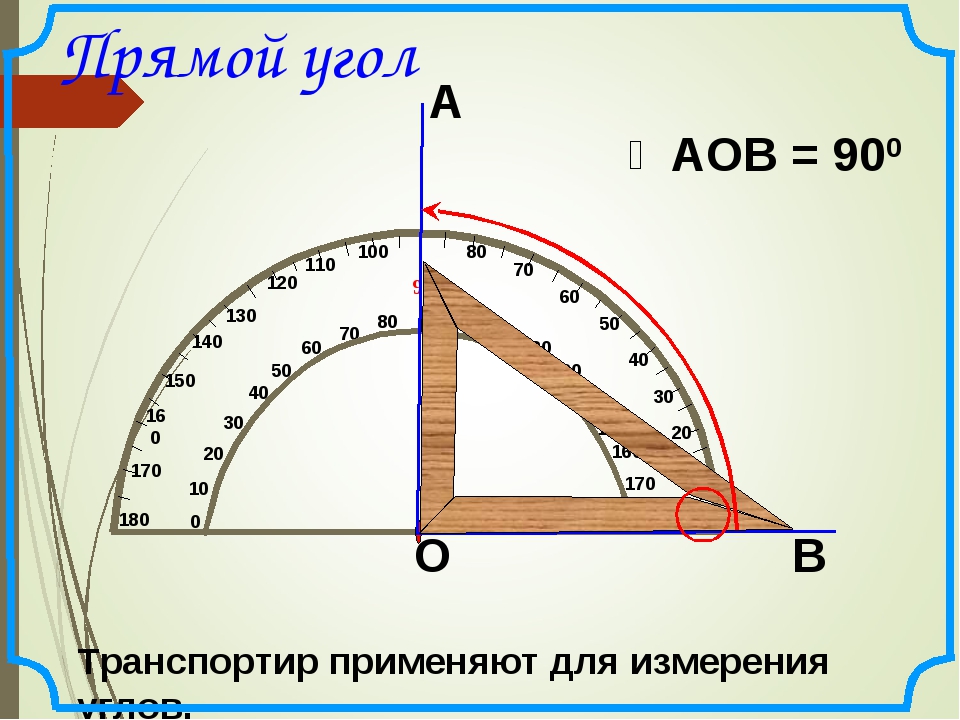
Сторона, противоположная прямому углу, называется гипотенузой.Боковые стороны, прилегающие к прямому углу, — это ноги. При использовании теоремы Пифагора гипотенуза или ее длина часто обозначаются строчными буквами c . Ножки (или их длина) обычно имеют маркировку a и b .
Любую из опор можно рассматривать как основание, а другую опору — за высоту (или высоту), потому что прямой угол автоматически делает их перпендикулярными. Если длина обеих сторон известна, то, задав одну из этих сторон как основание b , а другую как высоту h , площадь прямоугольного треугольника легко вычислить, используя стандартную формулу для треугольника. площадь:
Это интуитивно логично, потому что другой равный прямоугольный треугольник может быть помещен напротив него так, чтобы гипотенузы были одним и тем же отрезком прямой, образуя прямоугольник со сторонами, имеющими длину b и ширину h .Площадь прямоугольника равна ( b ) ( h ), поэтому любой из образующих его конгруэнтных прямоугольных треугольников имеет площадь, равную половине этого прямоугольника.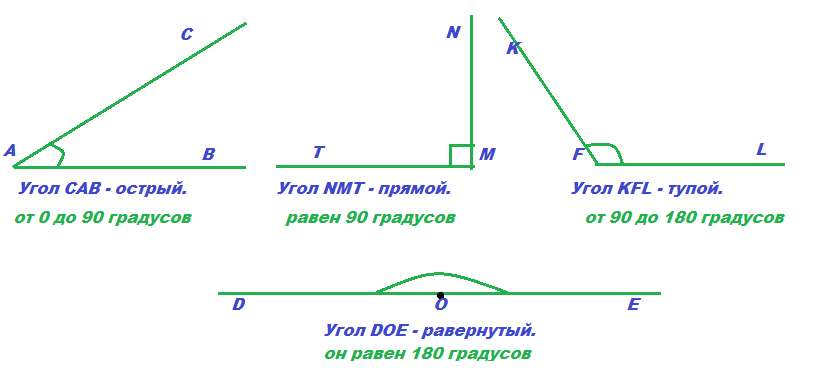
Теорема Пифагора
Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин двух других сторон.
Теорема Пифагора
Стороны, которые мы обозначили выше как b и h , теперь обозначены как b и a , поскольку при использовании теоремы Пифагора обычно используются переменные a, b и c. .Тем не менее важно понимать, что обе формулы относятся к одним и тем же сторонам. Например, в типичном вопросе GMAT вы можете использовать теорему Пифагора, чтобы определить основание и высоту треугольника, а затем в конечном итоге найти его площадь.
Довольно часто на экзамене GMAT вы попадаете в ситуацию, когда знаете, что конкретный треугольник является прямоугольным, и вы знаете длины двух из трех сторон. Затем вы сможете найти длину третьей стороны, вставив две известные длины в
. Ранее мы обсуждали, как теорему Пифагора можно использовать для вычисления расстояния между любыми двумя точками на координатной плоскости.
Распространенные тройки Пифагора
Определенные тройки чисел, удовлетворяющие теореме Пифагора, часто появляются на GMAT. Здесь вы должны запомнить хотя бы первые три тройки. Вам не нужно знать углы этих треугольников, только соотношение сторон:
На экзамене GMAT предполагается, что вы знаете углы и , боковые отношения для треугольников 45-45-90 и 30-60-90, но вы , а не , должны запомнить или уметь определять углы. для пифагорейских троек, перечисленных выше; вы можете определить длину сторон, просто используя формулу Пифагора.
45-45-90 Треугольник
Поскольку прямоугольный треугольник особенный, треугольник 45-45-90 особенный вдвойне. К нему применимы все общие правила треугольника, к нему применима теорема Пифагора, а затем он обладает некоторыми собственными особыми свойствами.
A 45-45-90 треугольник
Треугольник 45-45-90 — это то, что вы получаете, когда у вас есть равнобедренный прямоугольный треугольник. Если треугольник прямоугольный и равнобедренный, то две стороны, кроме прямого угла, должны составлять в сумме 90 градусов, и они должны быть равны, поэтому каждая должна быть равна 45 градусам.
Если треугольник прямоугольный и равнобедренный, то две стороны, кроме прямого угла, должны составлять в сумме 90 градусов, и они должны быть равны, поэтому каждая должна быть равна 45 градусам.
Кроме того, поскольку это прямоугольный треугольник, мы знаем, что
верно, но если a = b (потому что мы говорим о равнобедренном треугольнике), мы можем подставить это в теорему Пифагора, чтобы получить:
Если вы попытаетесь установить a = 1, то вы получите c = √2, как на диаграмме выше. Стороны каждого треугольника 45-45-90 имеют длину в соотношении 1: 1: √2.
Соотношение сторон не означает, что стороны, противоположные углам 45 градусов, обязательно равны 1, как они указаны выше.Скорее, какая бы длина ни была от 45 градусов, назовем ее длиной x , она будет сопровождаться поперек гипотенузы стороной, равной √2 или x √2.
30-60-90 Треугольник
Треугольник 30-60-90 похож на треугольник 45-45-90 в том, что это «дважды особый» прямоугольный треугольник. Также, как и в случае с треугольником 45-45-90, когда у нас есть один из этих треугольников, мы знаем меру углов и отношение длин сторон.
Также, как и в случае с треугольником 45-45-90, когда у нас есть один из этих треугольников, мы знаем меру углов и отношение длин сторон.
Треугольник 30-60-90 внутри равностороннего треугольника
Треугольник 30-60-90 имеет углы, которые составляют 30 градусов, 60 градусов и 90 градусов, а стороны, обращенные к этим углам, имеют длину в соотношении 1: √3: 2 соответственно. Как и в случае с любым соотношением, мы можем представить, что отсутствует число x , поэтому длины будут x : x √3: 2 x .
Если мы попробуем вставить эти длины в теорему Пифагора, мы получим следующее:
Наш результат подтверждает, что теорема верна — как и лучше, поскольку мы имеем дело с прямоугольным треугольником.
Вы можете запомнить, какая сторона и какой угол пересекают, используя тот факт, что большая длина стороны треугольника обращена к большим углам. Это означает, что сторона под углом 30 градусов будет самой маленькой стороной, сторона под углом 60 градусов будет стороной средней длины, а сторона под углом 90 градусов будет самой длинной стороной. При использовании этого трюка с памятью люди иногда задаются вопросом, больше ли √3 или 2. Вы можете помнить, что √3 меньше 2, потому что 2 равно √4, а √3 меньше √4.
При использовании этого трюка с памятью люди иногда задаются вопросом, больше ли √3 или 2. Вы можете помнить, что √3 меньше 2, потому что 2 равно √4, а √3 меньше √4.
Рисунок выше демонстрирует свойство, которое иногда проявляется в GMAT: обратите внимание, что изображенный треугольник 30-60-90 находится внутри равностороннего треугольника. Изучив схему, вы можете убедиться, что любой равносторонний треугольник содержит два «спрятанных» внутри треугольника 30-60-90. Этот факт может появиться в ответах на вопросы по более тонкой геометрии на GMAT, поэтому подготовьте себя к тому, чтобы видеть два треугольника 30-60-90, когда присутствует равносторонний треугольник.
Тригонометрия?
Вам не нужно знать тригонометрию для сдачи GMAT.Помните синусы, косинусы и тангенсы углов? Может быть, да, а может и нет, но вам не нужно знать их для GMAT. И, если вы изучали эти предметы, и они свежи в вашей памяти, не поддавайтесь искушению попытаться использовать их. Лучше поищите другой метод решения вопросов геометрии, используя материал этого резюме.
Практические вопросы
Закат на дороге:
http://www.gmatfree.com/decline-in-a-road
Периметр прямоугольного треугольника:
http: // www.gmatfree.com/perimeter-of-a-right-triangle
Вложенных треугольников:
http://www.gmatfree.com/nested-triangles/
углов треугольника — Бесплатная математическая справка
Углы могут быть добавлены
Так же, как и обычные числа, углы можно складывать для получения суммы, возможно, с целью определения меры неизвестного угла. Иногда мы можем определить недостающий угол, потому что знаем, что сумма должна быть определенным значением. Помните — сумма углов в любом треугольнике равна 180 градусам.Ниже изображен треугольник ABC, где угол A = 60 градусов, угол B = 50 градусов и угол C = 70 градусов.
Если сложить все три угла в любом треугольнике, мы получим 180 градусов. Итак, мера угла A + угол B + угол C = 180 градусов. Это верно для любого треугольника в мире геометрии. Мы можем использовать эту идею, чтобы найти величину угла (углов), для которой градус отсутствует или не указан.
Мы можем использовать эту идею, чтобы найти величину угла (углов), для которой градус отсутствует или не указан.
Нахождение недостающего угла
В треугольнике ABC ниже угол A = 40 градусов и угол B = 60 градусов.Какова мера угла C?
Мы знаем, что сумма мер любого треугольника равна 180 градусам. Используя тот факт, что угол A + угол B + угол C = 180 градусов, мы можем найти меру угла C.
угол A = 40
угол B = 60
угол C = мы не знаем.
Чтобы найти угол C, мы просто подставляем формулу выше и решаем относительно C.
A + B + C = 180
C = 180 — A — B
C = 180-40-60
C = 80
Чтобы проверить правильность 80 градусов, добавим все три угловые меры.Если мы получим 180 градусов, то наш ответ для угла C правильный.
Поехали:
40 + 60 + 80 = 180
180 = 180 … Проверяет!
Не всегда нужно подставлять эти значения в уравнение и решать. Как только вы освоитесь с такого рода проблемами, вы сможете сказать: «Хорошо, 40 + 60 = 100, поэтому другой угол должен быть 80!» и это намного быстрее.
Равносторонние треугольники
Если треугольник равносторонний, каков градус каждого из его углов?
Помните, что все стороны равностороннего треугольника имеют равной меры .У них также, как вы узнаете, равные углы! Пусть x = градус каждого угла. У треугольников три угла, поэтому мы прибавим x ТРИ раза.
У нас это:
x + x + x = 180
3x = 180
x = 60
Имеет смысл, правда? Если все углы равны и в сумме они равны 180, то это должно быть 60 градусов!
Соотношение углов
Градусы углов треугольника находятся в соотношении 4: 5: 9.
Какова величина НАИБОЛЬШЕГО угла треугольника в градусах?
Обратите внимание, что наименьший угол представлен наименьшим числом в данном соотношении.Наименьшее из приведенных чисел — 4, верно? Поскольку это соотношение, мы должны умножить все эти значения (4,5,9) на некоторый общий коэффициент, чтобы получить фактические углы. (Например, 60 и 80 находятся в соотношении 3: 4 с коэффициентом 20)
Пусть 4x = мера наименьшего угла треугольника. Теперь мы можем сказать, что 5x и 9x = градусные меры остальных углов треугольника. Мы просто складываем 4x + 5x + 9x, приравниваем сумму к 180 градусам и решаем относительно x. Найдя x, мы подставляем значение x в 4x и упрощаем, чтобы найти величину наименьшего угла треугольника.
Теперь мы можем сказать, что 5x и 9x = градусные меры остальных углов треугольника. Мы просто складываем 4x + 5x + 9x, приравниваем сумму к 180 градусам и решаем относительно x. Найдя x, мы подставляем значение x в 4x и упрощаем, чтобы найти величину наименьшего угла треугольника.
4x + 5x + 9x = 180
9x + 9x = 180
18x = 180
x = 180/18
x = 10
Мы нашли значение x, но это НЕ означает, что мы закончили.
Чтобы найти размер наименьшего угла треугольника, умножаем 4 на 10. Итак, 4 x 10 = 40.
Ответ — 40 градусов.
Помните, сумма углов треугольника равна 180 градусам. Просто возьмите то, что вам дано в задаче, и попытайтесь определить, в результате чего итоговый угол в сумме составит 180 градусов.
Урок, проводимый г-ном Фелизом
Воспользуйтесь «Калькулятором треугольников» ниже:
Сумма внутренних и внешних углов (многоугольники, пятиугольники …) // Tutors.com
Нахождение суммы внутренних и внешних углов
Полигоны подобны домикам в мире двумерной геометрии. Они создают внутреннее, называемое внутренним, и внешнее, называемое экстерьером. Вы можете измерять внутренние и внешние углы. Вы также можете сложить суммы всех внутренних углов и суммы всех внешних углов правильных многоугольников.Наша формула работает с треугольниками, квадратами, пятиугольниками, шестиугольниками, четырехугольниками, восьмиугольниками и многим другим.
Они создают внутреннее, называемое внутренним, и внешнее, называемое экстерьером. Вы можете измерять внутренние и внешние углы. Вы также можете сложить суммы всех внутренних углов и суммы всех внешних углов правильных многоугольников.Наша формула работает с треугольниками, квадратами, пятиугольниками, шестиугольниками, четырехугольниками, восьмиугольниками и многим другим.
- Видео
- Что такое правильный многоугольник?
- Сумма внутренних углов многоугольника
- Сумма внутренних углов
Что такое правильный многоугольник?
Чтобы многоугольник был правильным многоугольником, он должен удовлетворять этим четырем требованиям:
- Быть двумерным
- Заключите пространство, создав интерьер и экстерьер
- Использовать только отрезки для сторон
- Все стороны равны друг другу по длине и все внутренние углы равны по размеру.
Сумма внутренних углов многоугольника
Правильные многоугольники существуют без ограничений (теоретически), но по мере того, как у вас появляется все больше и больше сторон, многоугольник все больше и больше напоминает круг. Правильный многоугольник с наименьшим количеством сторон — тремя — и есть равносторонний треугольник. Правильный многоугольник с большинством сторон, обычно используемый в классах геометрии, вероятно, представляет собой двенадцатиугольник или 12-угольник с 12 сторонами и 12 внутренними углами:
Правильный многоугольник с наименьшим количеством сторон — тремя — и есть равносторонний треугольник. Правильный многоугольник с большинством сторон, обычно используемый в классах геометрии, вероятно, представляет собой двенадцатиугольник или 12-угольник с 12 сторонами и 12 внутренними углами:
Довольно необычно, не правда ли? Но только потому, что у него есть все эти стороны и внутренние углы, не думайте, что вы не можете много разобраться в нашем двенадцатиугольнике. Предположим, например, что вы хотите знать, к чему складываются все эти внутренние углы в градусах?
Сумма внутренних углов
Треугольники — это просто.Их внутренние углы складываются в 180 °. Точно так же квадрат (правильный четырехугольник) добавляет 360 °, потому что квадрат можно разделить на два треугольника.
Слово «многоугольник» означает «много углов», хотя большинство людей, кажется, замечают стороны больше, чем углы, поэтому они создали такие слова, как «четырехугольник», что означает «четыре стороны».
Правильный многоугольник имеет столько же внутренних углов, сколько и сторон, поэтому треугольник имеет три стороны и три внутренних угла. Квадрат? По четыре каждого.Пентагон? Пять и так далее. У нашего двенадцатиугольника 12 сторон и 12 внутренних углов.
Формула суммы внутренних углов
Формула суммы внутренних углов многоугольника очень проста. Пусть n равно количеству сторон любого правильного многоугольника, который вы изучаете. Вот формула:
Сумма внутренних углов = (n — 2) × 180 °
Сумма углов в треугольнике
Вы можете это сделать. Попробуйте сначала с нашим равносторонним треугольником:
(п — 2) × 180 °
(3 — 2) × 180 °
Сумма внутренних углов = 180 °
Сумма углов квадрата
И снова попробуйте для квадрата:
(п — 2) × 180 °
(4 — 2) × 180 °
2 × 180 °
Сумма внутренних углов = 360 °
Как найти один внутренний угол
Чтобы найти размер одного внутреннего угла, вы просто берете эту сумму для всех углов и делите ее на n, количество сторон или углов в правильном многоугольнике.
Новая формула очень похожа на старую:
Один внутренний угол = (n — 2) × 180 ° n
Опять же, проверьте его на равносторонний треугольник:
(3 — 2) × 180 ° 3
180 ° 3
Один внутренний угол = 60 °
А для квадрата:
(4 — 2) × 180 ° 4
2 × 180 ° 4
360 ° 4
Один внутренний угол = 90 °
Эй! Оно работает! И срабатывает каждый раз . Теперь займемся этим двенадцатигранником.
Примеры внутренних углов
Помните, как выглядит 12-сторонний двенадцатигранник? Найдем сумму внутренних углов, а также один внутренний угол:
Найдите сумму внутренних углов двенадцатиугольника
(п — 2) × 180 °
(12 — 2) × 180 °
10 × 180 °
Сумма внутренних углов = 1,800 °
А теперь найдем один внутренний угол
(п — 2) × 180 ° с
(12 — 2) × 180 ° 12
10 × 180 ° 12
1,800 ° 12
Один внутренний угол = 150 °
Отлично!
Сумма внешних углов
Каждый правильный многоугольник имеет внешних углов . Это , а не угол отражения (более 180 °), создаваемый вращением от внешней стороны одной стороны к другой. Это распространенное заблуждение. Например, в равностороннем треугольнике внешний угол равен , а не 360 ° — 60 ° = 300 °, как если бы мы вращались с одной стороны полностью вокруг вершины к другой стороне.
Это , а не угол отражения (более 180 °), создаваемый вращением от внешней стороны одной стороны к другой. Это распространенное заблуждение. Например, в равностороннем треугольнике внешний угол равен , а не 360 ° — 60 ° = 300 °, как если бы мы вращались с одной стороны полностью вокруг вершины к другой стороне.
Внешние углы создаются путем расширения одной стороны правильного многоугольника за пределы формы и последующего измерения в градусах от этой удлиненной линии до следующей стороны многоугольника.
Поскольку вы расширяете сторону многоугольника, этот внешний угол обязательно должен составлять дополнительных к внутреннему углу многоугольника. Вместе внутренние и внешние углы в сумме составляют 180 °.
Для нашего равностороннего треугольника внешний угол любой вершины равен 120 °. Для квадрата внешний угол составляет 90 °.
Формула внешнего угла
Если вы предпочитаете формулу, вычтите внутренний угол из 180 °:
Внешний угол = 180 ° — внутренний угол
Примеры внешних углов
Что осталось в нашей коллекции правильных многоугольников? Этот двенадцатигранник! Мы знаем, что любой внутренний угол составляет 150 °, поэтому внешний угол составляет:
.
180 ° — 150 °
Внешний угол = 30 °
Проверка вашей работы
Внимательно посмотрите на три внешних угла, которые мы использовали в наших примерах:
Треугольник = 120 °
Квадрат = 90 °
Додекагон = 30 °
Приготовьтесь удивляться.Умножьте каждое из этих измерений на количество сторон правильного многоугольника:
.- Треугольник = 120 ° × 3 = 360 °
- Квадрат = 90 ° × 4 = 360 °
- Додекагон = 30 ° × 12 = 360 °
Каждый раз, когда вы складываете (или умножаете, что является быстрым сложением) суммы внешних углов любого правильного многоугольника, вы всегда получаете 360 °.
Это похоже на магию, но геометрическая причина этого на самом деле проста: чтобы перемещаться вокруг этих фигур, вы делаете один полный оборот на 360 °.
Тем не менее, эту идею легко запомнить: каким бы суетливым и многогранным ни был правильный многоугольник, сумма его внешних углов всегда равна 360 ° .
Краткое содержание урока
После проработки всего этого теперь вы можете определить правильный многоугольник, измерить один внутренний угол любого многоугольника, а также определить и применить формулу, используемую для нахождения суммы внутренних углов правильного многоугольника. Вы также можете объяснить кому-нибудь, как найти меру внешних углов правильного многоугольника, и вы знаете сумму внешних углов каждого правильного многоугольника.
Следующий урок:
Соотношения и пропорции
Как рассчитать углы: 9 шагов (с изображениями)
Поддержите образовательную миссию wikiHow
Каждый день в Wikihow, мы упорно работаем, чтобы дать вам доступ к инструкции и информацию, которые помогут вам жить лучше, то ли это держать вас безопасным, здоровым, или улучшение Вашего благосостояния. В условиях нынешнего кризиса общественного здравоохранения и экономического кризиса, когда мир резко меняется, и мы все учимся и адаптируемся к изменениям в повседневной жизни, людям нужна wikiHow как никогда. Ваша поддержка помогает wikiHow создавать более подробные иллюстрированные статьи и видеоролики и делиться нашим надежным брендом учебного контента с миллионами людей по всему миру. Пожалуйста, подумайте о том, чтобы внести свой вклад в wikiHow сегодня.
Ваша поддержка помогает wikiHow создавать более подробные иллюстрированные статьи и видеоролики и делиться нашим надежным брендом учебного контента с миллионами людей по всему миру. Пожалуйста, подумайте о том, чтобы внести свой вклад в wikiHow сегодня.
Об этой статье
Соавтором этой статьи является наша обученная команда редакторов и исследователей, которые проверили ее точность и полноту. Команда управления контентом wikiHow внимательно следит за работой редакции, чтобы гарантировать, что каждая статья подкреплена достоверными исследованиями и соответствует нашим высоким стандартам качества.Эта статья была просмотрена 346 146 раз (а).Соавторы: 11
Обновлено: 9 февраля 2021 г.
Просмотры: 346,146
Резюме статьиX Чтобы вычислить углы в многоугольнике, сначала узнайте, к чему складываются ваши углы при суммировании, например, 180 градусов в треугольнике или 360 градусов в четырехугольнике. Как только вы узнаете, к чему складываются углы, сложите известные вам углы, а затем вычтите ответ из общих значений углов для вашей формы.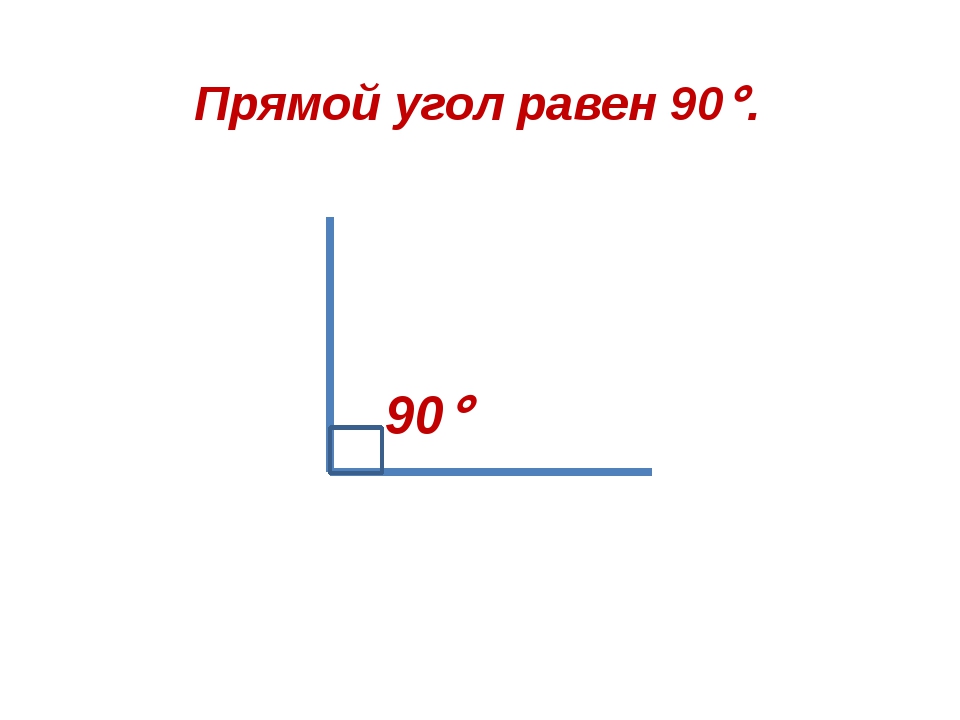 Например, сложите 60 и 80, чтобы получить 140 для 2 углов в треугольнике, затем вычтите 140 из 180, чтобы вычислить третий угол в треугольнике, который будет 40 градусов. Чтобы узнать, как рассчитать угол в прямоугольном треугольнике, читайте дальше!
Например, сложите 60 и 80, чтобы получить 140 для 2 углов в треугольнике, затем вычтите 140 из 180, чтобы вычислить третий угол в треугольнике, который будет 40 градусов. Чтобы узнать, как рассчитать угол в прямоугольном треугольнике, читайте дальше!
- Печать
- Отправить письмо поклонника авторам
Тригонометрия — Терминология
Чтобы лучше понять некоторые проблемы, связанные с самолетами
и двигательная установка
необходимо использовать некоторые математические идеи из тригонометрия , исследование треугольников.Большинство людей знакомятся с тригонометрией в средней школе.
В тригонометрии много сложных частей, но на этой странице
нас интересуют в основном определения и терминология.
Начнем с общего треугольника. Треугольник — это замкнутая форма, имеющая
три стороны и три внутренних угла. Сумма трех углов
любой треугольник равен 180 градусам. Если мы обозначим
углов треугольника c , d и e , тогда:
Если мы обозначим
углов треугольника c , d и e , тогда:
c + d + e = 180 градусов
Есть два способа измерить углы внутри треугольника.Один из способов — измерить угол в градусов , где 360 градусов составляют полный круг. В Другой способ — измерить угол в радиан , где 2 пи радиана равны полный круг. Следовательно;
360 (градусы) = 2 * пи (радианы)
1 градус = 0,01745 радиана
1 радиан = 57,2957 градуса
Прямоугольный треугольник является частным случаем общего треугольника с
один из его углов равен 90 градусам. Угол 90 градусов
называется прямым углом , и отсюда прямоугольный треугольник получил свое название. Прямоугольный треугольник обладает некоторыми особыми свойствами, которые очень полезны для решения задач.
Сумма трех углов прямоугольного треугольника равна 180 градусам и одному
углов равняется 90 градусам. Тогда сумма двух других углов тоже будет 90 градусов. Для прямоугольного треугольника:
Для прямоугольного треугольника:
c + d = 90 градусов = пи / 2 радиана
Важным фактором здесь является то, что если мы знаем (или измеряем) один угол прямоугольного треугольника, мы автоматически знаем значение другого угла.Если мы знаем значение d , то
c = 90 — d
Чтобы описать треугольник в целом, нам нужно знать значение двух углов; за право треугольник нам нужно знать (или измерить) только один угол.
Еще одна важная информация касается размер сторон прямоугольного треугольника. Назовем сторону прямоугольного треугольника противоположной от прямого угла гипотенуза .Это самая длинная из трех сторон. прямоугольного треугольника. Слово «гипотенуза» происходит от двух греческих слов. означает «растягивать», так как это самая длинная сторона. Обозначим гипотенузу символом h и мы обозначим две другие стороны a и b .
Независимо от размера гипотенузы
соотношение
от размера стороны a до гипотенузы h зависит
только
от величины угла между стороной и гипотенузой.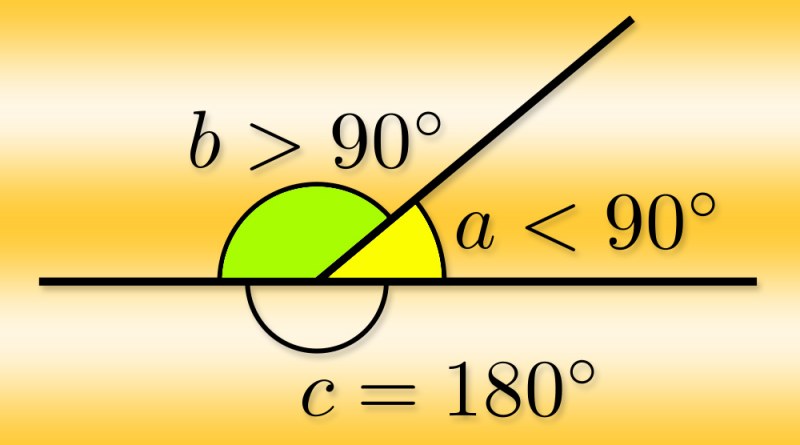 Величина отношения равна
функция
угла и получил название
косинус угла.
На рисунке,
Величина отношения равна
функция
угла и получил название
косинус угла.
На рисунке,
cos (c) = a / h
Из-за соотношения углов прямоугольного треугольника мы можем определить другая функция угла, называемая синус угла, который связывает стороны b и гипотенуза:
грех (с) = б / ч
Ключевым моментом здесь является то, что если мы измеряем один угол, мы знаем значение всех три угла в прямоугольном треугольнике.А если дополнительно измерить одну сторону, мы можем использовать эти тригонометрических функций для определения длины со всех трех сторон. Мы можем определить 5 единиц информации (2 угла и 3 стороны), сделав всего два измерения.
Между сторонами прямоугольного треугольника существует дополнительная связь. Если мы нарисуем квадрат на гипотенузе и квадрат на каждой из двух сторон, площадь квадрата на гипотенузе равна сумме квадраты по бокам.2
Теорема Пифагора может использоваться с тригонометрическими функциями
чтобы определить размер всех сторон прямоугольного треугольника.


 Поэтому можно легко вычислить один из них, если известен другой.
Поэтому можно легко вычислить один из них, если известен другой.