Как на местности построить прямой угол. Как быстро и точно разметить большой участок земли под фундамент сельского дачного дома.
Привязка зданий и сооружений к местности, разметка дома
Начиная изучение геометрии, на первом же уроке рассказывают, что геометрия с греческого переводится как измерение земли. А когда однажды приходится что-то строить или ремонтировать, и появляется необходимость мерить землю в прямом смысле этого слова, оказывается, что этого-то в школе и не преподавали! Потому что рисовать план дома на бумаге – это одно, а объяснять экскаваторщику, где и сколько копать, стоя на поросшем травой пустыре – совсем другое.Содержание1. Построение прямого угла на местности.2. Определение высоты и глубины на местности, высотные отметки.
Но не святые горшки лепят, после изучения информации далее, вы сумеете и выполнить разбивку котлована будущего здания, и осуществить привязку к местности сооружения, существующего только на бумаге, определить высоты, построить горизонтальную линию, при этом используя самые простые инструменты.
Построение прямого угла на местности
Начнем с самого важного – построения прямого угла на местности. Сделать это несложно, а из инструментария нужна только десятиметровая рулетка, четыре колышка и моток капронового шнура.
Определяем линию, от которой будем строить прямой угол. К примеру, это стена будущего здания. Забиваем два колышка и натягиваем между ними шнур. Расстояние между колышками берем произвольное, но несколько больше четырех метров.
Колышек А будет вершиной нашего угла, а натянутый шнур – одной из сторон. Отмеряем от колышка А вдоль шнура четыре метра и забиваем колышек С.
Теперь нам понадобятся помощники. Один из них держит начало, или ноль, рулетки на колышке А, второй – на колышке С держит отметку 8 метров. Вы берете ленту рулетки на отметке 3 м и натягиваете ее так, чтобы образовался треугольник, одним из катетов которого будет натянутый шнур, вторым катетом – отрезок рулетки от ноля до трех, а гипотенузой – отрезок от трех до восьми метров. Рулетку стараемся держать ближе к поверхности земли – так, чтобы все отрезки по возможности лежали в одной плоскости.
Рулетку стараемся держать ближе к поверхности земли – так, чтобы все отрезки по возможности лежали в одной плоскости.
И отрезок между нулем и тройкой (на рисунке синий цвет), и отрезок ленты между тройкой и восьмеркой метровыми отметками (красный) должны быть одинаково хорошо натянуты. Вбиваем колышек В точно в том месте, куда пришлась отметка три метра. Как это все выглядит, видно на рисунке.
Угол САВ будет равен 90 градусам, что и требовалось. Теперь, чтобы построить на местности любой прямоугольник, достаточно отложить длину и ширину на сторонах нашего угла, построить еще один прямой угол.
После построения прямоугольника, для проверки, измерьте его диагонали. Они не должны разниться больше чем на два – три сантиметра при размерах прямоугольника порядка пятнадцати метров.
Определение высоты и глубины на местности, высотные отметки
Теперь узнаем, как определить на местности высоту или глубину. Чтобы дать на местности высотную отметку, в строительстве используют прибор, называемый нивелиром. Но нивелир стоит недешево, да и научиться им пользоваться – дело не пяти минут. Но существует приспособление, точностью не уступающее самым дорогим приборам, а стоимостью равное нескольким батонам хлеба. Называется это чудо техники – гидроуровень. С его помощью можно на расстоянии пятнадцать метров поставить две точки на одинаковую высоту с точностью до двух миллиметров. Принцип гидроуровня основан на законе сообщающихся сосудов, а представляет он собой, в самом простом случае, прозрачную силиконовую трубку диаметром 8 мм, заполненную водой.
К примеру, вам необходимо выполнить бетонный фундамент здания, и, естественно, он должен быть по возможности горизонтальным.
В первую очередь нам нужно определить базовую отметку высоты. Если она не задана в проекте, то назначаем ее произвольно, согласуясь с рельефом, и вбиваем на ней гвоздь. Трубку гидроуровня элементарно затыкаете пальцем, чтобы не вылилась вода; ваш помощник остается возле первого – базового – гвоздя, а вы идете к следующему углу.
Помощник удерживает свой конец уровня вертикально, так чтобы поверхность столбика воды совпала с гвоздем. Вы свой подводите к месту, на котором необходимо указать отметку. Двигая трубку вверх-вниз, помощник добивается совпадения поверхности воды с гвоздем. Ждете, пока вода успокоится, и делаете отметку на опалубке по линии обреза столбика воды. На рисунке это показано достаточно наглядно. В полученную отметку вбиваете второй гвоздь. Так повторяете нужное количество раз. Натянув на вбитые гвозди прочную нить или леску, вы получите строго горизонтальные линии.
Освоив вышеуказанные приемы, комбинируя их, вы сможете осуществлять разбивку на местности весьма сложных конструкций, а также проверку качества их выполнения. Читайте так же о том, как работать тахеометром и нивелиром.
Задавайте вопросы в комментариях ниже либо по почте. Подписывайтесь на новостную рассылку. Успехов вам, и добра вашей семье!chonemuzhik.ru
Как построить прямой угол на земле при помощи простейших инструментов?
Это — древнейшая геометрическая задача.
Пошаговая инструкция
1й способ. — С помощью «золотого», или «египетского», треугольника. Стороны этого треугольника имеют соотношение сторон 3:4:5, а угол равен строго 90град. Этим качеством широко пользовались древние египтяне и другие пракультуры.
Илл.1. Построение Золотого, или египетского треугольника
- Изготавливаем три мерки (или веревочных циркуля – веревка на двух гвоздях или колышках) с длинами 3; 4; 5 метров. Древние в качестве единиц измерения часто пользовались способом завязывания узелков с равными расстояниями между ними. Единица длины — «узелок».
- Вбиваем в точке О колышек, цепляем на него мерку «R3 — 3 узелка».
- Протягиваем веревку вдоль известной границы – в сторону предполагаемой точки А.
- В момент натяжения на линии границы – точка А, вбиваем колышек.
- Затем — снова от точки О, протягиваем мерку R4 – вдоль второй границы. Колышек пока не вбиваем.

- После этого натягиваем мерку R5 – от А до В.
- В месте пересечения мерок R2 и R3 вбиваем колышек. – Это искомая точка В – третья вершина золотого треугольника, со сторонами 3;4;5 и с прямым углом в точке О.
2й способ. С помощью циркуля.
Циркуль может быть веревочный или в виде шагомера. См: …простейший землемерный инструмент
Наш циркуль-шагомер имеет шаг в 1 метр.
Илл.2. Циркуль-шагомер
Построение – также по Илл.1.
- От точки отсчета – точки О – угла соседа, проводим отрезок произвольной длины — но больше, чем радиус циркуля = 1м – в каждую сторону от центра (отрезок АВ).
- Ставим ногу циркуля в точку О.
- Проводим окружность с радиусом (шагом циркуля) = 1м. Достаточно провести короткие дуги – сантиметров по 10-20, в местах пересечения с отмеченным отрезком (через точки А и В.). Этим действием мы нашли равноудаленные точки от центра — А и В. Величина удаления от центра здесь не имеет значения. Можно эти точки просто отметить рулеткой.
- Далее нужно провести дуги с центрами в точках А и В, но несколько (произвольно) большего радиуса, чем R=1м. Можно перенастроить наш циркуль на больший радиус, если он имеет регулируемый шаг. Но для такой небольшой текущей задачи не хотелось бы его «дергать». Или когда регулировки нет. Можно сделать за полминуты веревочный циркуль.
- Ставим первый гвоздь (или ножку циркуля с радиусом больше, чем 1м) поочередно в точки А и В. И проводим вторым гвоздем — в натянутом состоянии веревки, две дуги — так чтобы они пересеклись друг с дружкой. Можно в двух точках: C и D, но достаточно одной – C. И снова хватит коротких засечек на пересечении в точке С.
- Проводим прямую (отрезок) через точки С и D.
- Все! Полученный отрезок, или прямая, — есть точное направление на север :). Простите, — на прямой угол.
- На рисунке показаны два случая несоответствия границы по участку соседа. На Илл.3а приведен случай, когда забор соседа уходит от нужного направления в ущерб себе.
 На 3б – он залез на Ваш участок. В ситуации 3а возможно построение двух «направляющих» точек: и C, и D. На 3б же – только С.
На 3б – он залез на Ваш участок. В ситуации 3а возможно построение двух «направляющих» точек: и C, и D. На 3б же – только С. - Поставьте на углу О колышек, а в точке C — временный колышек, и протяните от С шнур до задней границы участка. – Так, чтобы шнур едва касался колышка О. Замерив от точки О – в направлении D, длину стороны по генплану, получите достоверный задний правый угол участка.
Илл.3. Построение прямого угла – от угла соседа, с помощью циркуля-шагомера и веревочного циркуля
Если у Вас есть циркуль-шагомер, то можно и вовсе обойтись без веревочного. Веревочный в предыдущем примере мы применили для проведения дуг большего радиуса, чем у шагомера. Большего потому, что эти дуги должны где-нибудь пересечься. Для того чтобы дуги можно было провести шагомером с тем же радиусом – 1м с гарантией их пересечения, надо чтобы точки А и В находились внутри окружности c R =1м.
- Отмерьте тогда эти равноудаленные точки рулеткой — в разные стороны от центра, но обязательно по линии АВ (линии забора соседа). Чем точки А и В будут ближе к центру – тем дальше от него направляющие точки: C и D, и тем точнее измерения. На рисунке это расстояние принято равным около четверти радиуса шагомера = 260мм.
Илл.4. Построение прямого угла с помощью циркуля-шагомера и рулетки
- Не менее актуальна эта схема действий и при построении любого прямоугольника, в частности — контура прямоугольного фундамента. Вы получите его идеальным. Его диагонали, конечно, нужно проверить, но разве не уменьшаются усилия? – По сравнению, когда диагонали, углы и стороны контура фундамента двигают туда-сюда, пока углы не сойдутся..
Собственно, мы решили геометрическую задачу на земле. Для того чтобы Ваши действия были более уверенными на участке, потренируйтесь на бумаге – с помощью обычного циркуля. Что ничем в принципе не отличается.
www.remotvet.ru
Как построить прямой угол на местности – линейка без прямых углов
Соблюдайте правило прямого угла
Важную информацию о взаимоотношениях людей дает не только расстояние между ними, но и то, под каким углом они стоят или сидят по отношению друг к другу.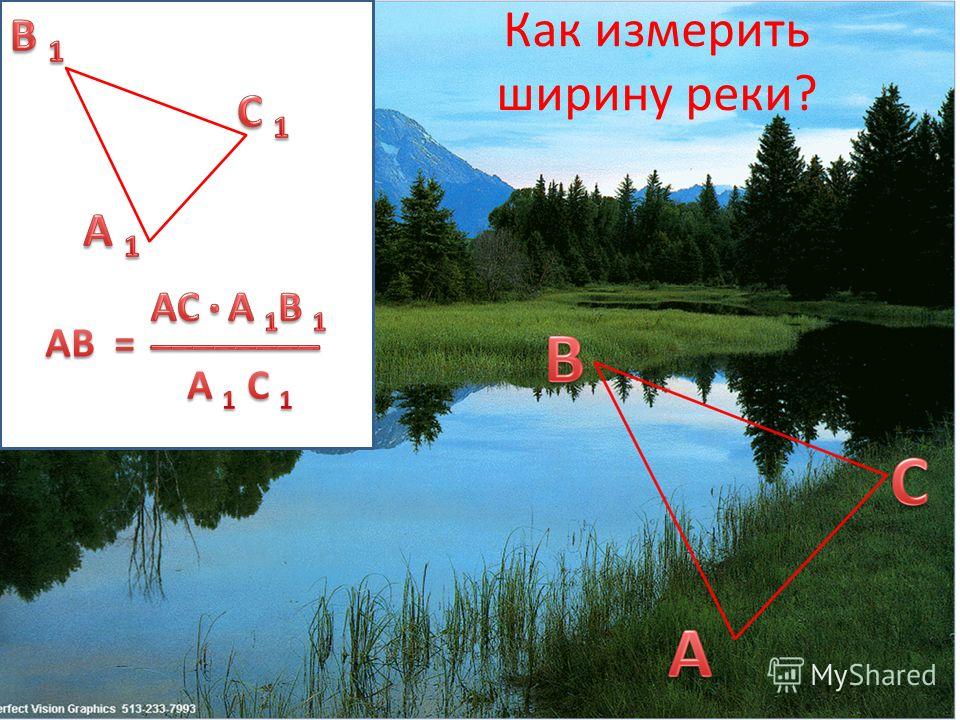 Оптимальный вариант – это расположение друг к другу под углом 90 градусов.
Оптимальный вариант – это расположение друг к другу под углом 90 градусов.
Правило прямого угла
Мысленно нарисуйте прямоугольный треугольник и представьте, что вы с собеседником стоите на его катетах лицом в центр треугольника. Это открытая позиция. Вы повернуты друг к другу, но перед вами остается свободное пространство для «маневра». Общаясь и постепенно узнавая друг друга, вы сможете доверительно развернуться уже лицом к лицу.
Этот прием всем мужчинам рекомендую использовать при знакомстве с женщиной! Вы должны подойти к ней не лицом к лицу, а сбоку, чтобы между вами образовался угол в 90 градусов. Затем, в процессе беседы, вы можете постепенно разворачивать корпус, чтобы оказаться лицом к лицу, и при этом уменьшать дистанцию между вами. Но только постепенно! Если вы поторопитесь, женщина воспримет это как наглое домогательство. А если будете терпеливы – у вас появится хороший шанс пригласить ее на свидание!
Объяснить действие правила прямого угла проще всего на конкретном примере.
…
Представьте себе, что вы идете по улице, и вдруг к вам обращается человек с просьбой показать, например, какой-то дом. Вы останавливаетесь, чтобы подсказать правильное направление. Куда будет развернут ваш корпус: по направлению движения или к остановившему вас человеку? Правильно: в ту сторону, куда вы и направлялись!
А теперь другой вариант. Снова вы идете по улице и вас окликают, но это – о боже, какая встреча! – ваш старый приятель. Вы останавливаетесь, чтобы поздороваться, перекинуться парой слов и бежать дальше по своим делам. Теперь в какую сторону будет развернут ваш корпус? Конечно же, к приятелю!
В первом случае вы не разворачиваетесь полностью к человеку, потому что он не знаком вам. Ваше подсознание, основная задача которого – биологическая защита, знает, что положение боком по отношению к другому человеку уменьшает площадь поражения при возможном нападении.
Если же мы доверяем собеседнику и хотим с ним общаться, мы неосознанно поворачиваемся к нему – лицом к лицу. Потому что подсознание уверено: угрозы нападения нет.
Потому что подсознание уверено: угрозы нападения нет.
Так что, если вы хотите найти общий язык с незнакомым собеседником, используйте правило прямого угла – треугольную диспозицию. И почаще обращайте внимание на то, как расположены ваши тела во время общения. Когда вы начинаете доверять друг другу, вы автоматически поворачиваетесь друг к другу лицом к лицу.
Добавлю еще одну маленькую хитрость. Если вы хотите убедить человека в чем-либо, стойте с левой стороны от него – там, где сердце. Доказано, что левая сторона более восприимчива к информации. Неслучайно цыганки на улице, когда подходят погадать, стараются встать с левой стороны, берут левую руку и тихим голосом нашептывают в левое ухо свои предсказания.
Поступайте так же – и будет вам счастье, к гадалке не ходи!
Следите за сигналами собеседника
Вспомните: иногда, общаясь с человеком, вы чувствуете, что он находится будто не с вами, не здесь. Вроде бы человек внимательно слушает вас, кивает головой, улыбается… Но вы ощущаете, что ваши слова пролетают мимо!
Внимание! Посмотрите на расположение тела вашего собеседника. Вы обязательно увидите, что либо поворот корпуса, либо носок ноги вашего партнера указывают в противоположную от вас сторону. Чаще всего к выходу из помещения, в котором вы общаетесь. Или направлены на другого человека, если вы общаетесь втроем.
Знайте: поворот корпуса и направление носка ноги всегда указывает на настоящее направление мыслей вашего собеседника!
Негативные сигналы
Если, проводя переговоры, вы вдруг заметили, что ваш собеседник откинулся назад, чуть отвернул корпус от вас, закинул ногу на ногу и остался в этом положении, срочно меняйте тактику поведения и общения!
Вы ошибаетесь, если думаете, что он расслабился и внимательно вас слушает. Ничуть! Наоборот, вы ему абсолютно неинтересны! Подобное положение тела является закрытым. Оно означает, что ваш собеседник закрылся от вас, удалился в мир своих мыслей.
Такие негативные сигналы могут означать для вас следующее:
• ваш собеседник услышал от вас нечто такое, что ему не понравилось;
• он понял, что ваша идея не представляет для него интереса;
• он уже принял решение отказать вам, не принимать ваше предложение.
Чтобы вновь заинтересовать вашего собеседника, рекомендую протянуть что-нибудь ему в руки. Таким образом он будет вынужден сменить позу, а вы должны использовать этот момент и сменить тактику ведения переговоров!
На что нужно обратить внимание? Во-первых, чтобы удержать внимание партнера, ваши движения и позы должны быть открытыми. Это значит, что ни в коем случае, никогда и ни при каких обстоятельствах, общаясь с людьми, вы не должны скрещивать руки и ноги. Это признак негативного или оборонительного отношения.
Ваша задача – научиться использовать положительные, открытые жесты для успешного общения с другими людьми. И, соответственно, избавиться от жестов закрытых, несущих отрицательную, негативную окраску. Используя открытые жесты, вы будете чувствовать себя более уютно в обществе людей и будете выглядеть более привлекательными для них.
Поза активного слушателя
Если вы хотите быть убедительными и одновременно внимательными к партнеру, обязательно освойте позу «активного слушателя». С ее помощью вы продемонстрируете свою заинтересованность в собеседнике!
Поставьте ноги прямо, параллельно друг другу. Корпус слегка подайте вперед, не откидывайтесь назад. Представьте, что вы слушаете увлекательную историю. Настолько интересную, что вы боитесь упустить даже слово. Поэтому не только ваше тело наклоняется вперед, но и голова слегка подается вперед и немного наклоняется вбок.
Потренируйтесь сперва на своих знакомых, чтобы ваши движения выглядели естественно. А оттачивать мастерство можно на совещаниях, собраниях и деловых встречах!
Концентрируйтесь на позитиве!
Чтобы все описанные выше приемы действовали наиболее эффективно, они должны выглядеть естественными.
Привязка зданий и сооружений к местности, разметка дома
Для этого ваше тело должно реагировать идеально в соответствии с вашими замыслами.
Как этого добиться? Самое простое – вспомнить такое состояние, когда вы чувствовали себя наиболее комфортно. Например, припомните, когда последний раз вы общались с близкими друзьями. Или сидели у камина на кресле-качалке под клетчатым пледом, с интересной книжкой в руках и мурлыкающей кошкой на коленях.
Например, припомните, когда последний раз вы общались с близкими друзьями. Или сидели у камина на кресле-качалке под клетчатым пледом, с интересной книжкой в руках и мурлыкающей кошкой на коленях.
Заметили? Ваши губы расплываются в улыбке, взгляд смягчается, ладони раскрываются… Уверяю вас: при этом зрачки ваших глаз расширяются, а тело автоматически поворачивается к источнику тепла и уюта, будь то близкий человек или любимая кошка.
Это состояние нужно запомнить! И ощущение комфорта и уюта использовать при общении с незнакомым для вас человеком. Просто мысленно представьте, что этот человек – ваш друг, тот самый источник тепла и уюта. Вы очень рады его видеть! Ничего больше не требуется: ваше тело автоматически настроится на нужный лад.
Воспоминания о приятных переживаниях общения запускают цепную реакцию: от подсознательного смягчения взгляда до поворота тела. И все это происходит само собой!
Более того, когда вы ведете себя так, будто только что встреченный и пока незнакомый вам человек необычайно вам нравится, вы и в самом деле начинаете проникаться к нему искренней симпатией!
Это одно из правил психологии.
Когда мы верим, что нравимся другому человеку и что он нравится нам – наше поведение делает эти предположения реальностью. И то же самое происходит, когда мы верим, что не нравимся окружающим – это становится правдой!
Как говорил Генри Форд: «Верите ли вы, что не можете, или верите, что можете – вы правы в обоих случаях».
Практика третьего шага
Запомните основные правила!
Обязательно зафиксируйте в памяти основные правила третьего шага. Чтобы лучше их запомнить, рекомендую записать правила на бумаге. Записав, вы точно сможете их запомнить! Запомнив, будете использовать в жизни. А используя эти правила, вы измените не только свое поведение, но и поведение своих собеседников и партнеров!
Напомню, правила простые: сохраняйте дистанцию, используйте треугольную диспозицию, стойте с левой стороны от собеседника и используйте при разговоре открытые жесты.
Наблюдайте за людьми
Поставьте себе задачу каждый день хотя бы 15 минут наблюдать за поведением людей при разговоре. Оценивайте расположение их тел по отношению друг к другу во время разговора, делайте выводы, набирайтесь опыта!
Шаг четвертый. Покажите ваши руки!
stroyvolga.ru
Как точно разметить прямой угол на местности, не имея транспортира?
Как точно разметить прямой угол на местности, не имея транспортира?
В этом случае для построения прямого угла применяется всем известная формула Пифагора — в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Еще такое построение называют quot;египетским треугольникомquot;, так как по такому же принципу строились углы пирамид. Натяните строительный шнур по главному фасаду одной из сторон будущего строения. Эта линия свое положение НЕ меняет. На шнуре, в точке где будет угол постройки привяжите еще один шнур и отойдите с ним в сторону, образуя другую, перпендикулярную сторону строения.На первом шнуре от точки, образующей угол отмерьте 4 метра. От этой же точки, но по другому шнуру отмерьте 3 метра. На совершенно отдельном шнуре зафиксируйте длину (расстояние) 5 метров (можно привязать яркие тесемки). Далее работают 2 человека. Один человек крайнюю точку пятиметрового шнура держит на шнуре главного фасада в точке 4 метра. Другой человекпостарается 5-и метровый шнур дотянуть до точки 3 м на другом шнуре.Вторая сторона на момент построения будет подвижной.Подтяните или отодвиньте боковую сторону так, чтобы крайние точки 5-иметрового и 3-х метрового шнура соединились. А угол между шнуром/линией главного фасада и линией бокового фасада у вас будет прямым, то есть 90 градусов. А по теореме это выглядит так — 4 (16) + 3 (9) = 5 (25) 25 = 25
Ну, если говоря quot;на местностиquot;, Вы предполагаете начертить прямой угол прямо на земле, к примеру размечая границы какого-то участка или фундамента будущего дома, то можно воспользоваться тремя колышками и шпагатом или вервкой, длинна которой кратна 12 метрам.
Говорят, этот метод был известен ещ в древнем Египте, а в его основе так называемое правило quot;золотого сеченияquot;.
quot;Золотое сечениеquot; — это треугольник со сторонами, длинны которых соотносятся, как 3:4:5
Вот так, более подробно, использование этого метода на практике описывается в интернете:
Как правило строили когда делают прямые углы меряют диагонали полученного прямоугольника. Если нужно сделать что-то маленькое, то можно этот прямой угол обвести по прямоугольному предмету. Самый простой способ это произвести замер диагоналей. Можно и с помощью веревки, смотрите какой вариант вам больше подходит.
Возьмите три брусочка (рейки, линейки, металлические полоски, какие-нибудь жесткие дюралевые элементы для строительства). Сделайте в них по два отверстия диаметром 4-6 мм. Расстояния между центрами отверстий должны относиться друг к другу как 3:4:5, (например 60 см, 80 см и 100 см, или 15 см, 20 см, 25 см). Скрепите брусочки винтами (болтами) в треугольник. Получится прямоугольный треугольник с прямым углом между короткими сторонами (катетами). Чем длиннее стороны треугольников тем точнее будет прямой угол. Но, слишком длинные брусочки могут оказаться кривыми, или прогнуться в процессе изготовления или эксплуатации.
Другой вариант: берете три кусочка мягкой проволоки, с тем же соотношением длин, например 3 4 и 5 м, реально где-то на 10-20 см длиннее. На концах проволоки делаете кольца. Вбиваете в землю два колышка (кусочки труб), допустим, сначала на расстоянии ровно 3 м, накидываете кольца на колышки и сделав петлю где-нибудь в средней части проволоки quot;скруткойquot; выбираете излишек длины, чтобы проволока натянулась как можно прямее между колышками. Точно так же натягиваете другую проволоку на колышки с расстоянием между ними 4 м, и третью — с расстоянием 5 м. Теперь, в вершине требующегося прямого угла вбиваете один колышек. На него накидываете концы 3-х и 4-ж метровых проволок. Другие концы этих проволок продеваете в другие колышки, которые держат в руках Ваши помощники. кольца третьей проволоки (5 м) тоже продеваете в эти колышки. Затем помощники расходятся по требуемым направлениям и подбирают положения колышков, которые у них в руках (удерживая их строго вертикально) так, чтобы все три проволоки были натянуты. Когда такое положение достигнуто, угол будет близок к прямому.
кольца третьей проволоки (5 м) тоже продеваете в эти колышки. Затем помощники расходятся по требуемым направлениям и подбирают положения колышков, которые у них в руках (удерживая их строго вертикально) так, чтобы все три проволоки были натянуты. Когда такое положение достигнуто, угол будет близок к прямому.
Можно и другие соотношения, лишь бы между ними соблюдалась теорема Пифагора, например 5, 12 и 13, или 7,24 и 25.
Отсутствие транспортира вполне компенсирует теодолит.
Ну и не забываем что диагонали прямоугольника равны между собой.
info-4all.ru
Полезная геометрия | Наука и жизнь
В школе мы несколько лет подряд прилежно изучаем геометрию. Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться.Вешаем зеркало
Вы решили повесить в прихожей зеркало. Тут же возникает вопрос: какой минимальной высоты должно быть зеркало, чтобы человек среднего роста мог видеть себя в нём целиком? И ещё: имеет ли при этом значение размер помещения, где будет висеть зеркало? Решение. Предмет и его отражение симметричны относительно плоскости зеркала. Построим в нём изображение человека (рис. 1): АВ — человек, А1В1 — его изображение, точка С — глаз, DE — зеркало. Из рисунка видно, что минимальная высота зеркала приблизительно равна половине роста человека, считая от уровня глаз. При этом высота Е нижнего края зеркала от пола должна быть вдвое меньше расстояния от пола до глаз. Легко понять, что, на каком бы расстоянии от такого зеркала ни находился человек, он сможет увидеть себя в нём с головы до ног, значит, размер помещения значения не имеет.Завариваем чай
Перед вами стеклянные чайники четырёх моделей одинаковой вместимости (рис. 2). В каком чайнике заваренный чай останется тёплым дольше? Решение. Из курса физики известно, что время охлаждения пропорционально площади поверхности тела. Значит, чем меньше поверхность чайника, тем дольше остывает чай. Самая маленькая площадь поверхности у четвёртого чайника, так как его форма близка к сфере (S = d2).
Значит, чем меньше поверхность чайника, тем дольше остывает чай. Самая маленькая площадь поверхности у четвёртого чайника, так как его форма близка к сфере (S = d2).Выдерживаем прямые углы
Если вы решили склеить коробку, сделать шкатулку или выложить плитку, важно, чтобы все детали были точными прямоугольниками или квадратами. В противном случае всё пойдёт наперекосяк. Как проверить, имеет ли деталь нужную «геометрию»? Решение. Чтобы проверить, у всех ли деталей, с которыми вы работаете, прямые углы и одинаковые линейные размеры, можно использовать строи-тельный угольник (рис. 3), а можно применить знания по геометрии. Убедитесь в том, что противоположные стороны четырёхугольника равны и при этом диагонали тоже имеют одинаковую длину. Как вы и сами знаете, сделать это можно с помощью линейки. Но вот вопрос: обязательно ли проверять и стороны и диагонали? Геометрия утверждает, что да! Например, на рис. 4 диагонали в четырёхугольнике слева равны, но очевидно, что его углы совсем не прямые. А в четырёхугольнике справа противоположные стороны равны, но это тоже не прямоугольник. Для проверки прямоугольности геометрия ещё советует убедиться в равенстве всех четырёх отрезков, на которые разбиваются диагонали в точке их пересечения.Строим прямой угол на земле
Известен старинный способ постро-ения прямого угла на поверхности земли. Его использовали ещё древние египтяне. Они строили прямой угол с помощью обычной верёвки, на которой через равные расстояния завязаны тринадцать узелков. Чтобы отрезки на верёвке были одинаковые, узелки завязывали вокруг колышков, вбитых в землю на равном расстоянии друг от друга. В чём состоит этот «верёвочный» способ? Решение. В древности при закладке храма такую верёвку с узелками использовали для определения направлений его стен. Концы верёвки на месте крайних узелков связывали, а затем натягивали её на три колышка так, как показано на рис. 5. Стороны при этом имели соотношение 3:4:5. В таком треугольнике один из углов получается прямым. Впоследствии этот факт был доказан в теореме Пифагора. Поэтому первых геометров называли ещё «натягивателями верёвок». Нужно отметить, что таким способом построения прямого угла на местности пользуются и сегодня, например при закладке фундамента небольшого строения.
Впоследствии этот факт был доказан в теореме Пифагора. Поэтому первых геометров называли ещё «натягивателями верёвок». Нужно отметить, что таким способом построения прямого угла на местности пользуются и сегодня, например при закладке фундамента небольшого строения.Проверяем перпендикулярность стен
Как проверить, перпендикулярны ли друг другу соседние стены в комнате, воспользовавшись верёвкой с узелками из предыдущей задачи? Решение. Если предположить, что стены в комнате вертикальны, а пол горизонтален, то проверку проводят так. От точки на полу в углу между стенами откладывают отрезки длиной 3 и 4 единицы (рис. 6). Если стены перпендикулярны, то расстояние между концами отрезков будет равно 5 единицам, так как построенный тре-угольник со сторонами 3, 4, 5 — прямоугольный.Отмеряем нужный объём
Часто в рецептуре того или иного блюда требуется взять четверть (или половину) стакана жидкости, муки либо какого-либо другого продукта. Как отмерить такой объём с наибольшей точностью, не прибегая к дополнительным измерительным средствам? Решение. Воспользуемся стаканом цилиндрической формы — это важно для точности измерений. Чтобы отмерить четверть стакана жидкости, надо из наполненного стакана вылить столько, чтобы оставшаяся в нём жидкость закрыла половину дна (рис. 7). Она займёт примерно четверть объёма стакана-цилиндра. Аналогично поступаем, если надо отмерить половину стакана. Наклоняем стакан так, чтобы оставшаяся в нём жидкость закрыла всё дно (рис. 8). А можно ли геометрическим способом узнать объём бутылки? Конечно! Для этого надо заполнить бутылку водой чуть меньше чем наполовину (рис. 9, слева) и измерить объём воды, умножив площадь дна бутылки на высоту налитой в неё воды (напомним, что объём цилиндра вычисляется как произведение площади основания на высоту). Затем нужно перевернуть бутылку горлышком вниз так, чтобы вода не вытекла, и измерить объём верхней цилиндрической части бутылки, оставшейся пустой (рис. 9, справа). Полный объём бутылки равен сумме найденных объёмов. Для точности можно учесть толщину стенок бутылки.
Для точности можно учесть толщину стенок бутылки.Укрепляем калитку
Прямоугольная калитка (рис. 10, слева) со временем расшатывается и становится похожей на параллело-грамм. Этого можно избежать, прибив к ней ещё одну планку. Только надо знать, как это сделать. Решение. Выбор такого положения планки, как показано на рис. 10, справа, основан на свойстве жёсткости треугольника. Оно гласит: существует единственный треугольник с заданными длинами сторон. Планка и есть гипотенуза такого треугольника.Выбираем табурет
Если вы решили предыдущую задачу, то без труда определите, на какой табурет (рис. 11) можно сесть без риска оказаться на полу. Решение. Безопасный табурет изображён на правой картинке, так как его сиденье и ножки образуют треугольник.Исправляем ошибку кроя
Предположим, вам нужно вырезать для аппликации два разносторонних треугольника из цветной бумаги — «левый» и «правый». Вы случайно вырезали их одинаковыми — оба «левые». Можно ли, не используя новый кусок бумаги, исправить ошибку? Решение. Для исправления ошибки вы можете разрезать один из треугольников, например так, как показано на рис. 12, а затем сложить из него нужный треугольник.Находим середину
Как без всяких измерений найти середину негнущегося прута, доски или металлического стержня? Решение. Можно отмерить размеры стержня на шнуре, затем сложить его пополам и отложить полученную длину. А можно воспользоваться геометрическим построением середины отрезка с помощью циркуля и линейки, если, конечно, размеры позволяют это сделать. Ещё более рациональное решение даёт физика. Середину однородного стержня легко найти, используя понятие центра тяжести (рис. 13).www.nkj.ru
Как быстро и точно разметить большой участок земли под фундамент сельского дачного дома.
Мы живем в «прямоугольном» мире, в Декартовой системе координат. Все стройматериалы также выпускаются в виде прямоугольных заготовок. От доски до рулонов утеплителя. От кирпичей, до бетонных плит перекрытия. Только сыпучие материалы меряются ведрами, мешками, кубометрами (кстати, тоже прямоугольными…).
Только сыпучие материалы меряются ведрами, мешками, кубометрами (кстати, тоже прямоугольными…).
Поэтому крайне важно при разметке большого участка земли под фундамент выдержать эту прямоугольность. Хотя сделать это самодеятельному строителю бывает не всегда легко. Но приходится.
Хотя, если знать основополагающие принципы разметки и знать некоторые приемы, сделать это можно и самостоятельно, и даже в одиночку.
Принцип первый: Диагонали у прямоугольника — равны. Если длины диагоналей не равны — значит это НЕ прямоугольник, а что то иное. Ромб, параллелограмм, или вообще фигура не поддающаяся классификации, просто четырехугольник.
Есть однако и исключение. Диагонали равны и у равнобедренной трапеции! Диагонали у нее одинаковые, но она — не прямоугольник! Это тоже полезно знать, и не радоваться раньше времени, добившись равности диагоналей.
Поэтому необходимо применять
Принцип второй: Для гарантированного построения прямого угла надо построить т.н. «египетский» или «золотой» треугольник. Такой треугольник, согласно многократно доказанной теореме Пифагора, имеет стороны 3, 4, и 5 единиц. Т.е. катеты длиной по 3 и 4 единицы, а гипотенуза равна 5 единицам. Такой треугольник ВСЕГДА прямоугольный. Несмотря на то, что бы вы не подразумевали под «единицами» — метры, сантиметры, длину какой то палочки, удавов или попугаев. Главное, что бы единицы для измерения катетов и гипотенузы были одни и те же.
Эти два принципа — необходимы и достаточны для того, что бы правильно, и с достаточной для строительства точностью разметить участок под фундамент дома или что вам надо.
Итак, переходим к практическим упражнениям на местности.
Для этого нам потребуется рулетка (желательно длиной больше диагонали, что бы не пользоваться узелками на веревочках). И прочный и длинный шнурок (веревочка). Шнурка должно быть много. Весьма полезно иметь несколько тугих прищепок, что бы не возиться с колышками.
Кстати, прежде чем приступать к разметке и вообще к проектированию, неплохо бы определиться с типом строения, из чего будут стены и т. д. Дело в том, что материалы выпускаются определенных размеров. И бывает весьма обидно, когда впоследствии при постройке, вам, например, придется аккуратно отпиливать от каждого куска пенопласта «лишних 5 сантиметров». И так — 170 раз подряд… Может проще было делать каркас сразу под имеющиеся в продаже материалы?
д. Дело в том, что материалы выпускаются определенных размеров. И бывает весьма обидно, когда впоследствии при постройке, вам, например, придется аккуратно отпиливать от каждого куска пенопласта «лишних 5 сантиметров». И так — 170 раз подряд… Может проще было делать каркас сразу под имеющиеся в продаже материалы?
Т.е. поинтересуйтесь, а каких ЭТО (из чего вы будете строить дом и отделывать его) бывает типо-размеров? Весьма полезно и с экономической точки зрения — отходов не будет. Ну почти не будет…
После того, как с размерами вы определились, размечают ПЕРВУЮ стену. Неважно какую, фасад, боковую или заднюю. Ее же ориентируют в нужном вам направлении. Причем длину этой стены никак не учитывают, а берут с запасом, минимум по полметра — метру от предполагаемых углов. Там забивают колышки и туго натягивают шнурок. Т.е. мы разметили не саму стену, а только ее НАПРАВЛЕНИЕ и примерное месторасположение.
Для чего это делается? Дело в том, что в дальнейшем вам ведь придется вынимать грунт для устройства фундамента. Если мы вобьем колышек сразу в место предполагаемого угла фундамента, то при выемке грунта колышек попросту упадет.
Кстати, вместо колышков удобнее использовать 1-2 х метровую доску, к которой прибиты два колышка. Тогда в боковой торец доски можно вбивать гвозди в любом месте и очень оперативно двигать шнуров влево — вправо. Таким образом можно разметить фундамент просто идеально, с точностью до миллиметров. Такой способ разметки называется «обноска» и работать с ней значительно удобнее, чем с колышками.
Когда мы натягиваем первый шнурок и намечаем место первой стены, у нас появляется «печка», от которой мы будем плясать.
Вот теперь пришло время определиться с местом, где будет угол фундамента. Вешаем на это место прищепку на шнурок (или забиваем колышек) и отмечаем длину стены. Теперь у нас есть уже целых два угла.
А вот тут начинается самое интересное.
Точно такую же обноску мы делаем и для другой стены, перпендикулярной первой.
На первом шнурке мы отмеряем 3 единицы ( кстати, чем единицы длиннее , тем точнее будет прямой угол). Например, ровно 3 метра. И вешаем в этом месте прищепку.
От места пересечения шнурков (желательно что бы они были почти на одной высоте), отмеряем 4 единицы ( ровно 4 метра в данном случае) и тоже вешаем прищепку.
Измеряем расстояние между 2-мя прищепками (с помощью рулетки и помощника). Оно должно быть равно ровно (!!!) 5 метров. Разумеется, с первого раза вы вряд ли получите такой результат. Если он МЕНЬШЕ, это значит, что угол более острый, чем 90 градусов. Если БОЛЬШЕ 5-ти метров — значит угол больше 90 градусов. В этом случае необходимо сдвинуть один конец второго шнурка в ту или иную сторону. После этого снова отмерить 3 единицы от перекрестка шнурков по первому шнурку и 4 единицы по второму. И снова измерить гипотенузу…
Такие перемещения и измерения делаются несколько раз и в конце концов вы получаете желаемый результат — гипотенуза треугольника равна 5 метрам, и стены у нас (вернее их разметка) расположены строго перпендикулярно.
Теперь мы можем отмерить длину второй стены и повесить прищепку там (или забить колышек. Это будет уже 3-й угол дома. И у нас уже появилась диагональ. (А мы помним, что нам важна не ее абсолютная длина, а равенство диагоналей. )
Поэтому найти место для 4-го угла — дело техники. Устроив обноску надо просто найти место пересечения третьего и четвертого шнурка при условии равенства длин противоположных стен.
Ну вот и готова ВНЕШНЯЯ обноска фундамента. Если фундамент — плита, этого достаточно. А если фундамент ленточный — устраиваю внутреннюю обноску так же как и первую, с учетом ширины ленты фундамента. Разумеется сделать ее гораздо проще, чем внешнюю.
Этот способ разметки фундамента проверен веками.. А в те времена не было калькуляторов и сельские строители понятия не имели о квадратных корнях.
Поэтому считаю нужным рассказать, как я размечал свой фундамент. Напомню, его внешний размер у меня 15 х 12 метров. Диагональ, соответственно 19.21 метр
Диагональ, соответственно 19.21 метр
Рассчитав все на бумаге, я купил нужное количество шнурка и попросту отмерил весь периметр фундамента. А затем, наметив «углы» я перевязал его крест накрест абсолютно равными диагоналями.
Т.е. я сразу пошел от желаемого результата…
Выйдя на местность, я вбил первый колышек в желаемом месте и сориентировал первую стенку. Соответственно вбил колышек в месте второго угла.
Ну а дальше было дело техники. Взял колышек и натянув «паутину» так, что бы была натянута одновременно и «стенка» и диагональ, я нашел место третьего угла. Ну и точно так же — место для четвертого. Вся процедура не заняла и 30 минут. Причем размечал ее фундамент в одиночку.
А выносную обноску я устроил уже сверху фактически размеченного фундамента. После этого убрал свою «паутину», что бы она не мешала работать.
dom.delaysam.ru
Разбивка на местности. Обноска.[Razbivka-na-mestnosti-Obnoska] | Мой загородный дом
Поскольку здания и сооружения на местности имеют прямые углы, попробуем построить такой угол на местности. Нам понадобится: три штыря из проволоки, диаметром 6-8 мм и длиной 40 см, а так же полипропиленовый шпагат- около 15 метров.
Отрежем два куска шпагата – 4м и 5 м.Выберем исходную точку на участке, где у нас планируется один из углов будущего сооружения. Возьмём один штырь, привяжем к нему оба куска шпагата и воткнём штырь в нашу исходную точку. Это и будет вершина первого прямого угла.
Затем рулеткой отмеряем на длинном куске шпагата ровно 4 м.На этом месте привязываем ещё один штырь.
Теперь на коротком куске шпагата отмеряем ровно 3 м и, точно так же, привязываем третий штырь.
У нас получилось, что один штырь воткнут в исходной точке, и к нему привязаны 2 отрезка шпагата- 3 и 4 м со штырями на концах. Берём третий отрезок шпагата и привязываем его к одному из не воткнутых в землю штырей. От штыря по этому отрезку отмеряем ровно 5 м и завязываем на этой отметке узелок.
Получился простейший, но довольно точный инструмент для построения прямых углов на местности.
Как им пользоваться? Воткнём в землю второй штырь. Обычно это штырь с четырёхметровым отрезком шпагата. Ориентируем его так, как пойдет длинная стена нашего будущего сооружения. Далее, совмещаем место 5и метровой отметки и место третьего штыря, как показано на рисунке 1.
Получился прямой угол на местности.
Таким же образом строим весь прямоугольник будущего сооружения. Теперь правим его диагональю.
Допустим, наше сооружение имеет размер по осям 6м на 8 м.Рассчитаем размер диагонали Д.
Д=6*6+8*8=36+64=100
Извлекаем корень квадратный из 100, получим 10 м
Берём отрезок шпагата чуть более 10м и двумя узелками отметим 10 м. Проверим диагонали, как показано на рисунке 2.
Если диагонали не попадают в углы, переставим штыри. Таким образом, мы вынесли план будущего сооружения в осях.
Выполнение обноски
myzagdom.ru
Как сделать прямой угол для фундамента. Общие правила для любого фундамента
Как сделать прямой угол для фундамента. Общие правила для любого фундамента
Выбираем точку отсчета. Первую сторону нашего фундамента нужно привязать к какому-нибудь объекту нашего участка.
Пример. Сделаем так, чтобы наш фундамент (дом) был параллелен одной из сторон забора. Следовательно, первую бечевку натягиваем равноудалено от этой стороны забора на нужное нам расстояние.
Построение прямого угла (90⁰). В качестве примера будем рассматривать прямоугольный фундамент, в котором все углы максимально близки к 90⁰.
Существует несколько способов как это сделать. Мы рассмотрим 2 основных. © www.gvozdem.ru
Способ 1. Правило золотого треугольника
Для построения прямого угла будем применять теорему Пифагора.
Формула
Чтобы не углубляться в геометрию попробуем описать проще. Чтобы между двумя отрезками a и b сделать угол в 90⁰ нужно сложить длины этих отрезков и вывести корень из этой суммы. Получившиеся число будет являться длинной нашей диагонали соединяющей наши отрезки. Очень просто расчет сделать с помощью калькулятора.
Очень просто расчет сделать с помощью калькулятора.
Обычно при разметке фундамента берут размеры сторон, чтобы при выведении из корня получалось целое число. Пример: 3х4х5; 6х8х10.
Если у вас есть рулетка, то в целом проблем не возникнет, если вы будете брать отрезки отличные от общеиспользуемых. Например: 3х3х4,24; 2х2х2,83; 4х6х7,21
Если измерения мы производили в метрах, то значения получаются очень даже понятными: 4м24см; 2м83см; 7м21см.
Калькулятор
Также стоит отметить, что измерения можно производить в любых системах измерения длины главное использовать известное нам соотношение сторон: 3х4х5 метра, 3х4х5 сантиметра и т.п. То есть, если даже у вас нет инструмента для измерения длины, то можно взять, например, рейку (длина рейки не имеет значения) и померить ей (3 рейки х 4 рейки х 5 реек).
Теперь давайте посмотрим как это применить на практике.
Как найти прямой угол на земле. Как пользоваться правилом 3-4-5
1
Поймите, в чем суть правила 3-4-5. Если у треугольника есть три стороны со значениями 3, 4 и 5 см (или кратное им значение), это прямоугольный треугольник, угол между сторонами с меньшими значениями составляет 90 градусов. Если у вас получилось построить треугольник, исходя из значений угла, то можно точно сказать, что угол прямоугольный. Это правило основано на теореме Пифагора :A2+ B2= C2(в прямоугольном треугольнике). Где С – самая длинная сторона (гипотенуза), А и В –остальные стороны (катеты).
- Правило 3-4-5 очень удобно проверить благодаря целым числам. Итак, опираясь на математические расчеты:32+ 42= 9 + 16 = 25 =52.
2
Отмерьте от угла 3 см (или 3 м) на одной стороне. Можно взять любую меру длины. Пометьте отмеренный участок точкой.
- Можно умножить каждое число на одно и то же число – и это правило все равно сработает. Например, это правило будет работать для треугольника со сторонами 30-40-50 сантиметров или метров.
 Если у вас большая комната, можно использовать следующие числа: 9-12-15, 6-8-10 метров.
Если у вас большая комната, можно использовать следующие числа: 9-12-15, 6-8-10 метров.
3
Отмерьте четыре метра (или длину со значением, которое кратно четырем) на другой стороне. То же самое, если у вас получится сделать треугольник, то угол между этими двумя сторонами будет равен 90 градусам. Снова пометьте отмеренный участок точкой.
4
Теперь измерьте расстояние между этими двумя метками. Если расстояние кратно пяти, то можно точно сказать, что угол составляет 90 градусов.
- Если расстояние меньше, чем 5 единиц (метров), значит, угол острый (меньше 90 градусов). Если есть такая возможность, нужно немного раздвинуть стороны, образующие этот угол.
- Если расстояние между метками составляет больше 5 единиц (метров), значит, угол тупой (то есть больше 90 градусов). Если есть такая возможность, нужно свести стороны, образующие угол, поближе друг к другу, чтобы угол получился прямым. Строя прямой угол, можно использовать прямой угол рамки.
- Получив прямой угол в 90 градусов, можно проверить остальные углы комнаты, чтобы убедиться в том, что они прямые.
Как ровно разметить фундамент. Подготовка к разметке фундамента
Перед тем как разметить фундамент своими руками составляется проект будущего здания . При этом определяется площадь объекта, внешний вид строения и планировка отдельных помещений. Проект привязывается к участку, где будет проводиться строительство. Сначала проводятся работы по исследованию грунта, а затем осуществляется разметка основания.
Для проведения разметки потребуются следующие инструменты:
- Колышки из металла или дерева.
- Строительные уровни.
- Рулетка и отвес.
- Нивелир и лазерный дальномер.
- Шнур.
- Доски и обрезки арматуры.
Перед тем как сделать разметку под фундамент, необходимо произвести подготовительные работы:
- Демонтируются старые строения , убирается мусор и лишние насаждения на участке.

- Площадка выравнивается в горизонтальной плоскости , устраняются все углубления и холмы.
- Подготавливается проезд для транспортных средств, которые будут подвозить строительные материалы и вывозить ненужный мусор. После очищения дороги, ее рекомендуется присыпать гравием для удобного проезда во время дождя.
- Отдельно подготавливается место для складирования разнообразных материалов.
- Перед строительными работами стоит возвести забор, чтобы защитить строительные материалы.
- Продумайте подведение электричества , воды, монтаж санузла, а также временное жилье.
После этого проводится разметка фундамента под дом. Технология монтажа предполагает наличие прямоугольных форм. Общие правила и нормы для разметки подходят для всех разновидностей оснований, на них не влияет материал изготовления или наличие подвального помещения.
Разметка начинается с любой стороны строения . Это может быть фасад или боковая часть постройки. При использовании рулетки стоит отдать предпочтение изделиям из металла, которые имеют длину более 10 м. Модели из ткани не гарантируют точность измерений и провисают при замерах.
Для осуществления обноски рекомендуется использовать бруски (не менее 10 штук), колья (примерно 19 штук), а также шнуры, доски и веревки. Иногда применяются куски арматуры, которые вбиваются в грунт. Они должны быть п-образной формы.
Участок выбирается с учетом следующих факторов:
- Перспектива проведения всех коммуникаций.
- Состояние дорог.
- Географическая привязка к сторонам света .
Важнейшим предназначением разметки является осуществление правильной ориентации будущего строения, относительно местности. Это позволит возвести строение с учетом стандартных технологических правил.
Видео как отмерить прямой угол в помещении или на местности без угольника
Привязка зданий и сооружений к местности, разметка дома
Начиная изучение геометрии, на первом же уроке рассказывают, что геометрия с греческого переводится как измерение земли. А когда однажды приходится что-то строить или ремонтировать, и появляется необходимость мерить землю в прямом смысле этого слова, оказывается, что этого-то в школе и не преподавали! Потому что рисовать план дома на бумаге – это одно, а объяснять экскаваторщику, где и сколько копать, стоя на поросшем травой пустыре – совсем другое.
А когда однажды приходится что-то строить или ремонтировать, и появляется необходимость мерить землю в прямом смысле этого слова, оказывается, что этого-то в школе и не преподавали! Потому что рисовать план дома на бумаге – это одно, а объяснять экскаваторщику, где и сколько копать, стоя на поросшем травой пустыре – совсем другое.
Содержание
1. Построение прямого угла на местности.
2. Определение высоты и глубины на местности, высотные отметки.
Но не святые горшки лепят, после изучения информации далее, вы сумеете и выполнить разбивку котлована будущего здания, и осуществить привязку к местности сооружения, существующего только на бумаге, определить высоты, построить горизонтальную линию, при этом используя самые простые инструменты.
Построение прямого угла на местности
Определяем линию, от которой будем строить прямой угол. К примеру, это стена будущего здания. Забиваем два колышка и натягиваем между ними шнур. Расстояние между колышками берем произвольное, но несколько больше четырех метров.
Колышек А будет вершиной нашего угла, а натянутый шнур – одной из сторон. Отмеряем от колышка А вдоль шнура четыре метра и забиваем колышек С.
Теперь нам понадобятся помощники. Один из них держит начало, или ноль, рулетки на колышке А, второй – на

И отрезок между нулем и тройкой (на рисунке синий цвет), и отрезок ленты между тройкой и восьмеркой метровыми отметками (красный) должны быть одинаково хорошо натянуты. Вбиваем колышек В точно в том месте, куда пришлась отметка три метра. Как это все выглядит, видно на рисунке.
Угол САВ будет равен 90 градусам, что и требовалось. Теперь, чтобы построить на местности любой прямоугольник, достаточно отложить длину и ширину на сторонах нашего угла, построить еще один прямой угол.
После построения прямоугольника, для проверки, измерьте его диагонали. Они не должны разниться больше чем на два – три сантиметра при размерах прямоугольника порядка пятнадцати метров.
Определение высоты и глубины на местности, высотные отметки
Теперь узнаем, как определить на местности высоту или глубину. Чтобы дать на местности высотную отметку, в строительстве используют прибор, называемый нивелиром. Но нивелир стоит недешево, да и научиться им пользоваться – дело не пяти минут. Но существует приспособление, точностью не уступающее самым дорогим приборам, а стоимостью равное нескольким батонам хлеба. Называется это чудо техники –
К примеру, вам необходимо выполнить бетонный фундамент здания, и, естественно, он должен быть по возможности горизонтальным.
В первую очередь нам нужно определить базовую отметку высоты. Если она не задана в проекте, то назначаем ее произвольно, согласуясь с рельефом, и вбиваем на ней гвоздь. Трубку гидроуровня элементарно затыкаете пальцем, чтобы не вылилась вода; ваш помощник остается возле первого – базового – гвоздя, а вы идете к следующему углу.
Помощник удерживает свой конец уровня вертикально, так чтобы поверхность столбика воды совпала с гвоздем. Вы свой подводите к месту, на котором необходимо указать отметку. Двигая трубку вверх-вниз, помощник добивается совпадения поверхности воды с гвоздем. Ждете, пока вода успокоится, и делаете отметку на опалубке по линии обреза столбика воды. На рисунке это показано достаточно наглядно. В полученную отметку вбиваете второй гвоздь. Так повторяете нужное количество раз. Натянув на вбитые гвозди прочную нить или леску, вы получите строго горизонтальные линии.
Вы свой подводите к месту, на котором необходимо указать отметку. Двигая трубку вверх-вниз, помощник добивается совпадения поверхности воды с гвоздем. Ждете, пока вода успокоится, и делаете отметку на опалубке по линии обреза столбика воды. На рисунке это показано достаточно наглядно. В полученную отметку вбиваете второй гвоздь. Так повторяете нужное количество раз. Натянув на вбитые гвозди прочную нить или леску, вы получите строго горизонтальные линии.
Освоив вышеуказанные приемы, комбинируя их, вы сможете осуществлять разбивку на местности весьма сложных конструкций, а также проверку качества их выполнения. Читайте так же о том, как работать тахеометром и нивелиром.
Оставляйте ваши советы и комментарии ниже. Подписывайтесь на новостную рассылку. Успехов вам, и добра вашей семье!Глава I Основные понятия
ГЛАВА I.
ОСНОВНЫЕ ПОНЯТИЯ.
§ 4. Прямой угол. Смежные и вертикальные углы.
Прямой угол.
49. Из листа бумаги, согнув его соответствующим образом, сделать модель прямого угла.
50. Найти острые, прямые и тупые, углы на окружающих предметах.
51. Проверить при помощи чертёжного треугольника углы ученической тетради.
52. На чертеже 18 изображено несколько углов. Указать, какие из этих углов прямые. Назвать тупые углы.
53. Начертить на глаз несколько прямых углов в различных положениях и проверить их чертежным треугольником.
54. При помощи линейки построить прямой угол с вершиной, совпадающей с вершиной данного прямого угла. Сколько таких прямых углов можно построить?
55. На сторонах прямого угла расположены две точки. Одна из них — на расстоянии 30 мм от вершины, другая — на расстоянии 40 мм. Построить эти точки и измерить расстояние между ними.
56. 1) Вычислить величину каждого из двух углов, полученных при делении угла, равного 0,6 d, его биссектрисой.
2) Решить задачу 56 (1), если данный угол равен: а) 1 2/3d; б) 15/
Смежные углы.
57. Начертить два неравных смежных угла так, чтобы их общая сторона была:
а) вертикальной; б) горизонтальной; в) наклонной.
58. Среди углов, данных на чертеже 19, указать смежные углы. Объяснить, почему углы на чертеже 19, в нельзя назвать смежными.
59. Всегда ли верно, что: а) если два угла смежные, то их сумма равна двум прямым углам; б) если сумма двух углов равна двум прямым, то углы смежные? Привести примеры.
60. 1) Построить для данного угла (острого или тупого) угол, дополняющий его до развёрнутого.
2) Сколько можно построить углов, смежных данному? Доказать, что эти углы равны.
61. Один из смежных углов тупой (острый). Каким является другой угол?
62. Один из смежных углов равен: а) 0,9 d; б) 7/8d. Найти величину другого угла.
63. Один из смежных углов больше другого на: а) 1/3d; б) d. Найти величину каждого из этих углов.
64.1) Один из смежных углов в три раза больше другого. Найти величину каждого из этих углов.
2) Один из смежных углов составляет 20% другого. Найти величину каждого из этих углов.
65. Угол ABC равен: a) 0,8d; б) 11/3d. Продолжить стороны этого угла за вершину и вычислить величину каждого из образовавшихся углов.
66. Найти величину угла, образованного биссектрисами двух смежных углов.
67. Из точки С, взятой на прямой АВ, проведены два луча СМ и CN так, что они образуют с прямой АВ равные острые углы (черт. 20), / 1 = / 2. Объяснить, почему
/ 3 = / 4.
68. 1) Из точки, взятой на прямой, по одну сторону этой прямой проведены два луча (черт. 21) так, что / 1 = 0,5 d, / 2 =7/8 d. Найти величину третьего угла.
2) На прямой дана точка, из которой по одну сторону прямой проведены два луча (черт. 22) так, что / 1 = 3/5 d, / 2 составляет половину первого угла. Найти величину третьего угла.
69. 1) Через вершину угла, равного 8/9d, вне его проведена прямая, образующая с одной из его сторон угол, равный d/3. Найти величину угла, образованного прямой с другой стороной данного угла.
2) Через вершину угла, равного 8/9 d, проведена прямая, делящая угол на два угла, один из которых равен d/3. Найти каждый из образовавшихся углов, меньших развёрнутого.
70.1) Два луча, проведённые по одну сторону прямой из взятой на ней точки, образуют между собой и с прямой равные острые углы. Найти величину каждого из этих углов.
2) Решить эту же задачу для случая: а) трёх лучей, б) четырёх лучей.
Вертикальные углы.
71. Дан угол. Построить для него смежный и вертикальный углы.
72. При помощи линейки построить угол, равный данному и имеющий с ним общую вершину.
73. Один из углов, образованных двумя пересекающимися прямыми, равен d. Чему равны остальные углы?
74. Один из углов, образовавшихся при пересечении двух прямых, равен 0,6 d. Чему равны остальные углы?
75. Сумма двух вертикальных углов, образованных двумя прямыми, равна 8/9 d. Найти величину каждого из полученных четырёх углов.
76. Найти величину каждого из четырёх углов, образованных двумя пересекающимися прямыми, если сумма трёх из них равна 2,5 d.
77. Какой угол образуют биссектрисы двух вертикальных углов?
78. Даны три прямые, пересекающиеся в одной точке (черт. 23).
Доказать, что / 1 + / 2 + / 3 = 2d. Вычислить сумму / 1 + / 3, если / 2 = d/5.
Сумма углов, имеющих общую вершину.
79. Четыре луча, проведённые из одной точки (черт. 24), образуют следующие углы:
/ 1 = 7/8 d; / 2 = 1 1/4 d; / 3 = 11/5d. Найти величину четвёртого угла.
80. Из одной точки проведены пять лучей так, что углы, образованные каждыми двумя соседними лучами, равны между собой. Найти эти углы.
81.1) Из одной точки проведены четыре луча. Могут ли все углы, образованные смежными лучами, быть одновременно: а) тупыми; б) острыми?
2) Задачу 81 (1) решить для случая трёх лучей.
82. На чертеже 25 указать, не измеряя углов, ошибки, допущенные при простановке их величин.
Перпендикуляр к прямой.
83. 1) Начертить прямую и вне её взять некоторую точку (черт. 26, а). Через эту точку при помощи чертёжного треугольника провести перпендикуляр к прямой. Измерить (по перпендикуляру) расстояние от точки до прямой.
2) Выполнить то же задание при другом положении точки и, прямой (черт. 26, б).
84. Через данную точку О провести перпендикуляры к трём данным прямым (черт. 27).
85. При помощи эккера построить на поверхности земли (или в классной комнате) прямой угол.
86. 1) При помощи эккера построить на поверхности земли (или в классной комнате) прямую, перпендикулярную данной прямой и проходящую через данную на ней точку.
2) Как при помощи эккера построить прямую, перпендикулярную данной прямой и проходящую через точку, не лежащую на данной прямой?
87. 1) Через вершину угла ABC, равного l,2d, проведена прямая MN, перпендикулярная его биссектрисе. Вычислить углы, которые образует прямая MN со сторонами угла ABC.
2) Через вершину данного угла провести прямую, образующую с его сторонами равные углы.
ОТВЕТЫ
Как начертить прямой угол. Измерительные работы на местности в курсе геометрии основной школы
31*. Провести из точки С перпендикуляр на прямую АВ (рис. 29,а, где AB || пл. V).
Решеиие. Известно, прямой угол проецируется на плоскость в виде прямого угла в том случае, если одна из его сторон параллельна плоскости проекции, а другая пересекает эту плоскость под острым углом.
В данном случае (рис. 29, а) прямая АВ параллельна пл. V. Поэтому можно из точки с» (рис. 29, б) провести прямую перпендикулярно к а»b» и найти проекции точки К, в которой СК пересекает АВ. Получаем проекции c»k» и ck искомого перпендикуляра.
32. Провести ив точки С прямую перпендикулярно к прямой АВ: 1) AB || пл. H (рис. .30, а), 2) AB || пл. W (рис. 30, б).
33*. Пересечь прямые АВ и CD (рис. 31, а) третьей прямой, перпендикулярной к ним, т. е. найти кратчайшее расстояние между скрещивающимися прямыми АВ и CD, из которых одна прямая (CD) перпендикулярна к пл. проекций Н.
Решение. Так как прямая CD перпендикулярна к пл. Н, то любой перпендикуляр к ней располагается параллельно пл. Н. Поэтому прямой угол между искомой прямой и прямой АВ изображается на пл. Н в виде прямого угла. Горизонт. проекция точки пересечения искомой прямой с прямой CD — точка m — совпадает с с (d) (рис. 31, б). Проводим через точку m горизонт. проекцию прямой перпендикулярно к ab до пересечения с ней в точке k и находим k». Фронт, проекция искомой прямой (k»m») располагается параллельно оси х.
34*. Построить ромб ABCD, зная, что отрезок BD является одной из его диагоналей (BD || пл. V), а вершина А должна быть на прямой EF (рис. 32, а).
Решение. Диагонали ромба взаимно перпендикулярны и делятся в точке пересечения пополам. Поэтому делим (рис. 32, б) проекции диагонали BD пополам. Так как BD || пл. V, то из точки k» проводим перпендикуляр к прямой b»d». Это соответствует правилам построения проекции прямого угла на плоскости, по отношению к которой диагональ BD параллельна. Точка пересечения этого перпендикуляра с проекцией e»f» представляет собой фронт, проекцию а» искомой вершины ромба А. Для построения точки с» откладываем на продолжении прямой a»k» отрезок k»с», разный отрезку а»k». По точке а» строим на ef точку а. Дальнейшее ясно из чертежа.
35. Построить равнобедренный треугольник ABC с основанием, равным ВС (ВС || пл. Н). Вершина А должна быть на прямой ЕF (рис. 33).
36. Построить прямоугольный треугольник ABC, у которого катет А В лежит на прямой MN (MN || пл. V) и равен l. Для катета ВС дана его проекция bс (рис. 34).
37*. Построить равнобедренный треугольник с основанием ВС на прямой MN (MN || пл. H) и вершиной А на прямой EF (рис. 35, а). Основание ВС должно равняться высоте треугольника АК, причем для точки К дана ее горизонт, проекция.
Решение. Для построения треугольника надо найти его высоту АК и отложить половину ее величины на прямой М N по обе стороны от точки К. На рис. 35, б по точке k строим точку k». Из точки k проводим перпендикуляр к прямой mn (прямой угол между высотой АК и основанием ВС, лежащим на MN, изображается на пл. проекций Н в виде прямого же угла, так как прямая MN параллельна пл. Н). Продолжаем зтст перпендикуляр до пересечения с ef. По точке а строим а» на е»f»; получаем фронт. проекцию высоты АК.
Теперь можно найти натуральную величину высоты АК. Для этого строим прямоугольный треугольник akK , у которого катет kK равен разности расстояний точек А и К от пл. Н. Гипотенуза аK выражает высоту АК. Откладывая на прямой mn отрезки kb н kc, равные половине высоты АК (т. е. половине отрезка аK ), получаем точки b и с, а по ним проекции b» и с». Дальнейшее ясно из чертежа.
38. Построить квадрат ABCD со стороной ВС на прямой ММ, которая || пл. V (рис. 36).
39. Построить прямоугольный треугольник ABC с катетом ВС на прямой MN (MN || пл. H). Для катета АВ дана проекция а»b». Катет ВС должен быть в 1,5 раза больше катета АВ (рис. 37).
В курсе изучения геометрии основной школы рассматриваются задачи, связанные с практическим применением изученных знаний: измерительные работы на местности, измерительные инструменты. Практические работы на местности являются одной из наиболее активных форм связи обучения с жизнью, теории с практикой. Учащиеся учатся пользоваться справочниками, применять необходимые формулы, овладевают практическими приёмами геометрических измерений и построений.
Практические работы с использованием измерительных инструментов повышают интерес учащихся к математике, а решение задач на измерение ширины реки, высоты предмета и определение расстояния до недоступной точки позволяют применить их в практической деятельности, увидеть масштаб применения математики в жизни человека.
По мере изучения материала способы решения этих задач изменяются, одну и ту же задачу можно решить многими способами. При этом используются следующие вопросы геометрии: равенство и подобие треугольников, соотношения в прямоугольном треугольнике, теорема синусов и теорема косинусов, теорема Пифагора, свойства прямоугольных треугольников и т.д.
Цели проведения уроков “Измерение на местности”:
Задачи:
- научности;
- наглядности;
- дифференцированного подхода;
Критерии оценки достижения ожидаемых результатов:
- активность учащихся;
Подготовка и проведение таких уроков позволяют в результате:
Одной из наиболее активных форм связи обучения с жизнью, теории с практикой является выполнение учащимися на уроках геометрии практических работ, связанных с измерением, построением, изображением. В курсе изучения геометрии основной школы рассматриваются задачи, связанные с практическим применением изученных знаний: измерительные работы на местности, измерительные инструменты. На уроках математики параллельно с изучением теоретического материала учащиеся должны научиться производить измерения, пользоваться справочниками и таблицами, свободно владеть чертёжными и измерительными инструментами. Работа проводится как на местности, так и решение задач в классе различными способами на нахождение высоты предмета и определение расстояния до недоступной точки. По программе в курсе геометрии рассматриваются следующие вопросы:
7 класс
- “Провешивание прямой на местности” (п.2),
- “Измерительные инструменты” (п.8),
- “Измерение углов на местности” (п.10),
- “Построение прямых углов на местности” (п.13),
- “Задачи на построение. Окружность” (п.21),
- “Практические способы построения параллельных прямых” (п.26),
- “Уголковый отражатель” (п.36),
- “Расстояние между параллельными прямыми” (п.37 – рейсмус),
- “Построение треугольника по трём элементам” (п.38)
8 класс.
- “Практические приложения подобия треугольников” (п.64 – определение высоты предмета, определение расстояния до недоступной точки)
9 класс.
Практические работы на уроках геометрии позволяют решать педагогические задачи: ставить перед учащимися познавательную математическую проблему, актуализировать их знания и готовить к усвоению нового материала, формировать практически умения и навыки в обращении с различными приборами, инструментами, вычислительной техникой, справочниками и таблицами.. Они позволяют реализовать в обучении важнейшие принципы взаимосвязи теории и практики: практика выступает в качестве исходного звена развития теории и служит важнейшим стимулом её изучения учащимися, она является средством проверки теории и областью её применения.
Система проведения уроков “Измерение на местности” ставит цели:
- практическое применение теоретических знаний учащихся;
- активизация познавательной деятельности учащихся;
Предусматривает выполнение следующих задач:
- расширение кругозора учащихся;
- повышение интереса к предмету;
- развитие смекалки, любознательности, логического и творческого мышления;
- формирование качеств мышления, характерных для математической деятельности и необходимых для продуктивной жизни в обществе.
При отборе содержания каждого урока по данной теме и форм деятельности учащихся используются принципы:
- взаимосвязи теории с практикой;
- научности;
- наглядности;
- учёта возрастных и индивидуальных особенностей учащихся;
- сочетания коллективной и индивидуальной деятельности участников;
- дифференцированного подхода;
Критерии оценки достижения ожидаемых результатов:
- активность учащихся;
- самостоятельность учащихся в выполнении заданий;
- практические применения математических знаний;
- уровень творческих способностей участников.
Подготовка и проведение таких уроков позволяют в результате:
- подключить, пробудить и развить потенциальные способности учащихся;
- выявить наиболее активных и способных участников;
- воспитывать нравственные качества личности: трудолюбие, упорство в достижении цели, ответственность и самостоятельность.
- научить применять математические знания в повседневной практической жизни;
- обращаться с различными приборами, инструментами, вычислительной техникой, справочниками и таблицами.
Измерительные инструменты, используемые при измерении на местности:
- Рулетка – лента, с нанесёнными на ней делениями, предназначена для измерения расстояния на местности.
- Экер – прибор для построения прямых углов на местности.
- Астролябия – прибор для измерения углов на местности.
- Вехи (вешки) – колья, которые вбивают в землю.
- Землемерный циркуль (полевой циркуль – сажень) – инструмент в виде буквы А высотой 1,37 м и шириной 2 м. для измерения расстояния на местности, для учащихся удобнее расстояние между ножками взять 1 метр.
Экер
Экер представляет собой два бруска, расположенных под прямым углом и укреплённых на треножнике. На концах брусков вбиты гвозди так, что прямые, проходящие через них, взаимно перпендикулярны.
Астролябия
Устройство: астролябия состоит из двух частей: диска (лимб), разделённого на градусы, и вращающейся вокруг центра линейки (алидады). При измерении угла на местности она наводится на предметы, лежащие на его сторонах. Наведение алидады называется визированием. Для визирования служат диоптры. Это металлические пластинки с прорезами. Диоптров два: один с прорезом в виде узкой щели, другой с широким прорезом, посередине которого натянут волосок. При визировании к узкому прорезу прикладывается глаз наблюдателя, поэтому диоптр с таким прорезом называется глазным. Диоптр с волоском направляется к предмету, лежащему на стороне измеряемого; он называется предметным. В середине алидады прикреплён к ней компас.
астролябия
Практические работы
1. Построение прямой на местности (провешивание прямой линии)
Отрезки на местности обозначают с помощью вех. Чтобы вешка стояла прямо, применяют отвес (какой – либо грузик, подвешенный на нитке). Ряд вбитых в землю вех и обозначает отрезок прямой линии на местности. В выбранном направлении ставят две вехи на расстоянии друг от друга, между ними другие вехи, так, чтобы глядя через одну, другие прикрывались друг другом.
Практическая работа: построение прямой на местности.
Задание: отметьте на ней отрезок в 20 м, 36 м, 42 м.
2. Измерение средней длины шага.
Считается некоторое число шагов (например, 50), измеряется данное расстояние и вычисляется средняя длина шага. Опыт удобнее провести несколько раз и сосчитать среднее арифметическое.
Практическая работа: измерение средней длины шага.
Задание: зная среднюю длину шага, отложите на местности отрезок 20 м, проверьте с помощью рулетки.
3. Построение прямых углов на местности.
Чтобы построить на местности прямой угол АОВ с заданной стороной ОА, устанавливают треножник с экером так, чтобы отвес находился точно над точкой О, а направление одного бруска совпало с направлением луча ОА. Совмещение этих направлений можно осуществить с помощью вехи, поставленной на луче. Затем провешивают прямую линию по направлению другого бруска (ОВ).
Практическая работа: построение прямого угла на местности, прямоугольника, квадрата.
Задание: измерьте периметр и площадь прямоугольника, квадрата.
4. Построение и измерение углов с помощью астролябии.
Астролябию устанавливают в вершине измерительного угла так, чтобы лимб её был расположен в горизонтальной плоскости, а отвес, подвешенный под центром лимба, проектировался бы в точку, принимаемую за вершину угла на поверхности земли. Затем визируют алидадой по направлению одной стороны измеряемого угла и отсчитывают на лимбе градусные деления против метки предметного диоптра. Повёртывают алидаду по ходу часовой стрелки в направлении второй стороны угла и делают второй отсчёт. Искомый угол равен разности показаний при втором и первом отсчётах.
Практическая работа:
- измерение заданных углов,
- построение углов заданной градусной меры,
- построение треугольника по трём элементам – по стороне и двум прилежащим к ней углам, по двум сторонам и углу между ними.
Задание: измерить градусные меры заданных углов.
5. Построение окружности на местности.
На местности устанавливается колышек, к которому привязывается верёвка. Держась за свободный конец верёвки, двигаясь вокруг колышка, можно описать окружность.
Практическая работа: построение окружности.
Задание: измерение радиуса, диаметра; вычисление площади круга, длины окружности.
6. Определение высоты предмета.
а) С помощью вращающейся планки.
Предположим, что нам нужно определить высоту какого – нибудь предмета, например высоту столба А 1 С 1 (задача № 579). Для этого поставим на некотором расстоянии от столба шест АС с вращающейся планкой и направим планку на верхнюю точку С 1 столба. Отметим на поверхности земли точку В, в которой прямая А 1 А пересекается с поверхностью земли. Прямоугольные треугольники А 1 С 1 В и АСВ подобны по первому признаку подобия треугольников (угол А 1 = углу А = 90 о, угол В – общий). Из подобия треугольников следует;
Измерив расстояния ВА 1 и ВА (расстояние от точки В до основания столба и расстояние до шеста с вращающейся планкой), зная длину АС шеста, по полученной формуле определяем высоту А 1 С 1 столба.
б) С помощью тени.
Измерение следует проводить в солнечную погоду. Измерим длину тени дерева и длину тени человека. Построим два прямоугольных треугольника, они подобны. Используя подобие треугольников составим пропорцию (отношение соответственных сторон), из которой и найдём высоту дерева (задача №580). Можно таким образом определить высоту дерева и в 6 кл, используя построение прямоугольных треугольников в выбранном масштабе.
в) С помощью зеркала.
Для определения высоты предмета можно использовать зеркало, расположенное на земле горизонтально (задача №581). Луч света, отражаясь от зеркала попадает в глаз человека. Используя подобие треугольников можно найти высоту предмета, зная рост человека (до глаз), расстояние от глаз до макушки человека и измеряя расстояние от человека до зеркала, расстояние от зеркала до предмета (учитывая, что угол падения луча равен углу отражения).
г) С помощью чертёжного прямоугольного треугольника .
На уровне глаз расположим прямоугольный треугольник, направив один катет горизонтально поверхности земли, другой катет направив на предмет, высоту которого измеряем. Отходим от предмета на такое расстояние, чтобы второй катет “прикрыл” дерево. Если треугольник ещё и равнобедренный, то высота предмета равна расстоянию от человека до основания предмета (прибавив рост человека). Если треугольник не равнобедренный, то используется снова подобие треугольников, измеряя катеты треугольника и расстояние от человека до предмета (используется и построение прямоугольных треугольников в выбранном масштабе). Если треугольник имеет угол в 30 0 , то используется свойство прямоугольного треугольника: против угла в 30 0 лежит катет вдвое меньше гипотенузы.
д) Во время игры “ Зарница” учащимся не разрешается использовать измерительные приборы, поэтому можно предложить следующий способ:
один ложится на землю и направляет глаза на макушку другого, находящегося от него на расстоянии своего роста, так чтобы прямая проходила через макушку товарища и верхушку предмета. Тогда треугольник получается равнобедренным и высота предмета равна расстоянию от лежавшего до основания предмета, которое измеряется, зная среднюю длину шага учащегося. Если же треугольник не равнобедренный, то зная среднюю длину шага измеряется расстояние от лежавшего на земле до стоявшего и до предмета, рост стоявшего заведомо известен. А далее по признаку подобия треугольников вычисляется высота предмета (или построение прямоугольных треугольников в выбранном масштабе).
7. Определение расстояния до недоступной точки.
а) Предположим, что нам нужно найти расстояние от пункта А до недоступного пункта В. Для этого на местности выбираем точку С, провешиваем отрезок АС и измеряем его. Затем с помощью астролябии измеряем углы А и С. На листке бумаги строим какой – нибудь треугольник А 1 В 1 С 1 , у которого угол А 1 = угол А, угол С! = угол С и измеряем длины сторон А 1 В 1 и А 1 С 1 этого треугольника. Так как треугольник АВС подобен треугольнику А 1 В 1 С 1 , то АВ: А 1 В 1 = АС: А 1 С 1 , откуда находим АВ по известным расстояниям АС, А 1 С 1 , А 1 В 1. . Для удобства вычислений удобно построить треугольник А 1 В 1 С 1 так, чтобы А 1 С 1: АС = 1: 1000
б) Для измерения ширины реки на берегу измеряем расстояние АС, с помощью астролябии устанавливаем угол А = 90 0 (направив на объект В на противоположном берегу), измеряем угол С. На листке бумаги строим подобный треугольник (удобнее в масштабе 1: 1000) и вычисляем АВ (ширину реки).
в) Ширину реки можно определить и так: рассматривая два подобных треугольника АВС и АВ 1 С 1 . Точка А выбрана на берегу реки, В 1 и С у кромки поверхности воды, ВВ 1 – ширина реки (зад №583, рис 204 учебника), измеряя при этом АС, АС 1 , АВ 1 .
Практическая работа: определить высоту дерева, ширину реки.
В 9 классе в пункте 100 тоже рассматриваются измерительные работы на местности, но используется тема “Решение треугольников”, при этом применяется теорема синусов и теорема косинусов. Рассматриваются задачи с конкретными данными, решая которые можно увидеть различные способы нахождения и высоты предмета и определить расстояние до недоступной точки, что можно применить в будущем практически.
1. Измерение высоты предмета .
Предположим, что требуется определить высоту АН какого – то предмета. Для этого отметим точку В на определённом расстоянии а от основания Н предмета и измерим угол АВН. По этим данным из прямоугольного треугольника АНВ находим высоту предмета: АН = НВ tgАВН.
Если основание предмета недоступно, то можно поступить так: на прямой, проходящей через основание Н предмета, отметим две точки В и С на определенном расстоянии а друг от друга и измерим углы АВН и АСВ: угол АВН = a , угол АСВ = b , угол ВАС = a – b . Эти данные позволяют определить все элементы треугольника АВС; по теореме синусов находим АВ:
АВ = sin (a – b ). Из прямоугольного треугольника АВН находим высоту АН предмета:
АН = АВ sin a .
№ 1036
Наблюдатель находится на расстоянии 50 м от башни, высоту которой хочет определить. Основание башни он видит под углом 10 0 к горизонту, а вершину – под углом 45 0 к горизонту. Какова высота башни? (рис.298 учебника)
Решение
Рассмотрим треугольник АВС – прямоугольный и равнобедренный, т.к угол СВА =45 0 , то и угол ВСА =45 0 , значит СА=50м.
Рассмотрим треугольник АВН – прямоугольный, tg (АВН) = АН/ АВ, отсюда
АН = АВ tg (АВН), т.е АН = 50tg 10 0 , отсюда АН =9м. СН= СА+АН =50+9 = 59(м)
№ 1038
На горе находится башня, высота которой равна 100м. Некоторый предмет А у подножия горы наблюдают сначала с вершины В башни под углом 60 0 к горизонту, а потом с её основания С под углом 30 0 . Найдите высоту Н горы (рисунок 299 учебника).
Решение:
угол ЕВА = 60 0
угол КСА =30 0
Найти СР.
Решение:
Угол СВК = 30 0 , т.к. угол ЕВС =90 0 и угол ЕВА =60 0 , отсюда угол СКА =60 0 , значит уголСКА = 180 0 – 60 0 = 120 0 .
В треугольнике СКА видим, что угол АСК = 30 0 , уголСКА = 120 0 , то уголСАК = 30 0 , получим, что треугольник ВСА равнобедренный с основанием АВ, т.к. уголСВК = 30 0 и уголВАС = 30 0 , значит АС = 100м (ВС = АС).
Рассмотрим треугольник АСР, прямоугольный с острым углом в 30 0 (РАС = АСК, накрест лежащие углы при пересечении параллельных прямых СК и АР секущей АС), а против угла в 30 0 лежит катет вдвое меньше гипотенузы, поэтому РС = 50м.
2. Измерение расстояния до недоступной точки (измерение ширины реки).
Случай 1. Измерение расстояния между точками Аи В, разделёнными препятствием (рекой).
Выберем на берегу реки две доступные точки А и В, расстояние между которыми может быть измерено. Из точки А видны и точка В и точка С, взятая на противоположном берегу. Измерим расстояние АВ, с помощью астролябии измеряем углы А и В, угол АСВ = 180 0 — угол А — угол В
Зная одну сторону треугольника и все углы, по теореме синусов находим искомое расстояние.
2 случай.
Измерение расстояния между точками А и В, разделёнными препятствием (озером). Точки А и В доступны.
Выбирают третью точку С, из которой видны точки А и В и могут быть непосредственны измерены расстояния до них. Получается треугольник, у которого даны угол АСВ (измеряется с помощью астролябии) и стороны АС и ВС. На основании этих данных по теореме косинусов можно определить величину стороны АВ – искомое расстояние. АВ 2 = АС 2 + ВС 2 – 2 АС * ВС cos угла С.
3 случай:
Измерение расстояния между точками А и В, разделёнными препятствием (лесом) и недоступными определяющему расстояние (точки находятся по ту сторону реки).
Выбирают две доступные точки С и К, расстояние между которыми может быть измерено и из которых видны как точка А, так т точка В.
Устанавливают астролябию в точке С и измеряют углы АСК и ВСК. Затем измеряют расстояние СК и переносят астролябию в т. К, из которой измеряют углы АКС и АКВ. На бумаге по стороне СК, взятой в определённом масштабе и двум прилежащим углам строят треугольники АСК и ВСК и вычисляют элементы этих треугольников. Проведя на чертеже линию АВ, определяют длину её непосредственно по чертежу или путём вычисления (решают треугольники АВС и АВК, в которые входит определяемая линия АВ).
Практическая работа в 9 кл на уроках геометрии:
- измерить высоту предмета;
- расстояние до недоступной точки (ширину реки).
Работу провести и через подобие треугольников и через тему “Решение треугольников”.
Задание: сравнить полученные результаты.
В результате проведения цикла уроков по вопросам рассмотрения практического применения геометрии, учащиеся убеждаются в непосредственном применении математики в практической жизни человека (измерение расстояния до недоступной точки, определение высоты предмета различными способами к концу обучения в основной школе, использование измерительных приборов). Решение задач этого типа вызывает заинтересованность учащихся, которые с нетерпением ждут уроков, связанных с непосредственным измерением на местности. А задачи, предложенные в учебнике, знакомят с различными способами решения этих задач.
Литература:
- Атанасян Л.С. Геометрия 7 -9. – Москва: Просвещение, 2000 г.
Тема урока: «Углы. Виды углов. Построение прямого угла»
Демонстрационный материал: презентация
Цели урока:
1.Проверить уже полученные знания и умения учащихся о
геометрических фигурах и их свойствах.
2.Научить правильно называть элементы угла – вершины и его стороны, правильно называть и обозначать угол, с помощью трех и одной букв; научить распознавать острые, тупые и прямые углы, и применять определения углов для их распознания (т.е. применять определение острого угла, тупого угла, прямого угла).
3. Совершенствовать умение работать с чертежными инструментами – линейкой, угольником и циркулем;
совершенствовать устные и письменные вычислительные навыки;
совершенствовать навык самостоятельности в работе.
4. Оценить образно-логическое мышление учащихся с помощью теста: “Выбери правильное определение.”
5. Развивать логическое мышление; развивать внимание учащихся, память, математическую речь.
5. Воспитывать аккуратность при построении чертежей и оформлении упражнений; воспитывать интерес к математике через занимательные задания, конструирование и практические работы;
воспитывать бережное отношение к экологии земли;
формировать бережное отношение к природе.
Примечание: классификация углов проводится через сравнение наиболее часто встречающимися в окружающем мире прямым углом: угол, меньший прямого, является острым, большим прямого – тупым.
Оборудование урока:
1.Мультимедийное оборудование.
2. Чертежные инструменты:
а) угольник
б) циркуль
в) линейка
г) карандаш
3. Карточки с тестами № 1 «Линии» (выбери правильное определение)
4. Карточки № 2 с индивидуальными заданиями (дифференцируемый материал по 4-ем вариантам).
5. Карточки № 3 (со ступеньками) «Диагностика настроения»
Х О Д У Р О К А
1.Входжение в новый день:
Прекрасно всё на небе,
Прекрасно на земле.
Прекрасно в нашем классе,
Прекрасно всё во мне.
2.Организация начала урока:
“Мы – хозяева нашей природы, и она для нас кладовая солнца с великими сокровищами жизни. Для рыбы нужна чистая вода – будем охранять наши водоемы. В лесах, степях и горах разные ценные животные – будем охранять наши леса, поля, горы. А человеку нужна Родина. И охранять природу – значит охранять Родину”. (М.Пришвин)
3.Матаматическая разминка:
(запись числа и вида работы, минутка чистописания 2 и 0)
Решить задачи устно.
На семью из трёх человек в сутки требуется 60 кг чистого воздуха. Сколько кг воздуха потребуется на наш класс, если в классе 23 ученика?
(60:3=20кг на каждого, 20х23=460 кг в сутки)
В квартире подтекает водопроводный кран. За 6 минут набегает полный стакан воды. Сколько воды вытечет из такого крана за 1 час, если в 1 литре 5 стаканов воды?
(60:6=10 стаканов за 1 час, 10:5=2 литра за 1 час)
Из 250000 видов растений Земли 1/10 часть находится на грани исчезновения. Сколько видов растений на Земле на грани исчезновения?
(250 000:10=25 000 видов на грани)
Решить в тетради столбиком:
(Как называется неизвестный компонент, как его найти?)
3234 — *** = 2484 (3234 – 2484=750)
(Столько жуков-короедов съедает за 1 день дятел.)
*** + 263 = 423 (423-263=160)
(Столько в среднем съедает за день тли божья коровка.)
**** — 438 = 562 (438+562=1000)
(Столько полевых мышей уничтожает сова за 1 год.)
Молодцы!
И зачем же мы выполняли все эти задания?
Мы хотим, чтоб птицы пели!
Чтобы были голубыми небеса!
Чтобы речка серебрилась,
Чтобы белочка резвилась!
Мы хотим, чтоб солнце грело,
И берёзка зеленела.
Чтобы этого добиться,
Надо хорошо учиться!
3.Проверка домашнего задания
Но не достаточно хорошо учиться только в школе, нужно ещё и дома повторять и закреплять знания полученные на уроках.
Проверим домашнее задание.
(работа по карточкам № 1)
Тест «Линии»
1.При названии какой линии имеет значение порядок букв?
Варианты ответов:
Варианты ответов:
одной большой буквой,
двумя маленькими латинскими буквами,
нет правильного ответа.
3.Луч- это…
Варианты ответов:
4. Отрезок- это…
Варианты ответов:
5. Длину можно измерить у…
Варианты ответов:
Самопроверка по ключу. Молодцы!
Ф И З М И Н У Т К А Д В И Г А Т Е Л Ь Н А Я
Мы проверили осанку
И свели лопатки,
Мы походим на носках,
А потом на пятках.
Пойдем мягко, как лисята,
И как мишка косолапый,
И как заинька-трусишка,
И как серый волк-волчишка.
Вот свернулся еж в клубок,
Потому что он продрог.
Лучик ежика коснулся,
Ежик сладко потянулся.
4. Актуализация знаний.
(определение раздела математики)
Как вы думаете, почему я просила вас дома повторить тему «Линии»?
(читают хором по слайду)
Удивительная страна — Геометрия!
Фигуры и линии в ней живут,
Меряют, чертят и узнают:
Периметр, площадь, длину, ширину,
Диаметр, радиус и высоту!
Скорей собирай своих знаний багаж!
Готовь поскорее свой карандаш!
Но не только карандаши должны лежать на ваших партах.
Что ещё вы приготовили для урока?
(проверка готовности к уроку)
(актуализация знаний)
(работа по слайдам)
Что вы видите на экране? (угол)
Как образовался угол? (из двух лучей, вышедших из 1 точки)
Как называется эта точка теперь? (вершина угла)
Как теперь называются лучи? (стороны угла)
Точка: «От вершины по лучу
Словно с горки покачу.
Только луч теперь – она.
Он зовётся «сторона»».
Как дать углу имя? (обозначить вершину угла латинской буквой
или как в треугольнике – тремя буквами, но
средняя буква должна обозначать вершину
Какие бывают углы? (острые, прямые, и тупые)
Как различать углы? (при помощи прямоугольного треугольника)
(практическая работа на карточках № 2)
Алгоритм
1. начертить угол
2. дать название
3. написать основное свойство
(взаимная проверка по слайдам и оценивание)
Ф И З М И Н У Т К А Д Л Я П А Л Ь Ч И К О В
Это пальчик – дедушка (сгибают мизинцы),
Этот пальчик-бабушка (сгибают безымянные пальцы),
Этот пальчик-папа (сгибают средние пальцы),
Этот пальчик – мама (сгибают указательные пальцы),
Этот пальчик – я.(сгибают большие пальцы)
Вот и вся моя семья (хлопают в ладоши).
5. Работа над новым материалом.
Какой угол было проще всего строить по треугольнику?
(прямой угол)
ПОСТАНОВКА ПРОБЛЕМНОЙ СИТУАЦИИ №1
А если я усложню вам задачу и попрошу вас построить
прямой угол без треугольника?
Что вы будете делать?
(по клеточкам: 1 луч горизонтально, 2 луч вертикально)
(если лист нелинованный, то сложить его 2 раза, получится даже 4 прямых угла)
(обвести любой предмет, имеющий прямой угол, например…)
(по угольнику)
ПОСТАНОВКА ПРОБЛЕМНОЙ СИТУАЦИИ №2
Я хочу предложить вам построить прямой угол при других инструментов.
Отгадайте каких.
Кто я, если прямота главная моя черта? (линейка)
Мой циркач, циркач лихой, чертит круг одной ногой,
А другой проткнул бумагу, уцепился и ни шагу. (циркуль )
Чтобы безопасно пользоваться такими инструментами, нужно помнить
правила безопасности:
Нельзя подносить циркуль к лицу, на конце есть игла, можно уколоться.
Нельзя передавать циркуль иглой вперёд, можно уколоть своего товарища.
На рабочем столе должен быть порядок.
− Что же надо нам сделать? (построить прямой угол)
Поставьте перед собой цель.
(Я должен научиться строить прямой угол пользуясь линейкой и циркулем)
− Сформулируйте тему урока.
(Построение прямого угла при помощи циркуля и линейки)
«Открытие» новых знаний
Решение проблемы с помощью практической работы.
(дети работают на доске, делают попытки построения)
(когда решение проблемы найдено, составляется алгоритм)
Алгоритм построения прямого угла
1.начерти прямую линию
2.на ней поставь две точки А и В
3. проведи две окружности, чтобы точки А и В стали центрами окружностей
4.точки пересечения окружностей обозначь буквами С и D
5.через полученные точки С и D проведи прямую линию
6.точку пересечения двух прямых линий обозначь буквой О
Назовите углы которые получились.
(L COB, L BOD, L AOC, L AOD)
Назовите эти углы по-другому. (2 и 3 способ)
Ф И З М И Н У Т К А Д Л Я Г Л А З
6. Закрепления полученных знаний.
Выполните чертёж в тетради, пользуясь этим алгоритмом.
(практическая самостоятельная работа в тетрадях)
Поднимите руки у кого получилось. Молодцы!
7. Подведение итогов урока.
Что нового вы сегодня узнали?
(узнали, что можно построить прямой угол разными способами)
Чему вы научились на уроке?
(строить прямой угол с помощью линейки и циркуля)
Сколько способов построения прямого угла вы теперь знаете?
А ещё мы обозначали точки в чертежах латинскими буквами.
А на латинском языке слово “Логос” – наука, а “Эко” — “дом». Получается, это наука о доме. Но не о доме в обычном смысле, нет, это наука о нашем общем доме – природе.
В родном доме я тоже желаю вам чувствовать себя отлично, но не забывать выполнять домашнюю работу.
8. Задание на дом:
стр. 34, № 158. (чтение условия задачи)
Выберите задание по своему усмотрению:
1. выполнить решение задачи
2. составить краткую запись и решить задачу
3. составить краткую запись, решить задачу и сделать чертёж
9.Диагностика настроения на конец урока.
Встаньте, пожалуйста, те,
кто устал от сегодняшнего урока;
кому было трудно;
а кто был уверен в себе;
у кого осталось отличное настроение.
Возьмите последнюю карточку № 3.
И поставьте себя на ту ступеньку, где вы себя сейчас чувствуете.
Ф.И. ____________________________ ТЕСТ «ЛИНИИ» одной большой буквой двумя маленькими латинскими буквами двумя большими латинскими буквами или одной маленькой нет правильного ответа 3.Луч- это… часть прямой, не имеющая начала и конца часть прямой часть прямой, имеющая начало, но не имеющая конец часть прямой, имеющая начало и конец 4. Отрезок- это… часть прямой, не имеющая начала и конца часть прямой часть прямой, имеющая начало, но не имеющая конец часть прямой, имеющая начало и конец 5. Длину можно измерить у… | Ф.И. _____________________________ ТЕСТ «ЛИНИИ» 1.При названии какой линии имеет значение порядок букв? одной большой буквой двумя маленькими латинскими двумя большими латинскими буквами или одной маленькой нет правильного ответа 3.Луч- это… часть прямой, не имеющая начала и конца часть прямой часть прямой, имеющая начало, но не имеющая конец часть прямой, имеющая начало и конец 4. Отрезок- это… часть прямой, не имеющая начала и конца часть прямой часть прямой, имеющая начало, но не имеющая конец часть прямой, имеющая начало и конец 5. Длину можно измерить у… |
Приложение 1 (тест для проверки домашнего задания)
«Свойства равнобедренного треугольника» — Н. Равнобедренный. Виды треугольников (по сторонам)?. 1. Виды треугольников (по углам)?. Т. Р. АВС -равнобедренный. В равнобедренном треугольнике углы при основании равны. Боковая сторона.
«Равенство прямоугольных треугольников» — Треугольник, в котором один угол прямой, называется прямоугольным. Катет. 45°. 150°. Проверь себя. 3,5. Ответ: Падающий луч и отражённый луч параллельны. Подсказка. 1. Сумма двух острых углов прямоугольного треугольника равна 90°.
«Свойства прямоугольного треугольника» — 3. 4. Доказательство. 5. Первое свойство Второе свойство Третье свойство Задачи. Некоторые свойства прямоугольных треугольников. Сумма двух острых углов прямоугольного треугольника равна 90°. Первое свойство. 2.
«Признаки треугольника» — Первый признак равенства треугольников. (По двум сторонам. 4. Сформулируйте признак равенства треугольников, который изображен на рисунке. 3. 2. Назад. 1.
«Медиана биссектриса и высота треугольника» — отрезок, соединяющий вершину треугольника с серединой противолежащей стороны Биссектриса треугольника Медиана треугольника Высота треугольника. Медиана, биссектриса и высота треугольника. отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противолежащей стороны Медиана треугольника Высота треугольника Биссектриса треугольника.
«Первый признак равенства треугольников» — Теоремой. Равными. А. Вершинами. Вставь слово. Цель урока. В. Периметром. Познакомиться с формулировкой теоремы, выражающей первый признак равенства треугольников. Первый признак равенства треугольников. План урока. Треугольником. С. В некотором царстве-государстве в стране Геометрия жил вот такой треугольник.
прямая, периметр, ломаная, круг, окружность, угол, прямоугольник. Перпендикулярность прямых а) существенные признаки понятия «прямой угол»
МБОУ « Окская СОШ»
Конспект открытого урока по математике
в 4-ом классе на тему:
« Построение прямоугольника на нелинованной бумаге».
Учитель начальных классов: Яшина Татьяна Васильевна
2013 год
Урок « Построение прямоугольника на нелинованной бумаге» 4 класс
Цели урока: Научить построению прямоугольника и квадрата на нелинованной бумаге с помощью циркуля и линейки.
Задачи:
1. Образовательные:
актуализировать прежние знания о прямоугольнике и квадрате;
формировать практические навыки построения геометрических фигур, используя знания о них;
закрепить навыки решения текстовых задач, сравнения именованных чисел;
развивать вычислительные навыки, логическое мышление.
2. Развивающие:
развивать пространственное воображение учащихся;
развивать коммуникативные навыки учащихся в ходе парной работы, способность к взаимоконтролю и самоконтролю.
3. Воспитывающие:
воспитывать аккуратность при выполнении построений;
пробуждать в ученике чувство гордости за свои личные достижения и успехи своих товарищей.
Тип урока:
комбинированный
Форма урока:
практическая работа.
Оборудование:
для учащихся: учебник, угольник, лист нелинованной белой бумаги, простой карандаш, циркуль
для учителя: учебник, ноутбук, телевизор , презентация.
Ход урока .
1.Организационный момент.
2.Мотивация к деятельности.
О, сколько нам открытий чудных
Готовит просвещенья дух.
И опыт, сын ошибок трудных,
И гений, парадоксов друг.
И случай, бог изобретатель.
Я надеюсь, что этот урок математики станет ещё одним подтверждением нашего девиза « Математика – королева наук», а великие люди прошлого и современности помогут нам в этом.
3.Устный счёт.
Тест (Слайд) Каждое задание будем оценивать.
1. Даны числа: 713754, 713654, 713554, … Выбери следующее число :
а) 713854
б) 713554
в) 713454
2. Чему равно уменьшаемое, если вычитаемое 73, а разность 600?
а) 527
б) 673
в) 763
3. Найди наименьшее из чисел:
а) 18215
б) 18152
в) 18125
г) 18521
4. Сколько всего десятков содержится в числе 387 560 ?
а) 6
б) 38
в) 38 756
5.Сколько цифр будет в частном 64 080: 9
а) 1
б) 2
в) 3
г) 4
6. Закончи предложение “Чтобы найти неизвестное делимое, надо значение частного…”
а) умножить на делитель;
б) разделить на делитель;
в) разделить на делимое.
4. Актуализация опорных знаний.
1. Отгадайте загадку:
Эта важная наука
Изучает всё вокруг:
Точки, линии, квадраты,
Треугольники и круг…
Для неё линейка, циркуль-
Это лучшие друзья.
Но и вам науку эту
Забывать никак нельзя!
Правильно, эта наука называется ГЕОМЕТРИЕЙ.
Что означает это слово?
В переводе с греческого это слово означает «землемерие» («гео» — земля, «метрио» — мерить). Такое название объясняется тем, что зарождение геометрии было связано с различными измерительными работами, которое приходилось выполнять при разметке земельных участков, проведении дорог, строительстве зданий и других сооружений. В результате этой деятельности появились и постепенно накапливались различные правила, связанные с геометрическими измерениями. Таким образом, геометрия возникла на основе практической деятельности людей и в начале своего развития служила преимущественно практическим целям.
В дальнейшем геометрия сформировалась как самостоятельная наука, в который изучаются геометрические фигуры и их свойства.
Окружающий нас мир – это мир геометрии. А.Д. Александров (Слайд)
2.Ребята, посмотрите внимательно на чертёж.
Назовите сколько треугольников?(9)
Сколько на чертеже четырёхугольников? (2).
Чем они отличаются друг от друга?
(Один является прямоугольником, а другой нет).
— Что вы знаете о прямоугольнике?
В прямоугольнике все углы прямые.
Противоположные стороны прямоугольника равны.
Диагонали в точке пересечения делятся пополам
Диагональ прямоугольника делит его на два равных треугольника.
3.Молодцы! Вы много рассказали о прямоугольнике.
Сейчас решите задачу: (Слайд)
В прямоугольнике проведена диагональ. Площадь одного из полученных треугольников равна 25 см 2 . Чему равна площадь прямоугольника?
Решите задачу.
Как вы нашли площадь прямоугольника?
(Мы знаем, что диагональ прямоугольника делит его на два одинаковых треугольника. Площадь одного треугольника равна 25 кв. см, значит площадь всего прямоугольника будет равна 25*2=50 см 2 ).
Верно, молодцы! А как начертить прямоугольник, если мы знаем только его площадь?
Что для этого надо знать? (Его длину и ширину).
Как узнать размеры прямоугольника?
(Методом подбора. Зная, что площадь находится путём умножения длины на ширину, 50 кв. см можно получить умножая 5 см на 10 см или 25см умножить на 2 см.).
Правильно. Выберите, какой прямоугольник удобнее начертить в тетради.(Удобнее начертить прямоугольник со сторонами 5 см и 10см.).
Верно. Начертите такой прямоугольник.
5.Целеполагание.
–Ребята, скажите, легко ли вам было начертить прямоугольник в тетради? (Да, легко).
Почему? (есть клеточки)
На прошлом уроке мы учились чертить прямоугольник на нелинованной бумаге с помощью угольника, и я просила вас дома начертить узор . Давайте проверим, что у вас получилось, а один человек у доски начертит прямоугольник с помощью угольника.
(Выставка работ, проверка ученика у доски – алгоритм построения)
А как вы думаете, легко ли начертить прямоугольник на нелинованной бумаге, например на альбомном листе, если у вас нет угольника? (трудно)
Значит, существует способ построения с помощью других инструментов. Сегодня на уроке нам потребуются циркуль и линейка.
Как вы думаете, какая же тема урока ? ( Построение прямоугольника на нелинованной бумаге с помощью циркуля и линейки) (Слайд)
Какая цель урока может быть поставлена в связи с темой? (Научиться строить прямоугольник на нелинованной бумаге с помощью циркуля и линейки) (Слайд)
– Где в нашей жизни могут пригодиться умения производить построения прямоугольника или квадрата именно на нелинованной бумаге?
Задачи:
1) Формировать практические навыки построения геометрических фигур, используя знания о них.
2)Развивать пространственное воображение.
3)Воспитывать аккуратность при выполнении построений.
Тема определена, цели поставлены – в путь за новыми знаниями!
6.Открытие новых знаний
Для работы нам понадобятся циркуль и линейка.
Чтобы безопасно пользоваться такими инструментами, нужно помнить
правила безопасности:
Нельзя подносить циркуль к лицу, на конце есть игла, можно уколоться.
Нельзя передавать циркуль иглой вперёд, можно уколоть своего товарища.
На рабочем столе должен быть порядок.
Может кто-то догадался, что нужно делать?
Если нет, посмотрите на доску.
B СK M
A D
Рис. 1 Рис. 2
Что делаем сначала? (Надо начертить окружность).
Что такое «диаметр»? (Это отрезок, соединяющий две точки на окружности и проходящий через её центр).
Составим алгоритм построения прямоугольника. (Слайд)
Начертите окружность.
Проведите в ней два диаметра.
Соедините концы диаметров отрезками. Получился прямоугольник.
7.Практическая работа
Возьмите альбомный лист.
Чертим окружность, радиус которой равен 5 см.
Проводим два диаметра.
Соединяем концы диаметров.
Обозначим вершины прямоугольника
Как проверить, что получился прямоугольник? (Можно измерить стороны фигуры, противоположные стороны должны быть одинаковые, можно измерить углы с помощью прямого угла, углы должны быть прямыми).
Проверьте, получился ли у вас прямоугольник.
Интересно вам было заниматься построением?
« Вдохновение нужно в геометрии не меньше чем в поэзии» А.С.Пушкин
(Слайд)
Вспомните свойства диагоналей квадрата
Диагонали квадрата равны,
при пересечении образуют прямые углы,
точка пересечения диагоналей делит их на равные отрезки.
С чего начнём построение? (Начертим окружность).
Мы нашли только две вершины квадрата, как найти ещё две? (Проведём перпендикулярную прямую к диаметру, получился ещё один диаметр . Эти прямые пересекаются под прямым углом как у квадрата. Таким образом мы нашли ещё две вершины квадрата).
Составим алгоритм построения квадрата. (Слайд)
Начертите окружность.
Проведите один диаметр.
Проведите перпендикулярную прямую к этому диаметру.
Точки пересечения с окружностью соедините отрезками. Получился квадрат.
8. Практическая работа по алгоритму.
9.Физкультминутка.
10.Включение в систему знаний .
Выбери свой уровень. (Слайд)
1.Найдите площадь и периметр прямоугольника и квадрата.
Р пр. = (6+8)*2=24(см)
S пр =6*8=48(см 2 )
Р кв =7*4=28(см)
S кв =7*7=49(см 2 )
2.У семьи Ивановых дачный участок размером 20 метров на 40 метров, а у семьи Сидоровых 30 метров на 30 метров. Чья ограда длиннее?
Р= (20+40)*2=120(м.)
Р=30*4=120(м)
Ответ: их ограды имеют одинаковую длину, значит равны.
3.Рассмотри план школьного сада, на котором 1 см изображает 10 м. Найди площадь этого сада в арах (стр.7) (Выбор лучшего варианта).
перемещение треугольника;
измерение сторон полученного прямоугольника;
нахождение площади в м 2 ;
выразить в арах.
S =60*30=1800(м 2 .)=18 а.
Легко ли вам давались все построения и вычисления?
-«Нет царского пути в геометрии» Евклид. (Слайд)
Молодцы! Вы хорошо справились с этим заданием. Вы доказали, что можете вправе называть себя друзьями ГЕОМЕТРИИ.
11. Закрепление пройденного материала.
1) Геометрия показалась мне очень интересной и какой- то волшебной наукой. И.К.Андронов (Слайд)
а) Найди равные величины.
б)Какая величина лишняя?
в) Продолжи закономерность:
Молодцы, теперь вы легко справитесь с № 33 стр.7
Проверим решение. (Слайд)
(6 км 5 м = 6 км 50 дм
2 сут.20 ч = 68 ч
3 т 1 ц > 3 т 10 кг
90 см 2
2) Решение задачи.
Решение трудной математической задачи можно сравнить с взятием крепости. Н.Я.Виленкин (Слайд)
Прочитайте задачу № 31. Составим краткую запись
Сколько мальчиков занималось в кружке?
Сколько девочек?
Каков рост всех мальчиков?
Каков рост всех девочек?
Что спрашивается в задаче? (Заполняется таблица в процессе работы).
Составьте план решения задачи:
найди средний рост мальчиков;
найди средний рост девочек;
сравни.
Решите задачу самостоятельно.
11м04см=1104см
12м60см=1260см
1)1104:8=138(см)-средний рост мальчиков
2)1260:9=140(см)-средний рост девочек
3)140-138=2(см)-больше
Ответ: на 2 см. в среднем рост мальчиков больше, чем рост девочек.
Проверим решение. Молодцы, мы взяли ещё одну математическую крепость! Оцените свою работу.
3)Работа над вычислительными навыками.
Решите 1 пример №34 на странице 7.
Вспомним порядок действий. Какое действие выполняем первым?
После выполнения — взаимопроверка.
(100 000 — 62 600) : 4 + 3 * 108 = 9 674
37 400
9 350
324
9674
— Оцените работу.
12) Подведение итогов урока и рефлексия.
1)-Какая была тема нашего урока?
Какие цели и задачи ставили перед собой?
Достигли мы их?
– С помощью каких инструментов можно построить прямоугольник на нелинованной бумаге? (С помощью циркуля и линейки, с помощью угольника)
— Повторим алгоритм построения прямоугольника и квадрата.
-Что осталось непонятным?
2 ) Вернёмся к прямоугольнику, который построили в начале урока. Закрасьте на нём ту часть заданий, с которыми вы справились и оцените свою работу на уроке.
МОЛОДЦЫ!!!
13) Домашнее задание.
По желанию: (Слайд)
Построить на нелинованной бумаге прямоугольник и квадрат, найти и сравнить их площади.
Составить геометрический узор, используя новые знания.
Литература.
М.И.Моро и др. учебник «Математика, 4 класс», М. «Просвещение» 2011г.
Л.И.Семакина «В помощь учителю», М., «Вако», 2011г.
Сначала вспомним, какая фигура называется прямоугольником (Рис. 1).
Рис. 1. Определение прямоугольника
Посмотрите на изображенные фигуры (Рис. 2).
Рис. 2. Фигуры
Нам нужно определить, есть ли среди них прямоугольник.
Для этого нам понадобится угольник. Найдем прямой угол у угольника и приложим его к каждому из углов наших фигур. Приложив угольник ко всем углам первой фигуры, мы видим, что он совпал со всеми углами. Это значит, что фигура под номером 1 — это прямоугольник.
Прикладываем прямой угол угольника к фигуре № 2 и видим, что угол не совпадает с прямым углом. Это значит, что фигура № 2 не прямоугольник.
Прикладываем прямой угол угольника к фигуре № 3. Первый угол прямой. Второй угол фигуры прямой. Третий угол фигуры тоже прямой. И четвертый угол тоже прямой. Третья фигура является прямоугольником.
Фигура № 4. Прикладываем прямой угол угольника, и он совпадает с углом фигуры. Прикладываем его ко второму углу фигуры, и он тоже совпадает. Прикладываем прямой угол угольника к третьему углу. Третий угол тоже совпадает. Четвертый угол тоже совпадает. Это значит, что фигура № 4 является прямоугольником.
Фигура № 5. Прикладываем прямой угол угольника к первому углу. Этот угол не совпадает с прямым углом угольника. Это значит, что фигура № 5 не является прямоугольником.
У нас получается, что прямоугольники — фигуры под номерами 1, 3, 4 (Рис. 4).
Рис. 3. Прямоугольники
Мы установили, что прямые углы есть у фигур 1, 3 и 4.
Угольник — это чертежный инструмент для построения углов. Угольники изготовляют из металла, пластмассы или дерева (Рис. 3).
Рис. 4. Угольник
У фигур 1 и 3 равны стороны, которые лежат напротив друг друга. А у фигуры № 4 равны все стороны. Такие фигуры имеют специальное название.
Четырехугольник, у которого стороны попарно равны, называется прямоугольник.
Прямоугольник, у которого все стороны равны, называется квадратом.
Давайте построим прямоугольник с помощью угольника и линейки.
Для этого сначала поставим на плоскости точку. Затем найдем угол на угольнике и приложим его так, чтобы точка была вершиной угла (Рис. 5).
Рис. 5. Точка — вершина угла
Теперь обводим стороны угла (Рис. 6).
Рис. 6. Стороны угла
То же самое мы делаем со вторым углом прямоугольника (Рис. 7).
Рис. 7. Стороны двух углов
Теперь мы возьмем линейку и с ее помощью отмерим отрезки данной длины. С помощью той же линейки мы начертим четвертую сторону (Рис. 8).
Рис. 8. Чертеж сторон фигуры
У нас получилась геометрическая фигура. Давайте ее назовем. Назовем каждую вершину нашего прямоугольника (Рис. 9).
Рис. 9. Обозначение вершин прямоугольника
Мы построили с помощью линейки и угольника прямоугольник АВСD.
На уроке мы узнали, как отличить прямоугольник от других четырехугольников. Так же мы узнали, как построить прямоугольник на листе бумаге, используя угольник и линейку.
Список литературы
- Александрова Э.И. Математика. 2 класс. — М.: Дрофа — 2004.
- Башмаков М.И., Нефёдова М.Г. Математика. 2 класс. — М.: Астрель — 2006.
- Дорофеев Г.В., Миракова Т.И. Математика. 2 класс. — М.: Просвещение — 2012.
- Proshkolu.ru ().
- Социальная сеть работников образования Nsportal.ru ().
- Illagodigardarivista.com ().
Домашнее задание
- Выберите из предложенных фигур прямоугольники (Рис. 10):
Рис. 10. Рисунок к заданию
- Докажите, что изображенная на рисунке 11 фигура — прямоугольник.
Рис. 11. Рисунок к заданию
- Самостоятельно постройте прямоугольник со сторонами 5 см и 8 см при помощи угольника и линейки.
Класс: 4
Презентация к уроку
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цель урока: Научить построению прямоугольника на нелинованной бумаге с помощью угольника.
1. Образовательные:
- актуализировать прежние знания о прямоугольнике и квадрате;
- формировать практические навыки построения геометрических фигур, используя знания о них;
- закрепить навыки решения текстовых задач на пропорциональное деление, сравнения именованных чисел.
2. Развивающие:
- развивать пространственное воображение учащихся;
- развивать коммуникативные навыки учащихся в ходе парной работы, способность к взаимоконтролю и самоконтролю.
3. Воспитывающие:
- воспитывать аккуратность при выполнении построений;
- пробуждать в ученике чувство гордости за свои личные достижения и успехи своих товарищей.
Тип урока: изучение нового материала.
Форма урока: практическая работа.
Оборудование:
для учащихся: учебник, угольник, лист нелинованной белой бумаги, простой карандаш;
для учителя: учебник, компьютер, мультимедийный проектор, экран.
Ход урока
1. Организационный момент.
2. Устный счет.
– Найдите ошибки в вычислениях на доске.
Правильные ответы: 100 024; 12 548; 6 504.
3. Проверка домашнего задания.Проверка квадратов на нелинованной бумаге. (Показать на доске способ построения квадрата с помощью циркуля и линейки.)
– Какие знания о квадрате помогли справиться с построением? (Диагонали квадрата равны, пересекаются, образуя четыре прямых угла.)
4. Актуализация знаний учащихся о прямоугольнике.– На прошлом уроке мы с вами научились строить прямоугольник с помощью циркуля и линейки. Вспомните, пожалуйста, что это за геометрическая фигура – прямоугольник. (Прямоугольник – это четырехугольник, у которого все углы прямые.)
– Что еще вы знаете о прямоугольнике? (Противоположные стороны равны. Диагонали равны.)
– Эти знания пригодятся нам сегодня.
5. Демонстрация презентации. Объяснение нового материала.СЛАЙД 1. Объявление темы урока: “Построение прямоугольника на нелинованной бумаге”.
– Какие инструменты понадобятся для практической работы? (Угольник, карандаш)
СЛАЙД 2. Цель: Научиться построению прямоугольника на нелинованной бумаге с помощью угольника.
СЛАЙД 3. Задачи: 1. Формировать практические навыки построения геометрических фигур, используя знания о них.
2. Развивать пространственное воображение.
3. Воспитывать аккуратность при выполнении построений.
СЛАЙД 4. Алгоритм построения прямоугольника с помощью угольника.
СЛАЙД 5. Начертили произвольный луч АД. Одну из сторон угольника приложили к лучу так, чтобы вершина прямого угла совпала с началом луча точкой А. Провели карандашом вдоль второй стороны угольника луч АВ. Получили один прямой угол ВАД.
СЛАЙД 6. Одну из сторон угольника приложили к лучу АВ так, чтобы вершина прямого угла совпала с точкой В. Провели карандашом вдоль второй стороны угольника луч ВС. Получили второй прямой угол АВС.
СЛАЙД 7. Одну из сторон угольника приложили к лучу АД так, чтобы вершина прямого угла совпала с точкой Д. Провели карандашом вдоль второй стороны угольника луч ДС. Получили третий прямой угол АДС.
СЛАЙД 8. Перед учащимися ставится проблемный вопрос – получился ли прямоугольник.
Ученики высказывают свои предположения и предлагают способы решения этой проблемы.
СЛАЙД 9. Проверка предположений учащихся.
Нужно выяснить, окажется ли угол ВСД прямым. Если да, то прямоугольник получился (так как по определению прямоугольник – это четырехугольник, у которого все углы прямые). Если нет, то фигура АВСД – не прямоугольник.
Проверка проводится с помощью угольника. Одну из его сторон нужно приложить к лучу ВС так, чтобы вершина прямого угла совпала с точкой С. Далее смотрим, совпал ли луч СД со второй стороной угольника. В нашем случае это произошло, то есть можно сделать вывод, что угол ВСД прямой и четырехугольник АВСД является прямоугольником.
Дальнейшая самостоятельная работа учащихся по построению прямоугольника на нелинованной бумаге с помощью угольника на материале алгоритма презентации предполагает возвращение к слайдам 4-9 (используя гиперссылку).
Учитель в это время контролирует процесс построения и оказывает индивидуальную помощь учащимся.
6. Физкультминутка для глаз (с использованием СЛАЙДОВ 10-12 презентации)7. Работа с учебником.
– Откройте учебник на стр.7. Задание №33. (Работа по вариантам. У доски 2 учащихся.)
– Какие величины нужно будет нам вспомнить? (Массу и время.)
Сравните именованные числа.
| (6 км 5 м = 6 км 50 дм | 2 сут.20 ч = 68 ч |
| 3 т 1 ц > 3 т 10 кг | 90 см 2 |
Проверяют 2 учащихся. За партами – взаимопроверка.
– Задание 34. Вычислите значение первого выражения. У доски 1 учащийся.
(100 000 – 62 600) : 4 + 3 108 = 9 674
Проверяет 1 учащийся.
– Задание 30. На доске подготовлена таблица для краткой записи. Заполняем все вместе. Как назовем столбики таблицы? (На 1 стр./Кол-во стр./Всего)
На доске задачу решает 1 учащийся.
1) 90: 6 = 15 (п.) – на одной странице
2) 75: 15 = 5 (стр.)
Ответ: потребуется 5 страниц.
Проверяет 1 учащийся.
*Дополнительное задание – №31.
8. Итог урока.
– Что нового узнали?
– Чему научились?
– С помощью каких инструментов можно построить прямоугольник на нелинованной бумаге? (С помощью циркуля и линейки, с помощью угольника)
– Где в нашей жизни могут пригодиться умения производить построения прямоугольника или квадрата именно на нелинованной бумаге?
Что осталось непонятным?
Выставление отметок ученикам, активно работающим на уроке.
9. Домашнее задание.
1. Построить на нелинованной бумаге квадрат с помощью угольника и линейки.
– Что такое квадрат? (Прямоугольник, у которого все стороны равны.)
Используйте это определение в домашней работе.
– Как выполните краткую запись? (В виде таблицы.)
– Сколько дней в ателье шили куртки? (Два дня.)
– Как назовете столбики своей таблицы? (Расход на 1 куртку/кол-во курток/всего метров)
Понятия «перпендикулярные прямые», «перпендикуляр». Построение прямого угла на нелинованной бумаге (с помощью циркуля).
Построение симметричных фигур с помощью угольника, линейки и циркуля.
Построения симметричных отрезков, фигур с помощью чертежных инструментов на клетчатой и нелинованной бумаге.
Параллельность прямых.
Построение параллельных прямых при помощи угольника и линейки.
Построение прямоугольников.
Повторение основных свойств противоположных сторон прямоугольника и квадрата. Построение чертежей с помощью линейки и угольника на нелинованной бумаге.
Измерение времени.
Единицы времени. Соотношение между единицами времени. Приборы для измерения времени.
Проект «Как измеряли время в древности»
Примеры подтем: древний календарь, солнечные часы, водные часы, часы-цветы, измерительные приборы в древности.
Решение логических задач. Шифрование текста.
Логические задачи, связанные с мерами длины, площади, времени. Графические модели, схемы, карты. Моделирование из бумаги с опорой на графическую карту с инструкцией.
Проект «Шифрование местонахождения» (или «Передача тайных сообщений»)
Примеры подтем: способы шифрования текстов, приспособления для шифрования, шифрование местонахождения, знаки в шифровании, игра «Поиск сокровищ», конкурс дешифраторов, создание приспособления для шифрования.
Класс (34 ч)
Десятичная система счисления.
Значение цифры в зависимости от места в записи числа. Десятичная система счисления: почему так называется? (исследование)
Проект «Системы счисления»
Примеры подтем: десятичная система счисления, двоичная система счисления, ЭВМ и система счисления, системы счисления в разных профессиях.
Координатный угол.
Знакомство с координатным углом, осью ординат и осью абсцисс. Ввести понятие передачи изображений, умение ориентироваться по координатам точек на плоскости. Построение координатного угла. Чтение, запись названных координатных точек, обозначение точек координатного луча с помощью пары чисел.
Графики. Диаграммы. Таблицы. Построения диаграмм, графиков, таблиц с помощью MS Office.
Использование в справочной литературе и СМИ графиков, таблиц, диаграмм. Сбор информации по таблицам, графикам, диаграммам. Виды диаграмм (столбчатая, круговая). Построение диаграмм, графиков, таблиц с помощью MS Office.
Проект «Стратегии».
Примеры подтем: игры с выигрышными стратегиями, стратегии в играх, стратегии в спорте, стратегии в компьютерных играх, стратегии в жизни (стратегии поведения), боевые стратегии, стратегии в древности, стратегия в рекламе, чемпионат по компьютерной игре в жанре «Стратегии», коллекция игр с выигрышными стратегиями, альбом со схемами сражений, выигранных благодаря правильно выбранным стратегиям, спортивные командные игры, рекламные ролики и плакаты.
Многогранник.
Понятие «многогранника» как фигуры, поверхность которой состоит из многоугольников. Грани, ребра, вершины многогранника.
Прямоугольный параллелепипед.
Определение количества вершин, углов, граней многогранника. Знакомство с прямоугольным параллелепипедом. Площадь поверхности прямоугольного параллелепипеда.
Куб. Развертка куба.
Куб – прямоугольный параллелепипед, все грани которого квадраты. Строим развертку геометрического тела (параллелепипед и куб) из бумаги. Площадь поверхности прямоугольного параллелепипеда и куба.
Каркасная модель параллелепипеда.
Изготовление каркасной модели прямоугольного параллелепипеда и куба из проволоки. Решение практических задач (расчет материала).
Игральный кубик. Игры с кубиком.
Изготовление игрального кубика для настольных игр. Коллекция игр с кубиком.
Объем прямоугольного параллелепипеда.
Понятие «объём геометрического тела». Кубический сантиметр. Изготовление модели кубического сантиметра. Кубический дециметр. Кубический метр. Два способа нахождения площади прямоугольного параллелепипеда.
Сетки. Игра «Морской бой», «Крестики-нолики» (в том числе на бесконечной доске)
Новый вид наглядного соотношения между величинами. Построение координаты на луче, на плоскости. Организация игр «Морской бой», «Крестики-нолики» на бесконечной доске.
13. Деление отрезка на 2, 4, 8,… равных частей с помощью циркуля и линейки.
Практическое задание: как разделить отрезок на 2 (4, 8, …) равные части, пользуясь только циркулем и линейкой (без шкалы)?
Угол и его величина. Транспортир. Сравнение углов.
Повторение и обобщение знаний об угле как геометрической фигуре. Величина угла (градусная мера). Измерение величины угла в градусах при помощи транспортира. Разные способы сравнения углов. Построение углов заданной величины.
Виды углов.
Классификация углов в зависимости от величины угла. Острый, прямой, тупой, развернутый угол. Построение и измерение.
Классификация треугольников.
Классификация треугольников в зависимости от величины углов и длины сторон. Остроугольный, прямоугольный, тупоугольный треугольник. Разносторонний, равнобедренный, равносторонний треугольник.
Построение прямоугольника с помощью линейки и транспортира.
Практическое задание: как можно построить прямоугольник с заданными сторонами с помощью транспортира и линейки. Повторение способов нахождения площади и периметра прямоугольника.
План и масштаб.
План. Понятие «масштаб». Чтение масштаба, определение соотношения длины на плане и местности. Запись масштаба плана. Чертеж плана классной комнаты, одной из комнат своей квартиры (по выбору). Соблюдение масштаба.
3. Закончить определения: «Прямоугольником называется…», «Квадратом…», «Равнобедренным треугольником…», «Параллелограммом…».
Назвать не менее трех обучающих игр, в которых в качестве игрового материала используются геометрические фигуры. Указать главную цель каждой из этих игр.
5. Привести конкретные и убедительные примеры разных видов заданий (не менее 5) с использованием геометрического материала, но направленные на достижение целей, связанных с изучением арифметики.
6. Привести не менее трех примеров заданий, связанных с разбиением многоугольников на части.
Указать оборудование, которым полезно обеспечить урок ознакомления с видами углов.
8. Назвать виды практических работ учащихся, в ходе выполнения которых дети выявляют:
а) существенные признаки понятия «прямой угол»;
б) свойство сторон прямоугольника.
9. Соединить стрелками или записать с помощью пар вида (а ;а ), (а,б ) те понятия, при формировании которых полезно использовать прием их сравнения (сопоставления или противопоставления):
Составить алгоритм построения прямоугольника с заданными сторонами с помощью циркуля, линейки, угольника.
Сформулировать (в обобщенном виде) задачи на построение, которые должны уверенно выполнять учащиеся начальных классов.
Построить выпуклый и невыпуклый семиугольник. Существуют ли невыпуклые четырехугольники? Какие признаки моделей многоугольников должны варьироваться, а какие оставаться неизменными при формировании понятия «семиугольник»?
13. Придумать не менее 5 примеров заданий на распознавание геометрических фигур.
Предложить три геометрические задачи на доказательство, доступные для учащихся начальных классов. Когда младшим школьникам можно предлагать задачи на доказательство? Почему?
Билет № 24
Решение задач с помощью уравнений
В решении задач с помощью уравнений, необходимо соблюдать следующее: во-первых, записать условие задачи алгебраическим языком, т.е. таким образом, чтобы получить уравнение; во-вторых, упростить это уравнение до такого вида, в котором неизвестная величина будет стоять с одной стороны, а все известные величины — на противоположной стороне. Способы этого уже были рассмотрены ранее.Один из основных принципов алгебраических решений, это то, что величина должна присутствовать в уравнении. Это позволит нам записать условия так, как если бы задача уже была решена. После этого, останется лишь решить уравнение и найти общее значение всех известных величин. Так как эти величины равны неизвестной величине на другой стороне уравнения, то величина всех известных значений будет означать, что задача решена.
Задача 1. Человек на вопрос, сколько он заплатил за часы, ответил: «Если умножить цену на 4, и к результату прибавить 70, а из этой суммы вычесть 50, то остаток будет равен 220 долларов». Сколько он заплатил за часы?Чтобы решить эту задачу, мы должны сначала записать условие задачи как алгебраическое выражение, то есть как уравнение.Пусть цена часов равна xx
Эта цена была умножена на 4, то есть получаем 4x4x
К произведению прибавили 70, то есть 4x+704x+70
Из этого вычли 50, то есть 4x+70−504x+70−50Таким образом, мы записали условие задачи с помощью чисел в алгебраической форме, но у нас еще нет уравнения . Однако, согласно последнему условию задачи, все предыдущие действия в итоге привели к результату, который равен 220220.Поэтому, это уравнение выглядит так: 4x+70−50=2204x+70−50=220
После проведения операций с уравнением, получаем, что x=50x=50.
То есть, значение xx равно 50 долларов, что и есть искомой ценой часов.Чтобы проверить , что мы получили верное значение искомой величины, мы должны подставить это значение вместо хх в уравнение, которое мы записали по условию задачи. Если в результате этой подстановки значения сторон будут равны, мы провели вычисление правильно.
Уравнение задачи имело вид 4x+70−50=2204x+70−50=220
Подставляя 50 вместо xx, получаем 4⋅50+70−50=2204⋅50+70−50=220
Отсюда, 220=220220=220.
2) ВЕЛИЧИНА — это особое свойство реальных объектов или явлений, и особенность заключается в том, что это свойство можно измерить, то есть назвать количество величины, которые выражают одно и тоже свойство объектов, называются величинами одного рода илиоднородными величинами . Например, длина стола и дли на комнаты — это однородные величины. Величины — длина, площадь, масса и другие обладают рядом свойств.Методика изучения площади геометрической фигуры
В методике работы над площадью фигуры имеется много общего с работой над длиной отрезка.
Прежде всего, площадь выделяется как свойство плоских предметов среди других их свойств. Уже дошкольники сравнивают предметы по площади и правильно устанавливают отношения «больше», «меньше», «равно», если сравниваемые предметы резко отличаются друг от друга или совершенно одинаковые. При этом дети пользуются наложением предметов или сравнивают их на глаз, сопоставляя предметы по занимаемому месту на столе, на земле, на листе бумаги и т.п. однако, сравнивая предметы, у которых форма различна, а различие площадей не очень четко выражено, дети испытывают затруднения. В этом случае они заменяют сравнение по площади сравнением по длине или по ширине предметов, т.е. переходят на линейную протяженность, особенно в тех случаях, когда по одному из измерений предметы сильно отличаются друг от друга.
В процессе изучения геометрического материала в I — II классах у детей уточняются представления о площади как о свойстве плоских геометрических фигур. Более четким становится понимание того, что фигуры могут быть различными и одинаковыми по площади. Этому способствуют упражнения на вырезание фигур из бумаги, черчение и раскрашивание их в тетрадях и т.п. В процессе решения задач с геометрическим содержанием учащиеся знакомятся с некоторыми свойствами площади. Они убеждаются, что площадь не изменяется при изменении положения фигуры на плоскости (фигура не становится ни больше, ни меньше). Дети многократно наблюдают соотношение между всей фигурой и ее частями (часть меньше целого), упражняются в составлении различных по форме фигур из одних и тех же заданных частей (т.е. построение равносоставленных фигур). Учащиеся постепенно накапливают представления о делении фигур на неравные равные части, сравнивая наложением полученные части, сравнивая наложением полученные части. Все эти знания и умения дети приобретают практическим путем попутно с изучением самих фигур.
Ознакомление с площадью можно провести так:
«Посмотрите на фигуры, прикрепленные к доске, и скажите, какая из них занимает больше всего места на доске (квадрат AMKD занимает места больше всех фигур). В этом случае говорят, что площадь квадрата больше, чем площадь каждого треугольника и квадрата CDMB. Сравните площадь треугольника АВС и квадрата AMKD (площадь треугольника меньше, чем площадь квадрата).
Эти фигуры сравниваются наложением — треугольник занимает только часть квадрата, значит, действительно площадь его меньше площади квадрата. Сравните на глаз площадь треугольника ФВС и площадь треугольника DOE (у них площади одинаковые, они занимают одинаковое место на доске, хотя расположены по-разному). Проверьте наложением.
Аналогично сравниваются по площади другие фигуры, а также предметы окружающей обстановки.
Билет № 25
У р о к 1. ПРЕДМЕТ «МАТЕМАТИКА». СЧЁТ ПРЕДМЕТОВ
Цели урока: познакомить учащихся с учебным предметом «Математика»; познакомить с учебным комплектом «Математика»; выявить умение учащихся вести счёт предметов.
Ход урока
I. Организационный момент.
II. Знакомство с предметом «Математика» и учебным комплектом «Математика».
Учитель, беседуя с детьми, рассказывает им в доступной форме о том, что изучает предмет «Математика», что они узнают, какие «открытия» сделают на уроках математики.
Учитель. Как вы думаете, ребята, для чего нужен предмет «Математика»?
Далее учитель сообщает детям, что в овладении математикой им поможет учебник, состоящий из двух книг, его написали для первоклассников М. И. Моро, С. И. Волкова и С. В. Степанова, а также нужны будут две тетради, в которых ученики смогут рисовать, раскрашивать, писать, но только на специально отведённых для этого местах.
Разбивка фундамента по осям своими руками
Содержание статьи
При разработке чертежей дома все конструктивные элементы привязываются к осям. Сделать это необходимо для обеспечения точности строительства. Перед началом возведения здания требуется вынести оси на местность или разметить расположение фундаментов. Оба этих действия в общем случае выполняются по одинаковой схеме.
Работы по выносу осей
Все опорные конструкции дома при разработке проекта в обязательном порядке должны быть привязаны к осям. Для точного расположения фундаментов на местности потребуется правильно разбить участок под дом в соответствии с чертежами. Этот этап строительства выполняют в следующем порядке:
- Обозначение первой оси. В качестве ее выбирают крайнюю, расположенную параллельно забору или границе участка.
- От забора отмеряют две точки, на равном расстоянии. Линия, соединяющая эти отрезки, и является искомой.
- На этой линии потребуется сделать отметки точек пересечения с перпендикулярными осями дома. Условные оси изготавливают из шнура, прикрепляя его к обноске с помощью гвоздей. Она в самом простом случае представляет собой деревянные колья, забитые на некотором отдалении от предполагаемого котлована или траншеи.
- От каждой отмеченной точки необходимо построить прямой угол, который задаст направление осям. Чтобы сделать это пользуются методом египетского треугольника. Результатом завершения построений становится разбивка осей дома в одном направлении.
- Чтобы сделать разметку в перпендикулярном направлении, необходимо отложить от первой построенной оси линии на проектном расстоянии (также как откладывались отрезки от забора).
Объяснения без наглядного примера могут запутать, поэтому рассмотрен дом прямоугольный в плане (на рисунке ниже). Помимо наружных стен строение имеет две внутренние, расположенные под прямым углом. На чертеже обозначены шесть осей, по три в каждом направлении.
Построения начинаем с оси «А», которая располагается вдоль забора. Разметив ее расположение, отмечают на ней точки пересечения с осями «1», «2», «3». Методом египетского треугольника выстраивают прямые углы и выполняют разбивку остальных линий. Чтобы правильно вынести ось «Б» потребуется от оси «А» отложить два отрезка длиной 3 м (по линиям 1 и 3). Соединив концы отрезков, получаем искомую линию. Далее точно также выполняют разбивку «В», откладывая 4,6 м от «Б».
Совет! Если дом вписан на территории под углом, построения усложняются дополнительными геометрическими замерами, поэтому рекомендуется использовать более простую схему параллельно забору или границе участка.
Система осей удобна тем, что к ней привязаны все конструкции дома: фундаменты, стены, перекрытия, перегородки и тому подобное. Если выполнять разбивку граней опорной части (приведена далее) при работах «нулевого» цикла потребуются новые ориентиры.
Привязка осей к фундаменту (и стенам) может быть центральная, нулевая или двухсторонняя. В первом случае чтобы обозначить границы конструкции потребуется отложить половину ширины в каждую сторону. Во втором ось совпадает с одной из поверхностей фундамента. Третий вариант предполагает разные расстояния от оси до двух граней фундамента. На чертеже обозначаются обе величины.
Обозначение границ фундамента
При самострое чаще всего не разрабатывают проект, а рисуют эскиз или схему. В этом случае редко используют оси, поэтому шнуром обозначают границы фундаментов дома. Разметка подземной части выполняется по аналогии с осями:
- Определяют расположение стены дома, параллельной забору или границе участка, отмечают ее бечевкой. Устанавливают обноску, размещая ее на некотором расстоянии от стен здания, чтобы не мешала при разработке грунта. Этот элемент разметки изготавливается из вертикальных стоек и горизонтальных перемычек между ними.
Устройство обноски
- Отмечают на обноске точку первого угла дома. От этой точки натягивают шнур перпендикулярно первой стене. Построения должны быть точными, насколько позволяет выполнение работы «на глаз».
- Делают проверку прямого угла. Для этого от выбранной точки на одном шнуре откладывают расстояние равное 3 м, а на другом 4 м.
- Измеряют расстояние между концами отложенных отрезков. Важно сделать это с максимальной точностью.
- Если величина равна 5 м, шнур расположен верно, можно вместо него устанавливать деревянную обноску. Если совпадения нет, бечевку смещают до тех пор, пока гипотенуза треугольника не станет равняться 5 м.
- После достижения этого значения построение прямого угла завершено.
- На линии стены (п. 1), параллельной забору, отмечают второй угол дома и повторяют действия с пункта 2. Получают третью сторону.
- На второй стороне обноски отмечают третий угол и выполняют те же действия, что и в предыдущих случаях. Получают четвертую сторону дома.
- Далее необходимо сделать отметки на линиях 3 и 4, равные размерам здания в плане. Метки должны совпасть, но если этого не происходит, их совмещают.
- Построение разметки прямоугольного или квадратного дома завершено.
- Чтобы убедится в точности, измеряют диагонали получившейся фигуры. Они должны быть равны.
Важно! В пунктах 3, 4, 5 описан метод египетского треугольника, о котором говорилось ранее.
После завершения выноса наружных граней дома для разных типов фундамента под дом есть отличия в построениях. Чтобы выполнить работу правильно, нужно ознакомиться с ними.
Ленточный фундамент
На обноске закрепляют два шнура, обозначающие обе грани ленты. Первый уже протянут, после выполнения приведенных выше действий. Чтобы натянуть второй потребуется отложить расстояние равное ширине фундамента от имеющегося шнура. Работы проводят после разработки грунта.
Погрешность измерений нормируется СП «Геодезические работы в строительстве» и назначается равной 1 см. Необходимо выполнить разметку не только для наружных стен, но и для внутренних.
Плитный фундамент
Для этой конструкции нет необходимости выполнять дополнительные построения. Достаточно разметки наружных граней. При работе важно помнить, что плиту чаще всего заливают так, чтобы она выступала на 10 см за наружные стены.
Важно! При разметке требуется учитывать пожарные требования, которые регламентируют минимальное расстояние между соседними зданиями. Особенно они строги для деревянных строений. Более подробные величины разрывов можно узнать в СП 4.13130.2009 таблица 1. Также строение не должно выступать за красные линии, которые указываются в градостроительном плане. При возведении дома в сельской местности в качестве красных линий выступают дороги и проезды. Минимальное расстояние от первых до стен дома составляет 5 м, от вторых — 3 м. Это актуально для всех типов фундаментов.
Столбчатый фундамент
Чтобы правильно вынести на местность расположение столбов или свай на обноске закрепляют две горизонтальные перемычки, одна над другой. Нижняя располагается в одном уровне с обрезом отдельных опор, а верхняя по обрезу ростверка. Работу выполняют в три этапа:
- Закрепляют шнуры на нижней перемычке обноски, расположение которых будет совпадать с центральными осями столбов или свай. Шаг равен шагу опорных конструкций. Из пересечений опускают отвес и отмечают точки бурения.
- Размеченные линии перемещаются к наружной грани фундаментов. Выполняют заливку.
- Следующий этап — изготовление ростверка. Для закрепления бечевки используют верхнюю перемычку на обноске. Разметку выполняют так же, как для ленточных конструкций. Работа упрощается тем, что на обноске уже имеется гвоздь, обозначающий центральные оси фундаментов. Он этой точки можно отложить в обе стороны расстояние равное половине ширины ростверка и натянуть шнуры.
Работы по выносу размеров дома на местность могут осуществляться двумя приведенными выше способами:
- разбивка фундамента по осям;
- разбивка граней фундамента без использования осей.
Каждый из них имеет свои сложности и преимущества. Профессиональные строители используют первый метод. Непрофессионалу, стоящему свой дом, будет проще понять и применить второй.
Совет! Если вам нужны строители для возведения фундамента, есть очень удобный сервис по подбору спецов от PROFI.RU. Просто заполните детали заказа, мастера сами откликнутся и вы сможете выбрать с кем сотрудничать. У каждого специалиста в системе есть рейтинг, отзывы и примеры работ, что поможет с выбором. Похоже на мини тендер. Размещение заявки БЕСПЛАТНО и ни к чему не обязывает. Работает почти во всех городах России.
Если вы являетесь мастером, то перейдите по этой ссылке, зарегистрируйтесь в системе и сможете принимать заказы.
Хорошая реклама
Читайте также
Сделайте прямой угол с узлами и веревкой
Автор: Сюзанна Элвидж, бакалавр (с отличием), магистр наук — Обновлено: 24 октября 2012 г. |Прямой угол — это угол квадратной или L-образной формы, который составляет 90 градусов (четверть круга). Квадрат состоит из четырех прямых углов.
Сделайте прямой угол из узлов и веревки
Найдите длинный кусок веревки и завяжите на нем 13 узлов. Не имеет значения, насколько далеко они друг от друга, главное, чтобы они находились на одинаковом расстоянии друг от друга. Выложите нить в виде треугольника с узлами по углам и тремя промежутками между узлами с одной стороны, четырьмя на следующей и пятью на последней стороне.Натяните веревку туго (пусть люди держатся за углы, или сделайте это снаружи и прикрепите ее к земле) — так получится треугольник с прямым углом.Это работает, потому что, согласно теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы (наклонная сторона) равен сумме квадратов на двух других сторонах.
В этом квадрате гипотенуза равна пяти, а две другие стороны равны трем и четырем.
Просто чтобы проверить…
5×5 = 3×3 + 4×425 = 9 + 1625 = 25
Другой способ сделать это — завязать узел на веревке.Используя это как начало длины веревки, трижды оберните ее вокруг книги и завяжите второй узел. Оберните книгу четыре раза и завяжите третий узел. Оберните книгу пять раз и завяжите четвертый узел. Чтобы сохранить точность, старайтесь не слишком сильно наматывать струну на себя. Удерживая веревку натянутой, сделайте треугольник, используя узлы в качестве углов — это будет прямоугольный треугольник.
Другие способы сделать прямые углы
Сложите квадрат бумаги пополам, чтобы получился прямоугольник, а затем еще раз пополам, чтобы получился квадрат.Разверните — две складки пересекаются под прямым углом друг к другу.Привяжите груз к концу веревки. Пусть гиря повиснет (может потребоваться некоторое время, чтобы она перестала раскачиваться) — как только она остановится, струна окажется под прямым углом к столу или земле.
Используйте транспортир (будет проще, если он будет четким). Проведите линию на листе бумаги, а затем нарисуйте на ней крест. Совместите крест с линией внизу транспортира (совместите его с центром транспортира — вероятно, будет пересечение точки или двух линий).Нарисуйте точку там, где транспортир показывает «90 градусов». Соедините точку и крест — прямой угол.
Сделайте три полоски бумаги или открытки: одну длиной 3 см, другую 4 см длиной и третью 5 см. Этот метод похож на метод завязанной нити, использующий теорему Пифагора. Сделайте треугольник из длинных сторон трех частей карты — когда все три части будут на своих местах, это будет прямоугольный треугольник.
Проведите линию. Откройте циркуль так, чтобы карандаш и острие находились на расстоянии более половины длины линии (например, если линия имеет длину около 10 см, циркуль должен быть открыт примерно на 6 или 7 см).Поместите конец циркуля (будьте осторожны, он острый) на одном конце линии и карандашом нарисуйте полукруг через линию.
Поместите точку циркуля на другой конец линии и нарисуйте еще один полукруг — он должен пересекать первый полукруг выше и ниже линии (если это не так, не волнуйтесь, просто вернитесь и сделать кривые больше).
Соедините две точки пересечения — так получится прямой угол с первой линией.
Вам тоже может понравиться…
Поделитесь своей историей, присоединитесь к обсуждению или обратитесь за советом ..
Заголовок:
MissMsMrsMrDrRev’dProf.Other(не показан)
Подтвердить:
Для захватывающих снимков береговых птиц, Go Low
Люди намного выше куликов. Это настолько очевидное наблюдение, что это может показаться глупым, но когда дело доходит до съемки этих разнообразных очаровательных птиц, падение до их уровня может вывести ваши фотографии на новый уровень.
Уесть много преимуществ, говорит фотограф дикой природы и редактор Audubon Мелисса Гроо. Падение вниз поможет и исчезнуть на заднем плане, что сделает вас менее опасным для диких птиц; они привыкнут к вашему присутствию, займутся своими делами и, возможно, подойдут ближе к вашей камере. «Это гораздо менее угрожающий профиль», — говорит Гроо. С технической точки зрения, уменьшение и использование очень малой глубины резкости с малой диафрагмой создает нечеткий фон, заставляя фокус — птицу — выделяться.Более того, когда вы находитесь на уровне глаз, снимки получаются более интимными. «Это переносит вас в мир животных», — говорит Гроо.
Это также приводит к прямому контакту с песком и навозом. Защитите свое оборудование и свою спину с помощью этих советов и продуктов.
Ground Pod
Присоедините SLR к Nature Scapes SKM-II Skimmer Ground Pod II (80 долларов США), чтобы скользить по любой местности. Легкая, но прочная наземная капсула не зацепится за свою сферическую форму и быстро смывает любую грязь, грязь или песок, в которые вы ее попадете, при этом защищая камеру от непогоды.Некоторые фотографы выбирают вариант «сделай сам», переоборудовав сковороду на общую сумму около 10 долларов.
Прямоугольный видоискатель
Съемка на земле — верный способ получить искривленную шею. Избегайте агонии с видоискателем с прямым углом. Г-образная насадка позволяет парить над камерой, глядя в расширенное окно, не вытягивая голову. У каждого производителя камеры есть своя модель, например, Cannon Angle Finder C (199 долларов).
Брезент
Защитите от грязи, установив поверх покрытого силиконом брезента, такого как ткань Globe Skimmer Ultralite Ground Cloth Equinox (43 доллара США).Как только вы найдете идеальное место, расстелите на земле водоотталкивающий брезент и расставьте свое снаряжение.
Наколенники
Даже на самых гладких пляжах могут быть зазубренные ракушки или палки. Увеличьте свою выносливость и уменьшите боли позже, наденьте наколенники для рисования, такие как те, которые доступны в Home Depot (от 5 долларов США) или в местном хозяйственном магазине.
Средство для удаления пыли
В поездке на пляж песок неизбежно попадет повсюду — даже на пугающе дорогую и чувствительную камеру и объектив.Держите под рукой новую кисть, чтобы смахнуть зерна; примерно по доллару за штуку в местном хозяйственном магазине, стоит держать пару под рукой. Если вам нужно больше мощности, чем предоставляет кисть, Giottos Rocket Blaster Dust Removal Tool (9 долларов США) выдувает песок из мельчайших щелей в вашем оборудовании.
Beach Buggy
Транспортировка снаряжения по пересеченной местности с Eckla Beach Rolly Cart (120 долларов США) — это легкий ветерок.Легко маневренный, но прочный вагончик может выдержать полную загрузку фотоаппарата, аксессуаров и средств жизнеобеспечения. И он служит стулом, когда пора сделать перерыв.
Забор для бассейна своими руками | Повороты на 90 градусов
Индивидуальная резка Повороты на 90 градусов
Существуют определенные обстоятельства, при которых ограждение не может быть установлено с использованием обычных поворотов, и вам необходимо повернуть
на 90 градусов. Обычно это происходит по двум причинам. Одна из причин заключается в том, что поворот слишком тугой для использования одной стойки в качестве поворотной стойки, другая причина заключается в том, что клиент хочет, чтобы он идеально очертил свою колоду, которая содержит повороты на 90 градусов, а клиент не хочет, чтобы
был обычным поворотом, потому что они не хотят срезать углы и терять пространство на палубе.Для этого вы будете делать больше пропилов
, чем при стандартной установке, поэтому рекомендуется взимать плату за дополнительную работу и материалы, которые будут потрачены впустую.
1. Первым шагом к установке поворота на 90 градусов является отметка вне поворота. См. Диаграмму A1. Самая важная часть разметки поворота на 90
градусов — убедиться, что вы повернули шаблон и отметили линию разметки на повороте. Это позволит провисать сетку ограждения
, позволяя полюсам поворачиваться, так что защелка может соединяться на стандартном расстоянии 2 1/2 дюйма, не будучи слишком тугой.Чтобы увидеть поворот крупным планом
, пожалуйста, обратитесь к диаграмме A2.
2. Следующий шаг — правильно просверлить эти углы, чтобы забор имел хорошее соединение с поворотом на 90 градусов. На диаграмме A3 показано, как нужно просверлить углы
для этого конкретного примера. Повороты на 90 градусов состоят из двух соединяемых полюсов. Это означает, что теперь вы имеете дело с
, имея дело с силой двух полюсов, которые будут втянуты при добавлении напряжения. Следовательно, вам не нужно наклонять сверло
так сильно, как если бы вы работали с одной вехой.ПРИМЕЧАНИЕ. Не пытайтесь повернуться на 90 градусов одной шестой. Если вы,
, попытаетесь выполнить поворот на 90 градусов с помощью одной шесты, это может привести к изгибу шеста. Слишком большая нагрузка на опору
увеличит вероятность ее поломки. Это также выглядит эстетически некорректно. На диаграмме A4 показано, как должно выглядеть ограждение
после просверливания и до соединения.
Как сделать клиновое приспособление
Это определенно курица до яичной ситуации. Приступая к проекту «Деревянная звезда», я быстро понял, что мне нужно приспособление для клина, чтобы сделать крутой косой пропил, поэтому я сделал его и поделился с вами практическими рекомендациями.Сделаем приспособление для вашей торцовочной пилы. Учебное пособие по созданию клинового приспособления для крутых пропилов на торцовочной пиле, а также проект деревянной звезды.
Если вы видели недавний каталог Pottery Barn, скорее всего, вы любите эти деревянные звезды не меньше меня: И вы быстро подумали: «Я могу это сделать своими руками!». Однако после долгих проб и ошибок я проконсультировался с коллегой-строителем-блоггером Джемисоном из Rogue Engineer, который быстро сообщил мне, что мне нужен угол в 54 градуса, чтобы получить форму пятиконечной звезды.НО МОЯ ПИЛА НЕ ОБРАБОТАНА 54 ГРАДУСОВ?
Не бойтесь, у меня есть решение. Если вы хотите сделать пятиконечную деревянную звезду, вам понадобится приспособление для клина, и я покажу вам, как его сделать, потому что я погуглил до смерти и не смог найти учебник :). PS — У меня есть новая модная торцовочная пила, которая делает рез под углом 60 градусов !! Но этот урок, приведенный ниже, по-прежнему отлично подходит для изготовления зажимного приспособления для клина, если вам нужен крутой пропил, превышающий возможности вашей торцовочной пилы.Этот кондуктор сделан из обрезков древесины со всего магазина, не нужно покупать какие-либо расходные материалы, просто используйте то, что у вас есть под рукой.В конце концов, это приспособление, и хотя оно чрезвычайно полезно, оно не является декоративным, так что не беспокойтесь о том, чтобы выглядеть здесь красиво.
Принадлежности:
- Фанерный лом 3/4 ″
- Лом доски сосновый 1 × 2
- Шурупы для дерева 2 ″
- столярный клей
- транспортир
- карандаш
- торцовочная пила
- сверла и сверла
(Вам не нужна рулетка для этого проекта, но каким-то образом она оказалась на картинке.)
Зажим для клина можно использовать для большинства пропилов под углом, которые превышают настройки вашей пилы. В этом случае мы делаем приспособление на 54 градуса, но вы можете сделать его так, чтобы он соответствовал вашему необходимому срезу под углом.
По сути, мы перемещаем ограждение вперед, чтобы получился более крутой угол.
Ниже приведено руководство по изготовлению зажимного приспособления для торцовочной пилы. Пожалуйста, прочтите все шаги, прежде чем приступить к пониманию процесса. Также это то, что сработало для меня, и, возможно, у вас есть лучшая версия или обновление, пожалуйста, не стесняйтесь добавлять свои заметки в комментарии.Другим очень полезно, когда они видят ваши идеи — спасибо!
Шаг 1: Настройте торцовочную пилу на распил под углом 30 градусов. Я выбрал 30 градусов, потому что это казалось хорошей золотой серединой, а не слишком крутым.
Шаг 2: Установите обрезок фанеры 3/4 дюйма заподлицо с ограждением и сделайте разрез.
Шаг 3: Примените старую школу и используйте транспортир, чтобы отметить угол 36 градусов от свежего среза под углом. Задача состоит в том, чтобы подрезать под углом до 54 градусов, поэтому 90–54 = 36.
Шаг 4: Проведите линию под углом 36 градусов от красной точки через вашу отметку.
Шаг 5: Приклейте и прикрепите сосновую доску 1 × 2 на узкой стороне заподлицо до линии, которую вы только что нарисовали (выделена красным наверху). Предварительно просверлите и утопите 2-дюймовые шурупы по дереву в доску 1 × 2. Не волнуйтесь, если на этом этапе 1 × 2 выступает за пределы фанеры.
Шаг 6: Установите угол наклона обратно на 0 градусов и обрежьте лишнее 1 × 2 заподлицо с фанерой. Сделайте это для обоих концов 1 × 2.
Ваш клиновой зажим готов и готов к использованию.
Не забудьте установить угол скоса на 30 градусов перед выполнением любых разрезов!
Также не забудьте использовать зажим для фиксации зажимного приспособления.Если вам нужна дополнительная безопасность, подумайте о добавлении перпендикулярного деревянного ограждения к фанере (там, где он встречается с ограждением для пилы), вы также можете прикрепить деревянный забор к ограждению для пилы.
Теперь поместите доску, которую нужно разрезать, перед клином — здесь я использовал кусок сосны размером 8 дюймов размером 1 × 3. Обязательно прижмите доску к упору и отрежьте.
Торцовка под углом 54 градуса на торцовочной пиле с использованием клинового приспособления.
МАГАЗИН ЭТОГО ПРОЕКТА:
Включите JavaScript для просмотра содержимого
Как построить А-образную раму
Одной из самых прочных конструкций является А-образная рама, каркас которой состоит просто из ряда треугольников.Основания треугольников — это балки, поддерживающие пол, а стороны — стропила, удерживающие совмещенные стены и крышу. Простота конструкции и сравнительно низкая стоимость делают его популярным выбором для загородных домиков или автономных домов. Его основой может служить любой стиль фундамента.
Планирование вашей А-образной рамы
Самая распространенная форма — равносторонняя — балки и балки одинаковой длины расположены под углом 60 градусов друг к другу. Однако вы можете использовать разные углы для изменения формы (см. «Общие углы между перекрытиями и стропилами» ниже).А-образную раму можно построить практически любого размера, просто варьируя количество треугольников и их размеры, но кабина со спальным чердаком должна иметь стропила длиной не менее 20 футов, чтобы обеспечить достаточное пространство для головы на обоих этажах. Для небольшой конструкции, подобной описанной здесь, три человека могут поднять собранные треугольники на место без помощи специального оборудования. Конструкция со стропилами более 24 футов может оказаться слишком громоздкой для команды любителей. Обрамляйте двери и окна в торцевых стенах.Для большой А-образной рамы запланируйте много окон, чтобы интерьер не был слишком темным.
Инструменты для А-образной рамы
- Отвертка
- Циркулярная пила
- Хомуты С-образные
- Электродрель
- Молот
- Уровень плотника
- Плотницкая площадь
- Отвес
- Гаечный ключ
- Сабельная пила
Материалы А-образной рамы
- 1 на 2, 2 на 4
- 2 на 6, 2 на 8
- Обработанные давлением 2 на 6, 2 на 10, 4 на 4
- Фанера для наружных работ (3/4 дюйма)
- Клей для дерева
- Обычные гвозди (2 дюйма, 2 1/2 дюйма, 3 1/2 дюйма)
- Гвозди обычные оцинкованные (2 1/2 дюйма, 3 дюйма, 3 1/2 дюйма)
- Гвозди с кольцевой стойкой (2 1/2 дюйма)
- Шурупы для дерева (1 3/4 дюйма No.8)
- Кровельные материалы
- Болты с квадратным подголовком (5/8 дюйма на 6 дюймов; 1/2 дюйма на 4 дюйма, 6 дюймов)
- Стяжные винты (1/2 дюйма на 4 дюйма)
- Анкеры и гвозди универсальные и обрамляющие
- Лестница деревянная
- Бетонная смесь
Анатомия А-образной рамы
Эта равносторонняя А-образная рама с шириной 20 футов с каждой стороны опирается на тройные балки размером 2 на 10, обработанные давлением, поддерживаемые опорами из кирпичных блоков. Треугольники, расположенные на расстоянии 24 дюймов друг от друга, образованы стропилами 2 на 8, соединенными в вершинах фанерными косынками и зажатыми внизу парами обработанных давлением балок 2 на 6.(Для кабины большего размера, чем эта конструкция, потребуется брус для каркаса соответственно большего размера.) На торцевых стенах и под спальным чердаком между стропилами крепятся горизонтальные воротниковые балки размером 2 на 6. Стропила торцевых стен удвоены, чтобы обеспечить ровную поверхность для крепления гвоздей для внешней обшивки. Спальный чердак, к которому ведет лестница, обрамлен перилами, прикрепленными к столбам и стропилам. Коленные перегородки по бокам кабины обеспечивают скрытые места для хранения вещей. Палуба опирается на балки размером 2 на 6, расстояние между которыми составляет 16 дюймов.Столбы для перил крепятся к балкам настила. Лестница установлена на бетонных основаниях и крепится к настилу металлическими анкерами. Вся открытая древесина — это пиломатериалы, обработанные под давлением. Показана кровля из битумной черепицы.
Угол между перекрытиями и стропилами общий
(Длина стропил, длина балки, угол стропила / балки, угол стропила / стропила)
16 футов, 12 футов, 68 градусов, 22 градусов
16 футов, 14 футов, 64,1 градуса, 26 градусов
16 футов, 16 футов, 60 градусов, 30 градусов
20 футов, 12 футов, 72.5 градусов, 17,5 градусов
20 футов, 14 футов, 69,5 градусов, 20,5 градусов
20 футов, 16 футов, 66,4 градусов, 23,6 градусов
20 футов, 20 футов, 60 градусов, 30 градусов
Резка А-образных балок и стропил
- Чтобы быстро разрезать балки и стропила, сделайте приспособление для каждого разрезаемого угла.
- Отметьте обрезную доску под углом балок или стропил и положите ее на рабочую поверхность.
- Поместите по 2 на 4 с каждой стороны доски и закрепите их винтами.
- Совместите 1 на 2 с меткой и прикрутите его к 2 на 4 в качестве направляющей для резки.
- Проведите циркулярной пилой по направляющей, прорезав пропил через все три доски.
- Удалите обрезную доску и замените ее балкой или стропильной балкой с размеченной длиной.
- Совместите метку с пропилом и обрежьте доску.
- Обрежьте другой конец так, чтобы оба среза были под углом к середине.
Сборка треугольников А-образной рамы
- Зажмите концы двух балок вокруг основания стропил, совместив концы и края досок, и просверлите отверстие диаметром 5/8 дюйма в трех слоях.
- Скрепите доски вместе с помощью болта с квадратным подголовком 5/8 на 6 дюймов, шайбы и гайки.
- Таким же образом прикрепите противоположные концы балок к основанию другого стропила.
- Из 3/4-дюймовой фанеры для наружных работ вырежьте две треугольные косынки под тем же углом, что и у А-образной рамы.
- Соедините верхние концы стропил вместе и закрепите косынки с каждой стороны шва с помощью столярного клея и 1 3/4 дюйма шурупов № 8.
- Добавьте второй болт с квадратным подголовком к каждому стыку балки и стропила.
- Соберите оставшиеся треугольники таким же образом, но прикрепите косынки только к одной стороне каждого торцевого треугольника.
- Оставляя по крайней мере 7 футов высоты над головой, отметьте оба стропила каждого треугольника на торцевых стенах и под чердаком для воротниковых балок. Для каждого треугольника вырежьте две опорные балки, чтобы они поместились между внешними краями стропил, а затем закрепите их болтами, как вы делали балки.
- Отрежьте распорки 1 на 2 по ширине балки и закрепите их 2-дюймовыми общими гвоздями между всеми парами балок балок и воротниковых балок с интервалом в 2 фута.
- Удвойте стропила концевых треугольников: отрежьте четыре куска стропильного бруса — два, чтобы поместиться между балками и воротником, и два — между балками и пиками стропил, и прибейте их к внешней стороне стропил гвоздями 2 1/2 дюйма. .
Возведение треугольников А-образной рамы
- Отметьте места треугольников на балках с интервалом в 2 фута.
- Струпья от гвоздей — 1 фут длиной 2 на 4 — на внутренней стороне внешних балок с каждой стороны меток для треугольника переднего конца.
- С помощью пары помощников поднимите и поместите концевой треугольник на балке между струпьями.
- Прикрепите треугольник по вертикали и закрепите его двумя гвоздями размером 2 на 4, прибитыми по диагонали между стропилами и внешними балками так, чтобы верх каждой распорки находился на расстоянии не менее 4 1/2 футов от основания стропил.
- Поместите и прикрепите оставшиеся треугольники таким же образом, закрепив их гвоздями 1 на 2 с каждой стороны соседнего треугольника.
- Когда все треугольники закреплены, удалите корки и прикрепите треугольники к балкам, установив универсальный каркасный анкер с каждой стороны каждой балки.В районе с сильным ветром используйте ураганные стяжки. Прибейте нижние уголки треугольников к балкам.
- Обшить внешнюю часть рамы, укладывая настил для встряхивания, или панели 4 на 8 из 5/8-дюймовой фанеры для наружных работ для металлической кровли или битумной черепицы. Работайте снизу вверх, закрепляя оболочку общими гвоздями на 2 1/2 дюйма. Оставьте зазор 1/8 дюйма вокруг панелей и расположите стыки в шахматном порядке. После того, как вы уложите нижний ряд панелей, снимите распорку.
- Покройте пол фанерой.
Последние штрихи
Если А-образная рама включает чердак, обеспечьте его лестницей или лестницей и прочными перилами. Положите колоду, если вы ее строите, на тот же фундамент, что и основная конструкция, и окружите ее перилами. Купите палубные лестницы в строительном центре или соорудите их на месте. При строительстве установите изоляцию между балками пола, стропилами и стойками торцевых стен.
Перепечатано с разрешения Cabins & Cottages , опубликовано Fox Chapel Publishing, 2011.
Первоначально опубликовано: 25 ноября 2011 г.
.
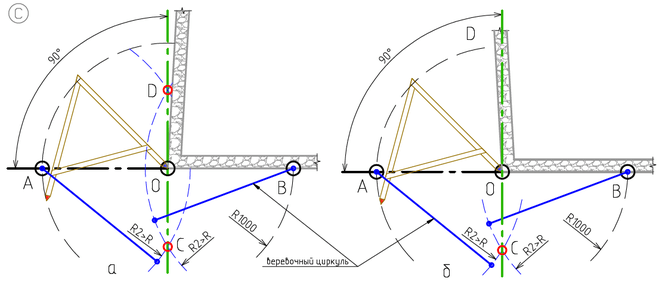
 На 3б – он залез на Ваш участок. В ситуации 3а возможно построение двух «направляющих» точек: и C, и D. На 3б же – только С.
На 3б – он залез на Ваш участок. В ситуации 3а возможно построение двух «направляющих» точек: и C, и D. На 3б же – только С.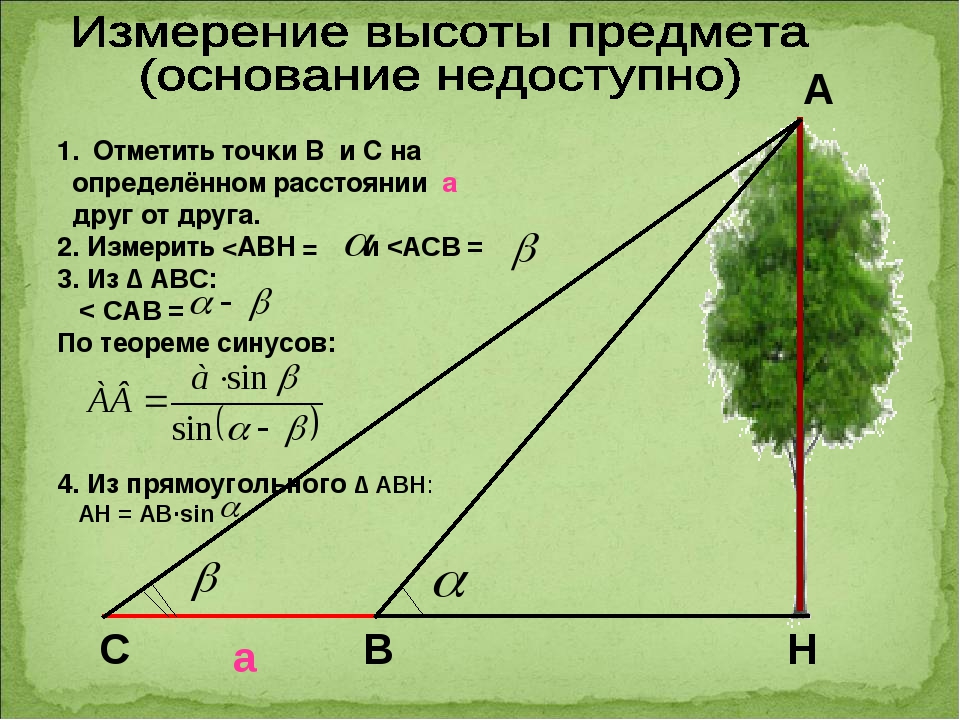 Если у вас большая комната, можно использовать следующие числа: 9-12-15, 6-8-10 метров.
Если у вас большая комната, можно использовать следующие числа: 9-12-15, 6-8-10 метров.