Измерение углов. Транспортир | Математика
Измерить угол — значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.
Обычно за единицу измерения углов принимают градус. Градус — это угол, равный части развёрнутого угла. Для обозначения градусов в тексте, используется знак °
, который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).
Измерение углов транспортиром
Для измерения углов используют специальный прибор — транспортир:
У транспортира две шкалы — внутренняя и внешняя. Начало отсчёта у внутренней и у внешней шкал располагается с разных сторон. Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.
Измерение углов производится следующим образом: транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах:
Говорят: угол BOC равен 60 градусов, угол MON равен 120 градусов
и пишут: ∠BOC = 60°, ∠MON = 120°.
Для более точного измерения углов используют доли градуса: минуты и секунды. Минута — это угол, равный
части градуса. Секунда — это угол, равный части минуты. Минуты обозначают знаком ‘
, a секунды — знаком »
. Знак минут и секунд ставится в правом верхнем углу числа. Например, если угол имеет величину 50 градусов 34 минуты и 19 секунд, то пишут:
50°34‘19».
Свойства измерения углов
Если луч делит данный угол на две части (на два угла), то величина данного угла равна сумме величин двух полученных углов.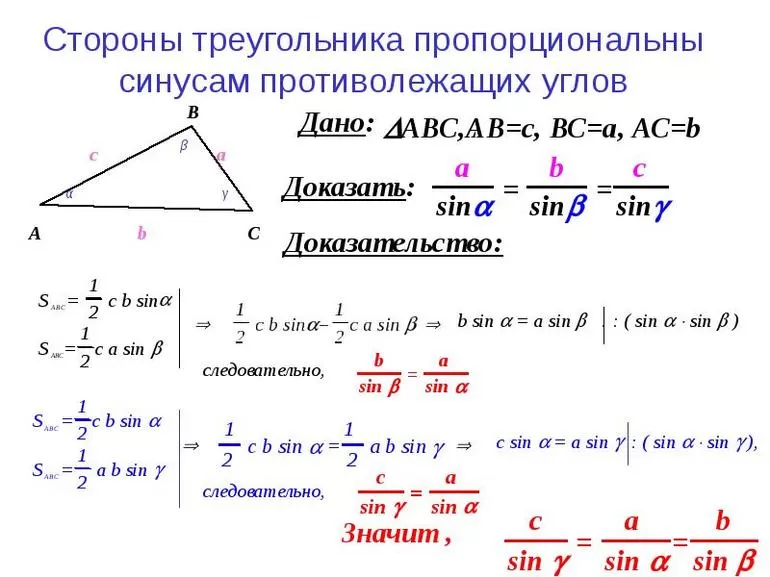
Рассмотрим угол AOB:
Луч OD делит его на два угла: ∠AOD и ∠DOB. Таким образом, ∠AOB = ∠AOD + ∠DOB.
Развёрнутый угол равен 180°.
Любой угол имеет определённую величину, большую нуля.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Тригонометрия
Рассмотрим тригонометрические круги, изображенные на рисунке 1 и рисунке 2.
Рис.1
Рис.2
На тригонометрическом круге, изображенном на рисунке 1, центральные углы измерены в градусах, а на тригонометрическом круге, изображенном на рисунке 2, те же центральные углы измерены в радианах.
Углом в 1 градус называют угол, составляющий полного угла. Углом в k° называют угол в k раз больший угла в 1° .
Углом в 1 радиан называют центральный угол тригонометрического круга, которому соответствует дуга окружности тригонометрического круга длиной 1 . Углом в k радиан называют центральный угол тригонометрического круга в k раз больший угла в 1 радиан.
Следствие 1. Углом в k радиан является центральный угол тригонометрического круга, которому соответствует дуга окружности тригонометрического круга длиной k .
Следствие 2. Полный угол является углом в 2π радиан.
Для того, чтобы найти формулы, связывающие градусную и радианную меры угла, рассмотрим рисунки 3 и 4
| Рис.3 | Рис.4 |
| Рис.3 |
| Рис.4 |
На этих рисунках изображены прямые углы, причем на рисунке 3 прямой угол измерен в градусах и равен 90° , а на рисунке 4 прямой угол измерен в радианах и равен радиан. Следовательно,
Следовательно,
Таким образом, формулы, связывающие градусную и радианную меры угла, имеют вид
Поскольку , то
По этой причине углы, составляющие целое число радиан, изображаются на тригонометрическом круге так, как это показано на рисунке 5.
Рис.5
Замечание. Тригонометрическая формула sin α означает, что рассматривается синус угла в α радиан, а тригонометрическая формула sin α° означает, что рассматривается синус угла в α градусов. По такому же правилу определяются значения косинуса, тангенса и котангенса.
Пример. Найти наименьшее из чисел:
Решение. Поскольку
то наименьшим числом является число cos 3 .
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Урок 5. измерение углов — Геометрия — 7 класс
Геометрия
Урок №5
Измерение углов
Перечень рассматриваемых вопросов:
- Измерительные инструменты.
- Градусная мера угла; биссектриса.
- Транспортир.
- Классификация углов.
Тезаурус:
Градус – угол, равный одной сто восьмидесятой части развернутого угла.
Градусная мера угла – положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.
Минута – 1/60 часть градуса.
Секунда – 1/60 часть минуты.
Луч – часть прямой, состоящий из всех точек, лежащих по одну сторону от заданной точки, которая является началом луча.
Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
Стороны угла – лучи, из которых состоит угол.
Вершина угла – общее начало сторон угла.
Биссектриса – это луч, исходящий из вершины угла и делящий его на два равных угла.
Основная литература:
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Ранее вы уже познакомились с геометрической фигурой – уголи его составными элементами.
Сегодня мы продолжим изучать углы, познакомимся с их классификацией и будем измерять углы с помощью транспортира.
Измерение углов аналогично измерению отрезков – оно основано на сравнении, только отрезки сравнивались с отрезком, принятым за единицу измерения, а углы с углом, тоже принятым за единицу измерения.
Обычно за единицу измерения углов принимают градус.
Градус – угол, равный 1/180 части развёрнутого угла.
Положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу, называется градусной мерой угла.
Для измерения углов используют транспортир. Вспомним, как проводить измерение углов с помощью транспортира.
Транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале.
Например:
∠О = 50°
Но обычно говорят кратко – угол О равен 50 градусам.
Если масштабныйугол не укладываетсяцелое число раз в измеряемом угле, тоединицу измерения делят ещё на части.
Определённые части градуса носят специальные названия.
Части градуса.
Минута – 1/60 часть градуса.
Обозначается «´».
Секунда – 1/60 часть минуты.
Обозначается «´´».
Например:
∠А = 40 ° 15´ 16 ´´
Далее, аналогично понятию равные отрезки, ведём понятие равные углы.
Дваугла считаются равными, если градус и его части укладываются в этих углах одинаковое число раз, т.е. равные углы имеют равные градусные меры.
Если один угол меньше другого, то градус в нём (или его часть) укладываются в этом углу меньшее число раз, чем в другом, т.е. меньший угол имеет меньшую градусную меру.
Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.
∠АОС =∠АОL + ∠LОС,
∠АОL = 64°,
∠LОС = 64°,
∠АОС = 64° + 64° = 128°.
Далее рассмотрим классификацию углов.
Но есть и другие углы.
Например, прямой угол, его градусная мера девяносто градусов;
острый угол, его градусная мера меньше девяноста градусов;
тупой угол, его градусная мера больше девяноста градусов, но меньше ста восьмидесяти.
Выполним практическое задание – построим биссектрису угла с помощью транспортира.
Мы знаем, что биссектриса – это луч, исходящий из вершины угла и делящий его на два равных угла.
∠АОС = 128°,
128° : 2 = 64°,
OL – биссектриса ∠АОС.
Поэтому для начала определим градусную меру ∠АОС, она составляет 128°, тогда биссектриса этого угла, исходя из определения, составит 64 °.
Итак, сегодня получили представление о том, как измерять и изображать угол с помощью транспортира. Перейдем к практическим заданиям.
Перейдем к практическим заданиям.
Способы измерения на местности.
Измерение углов на местности проводят с помощью различных приборов. Один из таких – астролябия, она состоит из диска (лимб), разбитого на градусы и вращающейся вокруг центра диска линейки (алидады). На концах алидады есть окошечки, которые нужны, чтобы устанавливать её в определённом направлении.
Опишем, как происходит измерение углов с помощью этого прибора. При измерении углов астролябию устанавливают в его вершине, например, точке О, при этом лимб должен находится горизонтально плоскости угла, а отвес, в центе диска, совпадать с вершиной угла.
Затем устанавливаем алидаду вдоль одной из сторон угла, например, АО, отмечаем деление, напротив которого находится указатель алидады.
Далее поворачиваем алидаду по часовой стрелке, пока она не совпадёт со второй стороной угла, у нас это сторона ОВ, отмечаем деление, напротив которого оказался указатель алидады. Теперь можно найти градусную меру измеряемого угла, как разность второго и первого измерения.
Тренировочные задания.
1. Луч ВК делит развернутый ∠ОВС на два угла, разность которых равна 56°. Найдите образовавшиеся углы.
Решение: нарисуем рисунок, исходя из условия задачи.
Обозначим ∠СВК за х, тогда ∠ОВК= х + 56°, исходя из условия задачи (разность углов равна 56°). Развёрнутый угол равен 180°. Составим уравнение и решим его.
х + х +56 =180,
2х= 180 – 56,
2х= 124,
х = 124:2,
х = 62° (∠СВК).
Тогда ∠ОВК= х + 56°= 62° +56° = 118°.
Ответ: ∠СВК = 62°; ∠ОВК = 118°.
2. Чему равен ∠ЕОА, если ∠ВОА = 130° 54´, а ∠ВОЕ = 105° 76´?
Решение: Найдём ∠ЕОА = ∠ВОА – ∠ВОЕ, т.к. ОЕ – луч, проведённый из вершины ∠ВОА и делящий этот угол на 2 части. Подставим в выражение градусные меры углов и найдём градусную меру ∠ЕОА. Так как в градусе 60 минут, то 105° 76´ = 106° 16´.
∠ЕОА = 130° 54´ – 106° 16´ = 24° 38´. \circ\).
\circ\).
\(\bullet\) Внешний угол \(\angle BCD\) треугольника \(ABC\) равен сумме двух углов треугольника, не смежных с ним.
Факт 4.
\(\bullet\) Биссектрисы смежных углов взаимно перпендикулярны.
\(\bullet\) Биссектрисы односторонних углов при параллельных прямых взаимно перпендикулярны.
Факт 5.
\(\bullet\) Прямая теорема: каждая точка биссектрисы угла равноудалена от сторон угла.
\(\bullet\) Обратная теорема: если точка равноудалена от сторон угла, то она лежит на его биссектрисе.
Факт 6.
\(\bullet\) Равнобедренный треугольник – треугольник, у которого две стороны равны. Третья сторона треугольника называется основанием.
Первое свойство равнобедренного треугольника:
Второе свойство равнобедренного треугольника: углы при основании равны.
Первый признак равнобедренного треугольника: если у треугольника два угла равны, то он равнобедренный.
Второй признак равнобедренного треугольника: если у треугольника совпадают высота и медиана (высота и биссектриса или медиана и биссектриса), проведенные к одной и той же стороне, то этот треугольник является равнобедренным.
Факт 7.
\(\bullet\) Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.
Факт 8.
\(\bullet\) Медианы в треугольнике точкой пересечения делятся в отношении \(2:1\), считая от вершины.
Факт 9.
\(\bullet\) Медиана треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.
Факт 10.
\(\bullet\) Высота, проведенная из вершины прямого угла треугольника, делит его на два треугольника, подобных исходному.
\(\bullet\) Квадрат этой высоты равен произведению отрезков, на которые она делит гипотенузу.
Факт 11.
\(\bullet\) Средняя линия треугольника – отрезок, соединяющий середины двух его сторон.
\(\bullet\) 1. Средняя линия треугольника параллельна третьей стороне.
\(\bullet\) 2. Средняя линия треугольника равна половине третьей стороны.
\(\bullet\) 3. Средняя линия отсекает от треугольника подобный ему треугольник.
Решение задач по теме «Смежные и вертикальные углы»
Тип урока: урок закрепления нового материала
Цели урока:
- Образовательные: повторить и закрепить понятия о смежных и вертикальных углах;
- Развивающие: развивать умение анализировать условие задачи;
- Воспитательные: воспитание аккуратности (аккуратное выполнение чертежей на доске и в тетрадях, рациональное распределение записей).
Структура урока:
- I этап. Организационный момент
- II этап. Актуализация опорных знаний
- III этап. Закрепление изученного материала
- IV этап. Зарядка для глаз
- V этап. Самостоятельная работа
- VI этап. Домашнее задание
- VII этап. Итог урока
(Слайд 1-2)
Приветствие, сообщение темы, целей и задач.
Учитель: Вам было задано домашнее задание: повторить п.14 и 15, ответить на вопросы 1, 2, 3, 6, 7. Сейчас проверим, как вы подготовились к уроку.
(Слайд 3)
Вопрос: Какие углы называются смежными? (Ответ. Два угла называются смежными, если у них одна сторона общая, а другие стороны являются дополнительными полупрямыми)
Вопрос. Из рисунка назвать смежные углы. (Ответ: ∠АОВ и ∠ВОС – смежные углы)
Из рисунка назвать смежные углы. (Ответ: ∠АОВ и ∠ВОС – смежные углы)
Вопрос. Какая сторона у них общая? (Ответ: ОВ – общая сторона.)
Вопрос. Назвать дополнительные полупрямые. (Ответ. ОС и ОА – дополнительные полупрямые.)
(Слайд 4) Вопрос. Какими свойствами обладают смежные углы?
Ответ.
- Сумма смежных углов равна 180° (теорема)
∠1 + ∠2 = 180°
- Если два угла равны, то и смежные с ними углы равны.
- Если угол не развернутый, то его градусная мера меньше 180°.
- Угол, смежный с прямым, есть прямой угол.
(Слайд 5)
Вопросы. Могут ли два смежных угла быть равными:
а) 75° и 80°; Ответ: (нет, т.к.75° + 80°=155°)
б) 94° и 96°; Ответ: (нет, т.к. 94° + 96°= 190°)
в) 83° и 97°? Ответ: (да, т.к. 83° + 97°= 180°)
(Слайд 6)
Устно.
| Дано:
∠АОВ а ∩ АО а ∩ ОВ ∠3 = ∠4 |
Доказательство.
1. ∠3 смежный с ∠1, ∠4 смежный с ∠2 . 2. Т.к. ∠3 = ∠4 (по условию), то ∠1 = ∠ 2, |
Доказать ∠1 = ∠2 |
(Слайд 7)
Вопрос. Какие углы называются вертикальными?
(Ответ. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого).
∠ 1 и ∠ 3 – вертикальные углы
∠ 2 и ∠ 4 – вертикальные углы
(Слайд 8)
Вопрос. Каким свойством обладают смежные углы?
Ответ. Вертикальные углы равны. (теорема)
∠ 1 = ∠ 3
∠ 2 = ∠ 4
III этап. Закрепление изученного материала. Решение задач.(Слайд 9)
№3 (учебник)
Дано: ∠1 и ∠2– смежные ∠1 больше ∠2 в 2 раза |
Решение. 1. Пусть ∠2 = х, тогда ∠1=2х 2. Т.к. ∠1 + ∠2 = 180°(по теореме о смежных углах), то х + 2х = 180° 3х = 180°, ⇒ х =180°: 3, х = 60°. 3. Следовательно: ∠2 = 60°, ∠1 = 2∙60°= 120° Ответ: ∠1= 120°, ∠2= 60°, |
| Найти ∠1 и ∠2 |
(Слайд 10)
№6(2)
Дано: ∠1 и ∠2 – смежные ∠1 : ∠2 = 3 : 7 |
Решение. 1. Пусть х. – коэффициент пропорциональности. Тогда ∠1 = 3х, ∠2 = 7х (по условию задачи) 2. Т.к ∠1 + ∠2 = 180°(по теореме о смежных углах), то 3х + 7х = 180°, 10х = 180°, х = 18°. 3. Следовательно: ∠1 =3 ∙ 18°=54°, ∠2 =7 ∙ 18°=126° Ответ: 54°; 126°. |
| Найти ∠1 и ∠2 |
(Слайд 11)
Дано: ∠1 и ∠2 – смежные ∠2 составляет 0,2 от∠1 |
Решение 1. Пусть ∠1 = х, тогда ∠2 = 0,2х (по условию). 2. Т.к. ∠1 + ∠2 = 180° (по теореме о смежных углах), 3. Следовательно: ∠1=150°, ∠2= 0,2∙ 150°= 30°. Ответ: 150°, 30° |
| Найти ∠1 и ∠2 |
(Слайд 12)
Дано: а ∩ b ∠2 меньше ∠1 в 4 раза |
Решение 1. Пусть ∠2 = х , тогда ∠1 = 4х (по условию), 2. Т.к. ∠1+ ∠2 = 180° (по теореме о смежных углах), 3. Следовательно: ∠2 = 36°, ∠1 = 4∙36° = 144° ∠3= ∠1, ∠4= ∠2 (по теореме о вертикальных углах), Ответ: 144°, 36°, 144°, 36°. |
| Найти ∠1, ∠2, ∠3 и ∠4 |
(Слайд 13)
Дано: AС ∩ ВD = O ∠ВОС = 23° |
Решение 1. 2. ∠АОВ + ∠ВОС = 180° (по теореме о смежных углах). Следовательно: ∠АОВ =180°– ∠ВОС, 3. ∠СОD = ∠АОВ = 157° (по теореме о вертикальных углах). Ответ: 157°, 157°, 23°. |
Найти: ∠СОD, ∠АОВ, ∠АОD. |
(Слайд 14)
Устно. Вопрос. Назовите смежные и вертикальные углы.
Ответ.
Смежные углы:∠ АОМ и ∠ АОD, ∠АОD и ∠NОD, ∠NОD и ∠NОМ, ∠NОМ и ∠АОМ .
Вертикальные углы: ∠АОМ и ∠NОD, ∠АОD и ∠NОМ.
IV этап. Зарядка для глаз(Слайд 15)
V этап. Самостоятельная работа (на листочках).| Вариант 1 | Вариант 2 |
| №1. Один из углов, получившихся при пересечении двух прямых, равен 87°. Найдите остальные углы. | №1. Один из углов, получившихся при пересечении двух прямых, равен 118°. Найдите остальные углы. |
№2. Разность смежных углов равна 50°. Найдите меньший угол. Разность смежных углов равна 50°. Найдите меньший угол. |
№2. Один из смежных углов в 4 раза меньше другого. Найдите больший угол. |
Ответы
| Вариант 1 | Вариант 2 |
| №1. 93°, 87°, 93°. | №1. 62°, 118°, 62° |
| №2. 75°. | №2. 36°. |
- §2. Пункты 14-15.
- Задачи на стр. 26. № 6(4), № 12.
- Повторили понятия смежных и вертикальных углов
- Научились решать задачи, используя знания о смежных и вертикальных углах.
- Стали еще на одну ступеньку выше в изучении геометрии.
Геометрия. Урок 2. Углы — ЁП
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.
Стороны угла – лучи, которые образуют угол.
Вершина угла – точка, из которой выходят лучи.
Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.
Важно: в названии буква, обозначающая вершину угла, стоит между двумя буквами, обозначающими точки на сторонах угла. Так, угол, изображенный на рисунке, можно назвать: ∠AOB или ∠BOA, но ни в коем случае не ∠OAB,∠OBA,∠ABO,∠BAO.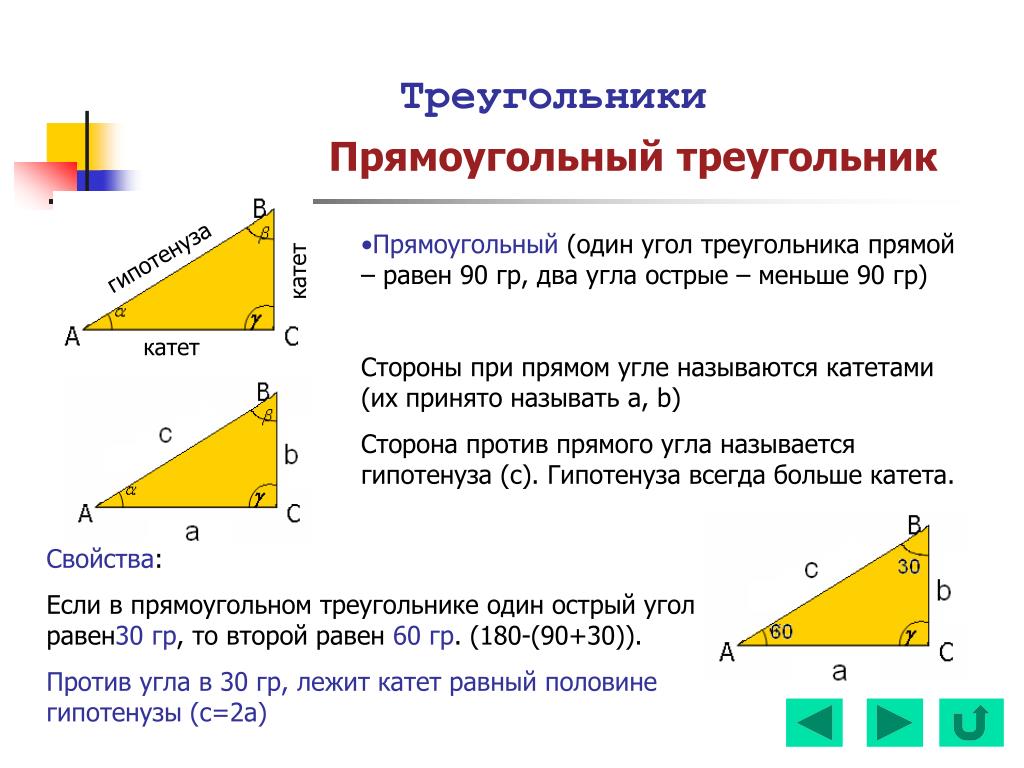
Величину угла измеряют в градусах. ∠AOB=24°.
Биссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла.
Или
Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.
OD – биссектриса угла ∠AOB. Она делит этот угол на два равных угла.
∠AOD=∠BOD=∠AOB2
Точка D – произвольная точка на биссектрисе. Она равноудалена от сторон OA и OB угла ∠AOB.
Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.
Свойство: вертикальные углы равны.
Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой.
Свойство: сумма смежных углов равна 180°.
Пример:
Пары углов
(1) и (3)
(2) и (4)
называются вертикальными.
По свойству вертикальных углов:
∠COD=∠AOB
∠BOD=∠AOC
Пары углов
(1) и (2)
(2) и (3)
(3) и (4)
(4) и (1)
называются смежными.
По свойству смежных углов:
∠COD+∠DOB=180°∠DOB+∠BOA=180°∠BOA+∠AOC=180°∠AOC+∠COD=180°
Прямая, пересекающая две заданные прямые, называется секущей этих прямых.
Существует пять видов углов, которые образуются при пересечении двух прямых секущей.
Пары углов:
(1) и (5)
(2) и (6)
(3) и (7)
(4) и (8)
называются соответственными.
(Легко запомнить: они соответствуют друг другу, похожи друг на друга).
Пары углов:
(3) и (5)
(4) и (6)
называются внутренними односторонними.
(Легко запомнить: лежат по одну сторону от секущей, между двумя прямыми).
Пары углов:
(1) и (7)
(2) и (8)
называются внешними односторонними.
(Легко запомнить: лежат по одну сторону от секущей по разные стороны от двух прямых).
Пары углов:
(3) и (6)
(4) и (5)
называются внутренними накрест лежащими.
(Легко запомнить: лежат между двумя прямыми, расположены наискосок друг относительно друга).
Пары углов:
(1) и (8)
(2) и (7)
называются внешними накрест лежащими.
(Легко запомнить: лежат по разные стороны от двух прямых, расположены наискосок друг относительно друга).
Если прямые, которые пересекает секущая, параллельны, то углы имеют следующие свойства:
- Соответственные углы равны.
- Внутренние накрест лежащие углы равны.
- Внешние накрест лежащие углы равны.
- Сумма внутренних односторонних углов равна 180°.
- Сумма внешних односторонних углов равна 180°.
Сумма углов произвольного n-угольника вычисляется по формуле:
Sn=180°⋅(n−2)
где n – это количество углов в n-угольнике.
Пользуясь этой формулой, можно вычислить сумму углов для произвольного n-угольника.
Сумма углов треугольника: S3=180°⋅(3−2)=180°
Сумма углов четырехугольника: S4=180°⋅(4−2)=360°
Сумма углов пятиугольника: S5=180°⋅(5−2)=540°
Так можно продолжать до бесконечности.
Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.
На рисунках изображены примеры правильных многоугольников:
Чтобы найти величину угла правильного n-угольника, необходимо сумму углов этого многоугольника разделить на количество углов.
αn=180°⋅(n−2)n
Модуль геометрия: задания, связанные с углами
Скачать домашнее задание к уроку 2.
Радиан, Углы больше 360 градусов, Положительные и отрицательные углы
Когда прямые пересекаются, то получается четыре разные области по отношению к точке пересечения.
Эти новые области называют углами. {\circ} = \frac{260}{360} = \frac{7}{9}$ кругов
{\circ} = \frac{260}{360} = \frac{7}{9}$ кругов
Объект описал $2\frac{7}{9}$ кругов
Когда объект вращается по часовой стрелки, то он образует отрицательный угол вращения, а когда вращается против часовой стрелке — положительный угол. До этого момента мы рассматривали только положительные углы.
В форме диаграммы отрицательный угол может быть изображен так, как это показано ниже.
Рисунок ниже показывает знак угла, который измеряется от общей прямой, 0 оси (оси абсцисс — х оси)
Это означает, что при наличии отрицательного угла, мы можем получить соответствующий ему положительный угол.
Например, нижняя часть вертикальной прямой это 270°. Когда измеряется в негативную сторону, то получим -90°. Мы просто вычитаем 270 из 360.
Имея отрицательный угол, мы прибавляем 360, для того чтобы получить соотвествующий положительный угол.
Когда угол равен -360°, это означает, что объект совершил более одного круга по часовой стрелке.
Пример 3
1. Найти соответствующий положительный угол
a) -35°
b) -60°
c) -180°
d) — 670°
2. Найти соответствующий отрицательный угол 80°, 167°, 330°и 1300°.
Решение
1. Для того, чтобы найти соответствующий положительный угол мы прибавляем 360 к значению угла.
a) -35°= 360 + (-35) = 360 — 35 = 325°
b) -60°= 360 + (-60) = 360 — 60 = 300°
c) -180°= 360 + (-180) = 360 — 180 = 180°
d) -670°= 360 + (-670) = -310
Это означает один круг по часовой стрелке (360)
360 + (-310) = 50°
Угол равен 360 + 50 = 410°
2. Для того, чтобы получить соответсвующий отрицательный угол мы вычитаем 360 от значения угла.
80° = 80 — 360 = — 280°
167° = 167 — 360 = -193°
330° = 330 — 360 = -30°
1300° = 1300 — 360 = 940 (пройден один круг)
940 — 360 = 580 (пройден второй круг)
580 — 360 = 220 (пройден третий круг)
220 — 360 = -140°
Угол равен -360 — 360 — 360 — 140 = -1220°
Таким образом 1300° = -1220°
Радиан — это угол из центра круга, в который заключена дуга, длина которой равна радиусу данного круга. {\circ}$
{\circ}$
c) 1 рад = 57,3°
$2,4 = \frac{2,4 \times 57,3}{1} = 137,52$
Отрицаетльные углы и углы больше, чем $2\pi$ радиан
Для того чтобы преобразовать отрицательный угол в положительный, мы складываем его с $2\pi$.
Для того чтобы преобразовать положительный угол в отрицательный, мы вычитаем из него $2\pi$.
Пример 5
1. Преобразовать $-\frac{3}{4}\pi$ и $-\frac{5}{7}\pi$ в позитивные углы в радианах.
Решение
Прибавляем к углу $2\pi$
$-\frac{3}{4}\pi = -\frac{3}{4}\pi + 2\pi = \frac{5}{4}\pi = 1\frac{1}{4}\pi$
$-\frac{5}{7}\pi = -\frac{5}{7}\pi + 2\pi = \frac{9}{7}\pi = 1\frac{2}{7}\pi$
Когда объект вращается на угол больший, чем $2\pi$;, то он делает больше одного круга.
Для того, чтобы определить количество оборотов (кругов или циклов) в таком угле, мы находим такое число, умножая которое на $2\pi$, результат равен или меньше, но как можно ближе к данному числу.
Пример 6
1. Найти количество кругов пройденных объектом при данных углах
a) $-10\pi$
b) $9\pi$
c) $\frac{7}{2}\pi$
Решение
a) $-10\pi = 5(-2\pi)$;
$-2\pi$ подразумевает один цикл в направлении по часовой стрелке, то это означает, что
объект сделал 5 циклов по часовой стрелке.
b) $9\pi = 4(2\pi) + \pi$, $\pi =$ пол цикла
объект сделал четыре с половиной цикла против часовой стрелки
c) $\frac{7}{2}\pi=3,5\pi=2\pi+1,5\pi$, $1,5\pi$ равно три четверти цикла $(\frac{1,5\pi}{2\pi}=\frac{3}{4})$
объект прошел один и три четверти цикла против часовой стрелки
Линейное программирование: таблица угловых точек
Линейное программирование: таблица угловых точекОпределите угловые точки
Угловые точки — это вершины допустимой области. Когда у вас есть график системы линейных неравенств, вы можете посмотреть на график и легко определить, где находятся угловые точки.
Вам может потребоваться решить систему линейных уравнений, чтобы найти некоторые координаты точек в середине. Например, решением пересечения прямых x + 2y = 16 и x + y = 9 является точка (2,7).Эту точку можно найти с помощью построения графика, замены, исключения, редукции по Гауссу, обращения матрицы или правила Крамера.
Например, решением пересечения прямых x + 2y = 16 и x + y = 9 является точка (2,7).Эту точку можно найти с помощью построения графика, замены, исключения, редукции по Гауссу, обращения матрицы или правила Крамера.
Для этой системы угловыми точками являются (0,0), (0,8), (2,7), (6,3) и (8,0).
Обратите внимание, что каждая угловая точка является пересечением двух линий, но не каждое пересечение двух линий является угловой точкой. Например, точка (6,3) является пересечением 3x + 2y = 24 и x + y = 9, но пересечение 3x + 2y = 24 и x + 2y = 16 находится за пределами допустимой области, поэтому это не угловая точка.
Оценить целевую функцию в каждой угловой точке
Наконец-то мы подошли к тому месту, где мы собираемся посмотреть на целевую функцию, P = 40x + 30y. Все, что мы сделали до сих пор, связано только с ограничениями или неравенством. Самый простой способ сделать это — сделать стол.
| x | л | P = 40x + 30y |
|---|---|---|
| 0 | 0 | 0 + 0 = 0 |
| 0 | 8 | 0 + 240 = 240 |
| 2 | 7 | 80 + 210 = 290 |
| 6 | 3 | 240 + 90 = 330 |
| 8 | 0 | 320 + 0 = 320 |
Поскольку целью было максимизировать P, а наибольшее значение P достигается, когда x = 6 и y = 3, мы можем дать ответ на задачу линейного программирования.
Максимальное значение P равно 330, когда x = 6 и y = 3.
Если бы целью было минимизировать P, то мы могли бы сказать, что минимальное значение P равно 0, когда x = 0 и y = 0.
Другие целевые функции с такими же ограничениями
Допустим, у вас была такая же допустимая область, но разные целевые функции.
- Максимизировать P = 40x + 30y (исходная целевая функция)
- Увеличить P = 20x + 30y
- Увеличить P = 10x + 30y
- Увеличить P = 50x + 30y
- Увеличить P = 30x + 30y
Самый простой способ добиться этого — просто расширить таблицу дополнительными столбцами для каждой из других целевых функций.
| x | л | 40x + 30лет | 20x + 30лет | 10x + 30лет | 50x + 30лет | 30x + 30лет |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 8 | 240 | 240 | 240 | 240 | 240 |
| 2 | 7 | 290 | 250 | 230 | 310 | 270 |
| 6 | 3 | 330 | 210 | 150 | 390 | 270 |
| 8 | 0 | 320 | 160 | 80 | 400 | 240 |
В каждом случае максимальное значение было выделено полужирным шрифтом , , поэтому вы можете видеть, где оно находится.
- Максимальное значение P = 40x + 30y равно 330, когда x = 6 и y = 3.
- Максимальное значение P = 20x + 30y равно 250, когда x = 2 и y = 7.
- Максимальное значение P = 10x + 30y равно 240, когда x = 0 и y = 8.
- Максимальное значение P = 50x + 30y составляет 400, когда x = 8 и y = 0.
- Максимальное значение P = 30x + 30y составляет 270, когда x = 2 и y = 7 ИЛИ, когда x = 6 и y = 3 ?????
Несколько решений
Обратите внимание, что последний дает нам небольшую проблему.Максимальное значение 270 встречается не только при x = 2 и y = 7, но также при x = 6 и y = 3. Фактически, это также происходит при x = 3 и y = 6, когда x = 4 и y = 5. , когда x = 5 и y = 4, когда x = 4.6 и y = 4.4, и любая другая точка на отрезке прямой между (2,7) и (6,3).
, когда x = 5 и y = 4, когда x = 4.6 и y = 4.4, и любая другая точка на отрезке прямой между (2,7) и (6,3).
Это тот случай, когда в основной теореме линейного программирования упоминается, что решение является границей между двумя угловыми точками. Каждая точка между (2,7) и (6,3) находится на прямой x + y = 9.
Но не каждая точка на прямой x + y = 9 является решением.Например, x = 1 и y = 8 даже не находятся в допустимой области. Итак, нам нужно ограничить наш домен только той частью линейного сегмента, которая нам нужна.
Итак, теперь мы можем ответить на эту последнюю проблему.
Максимальное значение P = 30x + 30y составляет 270, когда x + y = 9 и 2 ≤ x ≤ 6.
В качестве альтернативы вы можете использовать параметрическую форму и сказать, что максимальное значение P равно 270, когда x = 2 + 4t, y = 7-4t, 0 ≤ t ≤ 1. Большинство людей найдут первую форму проще.
Геометрия
— Учитывая отношения расстояний от трех углов прямоугольника, найдите координаты точки с указанными отношениями.2} $. Единичный вектор, указывающий из $ A $ в $ B $, равен $ U = \ frac {B-A} {d} $. Тогда $ V $ — это единичный вектор, перпендикулярный $ U $ — просто поменяйте координаты и измените знак. Наконец, мы можем найти (до) двух точек решения:
$$ P = A + uU \ pm vV $$
линейный Программирование: Введение (стр. 1 из 5) Разделы: Оптимизация линейных систем, Устранение проблем со словами Линейное программирование — это процесс принятия
различные линейные неравенства, относящиеся к некоторой ситуации, и нахождение
«лучшая» стоимость, достижимая в этих условиях.Типичный пример
будет принимать ограничения материалов и рабочей силы, а затем определять
«лучшие» уровни производства для максимальной прибыли при тех
условия. В «реальной жизни», линейное программирование является частью очень важной области математики под названием «оптимизация техники ». Эта область исследования (или хотя бы прикладные результаты его) используются каждый день при организации и распределении ресурсов.Эти «реальные» системы могут иметь десятки или сотни переменных, или больше. Однако в алгебре вы будете работать только с простыми (и наглядными) двухвариантный линейный случай. Общий процесс решения линейного программирования упражнения — графическое отображение неравенств (называемых «ограничениями») для формирования отгороженной области на плоскости x, y (так называемая «область осуществимости»). Затем вы выясняете координаты углов этой области допустимости (то есть вы найдете пересечение точки различных пар линий) и проверьте эти угловые точки в формула (называемая «уравнением оптимизации»), для которой вы пытаясь найти наибольшее или наименьшее значение.
Три неравенства в фигурных скобках это ограничения.Площадь самолета, которую они размечают, будет область осуществимости. Формула « z = 3 x + 4 y «равно уравнение оптимизации. Мне нужно найти ( x , у ) угловые точки выполнимости область, которая возвращает наибольшее и наименьшее значения z . Мой первый шаг — решить каждое неравенство для более наглядных эквивалентных форм: Легко построить график система: Авторские права Элизабет Стапель 2006-2011 Все права защищены Чтобы найти угловые точки, которых нет всегда ясно с графика — я соединю линии (таким образом формируя систему линейных уравнений) и решите:
Таким образом, угловые точки равны (2, 6), (6, 4) и (1, 3). Кто-то действительно умный доказал, что для такие линейные системы, максимальное и минимальное значения оптимизации уравнение всегда будет на углах области выполнимости. Так, чтобы найти решение этого упражнения, мне нужно подключить только эти три указывает на « z = 3 x + 4 y «. (2, 6): z = 3 (2) + 4 (6) = 6 + 24 = 30 Затем максимум z = 34 встречается
в (6,
4) , Верх | 1 | 2 | 3 | 4 | 5 | Вернуться к указателю Далее >>
|
Поиск линий и углов вашей собственности
При поиске памятников мы обычно используем три инструмента: обзорную карту, металлоискатель (или «пин-искатель») и лопату. Карты показывают нам, где искать, а металлоискатель дает нам более точную информацию.Памятники, как правило, со временем закапываются, поэтому может потребоваться лопата, чтобы копать где-нибудь на глубину от нескольких дюймов до нескольких футов.
Карты показывают нам, где искать, а металлоискатель дает нам более точную информацию.Памятники, как правило, со временем закапываются, поэтому может потребоваться лопата, чтобы копать где-нибудь на глубину от нескольких дюймов до нескольких футов.
Примечание: Люди (соседи) очень интересуются, когда кто-то копается в том, что они считают своей собственностью. Перед поиском памятников обязательно поговорите с соседями. Это вежливо, и кто знает? Может, они помогут с поиском.
С чего начать поиск?
Итак, мы знаем, как искать памятники. Но с чего начать? Начните с того, что спросите людей, которые, возможно, уже нашли ваши уголки: например, соседей и предыдущих владельцев недвижимости.Если кто-то строил на вашей собственности в прошлом, они также могут быть хорошим ресурсом, поскольку заявки на получение разрешения на строительство часто требуют расположения линий собственности.
Карты обзора обычно показывают, где находятся ваши памятники, если они существуют. Если вы живете в округе Бентон, штат Орегон, вы можете использовать инструмент съемочных карт, чтобы найти карты для своей собственности.
Нанять профессионала:
Если после исследования вы не можете найти свои памятники, есть другой вариант.Землемеры, такие как JD McGee, inc. может провести исследование и найти уголки вашей собственности по разумной цене. Если ваши углы не были отмечены памятниками, мы можем отметить их для вас или даже установить официальные памятники и записать новую карту. Чтобы узнать больше о том, как мы можем помочь вам с вашей недвижимостью, свяжитесь с нами сегодня!
Несколько полезных советов:
К сожалению, использование спортивного GPS-навигатора — не лучший способ определить местонахождение уголков вашей собственности. Для вашего угла нет GPS-координат, но если бы они были, то в большинстве распространенных GPS-устройств просто не хватало бы точности.
На вашей собственности не должно быть никаких памятников. Многие объекты были созданы, а не памятниками. Когда вы нанимаете профессионального геодезиста, такого как Джей Ди МакГи, мы можем использовать другие методы, чтобы найти уголки вашей собственности и отметить их для дальнейшего использования.
Многие объекты были созданы, а не памятниками. Когда вы нанимаете профессионального геодезиста, такого как Джей Ди МакГи, мы можем использовать другие методы, чтобы найти уголки вашей собственности и отметить их для дальнейшего использования.
Как найти углы на изображении с помощью OpenCv
Вот реализация, использующая cv2.goodFeaturesToTrack () для обнаружения углов. Подход
- Преобразовать изображение в оттенки серого
- Обнаружение тонких краев
- Обнаружение углов
- При желании выполнить преобразование перспективы по 4 точкам, чтобы получить вид сверху вниз изображения
Используя это начальное изображение,
После преобразования в оттенки серого мы выполняем точное обнаружение краев
Теперь, когда у нас есть достойный двоичный образ, мы можем использовать cv2.goodFeaturesToTrack ()
углов = cv2.goodFeaturesToTrack (ловкий, 4, 0,5, 50)
Для параметров мы даем ему хитроумное изображение, устанавливаем максимальное количество углов на 4 ( maxCorners ), используем минимально допустимое качество 0,5 ( qualityLevel ) и устанавливаем минимально возможное евклидово расстояние между возвращаемыми углами. до 50 ( мин Расстояние ). Вот результат
Теперь, когда мы определили углы, мы можем выполнить 4-точечное перспективное преобразование, чтобы получить вид сверху на объект.Сначала мы упорядочиваем точки по часовой стрелке, а затем рисуем результат на маске.
Примечание: мы могли бы просто найти контуры на изображении Canny вместо того, чтобы делать этот шаг для создания маски, но представьте, что у нас есть только 4 угловые точки для работы с
. Затем мы находим контуры на этой маске и фильтруем, используя cv2.arcLength () и cv2.approxPolyDP () . По идее, если у контура 4 точки, то это должен быть наш объект. Получив этот контур, мы выполняем перспективное преобразование
Получив этот контур, мы выполняем перспективное преобразование
Наконец, мы поворачиваем изображение в зависимости от желаемой ориентации.Вот результат
Код только для определения углов
импорт CV2
изображение = cv2.imread ('1.png')
серый = cv2.cvtColor (изображение, cv2.COLOR_BGR2GRAY)
canny = cv2.Canny (серый, 120, 255, 1)
corners = cv2.goodFeaturesToTrack (ловкий, 4,0.5,50)
для угла в углах:
x, y = corner.ravel ()
cv2.circle (изображение, (x, y), 5, (36,255,12), - 1)
cv2.imshow ('хитрый', хитрый)
cv2.imshow ('изображение', изображение)
cv2.waitKey ()
Код для определения углов и выполнения перспективного преобразования
импорт CV2
импортировать numpy как np
def rotate_image (изображение, угол):
# Возьмите размеры изображения, а затем определите центр
(h, w) = изображение.форма [: 2]
(cX, cY) = (w / 2, h / 2)
# захватить матрицу вращения (применяя отрицательное значение
# угол поворота по часовой стрелке), затем возьмите синус и косинус
# (т.е. компоненты вращения матрицы)
M = cv2.getRotationMatrix2D ((cX, cY), -angle, 1.0)
cos = np.abs (M [0, 0])
sin = np.abs (M [0, 1])
# Вычислить новые ограничивающие размеры изображения
nW = int ((h * sin) + (w * cos))
nH = int ((h * cos) + (w * sin))
# Отрегулируйте матрицу вращения, чтобы учесть перевод
M [0, 2] + = (nW / 2) - cX
M [1, 2] + = (nH / 2) - cY
# Выполните фактическое вращение и верните изображение
вернуть cv2.warpAffine (изображение, M, (nW, nH))
def order_points_clockwise (баллы):
# сортируем точки по их x-координатам
xSorted = pts [np.argsort (pts [:, 0]),:]
# берем крайнюю левую и крайнюю правую точки из отсортированных
# x-roodinate points
leftMost = xSorted [: 2,:]
rightMost = xSorted [2 :,:]
# теперь отсортируйте крайние левые координаты по их
# y-координаты, чтобы мы могли взять верхний левый и нижний левый
# балла соответственно
leftMost = leftMost [np. argsort (leftMost [:, 1]),:]
(tl, bl) = leftMost
# теперь отсортируйте крайние правые координаты по их
# y-координаты, чтобы мы могли взять верхний правый и нижний правый
# балла соответственно
rightMost = rightMost [np.argsort (rightMost [:, 1]),:]
(tr, br) = rightMost
# вернуть координаты в верхнем левом, верхнем правом,
# нижний правый и нижний левый порядок
return np.array ([tl, tr, br, bl], dtype = "int32")
def перспектива_трансформа (изображение, углы):
def order_corner_points (углы):
# Разделить углы на отдельные точки
# Индекс 0 - вверху справа
# 1 - вверху слева
# 2 - внизу слева
# 3 - внизу справа
corners = [(corner [0] [0], corner [0] [1]) для угла в углах]
top_r, top_l, bottom_l, bottom_r = углы [0], углы [1], углы [2], углы [3]
return (top_l, top_r, bottom_r, bottom_l)
# Порядок точек по часовой стрелке
Order_corners = order_corner_points (углы)
top_l, top_r, bottom_r, bottom_l = упорядоченные_уголки
# Определить ширину нового изображения, которая является максимальным расстоянием между
# (нижний правый и нижний левый) или (верхний правый и верхний левый) координаты x
width_A = np.sqrt (((bottom_r [0] - bottom_l [0]) ** 2) + ((bottom_r [1] - bottom_l [1]) ** 2))
width_B = np.sqrt (((top_r [0] - top_l [0]) ** 2) + ((top_r [1] - top_l [1]) ** 2))
ширина = макс (интервал (ширина_A), интервал (ширина_B))
# Определить высоту нового изображения, которая является максимальным расстоянием между
# (верхний правый и нижний правый) или (верхний левый и нижний левый) координаты Y
height_A = np.sqrt (((top_r [0] - bottom_r [0]) ** 2) + ((top_r [1] - bottom_r [1]) ** 2))
height_B = np.sqrt (((top_l [0] - bottom_l [0]) ** 2) + ((top_l [1] - bottom_l [1]) ** 2))
высота = макс (int (высота_A), int (высота_B))
# Построить новые точки для получения изображения сверху вниз в
# top_r, top_l, bottom_l, bottom_r порядок
размеры = np.
argsort (leftMost [:, 1]),:]
(tl, bl) = leftMost
# теперь отсортируйте крайние правые координаты по их
# y-координаты, чтобы мы могли взять верхний правый и нижний правый
# балла соответственно
rightMost = rightMost [np.argsort (rightMost [:, 1]),:]
(tr, br) = rightMost
# вернуть координаты в верхнем левом, верхнем правом,
# нижний правый и нижний левый порядок
return np.array ([tl, tr, br, bl], dtype = "int32")
def перспектива_трансформа (изображение, углы):
def order_corner_points (углы):
# Разделить углы на отдельные точки
# Индекс 0 - вверху справа
# 1 - вверху слева
# 2 - внизу слева
# 3 - внизу справа
corners = [(corner [0] [0], corner [0] [1]) для угла в углах]
top_r, top_l, bottom_l, bottom_r = углы [0], углы [1], углы [2], углы [3]
return (top_l, top_r, bottom_r, bottom_l)
# Порядок точек по часовой стрелке
Order_corners = order_corner_points (углы)
top_l, top_r, bottom_r, bottom_l = упорядоченные_уголки
# Определить ширину нового изображения, которая является максимальным расстоянием между
# (нижний правый и нижний левый) или (верхний правый и верхний левый) координаты x
width_A = np.sqrt (((bottom_r [0] - bottom_l [0]) ** 2) + ((bottom_r [1] - bottom_l [1]) ** 2))
width_B = np.sqrt (((top_r [0] - top_l [0]) ** 2) + ((top_r [1] - top_l [1]) ** 2))
ширина = макс (интервал (ширина_A), интервал (ширина_B))
# Определить высоту нового изображения, которая является максимальным расстоянием между
# (верхний правый и нижний правый) или (верхний левый и нижний левый) координаты Y
height_A = np.sqrt (((top_r [0] - bottom_r [0]) ** 2) + ((top_r [1] - bottom_r [1]) ** 2))
height_B = np.sqrt (((top_l [0] - bottom_l [0]) ** 2) + ((top_l [1] - bottom_l [1]) ** 2))
высота = макс (int (высота_A), int (высота_B))
# Построить новые точки для получения изображения сверху вниз в
# top_r, top_l, bottom_l, bottom_r порядок
размеры = np. array ([[0, 0], [ширина - 1, 0], [ширина - 1, высота - 1],
[0, высота - 1]], dtype = "float32")
# Преобразовать в формат Numpy
Order_corners = np.array (Order_corners, dtype = "float32")
# Найти матрицу перспективного преобразования
матрица = cv2.getPerspectiveTransform (упорядоченные_уголки, размеры)
# Вернуть преобразованное изображение
return cv2.warpPerspective (изображение, матрица, (ширина, высота))
изображение = cv2.imread ('1.png')
оригинал = image.copy ()
серый = cv2.cvtColor (изображение, cv2.COLOR_BGR2GRAY)
canny = cv2.Canny (серый, 120, 255, 1)
corners = cv2.goodFeaturesToTrack (ловкий, 4,0.5,50)
c_list = []
для угла в углах:
x, y = corner.ravel ()
c_list.append ([int (x), int (y)])
cv2.circle (изображение, (x, y), 5, (36,255,12), - 1)
corner_points = np.array ([c_list [0], c_list [1], c_list [2], c_list [3]])
order_corner_points = order_points_clockwise (угловые_поинты)
маска = np.zeros (image.shape, dtype = np.uint8)
cv2.fillPoly (маска, [точки_порядоченного_круга], (255,255,255))
маска = cv2.cvtColor (маска, cv2.COLOR_BGR2GRAY)
cnts = cv2.findContours (маска, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
cnts = cnts [0] if len (cnts) == 2 else cnts [1]
для c в центрах:
пери = cv2.arcLength (c, Истина)
приблизительно = cv2.approxPolyDP (c, 0,015 * пери, True)
если len (приблизительно) == 4:
transformed = перспектива_трансформа (оригинал, прибл.)
result = rotate_image (преобразованный, -90)
cv2.imshow ('хитрый', хитрый)
cv2.imshow ('изображение', изображение)
cv2.imshow ('маска', маска)
cv2.imshow ('преобразованный', преобразованный)
cv2.imshow ('результат', результат)
cv2.waitKey ()
array ([[0, 0], [ширина - 1, 0], [ширина - 1, высота - 1],
[0, высота - 1]], dtype = "float32")
# Преобразовать в формат Numpy
Order_corners = np.array (Order_corners, dtype = "float32")
# Найти матрицу перспективного преобразования
матрица = cv2.getPerspectiveTransform (упорядоченные_уголки, размеры)
# Вернуть преобразованное изображение
return cv2.warpPerspective (изображение, матрица, (ширина, высота))
изображение = cv2.imread ('1.png')
оригинал = image.copy ()
серый = cv2.cvtColor (изображение, cv2.COLOR_BGR2GRAY)
canny = cv2.Canny (серый, 120, 255, 1)
corners = cv2.goodFeaturesToTrack (ловкий, 4,0.5,50)
c_list = []
для угла в углах:
x, y = corner.ravel ()
c_list.append ([int (x), int (y)])
cv2.circle (изображение, (x, y), 5, (36,255,12), - 1)
corner_points = np.array ([c_list [0], c_list [1], c_list [2], c_list [3]])
order_corner_points = order_points_clockwise (угловые_поинты)
маска = np.zeros (image.shape, dtype = np.uint8)
cv2.fillPoly (маска, [точки_порядоченного_круга], (255,255,255))
маска = cv2.cvtColor (маска, cv2.COLOR_BGR2GRAY)
cnts = cv2.findContours (маска, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
cnts = cnts [0] if len (cnts) == 2 else cnts [1]
для c в центрах:
пери = cv2.arcLength (c, Истина)
приблизительно = cv2.approxPolyDP (c, 0,015 * пери, True)
если len (приблизительно) == 4:
transformed = перспектива_трансформа (оригинал, прибл.)
result = rotate_image (преобразованный, -90)
cv2.imshow ('хитрый', хитрый)
cv2.imshow ('изображение', изображение)
cv2.imshow ('маска', маска)
cv2.imshow ('преобразованный', преобразованный)
cv2.imshow ('результат', результат)
cv2.waitKey ()
Как найти очереди собственности
Фото: istockphoto.com
Хорошие заборы могут стать хорошими соседями, но случайное возведение ограды на участке соседа может привести к обидам или даже к судебному процессу. Если вы хотите построить пристройку, выяснить, кто несет ответственность за вырубку деревьев, или посадить живую изгородь, вам нужно знать, где законно заканчивается ваш двор и начинается следующий. Здесь мы собрали наиболее распространенные методы решения этой проблемы.Некоторые из них простые и недорогие, достаточные для удовлетворения вашего любопытства. Другие требуют навыков и будут стоить несколько долларов, но могут быть необходимы для определенных строительных проектов. Читайте дальше, чтобы узнать, как пройти черту — и убедитесь, что ваш дом и ландшафт остаются на вашей стороне.
Здесь мы собрали наиболее распространенные методы решения этой проблемы.Некоторые из них простые и недорогие, достаточные для удовлетворения вашего любопытства. Другие требуют навыков и будут стоить несколько долларов, но могут быть необходимы для определенных строительных проектов. Читайте дальше, чтобы узнать, как пройти черту — и убедитесь, что ваш дом и ландшафт остаются на вашей стороне.
Изучите линии, прорезанные на тротуаре перед вашим домом. Часто подрядчик, который заливал тротуар, начинал и останавливался на границах участка, поэтому эти линии разреза могут совпадать с краями вашего участка.Кроме того, внешний вид бетона на вашей стороне участка может немного отличаться от внешнего вида на стороне вашего соседа. Уличные фонари тоже часто устанавливают на границах владений. Хотя эти визуальные подсказки являются хорошим индикатором границ собственности, если вы собираетесь построить или установить что-то на своей земле, вам потребуется дополнительная проверка.
Посетите местный отдел зонированияДепартамент зонирования — это муниципальное управление, которое регистрирует таблички: карты, нарисованные в масштабе, которые показывают разделение земли.Если ваш дом не был построен более ста лет назад, вы, вероятно, сможете получить копию своего квартала и участка за минимальную плату. Это даст вам точные размеры вашего участка — другими словами, собственности, которой вы владеете на законных основаниях — по отношению к другим участкам в вашем квартале.
Повторение шагов геодезиста Когда геодезисты выкладывали исходную площадку, они определили отправную точку для всех участков на вашем участке. Вы можете проследить исходные шаги геодезиста, указав начальную точку, которая будет помечена на планшете как «общая точка» или «начальная точка» (POB).Часто это центр переулка. Все первоначальные измерения геодезиста будут указаны на табличке. С длинной рулеткой следите за платформой, как если бы вы делали карту сокровищ, измеряя свое физическое состояние по ходу движения. Ваши мерки должны соответствовать указанным на тарелке.
С длинной рулеткой следите за платформой, как если бы вы делали карту сокровищ, измеряя свое физическое состояние по ходу движения. Ваши мерки должны соответствовать указанным на тарелке.
Фото: istockphoto.com
Найдите скрытую геодезическую меткуГеодезическая булавка — это тонкие железные стержни длиной от двух до трех футов, иногда покрытые пластиком, которые первоначальная съемочная группа вставляла в границы участка.Если у вас есть доступ к металлоискателю, переместите устройство по земле вдоль тротуара к бордюру, чтобы определить местонахождение маркера. Булавки можно закопать прямо под поверхностью или на фут ниже. Однако за несколько дней до того, как вы начнете копать, вы должны позвонить 811 — бесплатному федеральному номеру, по которому вы попадете в местную коммунальную компанию. Попросите коммунальную компанию выйти и отметить любые заглубленные линии, чтобы случайно не попасть в них. Плата за эту услугу не взимается, но если вы повредите подземный коммуникационный трубопровод, вам придется заплатить за его ремонт.
Остерегайтесь перемещенных маркеров для обследованияМаркеры для обследования не являются надежными маркерами. За прошедшие годы предыдущие владельцы, коммунальные работники или даже лесозаготовительная компания могли выкопать геодезический значок и снова вставить его поблизости или просто выбросить в сторону. Однако ваша фактическая линия собственности не изменилась только потому, что кто-то испортил значок опроса. Например, если вы размещаете геодезические булавки на расстоянии 60 футов друг от друга на противоположных сторонах вашего участка, но на платформе указано, что ваш участок имеет ширину 50 футов, одна из этих булавок могла быть перемещена, а размер вашего участка все еще составляет всего 50 футов в поперечнике.
Найдите дополнительную информацию в своем документе В старых кварталах владельцы собственности могли купить или продать часть своих дворов. Если найти значок для опроса, это не даст вам этой информации, но в самом последнем юридическом описании, внесенном в ваш документ, будут перечислены все такие изменения. Если у вас нет копии вашего акта, зарегистрированного в записях домовладельца, получите ее в офисе реестра документов, который часто находится в здании окружного суда.
Если найти значок для опроса, это не даст вам этой информации, но в самом последнем юридическом описании, внесенном в ваш документ, будут перечислены все такие изменения. Если у вас нет копии вашего акта, зарегистрированного в записях домовладельца, получите ее в офисе реестра документов, который часто находится в здании окружного суда.
Если в вашем документе есть обзор меток и границ — опрос, который описывает точные расстояния и направления от одной установленной точки на вашей линии владения до другой, — у вас будет вся информация вам нужно определить местонахождение ваших границ собственности.К сожалению, этот тип юридического описания, как известно, трудно понять, если вы не геодезист.
Обследование границ и метража указывает отправную точку, расположенную в одном из углов вашего участка. Оттуда опрос предоставит вам подробные указания и расстояния, чтобы помочь вам найти остальные углы и границы вашего участка. Это похоже на игру «соедини точки», за исключением того, что вы делаете это пешком, а не на бумаге. Вам понадобится длинная измерительная лента, а также качественный направленный компас, чтобы вы могли систематически перемещаться от точки к точке.
Но егад! Вы обнаружите, что опрос по методу и границам читается как шекспировская пьеса. Типичная съемка может сказать вам «начать» с точки начала (POB), «пробежать оттуда на 100 футов на запад, затем на юг под внутренним углом 55 градусов к точке» и так далее, пока не вернет вас обратно к точке. исходная отправная точка.
Пригласите профессионального геодезиста Прежде чем вы слишком сильно сходите с ума с обследованием меток и границ, знайте, что это единственный юридически обязательный метод определения точных границ собственности, необходимый, например, если вы собираетесь построить дополнение к Ваш дом — это профессиональное обследование.Местные строительные нормы и правила определяют, насколько близко к вашей собственности вы можете построить закон. Профессиональное обследование может стоить от нескольких сотен до более тысячи долларов, в зависимости от размера вашей собственности и сложности обследования. Возможно, это дорого, но добавление к дому своей мечты при сохранении благосклонности соседей бесценно.
Профессиональное обследование может стоить от нескольких сотен до более тысячи долларов, в зависимости от размера вашей собственности и сложности обследования. Возможно, это дорого, но добавление к дому своей мечты при сохранении благосклонности соседей бесценно.
Пригласите профессионального геодезиста
Некоторые работы лучше оставить профессионалам. Сравните цитаты от проверенных местных геодезистов сегодня.
+Отметить только уголки собственности | Геодезия земли в Грузии
Если вам нужно уточнить границы вашей собственности, но вы не обязательно хотите или не должны оплачивать полное обследование границ или разбивку границ земельных участков, Геодезия Джорджии может прийти и отметить только углы собственности. Этот вариант можно выбрать, если собственнику недвижимости нужно найти только угловые штифты на своем участке. Разметка углов собственности часто бывает всем, что вам нужно, чтобы предотвратить посягательство на собственность вашего соседа или уладить любой существующий спор.
КОГДА МОЖНО НУЖНО ОТМЕТИТЬ УГОЛКИ ВАШЕЙ СОБСТВЕННОСТИ?
Вот несколько примеров, в которых маркировка углов участков может быть более реальной альтернативой полному обследованию границ:
- Если вы планируете построить забор вокруг своей собственности и хотите быть уверенным, что устанавливаете его на своей земле
- Если ваш участок достаточно мал, чтобы границы участков можно было визуализировать, только видя угловые булавки (на больших участках земли требуется больше деталей)
- Если ваш участок ограничен прямолинейными границами, которые можно определить только по углам
- Если вам требуется более подробное разъяснение границ собственности между вами и вашими соседями для разрешения спора, не имеющего временного характера
ПРОЦЕСС МАРКИРОВКИ ИМУЩЕСТВЕННЫХ УГЛОВ
Наша бригада проведет обследование границ вашего владения, чтобы убедиться, что найденные штифты верны, а затем четко пометить эти штифты оранжевым флажком.


 ∠АОD = ∠ВОС = 23° (по теореме о вертикальных углах)
∠АОD = ∠ВОС = 23° (по теореме о вертикальных углах)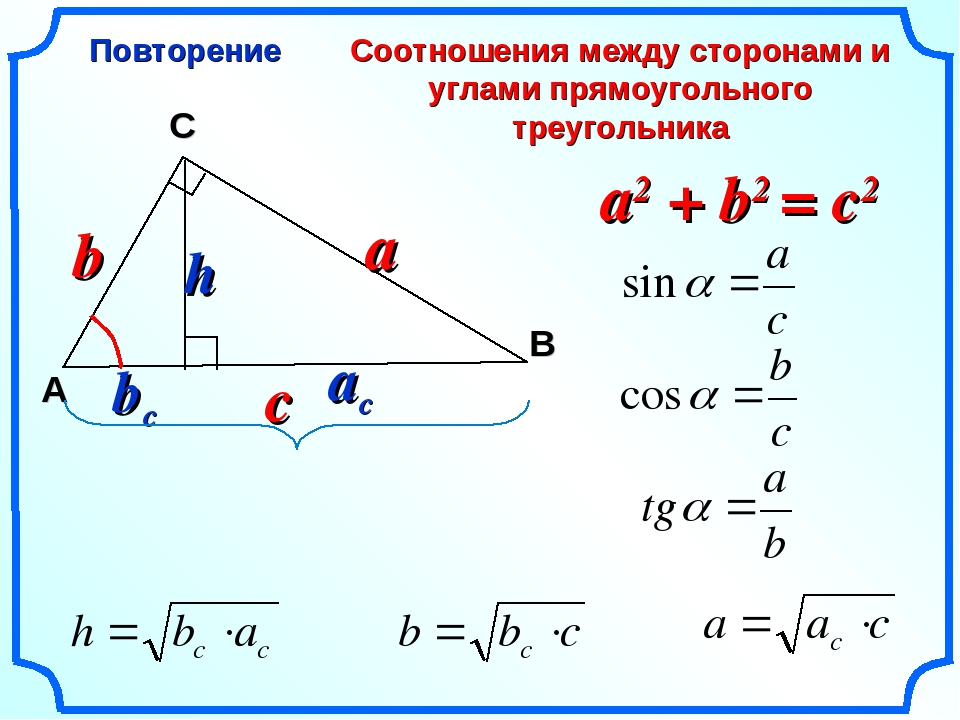
 при (1,
3)
при (1,
3) argsort (leftMost [:, 1]),:]
(tl, bl) = leftMost
# теперь отсортируйте крайние правые координаты по их
# y-координаты, чтобы мы могли взять верхний правый и нижний правый
# балла соответственно
rightMost = rightMost [np.argsort (rightMost [:, 1]),:]
(tr, br) = rightMost
# вернуть координаты в верхнем левом, верхнем правом,
# нижний правый и нижний левый порядок
return np.array ([tl, tr, br, bl], dtype = "int32")
def перспектива_трансформа (изображение, углы):
def order_corner_points (углы):
# Разделить углы на отдельные точки
# Индекс 0 - вверху справа
# 1 - вверху слева
# 2 - внизу слева
# 3 - внизу справа
corners = [(corner [0] [0], corner [0] [1]) для угла в углах]
top_r, top_l, bottom_l, bottom_r = углы [0], углы [1], углы [2], углы [3]
return (top_l, top_r, bottom_r, bottom_l)
# Порядок точек по часовой стрелке
Order_corners = order_corner_points (углы)
top_l, top_r, bottom_r, bottom_l = упорядоченные_уголки
# Определить ширину нового изображения, которая является максимальным расстоянием между
# (нижний правый и нижний левый) или (верхний правый и верхний левый) координаты x
width_A = np.sqrt (((bottom_r [0] - bottom_l [0]) ** 2) + ((bottom_r [1] - bottom_l [1]) ** 2))
width_B = np.sqrt (((top_r [0] - top_l [0]) ** 2) + ((top_r [1] - top_l [1]) ** 2))
ширина = макс (интервал (ширина_A), интервал (ширина_B))
# Определить высоту нового изображения, которая является максимальным расстоянием между
# (верхний правый и нижний правый) или (верхний левый и нижний левый) координаты Y
height_A = np.sqrt (((top_r [0] - bottom_r [0]) ** 2) + ((top_r [1] - bottom_r [1]) ** 2))
height_B = np.sqrt (((top_l [0] - bottom_l [0]) ** 2) + ((top_l [1] - bottom_l [1]) ** 2))
высота = макс (int (высота_A), int (высота_B))
# Построить новые точки для получения изображения сверху вниз в
# top_r, top_l, bottom_l, bottom_r порядок
размеры = np.
argsort (leftMost [:, 1]),:]
(tl, bl) = leftMost
# теперь отсортируйте крайние правые координаты по их
# y-координаты, чтобы мы могли взять верхний правый и нижний правый
# балла соответственно
rightMost = rightMost [np.argsort (rightMost [:, 1]),:]
(tr, br) = rightMost
# вернуть координаты в верхнем левом, верхнем правом,
# нижний правый и нижний левый порядок
return np.array ([tl, tr, br, bl], dtype = "int32")
def перспектива_трансформа (изображение, углы):
def order_corner_points (углы):
# Разделить углы на отдельные точки
# Индекс 0 - вверху справа
# 1 - вверху слева
# 2 - внизу слева
# 3 - внизу справа
corners = [(corner [0] [0], corner [0] [1]) для угла в углах]
top_r, top_l, bottom_l, bottom_r = углы [0], углы [1], углы [2], углы [3]
return (top_l, top_r, bottom_r, bottom_l)
# Порядок точек по часовой стрелке
Order_corners = order_corner_points (углы)
top_l, top_r, bottom_r, bottom_l = упорядоченные_уголки
# Определить ширину нового изображения, которая является максимальным расстоянием между
# (нижний правый и нижний левый) или (верхний правый и верхний левый) координаты x
width_A = np.sqrt (((bottom_r [0] - bottom_l [0]) ** 2) + ((bottom_r [1] - bottom_l [1]) ** 2))
width_B = np.sqrt (((top_r [0] - top_l [0]) ** 2) + ((top_r [1] - top_l [1]) ** 2))
ширина = макс (интервал (ширина_A), интервал (ширина_B))
# Определить высоту нового изображения, которая является максимальным расстоянием между
# (верхний правый и нижний правый) или (верхний левый и нижний левый) координаты Y
height_A = np.sqrt (((top_r [0] - bottom_r [0]) ** 2) + ((top_r [1] - bottom_r [1]) ** 2))
height_B = np.sqrt (((top_l [0] - bottom_l [0]) ** 2) + ((top_l [1] - bottom_l [1]) ** 2))
высота = макс (int (высота_A), int (высота_B))
# Построить новые точки для получения изображения сверху вниз в
# top_r, top_l, bottom_l, bottom_r порядок
размеры = np. array ([[0, 0], [ширина - 1, 0], [ширина - 1, высота - 1],
[0, высота - 1]], dtype = "float32")
# Преобразовать в формат Numpy
Order_corners = np.array (Order_corners, dtype = "float32")
# Найти матрицу перспективного преобразования
матрица = cv2.getPerspectiveTransform (упорядоченные_уголки, размеры)
# Вернуть преобразованное изображение
return cv2.warpPerspective (изображение, матрица, (ширина, высота))
изображение = cv2.imread ('1.png')
оригинал = image.copy ()
серый = cv2.cvtColor (изображение, cv2.COLOR_BGR2GRAY)
canny = cv2.Canny (серый, 120, 255, 1)
corners = cv2.goodFeaturesToTrack (ловкий, 4,0.5,50)
c_list = []
для угла в углах:
x, y = corner.ravel ()
c_list.append ([int (x), int (y)])
cv2.circle (изображение, (x, y), 5, (36,255,12), - 1)
corner_points = np.array ([c_list [0], c_list [1], c_list [2], c_list [3]])
order_corner_points = order_points_clockwise (угловые_поинты)
маска = np.zeros (image.shape, dtype = np.uint8)
cv2.fillPoly (маска, [точки_порядоченного_круга], (255,255,255))
маска = cv2.cvtColor (маска, cv2.COLOR_BGR2GRAY)
cnts = cv2.findContours (маска, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
cnts = cnts [0] if len (cnts) == 2 else cnts [1]
для c в центрах:
пери = cv2.arcLength (c, Истина)
приблизительно = cv2.approxPolyDP (c, 0,015 * пери, True)
если len (приблизительно) == 4:
transformed = перспектива_трансформа (оригинал, прибл.)
result = rotate_image (преобразованный, -90)
cv2.imshow ('хитрый', хитрый)
cv2.imshow ('изображение', изображение)
cv2.imshow ('маска', маска)
cv2.imshow ('преобразованный', преобразованный)
cv2.imshow ('результат', результат)
cv2.waitKey ()
array ([[0, 0], [ширина - 1, 0], [ширина - 1, высота - 1],
[0, высота - 1]], dtype = "float32")
# Преобразовать в формат Numpy
Order_corners = np.array (Order_corners, dtype = "float32")
# Найти матрицу перспективного преобразования
матрица = cv2.getPerspectiveTransform (упорядоченные_уголки, размеры)
# Вернуть преобразованное изображение
return cv2.warpPerspective (изображение, матрица, (ширина, высота))
изображение = cv2.imread ('1.png')
оригинал = image.copy ()
серый = cv2.cvtColor (изображение, cv2.COLOR_BGR2GRAY)
canny = cv2.Canny (серый, 120, 255, 1)
corners = cv2.goodFeaturesToTrack (ловкий, 4,0.5,50)
c_list = []
для угла в углах:
x, y = corner.ravel ()
c_list.append ([int (x), int (y)])
cv2.circle (изображение, (x, y), 5, (36,255,12), - 1)
corner_points = np.array ([c_list [0], c_list [1], c_list [2], c_list [3]])
order_corner_points = order_points_clockwise (угловые_поинты)
маска = np.zeros (image.shape, dtype = np.uint8)
cv2.fillPoly (маска, [точки_порядоченного_круга], (255,255,255))
маска = cv2.cvtColor (маска, cv2.COLOR_BGR2GRAY)
cnts = cv2.findContours (маска, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
cnts = cnts [0] if len (cnts) == 2 else cnts [1]
для c в центрах:
пери = cv2.arcLength (c, Истина)
приблизительно = cv2.approxPolyDP (c, 0,015 * пери, True)
если len (приблизительно) == 4:
transformed = перспектива_трансформа (оригинал, прибл.)
result = rotate_image (преобразованный, -90)
cv2.imshow ('хитрый', хитрый)
cv2.imshow ('изображение', изображение)
cv2.imshow ('маска', маска)
cv2.imshow ('преобразованный', преобразованный)
cv2.imshow ('результат', результат)
cv2.waitKey ()