Какие приборы применяют для построения прямых углов на местности
Теорема: если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180°, То прямые параллельны.
доказательство: даны две прямые а и b образуют с секущей АВ разные внутренние накрест лежащие углы. Допустим, пусть прямые a и b не параллельны, и пересекаются в некоторой точке С. секущая AB разбивает плоскость на две полуплоскости. В одной из них лежит точка C. Построим треугольник АBС1, равный треугольнику ABC, с вершиной C1 в другой полуплоскости. По условию внутренние накрест лежащие углы при прямых а b и секущей AB равны. и соответствующие углы треугольников ABC и ВАС1 совершенной А и В равны, то они совпадают с внутренними накрест лежащими углами. значит прямая АС1 совпадает с прямой а, а прямая BC1 совпадает с прямой b. получается, что через точки C и C1 проходят две различные Прямые a и b. А это невозможно, значит, Прямые a и b параллельны.
Ответ на фото. внешний угол при вершине противолежащий основанию равен сумме углов при основании.
Какие приборы применяют для построения прямых углов на местности?
Если имеется в виду как называются приборы ГАИшников, то это «радар» их очень много видов, вот сайт на котором подробно описываются многие из них, есть и с видео съёмкой, есть и обычные приборы, которые просто показывают скорость.
Если сжечь 1 кг метана, то он даст 55550 кДж тепла, а 1 кг пропана — 50350 кДж.
Если Вам для обогрева помещения нужно 20000 кДж тепла, то его можно получить только путём сожжения 0,360 кг метана или 0,397 кг пропана. И никакой «экономитель» не позволит Вам получить эти 20000 кДж, сжигая лишь 0,300 кг метана. Так что, чудо это или лохотрон, определяйте сами. Кстати то же самое относится и к «экономителям» электроэнергии.
Как показывает практика это лохотрон и никакую энергию этот прибор экономить не может да еще в такой маленькой коробочке. Посмотрите видео и тогда все станет понятно.
Посмотрите видео и тогда все станет понятно.
Два светодиода подключены к сети 220В и это вся схема которую предлагают купить для экономии электроэнергии.
В автомобильный прикуриватель можно «вставить» много чего полезного. Паяльник, вулканизатор, компрессор, переносной светильник, вентилятор, автомобильный телевизор (если эти приборы питаются от 12-ти вольт). Можно подключить устройство понижающее напряжение до необходимого значения, например до 5-ти вольт. Тогда через гнездо прикуривателя можно заряжать телефон и всё остальное, что заряжается от 5-ти вольт. Если использовать умножитель напряжения, то возможно подключение электроприборов питающихся от 220-ть вольт.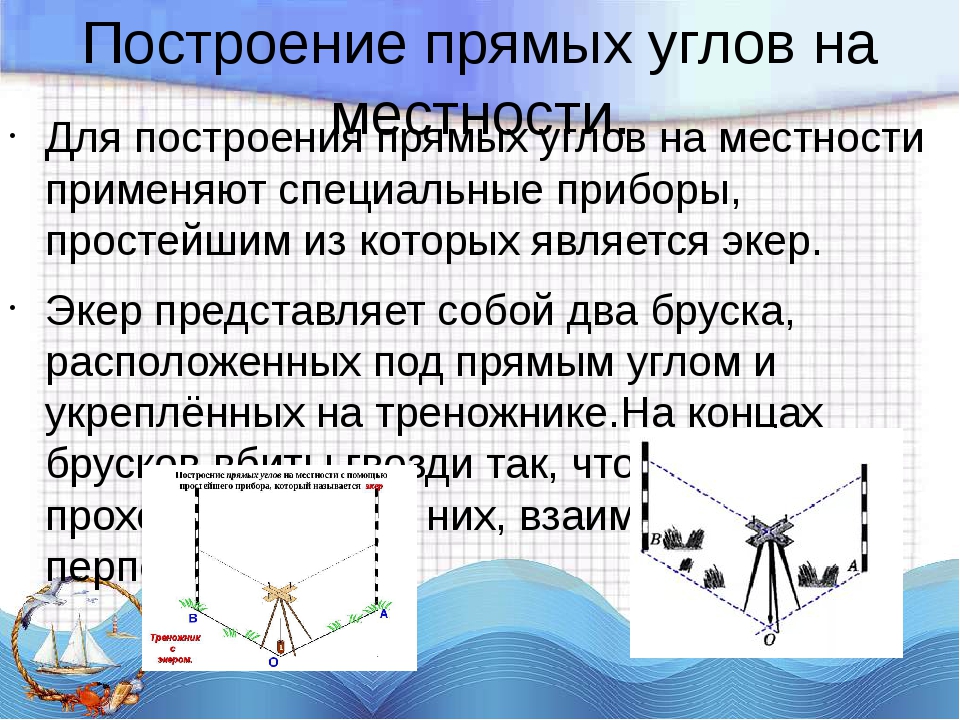
Гармонический анализатор — это прибор для вычисления коэффициентов входящих в разложение Фурье. Существуют различные типы такого рода приборов. Наиболее совершенные типы гармонического анализатора позволяют решить обратную задачу. Существуют также и самостоятельные прибора для этой цели. Например это классический прибор лорда Кельвина для предсказания приливов.
Урок 7. перпендикулярные прямые — Геометрия — 7 класс
Геометрия
7 класс
Урок № 7
Перпендикулярные прямые
Перечень рассматриваемых вопросов:
- Перпендикулярные прямые.

- Способы построения прямых углов на местности.
- Экер.
- Теодолит.
- Свойство перпендикулярных прямых.
Тезаурус:
Две пересекающиеся прямые называются перпендикулярными (или взаимно перпендикулярными), если они образуют при пересечении четыре прямых угла.
Основная литература:
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс.
 // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
// Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с. - Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения
Ранее вы уже познакомились с прямыми и выяснили, что они могут пересекаться или не пересекаться.
Сегодня мы продолжим изучать пересекающиеся прямые, которые являются перпендикулярными.
Введём понятие «перпендикулярные прямые».
Для этого рассмотрим две пересекающиеся прямые а и b. Они образуют четыре неразвёрнутых угла. Если один из этих углов будет прямой, то остальные тоже будут прямые, т.к.
∠1 и ∠2 – смежные (по определению смежных углов),
∠1 +∠2=180°(по свойству смежных углов),
∠2=180° – 90° = 90°,
∠1 =∠ 3 = 90° – вертикальные (по свойству вертикальных углов),
∠2 =∠ 4 = 90° – вертикальные (по свойству вертикальных углов).
Две пересекающиеся прямые называются перпендикулярными (или взаимно перпендикулярными), если они образуют при пересечении четыре прямых угла.
Обозначение перпендикулярных прямых:
а ┴ b
Построим перпендикулярные прямые.
Для этого воспользуемся чертёжным угольником и линейкой, как изображено на рисунке.
Рассмотрим свойство перпендикулярных прямых.
Две прямые, перпендикулярные к третьей, не пересекаются.
Дано:
АА1┴РQ
ВВ1┴РQ.
Доказать: АА1 и ВВ1 не пересекаются.
Доказательство.
Рассмотрим прямые АА1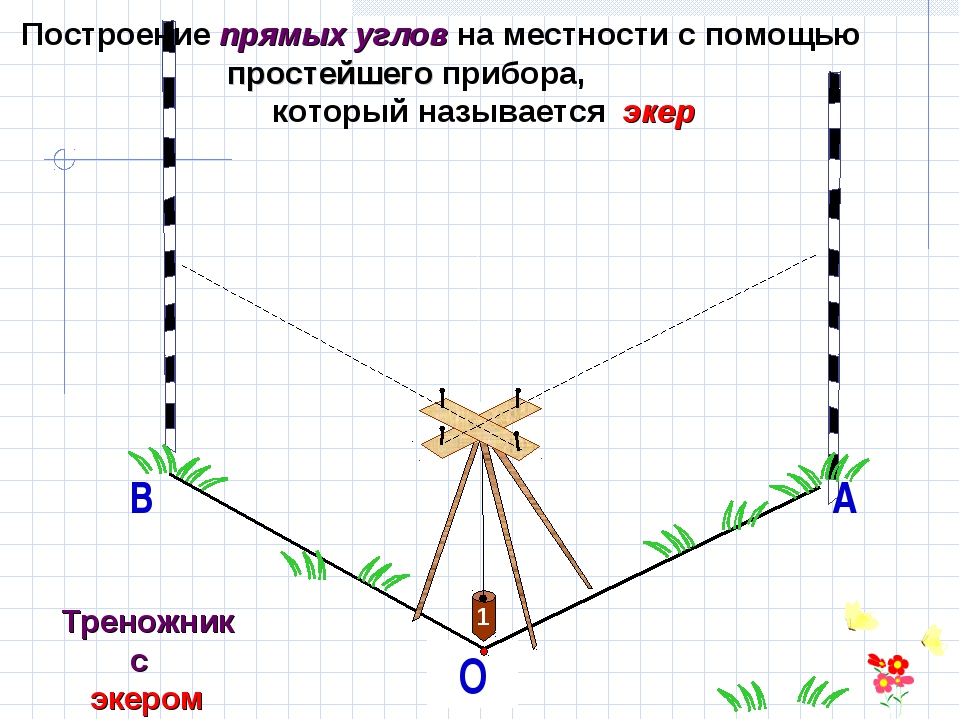
Предположим, что прямые АА1 и ВВ1пересекаются в точке М.
Мысленно перегнем плоскость по прямой РQ, точка М накладывается на точку М1.
Через точки М и М1
Данный метод доказательства называют методом от противного. Суть этого метода заключается в том, что предполагают противоположное тому, что требуется доказать. Исходя из предположения, путём рассуждений приходят к противоречию.
Этим методом можно воспользоваться для доказательства теоремыо единственности перпендикуляра к прямой.
Из точки, не лежащей на прямой, можно провести не более одного перпендикуляра к этой прямой.
Доказательство. Пустьточка не лежит на данной прямой a. Докажем, что из точки A нельзя провести два перпендикуляра к прямой a. Предположим, что из точки A можно провести два перпендикуляра AH и AK к прямой a. Мысленно перегнем плоскость по прямойaтак, чтобы полуплоскость с границей a, содержащая точку A, наложилась на другую полуплоскость. При этом точки H и K остаются на месте, точка A накладывается на некоторую точку B. Получается, что отрезки AH и AK накладываются на отрезки BH и BK.
Углы AHB и AKB – развернутые, так как каждый из них равен сумме двух прямых углов. Поэтому точки A, H и B лежат на одной прямой, и также точки A, K и B лежат на одной прямой.
Таким образом, мы получили, что через точки A и B проходят две прямые AH и AK. Но это невозможно (по аксиоме о взаимном расположении точек и прямых). Следовательно, из точки A можно провести единственный перпендикуляр к прямой а.
Следовательно, из точки A можно провести единственный перпендикуляр к прямой а.
Итак, сегодня получили представление о том, что такое перпендикулярные прямые, рассмотрели свойства перпендикулярных прямых, научились строить и обозначать перпендикулярные прямые, узнали о методе доказательства от противного.
Рассмотрим более сложный метод построения прямых углов на местности.
Для построения прямых углов на местности применяют специальные приборы, например, теодолит (в геодезии).
Но самый простой прибор для построения прямых углов на местности – это экер. Он состоит из двух брусков расположенных под углом 90° и укреплённых на треножнике. На концах брусков вбиты гвоздитак, что прямые, проходящие через них, перпендикулярны. Рассмотрим, как с его помощью построить прямые углы. На заданном луче, в нашем случае ОА, устанавливают экер так, что отвес находится точно над точкойО, а направление одного из брусков совпадает с лучом ОА, совмещение помогает осуществить веха, поставленная на луче ОА. Далее провешивают прямую с помощью другого бруска, получается ∠АОВ =90°.
Далее провешивают прямую с помощью другого бруска, получается ∠АОВ =90°.
Тренировочные задания.
1. Прямые СА и ВD взаимно перпендикулярны и пересекаются в точке О. Луч ОК – проведён из вершины прямого угла АОВ, так что∠КОВ = 52°. Найдите градусную меру ∠АОК.
Решение: нарисуем рисунок, исходя из условия задачи:
∠АОВ = 90°;
∠АОВ = ∠КОВ +∠АОК, следовательно, ∠АОК = ∠АОВ – ∠КОВ = 90° – 52° = 38°.
Ответ: ∠АОК = 38°.
2. Прямые СО и ОD взаимно перпендикулярны, найдите ∠МОВ, если ∠МОА = ∠СОА = 25°, ∠ВОD= ∠МОВ.
Решение. Т.к. прямые СО и ОD взаимно перпендикулярны, то ∠СОD = 90°
По условию задачи, ∠МОА = ∠СОА = 25°, ∠ВОD = ∠МОВ.
∠ СОD = ∠МОА + ∠СОА + ∠ВОD + ∠МОВ = 25° + 25° +2·∠МОВ = 50° + 2 · ∠МОВ = 90°
50° + 2 · ∠МОВ = 90°
∠МОВ = (90° – 50°) : 2
∠МОВ = 20°
Ответ: 20°.
Геометрия Атанасян Задачи к Главе 1
Практические задания и задачи из учебника геометрии для 7 класса к Главе 1 «Начальные геометрические сведения» (УМК Атанасян и др.) Ознакомительная версия перед покупкой книги. Цитаты из учебника представлены в учебных целях. Геометрия Атанасян Задачи к Главе 1.
Вернуться в Оглавление учебника по геометрии.
Геометрия 7 класс (УМК Атанасян)
Практические задания и задачи к Главе 1«Начальные геометрические сведения»
Практические задания к § 1 «Прямая и отрезок» (упр.№№ 1-7)
- Проведите прямую, обозначьте её буквой а и отметьте точки А и В, лежащие на этой прямой, и точки Р, Q и R, не лежащие на ней. Опишите взаимное расположение точек А, В, Р, Q, R и прямой а, используя символы ∈ и ∉.
- □ Отметьте три точки А, В и С, не лежащие на одной прямой, и проведите прямые АВ, ВС и СА.

- Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.
- Отметьте точки А, В, С, D так, чтобы точки А, В, С лежали на одной прямой, а точка D не лежала на ней. Через каждые две точки проведите прямую. Сколько получилось прямых?
- Проведите прямую а и отметьте на ней точки А и В. Отметьте: а) точки М и N, лежащие на отрезке АВ; б) точки Р и Q, лежащие на прямой а, но не лежащие на отрезке АВ; в) точки R и S, не лежащие на прямой а.
- Проведите прямую и отметьте на ней три точки. Сколько отрезков получилось на прямой?
- □ На рисунке 10 изображена прямая, на ней отмечены точки А, В, С и D. Назовите все отрезки: а) на которых лежит точка С; б) на которых не лежит точка В.
Практические задания к § 2 «Луч и угол» (упр.№№ 8-17)
- Проведите прямую, отметьте на ней точки А и В и на отрезке АВ отметьте точку С.
 а) Среди лучей АВ, ВС, СА, АС и ВА назовите совпадающие лучи; б) назовите луч, который является продолжением луча СА.
а) Среди лучей АВ, ВС, СА, АС и ВА назовите совпадающие лучи; б) назовите луч, который является продолжением луча СА. - Начертите три неразвёрнутых угла и обозначьте их так: ∠AOB, ∠hk, ∠M.
- Начертите два развёрнутых угла и обозначьте их буквами.
- Начертите три луча h, k и I с общим началом. Назовите все углы, образованные данными лучами.
- Начертите неразвёрнутый угол hk. Отметьте две точки внутри этого угла, две точки вне этого угла и две точки на сторонах угла.
- Начертите неразвёрнутый угол. Отметьте точки А, В, М и N так, чтобы все точки отрезка АВ лежали внутри угла, а все точки отрезка MN лежали вне угла.
- Начертите неразвёрнутый угол АОВ и проведите: а) луч ОС, который делит угол АОВ на два угла; б) луч OD, который не делит угол АОС на два угла.
- □ Сколько неразвёрнутых углов образуется при пересечении двух прямых?
- □ Какие из точек, изображённых на рисунке 17, лежат внутри угла hk, а какие — вне этого угла?
- Какие из лучей, изображённых на рисунке 18, делят угол АОВ на два угла?
 №№ 18-23)
№№ 18-23)- 18. На луче с началом О отмечены точки А, В и С так, что точка В лежит между точками О и А, а точка А — между точками О и С. Сравните отрезки ОВ и ОА, ОС и О А, ОВ и ОС.
- 19. Точка О является серединой отрезка АВ. Можно ли совместить наложением отрезки: а) ОА и ОВ; б) ОА и АВ?
- 20. □ На рисунке 25 отрезки АВ, ВС, CD и DE равны. Укажите: а) середины отрезков АС, АЕ и СЕ; б) отрезок, серединой которого является точка D; в) отрезки, серединой которых является точка С.
- 21. Луч ОС делит угол АОВ на два угла. Сравните углы АОВ и АОС.
- 22. □ Луч l — биссектриса угла hk. Можно ли наложением совместить углы: a) hl и lk; б) hl и hk?
- 23. □ На рисунке 26 углы, обозначенные цифрами, равны. Укажите: а) биссектрису каждого из углов АОС, BOF, АОЕ; б) все углы, биссектрисой которых является луч ОС.

- 24. Измерьте ширину и длину учебника геометрии и выразите их в сантиметрах и в миллиметрах.
- 25. Измерив толщину учебника геометрии без обложки, найдите толщину одного листа.
- 26. □ Найдите длины всех отрезков, изображённых на рисунке 31, если за единицу измерения принят отрезок: a) KL; б) АВ.
- 27. □ Начертите отрезок АВ и луч h. Пользуясь масштабной линейкой, отложите на луче h от его начала отрезки, длины которых равны 2АВ, 1/2АВ и 1/4АВ.
- 28. Начертите прямую и отметьте на ней точки А и В. С помощью масштабной линейки отметьте точки С и D так, чтобы точка В была серединой отрезка АС, а точка D — серединой отрезка ВС.
- 29. Начертите прямую АВ. С помощью масштабной линейки отметьте на этой прямой точку С, такую, что АС = 2 см. Сколько таких точек можно отметить на прямой АВ?
- 30.
 □ Точка В делит отрезок АС на два отрезка. Найдите длину отрезка АС, если АВ = 7,8 см, ВС = 25 мм.
□ Точка В делит отрезок АС на два отрезка. Найдите длину отрезка АС, если АВ = 7,8 см, ВС = 25 мм. - 31. □ Точка В делит отрезок АС на два отрезка. Найдите длину отрезка ВС, если: а) АВ = 3,7 см, АС = 7,2 см; б) АВ = 4 мм, АС = 4 см.
- 32. Точки А, В и С лежат на одной прямой. Известно, что АВ = 12 см, ВС = 13,5 см. Какой может быть длина отрезка АС?
- 33. □ Точки В, D и М лежат на одной прямой. Известно, что BD = 7 см, MD = 16 см. Каким может быть расстояние ВМ?
- 34. Точка С — середина отрезка АВ, равного 64 см. На луче С А отмечена точка D так, что СD = 15см. Найдите длины отрезков BD и DA.
- 35. Расстояние между Москвой и С.-Петербургом равно 650 км. Город Тверь находится между Москвой и С.-Петербургом в 170 км от Москвы. Найдите расстояние между Тверью и С.-Петербургом, считая, что все три города расположены на одной прямой.
- 36. Лежат ли точки А, Б и С на одной прямой, если АС = 5 см, АВ = 3 см, ВС = 4 см?
Решение.
Если точки А, В и С лежат на одной прямой, то больший из отрезков АВ, ВС и АС равен сумме двух других. По условию больший из данных отрезков (отрезок АС) равен 5 см, а сумма двух других (АВ + ВС) равна 7 см. Поэтому точки А, B и С не лежат на одной прямой. - 37. Точка С — середина отрезка АВ, точка О — середина отрезка АС. Найдите: а) АС, СВ, АО и ОВ, если АВ = 2 см; б) АВ, АС, АО и OB, если СB = 3,2 м.
- 38. □ На прямой отмечены точки О, А и В так, что ОА = 12 см, ОB = 9 см. Найдите расстояние между серединами отрезков ОА и ОB, если точка О: а) лежит на отрезке АВ; б) не лежит на отрезке АВ.
- 39. Отрезок, длина которого равна а, разделён произвольной точкой на два отрезка. Найдите расстояние между серединами этих отрезков.
- 40. □ Отрезок, равный 28 см, разделён на три неравных отрезка. Расстояние между серединами крайних отрезков 16 см. Найдите длину среднего отрезка.
 №№ 41-53)
№№ 41-53)- 41. Начертите три неразвёрнутых угла и один развёрнутый угол и обозначьте их так: ∠AOB, ∠CDE, ∠hk и ∠ С помощью транспортира измерьте углы и запишите результаты измерений.
- 42. Начертите луч ОА и с помощью транспортира отложите от луча ОА углы АОВ, АОС и AOD так, чтобы ∠AOB = 23°, ∠AOC = 67°, ∠AOD = 138°.
- 43. Начертите угол, равный 70°, и с помощью транспортира проведите его биссектрису.
- 44. Начертите угол АОВ и с помощью транспортира проведите луч ОС так, чтобы луч ОА являлся биссектрисой угла ВОС. Всегда ли это выполнимо?
- 45. □ Градусные меры двух углов равны. Равны ли сами углы?
- 46. На рисунке 37 изображены лучи с общим началом О.
а) Найдите градусные меры углов АОХ, BOX, АОВ, СОВ, DOX; б) назовите углы, равные 20°; в) назовите равные углы; г) назовите все углы со стороной ОА и найдите их градусные меры.
- 47. □ Луч ОЕ делит угол АОВ на два угла. Найдите ∠AOB, если:
а) ∠AOE = 44°, ∠EOB = 77°; б) ∠AOE = 12°37′, ∠EOB = 108°25′. - 48. Луч ОС делит угол АОВ на два угла. Найдите угол СОВ, если ∠AOB = 78°, а угол АОС на 18° меньше угла ВОС.
- 49. Луч ОС делит угол АОВ на два угла. Найдите угол АОС, если ∠AOB = 155°, а угол АОС на 15° больше угла СОВ.
- 50. □ Угол АОВ является частью угла АОС. Известно, что ∠AOC= 108°, ∠AOB = 3∠ Найдите угол АОВ.
- 51. □ На рисунке 38 угол AOD — прямой, ∠AOB = ∠BOC = ∠ Найдите угол, образованный биссектрисами углов АОВ и COD.
- 52. На рисунке 39 луч OV является биссектрисой угла ZOY, а луч OU — биссектрисой угла XOY. Найдите угол XOZ, если ∠UOV = 80°.
- 53. Луч l является биссектрисой неразвёрнутого угла hk. Может ли угол hl быть прямым или тупым?
 №№ 54-70)
№№ 54-70)- 58. □ Найдите угол, смежный с углом АВС, если: a) ∠ABC = 111°; б) ∠ABC = 90°; в) ∠ABC = 15°.
- 59. □ Один из смежных углов прямой. Каким (острым, прямым, тупым) является другой угол?
- 60. □ Верно ли утверждение: если смежные углы равны, то они прямые?
- 61. Найдите смежные углы hk и kl, если: а) ∠hk меньше ∠kl на 40°; б) ∠hk больше ∠kl на 120°; в) ∠hk больше ∠kl на 47°18′; г) ∠hk = 3∠kl; д) ∠hk : ∠kl = 5:4.
- 62. На рисунке 46 углы BOD и COD равны. Найдите угол AOD, если ∠COB = 148°.
- 63. Даны два равных угла. Равны ли смежные с ними углы?
- 64. □ Найдите изображённые на рисунке 41 углы: а) 1, 3, 4, если ∠2 = 117°; б) 1, 2, 4, если ∠3 = 43°27′.
- 65. □ Найдите неразвёрнутые углы, образованные при пересечении двух прямых, если: а) сумма двух из них равна 114°; б) сумма трёх углов равна 220°.

- 66. □ На рисунке 41 найдите углы 1, 2, 3, 4, если: а) ∠2 + ∠4 = 220°; б) 3 (∠1 +∠3) = ∠2 + ∠4; в) ∠2 – ∠1 = 30°.
- 67. □ На рисунке 47 изображены три прямые, пересекающиеся в точке О. Найдите сумму углов: ∠1 + ∠2 + ∠
- 68. На рисунке 48 ∠AOB = 50°, ∠FOE = 70°. Найдите углы АОС, BOD, СОЕ и COD.
- 69. □ Прямая а пересекает стороны угла А в точках Р и Q. Могут ли обе прямые АР и AQ быть перпендикулярными к прямой а?
- 70. □ Через точку А, не лежащую на прямой а, проведены три прямые, пересекающие прямую а. Докажите, что по крайней мере две из них не перпендикулярны к прямой а.
- 1. Сколько прямых можно провести через две точки?
- 2. Сколько общих точек могут иметь две прямые?
- 3. Объясните, что такое отрезок.

- 4. Объясните, что такое луч. Как обозначаются лучи?
- 5. Какая фигура называется углом? Объясните, что такое вершина и стороны угла.
- 6. Какой угол называется развёрнутым?
- 7. Какие фигуры называются равными?
- 8. Объясните, как сравнить два отрезка.
- 9. Какая точка называется серединой отрезка?
- 10. Объясните, как сравнить два угла.
- 11. Какой луч называется биссектрисой угла?
- 12. Точка С делит отрезок АВ на два отрезка. Как найти длину отрезка АВ, если известны длины отрезков АС и СВ?
- 13. Какими инструментами пользуются для измерения расстояний?
- 14. Что такое градусная мера угла?
- 15. Луч ОС делит угол АОВ на два угла. Как найти градусную меру угла АОВ, если известны градусные меры углов АОС и СОВ?
- 16.
 Какой угол называется острым? прямым? тупым?
Какой угол называется острым? прямым? тупым? - 17. Какие углы называются смежными? Чему равна сумма смежных углов?
- 18. Какие углы называются вертикальными? Каким свойством обладают вертикальные углы?
- 19. Какие прямые называются перпендикулярными?
- 20. Объясните, почему две прямые, перпендикулярные к третьей, не пересекаются.
- 21. Какие приборы применяют для построения прямых углов на местности?
Дополнительные задачи (упр.№№ 71-86)
- 71. Отметьте четыре точки так, чтобы никакие три не лежали на одной прямой. Через каждую пару точек проведите прямую. Сколько получилось прямых?
- 72. Даны четыре прямые, каждые две из которых пересекаются. Сколько точек пересечения имеют эти прямые, если через каждую точку пересечения проходят только две прямые?
- 73. Сколько неразвёрнутых углов образуется при пересечении трёх прямых, проходящих через одну точку?
- 74.
 Точка N лежит на отрезке МР. Расстояние между точками М и Р равно 24 см, а расстояние между точками N и М в два раза больше расстояния между точками N и Р. Найдите расстояние: а) между точками N и Р; б) между точками N и М.
Точка N лежит на отрезке МР. Расстояние между точками М и Р равно 24 см, а расстояние между точками N и М в два раза больше расстояния между точками N и Р. Найдите расстояние: а) между точками N и Р; б) между точками N и М. - 75. Три точки К, L, М лежат на одной прямой, КL = 6 см, LM = 10 см. Каким может быть расстояние КМ? Для каждого из возможных случаев сделайте чертёж.
- 76. Отрезок АВ длины а разделён точками Р и Q на три отрезка АР, PQ и QB так, что АР = 2PQ = 2QB. Найдите расстояние между: а) точкой А и серединой отрезка QB; б) серединами отрезков АР и QB.
- 77. Отрезок длины m разделён: а) на три равные части; б) на пять равных частей. Найдите расстояние между серединами крайних частей.
- 78. Отрезок в 36 см разделён на четыре не равные друг другу части. Расстояние между серединами крайних частей равно 30 см. Найдите расстояние между серединами средних частей.
- 79* □ Точки А, В и С лежат на одной прямой, точки М и N — середины отрезков АВ и АС.
 Докажите, что BC = 2MN.
Докажите, что BC = 2MN. - 80. Известно, что ∠AOB = 35°, ∠BOC = 50°. Найдите угол АОС. Для каждого из возможных случаев сделайте чертёж с помощью линейки и транспортира.
- 81. Угол hk равен 120°, а угол hm равен 150°. Найдите угол km. Для каждого из возможных случаев сделайте чертёж.
- 82. Найдите смежные углы, если: а) один из них на 45° больше другого; б) их разность равна 35°.
- 83. Найдите угол, образованный биссектрисами двух смежных углов.
- 84. Докажите, что биссектрисы вертикальных углов лежат на одной прямой.
- 85* □ Докажите, что если биссектрисы углов АВС и CBD перпендикулярны, то точки А, В и D лежат на одной прямой.
- 86. □ Даны две пересекающиеся прямые а и b и точка А, не лежащая на этих прямых. Через точку А проведены прямые m и n так, что m ⊥ а, n ⊥ Докажите, что прямые m и n не совпадают.
Вы смотрели: Практические задания и задачи из учебника геометрии для 7 класса к Главе 1 «Начальные геометрические сведения» (УМК Атанасян и др. ) Ознакомительная версия перед покупкой книги. Цитаты из учебника представлены в учебных целях.
) Ознакомительная версия перед покупкой книги. Цитаты из учебника представлены в учебных целях.
Вернуться к Оглавлению учебника по геометрии (Атанасян).
«Какие геодезические приборы применяются в строительстве?» – Яндекс.Кью
Геодезические работы на стройплощадке заключаются в составлении топографии участка, переносе на местность и контроле геометрических размеров строящихся сооружений. Одной из основных геодезических работ является разбивка (разметка) здания, которая заключается в нахождении высот и пересечений осей углов здания и закреплении их на участке строительства.
Обоснованием начала строительства служит разрешение, выданное местной администрацией. При выдаче которого решается ряд вопросов, связанных с будущим подключением дома к дорогам, сетям электро-, газо-, водоснабжения и канализирования, с расположением дома относительно сторон света и относительно других уже существующих зданий и сооружений. В городской среде это очень важные условия и обычно будущее здание вносится в генплан застройки, а его привязку к местности (разбивку) производят геодезисты районного отдела архитектуры. Иными словами, если будущее здание может быть построено только в том месте, где его запроектировали, то на стройплощадку выезжают местные геодезисты и забивают колышки там, где его нужно строить. Они же выносят и закрепляют высотную отметку. Задача застройщика заключается в вызове и оплате этих специалистов и последующем закреплении разбивки на месте строительства. Если же требования к расположению здания мягче, то его разбивку можно сделать собственными силами. Этому и будет посвящен данный раздел сайта.
Иными словами, если будущее здание может быть построено только в том месте, где его запроектировали, то на стройплощадку выезжают местные геодезисты и забивают колышки там, где его нужно строить. Они же выносят и закрепляют высотную отметку. Задача застройщика заключается в вызове и оплате этих специалистов и последующем закреплении разбивки на месте строительства. Если же требования к расположению здания мягче, то его разбивку можно сделать собственными силами. Этому и будет посвящен данный раздел сайта.
Для переноса на местность углов и осей стен запроектированного здания используются геодезические и мерные инструменты: измерительные ленты или длинномерные рулетки, штыри длиной 80–100 см из арматуры диаметром 8–12 мм, легкая кувалда или тяжелый молоток, прочный шнур (тонкая стальная проволока или толстая леска) и нивелир либо водяной уровень. В качестве полезной опции неплохо иметь геодезический инструмент — экер.
- Мерными лентами измеряют длину осей, чем длиннее лента, тем точнее измерение.

- Арматурными штырями закрепляют углы здания на местности используя их в роли колышков. Железный штырь легче забить в грунт на большую глубину. Они, в отличие от деревянных колышков, имеют небольшие поперечные размеры уменьшающие измерительную погрешность.
- Легкую кувалду или тяжелый молоток используют для забивания штырей в грунт. Некоторые штыри, во избежание вандализма, нужно забивать почти на полную глубину.
- Тонкой стальной проволокой или леской визуально закрепляют размеченные оси стен. Шнур, обозначающий оси нужно сильно натягивать, не допуская сильного провисания и раскачивания ветром, поэтому выбор падает на тонкую стальную проволоку или толстую синтетическую леску.
- Нивелиром выносится нулевая отметка здания — закрепляется горизонтальная плоскость, от которой в процессе строительства будут производиться все высотные вычисления.
- Экером на стройплощадке размечают прямые углы.
Большая Энциклопедия Нефти и Газа, статья, страница 1
Эккер
Cтраница 1
Эккер и Будар [18] удачно применили уравнение (1.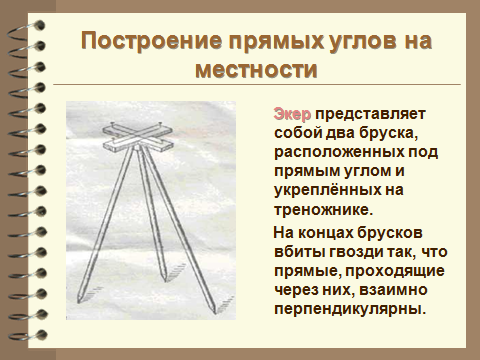 14) для реакции, имевшей место в неидеальной газовой смеси.
[1]
14) для реакции, имевшей место в неидеальной газовой смеси.
[1]
Эккер т, Дрейк Р. М. Теория тепло — и массообмена. [2]
Эккер т Э. Р. Введение в теорию тепло — и массоюбмена. [3]
Эккер ( рис. 60) применяют для построения прямых углов на местности. Коробка крепится на деревянцой ручке. [4]
Эккеры бывают простые и оптические. [6]
Эккером размечают направление, перпендикулярное оси пути. На этом направлении устанавливают два медносульфатных электрода: первый — на расстоянии d от оси пути; второй — на расстоянии / от первого. Синхронно с измерением разности потенциалов рельс — земля измеряют регистрирующим прибором типа Я-39 разность потенциалов At / между электродами, причем положительная клемма прибора должна быть подключена к электроду, ближайшему к рельсам.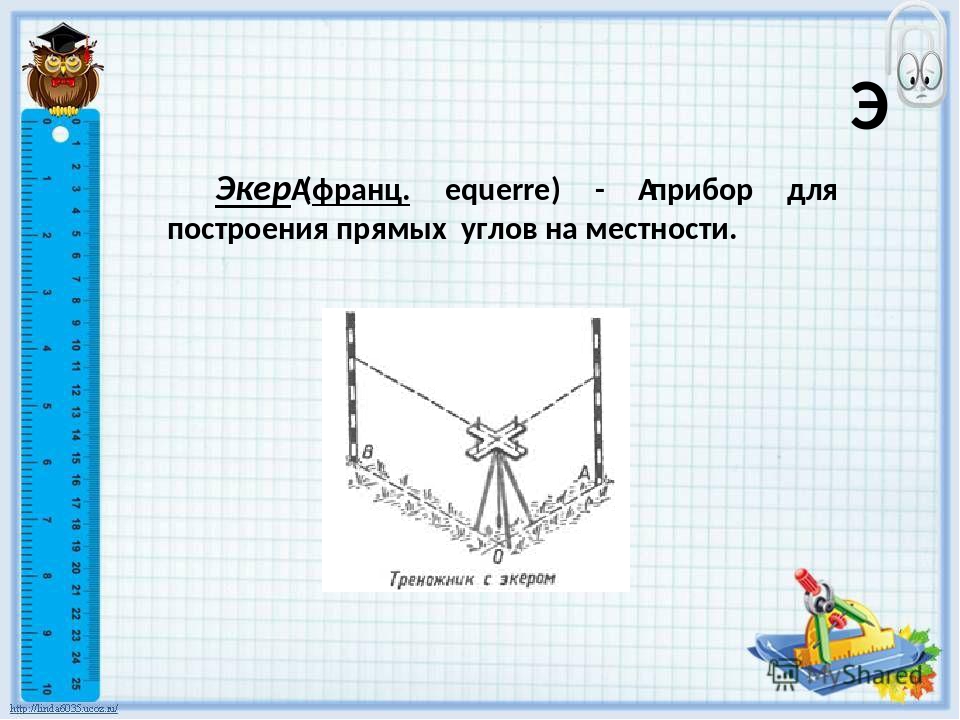 [7]
[7]
Эккером [48] было показано, что коэффициенты приведения at для наполненных и ненаполненных вулканизатов. [8]
Снизу эккер имеет ручку. [9]
Из оптических эккеров наиболее распространен двух-зеркальный ( рис. 26 6), у которого внутри оправы укреплены два зеркала а и Ъ, под углом 45 одно к другому. [10]
По мнению Эккера [48], введение сажи увеличивает вязкость каучуковой матрицы, что приводит к возрастанию модуля потерь эластомера с концентрацией наполнителя. [11]
Ответ: Работы Эккера, а также Бэйда и Йоса имеют целью более глубокое исследование различных физических процессов, происходящих на поверхности раздела между твердым телом и газом, через которую проходит электрический ток. Ни одна из этих работ не касается сложностей, появляющихся при движении газа относительно твердого катода.
[12]
Ни одна из этих работ не касается сложностей, появляющихся при движении газа относительно твердого катода.
[12]
Затем при помощи эккера, установленного над центром опоры, разбивается прямая, перпендикулярная к оси трассы. [13]
Прямой угол с помощью эккера отбивают следующим образом. На линии, к которой нужно восстановить перпендикуляр, произвольно устанавливают вешку. В вершине прямого угла лицом к восстанавливаемому перпендикуляру встает рабочий ( направляющий) и устанавливает эккер так, чтобы в середине зеркал отразилась закрепленная на линии вешка. Второй человек с другой вешкой идет по предполагаемой перпендикулярной линии и устанавливает ее по указанию направляющего так, чтобы она была видна в окошке эккера как продолжение отраженной в зеркале вешки, закрепленной на исходной линии. [14]
Поэтому исследования, выполненные Эккером и Валентинотти, можно считать наиболее серьезным подтверждением существующей теории шприцевания, так как их результаты хорошо совпадают с выводами теории. Особенно это относится к теоретическому распределению скоростей в потоке, изображенному на рис. 4 17 или 4 18, которое полностью подтверждается результатами их исследования.
[15]
Особенно это относится к теоретическому распределению скоростей в потоке, изображенному на рис. 4 17 или 4 18, которое полностью подтверждается результатами их исследования.
[15]
Страницы: 1 2 3 4
Урок «Измерение углов. Транспортир» (5 класс) – Документ 1 – УчМет
УРОК ПО ТЕМЕ
«ИЗМЕРЕНИЕ УГЛОВ. ТРАНСПОРТИР»
ЦЕЛИ УРОКА:
дидактическая— научить измерять углы с помощью транспортира, дать понятие «градус», познакомить с другими единицами измерения углов, с приборами: теодолит, гониометр, нивелир, кипрегель, познакомить с историей возникновения градусной единицей измерения углов
развивающая — развивать память, внимание, логическое мышление, уметь обобщать и делать
выводы, развивать навыки сравнения
воспитательная — воспитывать усидчивость, аккуратность выполнения построения, культуру общения
ТИП
УРОКА — Урок изучения новых знаний.
ОБОРУДОВАНИЕ: заготовки для измерения углов, разноцветные макеты углов, часы, «мордочки» для определения настроения.
МЕТОДЫ ОБУЧЕНИЯ:
1) словесный
наглядный
частично- поисковый
репродуктивный
практический
ПРИНЦИПЫ: актуализации и проблемности.
ФОРМЫ ОРГАНИЗАЦИИ ПОЗНАВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ УЧАЩИХСЯ:
фронтальный
работа в парах
индивидуальный
ХОД УРОКА:
Организационный момент.
Активизация мыслительной деятельности.
Объяснение новой темы
Закрепление по ходу изложения нового материала.
Домашнее задание.
1.ВОПРОС Ы :
1. Что называют углом?
Какой угол называют развернутый?
Какой угол называют прямым ?
Сколько прямых углов содержит развернутый угол?
какой угол называют острым?
Какой угол называется тупым?
7. Какое
время показывают часы если угол между
стрелками прямой, развернутый?
Какое
время показывают часы если угол между
стрелками прямой, развернутый?
2. С помощью чертежного угольника определить вид угла
На правильные ответы на вопросы в течении урока раздавать жетоны.
3. Работа в парах: Цветной набор моделей углов, разложить на парте в порядке их уменьшения. Повторить название видов углов.
Как легко проверить, правильно ли вы выполнили задачу? (наложением)
ИЗУЧЕНИЕ НОВОЙ ТЕМЫ:
ПРОБЛЕМА: На доске начерчены углы и даны градусы . Установить соответствие между углами и градусами.
1800, 300, 1500, 900.
Вам знакома эта запись? Что она обозначает?
Цель
урока: Сегодня на уроке мы научимся
измерять углы! Сейчас я предлагаю вам
отгадать загадку.
ЗАГАДКА:
Согласно словарю Даля: этот прибор — угломер.
Согласно словарю Ожегова: он — чертежный прибор — разделенный на градусы полукруг для измерения углов и нанесения их на чертеж
Большая Советская Энциклопедия говорит: это -приспособление для построения и измерения углов на чертежах.
Итак тема сегодняшнего урока «ИЗМЕРЕНИЕ УГЛОВ. ТРАНСПОРТИР».
Рассмотреть шкалу транспортира. Мы уже знаем один измерительный инструмент- линейка. Положите рядом линейку и транспортир. Что общего между ними? Обратить внимание на центр транспортира. Послушаем сообщения об истории возникновения транспортира:
Углы
меряют в градусах, минутах и секундах.
Эти угловые меры возникли в глубокой
древности. Предполагают, что это было
связано с созданием календаря. Древние
математики нарисовали круг и разделили
его на столько частей, сколько дней в
году. Но они думали, что в году не 366 и
не 365 дней, а 360. Поэтому круг они разделили
на 360 частей. Такое изображение года
было очень полезным: на нем можно было
отметить любой день.
Поэтому круг они разделили
на 360 частей. Такое изображение года
было очень полезным: на нем можно было
отметить любой день.
Полукруглая шкала транспортира разделена на 180 частей. А на всей окружности таких делений 360, как на древнем календаре. Древние греки уже знали, что в году не 360 дней, а больше, но деление круга на 360 равных частей сохранили. Древние римляне дали каждой такой части название «градус». Обозначается специальным значком 1°.
Слово «градус» — латинское слово, означает «шаг», «ступень». Измерение углов в градусах появилось более 3 тыс. лет назад в Вавилоне. В расчетах там использовалась шестидесятеричная система счисления, шестидесятеричные дроби. Поэтому вавилонские математики, а за ними и греческие и индийские, полный оборот делили на 360 частей — градусов. Градусная мера сохранилась до наших дней. Используются более мелкие единицы измерения угла: минута и секунда. 1 градус=60 минутам, 1минуга=60 секундам, обозначается так:
1°=
60/. 1/=60″
1/=60″
Прочитать определение градуса в учебнике .Итак : 1/180 часть развернутого угла называют градусом. В каких единицах измеряют углы ?
На уроках математики мы с вами углы будем измерять только в градусах, а на уроках географии, астрономии будете измерять в других единицах: минутах и секундах. А сейчас ,ребята мы с вами научимся измерять углы с помощью транспортира. Транспортиры бывают с одной шкалой и двумя шкалами. Поднимите руки у кого транспортир с одной шкалой, а у кого с двумя.
Измерим угол АОВ (уже начерчен на доске, учитель показывает как его измерять, и рассмотреть неправильное приложение транспортира).
Ученики измеряют углы на заготовках, по рядам углы в 26, 60,154 градусов.
ЗАДАНИЕ КЛАССУ : Измерить на заготовке прямые углы (по рядам: 1 ряд — угол 1, 2 ряд- угол 3. 3 ряд – угол 6. ВЫВОД: Прямой угол =90 градусам. Углы 1, 3, 6 равны 90 градусам
Как
не измеряя развернутый угол узнать его
величину? Рассмотри рис. 183. Проверить
угол МКР=180 градусов?
183. Проверить
угол МКР=180 градусов?
На этом же рисунке:
а) Назовите градусные меры углов АСЕ и FHL
б) Назовите углы равные 180 градусам, 90 градусам. Прочитать определение прямого угла.
Что можно сказать о градусных мерах равных углов? равные углы имеют равные градусные меры, больший угол имеет большую градусную меру, меньший угол имеет меньшую градусную меру.
ВЕРНЕМСЯ К ПРОБЛЕМЕ: найдем соответствие между углами и их градусными мерами.
Ребята! Какой угол мы называли острым? Попробуйте дать определение острого угла, используя градусную меру; также тупого, прямого и развернутого.
СОСТАВИМ ОПОРНЫЙ КОНСПЕКТ
На заготовке самостоятельно измерить все углы кроме прямых углов (по одному). Ученики измеряют каждый угол, проговаривают алгоритм измерения.
угол
2=133°, угол 4 =32°, угол 5= 112°, угол 7= 35°.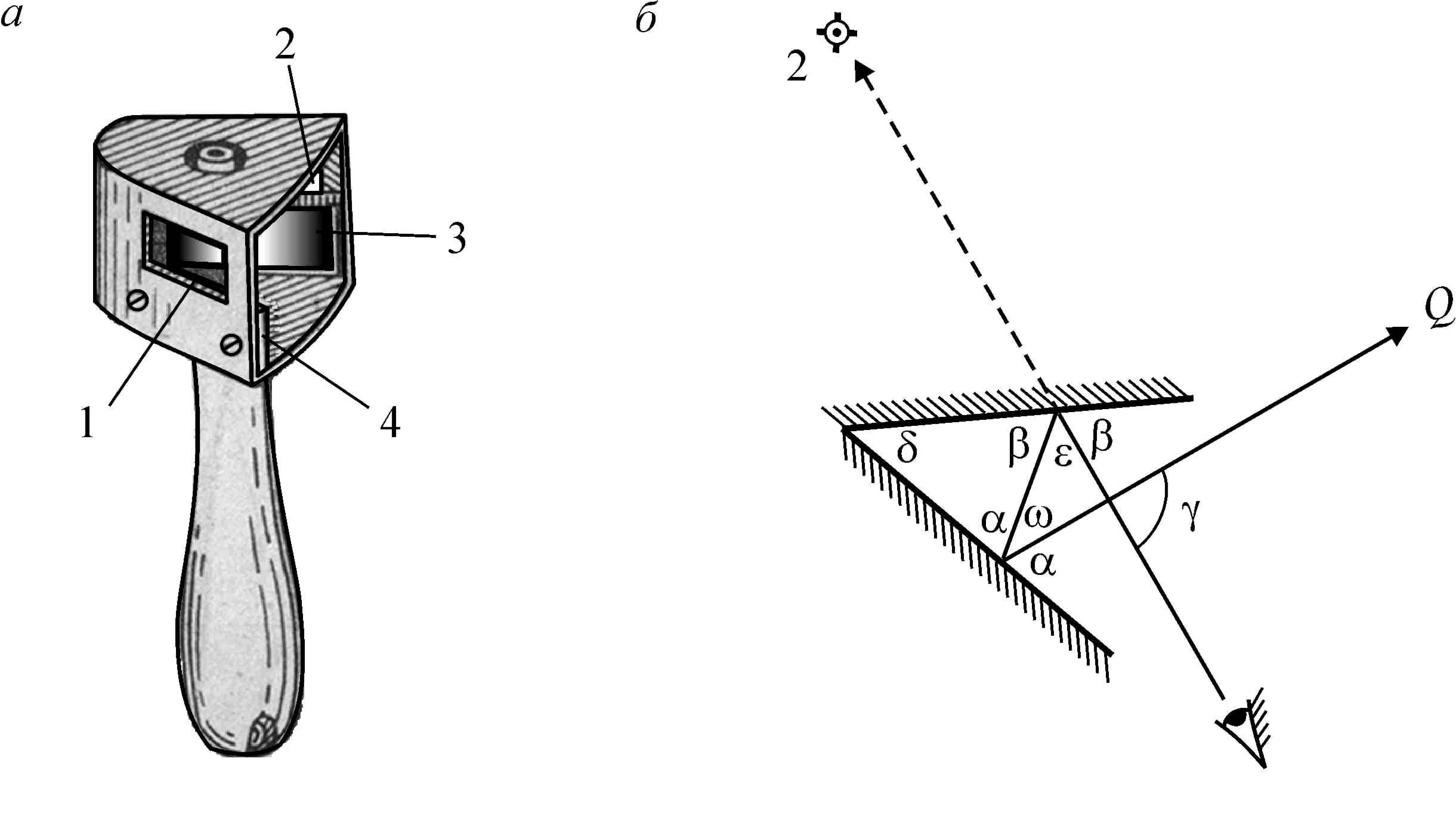
ИСТОРИЧЕСКАЯ СПРАВКА:
В конце 8-го века при разработке метрической системы мер, французские ученые предложили делить прямой угол не на 90, а на 100 частей. Такой угол называют «град»: 90° = 100 град.
В градах измеряют углы в геодезии; в некоторых строительных расчетах, но широкого распространения она не получила. Для точного измерения углов созданы различные инструменты. Основная часть этих приборов — шкала, похожая на шкалу транспортира.
Например: ТЕОДОЛИТ- для измерения углов при съемке ( круг- лимб, с угловыми делениями: градусы, полуградусы, грады и др.)
ГОНИОМЕТР- небольшой, удобный при передвижении инструмент , служит для измерения углов, построения прямых углов.
НИВЕЛИР
-инструмент при помощи которого
получается горизонтальная плоскость
й-ти горизонтальный луч. позволяющий
определять насколько точка находится
выше или ниже другой.
КИПРЕГЕЛЬ- для визирования на определяемые точки местности.
Транспортир применяют и для построения углов.
Построим угол АОВ=50 градусам. Учитель объясняет построение.
Peбята! Кроме того, что мы должны научиться строить углы с помощью транспортира, но и строить их на глазок. Для этого проведем практическую работу: построим из одного узла клетки углы 10, 20, ….. 80 градусов.
Строят. Находят узлы. Заполняют таблицу для своего угла. Проверяем вместе с помощью таблицы. Меняются табличками: теперь сосед используя координаты из соседней таблички строит угол и проверяет его с помощью транспортира.
УГОЛ | | |
100 | 6 | 1 |
200 | 8 | 3 |
300 | 7 | 4 |
400 | 6 | 5 |
500 | 5 | 6 |
600 | 4 | 7 |
700 | 3 | 8 |
800 | 1 | 6 |
ИТОГ УРОКА:
1) Для чего служит транспортир?
На сколько делений разделена шкала транспортира?
Что такое градус?
Сколько градусов содержит развернутый угол?
Сколько градусов содержит прямой угол?
Какой угол называют острым?
Какой угол называют тупым?
Какой угол можно построить без транспортира?
Кому
понравился урок тот пусть возьмет
зеленую улыбающуюся рожицу, а кому нет-
желтую .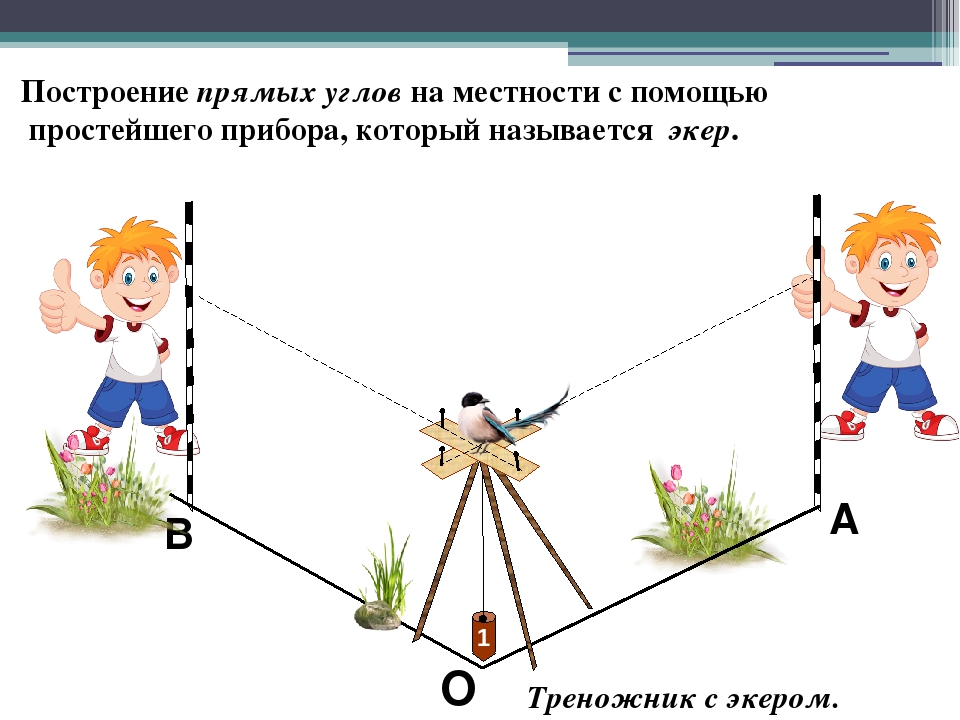
ДОМАШНЕЕ ЗАДАНИЕ: п. 42 -выучить определения, № 1620, 1654, 1655.
ПРИЛОЖЕНИЕ:
АСТРОЛЯБИЯ
Установка теодолита в вершине угла
Гониометр
Кипрегель
Нивелир технический НВ-1
ТЕОДОЛИТ
Названия инструментов, используемых для измерения углов
Мир наполнен углами. Вам нужны инструменты, чтобы точно измерить эти углы, от угла поперечной балки до уклона крыши. У каждой профессии есть свои специальные инструменты для определения углов, но некоторые из них используются в разных профессиях и в классе. Выберите измерительный инструмент, который подходит для вашего применения.
Вам нужны инструменты, чтобы точно измерить эти углы, от угла поперечной балки до уклона крыши. У каждой профессии есть свои специальные инструменты для определения углов, но некоторые из них используются в разных профессиях и в классе. Выберите измерительный инструмент, который подходит для вашего применения.
TL; DR (слишком долго; не читал)
Т-образные квадраты, регулируемые треугольники, уровни перехода, транспортиры и установочные квадраты — это некоторые из инструментов, используемых для измерения углов в архитектуре, геодезии, геометрии и плотницких работах.
Углы в архитектуре
Архитекторы, составляющие вручную чертежи мостов или ландшафтного дизайна, используют различные инструменты для точного измерения расстояний и углов. Используйте Т-образный квадрат, чтобы нарисовать горизонтальные линии и измерить углы 90 градусов по отношению к этим линиям. Используйте регулируемый треугольник для измерения углов от 0 до 90 градусов, поместив его на горизонтальную ось и отрегулировав шарнирный край, пока он не совпадет с наклонной линией, которую вы хотите измерить. Если вам нужно точно скопировать угол, соедините циркуль с линейкой, чтобы измерить угол, и начертите такой же.
Если вам нужно точно скопировать угол, соедините циркуль с линейкой, чтобы измерить угол, и начертите такой же.
Углы в съемке
Геодезисты используют инструменты для измерения горизонтальных и вертикальных углов по отношению к поверхности земли. Транзитный уровень имеет подвижный телескоп, который направлен на стержень для определения горизонтального уровня и угла наклона в градусах, минутах и секундах. Это определяет класс дорожного полотна или фундамент дома. Специалисты лесного хозяйства используют клинометр для вычисления высоты дерева по углу, образованному между клинометром и деревом. Чтобы измерить общую высоту дерева, посмотрите в окуляр клинометра на самом верхнем конце дерева, затем снимите показания на шкале.Добавьте измерение к высоте от инструмента до земли.
Углы в геометрии
В классе геометрии транспортир — это линейка с прикрепленным к ней полукругом. Положите линейку на горизонтальную сторону угла и прочтите, где гипотенуза — или наклонная сторона — пересекает транспортир, чтобы определить угол в градусах.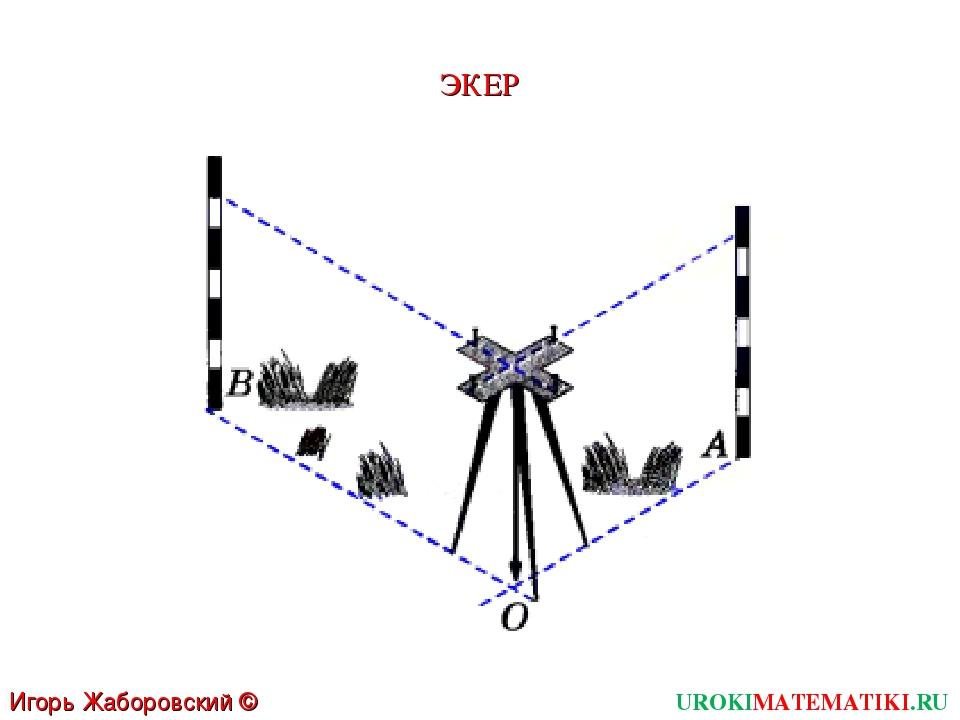 Положите установленный квадрат под углом 30, 45, 60 или 90 градусов, чтобы определить градусы. Угол треугольника для одного типа предварительно установлен на 30, 60 и 90 градусов, а его направление определяет градусы угла.Используйте второй квадрат, чтобы измерить углы 45 и 90 градусов.
Положите установленный квадрат под углом 30, 45, 60 или 90 градусов, чтобы определить градусы. Угол треугольника для одного типа предварительно установлен на 30, 60 и 90 градусов, а его направление определяет градусы угла.Используйте второй квадрат, чтобы измерить углы 45 и 90 градусов.
Углы в плотницких работах
В плотницких работах скоростной квадрат представляет собой трехсторонний «квадрат» с размерами углов от 0 до 60, нанесенными на его диагональную сторону. Измерьте углы, положив его вдоль края доски и считывая градусы угла. С помощью транспортира измерьте угол на конце доски, повернув регулируемый рычаг транспортира, пока он не зафиксируется на дереве. Просто прочитайте градусы на циферблате, чтобы узнать, под каким углом пропиливается древесина.
Мифы об угле разводки печатной платы: угол 45 градусов против угла 90 градусов | Блог о проектировании печатных плат
Altium Designer | & nbsp 4 мая 2018 г.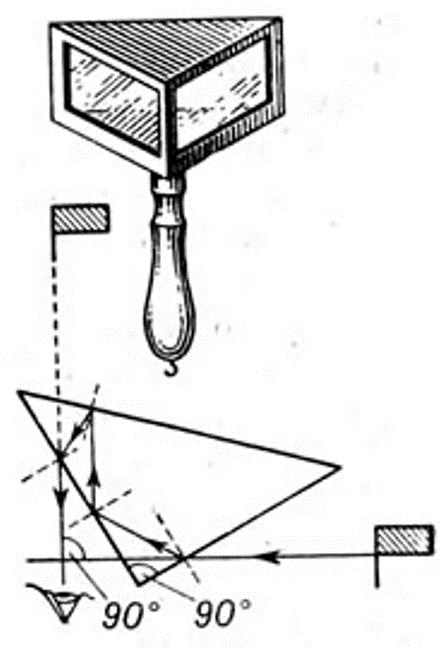
Нет ничего плохого в здоровом споре, касается ли он самого худшего покрытия для пиццы или лучшей паяльной маски.В мире редакторов печатных плат споры, которые беспокоят дизайнеров и исследователей, вращаются вокруг углов прокладки печатных плат. Следует ли прокладывать медные дорожки на печатной плате под углом 45 градусов или лучше прокладывать печатную плату под углом 90 градусов?
Однако при современном оборудовании оказывается, что обычно не имеет значения, какой угол вы используете. Используя современное программное обеспечение для проектирования печатных плат, инструменты трассировки могут приспособиться к выбору любого угла, за которым вы стоите, или того, что необходимо для нужд вашего устройства.
Влияние траекторий под прямым углом на эмиссию электромагнитных помех
Инженеры часто беспокоятся о наличии прямоугольных дорожек на печатной плате из-за возможности электромагнитных помех (EMI), излучаемых на острых углах. Популярная теория состоит в том, что высокочастотные сигналы излучают радиочастотное излучение на каждом повороте медной дорожки на 90 °. Этого простого предположения достаточно для большинства разработчиков оборудования, чтобы исключить любые правильные углы разводки печатной платы из конструкции дорожек или программного обеспечения автоматического маршрутизатора.
Популярная теория состоит в том, что высокочастотные сигналы излучают радиочастотное излучение на каждом повороте медной дорожки на 90 °. Этого простого предположения достаточно для большинства разработчиков оборудования, чтобы исключить любые правильные углы разводки печатной платы из конструкции дорожек или программного обеспечения автоматического маршрутизатора.
Однако теория о том, что электроны в высокоскоростном сигнале не могут совершать повороты под прямым углом, была опровергнута опытным инженером-электриком доктором Ховардом Джонсоном. На самом деле электроны миллиарды раз отскакивают в разных направлениях даже при небольшой длине; у них минимальные проблемы с перемещением под прямым углом.
Есть исключение — когда вы проектируете сверхвысокоскоростную заземляющую поверхность печатной платы в диапазоне 10 ГГц или более, или когда вы участвуете в разработке микроволновых схем, в которых используются дорожки с большой шириной 100 мил. В таких экстремальных условиях вам действительно нужно беспокоиться об углах 90 °. В противном случае они не должны вызывать серьезного беспокойства.
В противном случае они не должны вызывать серьезного беспокойства.
Позаботьтесь только о прямых углах в сверхскоростном исполнении.
Чтобы разрешить этот спор раз и навсегда, был проведен тест по измерению и сравнению излучаемого излучения между прямым углом и углом 45 ° для высокочастотного сигнала, для сигналов с нарастанием импульса до 17ps.Результаты подтверждают аргумент д-ра Говарда Джонсона о том, что нет разницы в уровнях излучения электромагнитных помех между прямым углом и углом 45 ° в пределах испытаний.
Почему так широко используются углы 45 °?
Вердикт вынесен, и можно безопасно использовать прямоугольные дорожки в своем дизайне, если вы не работаете над разработками сверхвысокочастотных микроволновых устройств. Миф о фрезеровании под углом 45 ° окончательно развенчан. Но если изначально это было неправильным представлением, почему программное обеспечение для проектирования печатных плат продолжает включать углы 45 ° в свою стратегию трассировки? Кроме того, почему люди вообще начали фрезерование с углом 45 °?
Каждый миф имеет свое происхождение. В случае фрезерования под углом 45 ° миф восходит к тем временам, когда производство печатных плат не было таким передовым, как сегодня. В то время прямоугольные или любые острые углы представляли реальную угрозу технологичности. Острые углы могут привести к образованию кислотных ловушек, где некоторые кислоты, используемые при травлении, задерживаются и продолжают разъедать медь на острых углах. В то время инженеры также были обеспокоены тем, что прямоугольные углы не так прочны, как 45 °, и их легко отклеить.
В случае фрезерования под углом 45 ° миф восходит к тем временам, когда производство печатных плат не было таким передовым, как сегодня. В то время прямоугольные или любые острые углы представляли реальную угрозу технологичности. Острые углы могут привести к образованию кислотных ловушек, где некоторые кислоты, используемые при травлении, задерживаются и продолжают разъедать медь на острых углах. В то время инженеры также были обеспокоены тем, что прямоугольные углы не так прочны, как 45 °, и их легко отклеить.
К счастью, эти опасения остались в прошлом, поскольку новая технология производства печатных плат гарантирует, что заземляющая поверхность вашей печатной платы будет правильно вытравлена, под прямым углом или нет. Инженеры-ветераны с тех времен, когда избегали прямых углов, часто по-прежнему неодобрительно относятся к использованию углов 45 ° в современных конструкциях. Однако для многих из них это скорее привычка, чем правило.
Острые углы вызывают проблемы с производительностью.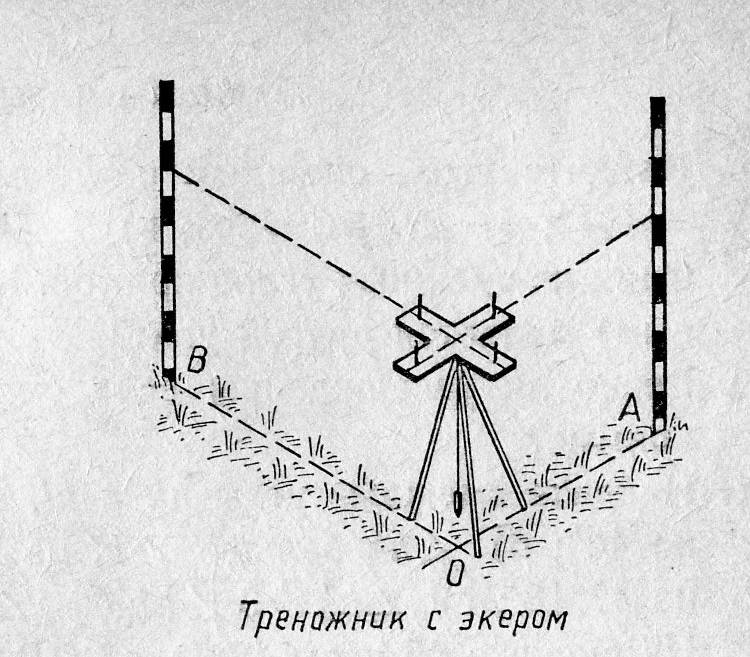
Почему я предпочитаю углы под углом 45 °?
Несмотря на то, что в моем дизайне нет ничего плохого в том, чтобы иметь прямые углы, я тщательно проверяю, чтобы каждый угол составлял 45 °, прежде чем отправлять макет печатной платы на изготовление.Это не потому, что я разработчик радиочастот, а не потому. Моя одержимость углом 45 ° довольно проста. Выглядят они стильно и, на мой взгляд, намного красивее, чем углы 90 °.
Проще говоря, это вопрос личных предпочтений. В конце концов, Altium Designer® уже настроен для красивой трассировки трасс под углом 45 °, и я не видел острой необходимости изменять эти настройки по умолчанию. Убедитесь, что вы используете программное обеспечение для проектирования печатных плат, которое позволяет реализовать любые ваши дизайнерские предпочтения.
Вас беспокоят прямые углы в конструкции печатной платы? Поговорите с экспертом по Altium Designer, чтобы узнать его мнение.
5.
 5 Геодезическая съемка и традиционные методы измерения местоположения на поверхности Земли
5 Геодезическая съемка и традиционные методы измерения местоположения на поверхности ЗемлиПростота, точность и доступность во всем мире сделали термин «GPS» нарицательным. Тем не менее, никакая мощность или возможности GPS были бы невозможны без традиционных геодезистов. Методы и инструменты традиционной съемки все еще используются и, как вы увидите, основаны на тех же самых концепциях, которые лежат в основе даже самого передового спутникового позиционирования.
Географические позиции указываются относительно фиксированной ссылки. Позиции на земном шаре, например, могут быть указаны в виде углов относительно центра Земли, экватора и нулевого меридиана.
Геодезисты измеряют горизонтальные позиции в географических или плоских системах координат относительно ранее исследованных позиций, называемых контрольными точками, большинство из которых физически указаны в мире с помощью металлического «ориентира», который фиксирует местоположение и, как показано здесь, может также указывают высоту относительно среднего уровня моря (Рисунок 5. 10). В 1988 году NGS установила с точностью до контрольной точки с четырьмя порядками, в пределах максимальной базовой ошибки от 3 мм до 5 см. В США Национальная геодезическая служба (NGS) поддерживает Национальную систему пространственной привязки (NSRS) , которая состоит из примерно 300 000 горизонтальных и 600 000 вертикальных контрольных станций (Doyle, 1994).
10). В 1988 году NGS установила с точностью до контрольной точки с четырьмя порядками, в пределах максимальной базовой ошибки от 3 мм до 5 см. В США Национальная геодезическая служба (NGS) поддерживает Национальную систему пространственной привязки (NSRS) , которая состоит из примерно 300 000 горизонтальных и 600 000 вертикальных контрольных станций (Doyle, 1994).
Дойл (1994) указывает, что горизонтальная и вертикальная системы отсчета совпадают менее чем на десять процентов. Это потому, что:
…. горизонтальные станции часто располагались на высоких горах или вершинах холмов, чтобы уменьшить необходимость в строительстве наблюдательных вышек, которые обычно требуются для обеспечения прямой видимости для измерений триангуляции, траверса и трилатерации. Однако вертикальные контрольные точки были установлены с помощью техники спиритического выравнивания, которая больше подходит для проведения на пологих склонах, таких как автомобильные и железные дороги, которые редко поднимаются на горные вершины.
(Дойл, 2002, стр. 1)
Вы можете задаться вопросом, как запускается сеть управления.Если позиции измеряются относительно других позиций, относительно какой позиции измеряется первая позиция? Ответ: звезды. До появления надежных часов астрономы могли определять долготу только путем тщательного наблюдения повторяющихся небесных событий, таких как затмения лун Юпитера. В настоящее время геодезисты получают чрезвычайно точные данные о местоположении, анализируя радиоволны, излучаемые далекими звездами. Однако после создания сети управления геодезистов определяют положения, используя инструменты, которые измеряют углы и расстояния между точками на поверхности Земли.
Рисунок 5.10: Контрольная точка, используемая для отметки вертикальной контрольной точки.
Кредит: Томпсон, 1988.
.5.5.1 Измерение углов и расстояний
Вы, наверное, видели геодезистов, работающих на улице, например, когда ремонтируют шоссе или строятся новые жилые дома. Часто один геодезист использует оборудование на штативе, а другой держит штангу на некотором расстоянии. Геодезисты и их оборудование тщательно измеряют углы и расстояния, по которым можно рассчитать положение и высоту.Кратко обсудим это оборудование и их методику. Давайте сначала посмотрим на углы и на то, как они применяются при съемке.
Часто один геодезист использует оборудование на штативе, а другой держит штангу на некотором расстоянии. Геодезисты и их оборудование тщательно измеряют углы и расстояния, по которым можно рассчитать положение и высоту.Кратко обсудим это оборудование и их методику. Давайте сначала посмотрим на углы и на то, как они применяются при съемке.
Хотя стандартный компас может дать вам приблизительную оценку углов, магнитное поле Земли непостоянно, и магнитные полюса, которые медленно перемещаются во времени, не идеально совпадают с осью вращения планеты; в результате последнего истинный (географический) север и магнитный север различны. Кроме того, при использовании компаса некоторые камни могут намагничиваться и вносить небольшие локальные аномалии.По этим причинам геодезисты полагаются на транзитов (или их более современные эквиваленты, называемые теодолитами ) для измерения углов. Транзит (рис. 5.11) состоит из телескопа для наблюдения за удаленными целевыми объектами, двух измерительных колес, которые работают как транспортиры для считывания горизонтальных и вертикальных углов, и пузырьковых уровней, чтобы гарантировать, что углы верны. Теодолит — это, по сути, тот же инструмент, за исключением того, что он несколько сложнее и обладает большей точностью.В современных теодолитах некоторые механические части заменены электроникой.
Теодолит — это, по сути, тот же инструмент, за исключением того, что он несколько сложнее и обладает большей точностью.В современных теодолитах некоторые механические части заменены электроникой.
Рисунок 5.11: Традиционный транзит, когда-то использовавшийся геодезистами.
Кредит: Raisz, 1948, используется с разрешения.
Когда геодезисты измеряют углы, результирующие вычисления обычно представляются как азимут , или азимуты , , как показано на рис. 5.12. Пеленг — это угол менее 90 ° в квадранте, определяемом сторонами света. Азимут — это угол между 0 ° и 360 °, измеренный по часовой стрелке с севера.«Юг, 45 ° восточной долготы» и «135 °» — это одно и то же направление, выраженное как азимут и азимут.
Рисунок 5.12: Азимуты и пеленги. Обратите внимание, что азимут 360 ° совпадает с 0 °.
Кредит: Географический факультет Университета штата Пенсильвания.
5.5.2 Измерение расстояний
Для измерения расстояний геодезисты когда-то использовали металлические ленты длиной 100 футов с градуировкой в сотых долях фута. Пример этого метода показан на рисунке 5.13. Расстояния по склонам измерялись короткими горизонтальными отрезками. Квалифицированные геодезисты могут достичь точности до одной десятой части (погрешность в 1 сантиметр на каждые 100 метров расстояния). Источники ошибки включают недостатки самой ленты, такие как перегибы; колебания длины ленты из-за экстремальных температур; и человеческие ошибки, такие как непоследовательное натяжение, позволяющее ленте отклоняться от горизонтальной плоскости, и неправильные показания.
Пример этого метода показан на рисунке 5.13. Расстояния по склонам измерялись короткими горизонтальными отрезками. Квалифицированные геодезисты могут достичь точности до одной десятой части (погрешность в 1 сантиметр на каждые 100 метров расстояния). Источники ошибки включают недостатки самой ленты, такие как перегибы; колебания длины ленты из-за экстремальных температур; и человеческие ошибки, такие как непоследовательное натяжение, позволяющее ленте отклоняться от горизонтальной плоскости, и неправильные показания.
Рис. 5.13: Съемочная группа измеряет базовое расстояние с помощью металлической (инварной) ленты.
Кредит: Ходжсон, 1916.
С 1980-х годов устройства электронного измерения расстояний (EDM) позволяют геодезистам измерять расстояния более точно и эффективнее, чем с помощью лент. Чтобы измерить расстояние по горизонтали между двумя точками, один геодезист использует инструмент EDM, чтобы направить энергетическую волну в сторону отражателя, удерживаемого вторым геодезистом. EDM регистрирует время, прошедшее между излучением волны и ее возвращением от отражателя. Затем он вычисляет расстояние как функцию прошедшего времени (мало чем отличается от того, что мы узнали о GPS!).Типичные дальномеры малого радиуса действия могут использоваться для измерения расстояний до 5 километров с точностью до одной части из 20 000, что в два раза точнее, чем при записи на ленту.
EDM регистрирует время, прошедшее между излучением волны и ее возвращением от отражателя. Затем он вычисляет расстояние как функцию прошедшего времени (мало чем отличается от того, что мы узнали о GPS!).Типичные дальномеры малого радиуса действия могут использоваться для измерения расстояний до 5 километров с точностью до одной части из 20 000, что в два раза точнее, чем при записи на ленту.
Инструменты, называемые тахеометрами (рис. 5.14), объединяют в одном устройстве электронное измерение расстояний и возможности теодолитов для измерения углов. Далее мы рассмотрим, как эти инструменты используются для измерения горизонтального положения по отношению к установленным сетям управления.
Рисунок 5.14: Современный тахеометр.
Кредит: Лукаш Фус.
5.5.3 Комбинирование углов и расстояний для определения позиций
Геодезисты разработали отдельные методы, основанные на отдельных сетях управления, для измерения горизонтального и вертикального положения. В этом контексте горизонтальное положение — это положение точки относительно двух осей: экватора и нулевого меридиана на земном шаре или осей x и y в плоской системе координат.
В этом контексте горизонтальное положение — это положение точки относительно двух осей: экватора и нулевого меридиана на земном шаре или осей x и y в плоской системе координат.
Теперь мы представим два метода, которые геодезисты используют для создания и расширения контрольных сетей (триангуляция и трилатерация), и два других метода, используемых для измерения положений относительно контрольных точек (открытые и закрытые переходы).
Сюрвейеры обычно измеряют позиции последовательно. Начиная с контрольных точек, они измеряют углы и расстояния до новых местоположений и используют тригонометрию для вычисления положений в системе координат плоскости. Такой способ измерения серии позиций известен как «перемещение». Ход, который начинается и заканчивается в разных местах, в которых хотя бы одна конечная точка изначально неизвестна, называется открытым ходом. Ход, который начинается и заканчивается в одной и той же точке или в двух разных, но известных точках, называется замкнутым ходом. «Замкнутый» здесь означает не геометрически замкнутый (как в многоугольнике), а математически замкнутый (определяемый как: или относящийся к интервалу, содержащему обе его конечные точки). «Замыкая» маршрут между одним известным местоположением и другим известным местоположением, геодезист может определить ошибки в походе.
«Замкнутый» здесь означает не геометрически замкнутый (как в многоугольнике), а математически замкнутый (определяемый как: или относящийся к интервалу, содержащему обе его конечные точки). «Замыкая» маршрут между одним известным местоположением и другим известным местоположением, геодезист может определить ошибки в походе.
Ошибки измерения в замкнутом траверсе, который соединяется в точке начала, можно количественно оценить путем суммирования внутренних углов многоугольника, образованного траверсой. Точность измерения одного угла неизвестна, но поскольку сумма внутренних углов многоугольника всегда (n-2) × 180, можно оценить ход в целом и распределить накопленные ошибки между всеми внутренние углы.Ошибки, возникающие при открытом походе, который не заканчивается там, где он начался, не могут быть оценены или исправлены. Единственный способ оценить точность открытого хода — это многократно измерять расстояния и углы, вперед и назад, и усреднять результаты расчетов. Поскольку повторные измерения являются дорогостоящими, другие методы съемки, которые позволяют геодезистам вычислять и учитывать погрешности измерения, для большинства приложений предпочтительнее открытых трасс.
5.5.4 Триангуляция
Закрытые переходы обеспечивают адекватную точность для съемки границ участков при условии, что установленная контрольная точка находится поблизости.Геодезисты проводят контрольные исследования для расширения и увеличения плотности точек в горизонтальных контрольных сетях. До того, как стало доступно спутниковое позиционирование для съемок, наиболее распространенной техникой проведения контрольных съемок была триангуляция (рис. 5.16).
Рисунок 5.15: Создание новых контрольных точек путем триангуляции из существующей контрольной точки (A).
Кредит: Географический факультет Университета штата Пенсильвания. Взято из оригинального текста DiBiase (1997).
- Используя тахеометр, оборудованный электронным устройством измерения расстояния, контрольная группа геодезистов начинает с измерения азимута , альфа и базового расстояния AB.
- Эти два измерения позволяют геодезической группе рассчитать позицию B как при открытом траверсе.

- Затем геодезисты измеряют внутренние углы CAB, ABC и BCA в точках A, B и C. Зная внутренние углы и длину базовой линии, тригонометрический «закон синусов» может быть использован для расчета длин любых других сторона.Зная эти размеры, геодезисты могут зафиксировать положение точки C.
- После измерения трех внутренних углов и длины одной стороны треугольника ABC группа контрольных изыскателей может рассчитать длину стороны BC. Эта расчетная длина затем служит базой для треугольника BDC. Таким образом, триангуляция используется для расширения сетей управления, точка за точкой и треугольник за треугольником.
5.5.5 Трилатерация
Альтернативой триангуляции является трилатерация , которая использует только расстояния для определения положения.Избегая угловых измерений, трилатерацию легче выполнять, она требует меньше инструментов и, следовательно, дешевле. Прочитав эту главу, вы уже познакомились с практическим применением трилатерации, поскольку это метод определения местоположения по спутнику, используемый в GPS.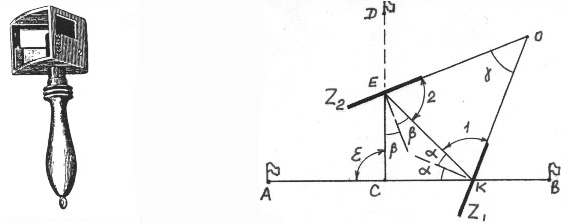
Вы видели пример трилатерации на рис. 5.8 в виде трехмерных сфер, отходящих от орбитальных спутников. В демонстрации 1 ниже показан этот процесс в двух измерениях.
Попробуйте это: пошагово выполните процесс двумерной трилатерации.
Демо: Трилатерация в двух измерениях.
Кредит: Институт электронного образования Джона А. Даттона, Государственный университет Пенсильвании.
Как только расстояние от контрольной точки установлено, человек может рассчитать расстояние, открыв траверс, или полагаться на известное расстояние, если оно существует. Единая контрольная точка и известное расстояние ограничивают возможные местоположения неизвестной точки краем круга, окружающего контрольную точку на этом расстоянии; вдоль этого круга есть бесконечное множество возможностей для неизвестного местоположения.Добавление второй контрольной точки вводит еще один круг с радиусом, равным его расстоянию от неизвестной точки. С двумя контрольными точками и дистанционными кругами количество возможных точек для неизвестного местоположения сокращается ровно до двух.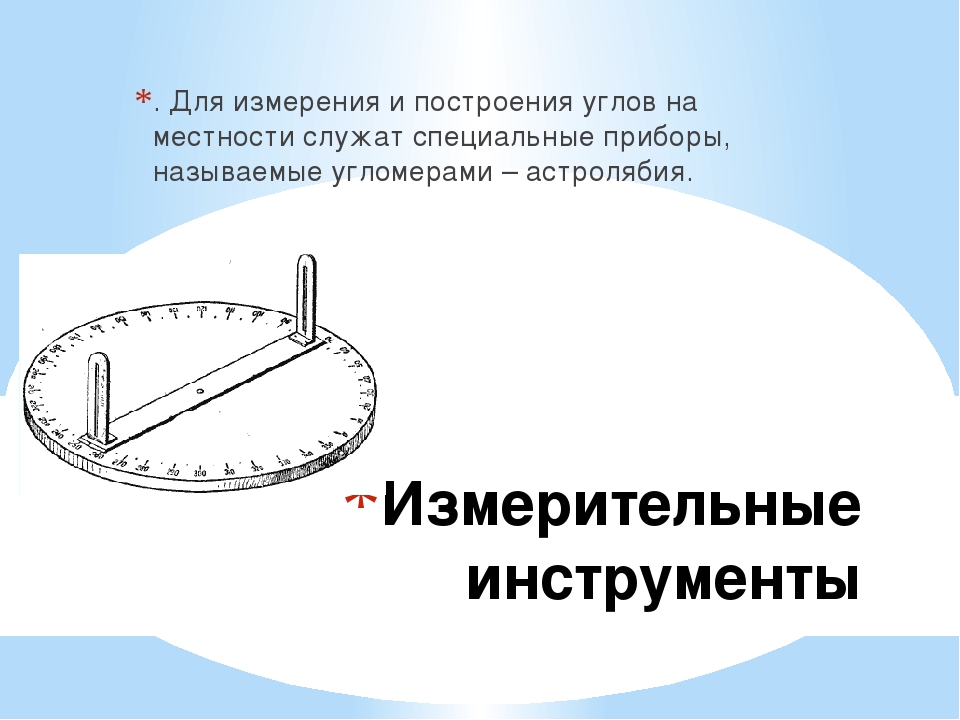 Третью и последнюю контрольную точку можно использовать, чтобы определить, какая из оставшихся возможностей является истинным местоположением.
Третью и последнюю контрольную точку можно использовать, чтобы определить, какая из оставшихся возможностей является истинным местоположением.
Трилатерация заметно проще триангуляции, и это очень ценный навык. Даже с очень приблизительными оценками можно с достаточным успехом определить общее местоположение.
Практическая викторина
Зарегистрированные студенты штата Пенсильвания должны вернуться, чтобы пройти тест для самооценки Land Surveying .
Вы можете проходить практические тесты столько раз, сколько хотите. Они не оцениваются и никак не влияют на вашу оценку.
Прямоугольные следы печатной платы: время убить мифы
Прямоугольные следы печатной платы: время уничтожить мифы
З. М. Петерсон и пуля; 27 декабря, 2019 Подходит к концу года, поэтому я подумал, что лучше всего завершить год, рассмотрев распространенный миф в дизайне печатных плат, который просто не умрет: никогда не использовать прямоугольные дорожки на печатной плате. Среди множества мифов о дизайне печатных плат, это один из самых известных мифов, которым все еще цепляются дизайнеры старой школы.
Среди множества мифов о дизайне печатных плат, это один из самых известных мифов, которым все еще цепляются дизайнеры старой школы.
Если вы читали некоторые руководства по проектированию печатных плат в Интернете, много говорится о трассировке под прямым углом и о том, как эти острые углы не следует использовать. Сюда входит блог Eagle, в котором конкретная производственная проблема (кислотные ловушки), основанная на технологии десятилетней давности, упоминается как причина отказа от трассировки трассировки под углом 90 градусов. Я видел, как все, от новичков до проектировщиков с многолетним опытом, заявляли, что трассировки под углом 90 градусов следует избегать любой ценой.Откуда взялась эта идея и почему ее до сих пор преподносят как пример плохой маршрутизации?
Возражения против прямоугольных следов печатной платы
Если вы посмотрите на возражения против маршрутизации под прямым углом, они часто представлены без доказательств или достаточных оснований. Эти возражения делятся на пять частей:
Эти возражения делятся на пять частей:
Утверждение 1: Электроны не могут двигаться по изгибам под прямым углом. Они сбиваются в кучу в углу и отталкиваются друг от друга.
Это полный бред.Фактически, если бы это было правдой, то сигналы не могли бы перемещаться между слоями через переходное отверстие. Это один из тех забавных фактов, которые, как я видел, упускают из виду многие старшие инженеры-проектировщики печатных плат.
Когда вы поймете, как в проводнике возбуждаются заряды, вы поймете, как поле может распространяться между двумя точками независимо от геометрии. Во-первых, давайте посмотрим на это электростатически. Когда проводник доводится до некоторого потенциала, некоторая плотность заряда затем переносится на поверхность проводника.Эта плотность заряда затем излучает электрическое поле, которое направлено перпендикулярно поверхности проводника. Если есть соседняя область отрицательного заряда (например, земля на печатной плате), то силовые линии электрического поля от положительной плотности заряда будут сходиться в область отрицательной плотности заряда. Это создает хорошо известные шаблоны полей, которые можно увидеть во многих учебных пособиях и при моделировании перекрестных помех на печатных платах.
Это создает хорошо известные шаблоны полей, которые можно увидеть во многих учебных пособиях и при моделировании перекрестных помех на печатных платах.
Если затем вы заставляете напряжение, подключенное к сигнальной дорожке, переключать полярность или каким-либо образом колебаться, это не означает, что электроны физически перемещаются от одного конца дорожки к другому.Электроны на самом деле перемещаются на очень короткое расстояние, прежде чем рассеиваются атомом, составляющим проводник, и тем не менее электронные сигналы все еще распространяются по следу, независимо от «группировки» или рассеяния.
Что действительно происходит в проводнике, так это то, что распространяющаяся электромагнитная волна возбуждает локализованные колебания электрического заряда от положительного до отрицательного. Другими словами, чистая плотность заряда в области распространения волны переключается с положительной на отрицательную, и это бегущее возмущение является распространяющейся электромагнитной волной.
Распределение электрического поля следует по траектории печатной платы независимо от прямых углов.
Ток не проходит от одного конца дорожки к другому. Вместо этого это локализованное колебание растет и затухает по мере прохождения волны, но колебание существует только в пределах области, которая охватывает пространственную протяженность (например, длину волны) электромагнитной волны.Для приемников с датчиком тока (например, буферов мощности) входной сигнал рассматривается только как колебательный электрический ток в непосредственной близости от входа приемника.
Для цифрового сигнала у вас действительно есть бесконечное количество локализованных колебаний (то есть на разных гармониках некоторой основной частоты), которые производят кажущееся непрерывное движение заряда по межсоединению. Опять же, суперпозиция этих локализованных колебаний тока создает то, что кажется движением заряда непосредственно от драйвера к приемнику, но заряд в проводнике на самом деле не движется таким образом.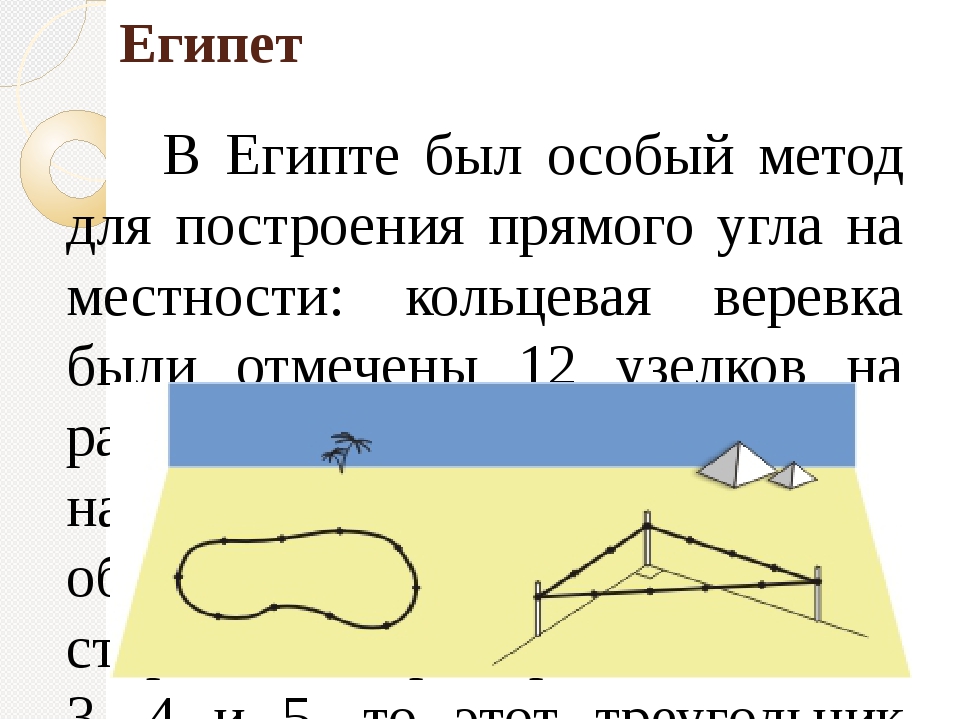
Пункт 2: Сигналы тока / напряжения полностью отражаются от прямоугольных дорожек
В этом есть крохотная доля правды, хотя это не имеет ничего общего с электронами, отскакивающими от края проводника. Да, это правда, что прямоугольные трассы создают разрыв импеданса, но он не более серьезен, чем разрыв импеданса, который можно увидеть на длинном переходном отверстии, слегка несовпадающей цепи фильтра / оконечной нагрузки, трассе под углом 45 градусов или серпантине. сегмент соответствия длины.Это означает, что вам следует позаботиться о создании трасс с согласованной геометрией, если вы хотите предотвратить скачки импеданса. Вы также должны свести к минимуму или исключить использование переходных отверстий в чрезвычайно высокоскоростных низкоуровневых ссылках.
Стенка прямоугольной дорожки не вызывает полного внутреннего отражения электромагнитных волн обратно в дорожку; Фактически, молодой студент знал бы из основ физики, что этого не происходит при нормальных условиях.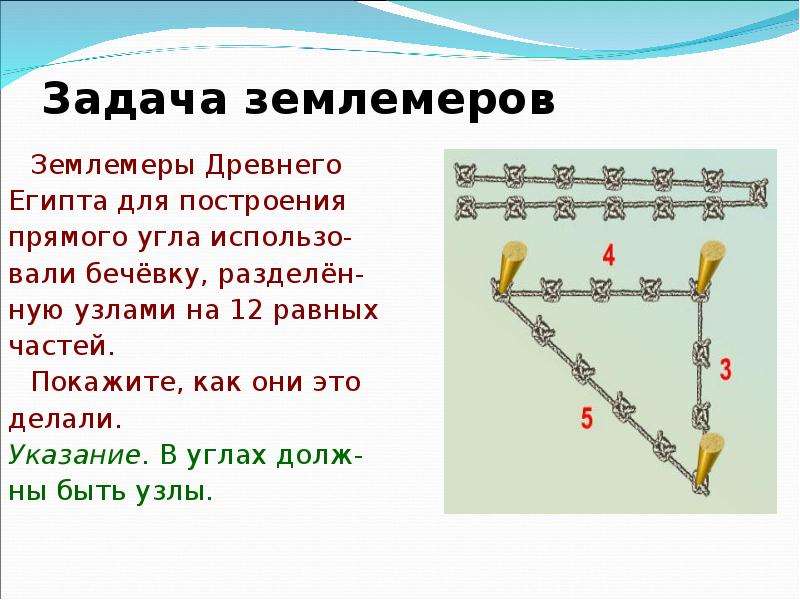 Точно так же не требуется след под углом 45 градусов, чтобы заставить электромагнитную волну повернуть за угол; если бы это было правдой, то только очень определенные пары изгиба под углом 45 градусов позволили бы сигналу достичь приемника на печатной плате.
Точно так же не требуется след под углом 45 градусов, чтобы заставить электромагнитную волну повернуть за угол; если бы это было правдой, то только очень определенные пары изгиба под углом 45 градусов позволили бы сигналу достичь приемника на печатной плате.
Что на самом деле происходит? Плотность электрического поля в углах прямоугольного следа немного выше, чем у гладкой стенки 45-градусного следа. Это фактически подводит нас к третьему утверждению в этом мифе о целостности сигнала…
Претензия 3: Прямоугольные дорожки на печатной плате являются источником электромагнитных помех
В этом утверждении есть доля правды, но это становится критичным только выше определенных частот. Большинство дизайнеров заявят, что вы никогда не должны прокладывать прямоугольные дорожки на печатной плате из-за электромагнитных помех, создаваемых в углу.Это создаст излучаемые электромагнитные помехи вдали от поверхности платы (излучение ближнего и дальнего поля), а также перекрестные помехи на близлежащих дорожках. Давайте сначала рассмотрим проблему перекрестных помех.
Давайте сначала рассмотрим проблему перекрестных помех.
Что касается перекрестных помех, то эту проблему целостности сигнала можно рассматривать как сигнал, индуцированный паразитной емкостью и / или индуктивностью между соседними дорожками, но перекрестные помехи будут возникать независимо от наличия прямоугольного угла на печатной плате. Более того, хотя поле, создаваемое внутри прямоугольного угла следа агрессора, будет сильнее, чем поле вдоль плоской стенки следа, поле может быть сконцентрировано во внешнем углу следа жертвы.В результате практически во всех ситуациях не наблюдается заметного влияния на перекрестные помехи.
Настоящий кусок истины можно найти, если рассмотреть излучение в дальней зоне. Математически существует несоответствие импеданса между краем прямоугольной дорожки печатной платы и диэлектриком. Всякий раз, когда у вас есть несоответствие импеданса в конструкции с волнами, распространяющимися вперед и назад, у вас есть отражение и потенциал для резонанса стоячей волны, подобный резонансу линии передачи. Однако электромагнитные помехи становятся серьезными только в том случае, если вы можете вызвать резонанс стоячей волны или несколько резонансов внутри частично открытой конструкции.
Однако электромагнитные помехи становятся серьезными только в том случае, если вы можете вызвать резонанс стоячей волны или несколько резонансов внутри частично открытой конструкции.
Пример распределения тока на прямоугольной кривой. Источник изображения.
Ограничивающим фактором, который определит, возбуждаются ли какие-либо резонансы, является размер квадратной области на прямоугольной дорожке печатной платы. В частности, поперечный размер области будет примерно равен четверти длины волны резонанса низшего порядка, так что это дает вам хорошую основу для оценки основных резонансных частот.Остальные гармоники будут примерно нечетными кратными основной частоте. Если мы допустим очень большую ширину следа 30 мил с эффективной диэлектрической проницаемостью 3,5, частота самого низкого порядка будет 112 ГГц! Если мы примем это как излом частоты для цифрового сигнала, это эквивалентно времени нарастания 3 пс, что намного ниже, чем у коммерчески доступных цифровых компонентов.
На сегодняшний день разработчикам цифровых технологий не нужно беспокоиться о прямоугольных следах печатной платы как источнике электромагнитных помех.Интеллектуальный ВЧ-разработчик уже должен использовать методы изоляции, чтобы предотвратить появление шума в других схемных блоках этой формой ЭМП. Даже дизайнеры, работающие за пределами режима mmWave, будут реализовывать достаточные меры изоляции в своей плате, независимо от частоты.
Пункт 4: Кислотные ловушки образуются во время производства
Раньше это возражение было справедливо в 1980-х годах, но с новыми решениями для травления, используемыми для травления меди во время производства, вы можете эффективно игнорировать эту проблему, если только вы не работаете с производителем, который сокращает углы.Несколько десятилетий назад растворы травителей имели тенденцию иметь более высокое поверхностное натяжение и вязкость, из-за чего они накапливались и располагались в углах под углом 90 градусов на прямоугольных дорожках печатной платы. Это может вызвать чрезмерное травление в углах, что приведет к чрезмерной шероховатости поверхности медных следов. Сегодня любой американский производитель, который хочет держать свои двери открытыми, знает, что нельзя использовать эти старые травители. Однако это по-прежнему является проблемой для зарубежных производителей низкого качества.
Это может вызвать чрезмерное травление в углах, что приведет к чрезмерной шероховатости поверхности медных следов. Сегодня любой американский производитель, который хочет держать свои двери открытыми, знает, что нельзя использовать эти старые травители. Однако это по-прежнему является проблемой для зарубежных производителей низкого качества.
Изображение под микроскопом показывает чрезмерное травление на некоторых следах меди.
Пункт 5: Электромиграция
Это, вероятно, наименее известное утверждение, которое чаще встречается у производителей, чем у дизайнеров. Считается, что высокая плотность тока вблизи углов (см. График выше) и результирующее высокое поле вызывают сильную электромиграцию. Однако экспериментальные тесты Croes et al. (см. источник ниже) обнаружили, что электромиграция около прямоугольных дорожек печатной платы была не более серьезной, чем миграция стандартных дорожек под углом 45 градусов или изогнутых дорожек.
- Источник: Croes, K., Li, Y., Lofrano, M., Wilson, C.J., and Tokei, Z. (2013). Внутреннее исследование влияния плотности тока и градиента плотности тока на электромиграцию в медных межсоединениях BEOL. В Proc. ИРПС , 2С.3.1-2С.3.4.
Существует связанное, законное утверждение, которое следует рассмотреть, которое касается электрического поля, создаваемого прямоугольными дорожками печатной платы. Более сильное поле, излучаемое этими дорожками, означает, что при проектировании высокого напряжения следует использовать большие расстояния утечки и зазоры.Поскольку поле выше, пробой диэлектрика между двумя проводниками легче, поэтому расстояние изоляции высокого напряжения между двумя точками должно быть увеличено. Это единственное законное объектирование прямоугольных следов печатной платы.
Приговор
К настоящему времени должно быть ясно; проблемы с прямоугольными дорожками на печатной плате являются мифами и не должны привлекать внимания , если вы не работаете с высоким напряжением . К сожалению, некоторые из этих мифов о дизайне просто не исчезнут в ближайшее время, но мы будем здесь, чтобы попытаться пролить свет на правду.
К сожалению, некоторые из этих мифов о дизайне просто не исчезнут в ближайшее время, но мы будем здесь, чтобы попытаться пролить свет на правду.
В NWES мы помогаем новаторам понять все аспекты их самых сложных технических проблем. Если вам нужно современное бюро по проектированию печатных плат и услуги по продвижению идей в области маркетинга, свяжитесь с NWES для консультации.
Простое руководство к треугольнику 30-60-90
Острый, тупой, равнобедренный, равносторонний… Когда дело доходит до треугольников, существует множество различных разновидностей, но лишь немногие из них являются «особенными».«У этих особых треугольников есть стороны и углы, которые согласованы и предсказуемы, и их можно использовать, чтобы сократить путь к решению ваших геометрических или тригонометрических задач. А треугольник 30-60-90 — произносится как« тридцать шестьдесят девяносто »- оказывается очень особенным действительно тип треугольника.
А треугольник 30-60-90 — произносится как« тридцать шестьдесят девяносто »- оказывается очень особенным действительно тип треугольника.
В этом руководстве мы расскажем, что такое треугольник 30-60-90, почему он работает и когда (и как) использовать свои знания о нем. Итак, приступим!
Что такое треугольник 30-60-90?
Треугольник 30-60-90 — это специальный прямоугольный треугольник (прямоугольный треугольник — это любой треугольник, который содержит угол 90 градусов), который всегда имеет углы градусов 30, 60 и 90 градусов.Поскольку это особый треугольник, у него также есть значения длины стороны, которые всегда находятся в постоянном соотношении друг с другом.
Базовое соотношение треугольника 30-60-90:
Сторона, противоположная углу 30 °: $ x
Сторона, противоположная углу 60 °: $ x * √3 $
Сторона, противоположная углу 90 °: 2 доллара x
доллара США.Например, треугольник 30-60-90 градусов может иметь длину стороны:
2, 2√3, 4
7, 7√3, 14
√3, 3, 2√3
(Почему более длинная ветвь равна 3? В этом треугольнике самая короткая ветвь ($ x $) равна $ √3 $, поэтому для более длинной ветви $ x√3 = √3 * √3 = √9 = 3 $. А гипотенуза — это 2 кратчайшего отрезка, или 2√3 $)
А гипотенуза — это 2 кратчайшего отрезка, или 2√3 $)
И так далее.
Сторона, противоположная углу 30 °, всегда является наименьшим , потому что 30 ° — наименьший угол. Сторона, противоположная углу 60 °, будет средней длиной , потому что 60 градусов — это средний угол в этом треугольнике. И, наконец, сторона, противоположная углу 90 °, всегда будет самой большой стороной (гипотенуза) , потому что 90 градусов — это наибольший угол.
Хотя треугольник 30-60-90 может выглядеть так же, как другие типы прямоугольных треугольников, он настолько особенный, что вам нужно всего три части информации, чтобы найти любое другое измерение. Пока вы знаете значение двух угловых мер и длины одной стороны (неважно, с какой стороны), вы знаете все, что вам нужно знать о своем треугольнике.
Например, мы можем использовать формулу треугольника 30-60-90, чтобы заполнить все оставшиеся информационные поля треугольников ниже.
Пример 1
Мы видим, что это прямоугольный треугольник, в котором гипотенуза вдвое больше длины одного из катетов. Это означает, что это должен быть треугольник 30-60-90, а меньшая заданная сторона противоположна 30 °.
Следовательно, более длинная полка должна располагаться напротив угла 60 ° и иметь размер $ 6 * √3 $ или 6√3 $.
Пример 2
Мы можем видеть, что это должен быть треугольник 30-60-90, потому что мы видим, что это прямоугольный треугольник с одним заданным размером 30 °.Тогда немаркированный угол должен составлять 60 °.
Поскольку 18 — это мера, противоположная углу 60 °, она должна быть равна $ x√3 $. Тогда самая короткая ветка должна иметь размер 18 $ / √3 $.
(обратите внимание, что длина отрезка на самом деле будет $ 18 / {√3} * {√3} / {√3} = {18√3} / 3 = 6√3 $, потому что знаменатель не может содержать радикальный / квадратный корень) .
А гипотенуза будет 2 $ (18 / √3)
$ (Обратите внимание, что, опять же, у вас не может быть радикала в знаменателе, поэтому окончательный ответ будет в два раза больше длины ноги $ 6√3 $ => $ 12√3 $).
Пример 3
Опять же, нам даны два измерения угла (90 ° и 60 °), поэтому третье измерение будет 30 °. Поскольку это треугольник 30-60-90, а гипотенуза равна 30, самый короткий отрезок будет равен 15, а более длинный отрезок будет равен 15√3.
Не нужно обращаться к волшебному шару восьмерки — эти правила работают всегда.
Почему это работает: 30-60-90 Доказательство теоремы о треугольнике
Но почему этот особый треугольник работает именно так? Как мы узнаем, что эти правила законны? Давайте подробно рассмотрим, как работает теорема о треугольнике 30-60-90, и докажем, почему эти длины сторон всегда будут согласованными.
Во-первых, давайте на секунду забудем о прямоугольных треугольниках и посмотрим на равносторонний треугольник .
Равносторонний треугольник — это треугольник, у которого все стороны и углы равны. Поскольку внутренние углы треугольника всегда составляют в сумме 180 ° и $ 180/3 = 60 $, равносторонний треугольник всегда будет иметь три угла по 60 °.
Теперь давайте опустим высоту от самого верхнего угла до основания треугольника.
Теперь мы создали два прямых угла и два конгруэнтных (равных) треугольника.
Как мы узнаем, что это равные треугольники? Поскольку мы опустили высоту равностороннего треугольника , мы разделили основание точно пополам. Новые треугольники также имеют одну длину стороны (высоту), и каждый из них имеет одинаковую длину гипотенузы. Поскольку у них три общих длины стороны (SSS), это означает, что треугольников совпадают.
Примечание: два треугольника совпадают не только на основе принципов длины стороны-стороны, или SSS, но также на основе измерений стороны-угла-стороны (SAS), угла-угла-стороны (AAS) и угла. -угловой (ASA).По сути? Они определенно совпадают.
Теперь, когда мы доказали конгруэнтность двух новых треугольников, мы видим, что каждый из верхних углов должен быть равен 30 градусам (потому что каждый треугольник уже имеет углы 90 ° и 60 ° и в сумме должно составлять 180 °). . Это означает, что мы сделали два треугольника 30-60-90.
. Это означает, что мы сделали два треугольника 30-60-90.
И поскольку мы знаем, что мы разрезаем основание равностороннего треугольника пополам, мы можем видеть, что сторона, противоположная углу 30 ° (самая короткая сторона) каждого из наших треугольников 30-60-90, составляет ровно половину длины треугольника. гипотенуза.2} / 4
долл. США$ b = {√3x} / 2 $
Итак, у нас осталось: $ x / 2, {x√3} / 2, x $
Теперь давайте умножим каждую меру на 2, чтобы облегчить жизнь и избежать всех дробей. Таким образом, у нас осталось:
$ x $, $ x√3 $, 2x $
Таким образом, мы можем видеть, что треугольник 30-60-90 всегда будет иметь одинаковую длину сторон $ x $, $ x√3 $ и $ 2x $ (или $ x / 2 $, $ {√3x } / 2 $ и $ x $).
К счастью для нас, мы можем доказать, что правила треугольника 30-60-90 верны без всего…это.
Когда использовать правила треугольника 30-60-90
Знание правил треугольника 30-60-90 поможет сэкономить время и силы при решении множества различных математических задач, а именно, большого разнообразия задач по геометрии и тригонометрии.
Геометрия
Правильное понимание треугольников 30-60-90 позволит вам решать вопросы геометрии, которые либо невозможно решить, не зная этих правил соотношения, либо, по крайней мере, потребуется значительное время и усилия для решения «долгого пути».«
С помощью специальных соотношений треугольников вы можете вычислить недостающие высоты или длины участков треугольника (без необходимости использовать теорему Пифагора), найти площадь треугольника, используя недостающую информацию о высоте или базовой длине, и быстро вычислить периметры.
Каждый раз, когда вам нужна скорость, чтобы ответить на вопрос, вам пригодятся такие ярлыки, как правила 30-60-90.
Тригонометрия
Запоминание и понимание соотношения треугольников 30-60-90 также позволит вам решать многие тригонометрические задачи без использования калькулятора или необходимости приближать ваши ответы в десятичной форме.
Треугольник 30-60-90 имеет довольно простые синусы, косинусы и тангенсы для каждого угла (и эти измерения всегда будут согласованы).
Синус 30 ° всегда будет $ 1/2 $.
Косинус 60 ° всегда будет $ 1/2 $.
Хотя другие синусы, косинусы и тангенсы довольно просты, их легче всего запомнить, и они, вероятно, обнаружатся на тестах. Таким образом, знание этих правил позволит вам как можно быстрее найти эти тригонометрические измерения.
Советы по запоминанию правил 30-60-90
Вы знаете, что эти правила соотношения 30-60-90 полезны, но как вы удерживаете информацию в своей голове? Чтобы помнить правила треугольника 30-60-90, нужно помнить о соотношении 1: √3: 2 и знать, что длина самой короткой стороны всегда противоположна самому короткому углу (30 °), а длина самой длинной стороны всегда противоположна наибольший угол (90 °).
Некоторые люди запоминают соотношение, думая: « $ \ bi x $, $ \ bo 2 \ bi x $, $ \ bi x \ bo √ \ bo3 $, », потому что последовательность «1, 2, 3» обычно легко запомнить. Единственная мера предосторожности при использовании этого метода — помнить, что самая длинная сторона на самом деле — это $ 2x $, , а не , $ x $ умноженное на $ √3 $.
Еще один способ запомнить ваши отношения — это использовать мнемоническую игру слов на соотношении 1: корень 3: 2 в их правильном порядке. Например, «Джеки Митчелл выбил Лу Герига и« выиграл и Рути тоже »»: один, корень три, два. (И это, кстати, настоящий факт из истории бейсбола!)
Поиграйте со своими собственными мнемоническими устройствами, если они вам не нравятся — спойте отношение к песне, найдите свои собственные фразы «один, корень три, два» или придумайте стихотворение о соотношении.Вы даже можете просто запомнить, что треугольник 30-60-90 — это половина равносторонней стороны, и вычислить оттуда размеры, если вам не нравится их запоминать.
Тем не менее, для вас имеет смысл запомнить эти правила 30-60-90, держать их в голове для будущих вопросов по геометрии и тригонометрии.
Запоминание — ваш друг, однако вы можете сделать это возможным.
Ваша школа сообщает ваш средний балл как взвешенный или невзвешенный? Каким будет ваш средний балл, с учетом 4. Шкала 0, 5.0 или 6.0? Воспользуйтесь нашим инструментом, чтобы рассчитать свой невзвешенный и взвешенный средний балл успеваемости, чтобы выяснить, как вы соотноситесь с другими поступающими в колледж. Вы также получите наш собственный расчет среднего балла среднего балла колледжа и советы о том, где можно улучшить, чтобы стать лучшим поступающим в колледж.
Шкала 0, 5.0 или 6.0? Воспользуйтесь нашим инструментом, чтобы рассчитать свой невзвешенный и взвешенный средний балл успеваемости, чтобы выяснить, как вы соотноситесь с другими поступающими в колледж. Вы также получите наш собственный расчет среднего балла среднего балла колледжа и советы о том, где можно улучшить, чтобы стать лучшим поступающим в колледж.
Пример 30-60-90 Вопросы
Теперь, когда мы рассмотрели «как и почему» 30-60-90 треугольников, давайте поработаем над некоторыми практическими задачами.
Геометрия
Строитель прислоняет 40-футовую лестницу к стене здания под углом 30 градусов от земли.Земля ровная, сторона здания перпендикулярна земле. Как далеко вверх по зданию до ближайшего подножия ведет лестница?
Не зная наших специальных правил треугольника 30-60-90, нам пришлось бы использовать тригонометрию и калькулятор, чтобы найти решение этой проблемы, поскольку у нас есть только одно измерение стороны треугольника. Но поскольку мы знаем, что это особый треугольник , мы можем найти ответ за считанные секунды.
Но поскольку мы знаем, что это особый треугольник , мы можем найти ответ за считанные секунды.
Если здание и земля перпендикулярны друг другу, это должно означать, что здание и земля образуют прямой (90 °) угол.Также известно, что лестница встречается с землей под углом 30 °. Таким образом, мы видим, что оставшийся угол должен составлять 60 °, что составляет треугольник 30-60-90.
Теперь мы знаем, что гипотенуза (самая длинная сторона) этого 30-60-90 составляет 40 футов, что означает, что самая короткая сторона будет вдвое меньше. (Помните, что самая длинная сторона всегда вдвое длиннее — $ 2x $ — самой короткой стороны.) Поскольку самая короткая сторона находится напротив угла 30 °, и этот угол является мерой лестницы от земли в градусах, это означает, что верхняя часть лестницы ударяется о здание на высоте 20 футов от земли.
Наш окончательный ответ — 20 футов.
Тригонометрия
Если в прямоугольном треугольнике sin Θ = $ 1/2 $, а длина самого короткого участка равна 8. Какова длина недостающей стороны, НЕ являющейся гипотенузой?
Какова длина недостающей стороны, НЕ являющейся гипотенузой?
Так как вы знаете свои правила 30-60-90, вы можете решить эту задачу без использования теоремы Пифагора или калькулятора.
Нам сказали, что это прямоугольный треугольник, и мы знаем из наших специальных правил прямоугольного треугольника, что синус 30 ° = $ 1/2 $.Следовательно, недостающий угол должен составлять 60 градусов, что делает треугольник 30-60-90.
И поскольку это треугольник 30-60-90, и нам сказали, что самая короткая сторона равна 8, гипотенуза должна быть равна 16, а недостающая сторона должна быть $ 8 * √3 $ или 8√3 $.
Наш окончательный ответ — 8√3.
На вынос
Запомнив правила для треугольников 30-60-90, вы сможете сократить свой путь через множество математических задач .Но имейте в виду, что, хотя знание этих правил — удобный инструмент, который нужно держать на поясе, вы все равно можете решить большинство проблем без них.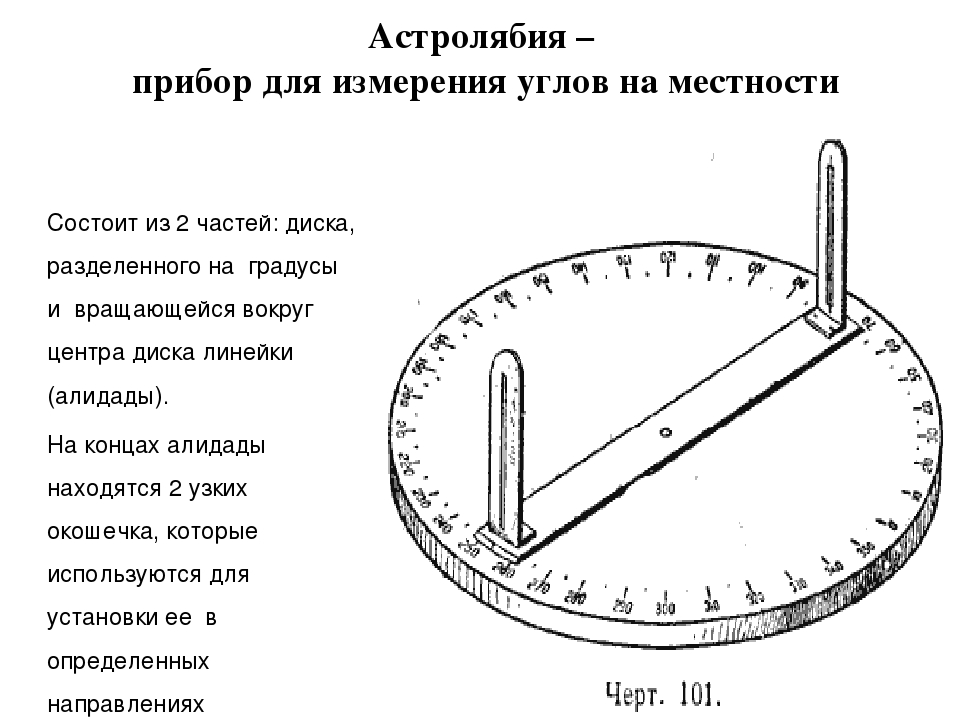
Следите за правилами $ x $, $ x√3 $, $ 2x $ и 30-60-90 любым понятным для вас способом и старайтесь придерживаться их, если можете, но не паникуйте, если вы ум исчезает, когда наступает время кризиса. В любом случае, у вас есть это.
И, если вам нужно больше практики, попробуйте эту викторину с треугольником 30-60-90. Удачной сдачи теста!
Углы заточки канавок — неожиданный ответ
Каков наилучший угол заточки канавок? «Правильный» угол строжки дежи зависит от ваших личных предпочтений.Угол наклона канавки будет определять, как вы стоите, маневрируете инструментом и как вы будете выполнять каждый проход на токарном станке. Несколько канавок с разными углами заточки фаски можно использовать в разных ситуациях токарной обработки.
Как и многие другие вещи в токарной обработке древесины, существует множество ответов.
Почему так много ответов?
Позвольте мне подчеркнуть, что следующие углы являются хорошей средней отправной точкой, но нам нужно углубиться в это немного глубже. Продолжайте читать, и я помогу вам узнать ВАШ персональный угол заточки долота.
Продолжайте читать, и я помогу вам узнать ВАШ персональный угол заточки долота.
Ниже приведены приблизительные углы заточки канавок для зубьев чаш для различных стилей канавок.
- 40-40 Шлифовка — 40 ° (конус меньшего размера)
- Традиционная шлифовка — 45 ° (крылья слегка отведены назад)
- Шлифовка ногтя — 50 ° (ширина крыльев канавки)
- Модифицированный ноготь — 50 ° (крылья ширина диаметра вала)
- Irish Grind — 55 ° (крылья в два раза больше диаметра инструмента)
- Micro Bevel Grind — 60-70 °
Углы заточки канавок для мерной чаши
Лучший способ точно измерить угол скоса канавки чаши — использовать транспортир.Поэкспериментировав с несколькими транспортирами, я решил, что мне действительно нравится этот простой стальной транспортир с фиксирующим винтом с накатанной головкой.
Поместите плоскую часть основания транспортира заподлицо с центром канавки канавки чаши. Отрегулируйте поворотный рычаг так, чтобы он плотно прилегал к углу скоса. Зафиксируйте винт с накатанной головкой и прочитайте угол под маленьким индикатором метки.
Зафиксируйте винт с накатанной головкой и прочитайте угол под маленьким индикатором метки.
Я испортил углы заточки канавок для чаши
Я помню, когда я только начал точить деревянные чаши, и заточка канавки для чаши казалась простой задачей.Мой наставник, Дэнни, нашел время, чтобы показать мне, как использовать джиг-приманку Wolverine Varigrind, чтобы вернуть прекрасную остроту моей долоте.
Шли месяцы, и я все больше и больше точил и затачивал, я начал получать комментарии от других токарных станков во время нашей группы токарной обработки в среду вечером. «Твоя долбина действительно сметена», — такой комментарий я слышал часто. Я пожал плечами и не особо об этом задумывался.
Поворот моей чаши улучшился, и я, по-видимому, продолжал опускать ручку долота для чаши ниже, когда я ее затачивал.Это действие резко отбросило назад боковые крылья. «О, вы используете гринд Элсворта», — сказал кто-то. «Конечно, я думаю. Кто бы это ни был? » РЖУНИМАГУ! Извини, Дэвид, тогда я был очень зеленым. Я чувствую, что мне нужно поклониться, чтобы показать свое недостоинство.
Я чувствую, что мне нужно поклониться, чтобы показать свое недостоинство.
Что я действительно знал, так это то, что эта выемка работала очень хорошо. Я мог агрессивно убирать отходы, а затем развернуться и сделать красивый скос на чистом толчке, прорезав поддерживаемую стенку зерна любой чаши.
Позже я научился переворачивать инструмент и использовать крылья для чистки скребков на внешней стороне чаш.Я любил свою долбленую чашу. В народе это называли «отброс», «ирландский гринд», «гринд Элсворта». Я назвал это «долбленой чашей».
Однажды я где-то прочитал статью, и там был пример моей выдолбленной задней чаши. «Круто», — думала я, пока не читала ближе.
Угол скоса для моего долота с задними крыльями с перегородкой должен составлять 65 °, говорится в статье. Я взял транспортир и измерил фаску долота. Было 55 °! О нет, что я делал? Судя по всему, я испортил долбан своей небрежной работой с болгаркой!
Я тихонько вернулся к кофемолке, надеясь, что никто не увидит, как я снимаю ценный металл с выемки чаши, отчаянно пытаясь вернуть мой скос под «правильный» угол.
Через некоторое время на шлифовальном станке и с более коротким инструментом я вернулся к токарному станку. По ощущениям царапина была примерно такой же, но что-то было по-другому. Что это было?
Потребовалось некоторое время, чтобы понять, что все движения и позиции моего тела были немного неправильными. Инструмент резал почти так же, только под немного другим углом, из-за смещения нового угла, который я только что заточил.
Углы заточки канавок для чаши персональные
Стоп! Не стачивайте долото только потому, что где-то прочли другой угол.Вместо того, чтобы воспринимать напечатанное число как Евангелие, подумайте о том, как вы используете свои инструменты.
Во-первых, вы используете долотки для чаш с различными стилями помола? В основном я использую два стиля.
Мои долота для чаши — это большие 3/4 дюйма и меньшие 1/2 дюйма со стреловидными задними кромками, каждый с углом скоса около 55 °, и долото для чаши с микро скосом, которое имеет режущий конец примерно 65-70 °. Это единственные долото для чаш, которые я использую и в которых я нуждаюсь регулярно. У меня есть другие, но они не так часто используются.
Это единственные долото для чаш, которые я использую и в которых я нуждаюсь регулярно. У меня есть другие, но они не так часто используются.
Я пытаюсь использовать то, что работает для вас. Если вам нравится использовать различные стили, размеры и углы фаски чаш, используйте их. Просто подумайте, как и когда вы используете каждую выемку и почему.
Я использую свои заостренные канавки для всех черновых и чистовых пропилов чаши снаружи и внутри. Если у чаши глубокая или угловатая внутренняя часть, я использую свое секретное оружие, как я люблю называть его, долото с микрокосом.
Если вы поворачиваете с группой других токарных станков, поспрашивайте вокруг и посмотрите, есть ли у кого-нибудь долота для чаш с углом скоса, резко отличающимся от вашего.Попросите одолжить их долото. Вам нужно будет на время повернуться, потому что поначалу странное чувство может заставить вас остановиться. Переверните всю чашу с другой долотой и посмотрите, что вы думаете.
Углы заточки канавок — неожиданный ответ
Углы заточки долота вашей чаши жизненно важны, потому что они определяют, как ВЫ стоите, занимаетесь позицией, двигаетесь и приспосабливаетесь к созданным чашам. Вы обратили внимание на «вы»?
Практически любой угол, в пределах разумного, на фаске канавки позволяет резать древесину.Однако, если у вас есть две выемки чаши со скосами на двадцать градусов друг от друга, и вы поворачиваете их обоими, вы почувствуете разницу.
Ответ на вопрос «Какие углы заточки канавок я должен использовать?» это просто. Используйте то, что работает для ВАС! Попробуйте другие углы, если хотите, но правильный ответ — тот, который больше подходит для ВАС!
Различные углы заточки канавок с разными эффектами
Используя совершенно разные скосы на шлифовке, вы почувствуете, как ваше тело вносит столь же экстремальные изменения.Например, способ вытягивания рук для внутренней выталкивания будет значительно отличаться.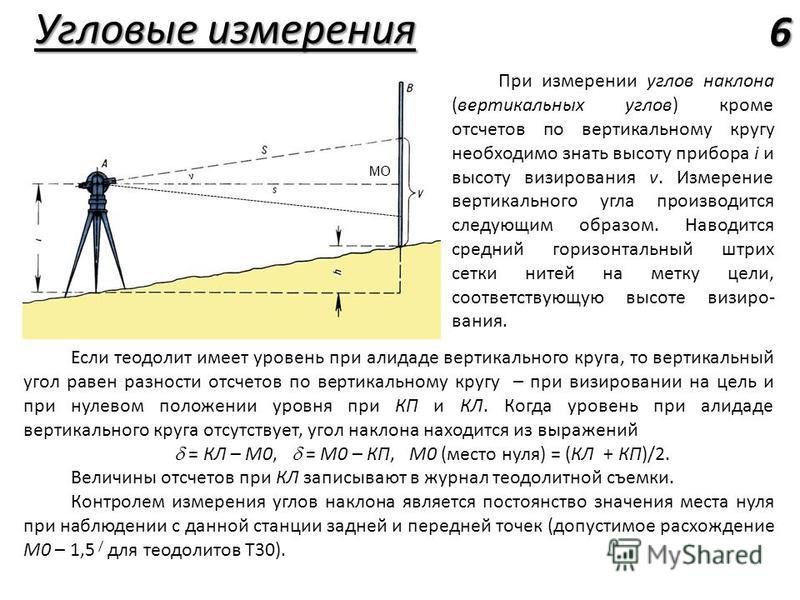
Вырезки для чаш с разными углами идеально подходят для определенных ситуаций. Я люблю иногда делать миски с загнутыми внутрь краями. Моя строжка чаши со скосом 55 ° не очень хорошо проходит под этим ободом.
Тем не менее, моя строжка со скосом под углом примерно 65-70 ° может попасть внутрь. И когда я переключаюсь на микроскос, мне также нужно перестроить свое тело, чтобы приспособиться к другому углу резания для этой строжки.Во многих случаях из-за совершенно разного угла строжки мне приходилось стоять на противоположной стороне токарного станка, чтобы использовать свой микрокосок.
Стандартного угла НЕТ
Если вы посмотрите на то, что эксперты по токарной обработке и в публикациях предлагают в качестве «правильного» угла скоса зареза чаши, скос резьбы чаши может составлять от 45 до 70 градусов.
Кто прав, а кто нет? Все они!
Не существует организационного органа, который подтверждает и проверяет правильные углы скоса зарезов чаши, и он не нужен. Вам нужно только подумать о том, что лучше всего подходит для ВАС.
Вам нужно только подумать о том, что лучше всего подходит для ВАС.
Во всяком случае, этот широкий диапазон углов заточки канавок должен указывать вам на то, что канавки для канавок — невероятно гибкий и настраиваемый инструмент.
Заставьте долбан для чаши делать то, что вам нужно.
Используйте то, что у вас есть в первую очередь
Надеюсь, вам пригодится мой опыт. Если долото для чаши вам подходит, не меняйте угол наклона. Даже если ваша точка зрения не соответствует популярной информации.
Не слушайте какой-нибудь фиксированный ответ на вопрос «правильный угол скоса». Нет такого. И все эксперты используют то, что им больше всего подходит. Это может сработать, а может и не сработать для вас. При всем уважении, Дэвид Эллсуорт (кланяясь).
Я не считаю, что эксперты или авторы в какой-то мере проявляют халатность. Они просто делятся тем, что им подходит или что может быть средним углом, который может стать хорошей отправной точкой для тех, кто начинает.
Независимо от того, сколько времени вы обтачивали, у вас, вероятно, есть углы заточки канавок, которые вам подходят.Теперь расспросите их. Почему они тебе нравятся? Хорошо ли они подходят для чаш, которые вы переворачиваете? Если так — отлично!
Если у вас есть долото, которое не работает так хорошо, спросите, почему? Это потому, что он не достигает определенной области чаш, которую вы поворачиваете? При повороте ощущается дискомфорт? Возможно, это изменит другой угол скоса.
Угол заточки канавок для дрейфующей чаши
При переходе к болгарке используйте точность. Тщательно проверьте угол, ваш угол, на котором вы ставите фаску.
Когда наша семья посетила Гранд-Каньон, наши дети были маленькими. Во время презентации рейнджеров кто-то спросил, можно ли им забрать домой несколько камней. Рейнджер объяснил, что если все принесут домой хотя бы один камень, в Гранд-Каньоне больше не останется камней. Логическая сторона меня хотела оспорить историю рейнджера, но общая идея сохранения парка была разумной.
Каждый раз, когда вы возвращаетесь к заточной шлифовальной машине, со временем могут произойти кардинальные изменения из-за незначительных нарушений.Важно следить за тем, чтобы кромка канавки совпадала с точильным кругом. Волосы, приподнятые на кончике или пятке, накапливаются намного быстрее, чем камни, покидающие эту дырку в Аризоне.
Если вы не потратите время на то, чтобы убедиться, что кромка канавки находится на одном уровне со шлифовальным кругом, ваша канавка может скоро сместиться под совершенно другой угол наклона.
Изменение и обслуживание угла заточки канавки стакана
Наилучший способ изменить угол заточки канавки дежи — постепенно. Если вы сомневаетесь в своем текущем угле пропахивания и хотите изменить его, возможно, на десять градусов, измените это медленно.
Каждый раз, когда вы возвращаетесь к заточно-шлифовальному станку, отрегулируйте угол на градус или около того и затачивайте канавку до тех пор, пока после нескольких заточек вы не достигнете желаемого конечного угла.
Не допускайте перегрева инструмента при шлифовании материала. ЗАПРЕЩАЕТСЯ погружать HSS (быстрорежущую сталь) в воду, если она слишком горячая для обработки или изменила цвет. Поставьте его и сделайте перерыв, пока он остынет. Резкие тепловые изменения в HSS могут вызвать стрессовые переломы.
Для охлаждения быстрорежущей стали можно использовать воду, если металл не слишком горячий или обесцвеченный.Приемлемо и рекомендуется частое охлаждение наконечника в воде. Однако охлаждение перегретой строжки в воде приведет к повреждению металла.
При формовании или заточке кончик долота не должен менять цвет. Синий или коричневый цвет на конце выемки означает, что металл перегрелся. Цветную область нужно удалить.
Если у вас колесо с большим ходом, используйте его для удаления материала, а затем вернитесь к колесу с более мелким ходом, чтобы восстановить острый край.
Заключение
Надеюсь, я убедил вас, что на самом деле нет единого правильного ответа на вопрос об угле заточки долота. Есть много хороших предложений и отправных точек, но единственный правильный ответ — это то, что работает для вас.
Есть много хороших предложений и отправных точек, но единственный правильный ответ — это то, что работает для вас.
Если вы готовы постоянно затачивать долбежку чаши до одного определенного угла скоса, вот три статьи, которые вам понадобятся, чтобы настроить станцию заточки, как эта Система заточки с вариативной сеткой Oneway Wolverine, понять и отрегулировать заточку Wolverine Vari-Grind Приспособьте, а затем последовательно выполняйте процесс заточки для получения легко предсказуемого угла скоса резьбы резца дежи каждый раз.
Пожалуйста, дайте мне знать, если вы нашли этот пост полезным. И, из любопытства, под каким углом вы затачиваете фаски канавок?
Хотите понять основы долбления чаш, прочтите это дальше.
— Помимо выемок для чаш, у меня есть много других предложений в моем Руководстве по рекомендуемому оборудованию. Проверь их.
Узнайте больше о канавке для чаши здесь:
• ШЛИФОВАНИЕ ДЛЯ ЧАШЕК 40-40 (ФОРМА, ЗАТОЧКА, ИСПОЛЬЗОВАНИЕ)
• ОСНОВНЫЕ ДАННЫЕ ДЛЯ ЧАШЕК — РУКОВОДСТВО ДЛЯ НАЧИНАЮЩИХ (ДЕТАЛИ, ИСПОЛЬЗОВАНИЕ, РАЗМЕРЫ, ЗАТОЧКИ) ШАГ ЗА ШАГОМ
Счастливый поворот ,
Кент
youtube.com/embed/o2dS0FWfLT4?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
прямоугольных следов печатной платы: время уничтожить мифы | by Northwest Engineering Solutions
Если вы читаете некоторые рекомендации по проектированию печатных плат в Интернете, много говорится о трассировке под прямым углом и о том, как нельзя использовать эти острые углы.Сюда входит блог Eagle, в котором конкретная производственная проблема (кислотные ловушки), основанная на технологии десятилетней давности, упоминается как причина отказа от трассировки трассировки под углом 90 градусов. Я видел, как все, от новичков до проектировщиков с многолетним опытом, заявляли, что трассировки под углом 90 градусов следует избегать любой ценой. Откуда взялась эта идея и почему ее до сих пор преподносят как пример плохой маршрутизации?
Если вы посмотрите на возражения против маршрутизации под прямым углом, они часто представлены без доказательств или достаточных оснований.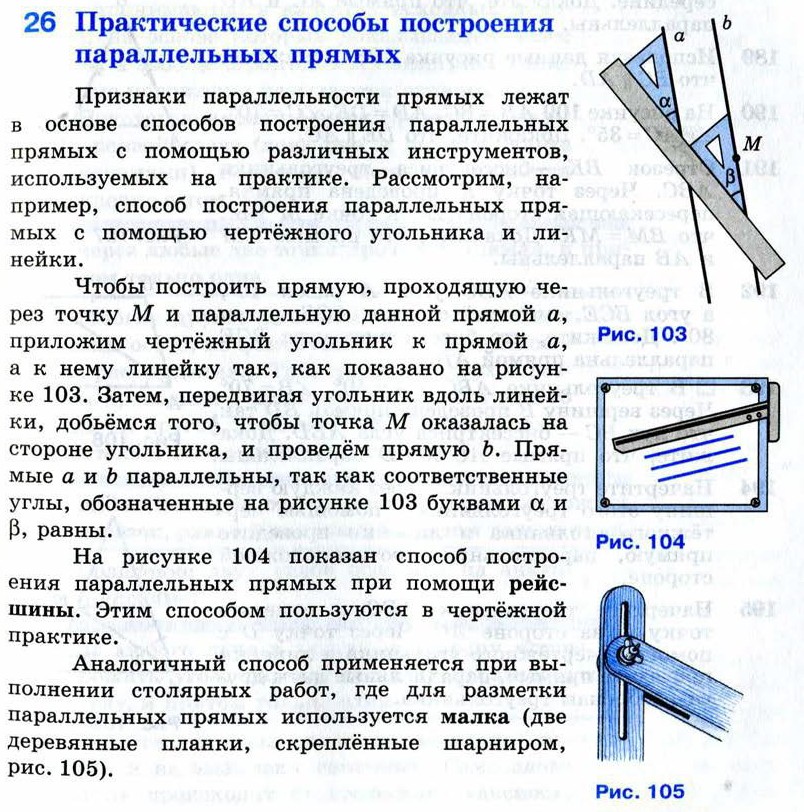 Эти возражения делятся на пять областей:
Эти возражения делятся на пять областей:
Это полная чушь. Фактически, если бы это было правдой, то сигналы не могли бы перемещаться между слоями через переходное отверстие. Это один из тех забавных фактов, которые, как я видел, упускают из виду многие старшие инженеры-проектировщики печатных плат.
Когда вы поймете, как в проводнике возбуждаются заряды, вы поймете, как поле может распространяться между двумя точками независимо от геометрии. Во-первых, давайте посмотрим на это электростатически. Когда проводник доводится до некоторого потенциала, некоторая плотность заряда затем переносится на поверхность проводника.Эта плотность заряда затем излучает электрическое поле, которое направлено перпендикулярно поверхности проводника. Если есть соседняя область отрицательного заряда (например, земля на печатной плате), то силовые линии электрического поля от положительной плотности заряда будут сходиться в область отрицательной плотности заряда. Это создает хорошо известные шаблоны полей, которые можно увидеть во многих учебных пособиях и при моделировании перекрестных помех на печатных платах.
Ток не проходит от одного конца дорожки к другому. Вместо этого это локализованное колебание растет и затухает по мере прохождения волны, но колебание существует только в пределах области, которая охватывает пространственную протяженность (например, длину волны) электромагнитной волны. Для приемников с датчиком тока (например, буферов мощности) входной сигнал рассматривается только как колебательный электрический ток в непосредственной близости от входа приемника.
Для цифрового сигнала действительно существует бесконечное количество локализованных колебаний (т.е.е., на разных гармониках некоторой основной частоты), которые создают непрерывное движение заряда кажущегося вдоль межсоединения. Опять же, суперпозиция этих локализованных колебаний тока создает то, что кажется движением заряда непосредственно от драйвера к приемнику, но заряд в проводнике на самом деле не движется таким образом.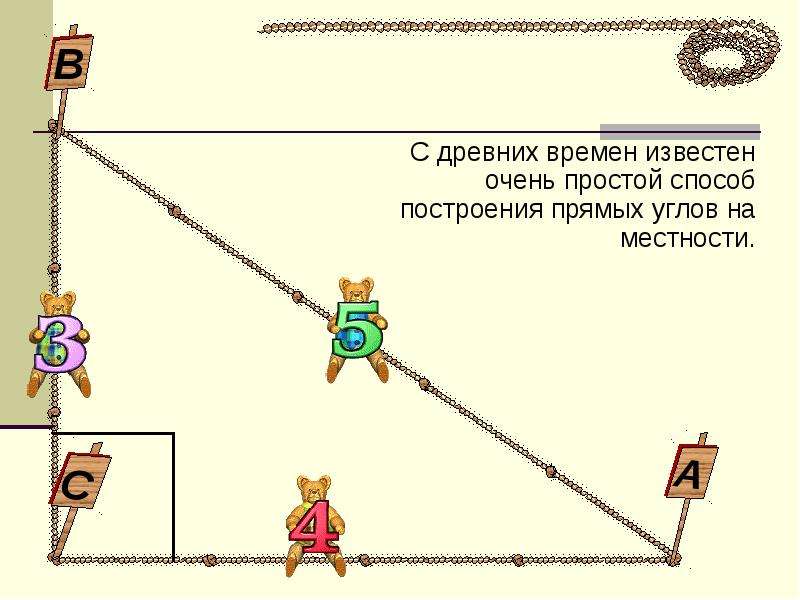
В этом есть крохотная доля правды, хотя это не имеет ничего общего с электронами, отскакивающими от края проводника.Да, это правда, что прямоугольные трассы создают разрыв импеданса, но он не более серьезен, чем разрыв импеданса, который можно увидеть на длинном переходном отверстии, слегка несовпадающей цепи фильтра / оконечной нагрузки, трассе под углом 45 градусов или серпантине. сегмент соответствия длины. Это означает, что вам следует позаботиться о создании трасс с согласованной геометрией, если вы хотите предотвратить скачки импеданса. Вы также должны свести к минимуму или исключить использование переходных отверстий в чрезвычайно высокоскоростных низкоуровневых ссылках.
Стенка прямоугольной трассы не вызывает полного внутреннего отражения электромагнитных волн обратно в трассу; Фактически, молодой студент знал бы из основ физики, что этого не происходит при нормальных условиях.Точно так же не требуется след под углом 45 градусов, чтобы заставить электромагнитную волну повернуть за угол; если бы это было правдой, то только очень определенные пары изгиба под углом 45 градусов позволили бы сигналу достичь приемника на печатной плате.
Что на самом деле происходит? Плотность электрического поля в углах прямоугольного следа немного выше, чем у гладкой стенки 45-градусного следа. Это фактически приводит нас к третьему утверждению в этом мифе о целостности сигнала …
В этом утверждении есть доля правды, но это становится критичным только выше определенных частот.Большинство дизайнеров заявят, что вы никогда не должны прокладывать прямоугольные дорожки на печатной плате из-за электромагнитных помех, создаваемых в углу. Это создаст излучаемые электромагнитные помехи вдали от поверхности платы (излучение ближнего и дальнего поля), а также перекрестные помехи на близлежащих дорожках. Давайте сначала рассмотрим проблему перекрестных помех.
Ограничивающим фактором, который определит, возбуждаются ли какие-либо резонансы, является размер квадратной области на прямоугольной дорожке печатной платы. В частности, поперечный размер области будет примерно равен четверти длины волны резонанса низшего порядка, так что это дает вам хорошую основу для оценки основных резонансных частот.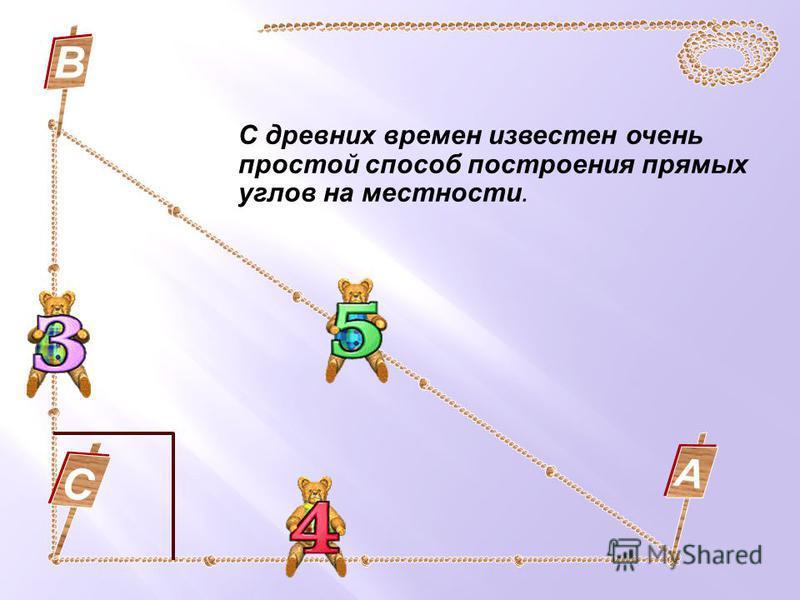 Остальные гармоники будут примерно нечетными кратными основной частоте. Если мы допустим очень большую ширину следа 30 мил с эффективной диэлектрической проницаемостью 3,5, частота самого низкого порядка будет 112 ГГц! Если мы примем это как излом частоты для цифрового сигнала, это эквивалентно времени нарастания 3 пс, что намного ниже, чем у коммерчески доступных цифровых компонентов.
Остальные гармоники будут примерно нечетными кратными основной частоте. Если мы допустим очень большую ширину следа 30 мил с эффективной диэлектрической проницаемостью 3,5, частота самого низкого порядка будет 112 ГГц! Если мы примем это как излом частоты для цифрового сигнала, это эквивалентно времени нарастания 3 пс, что намного ниже, чем у коммерчески доступных цифровых компонентов.
На сегодняшний день проектировщикам цифровых технологий не нужно беспокоиться о прямоугольных следах печатной платы как источнике электромагнитных помех.Интеллектуальный ВЧ-разработчик уже должен использовать методы изоляции, чтобы предотвратить появление шума в других схемных блоках этой формой ЭМП. Даже дизайнеры, работающие за пределами режима mmWave, будут реализовывать достаточные меры изоляции в своей плате, независимо от частоты.
Раньше это возражение было справедливо в 1980-х годах, но с новыми растворами травителей, используемыми для травления меди во время производства, вы можете эффективно игнорировать эту проблему, если только вы не работаете с производителем, который сокращает углы. Несколько десятилетий назад растворы травителей имели тенденцию иметь более высокое поверхностное натяжение и вязкость, из-за чего они накапливались и располагались в углах под углом 90 градусов на прямоугольных дорожках печатной платы. Это может вызвать чрезмерное травление в углах, что приведет к чрезмерной шероховатости поверхности медных следов. Сегодня любой американский производитель, который хочет держать свои двери открытыми, знает, что нельзя использовать эти старые травители. Однако это по-прежнему является проблемой для зарубежных производителей низкого качества.
Несколько десятилетий назад растворы травителей имели тенденцию иметь более высокое поверхностное натяжение и вязкость, из-за чего они накапливались и располагались в углах под углом 90 градусов на прямоугольных дорожках печатной платы. Это может вызвать чрезмерное травление в углах, что приведет к чрезмерной шероховатости поверхности медных следов. Сегодня любой американский производитель, который хочет держать свои двери открытыми, знает, что нельзя использовать эти старые травители. Однако это по-прежнему является проблемой для зарубежных производителей низкого качества.
Изображение под микроскопом, показывающее чрезмерное травление на некоторых следах меди.
Это, вероятно, наименее известное утверждение, которое чаще встречается у производителей, чем у дизайнеров. Считается, что высокая плотность тока вблизи углов (см. График выше) и результирующее высокое поле вызывают сильную электромиграцию. Однако экспериментальные тесты Croes et al. (см. источник ниже) обнаружили, что электромиграция около прямоугольных дорожек печатной платы была не более серьезной, чем миграция стандартных дорожек под углом 45 градусов или изогнутых дорожек.
Существует связанное, законное утверждение, которое следует учитывать, которое касается электрического поля, создаваемого прямоугольными дорожками печатной платы.Более сильное поле, излучаемое этими дорожками, означает, что при проектировании высокого напряжения следует использовать большие расстояния утечки и зазоры. Поскольку поле выше, пробой диэлектрика между двумя проводниками легче, поэтому расстояние изоляции высокого напряжения между двумя точками должно быть увеличено. Это единственное законное объектирование прямоугольных следов печатной платы.
К настоящему времени должно быть ясно; проблемы с прямоугольными дорожками на печатной плате являются мифами и не должны привлекать внимания , если вы не работаете с высоким напряжением .К сожалению, некоторые из этих мифов о дизайне просто не исчезнут в ближайшее время, но мы будем здесь, чтобы попытаться пролить свет на правду.
В NWES мы помогаем новаторам разобраться во всех аспектах их самых сложных технических проблем.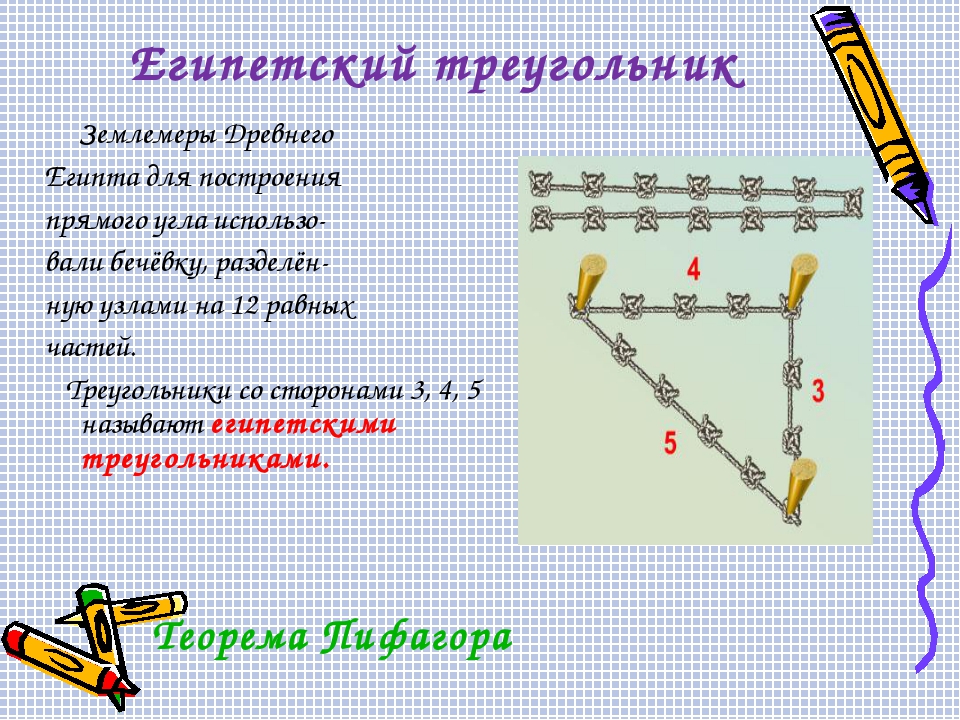

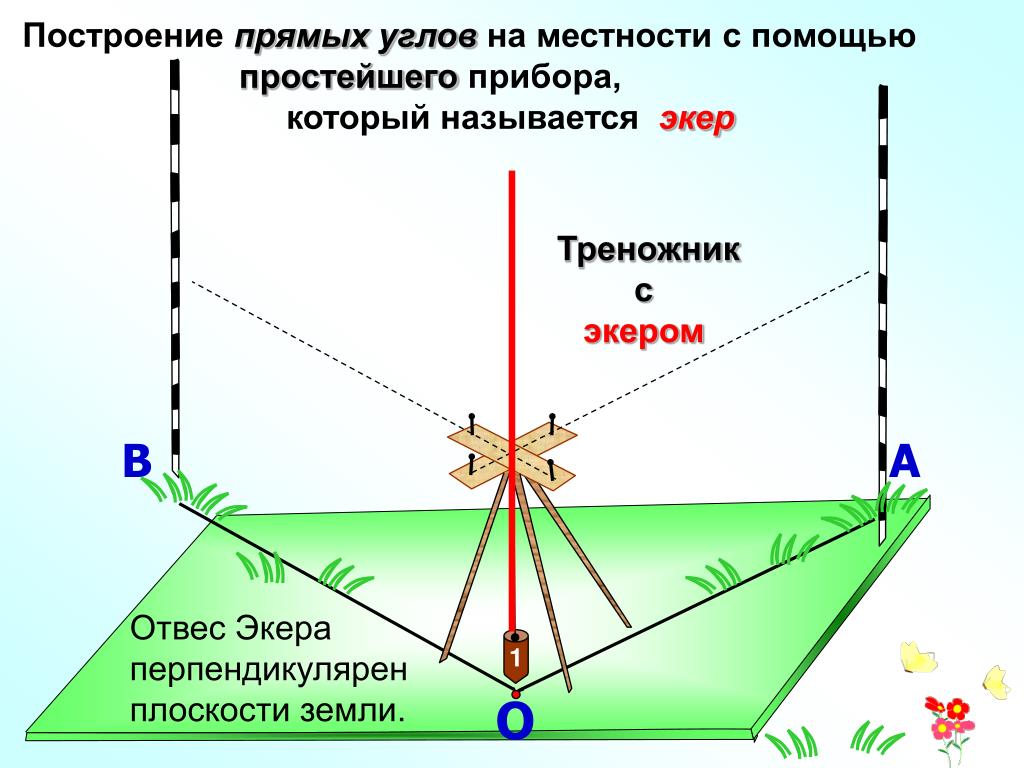
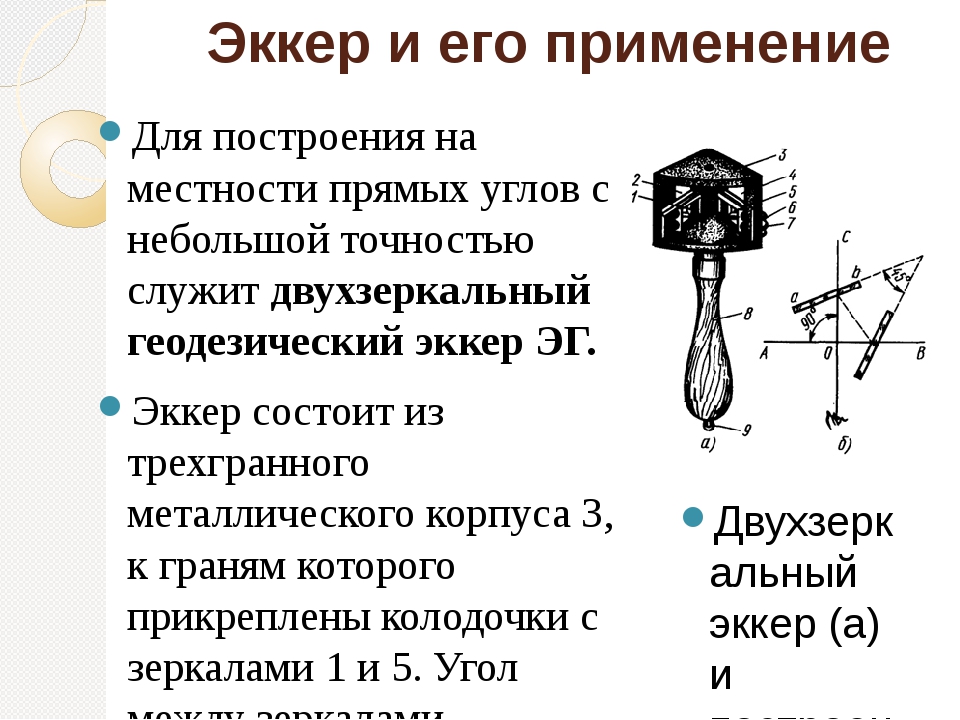 // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
// Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
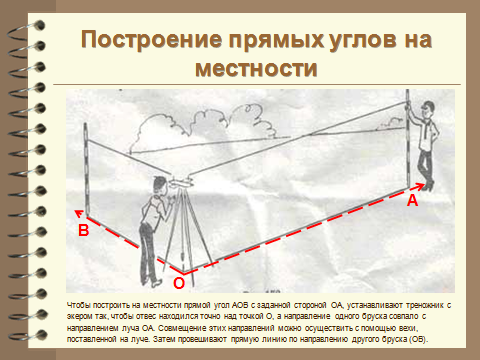 а) Среди лучей АВ, ВС, СА, АС и ВА назовите совпадающие лучи; б) назовите луч, который является продолжением луча СА.
а) Среди лучей АВ, ВС, СА, АС и ВА назовите совпадающие лучи; б) назовите луч, который является продолжением луча СА.
 □ Точка В делит отрезок АС на два отрезка. Найдите длину отрезка АС, если АВ = 7,8 см, ВС = 25 мм.
□ Точка В делит отрезок АС на два отрезка. Найдите длину отрезка АС, если АВ = 7,8 см, ВС = 25 мм.



 Какой угол называется острым? прямым? тупым?
Какой угол называется острым? прямым? тупым? Точка N лежит на отрезке МР. Расстояние между точками М и Р равно 24 см, а расстояние между точками N и М в два раза больше расстояния между точками N и Р. Найдите расстояние: а) между точками N и Р; б) между точками N и М.
Точка N лежит на отрезке МР. Расстояние между точками М и Р равно 24 см, а расстояние между точками N и М в два раза больше расстояния между точками N и Р. Найдите расстояние: а) между точками N и Р; б) между точками N и М. Докажите, что BC = 2MN.
Докажите, что BC = 2MN.
 (Дойл, 2002, стр. 1)
(Дойл, 2002, стр. 1)