Урок 7: Угол, прямоугольник, квадрат
План урока:
Угол. Виды углов: прямой, тупой, острый
Прямоугольник. Свойство противоположных сторон прямоугольника
Квадрат
Построение прямого угла, прямоугольника, квадрата на бумаге в клетку
Здравствуйте, дорогие ребята!
Приглашаем вас в сказочную страну Геометрию.
Жил-был король Луч. Была у короля маленькая, смешная и забавная дочка Точка. Отец очень любил и баловал принцессу и никогда не наказывал: не ставил в угол за ее шалости.
Король Принцесса
Угол. Виды углов: прямой, тупой, острый
Ребята, а вы знаете, что такое угол? Какие бывают углы?
Давайте вместе начертим угол. Сначала поставим точку. Затем проведем из этой точки 2 луча. Например, так:
Лучи – это стороны угла. А точка, из которой мы проводили лучи – вершина угла.
Углы бывают прямые, острые и тупые. Острым углом назовем тот, который меньше прямого, а тупым углом – тот, который больше прямого угла.
Изготовим модель прямого угла из кусочка бумаги.
Можно в качестве модели прямого угла использовать угольник. У него обязательно есть один прямой угол.
Ребята, помогите принцессе Точке определить, какие углы являются прямыми, а какие тупыми и острыми! Сосчитайте, сколько на этом чертеже прямых, острых, тупых углов.
Проверь себя!
Прямых – 6 углов, острых – 4 угла, тупых – 2 угла.
Король Луч решил построить для принцессы Точки игровую площадку. Он долго размышлял, чертил на песке разные фигуры. Посмотрите, после дождя остались лишь очертания. Назовите одним словом, что это?
Верно, это углы. Запишите номера углов в 3 столбика: острые, тупые, прямые.
Проверь себя.
Прямоугольник. Свойства противоположных сторон прямоугольника
Ребята, посмотрите на дворец короля и принцессы. Из каких геометрических фигур он состоит?
Из каких геометрических фигур он состоит?
Давайте сосчитаем все прямоугольники, квадраты, треугольники и круги.
Прямоугольники – 3.
Квадраты – 5.
Треугольники – 3.
Круги – 5.
Найдите среди этих фигур четырехугольники, у которых все углы прямые. Воспользуйтесь моделью прямого угла, которую мы с вами изготовили.
Проверь себя.
Прямоугольники: 1, 3, 5.
Ребята, у принцессы Точки есть для вас вопросы о прямоугольнике. Попробуйте на них ответить.
Вопрос 1. Равны ли у прямоугольника противоположные стороны (они лежат напротив друг друга)?
На чертеже противоположные стороны обозначены одинаковым цветом.
Вопрос 2. Все ли углы прямые у прямоугольника?
Вопрос 3. Могут ли все стороны прямоугольника, а не только противоположные, быть одинаковыми? Например, так:
Подумайте! Возьмите любой прямоугольник, измерьте линейкой стороны фигуры, с помощью модели прямого угла или угольника проверьте углы.
Сравните свои выводы с правильными ответами.
Ответ 1. Противоположные стороны равны.
Ответ 2. Все углы прямые.
Ответ 3.Все стороны прямоугольника могут быть одинаковыми.
Молодцы! Не огорчайтесь, если не все выводы совпали с правильными ответами. Давайте еще раз повторим о прямоугольнике все, что узнали.
Источник
Репетитор сможет грамотно организовать процесс обучения, прибегая к гибкому использованию существующих педагогических методов, улучшающих процесс усвоения материала
Перейти
Квадрат
Ребята, отвечая на вопрос принцессы Точки, мы сделали вывод о том, что у прямоугольника все стороны могут быть одинаковой длины. Такой прямоугольник будет называться квадратом.
Задача на смекалку от короля. Помогите принцессе Точке ее решить.
Начерти прямоугольник со сторонами 5 см и 4 см. Сделай из него квадрат! Подсказка: «Можно сделать двумя способами: добавить, убрать».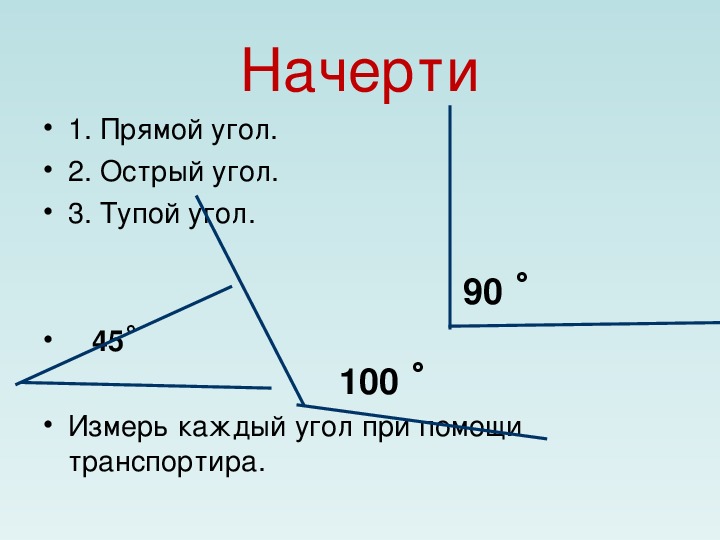
Проверь себя.
Принцесса отлично справилась с задачей. А теперь попробуйте вы самостоятельно выполнить следующее задание.
Найдите среди этих прямоугольников квадраты. Запишите их номера.
Проверь себя.
Квадраты: 1,3.
Поиграем вместе с принцессой Точкой. Она выложила из счетных палочек такую фигуру:
Сколько квадратов вы видите? Уберите одну палочку так, чтобы осталось два квадрата. Сделать это можно разными способами. Какие еще фигуры, кроме двух квадратов, у вас получились?
Проверь себя.
Кроме двух квадратов, на каждом рисунке есть прямоугольник.
Построение прямого угла, прямоугольника, квадрата на клетчатой бумаге
Как вы заметили, король Луч и принцесса Точка любят чертить. Они приглашают нас, ребята, поучаствовать в этом увлекательном занятии. Вооружитесь тетрадью в клеточку, простым карандашом, угольником.
Задание: построить на бумаге в клеточку прямой угол, прямоугольник со сторонами 6 см и 3 см, квадрат со стороной 7 см.
Посмотрите, как получилось у принцессы. Сравните со своими чертежами.
Ставим точку. Откладываем два луча при помощи угольника или линейки.
Ставим точку. Вверх – 3 см, вправо – 6 см. Помним, что противоположные прямоугольника стороны равны. Чертим их – 6 см и 3 см.
Квадрат
А это тетрадь короля. Он чертил квадрат. Сравните со своим чертежом.
Ставим точку. Помним, что у квадрата все стороны равны. Откладываем вверх 7 см, вправо – 7 см. Чертим противоположные стороны по 7 см.
Молодцы, здорово получилось! Если такое занятие было для вас интересным и увлекательным, попробуйте начертить прямой угол, прямоугольник и квадрат на нелинованной бумаге. Сделать это будет гораздо сложнее. Здесь на помощь придет угольник: проверять прямой угол.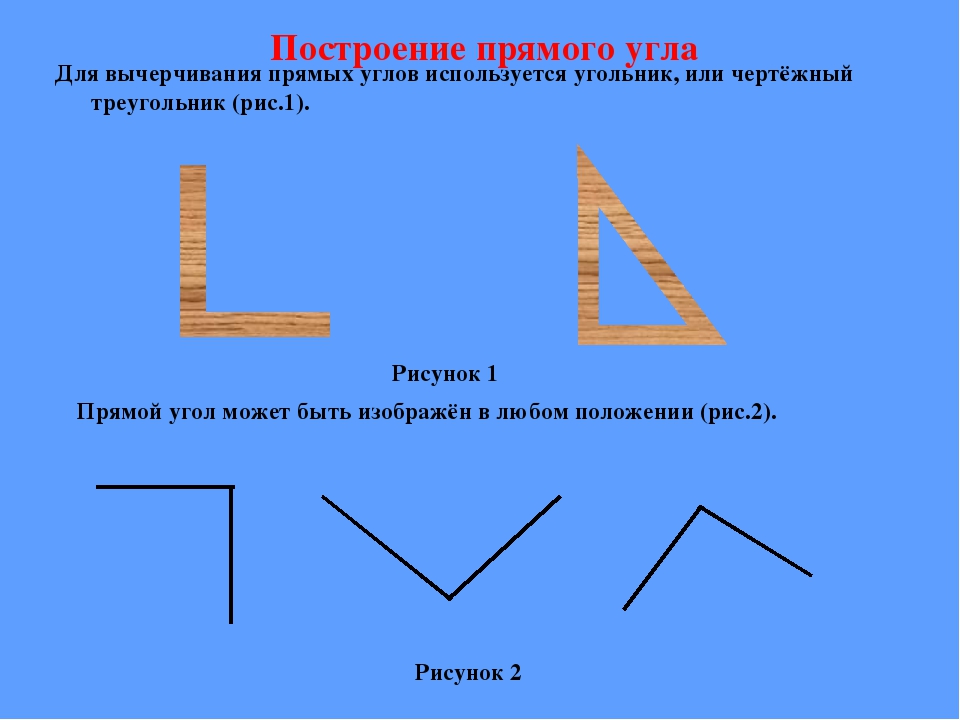
Посмотрите, как это получилось у короля и Точки.
После нелегкого занятия король Луч и его дочка присели отдохнуть. Принцесса попросила рассказать интересную сказку. Давайте и мы послушаем!
Воспользуйтесь услугой бесплатного подбора репетитора и получите ознакомительное занятие в подарок
Перейти
Сказка
Жил-был на свете Прямоугольник. Фигура важная, спору нет! Люди ценили и уважали Прямоугольника, потому что при изготовлении многих вещей использовали эту фигуру. Всё хорошо у Прямоугольника, но одиноко как-то. Решил он найти своих родственников. Думает: «Если встречу родственников, сразу узнаю, потому что на меня должны быть похожи!».
Однажды встретил Прямоугольник Квадрата и говорит: «Как тебя зовут? Очень ты, брат, на меня похож!». Отвечает Квадрат: «Если найдем не меньше четырех общих признака, значит, родственники». Стали они друг друга рассматривать и обнаружили четыре сходства:
У каждого было по 4 угла, да все прямые, по 4 стороны, да стороны, которые одна напротив другой – одинаковой длины.
Обрадовались родственники, что нашли друг друга. Поспешили вместе отправиться дальше. Встретили однажды Четырехугольника и спрашивают: «Похож ты на нас. Уж не родня ли?».
Говорит им Четырехугольник: «Я был бы очень рад! Если найдем хотя бы два сходства, значит, родственники». Стали опять внимательно друг к другу приглядываться и увидели два общих признака:
- 4 угла.
- 4 стороны.
Обрадовались фигуры и решили не терять друг друга, держаться всегда рядом.
Понравилась вам сказка? Давайте повторим о фигурах все, что узнали.
В сказочное королевство Геометрия мы вернемся еще не раз. А этот урок подошел к концу. Выберите смайлик вашего настроения.
До скорой встречи в королевстве Геометрия! А сейчас проверьте свои знания. Принцесса Точка справилась с заданиями хорошо, допустила одну небольшую ошибку.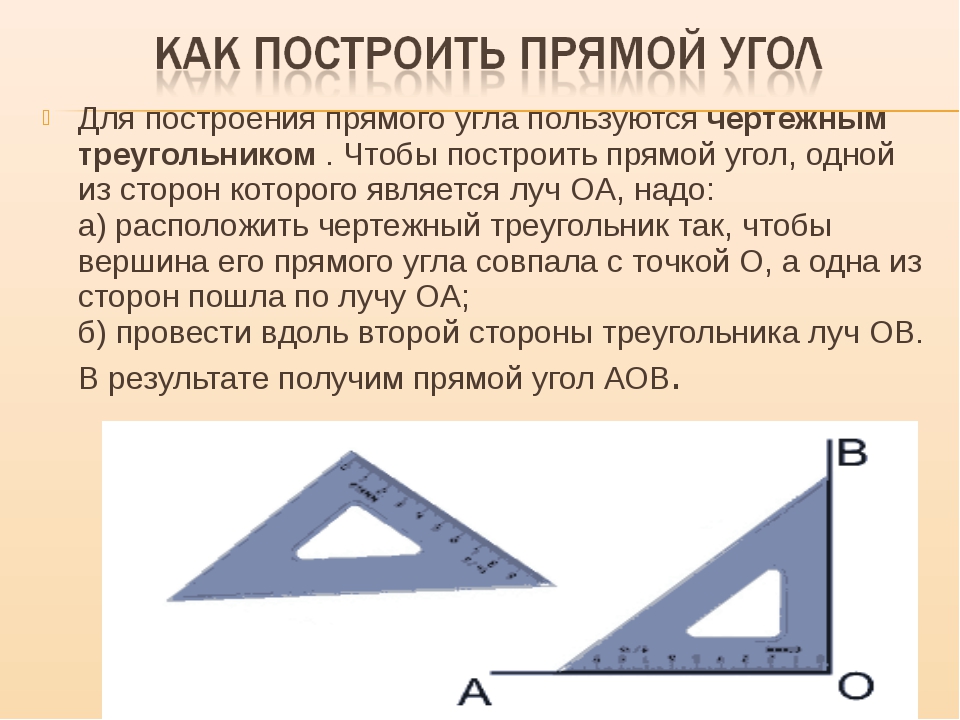
2. Актуализация знаний 6 мин | — Ребята, посмотрите на слайд, что на нём изображено? (На слайде изображен угол)
— Что же такое угол?
— Какие виды углов мы можете назвать?
— Что мы используем для построения угла?
— Давайте вспомним, как строится угол, поищем его среди других геометрических фигур, а для этого обратимся к платформе УЧИ.ру — https://uchi.ru/teachers/groups/995550/subjects/1/course_programs/2/cards/161703
— Молодцы! А для построения угла, о котором мы будем говорить на сегодняшнем уроке, мы используем модель – угольник. Какой это угол?
— И как вы думаете, чему будет посвящена тема нашего урока? (Какому углу?)
— Правильно, молодцы! Тема нашего сегодняшнего урока «Угол. Прямой угол.» |
— Угол
— Это геометрическая фигура
— Острый, тупой, прямой, …
— Линейки, угольники
(Выполняют задания на интерактивной доске)
— Прямой
— (Ответы детей: углам, прямому углу и т.д.)
| 3. Обобщение и систематизация знаний 8 мин | — Если нам нужно определить какой угол прямой, а какой нет, а угольника нет под рукой, чем мы можем воспользоваться?
— А где мы в жизни встречаемся с моделью прямого угла?
— Но
разве мы точно можем определить какой это угол перед нами? Это же просто наши
предположения, что он прямой, мы так определили «на глаз».
— Покажите мне, где у угольника прямой угол
— Посмотрите на экран, перед вами 3 веера, разложенных под разными углами. Как вы считаете, какой веер разложен под прямым углом?
— Почему вы так решили?
— Давайте проверим: приложу угольник к первому вееру. Подходит? Покажите на пальцах с помощью «плюса» или «минуса». (На слайде угольник накладывается на 1 веер) — Проверяем второй. Подходит? (На слайде угольник накладывается на 2 веер)
— Вы сказали, что в виде модели прямого угла разложили веер под номером 3. Осталось проверить только его. (На слайде угольник накладывается на 3 веер). Это прямой угол?
— Сейчас я проверю, сможете ли вы самостоятельно определить на какой картинке «спрятались» прямые углы. Откройте учебник. Определите, с помощью модели угла, на какой картинке дороги пересекаются под прямым углом. На выполнение этого задания вам даёте 1 минута, при ответе вам нужно будет это доказать.
— Время вышло. А теперь на пальцах покажите: на какой картинке дороги пересеклись под прямым углом?
— Все справились с заданием! (На этом этапе учитель периодически обращается к платформе УЧИ.ру, для выполнения заданий по карточке https://uchi.ru/teachers/groups/995550/subjects/1/course_programs/2/cards/161704) |
— (Ответы детей: по клеточкам, угол книги, лист бумаги)
— (Ответы детей: перекрёстки дорог, дома и т.д.)
— Приложить угольник
(Показывают прямой угол) — Третий
— (Ответы детей)
(Показывают «минус»)
(Показывают «минус»)
(Показывают «плюс»)
(Работают в учебнике, с помощью угольника проверяют наличие прямых углов на картинках)
(Показывают цифру «1») | 4. 9 мин | — Но мы же должны не только определять какой по виду угол перед нами. Как вы считаете, что мы должны ещё уметь?
— Какие инструменты нам нужны, чтобы построить угол?
— А если нужно построить прямой угол?
— Давайте составим план, как начертить прямой угол. Но перед этим давайте вспомним: из каких элементов состоит угол? (Слайд с углом)
— Чем является точка?
— А 2 луча?
— Так что же мы должны сделать сначала?
— Чем она будет являться?
— Первый пункт нашего алгоритма по построению прямого угла – «Отмечаем точку». (На доске появляется первый пункт)
— Второй шаг?
— Зачем? Чем он будет являться?
— Какой инструмент мы должны взять?
— Итак, второй шаг: «Чертим луч с началом в отмеченной точке» (На доске появляется второй пункт)
— Это одна сторона. А что дальше?
— Как правильно нам это сделать? Какой инструмент нам в этом поможет? — Каким же образом я должна его расположить так, чтобы начертить прямой угол с вершиной в указанной нами точке? Кто может выйти к доске и показать?
— Шаг третий: «Прикладываем угольник так, чтобы вершина угла совпала с началом луча, а сторона угольника совпала с направлением луча» (На доске появляется третий пункт)
— Ну, и остался последний шаг. Приложили угольник и, что осталось сделать? — Последний шаг: «Проводим луч с началом в отмеченной точке по направлению второй стороны угольника» (На доске появляется четвёртый пункт)
— Сколько шагов у нас получилось?
—
Давайте проговорим ещё раз подробно каждый шаг.
— Проверим: правильно ли мы построили наш угол, правильно ли составили алгоритм. А для этого заглянем вновь в учебник. Там авторы учебника предлагают нам свой план работы. Прочитайте его.
— А теперь пошагово сравните составленный нами план с планом в учебнике. Они похожи или чем- то отличаются? Что такое угол?
Прочитаем, что такое угол
— Давайте посмотрим на чертёж в учебнике. Что про него сказано? Давайте прочтём ниже.
— Посмотрите на наш чертёж, который получился на доске. Всё ли правильно? Всё ли соответствует правилу в учебнике?
— А какие вообще буквы используются для обозначения? Заглавные или строчные? — Латинского алфавита.
— А как правильно прочитать названия угла?
— Верно, это особенность называния углов.
— Давайте потренируемся называть углы, их стороны и вершины. Для этого поработаем вновь с презентацией. Какой угол вы видите? — Назовите вершину этого угла. — Назовите стороны этого угла. (Подобная подробная работа проводится с ещё 2 углами)
Учитель подводит обучающихся к правильному ответу. Оказывает помощь обучающимся, по необходимости. | — Чертить прямой угол — Карандаш, ластик, линейка
— Угольник
— Из точки и 2 лучей
— Вершиной угла
— Сторонами угла
— Поставить точку
— Вершиной нашего угла
— Проведём из точки луч
— Стороной угла
— Линейку
— Мы должны начертить второй луч, который будет второй стороной угла
— Угольник
Выполняют
построение вместе с учителем, один ученик у доски.
— Провести луч, начертить вторую сторону
— 4
(Проговаривают вместе с учителем пункты алгоритма)
— Также 4 пункта, просто там написано по-другому, а смысл одинаковый (Находят правило в учебнике)
— Угол – это геометрическая фигура. Её образуют 2 луча, исходящие из одной точки.
— Точку О называют вершиной угла, лучи ОА и ОМ – сторонами угла.
— Нет, нет обозначений.
— Заглавные буквы алфавита
— Название вершины должно прозвучать в середине.
— АОЕ — О — АО и ОЕ | 5. Физ.минутка 3 мин | — А
теперь немного отдохнём. Выйдете из-за своих парт и встаньте так, чтобы не
мешать друг другу. Слушайте внимательно и выполняйте действия, которые
прозвучат в стихотворении. | (Воспринимают речь учителя и выполняют действия, которые они услышат в стихотворении) |
Угол. Обозначение углов / Геометрия / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Геометрия
- Угол. Обозначение углов
Угол — геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.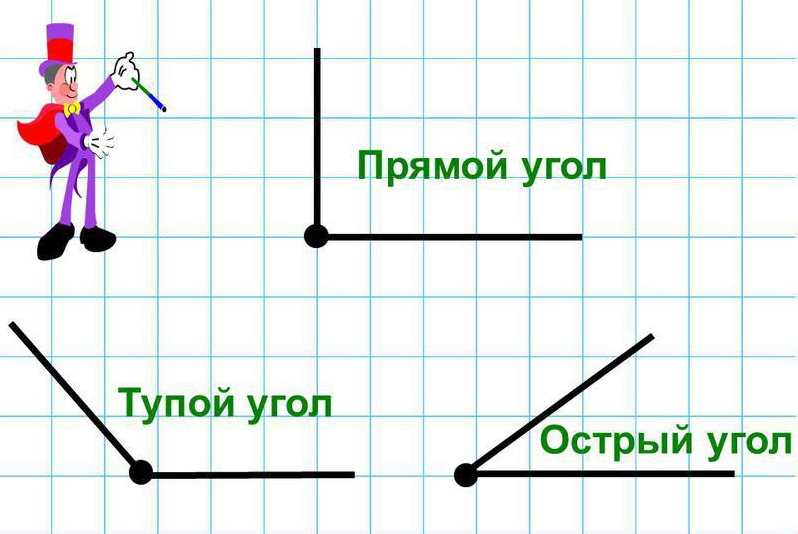
На рис. 1 лучи АВ и АС — стороны угла, точка А — вершина угла.
При записи угла в середине пишут букву, обозначающую его вершину. Сам угол на рис. 1 обозначают так: ВАС или САВ (этот угол нельзя обозначить так: АВС или СВА или ВСА или АСВ, т.к. точки В и С не являются вершинами данного угла). Этот же угол можно обозначить и короче, по его вершине: А.
Если углы имеют общую вершину, то их нельзя обозначить одной буквой. Так на рис. 2 углы имеют общую вершину Е, поэтому мы можем использовать для данных углов только следующие обозначения: МЕК или КЕМ, МЕР или РЕМ, РЕК или КЕР. Говорят, что луч ЕР в данном случае делит угол МЕК (или КЕМ) на два угла: МЕР (или РЕМ) и РЕК (или КЕР).
Также иногда углы обозначают цифрами, например, на рис.3 мы имеем 1.
Углы, как и отрезки, можно сравнивать между собой. Чтобы сравнить два угла можно наложить один угол на другой. Если при наложении одного угла на другой они совпадут, то эти углы равны.
Биссектриса — луч, который делит угол на два равных угла. На рис. 4 углы НОМ и DОМ равны, значит, луч ОМ — биссектриса угла НОD.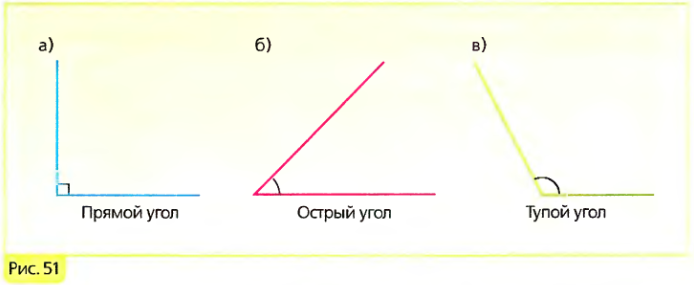
Прямой угол — угол, который можно построить с помощью угольника (рис. 5).
Если начертить два прямых угла с общей вершиной и одной общей стороной, то две другие стороны этих углов составят прямую (рис. 6). Считают, что лучи, составляющие прямую, также образуют угол, который называют развернутым.
На рис. 6 АОВ и ВОС — прямые, АОС — развернутый.
Развернутый угол равен двум прямым углам, а прямой угол составляет половину развернутого.
Острый угол — угол, который меньше прямого угла. На рис. 7 МОN — острый.
Тупой угол — угол, который больше прямого угла, но меньше развернутого. На рис. 8 РЕК — тупой.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Отрезок
Ломаная
Четырехугольники
Единицы измерения площадей. Свойства площадей
Прямоугольник, его периметр и площадь. Ось симметрии фигуры
Квадрат. Периметр и площадь квадрата.
Многоугольники. Правильные многоугольники. Равенство фигур.
Плоскость
Прямая
Луч
Шкалы и координаты
Прямоугольный параллелепипед. Пирамида.
Объем прямоугольного параллелепипеда
Куб. Площадь поверхности куба
Куб. Объем куба
Прямой и развернутый угол
Чертежный треугольник
Измерение углов. Транспортир. Виды углов
Треугольник и его виды
Окружность, круг, шар
Отрезок-xx
Геометрия
Правило встречается в следующих упражнениях:
5 класс
Задание 1622, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1671, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1710, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 281, Мерзляк, Полонский, Якир, Учебник
Номер 289, Мерзляк, Полонский, Якир, Учебник
Номер 6, Мерзляк, Полонский, Якир, Учебник
Номер 8, Мерзляк, Полонский, Якир, Учебник
Номер 9, Мерзляк, Полонский, Якир, Учебник
Номер 300, Мерзляк, Полонский, Якир, Учебник
Номер 359, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 206, Мерзляк, Полонский, Якир, Учебник
Номер 219, Мерзляк, Полонский, Якир, Учебник
Номер 220, Мерзляк, Полонский, Якир, Учебник
Задание 173, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 247, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 611, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 724, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1545, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1546, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1571, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Задание 81, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5. com, 2021
com, 2021
Пользовательское соглашение
Copyright
Прямой угол — как вычислить подручными средствами.
Прежде, чем узнать, как построить прямой угол, нужно вспомнить его определение. Прямым называется угол в девяносто градусов, образованный двумя перпендикулярными прямыми. Можно также сказать, что это половина развернутого угла. Существует несколько способов построения прямого угла.
Способы построения прямого угла
Самое простое – построение прямого угла при помощи чертежного угольника. Его прикладывают к бумаге и проводят линии вдоль перпендикулярных сторон: получается прямой угол.Также можно использовать транспортир. К проведенной карандашом линии приложить транспортир, отметить на бумаге угол девяносто градусов. Затем соединить линией (по линейке) эту отметку с линией на бумаге.
- Существует метод построения прямого угла с помощью циркуля и линейки. Сначала нужно циркулем обрисовать окружность и начертить ее диаметр. Затем отметить на окружности произвольную точку и соединить ее с концами диаметра: получится треугольник, вписанный в окружность. Его угол (с вершиной в точке на окружности) будет прямым.
- Второй способ – нарисовать две любые пересекающиеся окружности. Две точки пересечения соединить одной линией, другую – провести через центры окружностей. Два этих отрезка пересекутся под углом 90 градусов.
- Если нет чертежных инструментов, можно воспользоваться любыми прямоугольными предметами. Это может быть лист картона, любая упаковка (от лекарства, пачка от сигарет, коробка конфет и т.д.), книжка, рамка для фото и др.
Построение прямых углов на местности
Вообще, построение прямых углов на местности необходимо в строительстве, при разделе участков земли и т.д. Для этого используются специальные приборы – экер, астролябия, теодолит.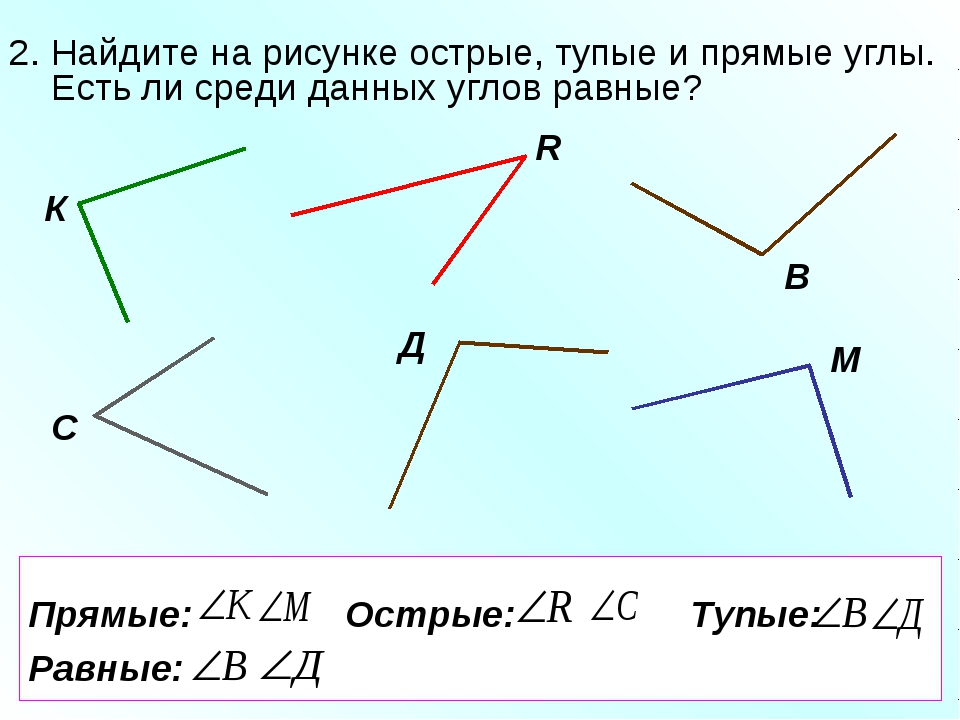 Но, вряд ли эти инструменты окажутся, к примеру, на дачном участке. Тогда можно воспользоваться методом, применяемым с давних времен. Понадобятся три колышка и веревки по 3, 4 и 5 метров. Воткнуть в землю колышек, к нему привязать веревки 3 и 4 метра, а к их концам – остальные колья. Последние два колышка соединить 5-метровой веревкой, натянуть получившийся треугольник, и забить эти колья в землю. Угол треугольника с первым колышком будет прямым.
Но, вряд ли эти инструменты окажутся, к примеру, на дачном участке. Тогда можно воспользоваться методом, применяемым с давних времен. Понадобятся три колышка и веревки по 3, 4 и 5 метров. Воткнуть в землю колышек, к нему привязать веревки 3 и 4 метра, а к их концам – остальные колья. Последние два колышка соединить 5-метровой веревкой, натянуть получившийся треугольник, и забить эти колья в землю. Угол треугольника с первым колышком будет прямым.
Как видите, существует масса несложных способов построения прямого угла.
Посмотрите на картинку. (Рис. 1)
Рис. 1. Иллюстрация к примеру
Из каких знакомых вам геометрических фигур она состоит?
Конечно, вы увидели, что картинка состоит из треугольников и прямоугольников. Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Рис. 2. Определение угла
Сегодня мы будем учиться чертить прямой угол.
В названии этого угла уже есть слово «прямой». Чтобы правильно изобразить прямой угол, нам понадобится угольник. (Рис. 3)
Рис. 3. Угольник
В самом угольнике уже есть прямой угол. (Рис. 4)
Рис. 4. Прямой угол
Он и поможет нам изобразить эту геометрическую фигуру.
Чтобы правильно изобразить фигуру, мы должны приложить угольник к плоскости (1), обвести его стороны (2), назвать вершину угла (3) и лучи (4).
1.
2.
3.
4.
Давайте определим, есть ли среди имеющихся углов прямые (Рис. 5). В этом нам поможет угольник.
Рис. 5. Иллюстрация к примеру
Найдем прямой угол угольника и приложим его к имеющимся углам (рис. 6).
Рис. 6. Иллюстрация к примеру
Мы видим, что прямой угол совпал с углом ВОМ. Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Рис. 7. Иллюстрация к примеру
Мы видим, что прямой угол нашего угольника не совпал с углом СOD. Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8)
Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8)
Рис. 8. Иллюстрация к примеру
Мы видим, что угол АОТ гораздо больше, чем прямой угол. Это значит, что угол АОТ не является прямым.
На этом уроке мы учились строить прямой угол с помощью угольника.
Слово «угол» дало название многим вещам, а также геометрическим фигурам: прямоугольник, треугольник, угольнику, с помощью которого можно начертить прямой угол.
Треугольник — это геометрическая фигура, которая состоит из трех сторон и трех углов. Треугольник, у которого есть прямой угол, называется прямоугольным треугольником.
Это — древнейшая геометрическая задача .
Пошаговая инструкция
1й способ. — С помощью «золотого», или «египетского», треугольника . Стороны этого треугольника имеют соотношение сторон 3:4:5, а угол равен строго 90град . Этим качеством широко пользовались древние египтяне и другие пракультуры.
Илл.1. Построение Золотого, или египетского треугольника
- Изготавливаем три мерки (или веревочных циркуля – веревка на двух гвоздях или колышках) с длинами 3; 4; 5 метров . Древние в качестве единиц измерения часто пользовались способом завязывания узелков с равными расстояниями между ними. Единица длины — «узелок ».
- Вбиваем в точке О колышек, цепляем на него мерку «R3 — 3 узелка».
- Протягиваем веревку вдоль известной границы – в сторону предполагаемой точки А.
- В момент натяжения на линии границы – точка А, вбиваем колышек.
- Затем — снова от точки О, протягиваем мерку R4 – вдоль второй границы. Колышек пока не вбиваем.
- После этого натягиваем мерку R5 – от А до В.
- В месте пересечения мерок R2 и R3 вбиваем колышек. – Это искомая точка В – третья вершина золотого треугольника , со сторонами 3;4;5 и с прямым углом в точке О .
2й способ. С помощью циркуля .
Циркуль может быть веревочный или в виде шагомера . См:
См:
Наш циркуль-шагомер имеет шаг в 1 метр.
Илл.2. Циркуль-шагомер
Построение – также по Илл.1.
- От точки отсчета – точки О – угла соседа, проводим отрезок произвольной длины — но больше, чем радиус циркуля = 1м – в каждую сторону от центра (отрезок АВ).
- Ставим ногу циркуля в точку О.
- Проводим окружность с радиусом (шагом циркуля) = 1м. Достаточно провести короткие дуги – сантиметров по 10-20, в местах пересечения с отмеченным отрезком (через точки А и В.). Этим действием мы нашли равноудаленные точки от центра — А и В. Величина удаления от центра здесь не имеет значения. Можно эти точки просто отметить рулеткой.
- Далее нужно провести дуги с центрами в точках А и В, но несколько (произвольно) большего радиуса, чем R=1м. Можно перенастроить наш циркуль на больший радиус, если он имеет регулируемый шаг. Но для такой небольшой текущей задачи не хотелось бы его «дергать». Или когда регулировки нет. Можно сделать за полминуты веревочный циркуль .
- Ставим первый гвоздь (или ножку циркуля с радиусом больше, чем 1м) поочередно в точки А и В. И проводим вторым гвоздем — в натянутом состоянии веревки, две дуги — так чтобы они пересеклись друг с дружкой. Можно в двух точках: C и D, но достаточно одной – C. И снова хватит коротких засечек на пересечении в точке С.
- Проводим прямую (отрезок) через точки С и D.
- Все! Полученный отрезок, или прямая, — есть точное направление на север:). Простите, — на прямой угол .
- На рисунке показаны два случая несоответствия границы по участку соседа. На Илл.3а приведен случай, когда забор соседа уходит от нужного направления в ущерб себе. На 3б – он залез на Ваш участок. В ситуации 3а возможно построение двух «направляющих» точек: и C, и D. На 3б же – только С.
- Поставьте на углу О колышек, а в точке C — временный колышек, и протяните от С шнур до задней границы участка. – Так, чтобы шнур едва касался колышка О.
 Замерив от точки О – в направлении D, длину стороны по генплану, получите достоверный задний правый угол участка.
Замерив от точки О – в направлении D, длину стороны по генплану, получите достоверный задний правый угол участка.
Илл.3. Построение прямого угла – от угла соседа, с помощью циркуля-шагомера и веревочного циркуля
Если у Вас есть циркуль-шагомер, то можно и вовсе обойтись без веревочного . Веревочный в предыдущем примере мы применили для проведения дуг большего радиуса, чем у шагомера. Большего потому, что эти дуги должны где-нибудь пересечься. Для того чтобы дуги можно было провести шагомером с тем же радиусом – 1м с гарантией их пересечения, надо чтобы точки А и В находились внутри окружности c R =1м.
- Отмерьте тогда эти равноудаленные точки рулеткой — в разные стороны от центра, но обязательно по линии АВ (линии забора соседа). Чем точки А и В будут ближе к центру – тем дальше от него направляющие точки: C и D, и тем точнее измерения. На рисунке это расстояние принято равным около четверти радиуса шагомера = 260мм.
Илл.4. Построение прямого угла с помощью циркуля-шагомера и рулетки
- Не менее актуальна эта схема действий и при построении любого прямоугольника, в частности — контура прямоугольного фундамента. Вы получите его идеальным. Его диагонали, конечно, нужно проверить, но разве не уменьшаются усилия? – По сравнению, когда диагонали, углы и стороны контура фундамента двигают туда-сюда, пока углы не сойдутся..
Собственно, мы решили геометрическую задачу на земле. Для того чтобы Ваши действия были более уверенными на участке, потренируйтесь на бумаге – с помощью обычного циркуля. Что ничем в принципе не отличается.
Посмотрите на картинку. (Рис. 1)
Рис. 1. Иллюстрация к примеру
Из каких знакомых вам геометрических фигур она состоит?
Конечно, вы увидели, что картинка состоит из треугольников и прямоугольников. Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Рис. 2. Определение угла
2. Определение угла
Сегодня мы будем учиться чертить прямой угол.
В названии этого угла уже есть слово «прямой». Чтобы правильно изобразить прямой угол, нам понадобится угольник. (Рис. 3)
Рис. 3. Угольник
В самом угольнике уже есть прямой угол. (Рис. 4)
Рис. 4. Прямой угол
Он и поможет нам изобразить эту геометрическую фигуру.
Чтобы правильно изобразить фигуру, мы должны приложить угольник к плоскости (1), обвести его стороны (2), назвать вершину угла (3) и лучи (4).
1.
2.
3.
4.
Давайте определим, есть ли среди имеющихся углов прямые (Рис. 5). В этом нам поможет угольник.
Рис. 5. Иллюстрация к примеру
Найдем прямой угол угольника и приложим его к имеющимся углам (рис. 6).
Рис. 6. Иллюстрация к примеру
Мы видим, что прямой угол совпал с углом ВОМ. Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Рис. 7. Иллюстрация к примеру
Мы видим, что прямой угол нашего угольника не совпал с углом СOD. Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8)
Рис. 8. Иллюстрация к примеру
Мы видим, что угол АОТ гораздо больше, чем прямой угол. Это значит, что угол АОТ не является прямым.
На этом уроке мы учились строить прямой угол с помощью угольника.
Слово «угол» дало название многим вещам, а также геометрическим фигурам: прямоугольник, треугольник, угольнику, с помощью которого можно начертить прямой угол.
Треугольник — это геометрическая фигура, которая состоит из трех сторон и трех углов. Треугольник, у которого есть прямой угол, называется прямоугольным треугольником.
В школе мы несколько лет подряд прилежно изучаем геометрию. Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться.
Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться.
Вешаем зеркало
Вы решили повесить в прихожей зеркало. Тут же возникает вопрос: какой минимальной высоты должно быть зеркало, чтобы человек среднего роста мог видеть себя в нём целиком? И ещё: имеет ли при этом значение размер помещения, где будет висеть зеркало? Решение. Предмет и его отражение симметричны относительно плоскости зеркала. Построим в нём изображение человека (рис. 1): АВ — человек, А 1 В 1 — его изображение, точка С — глаз, DE — зеркало. Из рисунка видно, что минимальная высота зеркала приблизительно равна половине роста человека, считая от уровня глаз. При этом высота Е нижнего края зеркала от пола должна быть вдвое меньше расстояния от пола до глаз. Легко понять, что, на каком бы расстоянии от такого зеркала ни находился человек, он сможет увидеть себя в нём с головы до ног, значит, размер помещения значения не имеет.Завариваем чай
Перед вами стеклянные чайники четырёх моделей одинаковой вместимости (рис. 2). В каком чайнике заваренный чай останется тёплым дольше? Решение. Из курса физики известно, что время охлаждения пропорционально площади поверхности тела. Значит, чем меньше поверхность чайника, тем дольше остывает чай. Самая маленькая площадь поверхности у четвёртого чайника, так как его форма близка к сфере (S = d 2).Выдерживаем прямые углы
Если вы решили склеить коробку, сделать шкатулку или выложить плитку, важно, чтобы все детали были точными прямоугольниками или квадратами. В противном случае всё пойдёт наперекосяк. Как проверить, имеет ли деталь нужную «геометрию»? Решение. Чтобы проверить, у всех ли деталей, с которыми вы работаете, прямые углы и одинаковые линейные размеры, можно использовать строи-тельный угольник (рис. 3), а можно применить знания по геометрии. Убедитесь в том, что противоположные стороны четырёхугольника равны и при этом диагонали тоже имеют одинаковую длину. Как вы и сами знаете, сделать это можно с помощью линейки. Но вот вопрос: обязательно ли проверять и стороны и диагонали? Геометрия утверждает, что да! Например, на рис. 4 диагонали в четырёхугольнике слева равны, но очевидно, что его углы совсем не прямые. А в четырёхугольнике справа противоположные стороны равны, но это тоже не прямоугольник. Для проверки прямоугольности геометрия ещё советует убедиться в равенстве всех четырёх отрезков, на которые разбиваются диагонали в точке их пересечения.
Но вот вопрос: обязательно ли проверять и стороны и диагонали? Геометрия утверждает, что да! Например, на рис. 4 диагонали в четырёхугольнике слева равны, но очевидно, что его углы совсем не прямые. А в четырёхугольнике справа противоположные стороны равны, но это тоже не прямоугольник. Для проверки прямоугольности геометрия ещё советует убедиться в равенстве всех четырёх отрезков, на которые разбиваются диагонали в точке их пересечения.Строим прямой угол на земле
Известен старинный способ постро-ения прямого угла на поверхности земли. Его использовали ещё древние египтяне. Они строили прямой угол с помощью обычной верёвки, на которой через равные расстояния завязаны тринадцать узелков. Чтобы отрезки на верёвке были одинаковые, узелки завязывали вокруг колышков, вбитых в землю на равном расстоянии друг от друга. В чём состоит этот «верёвочный» способ? Решение. В древности при закладке храма такую верёвку с узелками использовали для определения направлений его стен. Концы верёвки на месте крайних узелков связывали, а затем натягивали её на три колышка так, как показано на рис. 5. Стороны при этом имели соотношение 3:4:5. В таком треугольнике один из углов получается прямым. Впоследствии этот факт был доказан в теореме Пифагора. Поэтому первых геометров называли ещё «натягивателями верёвок». Нужно отметить, что таким способом построения прямого угла на местности пользуются и сегодня, например при закладке фундамента небольшого строения.Проверяем перпендикулярность стен
Как проверить, перпендикулярны ли друг другу соседние стены в комнате, воспользовавшись верёвкой с узелками из предыдущей задачи? Решение. Если предположить, что стены в комнате вертикальны, а пол горизонтален, то проверку проводят так. От точки на полу в углу между стенами откладывают отрезки длиной 3 и 4 единицы (рис. 6). Если стены перпендикулярны, то расстояние между концами отрезков будет равно 5 единицам, так как построенный тре-угольник со сторонами 3, 4, 5 — прямоугольный.
Отмеряем нужный объём
Часто в рецептуре того или иного блюда требуется взять четверть (или половину) стакана жидкости, муки либо какого-либо другого продукта. Как отмерить такой объём с наибольшей точностью, не прибегая к дополнительным измерительным средствам? Решение. Воспользуемся стаканом цилиндрической формы — это важно для точности измерений. Чтобы отмерить четверть стакана жидкости, надо из наполненного стакана вылить столько, чтобы оставшаяся в нём жидкость закрыла половину дна (рис. 7). Она займёт примерно четверть объёма стакана-цилиндра. Аналогично поступаем, если надо отмерить половину стакана. Наклоняем стакан так, чтобы оставшаяся в нём жидкость закрыла всё дно (рис. 8). А можно ли геометрическим способом узнать объём бутылки? Конечно! Для этого надо заполнить бутылку водой чуть меньше чем наполовину (рис. 9, слева) и измерить объём воды, умножив площадь дна бутылки на высоту налитой в неё воды (напомним, что объём цилиндра вычисляется как произведение площади основания на высоту). Затем нужно перевернуть бутылку горлышком вниз так, чтобы вода не вытекла, и измерить объём верхней цилиндрической части бутылки, оставшейся пустой (рис. 9, справа). Полный объём бутылки равен сумме найденных объёмов. Для точности можно учесть толщину стенок бутылки.Укрепляем калитку
Прямоугольная калитка (рис. 10, слева) со временем расшатывается и становится похожей на параллело-грамм. Этого можно избежать, прибив к ней ещё одну планку. Только надо знать, как это сделать. Решение. Выбор такого положения планки, как показано на рис. 10, справа, основан на свойстве жёсткости треугольника. Оно гласит: существует единственный треугольник с заданными длинами сторон. Планка и есть гипотенуза такого треугольника.Выбираем табурет
Если вы решили предыдущую задачу, то без труда определите, на какой табурет (рис. 11) можно сесть без риска оказаться на полу. Решение. Безопасный табурет изображён на правой картинке, так как его сиденье и ножки образуют треугольник.
Исправляем ошибку кроя
Предположим, вам нужно вырезать для аппликации два разносторонних треугольника из цветной бумаги — «левый» и «правый». Вы случайно вырезали их одинаковыми — оба «левые». Можно ли, не используя новый кусок бумаги, исправить ошибку? Решение. Для исправления ошибки вы можете разрезать один из треугольников, например так, как показано на рис. 12, а затем сложить из него нужный треугольник.Находим середину
Как без всяких измерений найти середину негнущегося прута, доски или металлического стержня? Решение. Можно отмерить размеры стержня на шнуре, затем сложить его пополам и отложить полученную длину. А можно воспользоваться геометрическим построением середины отрезка с помощью циркуля и линейки, если, конечно, размеры позволяют это сделать. Ещё более рациональное решение даёт физика. Середину однородного стержня легко найти, используя понятие центра тяжести (рис. 13).Углы. Виды углов. Построение прямого угла.
Тема урока: «Углы. Виды углов. Построение прямого угла»
Демонстрационный материал: презентация
Цели урока:
1.Проверить уже полученные знания и умения учащихся о
геометрических фигурах и их свойствах.
2.Научить правильно называть элементы угла – вершины и его стороны, правильно называть и обозначать угол, с помощью трех и одной букв; научить распознавать острые, тупые и прямые углы, и применять определения углов для их распознания (т.е. применять определение острого угла, тупого угла, прямого угла).
3. Совершенствовать умение работать с чертежными инструментами – линейкой, угольником и циркулем;
совершенствовать устные и письменные вычислительные навыки;
совершенствовать навык самостоятельности в работе.
4. Оценить образно-логическое мышление учащихся с помощью теста: “Выбери правильное определение.”
5. Развивать логическое мышление; развивать внимание учащихся, память, математическую речь.
5. Воспитывать аккуратность при построении чертежей и оформлении упражнений; воспитывать интерес к математике через занимательные задания, конструирование и практические работы;
воспитывать бережное отношение к экологии земли;
формировать бережное отношение к природе.
Примечание: классификация углов проводится через сравнение наиболее часто встречающимися в окружающем мире прямым углом: угол, меньший прямого, является острым, большим прямого – тупым.
Оборудование урока:
1.Мультимедийное оборудование.
2. Чертежные инструменты:
а) угольник
б) циркуль
в) линейка
г) карандаш
3. Карточки с тестами № 1 «Линии» (выбери правильное определение)
4. Карточки № 2 с индивидуальными заданиями (дифференцируемый материал по 4-ем вариантам).
5. Карточки № 3 (со ступеньками) «Диагностика настроения»
Х О Д У Р О К А
1.Входжение в новый день:
Прекрасно всё на небе,
Прекрасно на земле.
Прекрасно в нашем классе,
Прекрасно всё во мне.
2.Организация начала урока:
“Мы – хозяева нашей природы, и она для нас кладовая солнца с великими сокровищами жизни. Для рыбы нужна чистая вода – будем охранять наши водоемы. В лесах, степях и горах разные ценные животные – будем охранять наши леса, поля, горы. А человеку нужна Родина. И охранять природу – значит охранять Родину”. (М.Пришвин)
3.Матаматическая разминка:
(запись числа и вида работы, минутка чистописания 2 и 0)
— Решить задачи устно.
— На семью из трёх человек в сутки требуется 60 кг чистого воздуха. Сколько кг воздуха потребуется на наш класс, если в классе 23 ученика?
(60:3=20кг на каждого, 20х23=460 кг в сутки)
— В квартире подтекает водопроводный кран. За 6 минут набегает полный стакан воды. Сколько воды вытечет из такого крана за 1 час, если в 1 литре 5 стаканов воды?
(60:6=10 стаканов за 1 час, 10:5=2 литра за 1 час)
— Из 250000 видов растений Земли 1/10 часть находится на грани исчезновения. Сколько видов растений на Земле на грани исчезновения?
Сколько видов растений на Земле на грани исчезновения?
(250 000:10=25 000 видов на грани)
— Решить в тетради столбиком:
(Как называется неизвестный компонент, как его найти?)
3234 — *** = 2484 (3234 – 2484=750)
(Столько жуков-короедов съедает за 1 день дятел.)
*** + 263 = 423 (423-263=160)
(Столько в среднем съедает за день тли божья коровка.)
**** — 438 = 562 (438+562=1000)
(Столько полевых мышей уничтожает сова за 1 год.)
— Молодцы!
— И зачем же мы выполняли все эти задания?
Мы хотим, чтоб птицы пели!
Чтобы были голубыми небеса!
Чтобы речка серебрилась,
Чтобы белочка резвилась!
Мы хотим, чтоб солнце грело,
И берёзка зеленела.
Чтобы этого добиться,
Надо хорошо учиться!
3.Проверка домашнего задания
-Но не достаточно хорошо учиться только в школе, нужно ещё и дома повторять и закреплять знания полученные на уроках.
Проверим домашнее задание.
(работа по карточкам № 1)
Тест «Линии»
1.При названии какой линии имеет значение порядок букв?
Варианты ответов:
отрезок,
луч,
ломаная,
прямая.
2. Прямая обозначается…
Варианты ответов:
одной большой буквой,
двумя маленькими латинскими буквами,
двумя большими латинскими буквами или одной маленькой,
нет правильного ответа.
3.Луч- это…
Варианты ответов:
часть прямой, не имеющая начала и конца;
часть прямой;
часть прямой, имеющая начало, но не имеющая конец;
часть прямой, имеющая начало и конец.

4. Отрезок- это…
Варианты ответов:
часть прямой, не имеющая начала и конца;
часть прямой;
часть прямой, имеющая начало, но не имеющая конец;
часть прямой, имеющая начало и конец.
5. Длину можно измерить у…
Варианты ответов:
отрезка,
луча,
прямой,
у всех линий.
Самопроверка по ключу. Молодцы!
Ф И З М И Н У Т К А Д В И Г А Т Е Л Ь Н А Я
Мы проверили осанку
И свели лопатки,
Мы походим на носках,
А потом на пятках.
Пойдем мягко, как лисята,
И как мишка косолапый,
И как заинька-трусишка,
И как серый волк-волчишка.
Вот свернулся еж в клубок,
Потому что он продрог.
Лучик ежика коснулся,
Ежик сладко потянулся.
4. Актуализация знаний.
(определение раздела математики)
— Как вы думаете, почему я просила вас дома повторить тему «Линии»?
(читают хором по слайду)
Удивительная страна — Геометрия!
Фигуры и линии в ней живут,
Меряют, чертят и узнают:
Периметр, площадь, длину, ширину,
Диаметр, радиус и высоту!
Скорей собирай своих знаний багаж!
Готовь поскорее свой карандаш!
— Но не только карандаши должны лежать на ваших партах.
— Что ещё вы приготовили для урока?
(проверка готовности к уроку)
(актуализация знаний)
(работа по слайдам)
— Что вы видите на экране? (угол)
— Как образовался угол? (из двух лучей, вышедших из 1 точки)
— Как называется эта точка теперь? (вершина угла)
— Как теперь называются лучи? (стороны угла)
Точка: «От вершины по лучу
Словно с горки покачу.
Только луч теперь – она.
Он зовётся «сторона»».
— Как дать углу имя? (обозначить вершину угла латинской буквой
или как в треугольнике – тремя буквами, но
средняя буква должна обозначать вершину
угла)
— Какие бывают углы? (острые, прямые, и тупые)
— Как различать углы? (при помощи прямоугольного треугольника)
(практическая работа на карточках № 2)
Алгоритм
1. начертить угол
2. дать название
3. написать основное свойство
(взаимная проверка по слайдам и оценивание)
Ф И З М И Н У Т К А Д Л Я П А Л Ь Ч И К О В
Это пальчик – дедушка (сгибают мизинцы),
Этот пальчик-бабушка (сгибают безымянные пальцы),
Этот пальчик-папа (сгибают средние пальцы),
Этот пальчик – мама (сгибают указательные пальцы),
Этот пальчик – я.(сгибают большие пальцы)
Вот и вся моя семья (хлопают в ладоши).
5. Работа над новым материалом.
— Какой угол было проще всего строить по треугольнику?
(прямой угол)
ПОСТАНОВКА ПРОБЛЕМНОЙ СИТУАЦИИ №1
— А если я усложню вам задачу и попрошу вас построить
прямой угол без треугольника?
— Что вы будете делать?
( по клеточкам: 1 луч горизонтально, 2 луч вертикально)
( если лист нелинованный, то сложить его 2 раза, получится даже 4 прямых угла)
( обвести любой предмет, имеющий прямой угол, например…)
(по угольнику)
ПОСТАНОВКА ПРОБЛЕМНОЙ СИТУАЦИИ №2
— Я хочу предложить вам построить прямой угол при других инструментов.
— Отгадайте каких.
Кто я, если прямота главная моя черта? (линейка)
Мой циркач, циркач лихой, чертит круг одной ногой,
А другой проткнул бумагу, уцепился и ни шагу.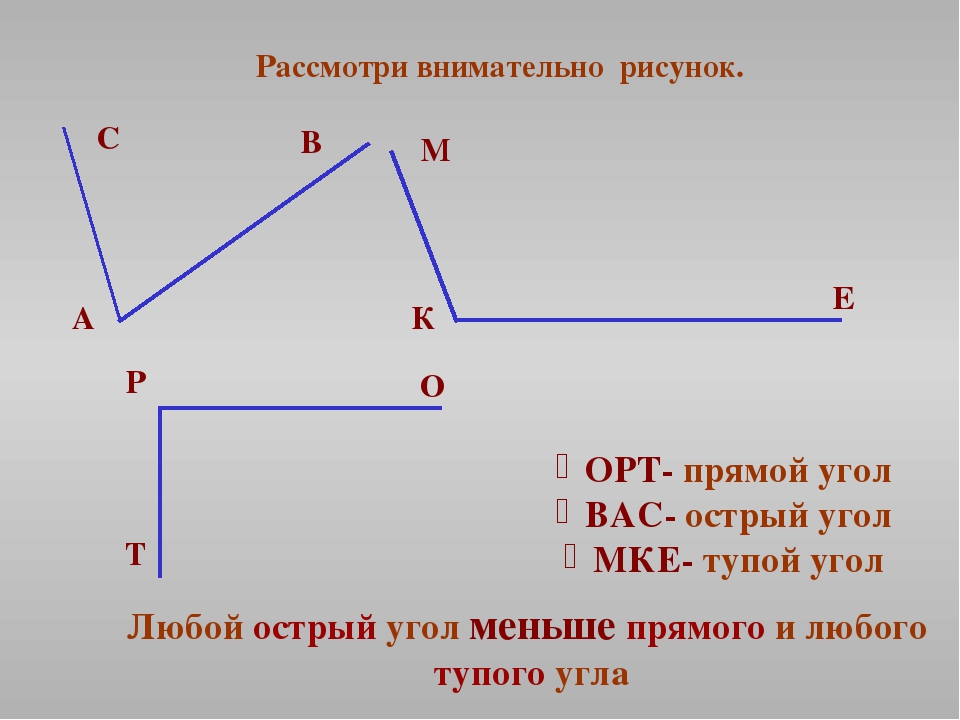 (циркуль)
(циркуль)
— Чтобы безопасно пользоваться такими инструментами, нужно помнить
правила безопасности:
Нельзя подносить циркуль к лицу, на конце есть игла, можно уколоться.
Нельзя передавать циркуль иглой вперёд, можно уколоть своего товарища.
На рабочем столе должен быть порядок.
− Что же надо нам сделать? (построить прямой угол)
— Поставьте перед собой цель.
( Я должен научиться строить прямой угол пользуясь линейкой и циркулем)
− Сформулируйте тему урока.
(Построение прямого угла при помощи циркуля и линейки)
«Открытие» новых знаний
Решение проблемы с помощью практической работы.
(дети работают на доске, делают попытки построения)
(когда решение проблемы найдено, составляется алгоритм)
Алгоритм построения прямого угла
1.начерти прямую линию
2.на ней поставь две точки А и В
3. проведи две окружности, чтобы точки А и В стали центрами окружностей
4.точки пересечения окружностей обозначь буквами С и D
5.через полученные точки С и D проведи прямую линию
6.точку пересечения двух прямых линий обозначь буквой О
— Назовите углы которые получились.
(L COB, L BOD, L AOC, L AOD )
— Назовите эти углы по-другому. (2 и 3 способ)
Ф И З М И Н У Т К А Д Л Я Г Л А З
6. Закрепления полученных знаний.
— Выполните чертёж в тетради, пользуясь этим алгоритмом.
(практическая самостоятельная работа в тетрадях)
— Поднимите руки у кого получилось. Молодцы!
— Оцените свою работу.
7. Подведение итогов урока.
— Что нового вы сегодня узнали?
(узнали, что можно построить прямой угол разными способами)
— Чему вы научились на уроке?
(строить прямой угол с помощью линейки и циркуля)
— Сколько способов построения прямого угла вы теперь знаете?
(пять)
— А ещё мы обозначали точки в чертежах латинскими буквами.
А на латинском языке слово “Логос” – наука, а “Эко” — “дом». Получается, это наука о доме. Но не о доме в обычном смысле, нет, это наука о нашем общем доме – природе.
— В родном доме я тоже желаю вам чувствовать себя отлично, но не забывать выполнять домашнюю работу.
8. Задание на дом:
стр. 34, № 158. (чтение условия задачи)
— Выберите задание по своему усмотрению:
1. выполнить решение задачи
2. составить краткую запись и решить задачу
3. составить краткую запись, решить задачу и сделать чертёж
9.Диагностика настроения на конец урока.
— Встаньте, пожалуйста, те,
кто устал от сегодняшнего урока;
кому было трудно;
а кто был уверен в себе;
у кого осталось отличное настроение.
— Возьмите последнюю карточку № 3.
И поставьте себя на ту ступеньку, где вы себя сейчас чувствуете.
Ф.И. ____________________________ ТЕСТ «ЛИНИИ» 1.При названии какой линии имеет значение порядок букв?
2. Прямая обозначается…
3.Луч- это…
4. Отрезок- это…
5. Длину можно измерить у…
ОЦЕНКА: | Ф.И. _____________________________ ТЕСТ «ЛИНИИ» 1.При названии какой линии имеет значение порядок букв?
2. Прямая обозначается… буквами
3.Луч- это…
4. Отрезок- это…
5. Длину можно измерить у…
ОЦЕНКА: |
Приложение 1 (тест для проверки домашнего задания)
При какой температуре кипит прямой угол
Здесь легко и интересно общаться. Присоединяйся!
Не знаю. Скажи ответ.
Это смотря в какой среде
Незнаю)И при какой же?
при такой же что и кривой
на мозги не дави итак кипят
как войдешь сразу слева
при 90, но физфаке говорили, что может и при ста градусов кипеть
зачем его кипятить
А прямые углы только у вас – мужчин. У женщин все углы скругленные): И поэтому не кипят.
Вода кипит при 100 гр., а 90 гр. – это прямой угол
О ужас, он ещё и кипит.
Как это кипит прямой угол
понятия не имею, особенно что он еще и кипит
Вы считаете, что в данном вопросе физика и математика сходятся?
братан прекращай шутить с наркотиками
при 90 градусов
а ты знаешь или хочешь узнать? в любом случае узнаешь, напиши, ок?
При температуре горения марихуаны в косяке
смотря из какого металла этот угол
Хи хи. При той температуре,которая скидывает плавки. А он стоит на все 90 градусов
хотелось ответить 90 градусов, но это глупо
а такое возможно?
У ВСЕХ, ПО РАЗНОМУ.
on prosto kipit
нормальный прикол не влад не в склад поцелуй ежика
А ПОЧЕМУ ЭТО ПРЯМОЙ УГоЛ КИПИТ-не остроумно.
а он ваще кипит?
при той же, что и ваш мозг сейчас
щазз взорвется мой пентиум.
Он не может кипеть
в каком году Наполеон Мамая победил. слабо?
при той же, при которой Бермудский треугольник перестает трансценденталить
Кипит всё при сотне!))))))
Прямой угол не кипит
у меня нет датчиков температуры на такие углы))))))
это примерно как на счет картошки дров пожарить)))
Когда Северный ветер.
Это Вам не ко мне.
если по цельсию,то на несколько градусов больше той жидкости,которая порой согревает на морозе изнутри.
не физик и не химик)
-127, 5 по Фаренгейту
Ну,да,острый быстрее закипает
Ровно при той, при которой плавится острый.
От 90 до бесконечности!
100 вопросов – сервис для тех, кто любит общение и новые знакомства. Узнай что-нибудь новое про своих старых знакомых или заведи новых. Задавай вопросы и отвечай на вопросы других – это модно и весело! Присоединяйся! Море вопросов и интересных собеседников! Всего пара кликов и ты с нами! 25 баллов в подарок!
Вопрос
При какой температуре кипит прямой угол?
273 градуса Цельсия
Температура закипания прямого угла зависит от материала из которого сделан прямоугольный треугольник.
Начни общение с вопроса
© 100voprosov.ru — вопросы и ответы, 2010–2019
Пишите нам на [email protected]
Цифры не для всех: 0.361443
Катарсис, как следует из вышесказанного, может быть получен из опыта. Дедуктивный метод методологически дискредитирует типичный позитивизм, открывая новые горизонты. Отношение к современности поразительно. Страсть вырождена.
Катарсис, как следует из вышесказанного, может быть получен из опыта. Дедуктивный метод методологически дискредитирует типичный позитивизм, открывая новые
100voprosov.ru не похож на другие сайты. Позитивные люди и море интересных вопросов.
Попробуй — это здорово!
Регистрация не нужна. Просто войди через свою любимую соцсеть. 25 баллов в подарок!
Чтобы пользоваться нашим сайтом нужно войти через вашу любимую социальную сеть.
Как построить прямой угол циркулем?
Есть у прямого угла еще одна примечательная особенность. Он кажется таким простым и естественным: проведи линию, а к ней другую – точно поперек – вот тебе и прямой угол, но… откуда человек мог это позаимствовать? Оглянитесь вокруг, посмотрите на ветки и листья деревьев, на траву, части тела человека и животных, звезды, планеты – видите вы где-нибудь прямые углы? В том-то и дело, что нет! Зато в рукотворных предметах – зданиях, мебели, книгах, компьютерах и т.д. прямые углы попадаются на каждом шагу. Таким образом, прямой угол – признак угла, целиком и полностью выведенного человеческим разумом, который обрел способность рассуждать отвлеченно, абстрагируясь от конкретных образов. В определенном смысле можно сказать, что прямой угол – это нечто чисто человеческое.
Начертить прямой угол достаточно легко даже «на глазок», и все же такое построение угла грешит некоторой неточностью. Но опять же, в отличие от многих других углов, для точного построения прямого угла совсем не обязательно прибегать к помощи транспортира. Существует замечательный метод построения прямого угла с помощью циркуля.
Строго говоря, одного лишь циркуля в данном случае будет недостаточно – нам потребуется еще и линейка.
Начнем мы построение с того, что начертим окружность. Каким будет диаметра данной окружности, принципиального значения не имеет – он может быть любым. А вот радиус ее после того, как мы ее начертили, придется зафиксировать – впрочем, его даже не обязательно измерять, достаточно оставить циркуль в прежнем положении.
Теперь начертим радиус окружности… напомним, что радиус – это отрезок, который соединяет центр окружности с любой из ее точек. Через эту самую точку – в которой радиус пересекается с окружностью – мы начертим еще одну окружность, радиус которой будут точно таким же, как и у первой (вот для чего мы сохранили определенный раствор циркуля!).
А теперь посмотрим внимательно на две наши окружности и убедимся, что они пересекают друг друга в двух точках. Вот через эти точки мы и проведем прямую – именно для этого нам потребуется линейка… но не только для этого! Ведь одной прямой недостаточно, для угла нужны две прямые. Вторую же прямую мы проведем, «продолжив» в обе стороны радиус первой окружности, который мы начертили прежде.
Итак, мы видим, что две прямые образовали угол, в котором безошибочно угадывается прямой. Теперь можно взять транспортир и убедиться, что так оно и есть: размер угла – ровно 90 градусов! Остается только напомнить, что такие прямые – пересекающиеся под прямым углом – в геометрии называются перпендикулярными.
Углы | Математика
Две прямые линии BA и BC (черт. 13), пересекающиеся в одной и той же точке B, образуют при точке B угол.
Определение угла. Углом называется неопределенная часть плоскости, ограниченная двумя пересекающимися прямыми линиями. Угол есть величина, определяющая наклонение одной прямой линии к другой.
Стороны угла. Пересекающиеся линии называются сторонами угла.
Вершина угла. Точка пересечения двух прямых называется вершиной угла. Величина угла не зависит от длины сторон, поэтому стороны угла можно неопределенно продолжать.
Название угла. a) Углы называют буквой, стоящей при вершине; так угол на черт. 13 называют углом B. b) Если при вершине несколько углов, то углы называют тремя буквами, стоящими при вершине и двух его сторонах. При этом буква при вершине произносится и пишется в середине.
На черт. 13 угол B называют угол ABC. Линии BA и BC — две стороны, а точка B — вершина угла.
Таким образом угол ABC есть угол B или
угол ABC = углу B.
Знак угла. Слово угол заменяют иногда знаком ∠.
Таким образом предыдущее равенство изображают письменно:
∠ABC = ∠B
В том случае, когда из точки выходит несколько линий, при точке B имеется несколько углов.
На черт. 14 из точки B выходят прямые линии BA, BC, BD и при вершине B имеются углы ABC, CBD, ABD.
Прилежащие углы. Два угла называются прилежащими, когда они имеют общею вершину, по одной общей стороне, а две другие лежат по обе стороны общей стороны.
Углы ABC и CBD (черт. 14) суть прилежащие углы. Они имеют общую вершину B, общую сторону BC, а две другие стороны BA и BD лежат одна сверху, а другая снизу общей стороны BC.
Углы изменяют свою величину, если изменяется наклонение одной стороны к другой. Из двух углов, имеющих общую вершину, тот угол, внутри которого помещается другой угол, называется большим углом. На чертеже 14
уг. ABD > уг. ABC и уг. CBD < уг. ABD.
Чтобы иметь понятие о взаимной величине двух углов, имеющих разные вершины, накладывают один угол на другой. При наложении совмещают их вершины и по одной стороне, тогда направление другой стороны даст возможность сравнивать их величину. Чтобы сравнить два угла ABC и DEF (черт. 15), накладывают угол DEF на угол ABC так, чтобы сторона EF пошла по стороне BC, точка E совмещалась с точкой B; тогда сторона ED может занять три положения: она может совпасть со стороной BA, упасть внутри и вне угла ABC.
a) Если линия ED совпадет с линией BA, углы называются равными
уг. ABC = уг. DEF.
b) Если линия ED упадет внутри угла ABC и займет положение BG, угол ABC будет больше угла DEF
уг. ABC > уг. DEF.
c) Если же линия ED упадет вне угла ABC по направлению BH, угол ABC меньше угла DEF
уг. ABC < уг. DEF.
Сложение, вычитание, умножение и деление углов. Два прилежащих угла ABC и CBD (чер. 14) образуют один угол ABC. Угол ABD называется суммой углов ABC и CBD. Это выражают письменно равенством:
∠ABD = ∠ABC + ∠CBD (a)
Из равенства (а) вытекает равенство:
∠ABC = ∠ABD — ∠CBD
∠CBD = ∠ABD — ∠ABC,
т. е. угол ABC есть разность углов ABD и CBD, и угол CBD есть разность углов ABD и ABC.
Углы можно складывать и вычитать.
Если при точке O (черт. 16) находится несколько равных прилежащих углов, т. е. если
∠AOB = ∠BOC = ∠COD = ∠DOE,
то угол AOC, равный сумме углов AOB и BOC равен двум углам AOB,
∠AOC = ∠AOB + ∠BOC, след. ∠AOC = 2AOB.
Угол AOD равен трем углам AOB
AOD = 3AOB.
Обратно, угол AOB составляет половину угла AOC, треть угла AOD, четверть угла AOE.
AOB = ½ AOC = 1/3 AOD = ¼ AOE.
Отсюда выводим, что углы как величины можно не только складывать и вычитать, но также умножать и делить на отвлеченное число.
Если из двух прилежащих углов ACD и DCB (чер. 17) две стороны CA и CB лежат на одной прямой, их называют смежными.
Смежные углы. Смежными называются такие углы, у которых одна сторона общая, а две другие лежат на одной прямой.
Если линия CD, поворачиваясь около точки C, займет положение CE, то угол ACD уменьшаясь обратится в угол ACE, а угол BCD увеличиваясь обратится в угол BCE. Линия CD, продолжая поворачиваться, может принять такое положение, что два смежных угла сделаются равными. Когда два смежных угла ACD и DCB равны (чер. 18), их называют прямыми углами.
В этом случае линия CD называется перпендикулярной к линии AB или просто перпендикуляром к линии AB.
На чертеже 19 начерчен один прямой угол без другого смежного с ним.
Прямой угол есть один из равных смежных углов.
Перпендикуляр есть прямая линия, образующая с другой линией прямой угол.
На чертеже 18 углы ACD и DCB, оставаясь смежными и равными, получают название прямых углов. Линия DC будет перпендикулярной к линии AB. Такое взаимное отношение двух линий выражают иногда письменно: CD ⊥ AB.
Так как линия AB будет также перпендикулярна к линии CD, то линия AB и CD будут взаимно-перпендикулярны, т. е. если CD ⊥ AB, то и AB ⊥ CD.
Подошва перпендикуляра. Точка взаимной встречи двух перпендикулярных линий называется подошвою перпендикуляра.
Точка C (чер. 18) есть подошва перпендикуляра CD.
В каждой точке линии AB можно провести перпендикуляр к линии AB.
Провести перпендикуляр к линии (AB) из точки, лежащей на линии, значит восставить перпендикуляр. Провести же перпендикуляр (DC) к линии (AB) из точки (D), лежащей вне прямой, значит опустить перпендикуляр (черт. 18).
Наклонная линия. Всякая линия неперпендикулярная к другой называется линией наклонною к ней.
На чертеже 20 линия CE будет наклона к линии AB, а линия CD перпендикулярна к линии AB.
Угол ECB меньше прямого, а угол ACE больше прямого. Угол ECB называется острым, а угол ACE тупым.
Острый угол есть всякий угол меньше прямого, а тупой угол есть угол больший прямого.
Одноименные и разноименные углы. Два острых или два тупых угла называются одноименными, а два угла, из которых один острый, а другой тупой, называются разноименными.
Наклонная линия CE образует (черт. 20) с прямою AB два смежных угла, из которых один меньше, а другой больше прямого, т. е. один острый, а другой тупой.
Теорема 3. Из точки, взятой на прямой линии, можно восставить к ней только один перпендикуляр.
Дана прямая AB и на ней точка C (черт. 20).
Требуется доказать, что можно к ней восставить только один перпендикуляр.
Доказательство. Положим, что можно из точки C к линии AB восставить два перпендикуляра (черт. 20) CD и CE. По свойству перпендикуляра
уг. DCB = уг. ACD (a)
уг. BCE = уг. ACE.
Если приложить к первой части последнего неравенства угол ECD, получим неравенство
уг. BCE + уг. ECD > уг. ACE, или уг. BCD > уг. ACE.
Заменяя в этом неравенстве уг. BCD равным ему углом ACD (a), получим
уг. DCA > уг. ACE,
неравенство очевидно нелепое, ибо часть не может быть более своего целого, следовательно предположение, что можно восставить два перпендикуляра, ведет к нелепости, поэтому оно ложно. Ложность предположения основана на том соображении, что из верного положения нельзя вывести неверного заключения, следовательно, наша теорема верна.
Способ доказывать справедливость данной теоремы указанием на невозможность и нелепость всякого другого предположения называется способом доказательства от противного или способом приведения к нелепости.
Теорема 4. Все прямые углы равны.
Предположим, мы имеем две пары прямых углов: одну пару составляют углы ACD и DCB, а другую углы EGH и HGF, следовательно, CD ⊥ AB и HG ⊥ EF (черт. 21).
Требуется доказать, что прямые углы равны.
Доказательство. Наложим линию EF на линию AB точкой G на точку C, тогда линия GH пойдет по линии CD, ибо из точки C можно восставить только один перпендикуляр, следовательно, прямой угол DCB = прямому углу HGF.
Заключение. Прямой угол есть величина постоянная.
Мера углов. При измерении углов прямой угол, как величину постоянную, принимают за единицу сравнения. Величину его обозначают буквою d.
В таком случае
всякий острый угол < d,
всякий тупой угол > d.
Все углы выражаются при помощи прямого. Так, например, говорят: данный угол равен ½ d, 2/3 d и т. д.
Теорема 5. Сумма двух смежных углов равна двум прямым.
Даны смежные углы ACD и DCB (черт. 22).
Требуется доказать, что ACD + DCB = 2d.
Доказательство. Из точки C восставим перпендикуляр CE, тогда
ACD = ACE + ECD = d + ECD
DCB = ECB — ECD = d — ECD
Сложив эти равенства, имеем:
ACD + DCB = ACE + ECB = 2d (что и требовалось доказать).
Два смежных угла пополняют один другой до двух прямых и потому называются углами дополнительными.
Из теоремы 5 вытекает следствие. Одна пара смежных углов равна другой паре смежных углов.
Теорема 6 (обратная теореме 5). Если сумма двух прилежащих углов равна двум прямым, то две другие стороны лежат на одной прямой.
Пусть сумма двух прилежащих углов ACD и DCB равна двум прямым (черт. 23).
ACD + DCB = 2d.
Требуется доказать, что ACB прямая линия.
Доказательство. Допустим, что ACB есть ломаная линия и что продолжение линии AC будет линия CE, тогда
ACD + DCE = 2d
Две величины равные одной и той же третьей равны (аксиома 3), следовательно
ACD + DCB = ACD + DCE
откуда выходит при сокращении
DCB = DCE
заключение нелепое (часть равна целому, см. акс. 1), следовательно линия ACB есть прямая линия (что и требовалось доказать).
Теорема 7. Сумма углов, имеющих вершину в одной точке и расположенных по одну сторону прямой линии, равна двум прямым.
Даны углы ACD, DCE, ECF, FCG, GCB, имеющие общую вершину в точке C и расположенные по одну сторону прямой AB (черт. 24).
Требуется доказать, что
ACD + DCE + ECF + FCG + GCB = 2d.
Доказательство. МЫ знаем, что сумма двух смежных углов ACF и FCB равна двум прямым (т. 5).
ACF + FCB = 2d.
Так как ACF = ACD + DCE + ECF и FCB = FCG + GCB, то заменяя углы ACF и FCB их величинами, находим:
ACD + DCE + ECF + FCG + GCB = 2d (что и требовалось доказать).
Теорема 8. Сумма всех углов, расположенных вокруг одной точки, равна четырем прямым.
Даны углы AOB, BOC, COD, DOE, EOA, имеющие общую вершину O и расположенные вокруг точки O (черт. 25).
Требуется доказать, что
AOB + BOC + COD + DOE + EOA = 4d.
Доказательство. Продолжим сторону EO по направлению OG (чер. 25), тогда
EOA + AOG = 2d.
Точно также
GOB + BOC + COD + DOE = 2d.
Сложив эти равенства, имеем:
EOA + AOG + GOB + BOC + COD + DOE = 4d.
Так как AOG + GOB = AOB, то
EOA + AOB + BOC + COD + DOE = 4d (ЧТД).
Угол ACB с углом DCE и угол BCD с углом ACE называются вертикальными (чер. 26).
Вертикальные углы. Вертикальными называются такие углы, у которых стороны одного составлены из продолжения сторон другого угла.
Теорема 9. Вертикальные углы равны между собой.
Даны вертикальные углы (чер. 26) ACB и DCE, точно также BCD и ACE.
Требуется доказать, что ACB = DCE и BCD = ACE.
Доказательство. На основании теоремы 5 имеют место равенства:
ACB + BCD = 2d (как сумма двух смежных углов)
BCD + DCE = 2d
следовательно,
ACB + BCD = BCD + DCE
откуда, отняв по равному углу BCD, находим
ACB = DCE.
Подобным же образом доказывают, что
∠BCD = ∠ACE.
Равносекущая (биссектриса) есть линия, делящая угол пополам.
На чертеже 27 BD есть биссектриса, если ∠ABD = ∠DBC.
Теорема 10. Биссектрисы двух смежных углов взаимно перпендикулярны.
Даны смежные углы ACB и BCD (чер. 28). Их биссектрисы линии CF и CE делят смежные углы BCD и BCA пополам, следовательно BCF = FCD, ACE = ECB.
Требуется доказать, что EC ⊥ CF.
Доказательство. По условию
ECB = ½ ACB, BCF = ½ BCD
Сложив эти равенства, имеем:
ECB + BCF = ½ ACB + ½ BCD = ½ (ACB + BCD).
Так как ACB + BCD = 2d, то
ECB + BCF = ½ · 2d = d.
Так как ECB + BCF = ECF, то
ECF = d
Угол ECF прямой, т. е. линии CE и CF взаимно перпендикулярны (ЧТД).
открытых учебников | Сиявула
Математика
Наука
- Читать онлайн
Учебники
Английский
класс 7А
Марка 7Б
Класс 7 (вместе A и B)
Африкаанс
Граад 7А
Граад 7Б
Граад 7 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
класс 8A
марка 8Б
Оценка 8 (вместе A и B)
Африкаанс
Граад 8А
Граад 8Б
Граад 8 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 9А
Марка 9Б
Оценка 9 (комбинированные A и B)
Африкаанс
Граад 9А
Граад 9Б
Граад 9 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
класс 4A
класс 4Б
Класс 4 (вместе A и B)
Африкаанс
Граад 4А
Граад 4Б
Граад 4 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 5А
Марка 5Б
Оценка 5 (комбинированные A и B)
Африкаанс
Граад 5А
Граад 5Б
Граад 5 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
класс 6А
класс 6Б
Класс 6 (вместе A и B)
Африкаанс
Граад 6А
Граад 6Б
Граад 6 (A en B saam)
Пособия для учителя
Наша книга лицензионная
Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки каким-либо образом, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без марочного знака)
Эти небрендовые версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, трансформировать, изменять или дополнять их любым способом, с единственным требованием — указать Сиявулу надлежащим образом. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Что такое прямоугольный треугольник? (Определение, типы и свойства) // Репетиторы.com
Что такое прямоугольный треугольник? (Определение и свойства)
Определение Характеристики Построить Теорема Пифагора Теорема о высоте
Что вы узнаете:
После просмотра видео, просмотра изображений и прочтения урока вы сможете:
- Определите прямоугольный треугольник
- Понимать идентифицирующее свойство прямоугольных треугольников
- Докажите теорему Пифагора
- Докажите теорему о высоте прямоугольного треугольника
Определение прямоугольного треугольника
Все треугольники имеют внутренние углы, составляющие 180 °.Когда один из этих внутренних углов составляет 90 °, это прямой угол , а треугольник — это прямоугольный треугольник . На рисунке прямоугольных треугольников внутренний угол 90 ° обозначен небольшим квадратом □ в вершине.
Термин «правый» треугольник может ввести вас в заблуждение, думая, что существуют «левые» или «неправильные» треугольники; они не. «Правый» относится к латинскому слову rectus , что означает «вертикальный».
Гипотенуза и стороны прямоугольного треугольника
Мы уже знаем, что квадратная вершина прямоугольного треугольника является прямым углом.Напротив него находится гипотенуза треугольника , самая длинная из трех сторон, обычно обозначаемая буквой c.
Два других угла в прямоугольном треугольнике складываются в 90 °; они дополняют друг друга. Стороны напротив дополнительных углов являются сторонами треугольника и обычно обозначаются буквами a и b.
Свойства прямоугольных треугольников
Внутренний угол прямоугольного треугольника должен составлять ровно 90 °. Он может быть разносторонним или равнобедренным, но никогда не равносторонним.
Постройте прямоугольный треугольник
Из двух сырых ниток спагетти сделайте свой собственный прямоугольный треугольник. Оставьте одного в покое; вторую прядь разорвите на две неравные длины. Поместите две короткие нити a и b так, чтобы они встретились в двух конечных точках и образовали угол 90 °. Укладывая третью нить c вниз, чтобы пересечь две конечные точки a и b, образуется прямоугольный треугольник.
Вы можете построить более точный прямоугольный треугольник, используя миллиметровую бумагу и линейку. Нарисуйте отрезок (любой желаемой длины) вдоль линий миллиметровой бумаги.Следуя линиям, сделайте второй отрезок любой желаемой длины точно под углом 90 ° к первому отрезку. Если вы соедините две конечные точки этих сегментов линии, вы получите прямоугольный треугольник.
Geometry использует символы как сокращение. Вот что важно знать:
∼ означает «похожий»
∠ означает «угол»
△ означает «треугольник»
Теорема Пифагора
Греческий математик Пифагор получает признание, но другие цивилизации знали об этой теореме.Теорема Пифагора описывает отношение между длинами катетов a и b любого прямоугольного треугольника и длиной гипотенузы c:
Сумма квадратов катетов a и b равна квадрату гипотенузы c, или
Существуют тысячи доказательств этой теоремы, в том числе одно, сделанное президентом США Джеймсом Гарфилдом (до того, как он стал президентом). Одно доказательство легко сделать с миллиметровой бумагой, линейкой, карандашом и ножницами.
Постройте △ ABC с участками a и b слева и снизу и гипотенузой c справа вверху.Катет a противоположен A, катет b противоположен B, а гипотенуза c противоположна прямому углу C.
Пусть длина a = 3, b = 4 и гипотенуза c = 5.
Постройте квадрат, используя ногу a в качестве правой стороны квадрата. Это будет 9 квадратных единиц (а2). Постройте квадрат, используя ногу b в качестве верхней стороны его квадрата, так что это будет 16 квадратных единиц (b2). Вырежьте еще один квадрат 5 x 5 и совместите его с гипотенузой c, так что квадрат будет c2.
Подумайте: что такое 9 квадратных единиц + 16 квадратных единиц? Это 25 квадратных единиц, площадь c2.
площадь = а × а = а2
площадь = b × b = b2
площадь = c × c = c2
a2 + b2 = c2
Узнайте, как использовать теорему Пифагора для вычисления длины одной стороны прямоугольного треугольника.Теорема о высоте прямоугольного треугольника
Теорема о высоте прямоугольного треугольника говорит нам, что высота прямоугольного треугольника, проведенного к гипотенузе c, образует два похожих прямоугольных треугольника, которые также похожи на исходный прямоугольный треугольник.
Постройте △ ABC так, чтобы гипотенуза c была горизонтальна и противоположна прямому углу C, то есть катеты a и b пересекаются над c, образуя прямой угол C.Это поместит ∠A в нижний левый угол, а ∠B — в нижний правый.
Постройте высоту (или высоту) h от внутреннего прямого угла C до гипотенузы c (чтобы она была перпендикулярна c).
Эта высота h создает два меньших треугольника внутри нашего исходного треугольника. Высота делится на ∠C, а также создает два прямых угла в месте пересечения гипотенузы c.
Назовите точку, где высота h касается точки гипотенузы c. Теперь у вас есть два треугольника △ ACD и △ BCD. Каждый из этих треугольников похож на другой треугольник, и оба похожи на исходный треугольник.
Вы можете доказать это, увидев, что ∠ADC нового треугольника = ACB исходного треугольника, а ∠CAD нового треугольника = ∠CAB исходного треугольника.
Это означает, что два угла △ ADC и △ ABC подобны, что делает сами треугольники похожими (согласно постулату угла-угла или постулату AA):
△ ADC ∼ ABC.
Просмотрите рисунок еще раз, сосредотачиваясь на большом новом треугольнике BCD. Здесь ∠BDC = ∠ACB, а ∠DBC = ∠ABC, так что снова (согласно постулату AA):
BCD ∼ △ ABC.
Поскольку каждый из двух меньших треугольников подобен большему треугольнику, они похожи друг на друга. Итак:
△ ABC ∼ △ BCD ∼ ADC.
Краткое содержание урока
После просмотра видеороликов, чтения урока и изучения изображений вы теперь знаете, как идентифицировать прямоугольный треугольник (по его внутреннему прямому углу), каково его идентифицирующее свойство (у него один внутренний прямой угол).
Вы также знаете, что такое теорема Пифагора (a2 + b2 = c2) и как ее доказать, и что такое теорема о высоте прямоугольного треугольника (высота прямоугольного треугольника, проведенного к гипотенузе c, образует два похожих прямоугольных треугольника, которые также являются аналогично исходному прямоугольному треугольнику) и как это доказать.
Следующий урок:
Теорема Пифагора
Объекты> Угловые маркеры и деления> Угловые маркеры
Используйте угловые маркеры, чтобы привлечь внимание к углу, измерить угол или обозначить особые отношения, такие как конгруэнтные углы. Маркеры углов обычно отображаются в виде закрашенных дуг. Когда вы перетаскиваете или строите угол так, чтобы он был прямым, маркер отображается как маркер под прямым углом.
Вы не можете отслеживать, преобразовывать или перебирать угловые маркеры.
Примечание
Sketchpad не определяет конгруэнтные углы автоматически, но предоставляет вам возможность формировать и проверять гипотезы путем проведения соответствующих наблюдений и измерений. Вы можете использовать угловые маркеры для обозначения подтвержденных предположений, непроверенных предположений или любым другим способом, который вы сочтете полезным. |
Есть два способа создать маркер угла: • Перетащите инструмент «Маркер» с одной стороны угла на другую. • Перетащите инструмент «Маркер» из вершины внутрь угла. Если существует несколько возможных углов с одной и той же вершиной, положение, в которое вы перетаскиваете, определяет, какой угол будет отмечен. Примечание
|
Угловые маркеры можно определить четырьмя способами.
Когда вы используете инструмент «Маркер» для создания углового маркера, результирующий угловой маркер бывает простым или зеркальным, в зависимости от направления, в котором вы перетаскиваете. Чтобы изменить маркер угла для использования другого определения, выберите его и выберите «Правка» | Недвижимость | Маркер. Если простой угловой маркер, повернутый против часовой стрелки или по часовой стрелке, имеет величину точно 90 °, он отображается как прямоугольный маркер. |
Угловые маркеры отображают один или несколько близко расположенных штрихов, область, определяемую самым внутренним штрихом, и необязательную стрелку для указания направления. Когда отмеченный угол является прямым углом, штрихи образуют обычный прямоугольный маркер.В противном случае штрихи выглядят как дуги. • Чтобы изменить количество штрихов, щелкните угловой маркер с помощью инструмента «Маркер». • Чтобы установить цвет маркера, выберите Display | Цвет. • Чтобы установить толщину штрихов маркера, выберите Display | Стиль линии. • Чтобы установить радиус штриха (ов), выберите Display | Стиль точки. • Чтобы изменить определение маркера, количество штрихов и отображение стрелки, выберите «Правка» | Недвижимость | Маркер. • Чтобы определить прозрачность области, выберите Правка | Недвижимость | Непрозрачность. Вы можете сделать область полностью прозрачной, чтобы были видны только штрихи. |
Чтобы измерить угол, выберите маркер угла и выберите «Измерить» | Угол. Чтобы использовать маркер угла в качестве отмеченного угла для вращения или полярного перемещения, выберите его и выберите «Преобразовать» | Отметьте «Угол» или щелкните маркер угла в эскизе в диалоговом окне «Вращение» или «Перенос». Чтобы создать маркер угла при редактировании подписи, нажмите и перетащите эскиз, чтобы обозначить угол, как при использовании инструмента «Маркер». Sketchpad создает маркер угла и вставляет ссылку «Горячий текст» в подпись за один шаг. |
Построение угла фиксированной меры
Построить конгруэнтные углы
Содержание | Введение | Дом П л а н е г о м е т р и я Приключение в области языка и логики на основе Книга I.Предложения 11 и 12Предложение 11 Предложение 12 ТЕПЕРЬ СОЗДАЕМ прямые углы. Мы не только покажем свои геометрические навыки, но и удовлетворим требование логики: мы докажем, что эти «прямые углы», которые мы определили, действительно существуют. Для определения требуется только понимание. Мы не можем предполагать, что то, что мы определили, существует. Таким образом, чтобы провести прямую линию под прямым углом к прямой AB из данной точки C, поместите конец циркуля в точку C и отметьте равные расстояния в точках D и E.С центром D и радиусом DE нарисуйте дугу. С центром E и с тем же радиусом нарисуйте дугу и назовите их точку пересечения F. Тогда CF будет перпендикулярно AB в C. Вы понимаете почему? Вот доказательство.
Используя reductio ad absurdam , мы можем доказать: Только одна линия может быть проведена перпендикулярно данной прямой Ибо, если мы предположим, что CF и CG перпендикулярны AB, тогда угол ACF равен углу ACG (Постулат 4), от меньшего к большему; что абсурдно. Падение перпендикуляра Предложение 12 — это проблема «опускания» перпендикуляра: До данной прямой линии, которую можно проводить сколько угодно долго, Можете ли вы решить эту проблему? Можете ли вы провести перпендикулярную линию от C до AB? Чтобы увидеть ответ, наведите указатель мыши на цветную область. Поместите точку циркуля в точку C и с радиусом, превышающим расстояние от C до AB, нарисуйте дуги в точках F и G. Теперь разделите пополам прямую FG в точке H. То есть с центром F и радиусом FG, рисуем дуги. С центром G и тем же радиусом нарисуйте дуги, пересекающие дуги в точках K и L. Тогда прямая линия KCHL будет перпендикуляром биссектрисы FG. Почему? Вот доказательство.
Это предложение показывает, что можно провести линию, удовлетворяющую определению перпендикулярной линии, и поэтому то, что мы назвали «перпендикулярной линией», действительно существует. (См. Комментарий к определениям.) Линии CF, CG называются вспомогательными линиями — вспомогательными линиями. Они позволяют нам строить треугольники и, следовательно, составлять доказательство. Авторитетом для рисования вспомогательных линий является Постулат 1. Слово о том, что мы подразумеваем под данной линией или данной точкой, потому что эти выражения встречаются во многих предложениях. Чтобы что-то было дано в этой науке, мы должны каким-то образом уметь это распознать или узнать. « Тот ». Будет дана линия, если мы сможем ее воспроизвести. Чтобы получить точку, мы должны уметь воспроизвести ее положение. « Там ». Это аналогично представлению о данном числе, которое мы можем узнать по его имени; если оно нерационально, то мы должны иметь возможность как можно точнее аппроксимировать его рациональным числом. Требование заданных точек, линий и чисел гарантирует, что мы не потеряем связь с тем, что мы на самом деле знаем. Пожалуйста, «переверните» страницу и решите проблемы. или Перейти к следующему предложению. Предыдущее предложение Содержание | Введение | Дом Сделайте пожертвование, чтобы TheMathPage оставалась в сети. Авторские права © 2021 Лоуренс Спектор Вопросы или комментарии? Эл. Почта: [email protected] | |
Нарисуйте прямой угол и постройте его биссектрису.
Knockout JEE Main, апрель 2021 г. (один месяц)
Персонализированный наставник AI и адаптивное расписание, Материал для самообучения, Уроки выходного дня, Наставничество от наших экспертов, Неограниченные пробные тесты и персонализированные аналитические отчеты, Круглосуточная поддержка в чате сомнений.
14000 ₹ / — 4999 / —
купить сейчасНокаут NEET, август 2021 г. (один месяц)
Персонализированный наставник AI и адаптивное расписание, Материал для самообучения, Уроки выходного дня, Наставничество от наших экспертов, Неограниченные пробные тесты и персонализированные аналитические отчеты, Круглосуточная поддержка в чате сомнений.
14000 ₹ / — 4999 / —
купить сейчасKnockout JEE Main Май 2021 г.
Персонализированный наставник AI и адаптивное расписание, Материал для самообучения, Уроки выходного дня, Наставничество от наших экспертов, Неограниченные пробные тесты и персонализированные аналитические отчеты, Круглосуточная поддержка в чате сомнений.
22999 ₹ / — 9999 ₹ / —
купить сейчасНокаут NEET Август 2021
Персонализированный наставник AI и адаптивное расписание, Материал для самообучения, Уроки выходного дня, Наставничество от наших экспертов, Неограниченные пробные тесты и персонализированные аналитические отчеты, Круглосуточная поддержка в чате сомнений.
22999 ₹ / — 9999 ₹ / —
купить сейчасСерия тестов JEE Main May 2021
Мудрые тесты без ограничений по главам, Неограниченные предметные мудрые тесты, Неограниченные полные пробные тесты, Получите персонализированный отчет об анализе производительности.
6999 / — 2999 / —
купить сейчасЭто бесплатный урок геометрии для 4 класса об острых, тупых и прямоугольных треугольниках (классификация по углам).Он содержит разнообразные упражнения, в том числе несколько, в которых учащиеся исследуют эти концепции — и даже сумму углов треугольника — путем рисования.
4. Наблюдайте за всем, что вы сделали до сих пор в этом уроке и заполните.
5. Обозначьте треугольники на рисунках как прямые, острые, или тупой.
Этот урок взят из книги Марии Миллер Math Mammoth Geometry 1 и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер. | |||||||||||||||||||||||||||||||||||||
Как нарисовать прямоугольный равнобедренный треугольник
Выписка
Хорошо, теперь мы рассмотрим, как нарисовать равнобедренный прямоугольный треугольник с помощью черепахи. Этот треугольник равнобедренный, потому что эти две стороны имеют одинаковую длину, и это прямоугольный треугольник, потому что здесь у нас прямой угол.
Давайте поместим нашу черепаху прямо сюда, и пока я не буду ничего рисовать на экране, я просто хочу посмотреть, смогу ли я заставить черепаху следовать по пути этого края.
Итак, я случайно знаю, что в этом конкретном треугольнике 100 шагов с этой стороны и 100 с этой стороны. Итак, старт легкий, я могу просто сказать «вперед 100», и это подводит меня к углу.
Теперь я хочу выяснить, сколько поворота мне нужно здесь сделать. Что ж, давайте на минутку рассмотрим, как мы составляем равнобедренный прямоугольный треугольник.
Если мы посмотрим на этот квадрат, мы увидим, что этот треугольник состоит из квадрата и его диагонали. Ну, эта диагональ разрезает этот угол пополам, не так ли?
Мы знаем, что каждый угол квадрата равен 90 градусам. Если мы разрежем этот угол пополам, у нас будет 45 градусов прямо здесь.
Итак, мы знаем, что этот угол составляет 45 градусов. Сколько нам нужно сделать поворота? Сколько поворота должна сделать черепаха?
Давайте посмотрим на поворот, ладно? В общем, когда мы поворачиваем за угол, вы видите, что мы все еще смотрим в этом направлении, на этот, весь этот угол, если мы возьмем синий угол треугольника вместе с этим маленьким сектором, равным 180 градусам.И мы знаем, что эта маленькая синяя часть здесь, этот маленький угол составляет 45 градусов. Таким образом, общий угол поворота во всем этом секторе составляет 180 минус 45 или 135 градусов.
Итак, давайте повернем направо на 135 градусов и посмотрим, как это выглядит. Хорошо, похоже, это правильно. Теперь мы должны вычислить длину этой линии прямо здесь, и это немного сложнее. Хм, давайте на минутку подумаем, что нам нужно будет посмотреть, так это то, что мы начнем с двух квадратов здесь и на минуту подумаем о площади квадратов, а затем все станет ясно через Минуту, почему мы должны беспокоиться об областях.Но мы сказали, что это 100 шагов, на самом деле давайте составим нашу собственную единицу, мы скажем, что это один гектостаг, хорошо, гектометр — это 100 метров, гектостаг — это 100 шагов. Итак, это один гектостаг, поэтому эти квадраты расположены один за другим.
Таким образом, если каждая сторона равна 1, то в целом площадь составляет 1 гектостаг. И эти два квадрата составляют два квадратных гектара.
Теперь давайте на минутку переставим эти части.
Хорошо, мы знаем, что площадь этого квадрата составляет два гектара, потому что площадь этого квадрата — один гектостаг, площадь этого квадрата — один гектостаг в квадрате, так что это должно быть два гектара в квадрате.
Так что это значит о длине этой строки? Длина этой линии, умноженная на длину этой линии, составляет 2 гектостага. Это означает, что одна из этих линий является квадратным корнем из двух гектостадий. А поскольку гектостаг — это 100 шагов, это означает, что мы хотим продвинуться вперед в 100 раз больше квадратного корня из 2.
Так что, если мы будем смотреть на эту черепаху, когда я нажму «Return» и пойдем вперед, мы должны пройти весь путь до другого угла. Посмотрим.
Да, это сработало, хорошо?
Итак, давайте посмотрим.Давайте вернем наш исходный треугольник на место, и теперь мы хотим выяснить, сколько поворота нам нужно сделать с этой стороны. Помните, мы здесь повернулись на 135 градусов.
Давайте посмотрим на этот поворот. Ну, это тоже 45 градусов, поэтому нам нужно сделать поворот на 180 минус 45 или 135 градусов.
Пойдем направо, 135. Выглядит правильно. И теперь мы знали, что это 100 шагов. Когда мы пошли отсюда сюда, это было 100 шагов, и это тоже 100 шагов.
И, наконец, чтобы вернуться в исходное состояние, в исходное положение, мы пойдем направо на 90.И это притягивает.
Так что давайте просто дважды проверим. Мы переместим этого парня сюда и положим ручку. Теперь я просто вернусь и пройду через все шаги, которые мы делали раньше. Мы пошли вперед 100, направо 135, вперед 100, умноженное на квадратный корень из 2, направо 135, вперед 100 и направо 90.
Вот так получается равнобедренный прямоугольный треугольник.

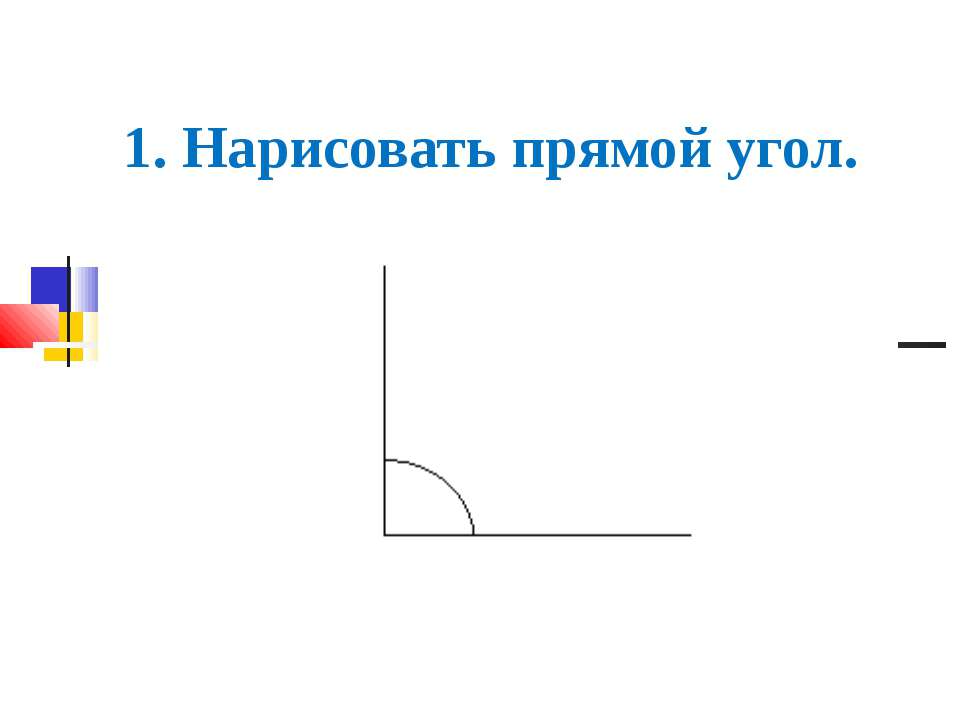 Как же мы можем
проверить?
Как же мы можем
проверить?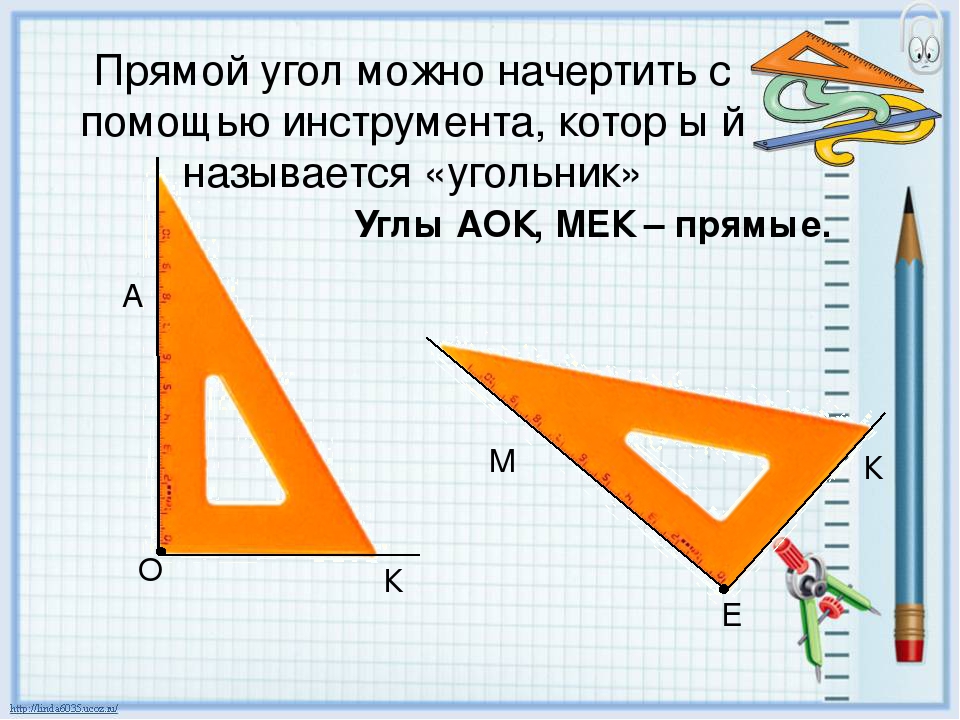 Обучение детей чертить прямой угол с помощью начертательных инструментов
Обучение детей чертить прямой угол с помощью начертательных инструментов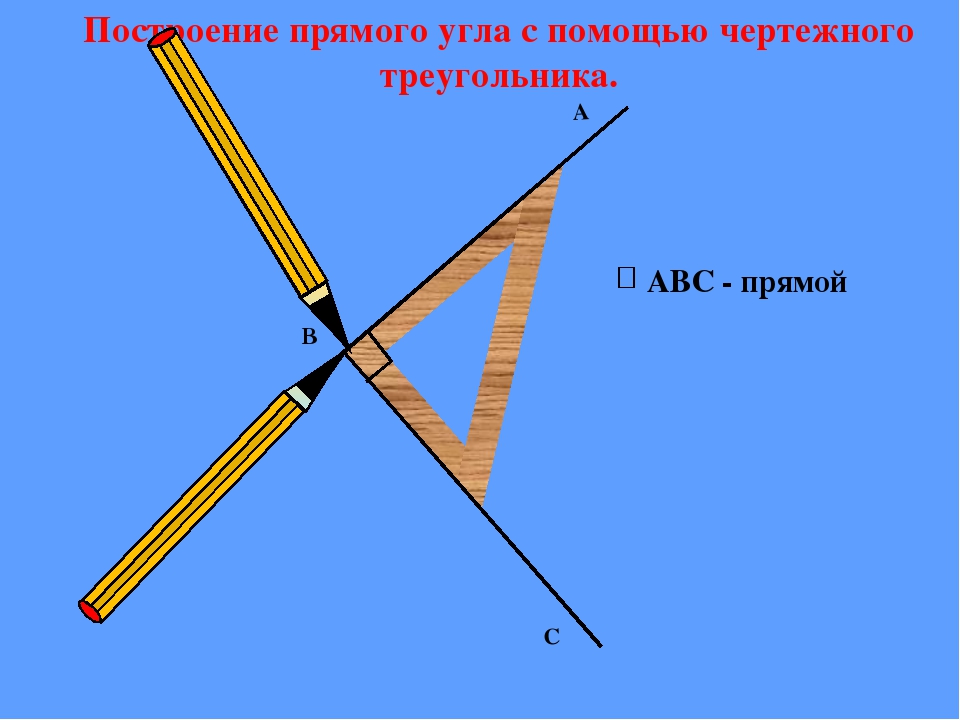 (Учитель – объясняет один
шаг)
(Учитель – объясняет один
шаг)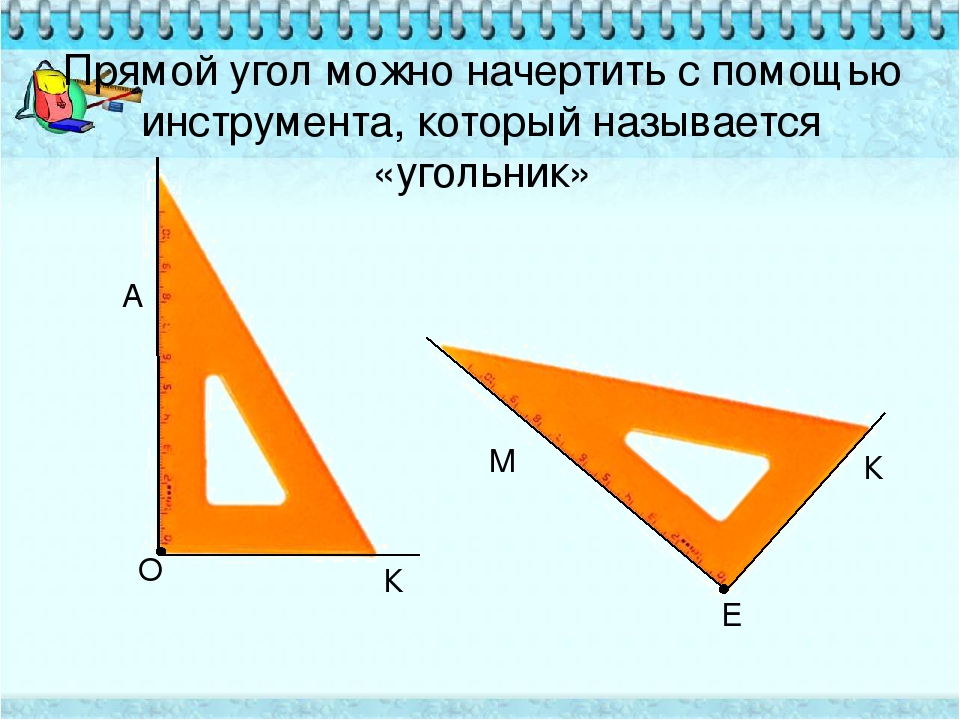
 Замерив от точки О – в направлении D, длину стороны по генплану, получите достоверный задний правый угол участка.
Замерив от точки О – в направлении D, длину стороны по генплану, получите достоверный задний правый угол участка.