План местности 6 класс
По планам можно получить много информации о местности, и они очень удобны в использовании. На планах показывают, что расположено на местности, отмечают названия и некоторые характеристики географических объектов.
Разновидности планов
Планы, подробно изображающие неровности земной поверхности и все географические объекты местности, называют топографическими (от греческих слов topos — место и grapho — пишу). Изображения на них уменьшаются не более чем в 5000 раз. Все объекты на топографических планах отображают общепринятыми условными знаками, а неровности поверхности — горизонталями и подписями отметок высот.
Для решения конкретных задач создают специальные планы с произвольными условными знаками. На таких планах отражают не все детали местности, а только те объекты и свойства, которые необходимы. Это, например, планы городов или туристических маршрутов, планы растительности участка с подробной характеристикой деревьев и кустарников и так далее.
Разные виды планов необходимы для людей многих специальностей. Их используют при строительстве разнообразных объектов и прокладке транспортных магистралей, поисках и добыче полезных ископаемых, проведении лесопосадок, решении военных задач. Специальные очень подробные планы создают для автомобилистов. А мы с вами, чтобы ориентироваться в незнакомом городе, приобретаем туристские планы.
Определение направлений
Планы местности ориентированы по основным сторонам горизонта. Специальная стрелка север—юг на них показывает направление на север. Если стрелка не изображена, то верхняя рамка плана считается северной, нижняя — южной, правая — восточной, левая — западной. Зная направление на север, можно от любой точки плана определить все другие стороны горизонта. Определять стороны горизонта на плане нужно для того, чтобы узнать о взаимном расположении объектов, установить направление на них.
Точное направление на какой-либо географический объект показывает азимут. На плане его определяют с помощью транспортира — специального чертёжного инструмента для измерения углов.
При измерении азимута на плане основание транспортира совмещают с направлением на север, а центр транспортира — с вершиной угла, од пой стороной которого служит направление на север, а другой — направление на объект. Далее определяют, через какую отметку на транспортире проходит сторона угла, представляющая собой направление на объект. Это и будет величина искомого азимута.
Как нарисовать план школьного двора по географии 6 класс
Составление плана школьного двора МКОУ «СОШ №3» способом полярной съёмки.
«Деятельность — единственный путь к знанию».
Б.Шоу
Географию невозможно изучать только сидя в классах и кабинетах. Увиденное своими глазами — самая ценная географическая информация. Описание географических объектов, сбор образцов, наблюдение явлений — все это тот фактический материал, который и является предметом изучения.

Объект исследования: территория школьного двора МКОУ «СОШ №3» г.Михайловска.
В данной работе нами был использован метод полевых исследований и наблюдений, а так же метод полярной и маршрутной съёмки местности.
Составить план местности (или, иначе говоря, произвести ее съемку) — значит изобразить эту местность на чертеже в выбранном масштабе с помощью условных знаков.
В своей работе мы использовали полярную и маршрутную съёмку местности.
2) Маршрутная съёмка
Маршрутная съёмка производится по ходовой линии.
По пути обозначаются предметы, угодья, находящиеся
слева и справа от дороги, насколько видно на открытой местности.
Для этого мы вспомнили классификацию виды условных знаков планов местности и что они обозначают.
— Площадные ( населённые пункты, здания, луг, поле и т.д.)
— Линейные (дорога, река и т.д)
— Внемасштабные (башни, памятники и т.д.)
— Пояснительные(направления течения реки, отметки высот и т.
 д.)
д.)Этапы работы на местности
1этап.Выбор точек отсчёта.
2 точка — Мастерская.
3 точка — с-з часть здания школы.
2 этап. Выбор оборудования.
Для составления плана местности нам потребовалось:
Жидкостный компас
Карандаш, ластик, цветные карандаши, булавка
Таблица 1
В первую очередь нам понадобилось вспомнить как измеряется расстояние на местности:
1. Вспомнить среднюю длину своих пар шагов
2. Измерить указанное расстояние парами шагов
например 110 п.ш.
3. Умножим среднюю длину пары шагов на число пар шагов
1,2 м х 110 п.ш. = 132 мТак же нужно знать, что расстояние до заданной точки можно измерить другим оборудованием.
Рулеткой
Полевым циркулем
Но мы использовали пары шагов.
4этап. Определение азимута до объектов.
Азимут – угол между направлением на север и направлением на какой-либо предмет.
5 этап. Заполнение таблицы.
6 этап.
 Камеральная обработка полученных данных.
Камеральная обработка полученных данных.Оформление работы
Взяли чистый лист бумаги
Отметили на нём стрелочку С-Ю , масштаб съёмки и свои Ф.И.
Положили свою работу выполненную на местности на чистый лист бумаги так, чтобы линии С-Ю совпадали по направлению
Булавкой проткнули нанесённые точки
Затем нанесли условные знаки
7.Результат.
Приложенные файлы
Запись опубликована автором uploader в рубрике Прочее.
Маршрутный способ съёмки удобен при составлении плана участка, вытянутого в длину. Его можно использовать и для изображения пути, пройденного в походе или на экскурсии.
Расстояния по маршруту составители плана определяют шагами.
На всех поворотах маршрута делаются остановки. На каждой остановке нужно отмечать её место на плане, ориентировать планшет, определять и прочерчивать направление на следующий объект.Следуя по маршруту, необходимо отмечать условными знаками всё, что встречается по обеим сторонам движения.
Можно описывать изменения характера рельефа, особенности растительного покрова, отдельные объекты природы и хозяйственной деятельности людей.
Маршрутная съёмка — съёмка местности,которая проводится при движении по какому-либо маршруту.Дронов В.
П., Савельева Л. Е. География. Землеведение. 5-6 кл.: учебник — М.: Дрофа, 2015. — 283 с.
По планам можно получить много информации о местности, и они очень удобны в использовании. На планах показывают, что расположено на местности, отмечают названия и некоторые характеристики географических объектов.
Разновидности планов
Планы, подробно изображающие неровности земной поверхности и все географические объекты местности, называют топографическими (от греческих слов topos — место и grapho — пишу).
Изображения на них уменьшаются не более чем в 5000 раз. Все объекты на топографических планах отображают общепринятыми условными знаками, а неровности поверхности — горизонталями и подписями отметок высот.
Для решения конкретных задач создают специальные планы с произвольными условными знаками. На таких планах отражают не все детали местности, а только те объекты и свойства, которые необходимы.
Это, например, планы городов или туристических маршрутов, планы растительности участка с подробной характеристикой деревьев и кустарников и так далее.
Разные виды планов необходимы для людей многих специальностей.
Их используют при строительстве разнообразных объектов и прокладке транспортных магистралей, поисках и добыче полезных ископаемых, проведении лесопосадок, решении военных задач. Специальные очень подробные планы создают для автомобилистов. А мы с вами, чтобы ориентироваться в незнакомом городе, приобретаем туристские планы.
Определение направлений
Планы местности ориентированы по основным сторонам горизонта. Специальная стрелка север—юг на них показывает направление на север.
Если стрелка не изображена, то верхняя рамка плана считается северной, нижняя — южной, правая — восточной, левая — западной. Зная направление на север, можно от любой точки плана определить все другие стороны горизонта. Определять стороны горизонта на плане нужно для того, чтобы узнать о взаимном расположении объектов, установить направление на них.
Точное направление на какой-либо географический объект показывает азимут.
На плане его определяют с помощью транспортира — специального чертёжного инструмента для измерения углов.
При измерении азимута на плане основание транспортира совмещают с направлением на север, а центр транспортира — с вершиной угла, од пой стороной которого служит направление на север, а другой — направление на объект.
Далее определяют, через какую отметку на транспортире проходит сторона угла, представляющая собой направление на объект.
Это и будет величина искомого азимута.
Буду благодарен, если Вы поделитесь этой статьей в социальных сетях:
План местности 6 класс википедия
Поиск по сайту:
1. План местности
Понятие о плане местности.
Условные знаки
Урок географии в 6 классе.
Автор: Карезина Нина Валентиновна,
учитель географии
МОУ СОШ №5 г.Светлого
Калининградской области
2.
Значение изображений местности
Строители
Геологи
Путешественники
Сельское хозяйство
Военные
…
3.
 Виды изображений местности
Виды изображений местностиРисунок
Аэрофотоснимок
Снимок из
космоса
План
местности
4.
5.
6.
7.
8. Условные знаки
9. Аэорфотоснимок и план местности
Сравните эти два изображения местности
10. Топографический план
Топографический план
местности –
это изображение на плоскости
небольшого участка
земной поверхности
в уменьшенном виде
при помощи условных знаков.
11.
Домашнее задание
• §4
• Нарисовать условные знаки в
тетрадь.
Выучить их.
• составить рассказ с их
использованием
План местности. Понятие о плане местности. Условные знаки. (6 клас)
English РусскийПравила
Откройте урок по географии в 6 классе. Тема урока: карта символов.
Цели обучения:
- Создайте представление об обычных признаках планов размещения и
карты, объемы и типы: именные, числовые, линейные. - Чтобы развить способность определять в соответствии с планом субъекты поля,
инструкции.
- Обучать студентов различным видам самостоятельной работы.
- Познакомьтесь с вашей страной и регионом.
Оборудование: учебники, атласы, упражнения, электронное дополнение к учебнику.
Методологическая поддержка:
А. А. Лобжанидзе «География, планета Земля». Москва, «Образование»,
Учебное пособие за 2006 год
А. А. Лобжанидзе «География, Планета Земля», симулятор ноутбука.
Москва,
«Образование», 2006 г.
Е. Мишняева «Атлас». Планета Земля. «Сферы. Москва,« Образование »,
2003
Электронное использование в учебнике. «Изображение Земли
поверхности «.
«Мультимедийный учебник: география: начальный курс» для 6-ти учащихся.
Общеобразовательные учреждения. Автор Петрова Н.Н.
республиканец
медиацентр, 2001 год.
План урока.
1. Организационный момент. Проверьте свою домашнюю работу.
Фронтальное исследование:
III.
Новая тема.
1. Сегодня, на уроке, мы узнаем, что такое общие персонажи,
Сегодня, на уроке, мы узнаем, что такое общие персонажи,
мы узнали, что такое масштаб, что он говорит.
— Теги не могли быть сохранены в течение длительного времени. Нам это было нужно
другие активы. Местность была заменена уменьшенной поверхностью модели
на земле. 20 000 лет назад ими моделировали
палочки и камни. Затем специальные
«Инструменты» — бары, камни, кости. Для углубления в песке или
глина. Затем они начали использовать такие материалы, которые можно хранить
долгое время.
Например, в Никарагуа, книги из кожи, B
Вавилония — глиняные плиты, в Египте — папирус.
2. Работа с учебником стр.10.
«Географический блокнот»
- Как древние картографы передавали индивидуальные характеристики
объекты? - электронное приложение — просмотр старых карт (слайд-шоу).
третий
Рисование — сложная задача. Они начали отправлять фотографии по плану
объекты, которые используют обычные символы.
— Условные символы — это символы, обозначающие разные объекты.
Условные символы — это тип алфавитной карты. Они не могут знать без знания
понять образ местности.
— Был предъявлен ряд требований к изображению традиционных символов:
а) простота;
б) разнообразие друг друга;
c) удаленное сходство с отображаемым объектом,
(Примечания в примечании)
Типы общих символов.
— В зависимости от уровня детализации, охвата территории и
Содержимое на картах использует множество общих символов.
Какой?
— работа с учебником стр.10, диаграмма.
a) Одноразовые символы — используются для указания точной позиции отдельных предметов.
— электронное приложение (слайд-шоу)
б) Линейные знаки — реки, дороги, границы. Они переусердствовали по ширине
объект, который точно обозначает область действия.
— электронное приложение (слайд-шоу)
c) Квадратные знаки являются реальными контурами объектов.
- электронное приложение (слайд-шоу)
- Условные символы разные.
Работа с атласом стр.8-9. - Цвет также является символом. Он предусматривает план
ландшафт и обогатите свой контент. - Перечислите традиционные цвета.
- Что показано синим цветом? Зеленый? Черный? Браун?
- Границы земли показаны небольшими точками.
- Значение условных символов показано в легенде карты.
Легенда — это изображение всех обычных символов, используемых на этой карте, с объяснением их значений.
- компьютерная работа — электронное приложение (слайд-шоу)
- работа с атласом с.12-13
- Что отображается на карте?
- Гимнастика для облегчения общей усталости и глаз.
- План диаграммы.
a) Когда вы показываете поле на листе бумаги,
Отрезать до сантиметров и миллиметров.
Вы должны выбрать его для этого
объем.
- Масштаб — это часть, из которой счетчик является единицей, а знаменатель —
Число, указывающее, сколько раз расстояние находится на плане или карте
Меньше самого ландшафта.
- Масштаб показывает, сколько раз план или поле
меньше, чем сам ландшафт.
b) Существует несколько типов шкал записи.
— Электронное приложение — типы шкалы записи (слайд).
c) Вы можете просмотреть все три записи громкости на всех картах.
— работайте с атласом.
d) В зависимости от масштаба, уровень детализации изменяется
изображения.
- работа с учебником с.
11
- электронная электронная таблица
Внутривенно Прикрепление.
1. Работа с симулятором ноутбука
Нет. 4, no. пятые
P. 11 номер задачи 1.
P. 12 номер задачи 4
2. Тестирование.
-электронное приложение для тестирования
Дети вводят свое имя в компьютер, выполняют задачу.
V. Подведение итогов.
VI.Организационный момент.
См. Также:
Урок по географии в 6 классе. Тема урока: карта символов. Цели занятий
1 стр.
Методологическое развитие географии 6-го класса. Тема: Тема: Реки. Воды страны. Изучение нового материала. Урок изучения
Тема: Тема: Реки. Воды страны. Изучение нового материала. Урок изучения
1 стр.
С точки зрения уроков, использующих информационные и коммуникационные технологии Краткое изложение географии Тема курсов: «Визит в Японию».
Тип урока: урок новых знаний. Тип урока: комбинированный
1 стр.
Урок в классе 3a. Тема урока: умные животные. Умные животные. Цели занятий
1 стр.
Урок на тему «Озера» в учителе географии 6-го класса Володина Лариса Николаевна. Урок вместе.
Задачи и
1 стр.
Чтение уроков мышления в классе Учитель 3 А Полякова В.Ф. 2007 Тема Тема: В. Л. Дуров «Наша ошибка». Цель урока: изучение жизни и работы В.
Л. Дурова: Цели урока
1 стр.
Открытый урок по физической географии Урок 7-го класса: «Антарктика» Ледяной Вселенной «Земля» Урок был разработан учителем географии Марияниной Е.И.
1 стр.
Урок по сжиганию в классе 11 Тема урока: военная форма военного персонала, военные типы и этикетки
1 стр.
Занятие в классе 2 грамма.
Тема курса: Даниил Хармс «Знаешь ли ты?» Учитель Блохин Н.Ю.
1 стр.
Резюме уроков по географии в 5 классе Тема урока «Первый круг путешествий в мире» Учитель Гобоу Сош нет. 852 Бровко С.Н.
1 стр.
Разработка урока в классе в географии класса 7 Тема урока: «Население и экономика США»
1 стр.
Информационный урок 10 класса. Аппаратное и программное обеспечение. ИКТ-тип обучения: урок.
Цели обучения: образование
1 стр.
План местности — урок. География, 6 класс.
На планах, как и на аэрофотоснимках и космических снимках, местность изображают сверху. Планы удобны в использовании и дают много информации о местности.
План местности — чертёж, который изображает земную поверхность сверху в уменьшенном виде с помощью условных знаков. Условные знаки планов отличаются от условных знаков географических карт.
Топографические планы (от греческих слов topos — «место» и grapho — «пишу») — планы, на которых подробно изображены неровности земной поверхности и все географические объекты местности.
Изображения на топографических планах уменьшаются не более чем в \(5000\) раз. Это означает, что масштаб может быть \(1 : 5000\) или крупнее («крупнее» означает, что цифра после знака « \(:\) » должна быть меньше).
Все объекты на топографических планах отображают общепринятыми условными знаками, а неровности поверхности — горизонталями и подписями отметок высот. Голубой линией показывают реку, лес закрашивают зелёным цветом, дома обозначают прямоугольниками.
По планам местности можно узнать, в каком направлении течёт река и какова её ширина, из каких пород деревьев состоит лес, из какого материала состоит лес и т. д.
Масштабными условными знаками на топографических планах обозначены: леса, сады, реки, озёра, населённые пункты и многое другое. Они позволяют определить размеры объектов и их площадь.
Внемасштабные условные знаки применяют для изображения объектов, которые из-за небольших размеров не могут быть показаны в масштабе плана (колодцы, столбы, родники и так далее).
Существуют специальные планы, которые создаются для решения конкретных задач. На них изображают только те объекты и свойства, которые необходимы в данном случае. К ним относятся планы городов или туристических маршрутов, планы растительности участка с подробной характеристикой деревьев и кустарников и так далее.
Планы используются при строительстве разнообразных объектов и прокладке транспортных магистралей, поисках и добыче полезных ископаемых, проведении лесопосадок, решении военных задач. Специальные, очень подробные, планы создают для автолюбителей. Для того чтобы ориентироваться в незнакомом городе, существуют туристские планы.
Источники:
Дронов В. П., Савельева Л. Е. География. Землеведение. 5-6 кл.: учебник — М.: Дрофа, 2015. — 283 с.
Страница 4 — 5. План местности
Комментарий: Работу лучше выполнять по шагам, последовательно выполняя задания к контурным картам. Для того, чтобы увеличить карту, просто нажмите на неё.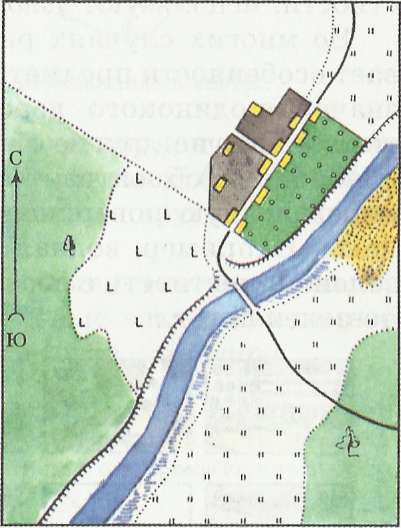 Также можно увеличивать и уменьшать размер страницы при помощи одновременного клавиш Ctrl и «+» или Ctrl и «-«.
Также можно увеличивать и уменьшать размер страницы при помощи одновременного клавиш Ctrl и «+» или Ctrl и «-«.
ЗАДАНИЯ
Для выполнения заданий будем рассматривать карту атласа на страницах 8 и 9.
1. Подпишите значения условных знаков.
2. Обозначьте принятыми условными знаками подписанные на плане объекты: редкий лес на болоте, еловый лес, редкий лес на лугу, луг с кустарником, плотину, кустарник.
3. Известно, что расстояние на местности от железнодорожного моста до перекрёстка автомобильных дорог составляет 600 м. Определите масштаб плана и впишите его в легенду плана.
Измерим это расстояние на карте линейкой. Получается, что 600 метров на местности = 6 см на карте. Значит 1 см на карте равен 100 метрам на местности. Переведем метры в сантиметры: 100 м = 10 000 см, то есть масштаб карты 1:10 000.
4. Определите, через сколько метров проведены сплошные и утолщённые горизонтали, и укажите их в легенде плана.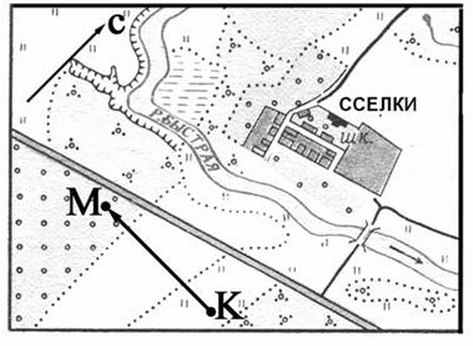
Рассмотрим карту. Для удобства обведём утолщенные горизонтали красной линией, а ближайшую сплошную горизонталь с обозначением высоты — фиолетовой линией.
Мы видим, что красная горизонталь с отметкой расположена на уровне 150 м, а ближайшая к ней фиолетовая — на уровне 155 м. Значит расстояние между сплошными горизонталями на этой карте составляет 5 метров.
По правилам, утолщенные диагонали проводятся по каждой пятой сплошной горизонтали. То есть расстояние между утолщенными горизонталями составляет 5 • 5 = 25 м. Можно вычислить, что вторая обведенная нами красным цветом утолщенная горизонталь находится на высоте 150 + 25 = 175 м.
5. Определите максимальную и минимальную абсолютные высоты, подписанные на плане. Проведите между ними линию и подпишите расстояние между отметками высот. Определите относительную высоту.
- Максимальная абсолютная высота, отмеченная на карте — это холм высотой 183 метра.

- Минимальная абсолютная высота, отмеченная на карте — это утолщенная горизонталь с отметкой 150 м (отмечена красной линией).
- Между максимальной и минимальной высотами проведена толстая розовая линия (перпендикуляр к горизонтали). Относительная высота равна 183 — 150 = 33 метра.
- Расстояние между этими точками на карте составляет 4 см. То есть на местности между самой высокой и самой низкой точкой расстояние составляет 400 метров.
6. Определите и подпишите абсолютную высоту домика лесника, расположенного в западной части плана.
Для удобства обведём ближайшие к домику лесника горизонтали синими линиями. Мы видим, что горизонталь, расположенная выше домика лесника имеет отметку 160 метров. Так как расстояние между сплошными горизонталями составляет 5 метров, то горизонталь, расположенная ниже домика лесника находится на отметке 155 м.
Можно предположить, что домик лесника находится на высоте 156 метров над уровнем моря.
7. Составьте план местности по описанию:
«От посёлка Лужки, расположенного на юго-западе, к хвойному лесу, расположенному на северо-востоке, ведёт грунтовая дорога. Примерно на середине пути к лесу протекает небольшая речка, перебраться через которую можно по деревянному мосту. Речка течёт с севера и вскоре после моста поворачивает на юго-восток. От посёлка и до речки, слева от дороги, тянутся фруктовые сады. На самом краю леса, к северу от дороги, стоит избушка лесника».
План местности — Рабочая тетрадь 6 класс Шатных (Ответы и гдз)
Понятие о плане местности.
1.Изучите особенности плана местности и аэрофотоснимка, помещенных на форзаце 1 учебника. Обозначьте в таблице знаком «+» признаки, характерные для каждого из этих видов изображений местности. Сделайте вывод.
Признаки План местности Аэрофотоснимок 1. Объекты более похожи на их реальный вид на местности
— + 2. Можно узнать название села, реки + — 3. Можно определить породы деревьев в лесу + — 4. Изображены все объекты, видимые сверху — + 5. Изображены только важные объекты + — 6. Объекты изображены условными знаками + — Вывод: План схематически изображает основные объекты местности, его удобно использовать для ориентирования на местности, проведения работ.
2. На форзаце 1 учебника и в атласе рассмотрите условные знаки, используемые для изображения объектов на плане местности. Какие условные знаки показаны на рисунке 1?
3. Пользуясь планом местности на форзаце 1 учебника, напишите, какие объекты может увидеть путник, идущий от реки Нара до Елагино по грунтовой дороге.
Мост, овраг, кустарник, луг, болото, линию электропередачи.
Масштаб.
1. Найдите масштаб плана местности на форзаце 1 учебника и запишите его. Назовите масштаб, записанный в таком виде
1:10 000 (числовой).
2. Определите, во сколько раз уменьшено расстояние на планах с масштабом:
а) 1:75 в 75 раз.
б) 1:250 в 250 раз.
в) 1:10 000 в 10 000 раз.
Какой из этих масштабов самый мелкий?
В.
3. Определите численный масштаб плана местности, на котором изображён мост, если его длина на местности в 1000 раз больше, чем на плане.
1:1000
4. Определите численный масштаб плана местности, если расстояние в 2 км показано на нём отрезком линии длиной 4 см.
1:50 000
5. При масштабе плана 1 : 2500 расстояние в 50 м надо выразить отрезком в см.
При масштабе плана 1 : 2500 расстояние в 50 м надо выразить отрезком в см.
В 2 см.
6. По известному численному масштабу запишите именованный:
а) 1 : 1000 в 1 см 10 м.
б) 1 : 25 000 в 1 см 250 м.
в) 1 : 50 000 в 1 см 500 м.
7. Именованный масштаб плана — в 1 см — 250 м. Рассчитайте, сколько сантиметров надо отложить на этом плане при изображении расстояния в:
а) 500 м = 2.
б) 1 км = 4.
в) 1250 м = 5.
8. Рассчитайте, во сколько раз расстояния на местности больше, чем на плане, если местность изображена в масштабе в 1 см — 90 м.
В 9000 раз.
9. Используя приём работы с линейным масштабом в учебнике, определите по плану местности на форзаце 1:
а) длину центральной улицы в деревне Елагино: 420 м.
б) ширину реки Нара у отметки уреза воды: 45 м.
10. Определите с помощью циркуля-измерителя длину ручья, впадающего в реку Нара.
110 м.
Стороны горизонта. Ориентирование.
1. На рисунке 2 обозначьте основные и промежуточные стороны горизонта.
2. Пользуясь компасом, определите:
а) в какую сторону горизонта обращены окна вашего класса
б) направление, в котором находится дверь класса
в) в каком направлении от окна расположен стол учите-
г) направление, в котором находится ваш дом
3. Определите стороны горизонта по азимуту и азимуты сторон горизонта. Заполните таблицу.
Азимут Сторона горизонта Азимут Сторона горизонта 45° СВ 315 СЗ 270° З 90 В 0° С 180 Ю 135° ЮВ 225 ЮЗ
4.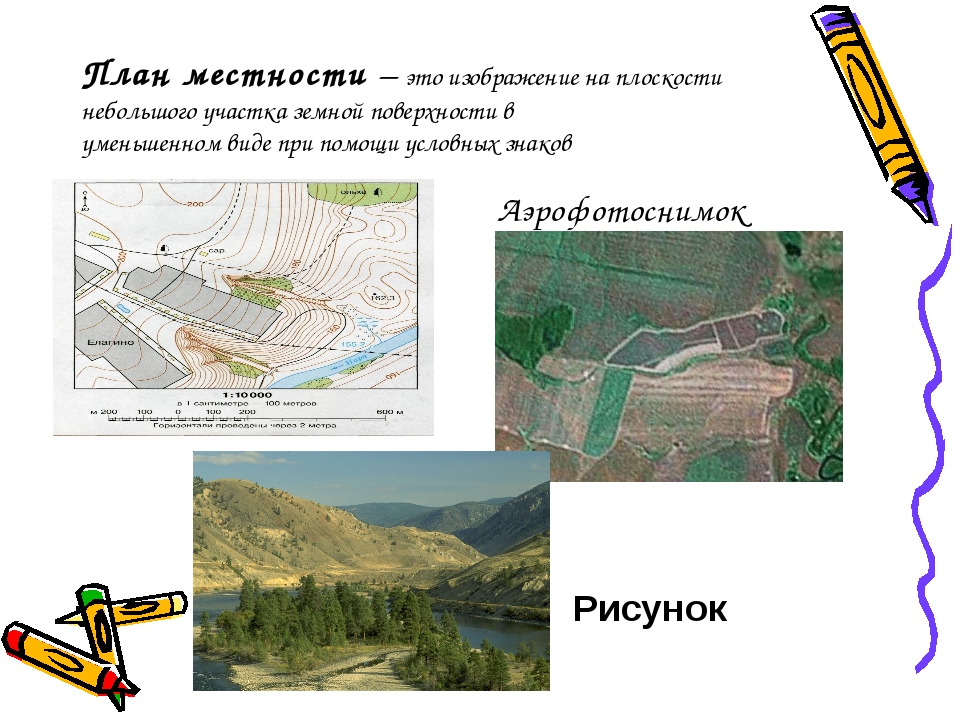 По плану местности на форзаце 1 учебника определите, в каком направлении от деревни Елагино находится:
По плану местности на форзаце 1 учебника определите, в каком направлении от деревни Елагино находится:
а) лиственный лес — севео-восток.
б) болото — юго-восток.
В каком направлении от сарая находится отдельно стоящее дерево?
Северо-запад.
5. От точки А до лагеря туристы должны пройти 400 м по азимуту 180°, затем 600 м по азимуту 45° и 800 м по азимуту 90°. Начертите их путь на рисунке 3. Используйте масштаб 1 : 20 000.
Рис. 3
Изображение на плане неровностей земной поверхности.
1. По рисунку 10 учебника определите:
а) абсолютную высоту холма — 150 м.
б) относительную высоту холма со стороны океана — 0.
в) относительную выосту холма со стороны суши — 50, 100 м.
2. На рисунке 4 с помощью горизонталей изобразите холм высотой 16 м. Горизонтали проведите через 4 м. Северный склон холма круче южного. Самый пологий склон — западный, самый крутой — восточный.
Горизонтали проведите через 4 м. Северный склон холма круче южного. Самый пологий склон — западный, самый крутой — восточный.
Рис.4.
3. Используя план местности, помещённый на форзаце 1 учебника, определите:
а) через сколько метров проведены горизонтали — 2.
б) где расположены самые низкие места территории — Юг, юго-запад.
в) где расположена самая высокая точка территории — запад.
Составление простейших планов местности.
1. Расскажите, что называют:
а) глазомерной съёмкой местности
съемка местности с планшетом.
б) полярной съёмкой местности
глазомерная съемка, проводящая из одной точки.
в) маршрутной съёмкой местности
глазомерная съемка в движении по какому-либо маршруту.
2.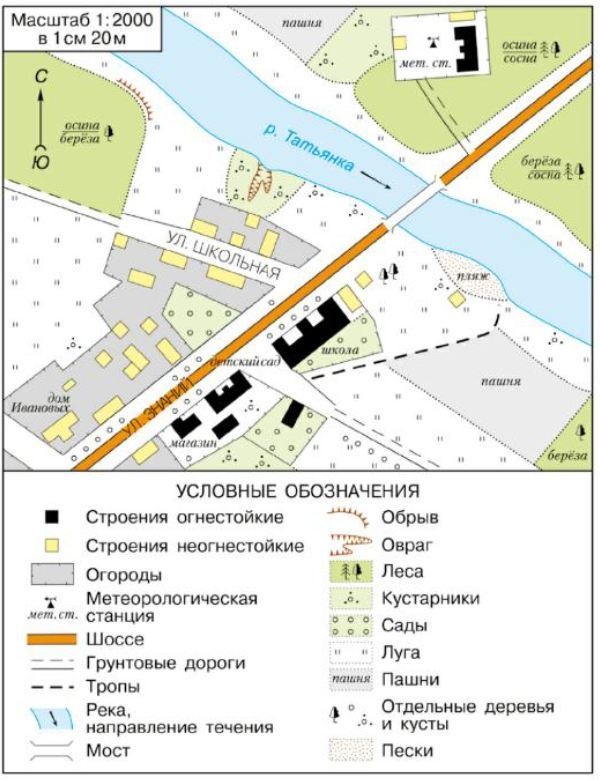 По заданию учителя проведите полярную и маршрутную съёмку местности. Оформите планы и вклейте их в тетрадь.
По заданию учителя проведите полярную и маршрутную съёмку местности. Оформите планы и вклейте их в тетрадь.
Географический диктант.
Чертёж, который изображает небольшую часть земной поверхности сверху в уменьшенном виде, — это план местности.
Показатель, по которому можно узнать, во сколько раз расстояния на местности уменьшены при изображении их на чертеже, — это масштаб.
Угол между направлением на север и направлением на какой-нибудь предмет местности — это азимут.
Все неровности земной поверхности — это рельеф.
Превышение по отвесу одной точки земной поверхности над другой — это относительная высота.
Превышение точки земной поверхности по отвесу
над уровнем моря — это абсолютная высота.Условная линия на плане, которая соединяет точки земной поверхности с одинаковой абсолютной высотой, — это горизонтали.
Глазомерная съёмка местности с одной точки — это полярная съемка.
Съёмка местности, применяемая при составлении плана участка, вытянутого в длину, или при изображении пути, пройденного в походе, — это маршрутная съемка.
Обобщение знаний по теме «План местности».
Пользуясь рисунком 5, заполните пропуски.
Вариант 1.
Смешанный лес находится на северо-западе от посёлка Речное. Расстояние от Речного до Берёзкино по грунтовой дороге равно 990 м . Железная дорога пересекает реку Каменка. Если двигаться по дороге от Березкино к домику лесника, то справа будет холм, а слева лес.
Электровоз у железнодорожной станции дал сигнал. Школьники, находящиеся на пароме, услышат его через 3 с. (Скорость распространения звука в воздухе 330 м/с.)
Фруктовый сад, расположенный северо-восточнее посёлка Речное, занимает 6400 м2.
Вариант 2.
Ширина реки Тихая равна 10 м. Длина моста через реку Каменку у посёлка Речное 5 м.
Расстояние по прямой от железнодорожной станции до холма с отметкой высоты 154,4 м равно 440 м. Длина участка реки Тихая, изображённого на плане, равна 640 м.
Азимут от колодца в Берёзкино на силосную башню равен 90°, на домик лесника — 0°, на электростанцию — 135°.
Площадь машинно-тракторной мастерской (МТМ) у Берёзкино равна 4096 м2.
Страница 6 — 7. План местности
Комментарий: Работу лучше выполнять по шагам, последовательно выполняя задания к контурным картам. Для того, чтобы увеличить карту, просто нажмите на неё. Также можно увеличивать и уменьшать размер страницы при помощи одновременного клавиш Ctrl и «+» или Ctrl и «-«.
ЗАДАНИЯ
Для выполнения заданий будем рассматривать атлас на странице 9.
1. Группа туристов находится на местности, обозначенной на плане точкой А.
а) Выберите по четыре объекта, расположенные к северу и югу от места нахождения туристов.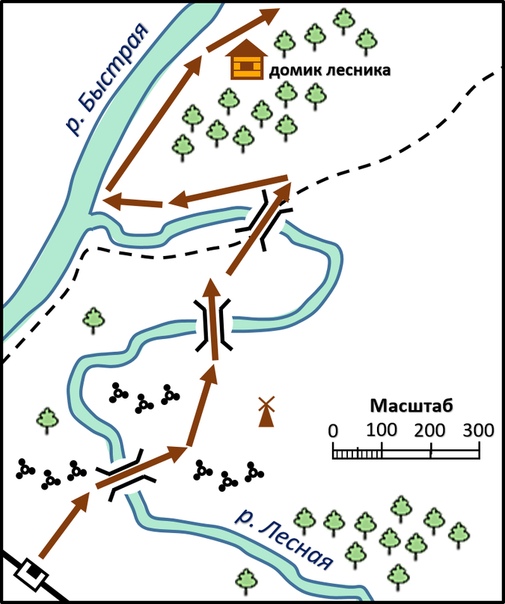 Обведите их синим карандашом, а расположенные к югу — красным.
Обведите их синим карандашом, а расположенные к югу — красным.
Объекты, расположенные к северу от точки А (обведены синей окружностью):
- отдельно стоящее дерево;
- посёлок Харино;
- мельница;
- дом лесника.
Объекты, расположенные к югу от точки А (обведены красной окружностью):
- школа;
- мост;
- пристань;
- песчаный карьер.
б) По каким азимутам должны следовать туристы, чтобы дойти до этих объектов?
Комментарий: Азимут маршрута — это угол между направлением движения по маршруту и северным направлением. Азимут маршрута измеряется в градусах и всегда только по часовой стрелке.
Для вычисления азимутов проведём вспомогательную линию — стрелку, указывающую строго на север (обозначена синим ветом и буквой С).
Теперь при помощи транспортира измерим азимуты маршрута к объектам (углы между направлениями к объектам и стрелкой на север):
- отдельно стоящее дерево — 308°;
- посёлок Харино — 324°;
- мельница — 3°;
- дом лесника — 40°;
- школа — 160°;
- мост — 195°;
- пристань — 232°;
- песчаный карьер — 213°.

в) С помощью масштаба определите расстояние до каждого из объектов.
При помощи линейки измерим расстояние от точки А до объектов, а потом определим реальное расстояние между объектами (масштаб карты 1 : 10 000 или 1 см = 100 метрам):
- до отдельно стоящего дерева — 4 см, то есть 400 метров;
- до посёлка Харино — 4 см, то есть 400 метров;
- до мельницы — 5,8 см, то есть 580 метров;
- до дома лесника — 3,1 см, то есть 310 метров;
- до школы- 4,7 см, то есть 470 метров;
- до моста — 2,3 см, то есть 230 метров;
- до пристани- 4,2 см, то есть 420 метров;
- до песчаного карьера — 12 см, то есть 1200 метров.
Результаты занесите в таблицу.
Объект | Азимут относительно точки А | Расстояние на местности от точки А |
| отдельно стоящее дерево | 308° | 400 метров |
| посёлок Харино | 324° | 400 метров |
| мельница | 3° | 580 метров |
| дом лесника | 40° | 310 метров |
| школа | 160° | 470 метров |
| мост | 195° | 230 метров |
| пристань | 232° | 420 метров |
| песчаный карьер | 213° | 1200 метров |
2.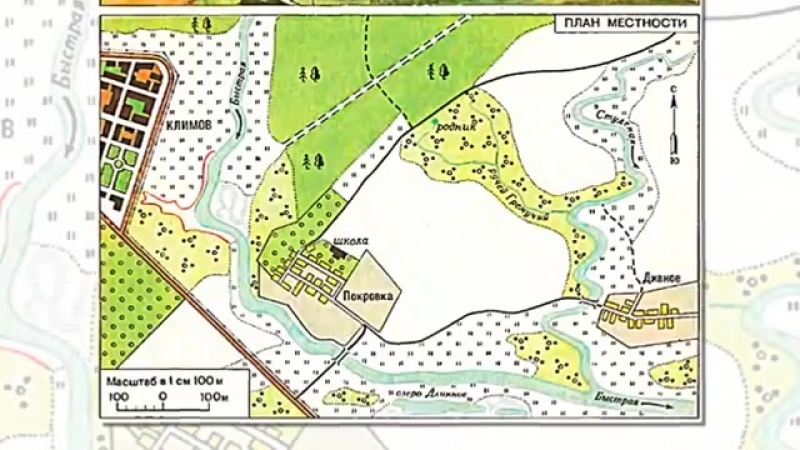 Внимательно рассмотрите план местности на с. 6. Где бы вы разместили футбольное поле? Почему вы выбрали именно это место? Свой ответ аргументируйте.
Внимательно рассмотрите план местности на с. 6. Где бы вы разместили футбольное поле? Почему вы выбрали именно это место? Свой ответ аргументируйте.
Я бы разместил поле уго-восточнее населенного пункта Арсентьево (место отмечено зелёным прямоугольником). Это место выбрал по следующим причинам:
- Это достаточно ровная поверхность без большого уклона. Определить ровность земной поверхности можно по карте — в этом месте расстояние между ближайшими горизонталями на карте 3 см или 300 метров на реальной местности (показано на карте фиолетово вспомогательной линией). Согласно легенде, горизонтали на данной карте проведены через 2,5 метра изменения уровня земной поверхности. То есть на протяжении 300 метров уклон составляет не более 2,5 метров. Так как длина стандартного футбольного поля примерно равна 100 метрам, то такой уклон не помешает сооружению этого спортивного объекта.
- Арсентьево — довольно крупный населённый пункт. В нем проживает 3 200 человек (цифры под названием населённого пункта обозначают количество жителей в тысячах человек).
 Кроме того, это место находится на пересечении дорог, ведущих из соседних населённых пунктов. То есть жителям окрестных деревень и поселков будет легко добраться до нового футбольного поля.
Кроме того, это место находится на пересечении дорог, ведущих из соседних населённых пунктов. То есть жителям окрестных деревень и поселков будет легко добраться до нового футбольного поля.
3. Напишите рассказ о своём пути в школу, заменив как можно больше слов условными знаками.
ГДЗ География 6 класс. Рабочая тетрадь Летягин А.А. 2020 » Страница 21 » Shkola.Center
Вопросы и задания
1. Съемка местности
• На схеме подпишите названия видов съемок местности в соответствии с их окончательными чертами.
Съёмка местности
— аэрофотоснимка
Не отличается большой точностью. Используются бытовые приспособления
— геодезическая
Отличается большой точностью. Используются инструменты и приборы (стальные ленты, нивелиры, теодолиты)
— инструментальная
Проводится из одной точки местности
— глазомерная
Проводится по пути движения во время походов
2.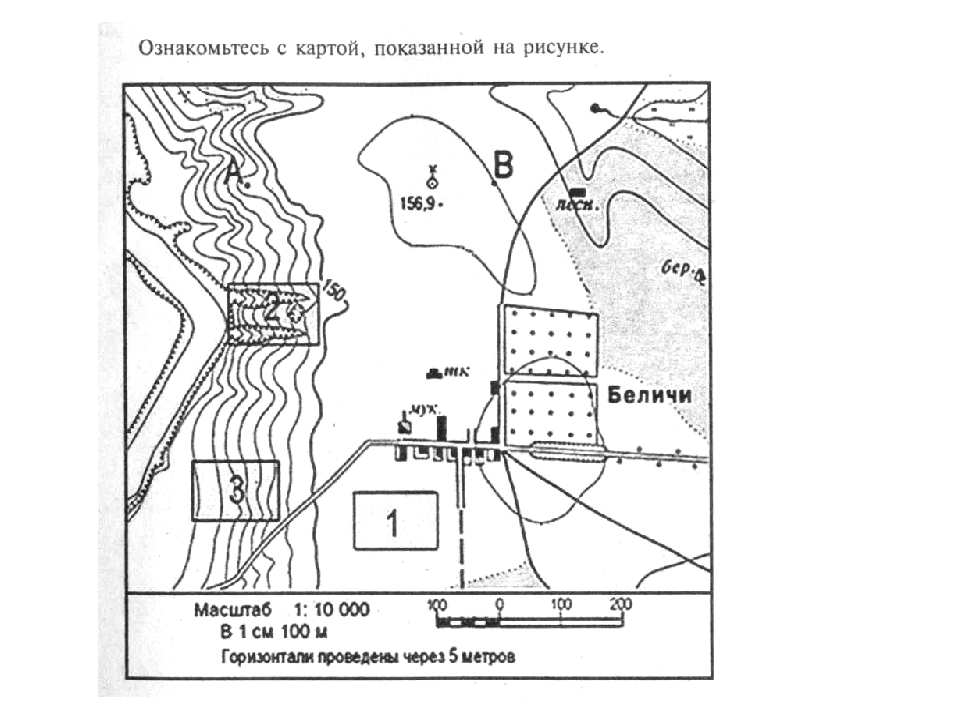 Полярная съемка
Полярная съемка
• Заполните таблицу.
| Составление плана пришкольного участка | ||
| Действия | Данные о местности | Данные для составления плана |
| 1. Выбрать масштаб съемки для планшета 30×40 см. | Размеры участка 60 х 80 м | Масштаб 1:200 |
| 2. Начертить линейный масштаб | В 1 см 2 м | |
| 3. Определить положение полюса на будущем плане с учетом расстояний до крайних объектов, которые будут нанесены на план | Измерить расстояния до крайних объектов и границ участка | Определить положение точки полюса на местности и на плане (в соответствии с масштабом) |
4. Встав в точке полюса,сориентировать планшет по компасу Встав в точке полюса,сориентировать планшет по компасу | Встать в исходной точке (полюсе). Закрепить компас на планшете так, чтоб направление стрелки компаса и стрелки север — юг, нарисованной на планшете совпали | |
| 5. Из полюсов провести визирование на объекты местности с помощью визирной линейки | Выбрать объекты местности для визирования, определить их ключевые точки | Провести визирование на объекты и их ключевые точки. На плане провести линии визирования |
| 6. Определить расстояния от полюса до объектов, на которые проводилось визирование | Пронумеровать объекты визирования. Доступными способами измерить расстояния от полюса до объектов визирования. Записать результаты измерений | |
| 7. Используя условные знаки для топографических планов и карт, обозначить объекты на плане | Определить размеры объектов и расстояния между ними и полюсом в соответствии с масштабом. Выбрать из таблицы те условные знаки и сокращения, которые необходимо использовать для составления плана. Нанести их на план. Проверить и окончательно оформить план местности Выбрать из таблицы те условные знаки и сокращения, которые необходимо использовать для составления плана. Нанести их на план. Проверить и окончательно оформить план местности | |
3. Составление плана местности на маршруте.
• Заполните таблицу.
| Проведение маршрутной съемки местности | ||
| Действия | Данные о местности | Данные для составления плана |
| 1 | 2 | 3 |
| 1. Выбрать масштаб съемки для планшета 30 х 40 см | Длинна маршрута 3500 м | Масштаб 1: 10000 |
| 2. Начертить линейный масштаб | 1 см.350 м. | |
3. Маршрутную съемку начнем выполнять от исходной точки до остановочных точек. Во всех точках нужно ориентировать планшет с помощью компаса. Во всех точках нужно ориентировать планшет с помощью компаса. | ||
| 4. От точки нашего местонахождения проведем визирование на следующую остановочную точку с помощью визирной линейки. | ||
| 5. Расстояние между точками будем определять на глаз, дальномером, шагами или по километровым столбам. Расстояние по направлениям визирования будем отмечать на плане в соответствие с выбранным масштабом. | ||
| 5. Обозначим на плане объекты, встреченные на маршруте, условными знаками для топографических карт. Местоположение объектов — ориентиров можно определить методом полярной съемки. | ||
Школа географа-следопыта
• Проведите полярную съемку пришкольного участка.
Работу лучше проводить по группам. План пришкольного участка будет совместным результатом работы каждой группы. Пометки и записи следует делать на плане в Дневнике географа-следопыта.
Первая группа определяет размеры пришкольного участка и выбирает масштаб съемки.
Длина пришкольного участка 60 м.
Ширина пришкольного участка 80 м.
Масштаб съемки 1:200
Втора группа определяет положение полюса съемки и основные направления и точки визирования, определяет азимуты по компасу.
Третья группа готовит планшет и визирную линейку, ориентирует планшет по направлению «север — юг», проводит визирование.
Четвертая группа готовит определяет расстояние между полюсами и точками визирования.
Пятая группа определяет размеры объектов, которые будут обозначены на плане пришкольного участка.
Получив необходимые данные, составьте черновой вариант плана пришкольного участка. В кабинете географии завершите работу по составлению окончательного варианта плана.
Математика для 6-го класса — Блок 7: Геометрия
Сводка по агрегату
В Блоке 7 шестиклассники исследуют измерения в геометрическом пространстве как в двухмерных, так и в трехмерных фигурах. На протяжении предыдущих классов учащиеся составляли и разбирали геометрические фигуры. В шестом классе ученики применяют эти концепции композиции и разложения к новым и знакомым формам, чтобы сформулировать свойства и формулы для поиска области (MP.7). Понимая площадь прямоугольных массивов и используя регулярность в повторении рассуждений, учащиеся могут определить площадь параллелограммов, треугольников и других многоугольников, образованных из этих фигур (MP.8). Студенты также повторно участвуют в основной работе класса несколькими способами. Они используют свои знания координатной плоскости и абсолютного значения для представления и измерения многоугольников в четырехквадрантной плоскости, они пишут уравнения для представления объема прямоугольных призм с дробными длинами сторон, а также они пишут и оценивают числовые выражения для представления площади поверхности призмы и пирамиды.
На протяжении предыдущих классов учащиеся составляли и разбирали геометрические фигуры. В шестом классе ученики применяют эти концепции композиции и разложения к новым и знакомым формам, чтобы сформулировать свойства и формулы для поиска области (MP.7). Понимая площадь прямоугольных массивов и используя регулярность в повторении рассуждений, учащиеся могут определить площадь параллелограммов, треугольников и других многоугольников, образованных из этих фигур (MP.8). Студенты также повторно участвуют в основной работе класса несколькими способами. Они используют свои знания координатной плоскости и абсолютного значения для представления и измерения многоугольников в четырехквадрантной плоскости, они пишут уравнения для представления объема прямоугольных призм с дробными длинами сторон, а также они пишут и оценивают числовые выражения для представления площади поверхности призмы и пирамиды.
В пятом классе ученики изучали объем как измерение трехмерного твердого тела с целыми числами сторон. В этом модуле учащиеся заново исследуют, как найти объем при упаковке твердых тел кубиками с дробными единицами. Они будут полагаться на свои навыки работы с дробями начиная с пятого класса и ранее в шестом классе.
В этом модуле учащиеся заново исследуют, как найти объем при упаковке твердых тел кубиками с дробными единицами. Они будут полагаться на свои навыки работы с дробями начиная с пятого класса и ранее в шестом классе.
На протяжении всего курса геометрических стандартов с шестого по восьмой классы учащиеся будут сталкиваться со все более сложными и состоящими из нескольких частей геометрическими задачами измерения, кульминацией которых станет восьмой класс со стандартом 8.G.9. Научиться понимать эти сложные проблемы, определять пути решения и систематизировать информацию будут важными навыками для учащихся по мере повышения требований и уровней строгости (MP.1).
Темп: 19 учебных дней (17 уроков, 1 гибкий день, 1 оценочный день)
Чтобы узнать, как изменить темп на 2020-2021 учебный год в связи с закрытием школ, см. Наши рекомендации по корректировке объема и последовательности занятий для 6-го класса.
Нарисовать многоугольники в координатной плоскости с заданными координатами вершин; используйте координаты, чтобы найти длину точек соединения сторон с той же первой или второй координатой.
 Применяйте эти методы в контексте решения реальных и математических задач. Сетка многоугольников:
Применяйте эти методы в контексте решения реальных и математических задач. Сетка многоугольников:Учащимся предлагается нарисовать многоугольник по координатам его вершин и определить длину диагоналей многоугольника.
Тип: Формирующее оценивание
Координаты многоугольника:Учащимся предлагается нарисовать многоугольник с учетом координат его вершин и определить как длины сторон, так и параллельность сторон.
Тип: Формирующее оценивание
Длина забора: Учащимся предлагается нарисовать многоугольник по координатам его вершин и определить периметр многоугольника.
Тип: Формирующее оценивание
Площадь патио:Учащимся предлагается нарисовать многоугольник по координатам его вершин и определить площадь многоугольника.
Тип: Формирующее оценивание
Координаты велосипедного участка:Учащимся предлагается построить график двух точек с учетом их координат и найти координаты двух других точек так, чтобы четыре точки представляли вершины квадрата.
Тип: Формирующее оценивание
Задачи кодирования геометрии # 1-7, 14 и 15: Этот набор задач по геометрии фокусируется на создании множества многоугольников по мере того, как учащиеся решают задачи и думают, когда они учатся кодировать с помощью программного обеспечения для блочного кодирования. Студенту необходимо будет использовать свои знания об атрибутах многоугольников и математических принципах геометрии для выполнения заданных задач. Задачи начинаются с довольно простых и переходят к более сложным ситуациям, в которых учащиеся могут исследовать в своем собственном темпе или работать в команде. Стандарты компьютерных наук неразрывно связаны со стандартами математики, в то же время предлагая «Шаг вперед!» и «Прыгай!» возможности для повышения строгости.
Студенту необходимо будет использовать свои знания об атрибутах многоугольников и математических принципах геометрии для выполнения заданных задач. Задачи начинаются с довольно простых и переходят к более сложным ситуациям, в которых учащиеся могут исследовать в своем собственном темпе или работать в команде. Стандарты компьютерных наук неразрывно связаны со стандартами математики, в то же время предлагая «Шаг вперед!» и «Прыгай!» возможности для повышения строгости.
Тип: План урока
Задача кодирования геометрии №16, 18 и 19: Этот набор задач по геометрии фокусируется на создании множества многоугольников с использованием координатной плоскости, когда учащиеся решают задачи и думают, когда они учатся кодировать с помощью программного обеспечения блочного кодирования. Студенту необходимо будет использовать свои знания об атрибутах многоугольников и математических принципах геометрии для выполнения заданных задач. Задачи начинаются с довольно простых и переходят к более сложным ситуациям, в которых учащиеся могут исследовать в своем собственном темпе или работать в команде. Стандарты компьютерных наук неразрывно связаны со стандартами математики, в то же время предлагая «Шаг вперед!» и «Прыгай!» возможности для повышения строгости.
Студенту необходимо будет использовать свои знания об атрибутах многоугольников и математических принципах геометрии для выполнения заданных задач. Задачи начинаются с довольно простых и переходят к более сложным ситуациям, в которых учащиеся могут исследовать в своем собственном темпе или работать в команде. Стандарты компьютерных наук неразрывно связаны со стандартами математики, в то же время предлагая «Шаг вперед!» и «Прыгай!» возможности для повышения строгости.
Тип: План урока
Profit Plaza: Этот урок требует от учащихся использования математических данных и логики / рассуждений для размещения продавцов в торговых помещениях в торговом центре.Студенты сначала ранжируют пять типов поставщиков по их рентабельности (на основе средних продаж и средних накладных расходов / затрат на содержание), а затем размещают типы поставщиков по 11-13 торговым площадям. От них также требуется определить площадь каждого помещения и рассчитать общую арендную плату. Планы площади даны на координатной плоскости, поэтому учащимся нужно будет найти длины горизонтальных и вертикальных отрезков (используя координаты конечных точек), чтобы вычислить площади прямоугольных и составных пространств.
От них также требуется определить площадь каждого помещения и рассчитать общую арендную плату. Планы площади даны на координатной плоскости, поэтому учащимся нужно будет найти длины горизонтальных и вертикальных отрезков (используя координаты конечных точек), чтобы вычислить площади прямоугольных и составных пространств.
Тип: План урока
Построение полигонов:Студентам предлагается нанести на график координаты, чтобы создать загадочный многоугольник, и определить длину его горизонтальной и вертикальной сторон, используя координаты.
Тип: План урока
Построение полигонов с помощью GeoGebra: Этот вводный урок знакомит студентов с процессом построения многоугольников на координатной плоскости и определения длин сторон по вертикали и горизонтали. Подробные инструкции даны учителям, которые плохо знакомы с GeoGebra. Подробная итоговая оценка включает дополнения и ключ для ответа.
Подробные инструкции даны учителям, которые плохо знакомы с GeoGebra. Подробная итоговая оценка включает дополнения и ключ для ответа.
Тип: План урока
Какова ваша точка зрения?:В этой игре ученик бросает вызов партнеру воссоздать его или ее четырехугольник или другую форму на географической доске, вызывая упорядоченные пары вершин четырехугольника.
Тип: План урока
Тайна кругов на полях … на координатной плоскости: На этом уроке учащиеся будут использовать свои знания построения точек в квадранте I координатной плоскости, чтобы вычислить другие пары координат в квадрантах II, III и IV. Учащимся предлагается сопоставить карточки с описанием и соответствующую «карту» (четырехкоординатную сетку). В качестве дополнения или следующего урока ученики будут рисовать свои собственные многоугольники на четырехкоординатной сетке и указывать координаты для каждого из них.
Учащимся предлагается сопоставить карточки с описанием и соответствующую «карту» (четырехкоординатную сетку). В качестве дополнения или следующего урока ученики будут рисовать свои собственные многоугольники на четырехкоординатной сетке и указывать координаты для каждого из них.
Тип: План урока
Эриксон / Блок 1: Масштабные чертежи
Studnets работают с масштабными чертежами в 7 классе, опираясь на более раннюю работу с геометрией и геометрическими измерениями.Ученики начали изучать двумерные и трехмерные формы в детском саду и продолжили эту работу в 1 и 2 классах, составляя, разлагая и идентифицируя формы. Работа студентов с геометрическим измерением началась с длины и продолжилась площадью. Студенты научились «структурировать двумерное пространство», то есть видеть прямоугольник с целочисленными длинами сторон как массив единичных квадратов или рядов или столбцов единичных квадратов. В 3 классе ученики различали периметр и площадь. Они соединили площадь прямоугольника с умножением, понимая, почему (для целых сторон) умножение длин сторон прямоугольника дает количество единичных квадратов, которые покрывают прямоугольник.Они использовали диаграммы с областями для представления экземпляров распределительного свойства. В 4 классе учащиеся применяли формулы площади и периметра прямоугольников для решения реальных и математических задач и научились пользоваться транспортиром. В 5 классе ученики расширили формулу для площади прямоугольника, включив в нее прямоугольники с дробными длинами сторон. В 6 классе учащиеся, основываясь на своих знаниях в области геометрии и геометрических измерений, составили формулы для площадей параллелограммов и треугольников, используя эти формулы для определения площади поверхности многогранников.
В 3 классе ученики различали периметр и площадь. Они соединили площадь прямоугольника с умножением, понимая, почему (для целых сторон) умножение длин сторон прямоугольника дает количество единичных квадратов, которые покрывают прямоугольник.Они использовали диаграммы с областями для представления экземпляров распределительного свойства. В 4 классе учащиеся применяли формулы площади и периметра прямоугольников для решения реальных и математических задач и научились пользоваться транспортиром. В 5 классе ученики расширили формулу для площади прямоугольника, включив в нее прямоугольники с дробными длинами сторон. В 6 классе учащиеся, основываясь на своих знаниях в области геометрии и геометрических измерений, составили формулы для площадей параллелограммов и треугольников, используя эти формулы для определения площади поверхности многогранников.
В этом разделе учащиеся изучают увеличенные копии картинок и плоских фигур, а затем применяют полученные знания для масштабирования чертежей, например карт и планов этажей. Это обеспечивает геометрическую подготовку к работе 7-го класса по пропорциональным отношениям, а также к работе 8-го класса по расширению и подобию.
Это обеспечивает геометрическую подготовку к работе 7-го класса по пропорциональным отношениям, а также к работе 8-го класса по расширению и подобию.
Студенты начинают с просмотра копий рисунков, некоторые из которых выполнены в масштабе, а некоторые — нет. Они используют свои собственные слова, чтобы описать, что отличает масштабированные и немасштабированные копии изображения.По мере продвижения модуля ученики узнают, что все значения длины в масштабированной копии умножаются на коэффициент масштабирования, а все углы остаются неизменными. Они рисуют копии фигур в масштабе. Они узнают, что если масштабный коэффициент больше 1, копия будет больше, а если масштабный коэффициент меньше 1, копия будет меньше. Они изучают, как изменяется область на масштабированных копиях изображения.
Далее студенты изучают масштабные чертежи. Они видят, что принципы и стратегии, которые они использовали для рассуждений о масштабированных копиях фигур, можно использовать с масштабными рисунками. Они интерпретируют и рисуют карты и планы этажей. Они работают со шкалами, в которых используются единицы измерения (например, «1 см представляет 10 км»), и шкалами, которые не включают единицы (например, «масштаб от 1 до 100»). Они учатся выражать шкалы с единицами измерения как шкалы без единиц, и наоборот. Они понимают, что фактическая длина является произведением коэффициента масштабирования и соответствующей длины на чертеже в масштабе, поэтому длины на чертеже являются произведением фактических длин и обратной величиной этого коэффициента масштабирования. Они изучают взаимосвязь между областями и длиной на масштабных чертежах.На протяжении всего модуля они обсуждают свои математические идеи и отвечают на идеи других (MP3, MP6). На завершающем уроке этого раздела учащиеся составляют план этажа своего класса или какой-либо другой комнаты или помещения в школе. Это возможность для них применить то, что они узнали на этом модуле, в повседневной жизни (MP4).
Они интерпретируют и рисуют карты и планы этажей. Они работают со шкалами, в которых используются единицы измерения (например, «1 см представляет 10 км»), и шкалами, которые не включают единицы (например, «масштаб от 1 до 100»). Они учатся выражать шкалы с единицами измерения как шкалы без единиц, и наоборот. Они понимают, что фактическая длина является произведением коэффициента масштабирования и соответствующей длины на чертеже в масштабе, поэтому длины на чертеже являются произведением фактических длин и обратной величиной этого коэффициента масштабирования. Они изучают взаимосвязь между областями и длиной на масштабных чертежах.На протяжении всего модуля они обсуждают свои математические идеи и отвечают на идеи других (MP3, MP6). На завершающем уроке этого раздела учащиеся составляют план этажа своего класса или какой-либо другой комнаты или помещения в школе. Это возможность для них применить то, что они узнали на этом модуле, в повседневной жизни (MP4).
В этом разделе несколько планов уроков предполагают, что каждый ученик имеет доступ к набору геометрических инструментов . Каждый набор инструментов содержит кальку, миллиметровую бумагу, цветные карандаши, ножницы, сантиметровую линейку, транспортир (рекомендуется использовать прозрачные транспортиры без отверстий, на которых видны радиальные линии), и учетную карточку для использования в качестве линейки или для разметки прямых углов.Предоставление студентам этих наборов инструментов дает им возможность развить способности к выбору подходящих инструментов и их стратегическому использованию для решения проблем (MP5). Обратите внимание, что даже учащиеся в классе с цифровым расширением должны иметь доступ к таким инструментам; приложения и моделирование следует рассматривать как дополнение к их инструментам, а не как замену физических инструментов.
Каждый набор инструментов содержит кальку, миллиметровую бумагу, цветные карандаши, ножницы, сантиметровую линейку, транспортир (рекомендуется использовать прозрачные транспортиры без отверстий, на которых видны радиальные линии), и учетную карточку для использования в качестве линейки или для разметки прямых углов.Предоставление студентам этих наборов инструментов дает им возможность развить способности к выбору подходящих инструментов и их стратегическому использованию для решения проблем (MP5). Обратите внимание, что даже учащиеся в классе с цифровым расширением должны иметь доступ к таким инструментам; приложения и моделирование следует рассматривать как дополнение к их инструментам, а не как замену физических инструментов.
Обратите внимание, что изучение масштабированных копий ограничено парами фигур, которые имеют одинаковый поворот и зеркальную ориентацию (т.е. которые не являются вращениями или отражениями друг друга), потому что модуль ориентирован на масштабирование, масштабные коэффициенты и масштабные чертежи. В 8 классе учащиеся расширят свои знания о масштабированных копиях, изучая переводы, повороты, отражения и растяжения.
В 8 классе учащиеся расширят свои знания о масштабированных копиях, изучая переводы, повороты, отражения и растяжения.
Студенты узнают о масштабировании фигур. Изображение представляет собой копию в масштабе оригинала, если форма растянута таким образом, чтобы не искажать ее.Например, вот оригинальная картинка и пять копий. Изображения C и D являются копиями оригинала в масштабе, а изображения A, B и E — нет.
В каждой масштабированной копии стороны в определенное количество раз длиннее соответствующих сторон оригинала. Мы называем это число масштабным коэффициентом . Размер масштабного коэффициента влияет на размер копии. Коэффициент масштабирования больше 1 делает копию больше оригинала. Коэффициент масштабирования меньше 1 делает копию меньше.
Вот задание, которое стоит попробовать со своим учеником:
- Для каждой копии укажите, является ли она масштабированной копией исходного треугольника.
 Если да, то каков масштабный коэффициент?
Если да, то каков масштабный коэффициент? - Нарисуйте еще одну масштабированную копию исходного треугольника с другим масштабным коэффициентом.
Решение:
- Копия 1 — это уменьшенная копия исходного треугольника. Коэффициент масштабирования равен 2, поскольку каждая сторона копии 1 вдвое длиннее соответствующей стороны исходного треугольника.5⋅2 = 10, 4⋅2 = 8, (6.4) ⋅2 = 12,8
- Копия 2 — это уменьшенная копия исходного треугольника. Коэффициент масштабирования равен 12 или 0,5, потому что каждая сторона Копии 2 вдвое короче соответствующей стороны исходного треугольника. 5⋅ (0,5) = 2,5, 4⋅ (0,5) = 2, (6,4) ⋅ (0,5) = 3,2
- Копия 3 не является масштабированной копией исходного треугольника. Форма была искажена. Углы бывают разных размеров, и нет одного числа, которое мы могли бы умножить на длину каждой стороны исходного треугольника, чтобы получить соответствующую длину стороны в Копии 3.
- Ответы разные.
 Пример ответа: прямоугольный треугольник с длиной стороны 12, 15 и 19,2 единицы будет масштабированной копией исходного треугольника с коэффициентом масштабирования 3.
Пример ответа: прямоугольный треугольник с длиной стороны 12, 15 и 19,2 единицы будет масштабированной копией исходного треугольника с коэффициентом масштабирования 3.
Студенты будут изучать масштабные рисунки. Чертеж в масштабе — это двухмерное представление реального объекта или места. Карты и планы этажей являются примерами масштабных чертежей.
Масштаб говорит нам, какую длину на чертеже в масштабе представляет в действительной длине. Например, масштаб «от 1 дюйма до 5 миль» означает, что 1 дюйм на чертеже представляет 5 фактических миль. Если на рисунке показана дорога длиной 2 дюйма, мы знаем, что на самом деле она имеет длину 2–5 или 10 миль.
Масштаб может быть записан с единицами измерения (например, от 1 дюйма до 5 миль) или без единиц (например, от 1 до 50 или от 1 до 400). Если на шкале нет единиц измерения, для расстояний на чертеже шкалы и фактических расстояний используются одни и те же единицы. Например, шкала «от 1 до 50» означает, что 1 сантиметр на чертеже соответствует 50 фактическим сантиметрам, 1 дюйм представляет 50 дюймов и т. Д.
Например, шкала «от 1 до 50» означает, что 1 сантиметр на чертеже соответствует 50 фактическим сантиметрам, 1 дюйм представляет 50 дюймов и т. Д.
Вот задание, которое стоит попробовать со своим учеником:
Киран нарисовал план этажа своего класса, используя масштаб от 1 дюйма до 6 футов.
- Рисунок Кирана имеет ширину 4 дюйма и длину 512 дюймов. Каковы размеры фактического класса?
- Стол в классе имеет ширину 3 фута и длину 6 футов. Какого размера она должна быть на чертеже в масштабе?
- Киран хочет сделать увеличенный чертеж того же класса.Какие из этих весов он мог использовать?
- от 1 до 50
- 1 до 72
- от 1 до 100
Решение:
- 24 фута в ширину и 33 фута в длину. Поскольку каждый дюйм на чертеже представляет собой 6 футов, мы можем умножить на 6, чтобы найти фактические размеры. Фактическая ширина классной комнаты составляет 24 фута, потому что 4 × 6 = 24.
 Длина класса 33 фута, потому что 512⋅6 = 5⋅6 + 12⋅6 = 30 + 3 = 33.
Длина класса 33 фута, потому что 512⋅6 = 5⋅6 + 12⋅6 = 30 + 3 = 33. - шириной 12 дюймов и длиной 1 дюйм. Мы можем разделить на 6, чтобы найти размеры на чертеже.6 ÷ 6 = 1 и 3 ÷ 6 = 12.
- A, от 1 до 50. Шкала «от 1 дюйма до 6 футов» эквивалентна шкале «от 1 до 72», потому что в 6 футах 72 дюйма. Масштаб «от 1 до 100» сделает чертеж в масштабе меньше, чем масштаб «от 1 до 72», потому что каждый дюйм на новом чертеже будет представлять более фактическую длину. Масштаб «от 1 до 50» сделает чертеж в масштабе больше, чем масштаб «от 1 до 72», потому что Kiran потребуется больше дюймов на чертеже для представления той же фактической длины.
План урока и мероприятия 6-8
Биология / экосистемы || География || Геология || Глобальное изменение || Природные опасности || Океаны / Побережья || Вода || Другое
Биология / экосистемы
USGS Kids- Activities
Мероприятия, игры, раскраски, проекты и рассказы, которые рассказывают детям младшего возраста о животных, изменении климата, сокращении популяции пчел, диких птицах и многом другом.
Раскраски животных — задания
Индивидуальные раскраски птиц, летучих мышей, рептилий, амфибий и выдр от наших друзей из Западного центра экологических исследований.
Дикая природа и загрязняющие вещества — уроки
Серия уроков, предназначенных для старшеклассников, которые знакомят с темой экотоксикологии и проводят студентов через научный процесс сбора исходных данных и выводов о воздействии загрязняющих веществ на дикую природу.
Станьте наблюдателем за фенологией — мероприятие
Национальная фенологическая сеть (спонсируемая Геологической службой США) ищет добровольцев для помощи в мониторинге видов растений и животных, встречающихся в Соединенных Штатах.Узнайте, как отслеживать фенологию растений и животных, и зарегистрируйтесь, чтобы вносить новые наблюдения в национальную базу данных по фенологии. Сделайте это классным проектом!
уроков на озере: руководство для педагогов по бассейну Пончартрейн — уроки
В бассейне озера Пончартрейн в Луизиане проживают 1,5 миллиона человек и имеется экосистема устья с огромным биоразнообразием. Упражнения в руководстве для преподавателя помогают учащимся 5–12 классов понять и оценить бассейн и научат их навыкам определять экологические проблемы, вносить изменения и решать проблемы.
Упражнения в руководстве для преподавателя помогают учащимся 5–12 классов понять и оценить бассейн и научат их навыкам определять экологические проблемы, вносить изменения и решать проблемы.
Земля и люди — мероприятие
Учащиеся изучают взаимодействие между людьми и окружающей средой в трех регионах США: Кейп-Код, Лос-Анджелес и Эверглейдс. Предназначен для 7–12 классов.
Interactive San Francisco Bay Data — Activity
Просмотрите графики данных, собранных из воды залива Сан-Франциско, затем создайте свои собственные графики, используя реальные данные. Как изменение проникновения света соотносится с температурой воды? Соответствует ли изменение солености изменению хлорофилла?
Североамериканская программа мониторинга амфибий (NAAMP) — мероприятие
NAAMP — это совместная работа, в которой добровольцы используются для мониторинга популяций голосящих амфибий.Участникам, отвечающим минимальным стандартам, назначаются придорожные маршруты, где данные собираются после наступления темноты. Эта программа в настоящее время активна только в штатах
Эта программа в настоящее время активна только в штатах
География
Ресурсы по топографическим картам для учителей — Уроки и занятия
Этот сайт уровня каталога содержит ссылки на различные ресурсы на топографических картах, информацию о том, как их получить, прочитать их, их историю и картографические проекции, а также ссылки на различные учебные мероприятия и модули.Это универсальный магазин для изучения, использования и обучения концепциям топографических карт.
Изучение карт — Урок
Изучение карт — это междисциплинарный набор материалов по картографированию для 7–12 классов. Студенты получат базовые навыки картографирования и чтения карт и увидят, как карты могут отвечать на фундаментальные географические вопросы. Изображения карт и занятия в этом пакете можно использовать на различных курсах, включая географию, историю, математику, искусство, английский язык и естественные науки.
Построение трехмерной топографической карты — Упражнение
В этом упражнении используются прозрачные пластиковые съемные крышки, каждая из которых отмечена отдельной линией возвышения и сложена друг над другом для создания трехмерной топографической карты. Он включает базовую карту острова Ангел (залив Сан-Франциско), но может быть адаптирован к любым местным топографическим особенностям.
27 идей для преподавания с использованием топографических карт — Activites
Содержит 27 идей для преподавания с использованием примерно 57 000 топографических карт, которые предлагает Геологическая служба США.
Тайны карт — справочная информация и задание
Примеры вопросов для использования с топографическими и тематическими картами Геологической службы США в качестве отправных точек для раскрытия тайн культурной и физической географии Земли.
География кукурузного лабиринта — Действия
Посетите кукурузный лабиринт и воспользуйтесь этими упражнениями, чтобы узнать о картах и географии.
Как использовать компас с топографической картой USGS — упражнение
Научитесь ориентироваться с помощью топографической карты и компаса.
Топографические карты, иллюстрирующие физические особенности — мероприятие
Топографические карты можно использовать для изучения широкого спектра физических объектов в Соединенных Штатах. Это помогает учащимся узнать о геологической эволюции природных ландшафтов страны и показывает, как топографические карты раскрывают больше о поверхности суши, чем просто ее форма и высота.Перемещайте курсор по картам и изображениям в этом онлайн-средстве просмотра, чтобы узнать об избранных особенностях американского ландшафта.
Map-It: простой генератор карт на основе форм — упражнение
Введите долготу и широту точек для нанесения на простую карту. Загрузите версию получившейся карты в формате postscript. Спутниковый снимок
Отслеживание изменений во времени — мероприятие
Повысьте уровень познания учащимися географии, чтения карт, наук о Земле и решения проблем с помощью изменений ландшафта, регистрируемых спутниками в космосе.
AmericaView- Lessons
USGS является партнером AmericaView, у которого есть планы уроков и другие образовательные ресурсы по работе со спутниковыми изображениями. В основном рассчитан на 6–12 классы.
Отслеживание изменений во времени — мероприятие
Повысьте уровень познания учащимися географии, чтения карт, наук о Земле и решения проблем с помощью изменений ландшафта, регистрируемых спутниками в космосе.
AmericaView- Lessons
USGS является партнером AmericaView, у которого есть планы уроков и другие образовательные ресурсы по работе со спутниковыми изображениями.В основном рассчитан на 6–12 классы.
Геология
Бумажные 3D-модели — упражнение
Трехмерные бумажные модели (с соответствующими руководствами для преподавателей) — это увлекательный и интерактивный способ обучения геологическим понятиям. Хотя эти модели были созданы в 1990-х годах и имеют несколько низкое разрешение, они все равно хороши! Анимации, упомянутые в руководствах для преподавателей, больше не доступны
Путешествие вдоль линии поля — Activity
Шестнадцатистраничный комикс о магнитном поле Земли. Путешествуйте вниз через недра Земли, а затем обратно в ионосферу, чтобы узнать, как работает магнитное поле.
Путешествуйте вниз через недра Земли, а затем обратно в ионосферу, чтобы узнать, как работает магнитное поле.
Как построить модель, иллюстрирующую распространение и субдукцию морского дна — упражнение
Постройте трехмерную модель, используя коробку из-под обуви.
Антарктический ледяной покров — уроки и мероприятия
Этот отчет иллюстрирует с помощью бумажной модели, почему происходят изменения в ледниковом покрове, покрывающем антарктический континент. Изучая бумажную модель, студенты лучше поймут эволюцию антарктического ледяного покрова.Анимации, упомянутые в руководствах для преподавателей, больше не доступны.
Столкновение с Чиксулубом — уроки и мероприятия
В этом отчете с помощью двух бумажных моделей показано, как динозавры могли вымереть в результате удара астероида. Изучая бумажные модели, студенты лучше поймут массовые вымирания, которые были частью истории Земли. Анимации, упомянутые в руководствах для преподавателей, больше не доступны.
Морские лилии — уроки и занятия
В этом отчете с помощью бумажной модели показано, как морские лилии жили и окаменели.Изучая бумажную модель, учащиеся лучше поймут похожее на цветок животное, называемое «морская лилия», и окружающую его среду на дне океана. Анимации, упомянутые в руководствах для преподавателей, больше не доступны.
Как построить четыре бумажные модели, описывающие островные коралловые рифы — мероприятие
Этот отчет содержит инструкции и шаблоны для создания набора из четырех трехмерных бумажных моделей, схематически иллюстрирующих развитие островных кораллов.
Сделайте свои собственные окаменелости из бумаги — уроки и задания
Этот отчет иллюстрирует с помощью бумажных моделей, как два организма, трилобит и наутилоид, стали окаменелостями.Отчет призван помочь студентам и другим людям визуализировать размер и форму трилобита и наутилоида, среду, в которой они жили, а также обстоятельства их окаменелости и последующего открытия. Анимации, упомянутые в руководствах для преподавателей, больше не доступны.
Анимации, упомянутые в руководствах для преподавателей, больше не доступны.
Создайте свою бумажную модель вулкана — уроки и занятия
Этот отчет содержит инструкции и образец для создания трехмерной бумажной модели вулкана. Эта модель предназначена для помощи студентам и другим людям в визуализации стратовулкана (внутри и снаружи) и в изучении некоторых терминов, используемых геологами при его описании.
Бумажная модель, показывающая движение разлома Сан-Андреас — активность
Этот отчет содержит инструкции и шаблоны для подготовки трехмерной модели, которая схематически иллюстрирует движение разлома, произошедшее во время землетрясения в Лома-Приета 17 октября 1989 г. в Калифорнии. Модель предназначена для того, чтобы помочь студентам и другим людям визуализировать процесс разлома во время землетрясений.
Песчаные дюны — уроки и занятия
В этом отчете с помощью компьютерной анимации и бумажных моделей показано, почему песчаные дюны могут принимать разные формы. Изучая анимацию и бумажные модели, ученики лучше поймут эволюцию песчаных дюн.
Изучая анимацию и бумажные модели, ученики лучше поймут эволюцию песчаных дюн.
Как построить 7 бумажных моделей, описывающих разломы Земли — Activity
Этот отчет содержит инструкции и шаблоны для подготовки семи трехмерных бумажных моделей, которые схематически иллюстрируют типичные разломы земли и связанные с ними формы рельефа.
2 Бумажные модели, показывающие влияние ледникового льда на горную долину — мероприятие
Этот отчет содержит инструкции и шаблоны для подготовки трехмерных бумажных моделей двух объектов: горной долины, частично заполненной ледником, и той же самой долины после таяния ледника .Включено краткое описание того, как формируются такие ледники, как они разрушают ландшафт и какие физиографические особенности они создают.
Последствия землетрясения — уроки и упражнения
Отчет предназначен для того, чтобы помочь учащимся и другим людям наглядно представить, что вызывает землетрясение и некоторые из возможных результатов сотрясения. Анимации, упомянутые в руководствах для преподавателей, больше не доступны.
Анимации, упомянутые в руководствах для преподавателей, больше не доступны.
Последствия оползней — уроки и мероприятия
В этом отчете показано, как возникают четыре различных типа оползней (оползни, обвалы, потоки и камнепады) и какие повреждения могут возникнуть.Отчет предназначен для того, чтобы помочь студентам и другим людям визуализировать причины оползней и некоторые возможные последствия оползней. Анимации, упомянутые в руководствах для преподавателей, больше не доступны.
Жизненный цикл месторождения полезных ископаемых — уроки и занятия
Это руководство для учителя включает 10 учебных упражнений, основанных на деятельности, которые знакомят студентов с основными геологическими концепциями; процессы поиска, идентификации и извлечения ресурсов из месторождения полезных ископаемых; и использование минералов.Пособие предназначено для учителей естественных наук и учащихся 5-8 классов.
Планета Тектоника Теннисный мяч — Упражнение
Создайте мини-глобус, на котором показаны основные границы плит мира (прокрутите до страницы 15).
Пакет дополнительных материалов для обучения «Динамическая планета» — уроки и задания
Этот помощник для преподавателей предназначен для помощи учителям в обучении тектонике плит, в первую очередь для 6–14 классов.
Геология школьного двора — мероприятия
В структурированных занятиях используются искусственные элементы, которые встречаются на обычном школьном дворе, для демонстрации геологических принципов.
Сбор камней — Упражнение
Узнайте о различных типах камней, а также о том, как их идентифицировать и собирать.
«Что находится в моей почве?» — Задание
Учащиеся разделяют, исследуют и определяют основные компоненты почвы, чтобы лучше понять, как эти компоненты придают почве ее уникальные физические характеристики.
Введение в почвы — Урок
Этот полный план урока показывает студентам, как развиваются почвы, и обеспечивает связь между почвами, климатом, растительностью и геологией.Включает материалы как для учителей, так и для студентов (раздаточный материал, головоломка, полевые и лабораторные листы).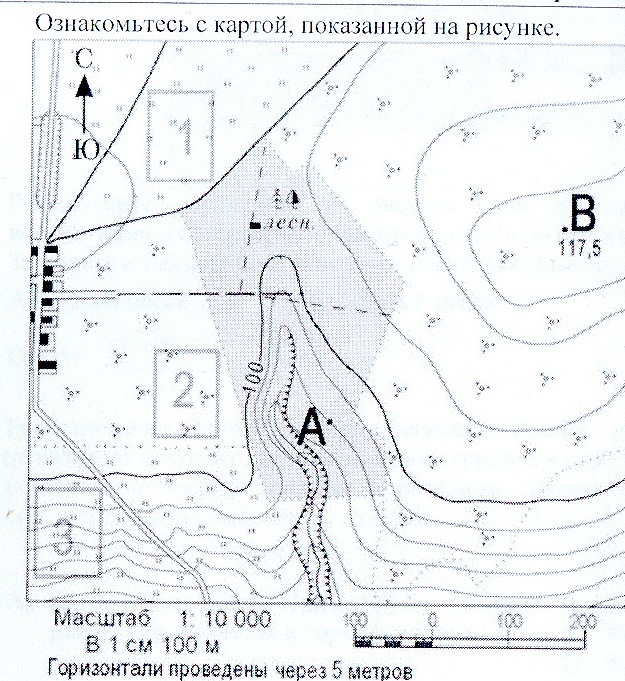
Градуированная подстилка — упражнение
Это упражнение знакомит студентов с концепцией сортировки материалов в различных средах и с особенностями отложений, называемыми градуированной напластовкой. Учащиеся обнаружат, что вода является хорошей средой для разделения и сортировки частиц, и что частицы ведут себя в воде иначе, чем в воздухе.
Геологический возраст — активность
Студенты изучают радиоактивность как инструмент для измерения геологического времени.
Глобальное изменение
Global Change- Activities
Включает введение, упражнения и учебное руководство по темам, связанным с глобальными изменениями, временем и системами Земли. Предназначен для 4–6 классов.
Отслеживание изменений во времени — мероприятие
Повысьте уровень познания учащимися географии, чтения карт, наук о Земле и решения проблем с помощью изменений ландшафта, регистрируемых спутниками в космосе.
Парниковые газы — мероприятие
Учащиеся наблюдают и сравнивают термические свойства трех основных парниковых изменений с течением времени для сухого воздуха, насыщенного водой воздуха, двуокиси углерода и метана.
Оценка изменения ледников и ландшафта — Урок
На этом уроке студенты интерпретируют данные Геологической службы США в различных форматах и делают выводы на основе представленных данных.
Природные опасности
Tabletop Earthquakes — Activity
Постройте простую машину для землетрясений, чтобы продемонстрировать принципы сейсмологии. Включает вспомогательные учебные материалы.
Размер и возникновение наводнений — мероприятие
Учащиеся используют макароны или бобы для расчета статистики повторяемости полов (см. Оборотную сторону плаката).
Жизнь с вулканом на заднем дворе — Урок
Руководство из трех частей, которое содержит научные материалы и основанные на запросах задания о вулканах Каскадного хребта для учащихся средней школы с акцентом на гору Ранье. Включает более 30 занятий, полевой справочник, глоссарий и дополнительную информацию.
Предскажите извержение! — Действия
Этот интерактивный сайт использует анимацию, иллюстрации, задания и викторины, чтобы показать, как извержения на горе Св. Хеленс была точно предсказана учеными Геологической службы США, а затем позволяет студентам предсказать фактическое извержение, используя реальные данные.
Хеленс была точно предсказана учеными Геологической службы США, а затем позволяет студентам предсказать фактическое извержение, используя реальные данные.
Мировой океан / побережье
Хрупкая окраина: руководство по обучению прибрежным водно-болотным угодьям — справочная информация и мероприятия
Материал для разработки всестороннего исследования прибрежных водно-болотных угодий. Включает справочную информацию, предлагаемые занятия, глоссарий, ссылки и список литературы. Действия могут быть продемонстрированы учителем или выполнены учениками.Особое внимание уделяется водно-болотным угодьям побережья Мексиканского залива.
Wise Wetland Ways — мероприятие
Учителя используют «артефакты» водно-болотных угодий, чтобы стимулировать обсуждение того, какую пользу мы получаем от водно-болотных угодий (см. Оборотную сторону плаката).
Вода
Школа наук о воде USGS — мероприятия и фотографии
Лучшая отправная точка для получения большого количества общей информации о науках о воде. Что такое вода? Каковы его свойства и как они измеряются? Как используется вода? Как USGS измеряет сток и собирает пробы воды? Глоссарий, картинная галерея и центр деятельности — это многие дополнительные функции.
Что такое вода? Каковы его свойства и как они измеряются? Как используется вода? Как USGS измеряет сток и собирает пробы воды? Глоссарий, картинная галерея и центр деятельности — это многие дополнительные функции.
Практические эксперименты по проверке кислотного дренажа шахт — Activity
В четырнадцати очень простых упражнениях используется самодельная лакмусовая бумага и предметы домашнего обихода для проверки воды ручья на кислотный дренаж шахт и изучения растений, бактерий и насекомых, живущих в воде.
Плакаты по образованию в области водных ресурсов — уроки и мероприятия
Все готовые плакаты, посвященные водным ресурсам, нарисованы в формате карикатуры одним и тем же художником-карикатуристом. Плакаты доступны в цветном или черно-белом цвете. На оборотной стороне цветных плакатов в формате PDF содержатся учебные задания: одна версия для детей 3-5 классов, а другая — задания для детей 6-8 классов.Черно-белые плакаты предназначены для раскрашивания детьми К-5 классов.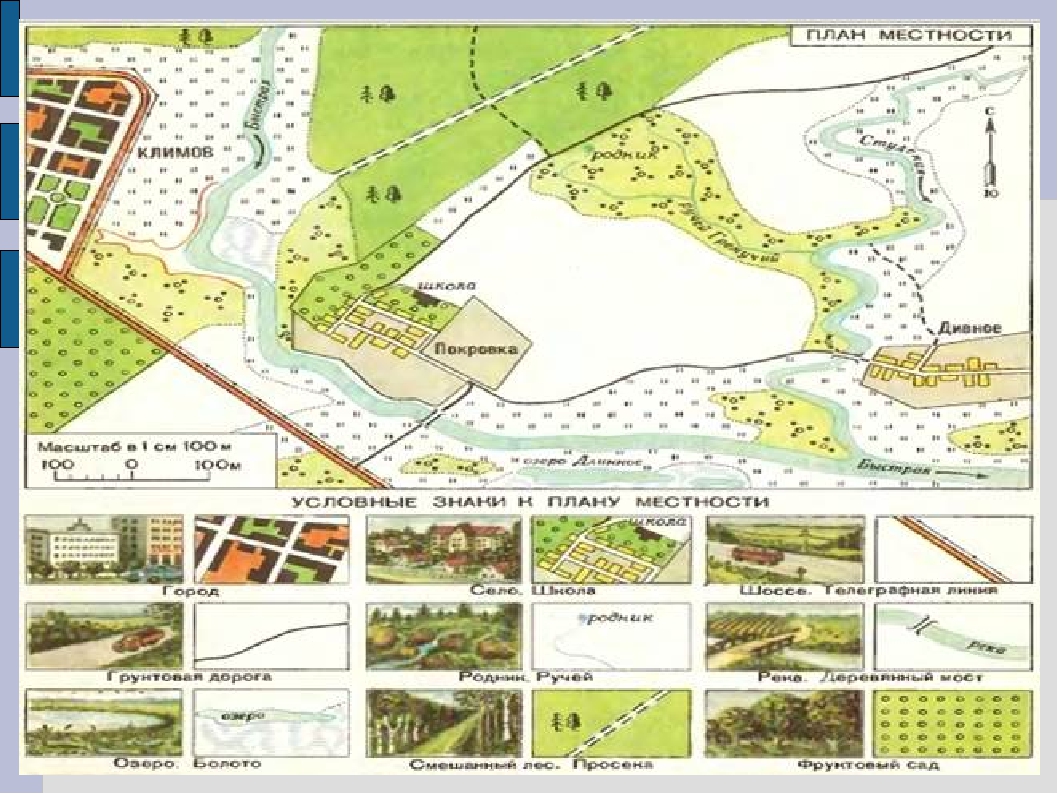
Информационная тетрадь по грунтовым водам — уроки
Пять планов уроков по грунтовым водам для 6–8 классов с формами, диаграммами и вспомогательной информацией. Хотя они были разработаны для совместной работы инструктора и специалиста по водным ресурсам, вдумчивый педагог мог легко справиться с уроками самостоятельно.
Размер и возникновение наводнений — мероприятие
Учащиеся используют макароны или бобы для расчета статистики повторяемости полов (см. Оборотную сторону плаката).
Другое
Площадь треугольников — урок геометрии с упражнениями
В этом уроке представлена идея, что площадь любого треугольника составляет ровно половину определенного параллелограмма — таким образом мы получаем знакомую формулу умножить базу на высоту и взять половину от этого. Урок содержит разнообразные упражнения для студентов.
|
1. Найдите площадь заштрихованного треугольника на картинке.
над.
2. Нарисуйте соответствующие параллелограммы для этих треугольников и найдите их
области.
Совет: нарисуйте линию, совпадающую с основанием
треугольник, начиная с верхней вершины.
а. _______ кв. | г. _______ кв. | г. _______ кв. |
Опять же, мы используем базу и высоту . Высота — перпендикуляр на базу, | Так как площадь треугольника равна половине Площадь | ||||
|
3. Нарисуйте высоту в каждом треугольнике и отметьте основание. Найдите площадь каждого
треугольник.
Нарисуйте высоту в каждом треугольнике и отметьте основание. Найдите площадь каждого
треугольник.
| а. _______ кв. | б. _______ кв. | г. _______ кв. |
| ||||||
|
| 5.Эта фигура называется _________________________. Вычислите его площадь. |
6. Нарисуйте как можно больше треугольников разной формы. как вы можете иметь площадь 12 квадратные единицы.
|
8. Нарисуйте свой собственный треугольник и найдите его площадь!
9. Нарисуйте треугольник площадью 3 квадратных дюйма.
Можно ли нарисовать только , один треугольник с
эту область, или можно нарисовать несколько, с
разные формы / размеры?
10. Нарисуйте треугольник, , ничего не измеряя, так, чтобы его площадь была близка к 20 см 2 .
Проверка по чертежу
Нарисуйте треугольник, , ничего не измеряя, так, чтобы его площадь была близка к 20 см 2 .
Проверка по чертежу
высота и замеры! Практикуйтесь, пока не получите
треугольник площадью примерно 20 см 2 .
Вы даже можете сделать игру
из этого: тот, кто получит область, ближайшую к данной области, — это
победитель
или получает наибольшее количество очков. Или по очереди с другом просите друга
нарисуйте треугольник с
конкретный район.Возможно, добавим условие, что
треугольник должен быть тупым / острым / правым, или
равносторонний / равнобедренный / разносторонний.
Этот урок взят из книги Марии Миллер Math Mammoth Geometry 2 и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер.
Глава 111. Подраздел B
Глава 111. Техас: основные знания и навыки математики
Подраздел Б. Средняя школа
Средняя школа
Законодательные органы: положения данного подраздела B выпущен в соответствии с Кодексом образования Техаса, 7.102 (c) (4), 28.002, 28.0021 (a) (1), и 28.008, если не указано иное.
111,25. Реализация Техасских основных знаний и навыков для математики, средняя школа, принята 2012.
(а) Положения пунктов 111.26-111.28 настоящего подраздела реализуются школьными округами.
(б) Не позднее 31 августа 2013 г., уполномоченный образование должно определить, было ли финансирование учебных материалов предоставлены в государственные школы Техаса для материалов, которые охватывают основные знания и навыки по математике, принятые в 111.26-111.28 из этого подраздел.
(c) Если комиссар принимает решение, что инструктивный
финансирование материалов было предоставлено в соответствии с подразделом (b) этого раздела,
111.26-111.28 настоящего подраздела вводить в действие, начиная с
2014-2015 учебный год и распространяется на 2014-2015 и последующие учебные годы.
(d) Если комиссар не принимает решение финансирование учебных материалов доступно в подразделе (b) данного раздела комиссар не позднее августа определяет 31 каждого последующего учебного года ли финансирование учебных материалов был доступен.Если комиссар определит, что инструкция выделено финансирование материалов, уполномоченный должен уведомить Государственное управление образования и школьных округов, 111.26-111.28 г. подраздел вводится в действие на следующий учебный год.
Источник: Положения настоящего стандарта 111.25 приняты для вступления в силу. 10 сентября 2012 г., 37 TexReg 7109; внесены изменения, вступающие в силу 31 декабря 2014 г., 39 TexReg 10470.
111.26. 6 класс, принято 2012.
(а) Введение.
(1) Стремление к совершенству в образовании
является движущей силой основных знаний и навыков Техаса по математике,
руководствуясь стандартами готовности к колледжу и карьере.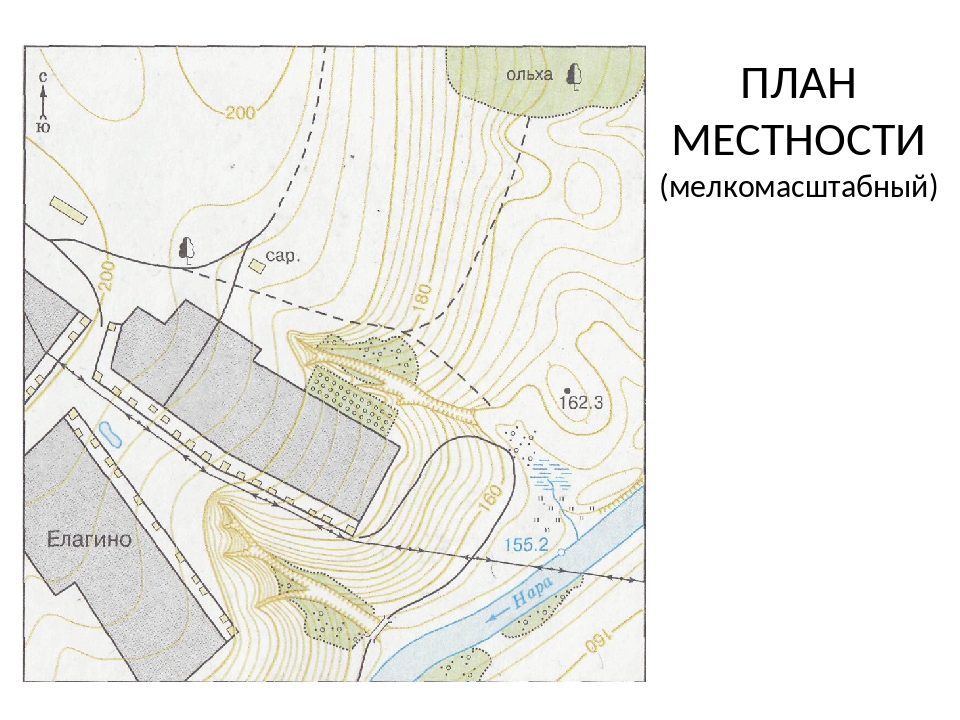 Встраивая статистику,
вероятность и финансы, уделяя особое внимание вычислительному мышлению, математическому
свободное владение языком и твердое понимание, Техас будет лидером в области математического образования
и подготовить всех студентов Техаса к испытаниям, с которыми они столкнутся в 21-м
век.
Встраивая статистику,
вероятность и финансы, уделяя особое внимание вычислительному мышлению, математическому
свободное владение языком и твердое понимание, Техас будет лидером в области математического образования
и подготовить всех студентов Техаса к испытаниям, с которыми они столкнутся в 21-м
век.
(2) Стандарты процессов описывают способы, которыми
Ожидается, что студенты будут вовлечены в содержание. Размещение процесса
стандарты в начале знаний и навыков, указанные для каждого класса
и конечно намеренно. Стандарты процессов объединяют другие знания
и навыки вместе, чтобы учащиеся могли успешно решать проблемы и
эффективно и результативно использовать математику в повседневной жизни. Стандарты процесса
интегрированы в каждый класс и курс.По возможности студенты будут
применять математику к проблемам, возникающим в повседневной жизни, в обществе и на рабочем месте.
Студенты будут использовать модель решения проблем, которая включает анализ заданных
информация, формулирование плана или стратегии, определение решения, обоснование
решение, а также оценка процесса решения проблем и разумности
решения. Студенты выберут соответствующие инструменты, такие как реальные объекты,
манипуляторы, алгоритмы, бумага и карандаш, а также технологии и методы
такие как мысленная математика, оценка, чувство чисел, а также обобщение и абстракция
решать задачи.Студенты будут эффективно передавать математические идеи,
рассуждения и их последствия с использованием нескольких представлений, таких как символы,
диаграммы, графики, компьютерные программы и язык. Студенты будут использовать математические
отношения для выработки решений, установления связей и прогнозов.
Студенты будут анализировать математические отношения, чтобы общаться и общаться
математические идеи. Студенты будут отображать, объяснять или обосновывать математические
идеи и аргументы с использованием точного математического языка в письменной или устной форме
общение.
Студенты выберут соответствующие инструменты, такие как реальные объекты,
манипуляторы, алгоритмы, бумага и карандаш, а также технологии и методы
такие как мысленная математика, оценка, чувство чисел, а также обобщение и абстракция
решать задачи.Студенты будут эффективно передавать математические идеи,
рассуждения и их последствия с использованием нескольких представлений, таких как символы,
диаграммы, графики, компьютерные программы и язык. Студенты будут использовать математические
отношения для выработки решений, установления связей и прогнозов.
Студенты будут анализировать математические отношения, чтобы общаться и общаться
математические идеи. Студенты будут отображать, объяснять или обосновывать математические
идеи и аргументы с использованием точного математического языка в письменной или устной форме
общение.
(3) Основное внимание в 6 классе уделяется количеству
и операции; соразмерность; выражения, уравнения и отношения;
и измерения и данные. Студенты используют концепции, алгоритмы и свойства
рациональных чисел, чтобы исследовать математические отношения и описывать
все более сложные ситуации. Студенты используют понятия соразмерности
исследовать, развивать и сообщать математические отношения. Ученики
использовать алгебраическое мышление, чтобы описать, как изменение одной величины в отношениях
приводит к изменению другого.Студенты соединяют словесные, числовые, графические,
и символические представления отношений, включая уравнения и неравенства.
Студенты используют геометрические свойства и отношения, а также пространственные рассуждения,
моделировать и анализировать ситуации и решать проблемы. Студенты передают информацию
о геометрических фигурах или ситуациях путем количественной оценки атрибутов, обобщить
процедуры, основанные на опыте измерений, и использовать эти процедуры для решения проблем.Студенты используют соответствующую статистику, представления данных и рассуждения.
Студенты используют концепции, алгоритмы и свойства
рациональных чисел, чтобы исследовать математические отношения и описывать
все более сложные ситуации. Студенты используют понятия соразмерности
исследовать, развивать и сообщать математические отношения. Ученики
использовать алгебраическое мышление, чтобы описать, как изменение одной величины в отношениях
приводит к изменению другого.Студенты соединяют словесные, числовые, графические,
и символические представления отношений, включая уравнения и неравенства.
Студенты используют геометрические свойства и отношения, а также пространственные рассуждения,
моделировать и анализировать ситуации и решать проблемы. Студенты передают информацию
о геометрических фигурах или ситуациях путем количественной оценки атрибутов, обобщить
процедуры, основанные на опыте измерений, и использовать эти процедуры для решения проблем.Студенты используют соответствующую статистику, представления данных и рассуждения. делать выводы, оценивать аргументы и давать рекомендации. В то время
важно использование всех видов техники, упор на готовность к алгебре
навыки требуют внедрения графической технологии.
делать выводы, оценивать аргументы и давать рекомендации. В то время
важно использование всех видов техники, упор на готовность к алгебре
навыки требуют внедрения графической технологии.
(4) Заявления, содержащие слово «включая» справочный контент, который необходимо освоить, а те, которые содержат фразу «такие как» предназначены в качестве возможных иллюстративных примеров.
(b) Знания и навыки.
(1) Стандарты математических процессов. Студент использует математические процессы для получения и демонстрации математического понимания. Ожидается:
(A) применять математику к возникающим проблемам в повседневной жизни, в обществе и на рабочем месте;
(B) использовать модель решения проблем, которая включает анализ данной информации, формулирование плана или стратегии, определение решение, обоснование решения и оценка процесса решения проблемы и разумности решения;
(C) выберите инструменты, включая реальные объекты, манипуляторы, бумагу и карандаш, и технология и методы, включая мысленную математику, оценку, и чувство числа, если необходимо, чтобы решить проблемы;
(D) передавать математические идеи, рассуждения и их последствия, используя несколько представлений, включая символы, диаграммы, графики и соответствующий язык;
(E) создавать и использовать представления для организации, записывать и передавать математические идеи;
(F) анализировать математические отношения к соединять и передавать математические идеи; и
(G) отображать, объяснять и обосновывать математические идеи и аргументы, используя точные
математический язык в письменном или устном общении.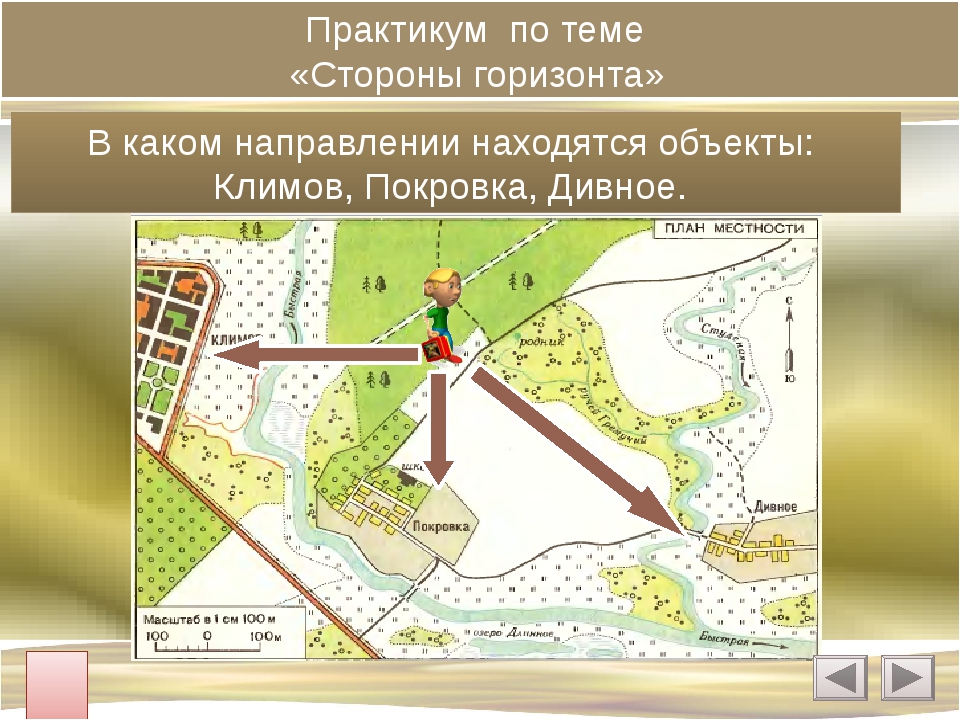
(2) Число и операции. Студент подает заявку стандарты математического процесса для представления и использования рациональных чисел в разнообразие форм. Ожидается:
(A) классифицирует целые числа, целые числа и рациональные числа с использованием визуального представления, такого как диаграмма Венна, для описания отношения между наборами чисел;
(B) идентифицирует число, его противоположность и его абсолютная величина;
(C) найти, сравнить, и упорядочивать целые и рациональные числа с помощью числовой строки;
(D) порядок набора рациональных чисел, возникающих из математического и реального контекстов; и
(E) распространяет представления о делении на включить дробное обозначение, например, a / b представляет то же число как a b , где b ≠ 0.
(3) Число и операции. Студент подает заявку
стандарты математического процесса для представления сложения, вычитания, умножения,
и разделение при решении проблем и обосновании решений. Студент
ожидается:
Студент
ожидается:
(A) признать, что деление на рациональное число и умножение на обратный результат в эквивалентных значениях;
(B) определяет, с расчетом и без него, увеличивается или уменьшается количество при умножении на дробь, в том числе значения больше или меньше единицы;
(C) представляют собой целочисленные операции с конкретными моделирует и связывает действия с моделями со стандартизованными алгоритмами;
(D) складывать, вычитать, умножать и делить целые числа свободно; и
(E) умножить и разделить положительное рациональное числа бегло.
(4) Пропорциональность. Студент применяет математические стандарты процесса для развития понимания пропорциональных отношений в проблемных ситуациях. Ожидается:
(A) сравнить два правила словесно, численно, графически и символически в форма y = ax или y = x + a , чтобы различать между аддитивными и мультипликативными отношениями;
(B) применять качественные и количественные рассуждения для решения задач прогнозирования и сравнения реальных проблем с использованием соотношений и ставки;
(C) приведены примеры соотношений как мультипликативных сравнения двух величин, описывающих один и тот же атрибут;
(D) приведены примеры ставок для сравнения путем деления двух величин с разными атрибутами, включая ставки как частные;
(E) представляют собой отношения и проценты с бетоном модели, дроби и десятичные дроби;
(F) представляют собой контрольные доли и проценты, такие как 1%, 10%, 25%, 33 1/3%, и кратные этих значений с использованием сеток 10 на 10, ленточных диаграмм, числовых линий и чисел;
(G) генерировать эквивалент формы дробей, десятичных знаков и процентов с использованием реальных задач, в том числе проблемы, связанные с деньгами; и
(H) преобразовать единицы измерения
система, включая использование пропорций и удельных ставок.
(5) Пропорциональность. Студент применяет математические стандарты процесса для решения проблем, связанных с пропорциональными отношениями. Ожидается:
(A) представляет математический и реальный мир проблемы, связанные с соотношениями и коэффициентами с использованием масштабных коэффициентов, таблиц, графиков и пропорции;
(B) решать реальные проблемы для найти целое с учетом части и процентов, чтобы найти часть с учетом целого и проценты, и найти проценты для части и целого, включая использование конкретных и графических моделей; и
(C) использовать эквивалентные дроби, десятичные дроби, и проценты, чтобы показать равные части одного и того же целого.
(6) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для использования нескольких представлений описывать алгебраические отношения. Ожидается:
(A) идентифицирует независимые и зависимые количества из таблиц и графики;
(B) напишите уравнение, которое представляет взаимосвязь между независимыми и зависимыми величинами из Таблица; и
(C) представляют
данный
ситуации с использованием словесных описаний, таблиц, графиков и
уравнения в виде y = kx или y = x + b .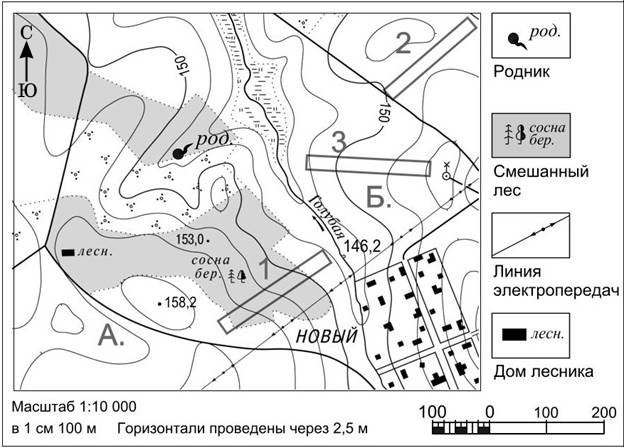
(7) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для разработки концепций выражения и уравнения. Ожидается:
(A) генерировать эквивалентные числовые выражения, использующие порядок операций, включая показатели целых чисел и разложение на простые множители;
(B) различать выражения и уравнения словесно, численно и алгебраически;
(C) определить, если два выражения эквивалентны с использованием конкретных моделей, графических моделей и алгебраических представлений; и
(D) генерирует эквивалентные выражения используя свойства операций: обратная, тождественная, коммутативная, ассоциативные и распределительные свойства.
(8) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса, чтобы использовать геометрию для представления отношения и решать проблемы. Ожидается:
(A) расширить предыдущие знания о треугольниках и их свойства включают сумму углов треугольника, отношение между длинами сторон и величиной углов в треугольнике, и определение когда три длины образуют треугольник;
(B) модель формулы площади для параллелограммов, трапеций, и треугольники, разложив и переставив части этих фигур;
(C) написать уравнения которые представляют собой проблемы, связанные с областью прямоугольники, параллелограммы, трапеции, треугольники и объем справа прямоугольные призмы с положительными рациональными размерами числа; и
(D) определить
решения проблем, связанных с областью
прямоугольники, параллелограммы, трапеции, треугольники и объем справа
прямоугольные призмы с положительными рациональными размерами
числа.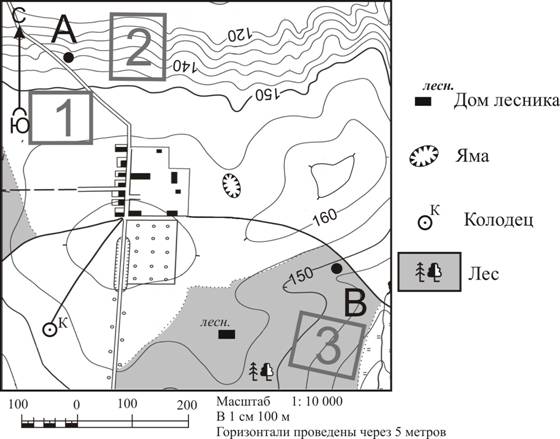
(9) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для использования уравнений и неравенств. представлять ситуации. Ожидается:
(A) написать уравнения с одной переменной и одним шагом и неравенства для обозначения ограничений или условий в рамках проблем;
(B) представляют решения для одной переменной, одношаговые уравнения и неравенства на числовых прямых; и
(C) написать соответствующие реальные проблемы с учетом уравнений или неравенств с одной переменной, одношаговых.
(10) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для использования уравнений и неравенств. решать задачи. Ожидается:
(A) и решить одну переменную, одношаговое уравнения и неравенства, представляющие проблемы, включая геометрические понятия; и
(B) определить, соответствует ли данное значение (я)
Однопеременные, одношаговые уравнения или неравенства верны.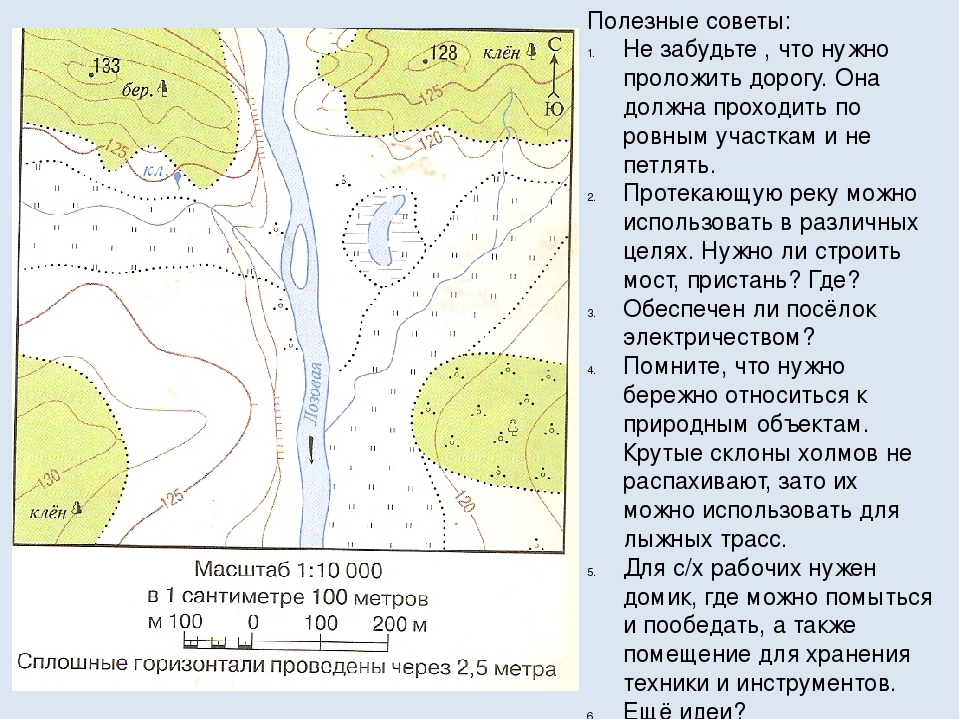
(11) Измерения и данные. Студент подает заявку стандарты математического процесса для использования координатной геометрии для определения местоположений на плоскости. Ожидается, что ученик наберет точки во всех четырех квадрантах. с помощью упорядоченные пары рациональных чисел.
(12) Измерения и данные. Студент подает заявку стандарты математических процессов для использования числовых или графических представлений анализировать проблемы. Ожидается:
(A) представляют числовые данные графически, включая точечные диаграммы, диаграммы стеблей и листьев, гистограммы и ящичковые диаграммы;
(B) использовать графическое представление числовых данные для описания центра, распространения и формы распределения данных;
(C) суммирует числовые данные с числовые сводки, включая среднее и медианное значение (меры центра), а также размах и межквартильный размах (IQR) (меры распространения), и используйте эти сводки для описания центра, распространения, и форма распределения данных; и
(D) резюмирует категориальные данные с числовыми
и графические сводки, включая режим, процент значений в каждом
категории (таблица относительной частоты) и гистограммы процентов, и используйте их
резюме для описания распределения данных.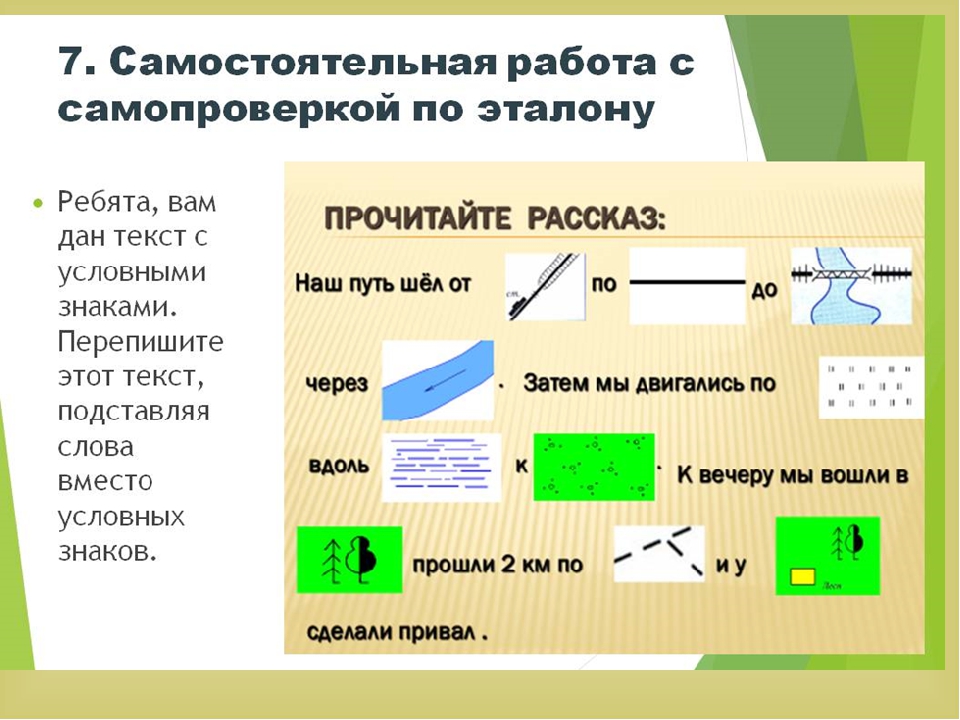
(13) Измерения и данные. Студент подает заявку стандарты математических процессов для использования числовых или графических представлений решать задачи. Ожидается:
(A) интерпретировать числовые данные, представленные в виде точечных диаграмм, стебель-лист графики, гистограммы и коробчатые диаграммы; и
(B) различать ситуации дающие данные с вариабельностью и без нее.
(14) Личная финансовая грамотность. Студент применяет стандарты математического процесса для развития экономического мышления и решение проблем, полезных в жизни знающего потребителя и инвестора.Ожидается:
(A) сравните характеристики и стоимость проверки счет и дебетовая карта, предлагаемые различными местными финансовыми учреждениями;
(B) различать дебетовые и кредитные карты открытки;
(C) балансировать регистр чеков, который включает депозиты, снятие средств и переводы;
(D) объясните, почему важно установить положительная кредитная история;
(E) описать информацию в кредитном отчете и как долго он сохраняется;
(F) описывает ценность кредитных отчетов для заемщикам и кредиторам;
(G) объясняет различные методы оплаты обучения в колледже, в том числе через сбережения, гранты, стипендии, студенческие ссуды и работу-учебу; и
(H) сравнить годовую зарплату нескольких профессий
требующие различных уровней послесреднего образования или профессионального обучения
и рассчитать влияние различных годовых зарплат на пожизненный доход.
Источник: Положения настоящего стандарта 111.26 приняты для вступления в силу. 10 сентября 2012 г., 37 TexReg 7109.
111,27. 7 класс, принято 2012.
(а) Введение.
(1) Стремление к совершенству в образовании является движущей силой основных знаний и навыков Техаса по математике, руководствуясь стандартами готовности к колледжу и карьере. Встраивая статистику, вероятность и финансы, уделяя особое внимание вычислительному мышлению, математическому свободное владение языком и твердое понимание, Техас будет лидером в области математического образования и подготовить всех студентов Техаса к испытаниям, с которыми они столкнутся в 21-м век.
(2) Стандарты процессов описывают способы, которыми
Ожидается, что студенты будут вовлечены в содержание. Размещение процесса
стандарты в начале знаний и навыков, указанные для каждого класса
и конечно намеренно. Стандарты процессов объединяют другие знания
и навыки вместе, чтобы учащиеся могли успешно решать проблемы и
эффективно и результативно использовать математику в повседневной жизни. Стандарты процесса
интегрированы в каждый класс и курс.По возможности студенты будут
применять математику к проблемам, возникающим в повседневной жизни, в обществе и на рабочем месте.
Студенты будут использовать модель решения проблем, которая включает анализ заданных
информация, формулирование плана или стратегии, определение решения, обоснование
решение, а также оценка процесса решения проблем и разумности
решения. Студенты выберут соответствующие инструменты, такие как реальные объекты,
манипуляторы, алгоритмы, бумага и карандаш, а также технологии и методы
такие как мысленная математика, оценка, чувство чисел, а также обобщение и абстракция
решать задачи.Студенты будут эффективно передавать математические идеи,
рассуждения и их последствия с использованием нескольких представлений, таких как символы,
диаграммы, графики, компьютерные программы и язык. Студенты будут использовать математические
отношения для выработки решений, установления связей и прогнозов.
Стандарты процесса
интегрированы в каждый класс и курс.По возможности студенты будут
применять математику к проблемам, возникающим в повседневной жизни, в обществе и на рабочем месте.
Студенты будут использовать модель решения проблем, которая включает анализ заданных
информация, формулирование плана или стратегии, определение решения, обоснование
решение, а также оценка процесса решения проблем и разумности
решения. Студенты выберут соответствующие инструменты, такие как реальные объекты,
манипуляторы, алгоритмы, бумага и карандаш, а также технологии и методы
такие как мысленная математика, оценка, чувство чисел, а также обобщение и абстракция
решать задачи.Студенты будут эффективно передавать математические идеи,
рассуждения и их последствия с использованием нескольких представлений, таких как символы,
диаграммы, графики, компьютерные программы и язык. Студенты будут использовать математические
отношения для выработки решений, установления связей и прогнозов.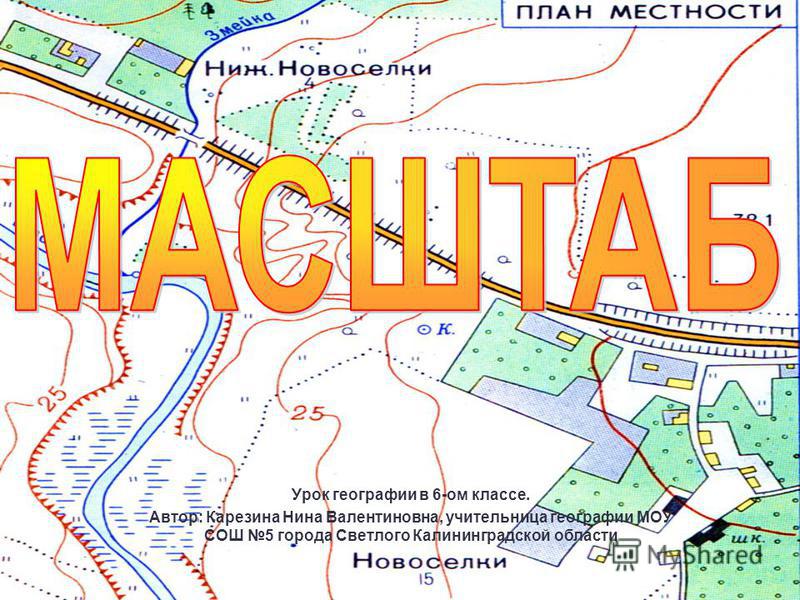 Студенты будут анализировать математические отношения, чтобы общаться и общаться
математические идеи. Студенты будут отображать, объяснять или обосновывать математические
идеи и аргументы с использованием точного математического языка в письменной или устной форме
общение.
Студенты будут анализировать математические отношения, чтобы общаться и общаться
математические идеи. Студенты будут отображать, объяснять или обосновывать математические
идеи и аргументы с использованием точного математического языка в письменной или устной форме
общение.
(3) Основное внимание в 7 классе уделяется количеству
и операции; соразмерность; выражения, уравнения и отношения;
и измерения и данные. Студенты используют концепции, алгоритмы и свойства
рациональных чисел, чтобы исследовать математические отношения и описывать
все более сложные ситуации. Студенты используют понятия соразмерности
для изучения, развития и передачи математических взаимосвязей, в том числе
число, геометрия и измерение, статистика и вероятность.Ученики
использовать алгебраическое мышление, чтобы описать, как изменение одной величины в отношениях
приводит к изменению другого. Студенты соединяют словесные, числовые, графические,
и символические представления отношений, включая уравнения и неравенства. Студенты используют геометрические свойства и отношения, а также пространственные рассуждения,
моделировать и анализировать ситуации и решать проблемы. Студенты передают информацию
о геометрических фигурах или ситуациях путем количественной оценки атрибутов, обобщить
процедуры, основанные на опыте измерений, и использовать эти процедуры для решения проблем.Студенты используют соответствующую статистику, представления данных и рассуждения.
делать выводы, оценивать аргументы и давать рекомендации. В то время
важно использование всех видов техники, упор на готовность к алгебре
навыки требуют внедрения графической технологии.
Студенты используют геометрические свойства и отношения, а также пространственные рассуждения,
моделировать и анализировать ситуации и решать проблемы. Студенты передают информацию
о геометрических фигурах или ситуациях путем количественной оценки атрибутов, обобщить
процедуры, основанные на опыте измерений, и использовать эти процедуры для решения проблем.Студенты используют соответствующую статистику, представления данных и рассуждения.
делать выводы, оценивать аргументы и давать рекомендации. В то время
важно использование всех видов техники, упор на готовность к алгебре
навыки требуют внедрения графической технологии.
(4) Заявления, содержащие слово «включая» справочный контент, который необходимо освоить, а те, которые содержат фразу «такие как» предназначены в качестве возможных иллюстративных примеров.
(b) Знания и навыки.
(1) Стандарты математических процессов. Студент
использует математические процессы для получения и демонстрации математического понимания. Ожидается:
Ожидается:
(A) применять математику к возникающим проблемам в повседневной жизни, в обществе и на рабочем месте;
(B) использовать модель решения проблем, которая включает анализ данной информации, формулирование плана или стратегии, определение решение, обоснование решения и оценка процесса решения проблемы и разумности решения;
(C) выберите инструменты, включая реальные объекты, манипуляторы, бумагу и карандаш, и технология и методы, включая мысленную математику, оценку, и чувство числа, если необходимо, чтобы решить проблемы;
(D) передавать математические идеи, рассуждения и их последствия, используя несколько представлений, включая символы, диаграммы, графики и соответствующий язык;
(E) создавать и использовать представления для организации, записывать и передавать математические идеи;
(F) анализировать математические отношения к соединять и передавать математические идеи; и
(G) отображать, объяснять и обосновывать математические идеи и аргументы, используя точные
математический язык в письменном или устном общении.
(2) Число и операции. Студент подает заявку стандарты математического процесса для представления и использования рациональных чисел в разнообразие форм. Ожидается, что студент расширит предыдущие знания наборы и подмножества с использованием визуального представления для описания отношений между наборы рациональных чисел.
(3) Число и операции. Студент подает заявку стандарты математического процесса для сложения, вычитания, умножения и деления решение проблем и обоснование решений.Ожидается:
(A) сложение, вычитание, умножение и деление рациональных чисел числа бегло; и
(B) применять и расширять предыдущие договоренности операций для решения задач с использованием сложения, вычитания, умножения, и деление рациональных чисел.
(4) Пропорциональность. Студент применяет математические стандарты процессов для представления и решения проблем, связанных с пропорциональными отношениями. Ожидается:
(A) представляют постоянную скорость изменения в математических и реальных задачах, заданных в графических, табличных, словесных, числовые, графические и алгебраические представления, в том числе d = rt ;
(B) рассчитать удельные расценки по ставкам в математической и проблемы реального мира;
(C) определить коэффициент пропорциональности ( k = y / x ) в рамках математических и реальных задач;
(D) решать проблемы, связанные с соотношения, ставки и проценты, включая многоэтапные задачи с процентами повышение и снижение процента, и проблемы с финансовой грамотностью; и
(E) преобразование между системами измерения, включая использование
пропорций и использования единичных ставок.
(5) Пропорциональность. Студент применяет математические стандарты процессов для использования геометрии для описания или решения проблем, связанных с пропорциональные отношения. Ожидается:
(A) обобщить критические атрибуты сходство, включая соотношения внутри и между подобными формами;
(B) описывает π как отношение длины окружности к ее диаметру; и
(C) решить математическую и реальные проблемы, связанные с чертежами аналогичной формы и масштаба.
(6) Пропорциональность. Студент применяет математические стандарты процессов для использования вероятности и статистики для описания или решения проблем включая пропорциональные отношения. Ожидается:
(A) представляют собой пробелы для простых и составные события с использованием списков и древовидных диаграмм;
(B) выбрать и использовать различные модели для представляют простые и сложные события с технологиями и без них;
(C) делать прогнозы и определять решения использование экспериментальных данных для простых и сложных событий;
(D) делать прогнозы и определять решения использование теоретической вероятности для простых и сложных событий;
(E) найти вероятности простого событие и его дополнение и описывают отношения между ними;
(F) использовать данные из случайной выборки для делать выводы о населении;
(G) решить проблемы с использованием данных, представленных в виде гистограмм, точечных диаграмм и круговых диаграмм, включая частичные сравнения и эквиваленты;
(H) решать проблемы с помощью качественные и количественные прогнозы и сравнения из простых экспериментов; и
(I) определяют экспериментальные и теоретические
вероятности, связанные с простыми и сложными событиями, с использованием данных и выборки
пробелы.
(7) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для представления линейных отношений. с использованием нескольких представлений. Ожидается, что ученик будет представлять линейные отношения с помощью словесных описаний, таблиц, графиков, и уравнения, которые упрощаются до формы y = mx + b .
(8) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для построения геометрических соотношений. с объемом.Ожидается:
(A) моделирование отношений между объемом прямоугольной призмы и прямоугольной пирамиды, имеющей оба совпадающих основания и высоты и соединяются это отношение к формулам;
(B) объяснять словесно и символически соотношение между объемом треугольной призмы и треугольной пирамида, имеющая одинаковое основание и высоту и соединяющая это отношение к формулам; и
(C) использовать модели для определения приблизительных формул
для окружности и площади круга и соедините модели с актуальными
формулы.
(9) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для решения геометрических задач. Ожидается:
(A) решить проблемы объемные прямоугольные призмы, треугольные призмы, прямоугольные пирамиды и треугольные пирамиды;
(B) определить окружность и площадь круги;
(C) определить площадь составных фигур содержащий комбинации прямоугольников, квадратов, параллелограммов, трапеций, треугольники, полукруги и четверти окружности; и
(D) решить проблемы, связанные с боковыми и общая площадь поверхности прямоугольной призмы, прямоугольной пирамиды, треугольная призма и треугольная пирамида путем определения площадь сетки фигуры.
(10) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для использования уравнений с одной переменной и неравенство для представления ситуаций. Ожидается:
(A) запись с одной переменной, двухступенчатая уравнения и неравенства для представления ограничения или условия в рамках проблем;
(B) представляют решения для одной переменной, двухступенчатой уравнения и неравенства на числовых линиях; и
(C) написать соответствующую реальную проблему
задано двухступенчатое уравнение с одной переменной или
неравенство.
(11) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для решения уравнений с одной переменной. и неравенство. Ожидается:
(A) моделирование и решение двухэтапных уравнений и неравенств с одной переменной;
(B) определить, значение (я) составляют двухступенчатые уравнения с одной переменной и неравенство правда; и
(C) писать и решать уравнения, используя геометрию концепции, включая сумму углов в треугольнике и угловые отношения.
(12) Измерения и данные. Студент подает заявку стандарты математических процессов для использования статистических представлений для анализа данные. Ожидается:
(A) сравнить две группы числовых данных, используя сравнительные точечные или коробчатые диаграммы путем сравнения их форм, центров и спреды;
(B) использовать данные из случайная выборка, чтобы сделать выводы о совокупности; и
(C) сравнить две популяции на основе данных
в случайных выборках из этих популяций, включая неофициальные сравнительные выводы
о различиях между двумя популяциями.
(13) Личная финансовая грамотность. Студент применяет стандарты математического процесса для развития экономического мышления и решение проблем, полезных в жизни знающего потребителя и инвестора. Ожидается:
(A) рассчитать налог с продаж для данной покупки и рассчитать подоходный налог с заработной платы;
(B) идентифицируют компоненты личного бюджет, включая доходы; запланированные сбережения на колледж, пенсию и чрезвычайные ситуации; налоги; постоянные и переменные расходы, и посчитайте, какой процент каждый категория состоит из общего бюджета;
(C) создание и организация финансовых активов и обязательства записывают и составляют отчет о чистой стоимости активов;
(D) используйте оценщик семейного бюджета для определения минимальный семейный бюджет и средняя почасовая оплата, необходимая семье для удовлетворить свои базовые потребности в студенческом городе или другом крупном городе поблизости;
(E) рассчитать и сравнить простые проценты и доход от сложных процентов; и
(F) анализировать и сравнивать денежные стимулы,
включая продажи, скидки и купоны.
Источник: Положения настоящего стандарта 111.27 приняты для вступления в силу. 10 сентября 2012 г., 37 TexReg 7109.
111,28. 8 класс, принято 2012.
(а) Введение.
(1) Стремление к совершенству в образовании является движущей силой основных знаний и навыков Техаса по математике, руководствуясь стандартами готовности к колледжу и карьере. Встраивая статистику, вероятность и финансы, уделяя особое внимание вычислительному мышлению, математическому свободное владение языком и твердое понимание, Техас будет лидером в области математического образования и подготовить всех студентов Техаса к испытаниям, с которыми они столкнутся в 21-м век.
(2) Стандарты процессов описывают способы, которыми
Ожидается, что студенты будут вовлечены в содержание. Размещение процесса
стандарты в начале знаний и навыков, указанные для каждого класса
и конечно намеренно. Стандарты процессов объединяют другие знания
и навыки вместе, чтобы учащиеся могли успешно решать проблемы и
эффективно и результативно использовать математику в повседневной жизни.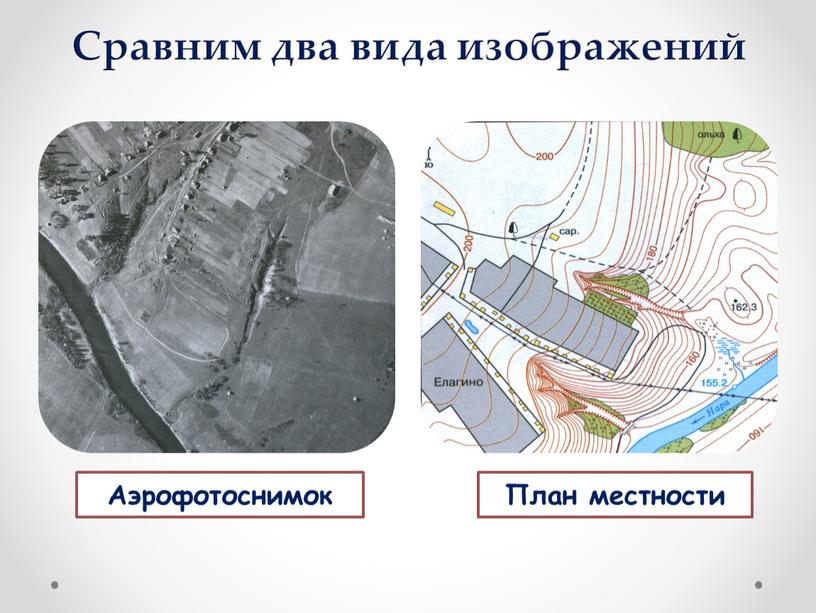 Стандарты процесса
интегрированы в каждый класс и курс.По возможности студенты будут
применять математику к проблемам, возникающим в повседневной жизни, в обществе и на рабочем месте.
Студенты будут использовать модель решения проблем, которая включает анализ заданных
информация, формулирование плана или стратегии, определение решения, обоснование
решение, а также оценка процесса решения проблем и разумности
решения. Студенты выберут соответствующие инструменты, такие как реальные объекты,
манипуляторы, алгоритмы, бумага и карандаш, а также технологии и методы
такие как мысленная математика, оценка, чувство чисел, а также обобщение и абстракция
решать задачи.Студенты будут эффективно передавать математические идеи,
рассуждения и их последствия с использованием нескольких представлений, таких как символы,
диаграммы, графики, компьютерные программы и язык. Студенты будут использовать математические
отношения для выработки решений, установления связей и прогнозов.
Стандарты процесса
интегрированы в каждый класс и курс.По возможности студенты будут
применять математику к проблемам, возникающим в повседневной жизни, в обществе и на рабочем месте.
Студенты будут использовать модель решения проблем, которая включает анализ заданных
информация, формулирование плана или стратегии, определение решения, обоснование
решение, а также оценка процесса решения проблем и разумности
решения. Студенты выберут соответствующие инструменты, такие как реальные объекты,
манипуляторы, алгоритмы, бумага и карандаш, а также технологии и методы
такие как мысленная математика, оценка, чувство чисел, а также обобщение и абстракция
решать задачи.Студенты будут эффективно передавать математические идеи,
рассуждения и их последствия с использованием нескольких представлений, таких как символы,
диаграммы, графики, компьютерные программы и язык. Студенты будут использовать математические
отношения для выработки решений, установления связей и прогнозов. Студенты будут анализировать математические отношения, чтобы общаться и общаться
математические идеи. Студенты будут отображать, объяснять или обосновывать математические
идеи и аргументы с использованием точного математического языка в письменной или устной форме
общение.
Студенты будут анализировать математические отношения, чтобы общаться и общаться
математические идеи. Студенты будут отображать, объяснять или обосновывать математические
идеи и аргументы с использованием точного математического языка в письменной или устной форме
общение.
(3) Основные направления в 8 классе — пропорциональность;
выражения, уравнения, отношения и основы функций; и измерения
и данные. Студенты используют концепции, алгоритмы и свойства действительных чисел
исследовать математические отношения и описывать все более сложные
ситуации. Студенты используют концепции соразмерности для изучения, развития,
и сообщать математические отношения. Студенты используют алгебраическое мышление
чтобы описать, как изменение одной величины в отношениях приводит к изменению
в другом.Студенты соединяют словесные, числовые, графические и символические представления
отношений, включая уравнения и неравенства. Студенты начинают
развить понимание функциональных отношений. Студенты используют геометрические
свойства и отношения, а также пространственные рассуждения для моделирования и анализа
ситуации и решать проблемы. Студенты сообщают информацию о геометрических
цифры или ситуации путем количественной оценки атрибутов, обобщить процедуры из
измерения и использовать процедуры для решения проблем.Ученики
использовать соответствующую статистику, представления данных и рассуждения для рисования
выводы, оценивать аргументы и давать рекомендации. Хотя использование
важны все виды техники, упор на навыки алгебры
требует внедрения графической технологии.
Студенты используют геометрические
свойства и отношения, а также пространственные рассуждения для моделирования и анализа
ситуации и решать проблемы. Студенты сообщают информацию о геометрических
цифры или ситуации путем количественной оценки атрибутов, обобщить процедуры из
измерения и использовать процедуры для решения проблем.Ученики
использовать соответствующую статистику, представления данных и рассуждения для рисования
выводы, оценивать аргументы и давать рекомендации. Хотя использование
важны все виды техники, упор на навыки алгебры
требует внедрения графической технологии.
(4) Заявления, содержащие слово «включая» справочный контент, который необходимо освоить, а те, которые содержат фразу «такие как» предназначены в качестве возможных иллюстративных примеров.
(b) Знания и навыки.
(1) Стандарты математических процессов. Студент
использует математические процессы для получения и демонстрации математического понимания. Ожидается:
Ожидается:
(A) применять математику к возникающим проблемам в повседневной жизни, в обществе и на рабочем месте;
(B) использовать модель решения проблем, которая включает анализ данной информации, формулирование плана или стратегии, определение решение, обоснование решения и оценка процесса решения проблемы и разумности решения;
(C) выберите инструменты, включая реальные объекты, манипуляторы, бумагу и карандаш, и технология и методы, включая мысленную математику, оценку, и чувство числа, если необходимо, чтобы решить проблемы;
(D) передавать математические идеи, рассуждения и их последствия, используя несколько представлений, включая символы, диаграммы, графики и соответствующий язык;
(E) создавать и использовать представления для организации, записывать и передавать математические идеи;
(F) анализировать математические отношения к соединять и передавать математические идеи; и
(G) отображать, объяснять и обосновывать математические идеи и аргументы, используя точные
математический язык в письменном или устном общении.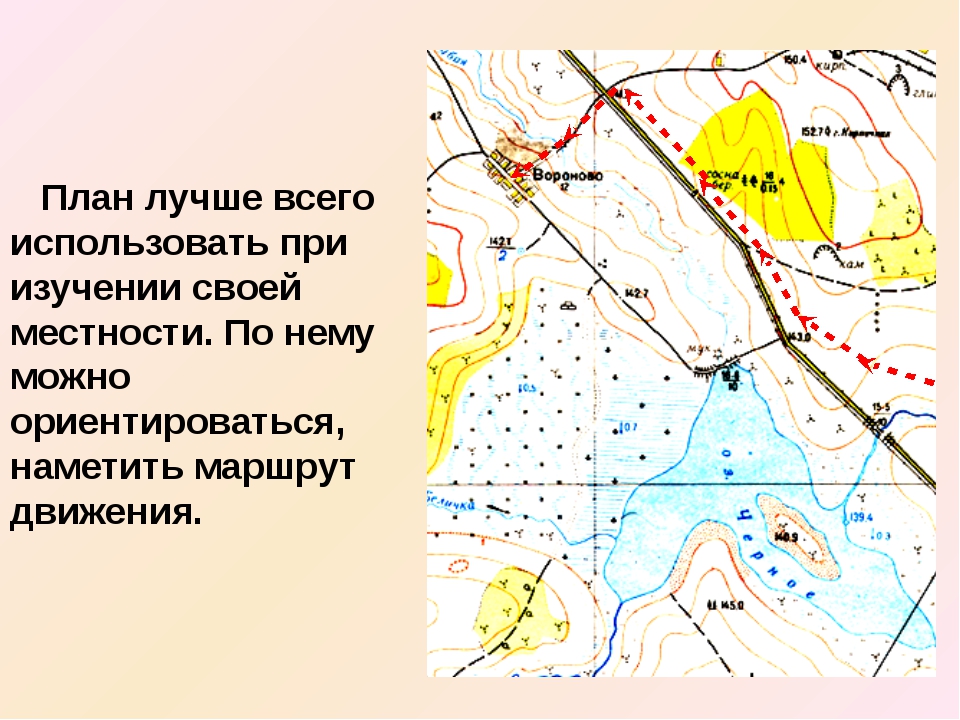
(2) Число и операции. Студент подает заявку стандарты математического процесса для представления и использования действительных чисел в различных форм. Ожидается:
(A) расширить предыдущие знания о множествах и подмножества с использованием визуального представления для описания отношений между наборами действительных чисел;
(B) приблизительное значение иррационального числа, включая π и квадрат корни чисел меньше 225 и расположите это приближение рационального числа на числовой прямой;
(C) преобразование между стандартным десятичным представлением и научная запись; и
(D) заказать набор настоящих числа, возникающие из математических и контексты реального мира.
(3) Пропорциональность. Студент применяет математические стандарты процесса для использования пропорциональных отношений для описания расширений. Ожидается:
(A) обобщают, что отношение соответствующих стороны одинаковых форм пропорциональны, включая форму и ее расширение;
(B) сравнить и сопоставить атрибуты формы и ее расширения (ов) на координатной плоскости; и
(C) использовать алгебраическое представление, чтобы объяснить влияние данного положительного рационального масштабного коэффициента, применяемого к двумерным фигурам, на координату
плоскость с центром в центре расширения.
(4) Пропорциональность. Студент применяет математические стандарты процесса для объяснения пропорциональных и непропорциональных отношений с уклоном. Ожидается:
(A) используйте аналогичные прямоугольные треугольники для построения понимание этого уклона, м, , заданного как скорость, сравнивая изменение в значениях и . к изменению x -значений, (y 2 — y 1 ) / (x 2 — x 1 ), то же самое для любых двух точек (x 1 , y 1 ) и (x 2 , y 2 ) на той же строке;
(B) график пропорциональных отношений, интерпретация единичная ставка как наклон линии, моделирующей взаимосвязь; и
(C) использовать данные из таблицы или графика для определения скорость изменения или наклона и y — перехват в математическом и реальном мире проблемы.
(5) Пропорциональность. Студент применяет математические
стандарты процесса использовать пропорциональные и непропорциональные отношения
разработать основные концепции функций. Ожидается:
Ожидается:
(A) представляют линейно-пропорциональный ситуации с таблицами, графиками и уравнениями в виде y = kx ;
(B) представляют линейные непропорциональные ситуации с таблицами, графики и уравнения в виде y = mx + b , где b ≠ 0;
(C) сопоставьте двумерные наборы данных, которые предполагают линейная связь с двумерными наборами данных, которые не предполагайте линейную зависимость от графического представления;
(D) используйте линию тренда, которая приближается к линейной взаимосвязь между двумерными наборами данных для прогнозирования;
(E) решать проблемы, связанные с прямая вариация;
(F) различать пропорциональные и непропорциональные ситуаций с использованием таблиц, графиков и уравнений в форма y = kx или y = mx + b , где b ≠ 0;
(G) идентифицирует функции, используя наборы упорядоченных пары, таблицы, отображения и графики;
(H) определяет примеры пропорциональных и непропорциональных функций, которые возникают из математических и проблемы реального мира; и
(I) напишите уравнение в форме y = mx + b для моделирования линейной зависимости
между двумя величинами с помощью словесного,
числовые, табличные и графические представления.
(6) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для разработки математических отношения и устанавливать связи с геометрическими формулами. Ожидается студент к:
(A) описывает формулу объема В = Bh цилиндра по площади основания и высоте;
(B) моделирование отношений между объемом цилиндра и конусом, имеющим равные основания и высоту, и соединяют это отношение к формулам; и
(C) используйте модели и схемы для объясните теорему Пифагора.
(7) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса, чтобы использовать геометрию для решения проблемы. Ожидается:
(А) решить задачи, связанные с объемом цилиндров, конусов, и сферы;
(B) использовать предыдущие знания площади поверхности чтобы сделать связи с формулами для боковой и общей площади поверхности и определять решения проблем с прямоугольными призмами, треугольными призмы и цилиндры;
(C) использовать теорему Пифагора и ее обратное решать задачи; и
(D) определить расстояние между двумя точками
на координатной плоскости с помощью теоремы Пифагора.
(8) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для использования уравнений с одной переменной или неравенство в проблемных ситуациях. Ожидается:
(A) напишите уравнения или неравенства с одной переменной с обеих сторон переменных, которые представляют проблемы, используя коэффициенты и константы рациональных чисел;
(B) напишите соответствующую реальную проблему когда задано уравнение с одной переменной или неравенство с переменными с обеих сторон знака равенства с использованием рационального числа коэффициенты и константы;
(C) и решите одну переменную уравнения с переменными по обе стороны от знака равенства, представляющие математические и реальные проблемы с использованием коэффициенты и константы рациональных чисел; и
(D) использовать неофициальные аргументы для установления фактов
о сумме углов и внешнем угле треугольников, углы, созданные при
параллельные прямые пересекаются трансверсалью, а критерий угол-угол для
подобие треугольников.
(9) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для использования нескольких представлений разработать основные концепции одновременных линейных уравнений. Студент ожидается определение и проверка значений x и y , которые одновременно удовлетворяют двум линейным уравнениям вида y = mx + b из пересечения графических уравнений.
(10) Двумерные формы.Студент подает заявку стандарты математических процессов для разработки концепций трансформационной геометрии. Ожидается:
(A) обобщают свойства ориентации и согласованность вращений, отражений, переводов и растяжения двумерных фигур по координате самолет;
(B) различать преобразования сохраняющие конгруэнтность и несоответствующие;
(C) объяснить эффект переводов, отражений по оси x или y , а вращение ограничено значениями 90, 180, 270 и 360, если применимо к двумерным фигурам на координатной плоскости с помощью алгебраической представление; и
(D) моделирует влияние на линейные и площадные измерения
расширенных двумерных форм.
(11) Измерения и данные. Студент подает заявку стандарты математических процессов для использования статистических процедур для описания данных. Ожидается:
(A) построить диаграмму рассеяния и описать наблюдаемые данные для решения таких вопросов ассоциации, как линейные, нелинейные и нет связи между двумерными данными;
(В) определить среднее абсолютное отклонение и используйте эту величину как меру данные о среднем расстоянии взяты от среднего с использованием набора данных не более 10 данных точки; и
(C) моделировать генерацию случайных выборок того же размера из популяции с известными характеристиками для развития понятие случайной выборки, репрезентативной для населения, из которого он был выбран.
(12) Личная финансовая грамотность. Студент
применяет стандарты математического процесса для развития экономического мышления
и решение проблем, полезных в жизни знающего потребителя и инвестора. Ожидается:
Ожидается:
(A) решить реальные проблемы, сравнивая процентная ставка и срок кредита влияют на стоимость кредита;
(B) рассчитать общую стоимость погашения ссуды, включая кредитные карты и легкодоступные ссуды, по различным ставкам проценты и за разные периоды с помощью онлайн-калькулятора;
(C) объясните, как вложены небольшие суммы денег регулярно, включая деньги, откладываемые на учебу и пенсию, со временем растут;
(D) рассчитать и сравнить простые проценты и доход от сложных процентов;
(E) определить и объяснить преимущества и недостатки разных способов оплаты;
(F) анализирует ситуации, чтобы определить, представлять финансово ответственные решения и определять преимущества финансовых ответственность и издержки финансовой безответственности; и
(G) оценка стоимости двухлетнего и четырехлетнего
высшее образование, включая семейный вклад, и периодически сберегать
план по накоплению денег, необходимых для вклада в общую стоимость
посещаемость не менее первого года обучения в колледже.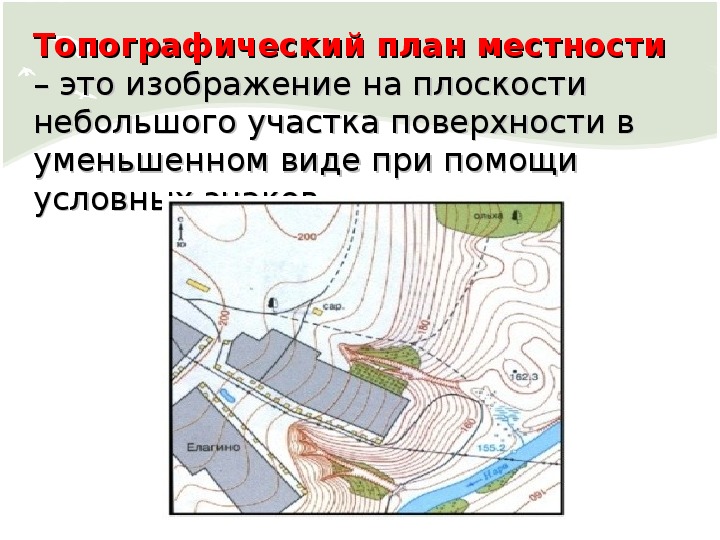
Источник: Положения настоящего стандарта 111.28 приняты для вступления в силу. 10 сентября 2012 г., 37 TexReg 7109.
Для дополнительная информация, электронная почта [email protected].
Средняя учебная программа / Планы и ресурсы по математике для 7-го класса
В 7-м классе учебное время должно быть сосредоточено на четырех важнейших областях: (1) развитие понимания и применение пропорциональных отношений; (2) развитие понимания операций с рациональными числами и работа с выражениями и линейными уравнениями; (3) решение задач, связанных с масштабными чертежами и
неформальных геометрических конструкций, и работа с двух- и трехмерными формами для решения задач, связанных с площадью, площадью поверхности и объемом; и (4) делать выводы о популяциях на основе выборок.
(1) Студенты расширяют свое понимание соотношений и развивают понимание пропорциональности для решения одно- и многоэтапных задач. Учащиеся используют свое понимание соотношений и пропорциональности для решения широкого круга задач, связанных с процентами, включая те, которые связаны со скидками, процентами, налогами, чаевыми и увеличением или уменьшением процентов
Учащиеся используют свое понимание соотношений и пропорциональности для решения широкого круга задач, связанных с процентами, включая те, которые связаны со скидками, процентами, налогами, чаевыми и увеличением или уменьшением процентов
. Учащиеся решают задачи о масштабных чертежах, соотнося соответствующие длины между объектами или используя тот факт, что отношения длин внутри объекта сохраняются в подобных объектах.Учащиеся составляют график пропорциональных соотношений и неформально понимают единичную ставку как меру
крутизны соответствующей линии, называемой наклоном. Они отличают пропорциональные отношения от других отношений.
(2) Учащиеся развивают единое понимание чисел, распознавая дроби, десятичные дроби (которые имеют конечное или повторяющееся десятичное представление) и проценты как различные представления рациональных чисел. Студенты расширяют сложение, вычитание, умножение и деление на все рациональные числа, сохраняя свойства операций и отношения между сложением и вычитанием, умножением и делением.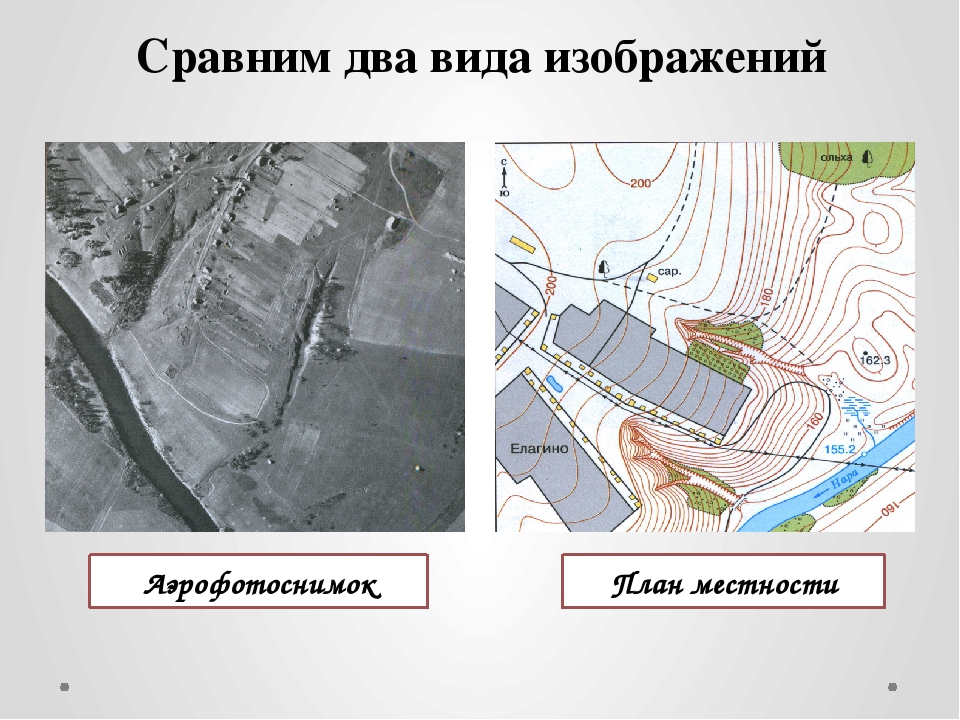 Применяя эти свойства и рассматривая отрицательные числа с точки зрения повседневных контекстов (например, суммы задолженности или температуры ниже нуля), студенты объясняют и интерпретируют правила сложения, вычитания, умножения и деления с отрицательными числами. Они используют арифметику рациональных чисел, когда формулируют выражения и уравнения с одной переменной и используют эти уравнения для решения задач.
Применяя эти свойства и рассматривая отрицательные числа с точки зрения повседневных контекстов (например, суммы задолженности или температуры ниже нуля), студенты объясняют и интерпретируют правила сложения, вычитания, умножения и деления с отрицательными числами. Они используют арифметику рациональных чисел, когда формулируют выражения и уравнения с одной переменной и используют эти уравнения для решения задач.
(3) Ученики продолжают свою работу с площадью с 6 класса, решая задачи, связанные с площадью и окружностью круга и площадью поверхности трехмерных объектов.При подготовке к работе над соответствием и сходством в 8 классе они рассуждают о взаимосвязях между двумерными фигурами, используя масштабные чертежи и неформальные геометрические конструкции, и они знакомятся с отношениями
между углами, образованными пересекающимися линиями. Студенты работают с трехмерными фигурами, связывая их с двухмерными фигурами, исследуя поперечные сечения. Они решают реальные и математические задачи, касающиеся площади, площади поверхности и объема двух- и трехмерных объектов
, состоящих из треугольников, четырехугольников, многоугольников, кубов и прямых призм.

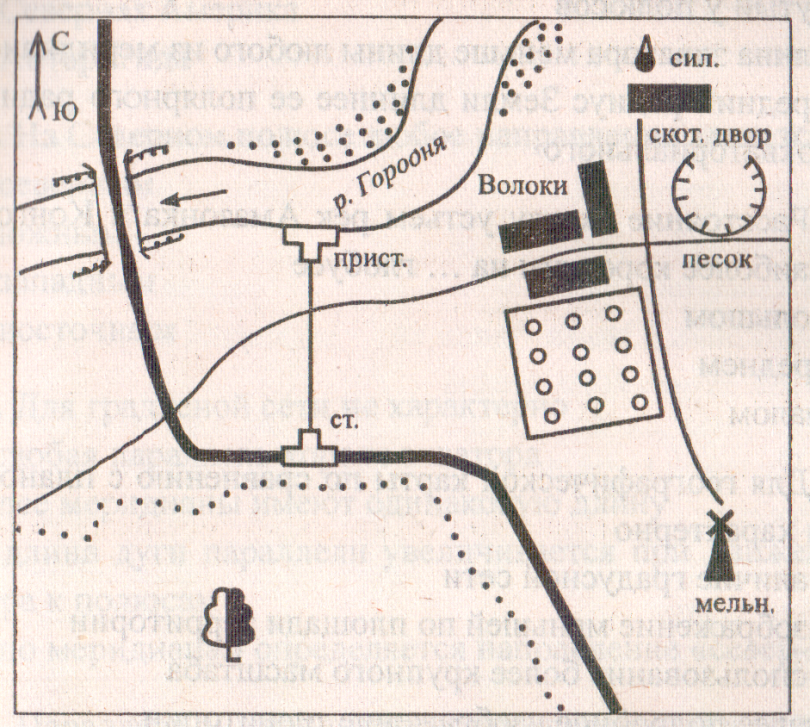


 Объекты более похожи на их реальный вид на местности
Объекты более похожи на их реальный вид на местности
 Расстояние по прямой от железнодорожной станции до холма с отметкой высоты 154,4 м равно 440 м. Длина участка реки Тихая, изображённого на плане, равна 640 м.
Расстояние по прямой от железнодорожной станции до холма с отметкой высоты 154,4 м равно 440 м. Длина участка реки Тихая, изображённого на плане, равна 640 м.
 Кроме того, это место находится на пересечении дорог, ведущих из соседних населённых пунктов. То есть жителям окрестных деревень и поселков будет легко добраться до нового футбольного поля.
Кроме того, это место находится на пересечении дорог, ведущих из соседних населённых пунктов. То есть жителям окрестных деревень и поселков будет легко добраться до нового футбольного поля. Если да, то каков масштабный коэффициент?
Если да, то каков масштабный коэффициент? Пример ответа: прямоугольный треугольник с длиной стороны 12, 15 и 19,2 единицы будет масштабированной копией исходного треугольника с коэффициентом масштабирования 3.
Пример ответа: прямоугольный треугольник с длиной стороны 12, 15 и 19,2 единицы будет масштабированной копией исходного треугольника с коэффициентом масштабирования 3.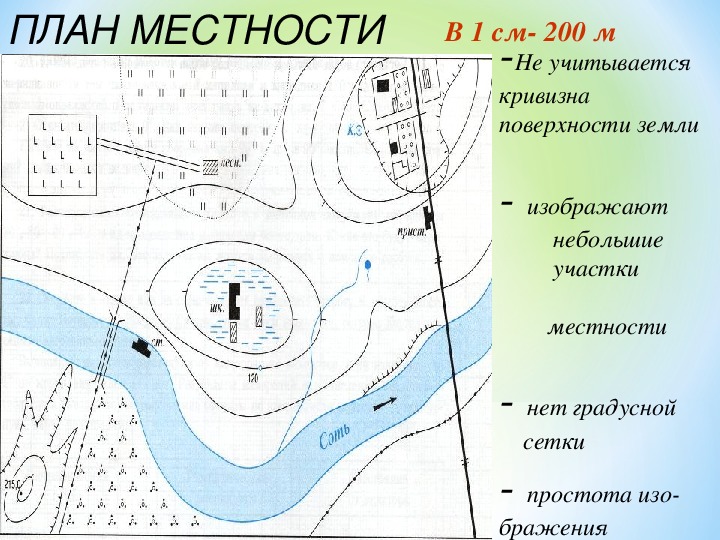 Длина класса 33 фута, потому что 512⋅6 = 5⋅6 + 12⋅6 = 30 + 3 = 33.
Длина класса 33 фута, потому что 512⋅6 = 5⋅6 + 12⋅6 = 30 + 3 = 33.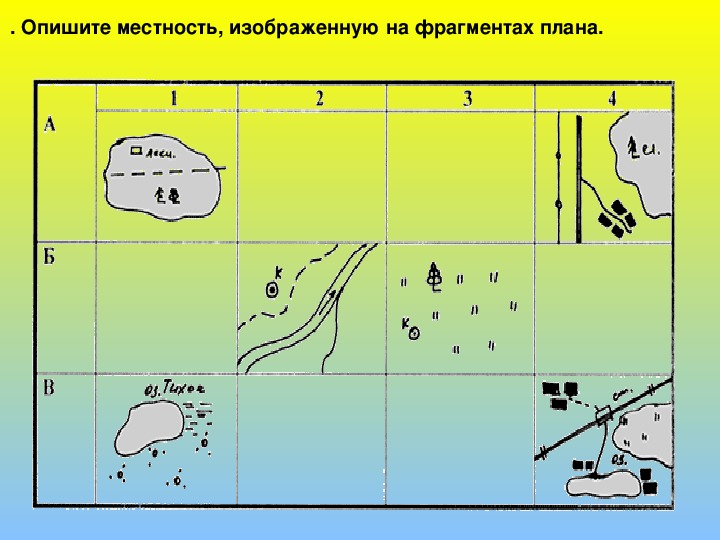
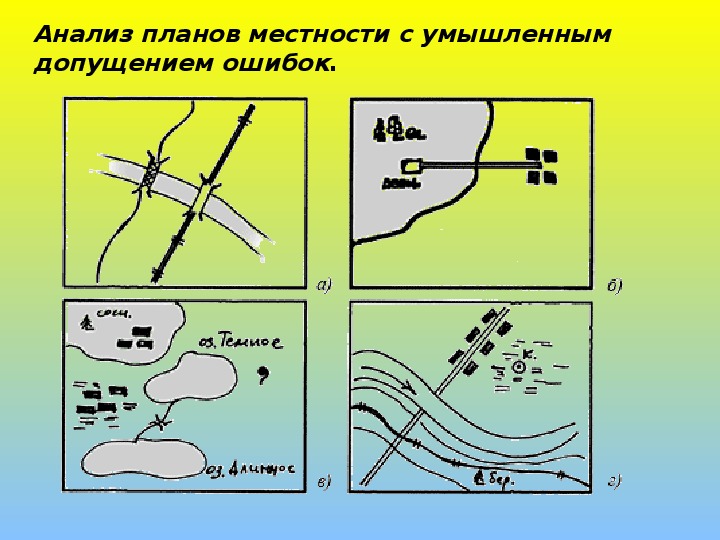
 Здесь легче всего придумать
база находится на «вершине».
Здесь легче всего придумать
база находится на «вершине».  Это
может быть любая из сторон!
Это
может быть любая из сторон!