Построение прямых углов на местности сообщение: Ошибка 404 — Запрашиваемая страница на сайте отсутствует. — kontakt-keramika.ru

Содержание

Построение прямых углов на местности. 5-й класс

Цели урока:

познакомить учащихся с принципом построения прямых углов на местности, применяемым в Древнем Египте;
развивать творческую самостоятельность мышления школьников и познавательный интерес к истории развития математики;
воспитывать добросовестное отношение к коллективной деятельности и умение работать в группе.

Оборудование: веревка длиной 10-14 м, деревянные колышки, молоток (для каждой группы).

Ход урока

1. Организационный момент, инструктаж.

2. Беседа об истории развития математики.

3. Работа в группах.

4. Защита своей работы.

5. Итоги урока.

Практическую работу лучше выполнять в школьном дворе, на свободной площади, например, на спортивной грунтовой площадке. Ребята заранее разбиты на группы по 5 человек и предупреждены о том, что нужно принести на урок. Проводится инструктаж об осторожном обращении с молотком. Желательно проводить работу в конце учебного года.

После инструктажа — беседа о том, как строились прямые углы на местности в Древнем Египте.

— Ребята, что вы знаете о Древнем Египте? Каким основным видом деятельности занимались жители? Чем это было обусловлено? (Земледелие, плодородные земли из-за разлива Нила).

Из истории известно, что примерно 4000 лет назад в долине реки Нил образовалось государство Египет. Правители этого государства — фараоны установили налоги за земельные участки на тех, кто ими пользовался. В связи с этим требовалось определять размеры площадей участков четырехугольной и треугольной формы. Река Нил после дождей разливалась и часто меняла свое русло, смывая границы участков. Приходилось исчезнувшие после наводнения границы участков восстанавливать, а после этого вновь измерять их.

Выполняли эту работу люди, которые умели измерять площади фигур. Появилась необходимость изучить приемы измерения площадей. К этому времени и относят зарождение геометрии. Слово «геометрия» состоит из двух слов: «гео» , что в переводе на русский язык означает земля, и «метрио» — мерю. Значит, в переводе «геометрия» означает землемерие. В своем дальнейшем развитии наука геометрия шагнула далеко за пределы землемерия и стала важным и большим разделом математики.

О зарождении геометрии в Древнем Египте крупнейший древнегреческий историк Геродот (V век до н. э.) написал: «Сезоострис, египетский фараон, разделил землю, дав каждому египтянину участок по жребию и взымал соответствующим образом налог с каждого участка. Случалось, что Нил заливал тот или иной участок, тогда пострадавший обращался к царю, а царь посылал землемеров, чтобы установить, на сколько уменьшился участок, и уменьшал налог. Так возникла геометрия в Египте, а оттуда перешла в Грецию».

Решения задач на вычисление площадей земельных участков содержится в египетских папирусах, в вавилонских клинописных табличках, в древнекитайских трактатах и других памятниках древности.

— Жителям приходилось каждый раз после разлива восстанавливать границы земельных участков. К тому же нужно было разбивать участки так, чтобы легче считать площадь.

Проще всего находить площадь участков в форме какой фигуры? (прямоугольника). Для этого было важным делом умение строить прямые углы на местности. Ученые того времени уже знали, что треугольник со сторонами 3, 4, 5 имеет прямой угол. Такой треугольник до сих пор называют египетским. Как вы думаете, как с помощью веревки и колышек построить такой треугольник на местности? (Группам дается 5 мин для совещания).

Если ни одна из групп не догадается, учитель дает подсказку о периметре треугольника.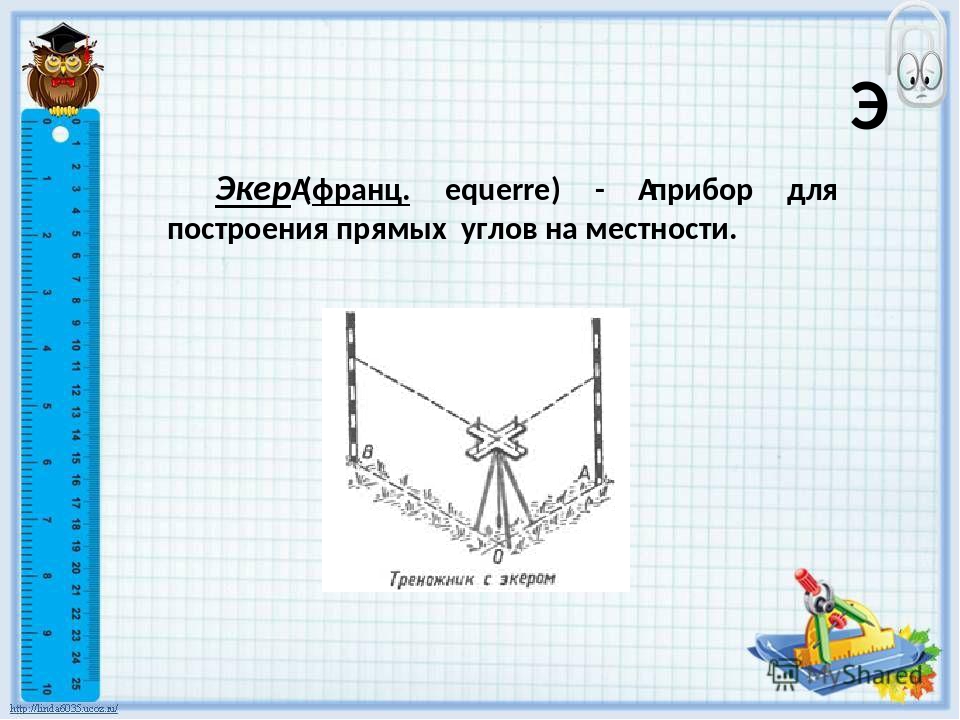

После того, как группы поняли принцип построения, ребята приступают к работе.

Принцип построения: веревка узлами делится на 12 равных частей и соединяются узлом начало и конец веревки. Колышком закрепляется один из узлов, отсчитывается сторона длиной в 3 отрезка, забивается следующий колышек и так же строится сторона длиной в 4 отрезка, веревка натягивается. По контуру веревки проводятся по земле отрезки. Получился египетский треугольник с прямым углом. Чтобы получить прямоугольник, нужно таким же образом достроить треугольник с общей стороной в 5 отрезков.

После построения ребята защищают свою работу, показывая построение.

Подводятся итоги, выставляются отметки, учитывая аккуратность и слаженность работы в группе, участие в беседе о Древнем Египте.

Если останется время, можно рассказать о теореме Пифагора и пифагоровых тройках чисел.

Тогда домашним заданием будет подбор троек натуральных чисел а, в и с, для которых с²= а²

+в².

Литература.

Г.И.Глейзер. История математики в школе: IV — VI классы. Пособие для учителей. — М.: Просвещение, 1981. — 239 с., ил.

Эккер и построение прямых углов на местности

Разбивка главных точек кривой. Закрепив на местности вершину угла и предшествующие ему пикеты, закрепляют главные точки кривой.

Середину кривой СК закрепляют, отложив от ВУ по направлению биссектрисы отрезок, равный Б (или Б_с).

На новом после вершины угла направлении трассы откладывают величину домера, после чего продолжают разбивку пикетажа. Обеим точкам домера (его началу и концу) присваивают одно и то же пикетажное наименование, благодаря чему пикетаж точки КК совпадает с пикетажем, считаемым по кривой.

Положение начала кривой НК и конца кривой КК определяют, используя разбитый пикетаж. Например, если ПК НК = 5 + 39,27, то от пикета № 5 откладывают вперёд 39,27 м и здесь колышком и сторожком закрепляют точку НК.

Детальная разбивка кривых. При детальной разбивке кривую закрепляют на местности через 10 или 20 м, применяя разные способы.

Способ ординат от касательной для круговой кривой

. Для каждой точки i (рис. 15.7, а), задавая расстояние k от начала кривой, вычисляют ее координаты:

x = R sinj; y = R (1 – cosj). (15.10)

Здесь угол j выражен в радианах и равен j = k/R.

Разбивку кривой ведут от ее начала и от конца к середине. Мерной лентой по оси x откладывают длину кривой k, от полученной точки отступают назад на величину k–x и здесь строят перпендикуляр – ординату y. Значения k–x и y обычно выбирают из таблиц для разбивки кривых.

а) б) в)

Рис. 15.7 Детальная разбивка кривых:

а – способом ординат от касательной для круговой кривой;

б – то же, для переходной и следующей за ней круговой кривой;

в – разбивка кривой электронным тахеометром

Способ ординат от касательной для переходной и следующей за ней круговой кривой (рис. 15.7, б). Для точек, расположенных в пределах переходной кривой, то есть при k £ l, координаты x, y вычисляют по формулам (15.8) и (15.9), принимая s = k. Для точек i, расположенных на круговой кривой, где k > l, вычисления выполняют по формулам:

l =

k – l; d = l/R; j = b + d;

x = m + R sinj; y = p + R (1 — cosj). (15.11)

Действия при разбивке кривой на местности аналогичны тем, что выполняют при разбивке круговой кривой.

Разбивка кривой с помощью электронного тахеометра. Выбирают на местности такую точку T (рис. 15.7, в), где обеспечена видимость точек будущей кривой и ее начала НК. В точке НК измеряют угол g и расстояние d. Вычисляют координаты точки Т:

x_T = d cosg; y

T = d sing.

По приведенным выше формулам вычисляют координаты точек кривой x_i, y_i (i = 1, 2, …).

Электронный тахеометр устанавливают в точке Т. Зная координаты точек Т, НК и i, вычисляют разбивочные элементы — углы b_i и расстояния d_i. Построив тахеометром вычисленные углы и расстояния, находят и закрепляют положение точек кривой на местности.

При выращивании сельскохозяйственных культур возникает необходимость проводить на местности линии под углом 90° (при квадратно-гнездовом способе посадки растений, при строгом соблюдении параллельности рядов и т.д.), чтобы облегчить работу сельскохозяйственной техники. Разбивка прямых углов на местности производится эккером. Эккеры бывают призменные, коробчатые, двухзеркальные и др.; применяются они также при съемке небольших участков местности с помощью мерной ленты или рулетки.

Работа двухзеркального эккера основана на принципе дважды отраженного от зеркала луча, составляющего со своим начальным направлением угол, в два раза больший угла между зеркалами.

С помощью эккера, использовав дополнительно ленты, эклиметр и рулетку в условиях производства, можно разбивать на местности территорию на отдельные прямоугольные участки (загонки) для выполнения технологических сельскохозяйственных работ; делать съемку небольшого участка местности и составлять на него план, схему.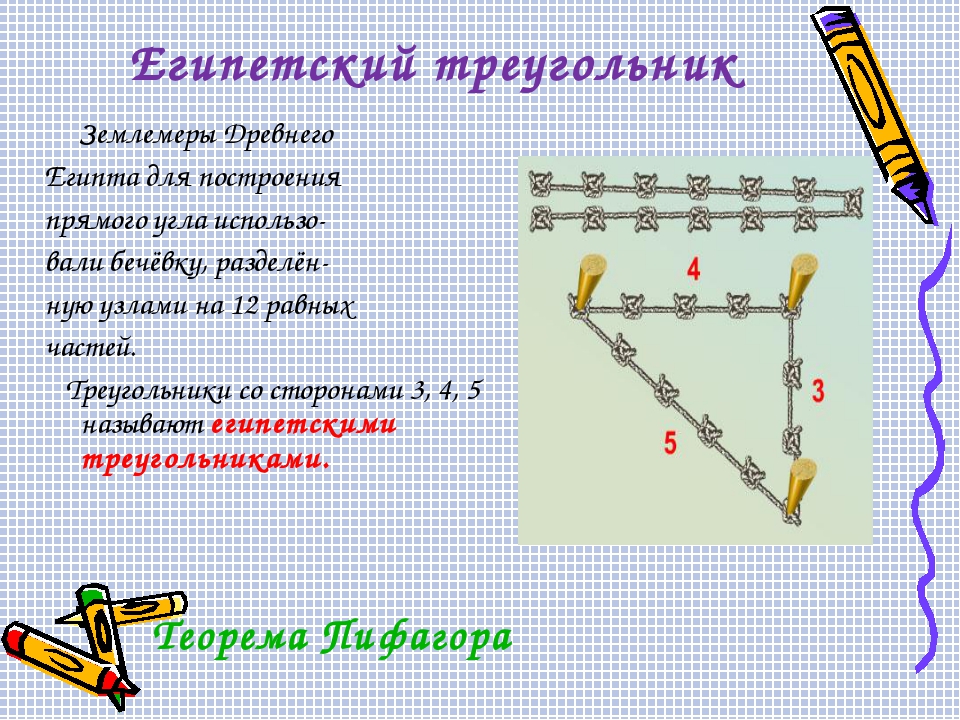

Точность построения угла эккером составляет 5—10′.

Съемка участка местности эккером и мерной лентой (рулеткой) проводится путем создания основы (опоры) для привязки и составления плана (схемы) в заданном масштабе. Наиболее распространенные способы съемки эккером и лентой: способ прямоугольных координат; способ обхода; способ разбивки участка на треугольники.

Способ обхода заключается в получении данных измерений недоступного участка, когда трудно проложить магистральный ход. Опираясь н!а ориентированную по румбам линию или используя естественный ру-брж (направление), эккер и ленту, методом построения прямых углов и в о оставления перпендикуляров определяем отдельные точки недоступного контура.

На основе полученного абриса описанным выше способом составляется план участка.

Сближение меридианов. Переход от геодезического азимута к дирекционному углу. Сближение меридианов у (гамма) — это угол в данной точке между ее меридианом и линией, параллельной оси абсцисс или осевому меридиану (рис.1). Направлению геодезического меридиана на топографической карте соответствуют боковые стороны ее рамки, а также прямые линии, которые можно провести между одноименными минутными делениями долгот. Счет сближения меридианов ведется от геодезического меридиана. Сближение меридианов считается положительным, если северное направление оси абсцисс отклонено к востоку от геодезического меридиана (рис.1), и отрицательным, если это направление отклонено к западу. Величина сближения меридианов, указанная на топографической карте в левом нижнем углу, относится к центру листа карты. При необходимости величину сближения меридианов можно вычислить по формуле:

где L — долгота данной точки; Lо — долгота осевого меридиана зоны, в которой расположена точка; В — широта данной точки.

Широту и долготу точки определяют по карте с точностью до 30′, а долготу осевого меридиана зоны рассчитывают по формуле:

Сближение меридианов равно нулю, если точка находится на осевом меридиане зоны или на экваторе. Для любой точки в пределах одной координатной шестиградусной зоны сближение меридианов по абсолютной величине не превышает 3°.

Геометрия. 7 — 9 классы. Атанасян Л.С. и др.

ОГЛАВЛЕНИЕ

Дорогие семиклассники! 3
Глава I Начальные геометрические сведения 5
§ 1. Прямая и отрезок —
1. Точки, прямые, отрезки —
2. Провешивание прямой на местности 6
Практические задания 7
§ 2. Луч и угол 8
3. Луч —
4. Угол —
Практические задания 10
§ 3. Сравнение отрезков и углов —
5. Равенство геометрических фигур —
6. Сравнение отрезков и углов 11
Задачи 12
§ 4. Измерение отрезков 13
7. Длина отрезка —
8. Единицы измерения. Измерительные инструменты 15
Практические задания 16
Задачи 17
§ 5. Измерение углов 18
9. Градусная мера угла —
10. Измерение углов на местности 19
Практические задания 20
Задачи 21
§ 6. Перпендикулярные прямые 22
11. Смежные и вертикальные углы —
12. Перпендикулярные прямые —
13. Построение прямых углов на местности 23
Практические задания 24
Задачи —
Вопросы для повторения к главе I 25
Дополнительные задачи 26
Глава II Треугольники 28
§ 1. Первый признак равенства треугольников —
14. Треугольник —
15. Первый признак равенства треугольников 29
Практические задания 30
Задачи 31
§ 2. Медианы, биссектрисы и высоты треугольника 32
16. Перпендикуляр к прямой —
17. Медианы, биссектрисы и высоты треугольника 33
18. Свойства равнобедренного треугольника 34
Практические задания 36
Задачи —
§ 3. Второй и третий признаки равенства треугольников 37
19. Второй признак равенства треугольников —
20. Третий признак равенства треугольников 38
Задачи 40
§ 4. Задачи на построение 42
21. Окружность —
22. Построения циркулем и линейкой 43
23. Примеры задач на построение 44
Задачи 47
Вопросы для повторения к главе II 48
Дополнительные задачи 49
Глава III Параллельные прямые 52
§ 1.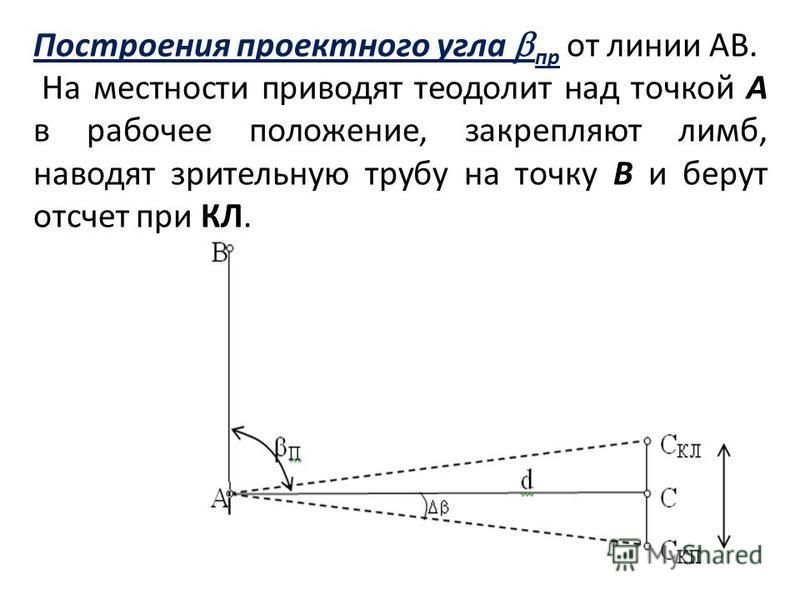 Признаки параллельности двух прямых —
24. Определение параллельных прямых —
25. Признаки параллельности двух прямых 53
26. Практические способы построения параллельных прямых 55
Задачи 56
§ 2. Аксиома параллельных прямых 57
27. Об аксиомах геометрии —
28. Аксиома параллельных прямых 58
29. Теоремы об углах, образованных двумя параллельными прямыми и секущей 60
30. Углы с соответственно параллельными или перпендикулярными сторонами 63
Задачи 65
Вопросы для повторения к главе III 66
Дополнительные задачи 67
Глава IV Соотношения между сторонами и углами треугольника 69
§ 1. Сумма углов треугольника —
31. Теорема о сумме углов треугольника —
32. Остроугольный, прямоугольный и тупоугольный треугольники 70
Задачи —
§ 2. Соотношения между сторонами и углами треугольника 71
33. Теорема о соотношениях между сторонами и углами треугольника —
34. Неравенство треугольника 73
Задачи —
§ 3. Прямоугольные треугольники 75
35. Некоторые свойства прямоугольных треугольников —
36. Признаки равенства прямоугольных треугольников 76
37. Уголковый отражатель 78
Задачи 79
§ 4. Построение треугольника по трём элементам 81
38. Расстояние от точки до прямой. Расстояние между параллельными прямыми —
39. Построение треугольника по трём элементам 83
Задачи 85
Вопросы для повторения к главе IV 88
Дополнительные задачи 89
Задачи повышенной трудности 92
Задачи к главе I —
Задачи к главе II —
Задачи к главам III и IV 93
Глава V Четырёхугольники 97
§ 1. Многоугольники —
40. Многоугольник —
41. Выпуклый многоугольник 98
42. Четырёхугольник 99
Задачи 100
§ 2. Параллелограмм и трапеция —
43. Параллелограмм —
44. Признаки параллелограмма 101
45. Трапеция 103
Задачи —
§ 3. Прямоугольник, ромб, квадрат 108
46. Прямоугольник —
47. Ромб и квадрат 109
48. Осевая и центральная симметрии 110
Задачи 112
Вопросы для повторения к главе V 113
Дополнительные задачи 114
Глава VI Площадь 116
§ 1. Площадь многоугольника —
49. Понятие площади многоугольника —
50. Площадь квадрата 119
51. Площадь прямоугольника 121
Задачи —
§ 2. Площади параллелограмма, треугольника и трапеции 122
52. Площадь параллелограмма —
53. Площадь треугольника 123
54. Площадь трапеции 125
Задачи 126
§ 3. Теорема Пифагора 128
55. Теорема Пифагора —
56. Теорема, обратная теореме Пифагора 129
57. Формула Герона 130
Задачи 132
Вопросы для повторения к главе VI 133
Дополнительные задачи 134
Глава VII Подобные треугольники 137
§ 1. Определение подобных треугольников —
58. Пропорциональные отрезки —
59. Определение подобных треугольников 138
60. Отношение площадей подобных треугольников 139
Задачи —
§ 2. Признаки подобия треугольников 141
61. Первый признак подобия треугольников —
62. Второй признак подобия треугольников 142
63. Третий признак подобия треугольников 143
Задачи —
§ 3. Применение подобия к доказательству теорем и решению задач 145
64. Средняя линия треугольника —
65. Пропорциональные отрезки в прямоугольном треугольнике 146
66. Практические приложения подобия треугольников 148
67. О подобии произвольных фигур 150
Задачи 152
§ 4. Соотношения между сторонами и углами прямоугольного треугольника 154
68. Синус, косинус и тангенс острого угла прямоугольного треугольника —
69. Значения синуса, косинуса и тангенса для углов 30°, 45° и 60° 156
Задачи 157
Вопросы для повторения к главе VII 158
Дополнительные задачи 159
Глава VIII Окружность 162
§ 1. Касательная к окружности —
70. Взаимное расположение прямой и окружности —
71. Касательная к окружности 164
Задачи 166
§ 2. Центральные и вписанные углы 167
72. Градусная мера дуги окружности —
73. Теорема о вписанном угле 168
Задачи 170
§ 3. Четыре замечательные точки треугольника 173
74. Свойства биссектрисы угла —
75. Свойства серединного перпендикуляра к отрезку 174
76. Теорема о пересечении высот треугольника 176
Задачи 177
§ 4. Вписанная и описанная окружности 178
77. Вписанная окружность —
78. Описанная окружность 181
Задачи 182
Вопросы для повторения к главе VIII 184
Дополнительные задачи 185
Глава IX Векторы 189
§ 1. Понятие вектора —
79. Понятие вектора —
80. Равенство векторов 191
81. Откладывание вектора от данной точки 192
Практические задания 193
Задачи 194
§ 2. Сложение и вычитание векторов 195
82. Сумма двух векторов —
83. Законы сложения векторов. Правило параллелограмма 196
84. Сумма нескольких векторов 197
85. Вычитание векторов 198
Практические задания 200
Задачи —
§ 3. Умножение вектора на число. Применение векторов к решению задач 202
86. Произведение вектора на число —
87. Применение векторов к решению задач 204
88. Средняя линия трапеции 205
Практические задания 206
Задачи —
Вопросы для повторения к главе IX 208
Дополнительные задачи 209
Задачи повышенной трудности 211
Задачи к главе V —
Задачи к главе VI 212
Задачи к главе VII 214
Задачи к главе VIII 217
Задачи к главе IX 219
Глава X Метод координат 222
§ 1. Координаты вектора —
89. Разложение вектора по двум неколлинеарным векторам —
90. Координаты вектора 224
Задачи 227
§ 2. Простейшие задачи в координатах 228
91. Связь между координатами вектора и координатами его начала и конца —
92. Простейшие задачи в координатах 230
Задачи 231
§ 3. Уравнения окружности и прямой 235
93. Уравнение линии на плоскости —
94. Уравнение окружности 236
95. Уравнение прямой 237
96. Взаимное расположение двух окружностей 238
Задачи 240
Вопросы для повторения к главе X 244
Дополнительные задачи 245
Глава XI Соотношения между сторонами и углами треугольника. Скалярное произведение векторов 248
§ 1. Синус, косинус, тангенс, котангенс угла —
97. Синус, косинус, тангенс, котангенс —
98. Основное тригонометрическое тождество. Формулы приведения 250
99. Формулы для вычисления координат точки —
Задачи 251
§ 2. Соотношения между сторонами и углами треугольника 252
100. Теорема о площади треугольника —
101. Теорема синусов —
102. Теорема косинусов 253
103. Решение треугольников 254
104. Измерительные работы 256
Задачи 257
§ 3. Скалярное произведение векторов 259
105. Угол между векторами —
106. Скалярное произведение векторов 260
107. Скалярное произведение в координатах 261
108. Свойства скалярного произведения векторов 263
Задачи 264
Вопросы для повторения к главе XI 266
Дополнительные задачи 267
Глава XII Длина окружности и площадь круга 270
§ 1. Правильные многоугольники —
109. Правильный многоугольник —
110. Окружность, описанная около правильного многоугольника —
111. Окружность, вписанная в правильный многоугольник 271
112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности 273
113. Построение правильных многоугольников 274
Задачи 276
§ 2. Длина окружности и площадь круга 278
114. Длина окружности —
115. Площадь круга 280
116. Площадь кругового сектора 281
Задачи 282
Вопросы для повторения к главе XII 284
Дополнительные задачи 285
Глава XIII Движения 287
§ 1. Понятие движения —
117. Отображение плоскости на себя —
118. Понятие движения 288
119. Наложения и движения 290
Задачи 292
§ 2. Параллельный перенос и поворот 294
120. Параллельный перенос —
121. Поворот —
Задачи 295
Вопросы для повторения к главе XIII 297
Дополнительные задачи —
Глава XIV Начальные сведения из стереометрии 300
§ 1. Многогранники —
122. Предмет стереометрии —
123. Многогранник 302
124. Призма 303
125. Параллелепипед 305
126. Объём тела 306
127. Свойства прямоугольного параллелепипеда 308
128. Пирамида 311
Задачи 313
§ 2. Тела и поверхности вращения 319
129. Цилиндр —
130. Конус 320
131. Сфера и шар 322
Задачи 323
Вопросы для повторения к главе XIV 327
Дополнительные задачи 328
Задачи повышенной трудности 330
Задачи к главе X —
Задачи к главе XI 331
Задачи к главе XII 332
Задачи к главе XIII 333
Задачи к главе XIV 334
Исследовательские задачи 335
Темы рефератов 336
Приложения
1. Об аксиомах планиметрии 337
2. Некоторые сведения о развитии геометрии 341
Ответы и указания 345
Предметный указатель 368
Список литературы 374

Учебник содержит 14 глав и 2 приложения, посвященные аксиомам геометрии и истории ее развития. В изложении материала учебника сочетаются наглядность и строгая логика. Основные геометрические понятия вводятся на основе наглядных представлений, что делает учебник доступным для самостоятельного изучения школьниками. Последовательность изложения различных разделов геометрии в данном учебнике отличается от других учебников. Так, например, достаточно рано (в 8 классе) вводится понятие площади многоугольника (вполне доступное и понятное школьникам). Это обеспечивает ряд методических преимуществ в построении курса планиметрии. В учебнике содержится богатый задачный материал. Общее число задач 1310. Большая их часть предлагается непосредственно после параграфов (это основные задачи). Среди них есть задачи всех типов — на вычисление, на доказательство, на построение, причем задачи на построение с помощью циркуля и линейки, играющие важную роль в изучении геометрии, появляются уже в середине 7 класса. Наряду с основными задачами в конце каждой главы даны дополнительные (комплексные) задачи, которые важны для понимания красоты геометрии, для развития эвристического и логического мышления учащихся. Эти задачи, как и задачи повышенной трудности по каждому классу, дают возможность учителю организовать индивидуальную работу с учениками, проявляющими особый интерес к геометрии, развить и повысить этот интерес. Среди задач повышенной трудности содержатся такие известные задачи, дополняющие школьный курс планиметрии, как задачи об окружности и прямой Эйлера, об окружностях Аполлония, теорема Птолемея и т.д. Ко всем задачам даны ответы, а к наиболее трудным задачам также и указания по их решению. Последняя глава учебника является введением в стереометрию, она знакомит учащихся с основными телами и поверхностями, формулами для вычисления их объемов и площадей.

Геометрия в геодезии

Зизень В.С. 1

1ГБПОУ ЛО «Мичуринский многопрофильный техникум»

Каштанова М.С. 1Романенко Е.О. 1

1ГБПОУ ЛО «Мичуринский многопрофильный техникум»

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

«Геодезия относится к числу прикладных математических наук, геодезию и называют иногда практическою геометриею» – С.М. Соловьев (1914 г.)

Для практических целей часто возникает необходимость производить геометрические построения на местности. Такие построения нужны и при строительстве зданий, и при прокладке дорог, и при различных измерениях объектов на местности. Можно подумать, что работа на ровной поверхности земли ничем, по существу, не отличается от работы циркулем и линейкой на обыкновенном листе бумаги. Это не совсем так. Ведь на бумаге циркулем мы можем проводить любые окружности или их дуги, а линейкой — любые прямые. На местности же, где расстояния между точками довольно велики, для подобных действий понадобилась бы длинная веревка или огромная линейка, которые не всегда имеются под руками. Да и вообще чертить прямо на земле, какие бы то ни было линии-дуги или прямые — представляется весьма затруднительным. Таким образом, построения на местности имеют свою специфику.

Ещё на уроках математики я узнала, что существует наука, которая занимается измерениями и построениями на местности — геодезия. Я заинтересовалась ею. Появилась гипотеза: если использовать знания о свойствах геометрических фигур, то можно решить практические задачи на местности.

Очень часто можно услышать такие высказывания: «Зачем нужно изучать математику, решать задачи? Где мне это пригодится?» Изучение математики развивает логическое мышление, приучает человека к точности, к умению видеть главное, сообщает необходимые сведения для понимания сложных задач, возникающих в различных областях деятельности современного человека.

Актуальность моего исследовательского проекта заключается в том, что наука геодезия не может развиваться без геометрии.

Плотное отношение между геодезией и геометрией показывает слово «геометрия», которое в переводе с греческого означает «землеизмерение».

Геодезия и геометрия долго взаимно дополняют и развивают друг друга. Развитию и совершенствованию методов геодезических работ способствовали научные достижения в области математики, физики, инструментальной техники. Для практических целей часто возникает необходимость производить геометрические построения на местности. Такие построения нужны и при строительстве зданий, и при прокладке дорог, и при различных измерениях объектов на местности, и при разведках месторождений полезных ископаемых. Геодезические работы ведутся при планировке, озеленении и благоустройстве городов и рабочих поселков. Осушение и орошение земель, лесоустройство требуют применения геодезии. Большую роль геодезия играет и в военном деле. «Карта — глаза армии». Карта используется для изучения местности, для отражения на ней боевой обстановки, для разработки боевых операций и т.д.

Цель исследовательского проекта: узнать, какова связь между геометрией и геодезией и каковы различия.

Для реализации поставленной цели я определил следующие задачи:

Изучить математическую литературу по данной теме;

ознакомиться с приборами для измерения на местности;

подобрать теоретический и практический материал, позволяющий продемонстрировать приложение геометрических фактов к решению задач;

применить полученные знания на практике.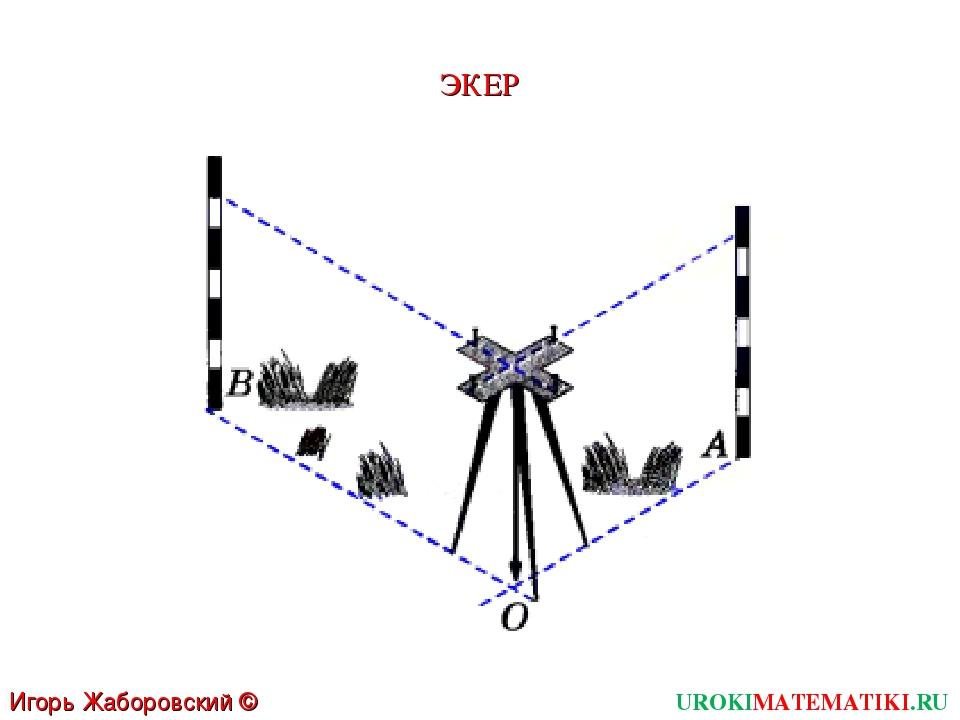

Объектом моих наблюдений стали:

Определение высоты предмета.

Определение расстояния до недоступной точки.

Методы исследования: Находить нужную литературу, обрабатывать информацию, выполнять и оформлять научно-исследовательскую работу с применением проектной технологии. Основной метод, который использовался в работе, — это метод систематизации и обработки данных.

Основная часть. Геометрия в геодезии

1.Что такое геодезия

Геодезия — наука о производстве измерений на местности, определении фигуры и размеров Земли и изображении земной поверхности в виде планов и карт. «Геодезия» — слово греческое и в переводе на русский язык означает «землеразделение». Название предмета показывает, что геодезия как наука возникла из практических потребностей человека. С развитием фотографии и особенно авиации стали широко применять для создания планов и карт фотоснимки земной поверхности. Геодезия развивается в тесной связи с другими научными дисциплинами. Огромное влияние на развитие геодезии оказывают математика, физика, астрономия. Математика вооружает геодезию средствами анализа и методами обработки результатов измерений. На основе физики рассчитывают оптические приборы и инструменты для геодезических измерений. Тесную связь геодезия имеет также с географией и геологией.

Из истории геодезии

Геодезия возникла в глубокой древности. Дошедшие до нас памятники свидетельствуют о том, что за много веков до нашей эры в Египте и Китае имелось представление о том, как в различных случаях измерять земельные участки. Приемы измерения земли были известны и в древней Греции, где они получили теоретическое обоснование и положили начало геометрии, что в переводе с греческого означает измерение земли. Геодезия и геометрия долго взаимно дополняли и развивали одна другую. Потребность в измерении Земли возникла на Руси еще в очень отдаленные времена.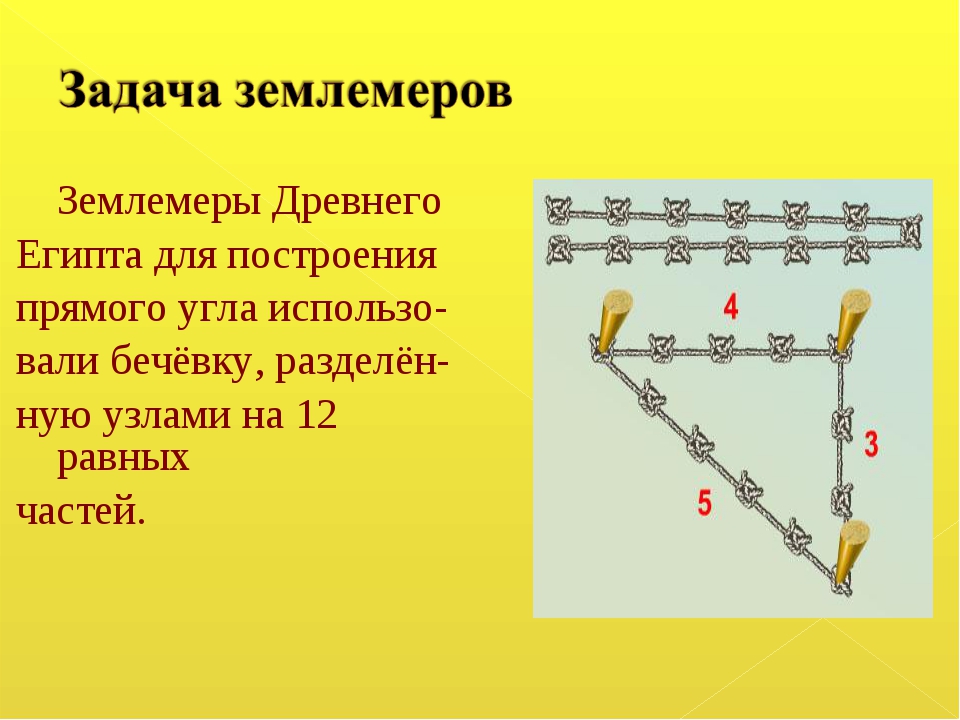 В 1068 г., т. е. в X I веке, было измерено расстояние между городами Таманью и Керчью через Керченский пролив по льду. В 1696 году начата первая съемка реки Дон. Преобладающая часть европейского цивилизованного мира также не имела точной географической карты, основанной на геодезических или астрономических работах. Петр I вместе с адмиралом Корнелием Крюйсом лично проводил эту съемку во время Азовского похода. Таким образом, русского царя можно назвать геодезистом. Измерения земной поверхности производились не только в интересах землевладения и земельного обложения налогами, но и для строительных и военных целей. [1].

Сегодня геодезия – это, по большей части, спутниковая геодезия, основанная на системах GPS (США) и ГЛОНАСС (РОССИЯ). Трудно представить современную геодезию без тесного взаимодействия с аэрокосмическим зондированием, геоинформатикой. Электронные карты и атласы, трехмерные картографические модели и другие геоизображения стали привычными средствами исследования для геодезистов.

Геодезия-геометрия (различия-аналогии)

Истоки геометрии, как это вытекает из названия (геометрия– землемерие), берут свое начало в землемерии. Формирование классической абстрактной геометрии началось еще с Фалеса и приняло свое заключительное выражение в «Началах» Евклида. Аристотель в своем трактате «Метафизика» положил четкую границу между геодезией и геометрией, применительно к «чувственным» и «умопостигаемым» абстрактным объектам. Геодезия к этому времени стала специфической системой профессиональных знаний, применявшихся в землеустройстве, земельном кадастре. Из самого термина (геодезия– землеразделение) вытекают характер и специфика этого рода знаний. Классическая геометрия (греческая) – «геометрия циркуля и линейки», а геодезия – геометрия прямого угла и мерной ленты (веревки). В совокупности вся система знаний разделилась на теоретическую и практическую геометрию, сохранивших свое деление и название практически до XXв. Но одновременно практическая система знаний именовалась геодезией. Геометрия развивалась и совершенствовалась благодаря заложенным в нее основам в виде постулатов и аксиом. По аналогии с теоретической геометрией, можно было бы в геодезии ввести постулаты и аксиомы, способствовавшие ее теоретическому развитию. В постулатах Евклида введены основные объекты геометрии: точки (то, что не имеет частей) и линия (не имеет ширины). В геодезии основными объектами являются введенные в работах [1, 2] структурные элементы (точки, линии, поверхности). Сохранив для точки и линии геометрическую интерпретацию, поверхность можно определить как то, что имеет ширину и длину. В геодезии использование и восприятие линии многофункционально:

— линия деления;

— линия границы

— линия как ориентир.

Особенно роль линии возросла, когда человек начал строиться и заниматься земледелием, т.е. при планировке земель и т.п.

Свои задачи геодезия решает, используя структурные элементы точки, линии, поверхности, углы. В геодезии существует ориентирование по четырем направлениям. В глобальной ориентировки формировались две важнейшие перпендикулярные линии (линии ориентирования), прямой угол сыграл роль мирового геометрического стандарта.

Понятие симметрии очень важно для геодезии. С учетом симметрии, пропорциональности формировались требования и технологии в строительстве и в геодезии. Главными фигурами в геодезических сетях были прямой угол и связанные с ним две простейшие фигуры: прямоугольный треугольник и квадрат (или прямоугольник) ( рис.1а,б,2)

Рис.1 Рис.2

Вся совокупность геодезических задач, решавшихся в древнее время под знаком практической геометрии, была представлена великим механиком и математиком Героном Александрийским. С позиций предмета «Практической геометрии» Герон излагает 17 известных геодезических задач:[1].

Измерить разность высот двух точек, невидимых одна от другой;

Провести прямую между двумя точками, невидимых одна от другой;

Найти расстояние места, где находишься, от другой недоступной точки;

Провести перпендикуляр на прямую, к которой нельзя приблизиться;

Измерить ширину реки;

Измерить глубину ямы;

Сквозь гору провести прямую, соединяющую две точки, данные с различных сторон горы;

Начертить контур реки;

Придать насыпи форму данного сферического сегмента;

Сообщить насыпи определенный уклон;

Измерить поле, не входя в него;

Разделить его на данное число частей посредством прямых, выходящих из одной точки;

Разделить трапецию и треугольник в данном отношении; и др. .

Рис. 3. Трассировка дорог, каналов, водопроводов, использовавшаяся

римскими агрименсорами.

Основной метод измерений, который используется в геодезии, называется триангуляционным. Этот термин произошѐ л от латинского слова «триангумом», что означает «треугольник». В основе этого метода лежат знания о треугольнике, которые мы уже изучили, и сегодня будем закреплять и применять.

В геометрии рассматриваются две типичные геодезические задачи: определение высоты объекта и определение расстояния до недоступной точки (рисунки 4 -8). Решение этих задач основано на использовании теоремы синусов, теоремы косинусов, теоремы о сумме треугольника, следствие из теоремы синусов (в треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол) [2].

Рис.4. Рис.5.

Рис.6. Рис.7. Рис.8. [2].

Метод Фалеса (построение триангуляции). Определение расстояния до корабля

Рис.9

Рассматривалась фигура прямоугольного треугольника в веревочном варианте —

узлы на веревке в интервале «Пифагоровы тройки»-3,4,5. Фалес при помощи такого построения треугольника определил расстояние до корабля (Рис. 9.) Применение такого треугольника использовалось при пробивке тоннеля на острове Самос (рис.2.)

Наконец известен исторический факт. Фалес определил высоту пирамиды при помощи её тени.(рис.10) [1,4].

Рис.10 ( Метод Фалеса) [3].

Прямоугольный треугольник использовался в Древнем Риме и других странах при проектировании водопроводов, каналов и городской канализации. Наклон стока воды задавался стандартным отклонением (1:200)

Рис.11. Вертикальный треугольник в определении уклона при проложении римских водопроводов .[1].

Теорема Пифагора для геодезии имела громаднейшее значение, так как она определяла метрику окружающего (евклидова) пространства. В плане оценки площади прямоугольного треугольника и использовалась формула S=1/2 ab/

Прямоугольный четырехугольник и квадрат нашли более раннее применение при планировке отдельных сооружений и особенно в землеустройстве, межевании, земельном кадастре.

В римском земледелии все угодья делились на центурии(квадратной формы) (рис.12). [1].

Рис.12.

Исследование. Измерение и построение на местности.

В своём исследовании я не ставила задачу изучить основы геодезии. Я подобрала практические задачи на построение и вычисление на местности, которые надо знать любому из нас. Построения на местности, основываясь на геометрических законах, имеют свою специфику: все прямые не проводятся на земле, а прокладываются, т. е. отмечается на них, например, колышками, достаточно густая сеть точек. Обычно прокладку прямых на местности называют провешиванием прямых. При геодезических работах используются специальные колышки длиной 15-20 см и диаметром 2-3 см, в торец которых забиваются гвоздики для более точного обозначения концов отмеряемого отрезка, и вехи – деревянные заостренные шесты длиной 1,5-2 м и диаметром 2-4 см. [3].

Приборы:

Теодолит ― геодезический инструмент для определения направлений и измерения горизонтальных и вертикальных углов при геодезических работах.

Тахеометр― геодезический инструмент для измерения расстояний, горизонтальных и вертикальных углов. Близок к классу неповторительных теодолитов, используется для определения координат и высот точек местности при топографической съёмке местности, при разбивочных работах, выносе на местность высот и координат проектных точек, прямых и обратных засечек, тригонометрического нивелирования и т. д.

Оптический нивелир ― геодезический инструмент для определения разницы высот точек земной поверхности.

Астролябия И.Э.Эслинга – угломерный прибор, которым пользовались геодезисты, посланные Петром Великим для геодезической съемки Камчатки и Курильских островов. Этот прибор предназначен, главным образом, для измерения горизонтальных углов. Не имеет уровней, горизонтальная установка, возможно, выполнялась с помощью съемного уровня. (рис 13)

Рулетка – лента, с нанесёнными на ней делениями, предназначена для измерения расстояний на местности.

Экер – прибор для измерения прямых углов на местности. (рис.12.)

Вехи (вешки) – колья которые вбивают в землю.

Земляной циркуль ( полевой циркуль – сажень) – инструмент в виде буквы А высотой 1,37 м. и шириной 2 м. для измерения на местности. [3,5].

Рис.12 Экер. Рис.13. Астролябия.

Как правило, участки местности представляют собой не идеально ровную поверхность, как тетрадный лист, на земле есть возвышения и углубления. Чтобы они не искажали геометрические образы прокладываемых линий, на местности строят не наклонные отрезки, а их ортогональные проекции на горизонтальную плоскость. Их можно определить, зная угол наклона – угол, образованный линией местности и ее проекцией на горизонтальную плоскость.

Эти углы измеряются специальными приборами эклиметрами.[1,3,5].

Построение окружности на местности.

На местности устанавливается колышек, к которому привязывается верёвка. Держась за свободный конец верёвки, двигаясь вокруг колышка, можно описать окружность (рис.14). Практическая работа: построение окружности. .[3].

Задание: измерение радиуса, диаметра; вычисление площади круга, длины окружности.

рис.14.

Построение прямой на местности (провешивание прямой линии)

Отрезки на местности обозначают с помощью вех. Чтобы вешка стояла прямо, применяют отвес (какой – либо грузик, подвешенный на нитке). Ряд вбитых в землю вех и обозначает отрезок прямой линии на местности. В выбранном направлении ставят две вехи на расстоянии друг от друга, между ними другие вехи, так, чтобы глядя через одну, другие прикрывались друг другом.[3].

Практическая работа: построение прямой на местности.

Задание: отметьте на ней отрезок в 20 м, 36 м, 42 м. (Рис.15) . [3].

Рис.15.

Измерение средней длины шага

Считается некоторое число шагов (например, 50), измеряется данное расстояние и вычисляется средняя длина шага. Опыт удобнее провести несколько раз и сосчитать среднее арифметическое.[3].

Практическая работа: измерение средней длины шага.

Задание: зная среднюю длину шага, отложите на местности отрезок 20м, проверьте с помощью рулетки.

Построение прямых углов на местности

Чтобы построить на местности прямой угол АОВ с заданной стороной ОА, устанавливают треножник с экером так, чтобы отвес находился точно над точкой О, а направление одного бруска совпало с направлением луча ОА. Совмещение этих направлений можно осуществить с помощью вехи, поставленной на луче. Затем провешивают прямую линию по направлению другого бруска (ОВ) (рис.16).[3,5].

Практическая работа: построение прямого угла на местности, прямоугольника, квадрата.

Задание: измерьте периметр и площадь прямоугольника, квадрата.

Рис.16.

Построение и измерение углов с помощью астролябии

Астролябию устанавливают в вершине измерительного угла так, чтобы лимб её был расположен в горизонтальной плоскости, а отвес, подвешенный под центром лимба, проектировался бы в точку, принимаемую за вершину угла на поверхности земли. Затем визируют алидадой по направлению одной стороны измеряемого угла и отсчитывают на лимбе градусные деления против метки предметного диоптра. Повёртывают алидаду по ходу часовой стрелки в направлении второй стороны угла и делают второй отсчёт. Искомый угол равен разности показаний при втором и первом отсчётах.[3,5].

Практическая работа:

измерение заданных углов,

построение углов заданной градусной меры,

построение треугольника по трём элементам – по стороне и двум прилежащим к ней углам, по двум сторонам и углу между ними.

Задание: измерить градусные меры заданных углов.

Измерение высоты горы.

У подножия горы прикрепим вертикальный шест, прикрепим горизонтальную палку так, чтобы один конец задел поверхность горы, измеряем высоту h_1.Таким образом поднимаемся до вершины горы M. Высота горы H=h₁+h₂+h₃+h₄+…(рис.17) [3].

Рис.17.

Измерение ширины реки.

Для измерения ширины реки останавливаемся в точке В и проводим мнимую прямую до дерева А, стоящего на том берегу реки и прикрепим шест в точке В. По реке проходим расстояние ВЕ и прикрепим шест в точке Е. От точки Е до точки С откладываем отрезок равный пятой части отрезка ВЕ Проводим мнимую прямую через точку Е к дереву А и прикрепим шест в точке К, измеряем расстояние СК. Расстояние АВ= 5× СК.(рис.18.) .[3].

Рис.18.

Заключение

В ходе выполнения данной работы я выяснил, что человек, не знающий геометрию, не сможет понять что – либо в геодезии, а значит, эти науки неразрывно связаны между собой. Геодезия и геометрии дополняют друг друга. В моей работе я подобрал задачи на построение и измерение на местности, которые можно применять нам в практической жизни. Профессия землеустроителя и геодезиста с древних времен и до настоящего времени остается одной из самых востребованных.

Список использованных источников и литературы:

Г.Н.Тетерин «Феномен и проблемы геодезии» Новосибирск:СТГА,2015,77 с.

В.Н. Клюшниченко « Многогранная геодезия» Новосибирск:СТГА,2016.-164 с.

В.Н.Ганьшин «Простейшие измерения на местности», Москва, «Недра», 2014г, 110с.

Г.И.Глейзер «История математики в школе», Москва, «Просвещение», 2014г, 240с.

Геометрия 7-9: Учебник для общеобразовательных учреждений /Л.С. Атанасян, В.Ф. Бутузов и др.- М: Просвещение, 2014г.

Просмотров работы: 1423

Способы определения положения проектных точек на местности

Способы определения положения проектных точек на местности.

1) способ полярных координат – когда есть возможность измерить расстояние от пункта до проектной точки. Точность зависит от точности построений проектного угла и расстояния. СКП положения проектной точки относительно разбивочной сети без учета погрешности закрепления;

2) способ прямоугольных координат – когда на территории густая сеть исходных пунктов. Проектные отрезки либо с плана, либо рассчитывается по координатам. Точность положения зависит главным образом от точности откладывания проектных расстояний, от точности построения прямых углов и длины проектных отрезков;

3) способ прямой засечки – когда есть густая сеть точек, но нет возможности измерить расстояние от опорной точки до проектной, аналитически рассчитываются углы с контрольными промерами (углами). Можно по 2 углам, но третий – для контроля;

4) способ линейных засечек – когда короткие расстояние, густая сеть, расстояния до точки не более длины мерного прибора, важно, чтобы углы пересечения были не Болье 1400 и не меньше 400;

5) способ проектного теодолитного хода – применяется при перенесении на местность трасс, линейных сооружений, при отводе земель на строительство. Определяются проектные координаты точки либо графически, либо из обратной геодезической задачи определяют дирекционные углы и расстояния, рассчитываются правые либо левые углы и с учетом наклона – расстояние. На местности привязывают ход к двум парам пунктов, прокладывают теодолитный ход, полученную невязку распределяют способом параллельных линий. Направление невязки определяют с помощью буссоли. Поправку вводят в каждую точку;

6) способ промеров по створу – измеряются расстояния 1-2, 2-3, 3-4 (по нарастающей)

Способы определения положения проектных точек на местности — 3. 5 out of 5 based on 2 votes

Построение прямых углов на местности. 5-й класс > Мастера спешат на помощь!

Конспект урока-путешествия по шкале ЭМВ (электромагнитных волн)

Данное мероприятие — урок-путешествие по шкале Э М В проводится для учащихся 11-го класса, дает возможность обобщить и систематизировать знания учащихся, использовать приобретенные знания для объяснения влияния различных участков спектра Э М В на здоровье человека, развивать интеллектуальные и творческие способности учащихся в процессе самостоятельного приобретения знаний по физике с использованием различных источников информации, а также представление результатов своей деятельности в различной форме: буклеты, брошюры, презентации, фотовыставки….

01 04 2021 3:49:50

Внеклассное мероприятие «КВН»

Задания для проведения К В Н направлены на развитие у учащихся восприятия, умения слышать и слушать, внимания, логического мышления, речи и воображения; коммуникативных навыков и навыков регуляции. Необычные задания способны заинтересовать многих учащихся. …

31 03 2021 3:17:35

Интерактивная доска на уроках геометрии

Цель работы: проанализировать возможности интерактивных технологий в школе и разработать методическое обеспечение темы « Треугольники» с интерактивной доской….

28 03 2021 1:41:52

Сообщающиеся сосуды

Представленный урок знакомит учащихся с сообщающимися сосудами, основными свойствами сообщающихся сосудов и их применением. Развитие творческих способностей обучающихся в рамках исследовательской работы….

27 03 2021 2:24:18

Введение в естественно-научные предметы (физика и химия)

Цель урока: создать условия для осознания и осмысления блока информации о методах изучения природы, для овладения начальными исследовательскими умениями проводить наблюдения, опыты и измерения, описывать их результаты, формулировать выводы. …

25 03 2021 10:11:45

Умножение десятичных дробей. 5-й класс

На уроке математики в 5-м классе учащиеся знакомятся с правилом умножения десятичных дробей на 0,1; 0,01; 0,001 и выполняют задания, которые требуют от учащихся наблюдательности, внимания, логического мышления, умения анализировать, делать выводы. На протяжении всего урока используется презентация….

24 03 2021 3:33:47

Элементы комбинаторики. Методы решения некоторых задач

Раздел » Теория вероятностей и математическая статистика» включен в новый государственный стандарт образовательной программы по математике. Существует ряд учебников, по которым рекомендовано вести обучение по данному разделу. Однако немного есть дидактических материалов, практических упражнений. Поэтому мы решили создать базу задач по комбинаторике с целью ее использования на уроках, кружках, факультативных занятиях. …

23 03 2021 12:35:18

Решение задач на проценты. 5-й класс

Одной из наиболее сложных тем, изучаемых в курсе математики в школе, является тема » Проценты». Я стараюсь с самого начала её изучения, т.е. с 5-го класса, уделять ей достаточно внимания, чтобы ученики имели навык решения самых разнообразных задач на применение процентов, так как подобные задачи есть в каждом варианте Г И А в 9-м классе и в каждом варианте Е Г Э в 11-м классе. Кроме того стараюсь показать практическую направленность таких задач – задач, с которыми ученики встретятся в жизни….

22 03 2021 0:28:14

Внеклассное мероприятие по математике. Интеллектуальная игра «Имя пришло со страниц учебника»

Интеллектуальная игра для старшеклассников, целью которой является развитие общего кругозора; развитие навыков поисковой и исследовательской работы, умения работать с научно-популярной литературой. Обучающиеся познакомятся с интересными фактами из жизни выдающихся учёных-математиков. В данной игре используется обширная наглядность, стихи, музыка, составлена компьютерная презентация. …

21 03 2021 22:19:45

Решение квадратных уравнений

Урок математики для учащихся 8-го класса закрепляет теоретические знания по изученной теме, совершенствует навыки решения квадратных уравнений. …

20 03 2021 21:30:49

Урок геометрии в 9-м классе «Длина окружности»

Что такое окружность? Как измерить её длину? Наглядное представление о длине окружности можно получить следующим образом. Представим себе нить в форме окружности. Разрежем её и растянем за концы. Длина полученного отрезка и есть длина окружности. Но не всегда длину окружности можно измерить с помощью нити. Поэтому вопрос о нахождении формулы для вычисления длины окружности волновал учёных с давних времён….

19 03 2021 1:59:55

Зачеты по алгебре. 7–8-е класссы

Разработанные вопросы по алгебре для 7–8-х классов продолжают систему зачётов для проверки усвоения материала в 5–6-х классах. Перед изучением новой главы раздаются вопросы к пунктам учебника, это облегчает подготовку к уроку, работу с учебником, позволяет быстро повторять теоретический материал. Эта форма зачётов повышает самооценку ученика, его авторитет в классе….

18 03 2021 19:39:19

Внеклассная работа по математике «Льюис Кэрролл»

Интегрированное внеклассное мероприятие предполагает расширение знаний учащихся, развитие познавательного интереса и творческой активности, что вызывает умение самостоятельно творчески работать с учебной и научно-популярной литературой. Важность этого проекта – залог успешной работы учащихся по предметам. В проекте используется обширная наглядность, сценки, стихи, музыка….

17 03 2021 13:48:54

Бинарный урок математики и географии по теме «Кавказ в цифрах»

Урок помогает закрепить математические знания учащихся по теме “ Проценты” с учетом их индивидуальных особенностей. Идёт процесс формирования умения самостоятельной работы с различными информационными источниками. Повышается интерес к изучению Кавказа, воспитывается чувство уважения между народами….

14 03 2021 18:26:46

Развитие мышления детей старшего дошкольного возраста в процессе решения задач

В процессе математического и общего умственного развития детей старшего дошкольного возраста существенное место занимает обучение решению и составлению простых арифметических задач. Цель рекомендации – показать, как развиваются наглядно-действенное, наглядно-образное и элементы логического мышления на занятиях по математическому развитию в процессе решения задач….

13 03 2021 19:32:32

Урок одного уравнения sinx+cosx=1

Урок решения одной задачи – это поиск способов решения этой задачи. Для одних уроки одной задачи – это соломинка для спасения в трудном мире математики, которая все же помогает найти свой, понятный путь решения задачи, для других – открывает мир красоты и изящества любимого предмета, для третьих – путь к пониманию в общении с одноклассниками и учителем. …

12 03 2021 0:35:56

Порядовка отопительной печи из кирпича: кирпичная печь своми руками, детали на фото и видео

На протяжении очень большого количества времени и по сей день одним из самых популярных средств отопления частных домов считается традиционная печь. Порядовка отопительной печи из кирпича заслужила свое распространение своими отличными функциональными свойствами, поскольку, как известно, с помощью печи можно не только обогреть помещение, но и приготовить еду, разогреть воду для бани (детальнее: » Порядовка… Читать дальше…

11 03 2021 10:56:19

Урок геометрии в 8-м классе «Прямоугольник, параллелограмм, куб»

Чтобы в увлекательной форме повторить данную тему, расширить общий кругозор учащихся, урок можно провести в нестандартной форме с занимательными, творческими заданиями, которые позволят активизировать мыслительную деятельность учащихся, развивать креативные способности. В одном из этапов применяю альтернативную технологию Эдварда де Боно «шесть шляп мышления». При таком методе общения ученик практически раскрепощен в выражении своих мыслей, не испытывает неловкостей при ответе. Учащиеся научатся анализировать, рассуждать, обобщать. Качество и прочность знаний при этом повышается. Все это создает высокую мотивацию при изучении данной темы….

10 03 2021 16:22:56

Физика и безопасность дорожного движения

Урок посвящен взаимосвязи физики и безопасности дорожного движения. Ученикам предстоит, опираясь на знание физических законов, выработать осознанную необходимость соблюдения правил дорожного движения….

09 03 2021 4:43:45

Сказка «Отважный Синий карандаш»

В сказке в доступной и запоминающейся форме представлено удивительное свойство воды – способность преломлять свет. Предложен вариант демонстрационного опыта для проведения в домашних условиях….

08 03 2021 21:17:47

Групповая работа на уроках математики по теме «Длина окружности и площади круга»

Данный урок математики в 6-м классе с использованием мультимедийной презентации по теме является уроком изучения нового материала, цель которого – познакомить учащихся с формулами длины окружности и площади круга, а также с числом π. Формулы выводятся учащимися в результате практической работы по измерению длины окружности и площади круга. …

07 03 2021 17:53:15

Урок-конференция «Наука и нравственность»

Цели и задачи урока: показать наиболее ярко ученого как человека, как личность; формировать у учащихся навыка самостоятельной работы с научно-популярной литературой по данной теме, вырабатывать у учащихся умение преподать полученные знания в простой и доступной форме, продолжить развитие у учащихся познавательного интереса к физике, формировать чувство гордости за ученых своей Родины. Для достижения результата используются презентации, подготовленные учителем….

06 03 2021 22:59:36

Урок геометрии в 7-м классе «Классификация треугольников»

Урок изучения и первичного закрепления новых знаний. Урок-исследование с применением маршрутного листа. На уроке используется презентация. Цель урока: познакомить учащихся с классификацией треугольников, определениями треугольников, элементами и свойствами прямоугольного треугольника….

05 03 2021 22:40:14

Шахтный твердотопливный котел: принцип работы и преимущества

В настоящее время большинство владельцев частных домов имеют у себя газовое отопление. Однако часто возникают ситуации, когда подключиться к центральной газовой трубе не представляется возможным. Тогда на помощь приходят твердотопливные котлы, мощные и надежные нагревательные приборы. Топить дровами или углем можно как в частном доме, так и на даче. По стоимости такой вид отопления будет… Читать дальше…

04 03 2021 11:49:40

Дифференцированное обучение по математике

Дифференцированное обучение — очень важная составляющая обучения. Оно направлено на развитие личности ребёнка, поэтому через дифференцированный подход в обучении математике повышается учебная мотивация учащихся и результаты обучения. …

03 03 2021 23:27:38

Решение неравенств и систем неравенств, алгебра, 8-й класс

Урок проводится с целью обобщения и систематизации умений и навыков выполнения действий с неравенствами и системами неравенств. Развивает творчество, сообразительность, смекалку учащихся, культуру их речи, познавательную активность учащихся. Воспитывает чувство ответственности, самоконтроля. Формирует интерес к изучению математики через использование И К Т. …

02 03 2021 21:26:53

Математика в событиях истории XIX века. 8-й класс

Урок позволяет объединить изучаемые дисциплины за счет использования взаимосвязей предметов; повысить эффективность достижения образовательных целей и задач; расширить социальное пространство личности; сформулировать познавательный интерес к математике; обобщить знания и умения по теме » Квадратные уравнения»….

01 03 2021 1:58:16

Внеклассное мероприятие в 6-м классе по математике «В гости к бабушке спешим»

С самого начала шестиклассники распределились на воображаемые семьи. И началось веселое путешествие на паровозике по математической стране. Станции были разные: Папинск, город знаков, Внимательная, Среднеарифметическая, И К С, Русская народная. Пройдя все испытания, каждая семья встретилась со своей «бабушкой». » И как это здорово, когда вся семья вместе», — подвели итог ребята. …

28 02 2021 15:19:39

Интегрированный урок алгебры и геометрии «Задача о Колодце Лотоса». 10–11-е классы

Данный материал позволяет соединить в одном уроке алгебру и геометрию, чтобы продемонстрировать неразрывную связь этих двух дисциплин. Презентация теперь является основой, главным элементом, на котором базируются этапы урока. Связь между различными предметами школьного курса, такими как история, информатика, алгебра, геометрия, литература, становится убедительной и неразрывной….

27 02 2021 4:29:49

Комбинаторика и ее применение

Представлена модель урока-проблематизации с элементами историзма по математике в 5-м классе, особенностью которого является то, что на нем рассматриваются задачи, требующие при решении логического мышления, а также задачи, наиболее приближенные к жизненным ситуациям. Такими задачами и являются задачи на комбинаторику. В задания Е Г Э с 2010 года тоже будет включен этот раздел. В урок включена презентация с элементами историзма, которая создана учащимися….

26 02 2021 19:28:19

Восхождение на пик «Задача». Решение задач с помощью рациональных уравнений

Решение текстовых задач развивает логическое и образное мышление, повышает эффективность обучения математике и смежным дисциплинам. На уроке учащиеся отрабатывают навыки и умения составлять математическую модель задачи на движение и на совместную работу; решают дробно-рациональные уравнения….

24 02 2021 22:35:30

Авторская программа элективного курса по геометрии «Решение планиметрических задач на вписанные и описанные окружности» для учащихся 9-х классов

Статистические данные анализа результатов проведения Е Г Э говорят о том, что наименьший процент верных ответов традиционно дается учащимися на геометрические задачи. Как известно, решению геометрических задач в школе уделяется мало внимания. Совершенно очевидно, что нужна специальная подготовка. Данный курс » Решение планиметрических задач на вписанные и описанные окружности» рассчитан на 12 часов для учащихся 9-х классов, желающих расширить и углубить свои знания по математике, сделать правильный выбор профиля обучения в старших классах и качественно подготовиться к Е Г Э….

23 02 2021 18:26:35

Внеклассная работа по математике. Игра «Великолепная семерка»

Игра » Великолепная семерка» относится к разделу » Внеклассная работа по математике». Цель: расширение кругозора учащихся, развитие математической культуры. В игре принимают участие не только игроки, но и болельщики. Рассматривается связь между различными областями деятельности (музыка, кино, история , литература, математика). Приводится экскурс истории числа семь. Развивается логическое мышление, сообразительность, память, внимание….

22 02 2021 12:13:53

Интегрирование методом замены переменной (метод подстановки)

Занятие « Интегрирование методом замены переменной (методом подстановки)» входит в изучение темы « Начала математического анализа». Тема рассчитана на 32 часа. Изучается в техникуме на 1-м курсе во втором семестре. На занятии прослеживаются межпредметные связи с дисциплинами « Физика» и « Техническая механика», которую будут изучать на втором курсе. Освоение студентами данной темы поможет в изучении спецдисциплин на старших курсах….

21 02 2021 0:22:26

Тема урока: «Треугольник – простейший и неисчерпаемый». 7-й класс

Содержание данного урока позволяет не только применить метод проектной работы в ходе занятия, но и показать, как можно неформально подходить к заданию домашней работы по предмету. В частности, результаты предыдущей домашней работы станут необходимыми для нового открытия, а последующее домашнее задание будет индивидуализированным (сформированным на основе рефлексивного итога занятия), построенным на Р Н О. …

20 02 2021 5:51:16

Введение в геометрию. 7-й класс

Увлечь на первых уроках учащихся предметом, развивать образное мышление, показать возможности применения на практике знаний, полученных на уроке, связать геометрию с другими школьными предметами, активизировать работу учащихся на уроках — задачи первого урока геометрии в 7-м классе. Сделать урок интересным, запоминающимся помогла мультимедийная презентация с элементами анимации. …

19 02 2021 19:16:52

Урок по физике «Рычаги. Условие равновесия». 7-й класс

Предлагаемый урок предназначен для учителей физики, работающих по программе курса физики 7-го класса (базовый уровень — 2 часа в неделю), ориентированной на учебник Пёрышкина А. В., при изучении темы » Простые механизмы». Цель данного урока — облегчить нелёгкий труд учителя, оказать методическую помощь в процессе подготовки к уроку, обеспечить сопровождение урока мультимедийной презентацией….

18 02 2021 12:59:42

Перпендикулярность прямых и плоскостей

Изучение предмета ведется по программе Л. С. Атанасяна и др. Основу урока составляет презентация, которая содержит все необходимые вопросы теории, иллюстрации к ним и готовые чертежи для решения задач. Для достижения эффективности восприятия материала в презентации используются эффекты анимации….

13 02 2021 4:56:20

Внеклассное мероприятие по физике. Тема: «Первые шаги в космосе»

Внеклассное мероприятие можно использовать в 7–9-х классах во время проведения декады по физике, что позволяет усилить интерес к предмету, повысить интеллектуальный уровень учащихся. Оно сопровождается красочной презентацией, а также творческой работой учащихся на тему « Космос». Заключительным этапом является викторина. …

12 02 2021 20:51:48

Проект по геометрии

Содержание материала расширяет представление учащихся об односторонних и двусторонних поверхностях, рассматриваемых на уроках геометрии в 11-м профильном классе, развивает интерес к математике. Проводится в форме игры по станциям: практическая, историческая, топологические свойства Л М, применение в науке и технике, в жизни человека. …

10 02 2021 0:41:57

Возможности применения информационных технологий в процессе обучения математике

Одна из основных задач образования — это вхождение в современное информационное общество. Основная цель информатизации образовательного пространства — повышение эффективности и качества образования. Этому способствует применение на занятиях различных Т С О. В статье раскрываются возможности применения на уроках математики компьютеров и мультимедийной установки. …

08 02 2021 16:35:11

Устный журнал «Законы Ньютона»

Цель и задачи урока: cистематизировать, обобщать, закреплять знания о законах Ньютона, показать границы применения этих законов, формировать умения комплексного применения полученных знаний при решении теоретических, экспериментальных, практических задач. Развивать познавательные интересы, интеллектуальные и творческие способности в процессе решения практических задач, коммуникативные навыки при работе в группах. …

07 02 2021 21:26:25

Решение систем показательных уравнений

В ходе урока учащиеся обобщают знания по теме » Показательная функция и простейшие показательные уравнения», знакомятся с методами решения систем показательных уравнений. Все задания, решаемые учащимися на уроке, взяты из открытого банка данных для подготовки к Е Г Э, что способствует повышению мотивации учащихся к изучению данной темы….

06 02 2021 8:34:26

Урок в 6-м классе по теме: «Координаты на прямой»

Объяснение нового материала проходит на реальных примерах и жизненных ситуациях. Учащиеся определяют показания термометра, повторяют изученное о линии времени, определяют положение точки на прямой по отношению к заданной точке, развивают умение записывать положительные и отрицательные числа. …

05 02 2021 9:34:45

Дверная вентиляционная решетка как способ вентиляции ванной

Свежий воздух внутри помещения – это залог не только здоровья людей, но и сохранности многих отделочных материалов. В большинстве помещений проблема притока кислорода решается просто – проветриванием. В ванной же комнате нет окон, поэтому в ней требуется организация качественной вентиляции – как принудительной, так и естественной. Для создания первой используются вентиляторы, а со второй могут… Читать дальше…

03 02 2021 1:53:41

Прямая и обратная пропорциональные зависимости

Урок обобщения и закрепления знаний учащихся о прямой и обратной пропорциональной зависимости, выработка навыка решения задач, используя жизненные занимательные задачи, развитие интереса к учебному материалу, используя занимательные задачи; воспитание коллективизма, развитие творческих способностей. …

02 02 2021 19:23:14

Деление с остатком. 5-й класс

Урок призван совершенствовать навыки выполнения действий деления с остатком, продолжить работу над текстовыми задачами, показать связь математики с жизнью….

01 02 2021 23:29:19

Обобщение материала по теме «Оптика». 11-й класс

Качество учебно-воспитательного процесса во многом зависит от того, какие методики и средства обучения используются, насколько эффективно происходит управление познавательной деятельностью учащихся и формирование учебно-познавательной компетенции на уроке. Такой урок, где я использую разные методические приемы, проведен в профильном 11-м классе. …

31 01 2021 3:48:12

Метод неопределенных коэффициентов и его универсальность

Автором подобраны и рассмотрены восемь видов заданий, при выполнении которых применяется метод неопределённых коэффициентов. Рассмотренные в работе примеры могут быть решены и другими способами. Но цель работы заключалась в том, чтобы показать универсальность этого метода, его оригинальность и рациональность, не отрицая того, что в некоторых случаях он приводит к громоздким, но несложным преобразованиям. …

30 01 2021 16:50:23

Предпрофильное обучение учащихся 8-х классов: гуманистические аспекты

Представлена програма элективного курса для учащихся 8-х классов по углублённому изучению математики, состоящая из следующих модулей: » Множества», » Делимость чисел», » Рациональные выражения», » Функции и их графики», » Квадратные уравнения», » Уравнения с параметрами». В основу этого элективного курса положен учебник » Алгебра 8″. Материал, излагаемый в этом учебнике, соответствует программе углублённого изучения математики и выходит за рамки действующих учебников алгебры для 8-го класса….

29 01 2021 18:41:21

Урок-игра по теме «Тепловые явления». 8-й класс

Цель урока: повторить и обобщить материал по теме » Тепловые явления». Класс разделен заранее на команды по 4–5 человек. Игра проходит в виде физической эстафеты. Состоит из 4 этапов. Каждая команда выбирает капитана и название команды. На каждом этапе каждую команду ждут определенного типа задания, подобранные заранее по данной теме. В конце каждого этапа идут обсуждения по заданным вопросам. За правильные ответы командам присуждаются баллы….

28 01 2021 4:53:39

Сложные проценты в ЕГЭ. 10–11-е классы

В новом формате Е Г Э сейчас значимое место занимает текстовая задача на проценты, вызывающая немалые трудности у учащихся. Из разных источников в работе собран практический материал о текстовых задачах на проценты. Рассматриваются задачи, которые иллюстрируют технику решения часто встречающихся задач на сложные проценты. В работе содержатся задачи, которые можно использовать на уроках и элективных курсах по математике….

26 01 2021 14:17:58

Урок математики в 4-м классе по теме «Сложение дробей»

Урок разработан по технологии проблемного обучения. Дети на уроке работают в группах, им предлагаются задания частично-поисковые и творческие, предлагается самим вывести формулу и составить алгоритм сложения дробей. На уроке учащиеся выступают в роли поварят, знакомятся с профессией повара и кондитера. Используемые приёмы способствуют созданию ситуации успеха для каждого ребенка, помогает каждому ученику проявить себя….

25 01 2021 3:55:48

Урок «Путешествие в мир Созвездий». «Десятичные дроби». 5-й класс

В своей работе автор хочет показать, как можно организовать урок накануне Дня космонавтики. Дети 5-го класса увлеченно работают на нестандартных уроках. Одним из таких является урок по теме » Десятичные дроби», посвященный Дню космонавтики, где дети знакомятся с созвездиями и решают задачи, примеры и уравнения, предложенные им. Урок сопровождается красочной презентацией. …

23 01 2021 6:20:40

Интегрированный урок по теме «Физика в живой природе (Бионика)»

Урок-конференция посвящен обсуждению результатов поисковых исследований учащихся по теме проекта, посвященного вопросу взаимосвязи между физическими явлениями – электричеством, ультразвуком, инфразвуком, радио- и эхолокацией и подобными устройствами у «живых моделей»- живых организмов различных видов….

20 01 2021 13:25:10

Действие с натуральными числами

Повторение свойств действий с натуральными числами. Отработка применения этих свойств к устному счёту. Выполняются задания «составь правило» и «лото». Повторение способов умножения чётных чисел на 5, 25, 125. Введение способов умножения нечётных чисел на 5, 25, 125….

19 01 2021 21:55:57

Программа развития технического творчества «Трансформер»

Программа развития технического творчества направлена на формирование основ системы научно-технического творчества, направленной на выявление, развитие и реализацию потенциала обучающихся Г Б П О У Р О « Т Мех К». В рамках научно-исследовательской деятельности формируется общая способность искать и находить новые решения, необычные способы достижения требуемого результата, новые подходы к рассмотрению различных технических задач. …

18 01 2021 22:37:46

Урок по теме «Площади фигур»

Урок проводится с использованием компьютерных технологий, что позволяет пройти больший объем материала, наглядно представить теоретический материал, быстро проконтролировать усвоение пройденного на уроке. На уроке использованы презентация PowerPoint и тест в Excel , составленные учителем. …

17 01 2021 22:47:51

Термоядерный синтез. Энергетика звезд

Предлагаемый читателю урок содержит учебный материал по основным вопросам термоядерного синтеза, включая и астрономический аспект. Показано, что звезда является природным «термоядерным котлом», огромная температура внутри которого способствует превращению водорода в гелий, затем образуется углерод и всё более сложные ядра. Выделяющаяся при этом энергия поддерживает высокую температуру в недрах звезды….

16 01 2021 20:10:38

Семинар-практикум «Решение логарифмических и показательных неравенств методом интервалов»

Для успешного решения большинства логарифмических и показательных неравенств требуется умение преобразовывать исходное неравенство в более простое. Нашими преобразованиями будут равносильные переходы. Преимущество и красота равносильных переходов (условий равносильности) состоит в том, что мы за один шаг освободимся от логарифмов и переменных оснований. Предлагаемые неравенства и метод их решения вполне доступны учащимся классов с углубленным изучением математики. В общеобразовательных классах они могут быть использованы на интегрированных уроках, на факультативных занятиях, элективных курсах или кружковых занятиях. …

15 01 2021 13:35:45

Плакат (слайд) к уроку «Вывод формулы корней квадратного уравнения»

В работе демонстрируется образец одного из уроков в 8-м классе, где на учебном плакате (слайде) в чёткой, доступной форме предложен вывод формулы корней квадратного уравнения. Этот плакат предоставляет учителю богатейшую возможность повторить и закрепить с обучаемыми многие базовые понятия курса алгебры основной школы. …

14 01 2021 3:10:19

Проект «Проценты в нашей жизни»

Предлагаемый проект демонстрирует учащимся применение математического аппарата к решению повседневных бытовых проблем, вопросов рыночной экономики и задач технологии производства. Познавательный материал курса будет способствовать не только выработке умений и закреплению навыков процентных вычислений, но и формированию устойчивого интереса учащихся к процессу и содержанию деятельности….

13 01 2021 20:39:16

Деление с остатком. 5-й класс

12 01 2021 7:13:14

Интегрированный урок-конференция. Тема: «Средства связи». 11-й класс

Урок интегрирует естественно-научные, гуманитарные и технические знания учебных курсов » Обществознание», » Физика», » Информатика» по темам » Общество и Н Т П», » Электромагнитные волны и их применение», » Телекоммуникационные сети». Образовательный процесс на уроке строится не в логике учебного предмета, а в логике деятельности, имеющей личностный смысл для ученика….

08 01 2021 4:34:27

Использование информационных технологий при обучении физики

В статье рассматриваются возможные пути использования современных информационных и коммуникационных технологий при обучении физике школьников. Проводится классификация информационных объектов и способов их применения на уроках физики, представлены некоторые варианты использования технических средств информационных и коммуникационных технологий при различной оснащенности учебного процесса….

05 01 2021 6:23:12

Методические особенности изучения темы «Задачи с параметрами». Основные понятия

Задачи с параметром – средство обобщения, систематизации, углубления, диагностики и контроля З У Н. Нами разработаны и успешно апробированы теория и методика обучения решению задач с параметром: даны четкие определения основных понятий; задания классифицированы по видам функций; используются ось параметра и графическая интерпретация ответа; задачи решаются аналитически и графически в разных системах координат; используется Н И Т. Нами подготовлена серия статей « Учимся решать задачи с параметром»….

04 01 2021 18:14:54

Внеклассное мероприятие «Звездный час»

Внеклассное мероприятие проводится в рамках предметной недели Ф И М (физика, информатика, математика). Можно провести и в День Космонавтики. Цель мероприятия: познакомить учащихся с достижениями в области космонавтики, формировать патриотические чувства, способствующие гражданскому воспитанию личности….

01 01 2021 23:49:27

Урок-игра по математике «Магазин» по теме «Действия с десятичными дробями», 5-й класс

Использование в учебном процессе игр позволяет решить многие дидактические цели. В процессе игры учащиеся сталкиваются с ситуацией выбора, в которой они могут проявить себя как личность, развивая свое творчество. Кроме того, участникам игры предоставляется возможность выбора не только вида деятельности, но и содержания заданий….

31 12 2020 9:29:22

«Масштаб 1:2, 1:5, 1:10, 1:100. Построение отрезков». 5-й класс

Урок знакомит с понятием «масштаб»; закрепляет умение переводить из одной меры в другую; расширяет знания о масштабе, придает им практическую направленность; корригирует и развивает устную и письменную речь; воспитывает интерес к предмету, бережное отношение к окружающему миру….

30 12 2020 21:51:12

Урок математики в 9-м классе по теме «Нахождение нескольких процентов числа»

Урок по обобщению и систематизации знаний и способов деятельности с постановкой и обсуждением проблемы « Жить или курить?». Основное обучающее воздействие принадлежит дидактическому материалу. В учебную деятельность вносится элемент заинтересованности в здоровом образе жизни. Создаются условия для самостоятельной мыслительной активности. …

29 12 2020 8:39:21

Зачет по геометрии в 8-м классе по теме «Четырехугольники»

Тематический зачет проводится в конце изучения темы и направлен на систематизацию, обобщение и проверку усвоения учащимися теоретического материала и умения применять его при решении задач. Зачет состоит из двух частей — теоретической и практической — и содержит задачи разного уровня. Каждый ученик имеет право сам выбрать для себя уровень сложности, что способствует психологическому комфорту ученика в школе, вырабатывает ответственность и способность к принятию решений. …

23 12 2020 20:51:17

Внеклассное мероприятие по математике на тему «12 апреля»

Урок опирается на анимационную презентацию, которая помогает учителю привлечь внимание к материалу и заинтересовать учеников. В презентации используются записи с голосом Ю. А. Гагарина. В ходе мероприятия ребята постоянно проводят самооценку, используя цветные звезды и звездную карту астронавта. Подводя итог мероприятия учитель может опереться на звездные карты….

22 12 2020 22:14:30

Урок-игра «Математический перекресток» по теме: «Арифметические действия с дробями»

Разработка открытого урока в игровой форме по обобщению знаний по теме: » Арифметические действия с дробями» в 5-м классе. Во время урока используется игровая технология, здоровье- сберегающая технология, а также ученики снабжаются раздаточным материалом. Материал урока связан с жизненными ситуациями. Основная цель урока систематизировать и обобщить знания учащихся по указанной теме. …

21 12 2020 23:10:11

Мысленный эксперимент по теме «Архимедова сила»

Спецификой физического научного знания является широчайшее применение в нём различных формально-математических средств. Эти средства помогают оттачивать строгость мышления, однако привычка мыслить только категориями математики может приводить к ошибочному пониманию сущности явлений природы. Выразить сущность процессов природы можно методами теоретического познания. Одним из них является метод мысленного экспериментирования. Метод мысленного экспериментирования рассмотрен на примере решения задач по теме » Архимедова сила»….

19 12 2020 6:41:59

Печь длительного горения: экономная печка на дровах своими руками, долгогорящая эконом печь

Популярность современной печки на дровах длительного горения постоянно растет, так как она позволяет получить больше тепловой энергии, причем с меньшими затратами твердого топлива.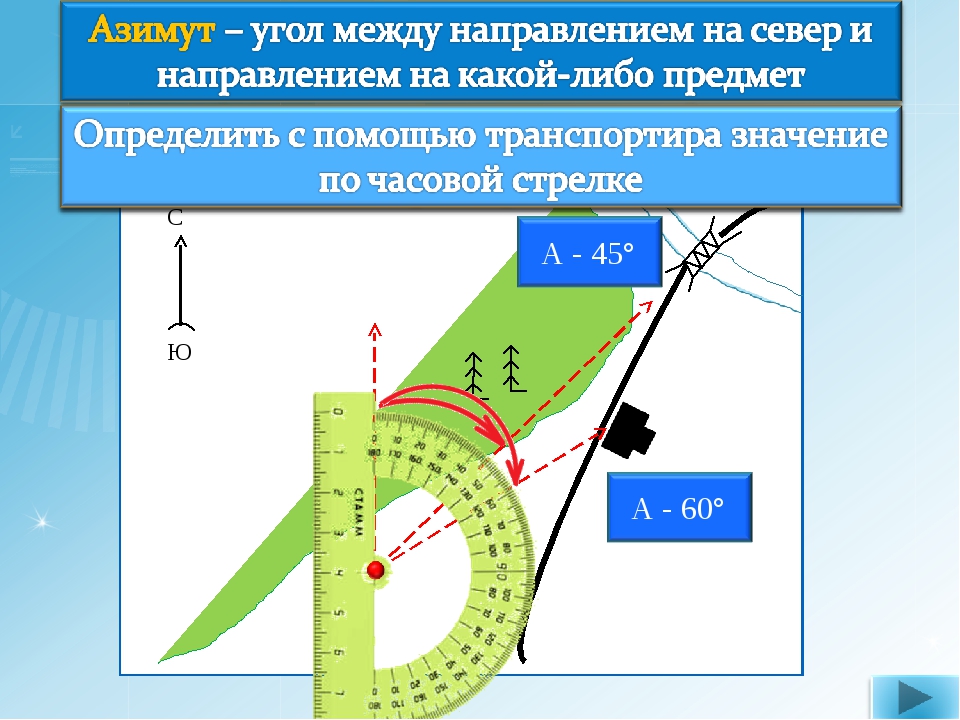 Особенно это актуально для населенных пунктов, где отсутствует централизованная подача газа, а с электроснабжением время от времени возникают проблемы. Эффект пиролиза и его применение в печах Функциональное назначение нагревательных агрегатов продолжительного горения… Читать дальше…

18 12 2020 11:35:15

Интегрированный урок по физике и биологии «Глаз как оптическая система»

Представленный урок подготовлен для 8-х классов. Урок проводится в кабинете при наличии мультимедийного проектора и персональных компьютеров. Урок по зрению предусмотрен как завершающий по теме » Геометрическая оптика» (непосредственно после рассмотрения задач на построение в линзах и принципиальных схем работы оптических приборов). …

17 12 2020 20:16:14

Урок повторения и обобщения «В стране треугольников»

Наверное, нет такого человека, который бы не встречался с таким геометрическим понятием как «треугольник». В школе уже, начиная с начальных классов, дети знают названия элементов, из которых состоит треугольник. Но более глубокое изучение треугольника начинается в 7-м классе на уроках геометрии. Первая теорема в школьном курсе геометрии тоже связана с треугольниками. Представленный урок — это урок обобщения темы » Треугольники» в 7-м классе….

16 12 2020 23:50:10

Геометрия с нуля

Несмотря на развитие науки, у многих школьников Р Ф такая наука, как геометрия, вызывает все больше затруднений, а какая-то часть детей и вовсе не может решать простейшие геометрические задачи. Необходимо признать тот факт, что восприятие у нового поколения совершенно иное. Дети все также хотят развиваться: читают книги, смотрят фильмы, проводят эксперименты. Но главное, чего они не хотят, так это заучивать то, чего не понимают. На основе этого утверждения и будет построена программа….

14 12 2020 6:21:14

Урок на тему «Чаша правосудия (Чаша Пифагора)»

Чаша Пифагора, также известная как Справедливая Чаша или Стакан Пифагора является одним из уникальных изобретений философа, математика и мистика Пифагора Самосского. Чаша Пифагора сыграла важную роль в развитии некоторых гидравлических компонентов, которые были изобретены и использовались в мире….

11 12 2020 5:53:37

Интегрированный урок (биология + физика) «За страницами учебника. Бионика»

Цель урока: создание условий для формирования познавательной активности учащихся. В ходе урока обобщаются знания учащихся по изучаемым предметам (биология и физика), а также расширяется их кругозор, формируется понятие о тесной взаимосвязи различных наук и взаимосвязи природы, науки и техники. Урок сопровождается презентацией и дополнительным занимательным материалом. Материал урока рекомендуется для учащихся 7-го класса….

10 12 2020 4:47:10

Тригонометрический бой

Данное мероприятие может использовать каждый учитель в своей работе, как при повторении темы « Тригонометрические формулы и преобразования», так и в дни проведения предметной недели в старших классах. …

09 12 2020 6:29:28

Организационные формы работы с обучающимися при подготовке к ЕГЭ по математике

Результативность сдачи Е Г Э во многом определяется тем, насколько эффективно организован процесс подготовки на всех ступенях обучения. А если у учащихся сформирована самостоятельность, ответственность и готовность к продолжению обучения, то выполняется не только заказ государства и общества, но и повышается собственная самооценка….

07 12 2020 11:21:16

Диагностическая работа в рамках подготовки к ИГА по алгебре в новой форме

Для подготовки девятиклассников к итоговой государственной аттестации по алгебре в новой форме можно провести диагностическую работу в конце II четверти по У М К А. Г. Мордковича. К этому времени будут изучены следующие темы: « Неравенства и системы неравенств», « Системы уравнений», « Понятие числовой функции». …

06 12 2020 17:29:50

Объем призмы. Решение задач

Организованная деятельность учащихся может способствовать успешному усвоению школьниками одной из самых замечательных наук — геометрии. Одним из способов организации, применяемых мною, является использование самоконтроля. Взаимный контроль проводится при проверке письменных работ, а также при рецензировании устных ответов и сообщений. Учащиеся обмениваются работами, и каждый из них выступает в роли рецензента. Они должны отметить допущенные их товарищем ошибки, объяснить их причины, способы исправления и предупреждения при выполнении аналогичной работы. Взаимный контроль позволяет углубить знания и умения учащихся, способствует развитию внимания, ответственного отношения к делу, формированию навыка самоконтроля. …

05 12 2020 15:53:21

«Женские истории». Сценарий вечера о женщинах-математиках

В данном сценарии рассказано о женщинах-математиках, которые добились славы своим талантом, они опровергли мнение о том, что математика – привилегия мужчин. Для этих женщин математика – смысл жизни, средство выражения своего «я». Сценарий предназначен для учителей и учащихся общеобразовательных школ, а также лицеев и гимназий. …

03 12 2020 1:51:34

Внеклассное мероприятие по математике

Это коллективная форма организации внеклассной работы по математике в 7-х классах, которая стимулирует познавательную деятельность учащихся, расширяет их кругозор в области математики, развивает способность учащихся к толерантному общению, чувство товарищества и взаимовыручки. Эту игру лучше проводить в рамках « Недели математики», когда чувствуется повышенный интерес к предмету….

02 12 2020 23:46:28

Урок по теме «Правильные многогранники» в гуманитарном классе

В статье предложен конспект первого урока по теме » Правильные многогранники» для гуманитарного класса. Выбор форм и методов работы с учащимися обоснован. На уроке применяется групповая форма работы. Авторы предлагают задания по моделированию правильных многогранников, использованию этих моделей, а также ряд заданий поискового характера. …

28 11 2020 5:15:48

Урок с ИКТ «Атомная энергетика: за и против». 11-й класс

Среди вопросов, представляющих научный интерес, немногие приковывают к себе постоянное внимание и вызывают так много споров, как вопрос о действии радиации на человека и окружающую среду. Урок не претендует на то, чтобы дать ответ на все вопросы….

27 11 2020 0:18:19

Программа элективного курса предпрофильной подготовки для учащихся 9-х классов «Решение текстовых задач»

Умение решать задачи является одним из основных показателей уровня математического развития, глубины освоения учебного материала, поэтому актуальность курса заключается в том, что здесь шире рассматриваются задачи на составление уравнений и систем уравнений, предлагаемые школьной программой. В данном курсе показаны методы и алгоритмы решения основных типов текстовых задач, встречающихся на итоговой аттестации в школе и на вступительных экзаменах в высшие учебные заведения; продемонстрированы принципы подходов к решению задач и структура процесса решения задач, на что не уделяется внимание при решении задач на уроках математике в школе….

24 11 2020 7:57:52

Урок-выставка «Физика и детская игрушка»

Урок — выставка » Физика и детская игрушка» проводится в конце 7-го класса. Ученики делятся на группы, готовят показ опытов и сообщения о звуковых, заводных, плавающих и других видах игрушек, принцип действия которых может быть понятен семиклассникам. На уроке демонстрируются несложные опыты. По ходу демонстраций ребята группы просят зрителей объяснить данный опыт, ответить на вопросы, отгадать загадки, показывают в действии те игрушки, которые ребята принесли к уроку из дома. Материал для выступления ребят можно взять из книги И. Я. Ланиной » Внеклассная работа по физике». …

23 11 2020 7:45:44

Шумоизоляция пола в квартире в стяжку

Шумоизоляция квартиры – один из столпов хорошего соседства. В домах без стяжки, где покрытие полов уложено непосредственно на плиты перекрытия, проблема шума от живущих внизу соседей часто бывает очень острой. Дело в том, что перекрытия состыкованы неидеально, всегда имеются небольшие щели, выбоины, технологические отверстия. Для защиты от шума снизу лучше всего поможет звукоизоляция под стяжку.… Читать дальше…

22 11 2020 12:52:41

Урок физики по теме «Использование явления электромагнитной индукции»

Урок физики в 11-м классе по теме « Использование электромагнитной индукции» формирует понятия об электромагнитном поле как виде материи и совершенствует навыки решения качественных и расчетных задач. В приложения 1 и 5 включены задания из К И Мов различных лет, что способствует на данном уроке осуществлять подготовку к Е Г Э по физике….

20 11 2020 15:28:32

Элективный курс по физике «Гравитация без формул»

Представленный элективный курс » Гравитация без формул» рассчитан на учащихся девятых общеобразовательных классов и предусматривает расширение программного материала по данной теме, совершенствование практических навыков и умений при выполнении творческих и лабораторных работ….

19 11 2020 23:20:38

Динамометры. Виды динамометров

Цели урока: ввести понятие «динамометр», познакомить учащихся с некоторыми видами динамометров и областью их применения. По презентации » Динамометры. Их виды» можно привести примеры использования динамометров в зависимости от их назначения. Применяя анимации, делается вывод о том, что любая сила, измеряемая динамометром, сравнивается с силой упругости. …

17 11 2020 18:38:39

Решение задач по теме «Нахождение процентов от данного числа»

При проведении урока использовались задачи, (составленные автором) с которыми мы часто встречаемся в повседневной жизни. Урок, проведенный в 7-м классе общеобразовательной школы для обучающихся с ограниченными возможностями здоровья (глухие и слабослышащие учащиеся), может быль использован для обучения школьников по программе 6-го класса….

16 11 2020 6:14:29

«Координатная плоскость»

Урок-исследование в 5-м классе. Целью урока является исследование координатной плоскости, закрепление, углубление и обобщение знаний учащихся по теме; повышение интереса к математике, развитие навыков логической, математической речи, умения делать выводы. …

14 11 2020 2:28:24

Обобщающий урок-соревнование по разделу «Сложение и вычитание десятичных дробей». 5-й класс

Интересные задания, нетрадиционная форма урока, групповая форма работы, применение различных видов дидактических и развивающих игр дают возможность ученикам активно включиться в учебную деятельность и формировать коммуникативную компетентность. Учащиеся работают по теме « Десятичная дробь». Вырабатываются навыки чтения, записи, сравнения десятичных дробей, их сложения и вычитания….

13 11 2020 3:30:56

Внеклассное мероприятие по математике: «Математические сутки»

Внеклассное мероприятие по математике для учащихся 6-х классов посвящено рассказу о режиме дня шестиклассника. Разнообразие творческих заданий способствует развитию у школьников не только находчивости и сообразительности, но и развивает интерес к учебному учреждению, в котором они учатся….

11 11 2020 15:12:49

Объем шара, объем шарового сегмента, шарового слоя и шарового сектора

Данная технология позволяет задействовать различные способности восприятия у различных учащихся, а именно: одни учащиеся воспринимают учебный материал через текст; другие – через восприятие изображения; третьи – через число, формулу, через письмо. Работа в группах взаимно дополняет особенности восприятия каждым учащимся и позволяет представить учебный материал максимально полно. …

10 11 2020 0:21:22

Новогоднее домашнее задание

В преддверии нового года, хочу поделиться с моими коллегами разработкой для учащихся 5-х классов. Данный материал может быть предоставлен учащимся как в виде домашнего задания, так и в виде печатной основы для проведения заключительного урока по итогам II четверти. …

09 11 2020 18:52:37

Задачи на проценты. Задачи на смеси и сплавы

В статье предлагаются разноуровневые текстовые задачи для подготовки к Г И А и Е Г Э по математике (и не только). Лишь небольшой процент учащихся пытаются решать задачи этого типа на экзамене, в проверочных работах. Еще меньший процент учащихся делает такие задания, если там присутствует значок «%» или слова «концентрация», «смеси», редко кто из учеников отважится дочитать условие до конца. Однако подобные текстовые задачи включены в проверочные или итоговые работы….

08 11 2020 11:24:43

Выбор обогревателя для воды: электрические, газовые

Горячая вода в быту необходима – это бесспорно, и в проекты современных жилых домов обязательно закладывается система горячего водоснабжения ( Г В С). Многоквартирные дома обеспечиваются горячей водой централизованно — подключением системы Г В С к магистральной теплоцентрали, а владельцы коттеджей при отсутствии такой возможности решают этот вопрос установкой водонагревающих устройств. Кроме дорогостоящих двухконтурных котлов отопления, рассчитанных также и на… Читать дальше…

04 11 2020 14:49:26

Урок-путешествие в 7-м классе «В царстве треугольников»

Урок-путешествие предлагается в качестве урока повторения и закрепления знаний за первое полугодие в 7-м классе. Содержание материала направлено на формирование интереса к предмету и соответствует требованиям стандарта образования. На уроке показана взаимосвязь математики с жизненными ситуациями….

03 11 2020 10:11:25

Геометрия 7 Атанасян Учебник | 7 класс Онлайн

Ознакомительная версия с цитатами из учебника для принятия решения о покупке книги: Геометрия. 7-9 классы. Учебник для общеобразовательных учреждений / Л.С. Атанасян и др. — М.: Мнемозина, 2018.

Содержание учебника позволяет достичь планируемых результатов обучения, предусмотренных ФГОС основного общего образования. Учебник включает трёхступенчатую систему задач, а также исследовательские задачи, темы рефератов, список рекомендуемой литературы, что позволит учащимся расширить и углубить свои знания по геометрии.

Геометрия 7 Атанасян Учебник

ОГЛАВЛЕНИЕ:

Глава I. Начальные геометрические сведения

§ 1. Прямая и отрезок (1. Точки, прямые, отрезки. 2. Провешивание прямой на местности)

Практические задания к § 1 «Прямая и отрезок» (упр.№№ 1-7)

§ 2. Луч и угол. (3. Луч. 4. Угол)

Практические задания к § 2 «Луч и угол» (упр.№№ 8-17)

§ 3. Сравнение отрезков и углов. (5. Равенство геометрических фигур. 6. Сравнение отрезков и углов)

Задачи к § 3 «Сравнение отрезков и углов» (упр.№№ 18-23)

§4. Измерение отрезков. (7. Длина отрезка. 8. Единицы измерения. Измерительные инструменты)

Практические задания и задачи к § 4 «Измерение отрезков» (упр.№№ 24-40)

§ 5. Измерение углов. (9. Градусная мера угла. 10. Измерение углов на местности)

Практические задания и задачи к § 5 «Измерение углов» (упр.№№ 41-53)

§ 6. Перпендикулярные прямые. (11. Смежные и вертикальные углы. 12. Перпендикулярные прямые. 13. Построение прямых углов на местности)

Глава II. Треугольники

§ 1. Первый признак равенства треугольников. (14. Треугольник. 15. Первый признак равенства треугольников)

§ 2. Медианы, биссектрисы и высоты треугольника. (16. Перпендикуляр к прямой. 17. Медианы, биссектрисы и высоты треугольника… 18. Свойства равнобедренного треугольника)

§ 3. Второй и третий признаки равенства треугольников (19. Второй признак равенства треугольников. 20. Третий признак равенства треугольников)

§ 4. Задачи на построение. (21. Окружность. 22. Построения циркулем и линейкой. 23. Примеры задач на построение)

Глава III. Параллельные прямые.

§ 1. Признаки параллельности двух прямых. (24. Определение параллельных прямых. 25. Признаки параллельности двух прямых. 26. Практические способы построения параллельных прямых)

§ 2. Аксиома параллельных прямых. (27. Об аксиомах геометрии. 28. Аксиома параллельных прямых. 29. Теоремы об углах, образованных двумя параллельными прямыми и секущей. 30. Углы с соответственно параллельными или перпендикулярными сторонами)

Глава IV. Соотношения между сторонами и углами треугольника

§ 1. Сумма углов треугольника. (31. Теорема о сумме углов треугольника. 32. Остроугольный, прямоугольный и тупоугольный треугольники)

§ 2. Соотношения между сторонами и углами треугольника. (33. Теорема о соотношениях между сторонами и углами треугольника. 34. Неравенство треугольника… 35. Некоторые свойства прямоугольных треугольников… 36. Признаки равенства прямоугольных треугольников. 37*. Уголковый отражатель)

§ 3. Построение треугольника по трём элементам. (38. Расстояние от точки до прямой. Расстояние между параллельными прямыми. 39. Построение треугольника по трём элементам)

Вы смотрели «Геометрия 7 Атанасян Учебник» (цитаты из пособия)

Обследование и выравнивание пирамиды Хуфу

Выравнивание пирамид и контроль формы пирамиды

На этой странице представлены различные методы древних египтян для съемки и измерения объяснены.
Исследование и контроль — Получение форма пирамиды — Возможные ошибки при строительстве пирамида — Египетские единицы измерения — Определение прямые углы — Угол наклона и секед — Точное выравнивание Север-Юг — Источники

Обследование и контроллинг

Строители пирамиды тщательно выбирали землю для строительства для пирамид.Пирамида Хуфу лежит на лучшей земле, существующей на плато Гиза и на вершине скального ядра высотой не менее 7,9 м. высота под пирамидой. Насколько важен выбор грунта под застройку был, показывает тот факт, что одна из спутниковых пирамид (G1c) вероятно пришлось переместить ближе к другим, потому что земля считалась недостаточно стабильный.

Major проблемы возникли ранее на других строительных площадках, потому что сила земли была завышена при возведении пирамиды.Например, земля под пирамидой Снефру (отца Хуфу) в Дахшуре дала под тяжестью груза и повредил корпус. Другой внешний слой обсадной колонны пришлось добавить, изменив угол наклона с 60 ° до 54,46 °. Но снова возникли структурные проблемы с проседанием, кожух соскользнул, и возникло больше повреждений. В итоге угол наклона пришлось резко снизить до 43.99 ° [6]. Теперь эта пирамида называется изогнутой пирамидой из-за ее формы.
Камни внешней облицовки пирамиды

Исследование плато Гиза показывает, что пирамиды выровнены по оси север-юг, а также по отношению друг к другу. Древние инженеры работали очень точно, не только идеально каждая из трех пирамид по центру, но угол наклона тоже одинаковый снизу вверх. вверху [4].

Карта: Плато Гиза с Великим Пирамиды ГПМП [8]. 100 м = 191 локоть. карта с GPS-координатами

Получение пирамиды

Пирамида — это простая форма, но при построении пирамидальной структуры размером с пирамиду Хуфу пришлось преодолеть множество препятствий.



Центр Центр пирамиды сдвинут в сторону.Пирамида выглядит однобокий.		Прямой угол Если углы не совпадают (например, 90 °), центр пирамида движется, и общая форма искажается.

Кромки / углы Края не расположены таким образом, чтобы образовывать постоянный угол.Форма пирамиды полностью искажена. Камни лежат в самом центре и в углу камни складывались особенно тщательно, а затем эти камни предоставит руководство по обеспечению геометрической точности четырех прямые углы и внешние камни между ними. [3].		Угол наклона Если угол наклона не контролируется, боковые поверхности пирамиды бывают выпуклыми или вогнутыми.Это было гарантировано, если внешние камни уже были разрезаны под прямым углом в карьере и до этого строго контролировались их принесли к пирамиде.

Высота и основание Пирамида определяется ее высотой и основанием.		Гладкость Блоки обсадных труб должны иметь гладкую боковую поверхность. Достигать это внешние камни были специально хорошо отполирован и все стыки залиты.

Устойчивость Для большей устойчивости некоторые слои камня слегка наклонены в сторону центр		Выравнивание По религиозным причинам все пирамиды на плато Гиза выровнены. ровно север-юг и по отношению друг к другу

Египетские единицы измерения

Древние египтяне использовали локти, ладони и пальцы в качестве единиц измерения.Локоть был разделен на 7 ладоней и ладонь на 4 пальца, в результате чего в 28 пальцев на один локоть.

Список иероглифов

Определение прямых углов

Натянув шнур между двумя колышками, воткнутыми в землю, можно получить длинный прямой линия была размечена. Затем к каждому колышку была привязана веревка одинаковой длины, более половины длины нарисованной линии.Держа струны натянутыми туго и вращая концы, египтяне могли нарисовать части двух идеальные круги. Эти дуги пересекают друг друга в двух точках. По рисунку прямая линия между этими двумя точками исходная линия делится пополам под прямым углом и линия разрезается на две равные части.

Египтяне не знали теории, объясняющей теорему Пифагора. но по опыту они знали, что могут образовывать прямые углы, используя так называемая примитивная пифагорейская тройка.Один из самых известных пример пифагорейской тройки равно 3-4-5, где 3² + 4² = 5² (9 + 16 = 25).

ср знать, что фараон нанял землемера, так называемого харпедонаптаи или гарпедонапты (канатные носилки или веревочные узловязатели). После ежегодного наводнения реки Нил, когда на дно долины откладывался богатый ил, границы собственности полей были разрушены, поэтому их пришлось восстанавливать.Харпедонаптаи использовали мерные шнуры с 11 одинаковыми узлами (или размечен краской) разделив его на 12 частей. С этими веревками они могли образуют прямоугольный треугольник со сторонами 3: 4: 5.

Тот же принцип можно использовать для определения прямого угла при площадь основания пирамиды Хуфу. Это очень точно — максимум отклонение от 90 ° составляет всего одну минуту! [5] Поскольку веревки могли быть слишком громоздкими, чтобы измерять такие большие расстояния также возможно, что вместо них использовались деревянные локтевые прутья.
Иллюстрация натяжителя веревки из гробницы Менны (здесь узлы на веревке видно, они, вероятно, делят его на расстояния в 1 локоть [2])
Глава «Инструменты и их применение» из книги Д. Арнольда

Угол наклона и секед

Как показано выше, очень важно контролировать угол наклона сторон пирамиды и гребня пирамиды.Любые ошибки сильно повлияли на форму пирамиды.

Поэтому было важно, чтобы внешних камней уже были скошен на прямой угол в карьерах Туры и не на плато пирамиды, где не хватало времени и места для выполнения этой важной задачи. По словам Франца Лёнера этот угол уже измерен как можно точнее в карьере а затем снова контролировали на строительной площадке у подножия пирамида с помощью специальной деревянный калибр.Когда камни достигнут необходимой высоты, внешние камни кладут друг на друга, а угол и Точная посадка проверяется снова. Положив сверху деревянную доску поверхности вы также можете контролировать, является ли поверхность ровной или вогнутый. Подгонку важных угловых камней можно контролировать натянув веревку по гребню пирамиды (или положив доску наверху).После завершения каждого каменного ряда поверхность пирамиды усеченная часть измерена, углы проверены, точно ли они измерены 90 градусов и если длина четырех краев одинакова. Если ошибки обнаружены, их еще можно исправить, либо путем замены камень или разрезав его на лучшую форму.
Камни внешней облицовки пирамиды
Камни для добычи пирамиды (детали скашивания камней)

От Ринд Математический папирус, который, как мы знаем, египтяне использовали так называемый seked (seqt, seqed или sqd) для определения углы.С помощью этого метода рассчитывается не фактический угол, а горизонтальное смещение стены. Другими словами, глядя на в один локоть измеряли древние египтяне, сколько ладонями или пальцами нижний край стены был смещен в сторону верхний край. Фактически, этот метод определяет прямоугольный треугольник, где один из двух катетов равен одному локтю, а другой соответствует самому секэду [7].

Для угла наклона сторон пирамиды Хуфу секед — это 5½ ладони. Другими словами, если стена 1 локоть высокий верхний край смещен на 5½ ладони (= 22 пальца) что дает угол наклона 51,84 ° или 51 ° 50’24 ». Это — с небольшой разницей — всего лишь официальный угол наклона. пирамиды Хуфу, которая дана как 51 ° 50’40 » [5].

Если мы хотим вычислить прямоугольный треугольник с помощью этого отношение ширины к высоте, используя как можно меньшие числа, мы выбираем a = 11 и b = 14, что переходит в c = 17,8 (это не пифагорейский тройной). Если мы посмотрим на высоту (280 локтей) и длину стороны (половина = 220 локтей) пирамиды Хуфу, конечно, мы находим соотношение ширины и высоты снова 14: 11.
Тройка Пифагора

Египтяне использовали секед для многих других построек. Хефрена пирамида состоит из 5 ладоней и 1 пальца (или 3-4-5 / 53,13 ° = 51 ° 06 ‘). Пирамида Джедефре состоит из 4 пальм (4-7-8 / 60,2 ° = 60 ° 12 ‘) [7].
Числа и фигуры пирамиды Хеопса (пирамида Хуфу)

Выравнивание основания пирамиды с помощью квадратного уровня

Базовая площадь или плато пирамиды Хуфу (включая окружающие тротуар) был выровнен с большой точностью, поэтому отклонение всего 2.1 см можно измерить [4]. В середине базы области осталось ядро горной породы.
Двор постройки пирамиды — центр строительный объект

Единственным инструментом для нивелирования, известным древним египтянам, был квадратный уровень. Это прямоугольный равнобедренный треугольник из дерева. Этот инструмент выполнен в форме буквы «А» и выглядит как линейка-треугольник или квадрат строителя.Отвес подвешен к верх соединенных уголков. Если отвес совпадает с отметкой в середине перекладины, поверхность, на которой две ножки подставка ровная. Поместив этот треугольник на камень, их можно было бы легко выровнен.

Равнобедренный треугольник из дерева с отвесом и отвес, который указывает на отметку на поперечине.

Для установления равных уровней на больших расстояниях этот Треугольник укладывался поверх балки.Сначала проверили треугольник и отрегулирован так, чтобы он лежал горизонтально и ровно на балке. Затем, по крепление на выравнивающей рейке на расстоянии, перепады высоты могут быть замеченным и исправленным. Полевые испытания показали, что на расстоянии до 45 м может быть обнаружена разница в 1 сантиметр [8]. Из-за ограниченного зрения людей большие расстояния не могли быть покрытым. Но потому что с этого можно смотреть в обе стороны. вид измерительной станции, наверное можно было правильно нивелировать дистанции до 90 метров.Квадраты уровней, как мы здесь описали, были найдено, например, в гробнице Сенеджема в Дейр-эль-Медине.

Еще одно предложение некоторых археологов — копать ровные канавы, окружающие пирамиды, с последующим заполнением их водой. В верхней части поверхности воды уровень будет отмечен по стороны канав в качестве ориентира. Другие археологи возражают, что Нил и канал Нила спускаются примерно на 44 м ниже, и эта вода испаряется. быстро в пустыне.Они думают, что такой способ выравнивания мог бы не использовались.

Точное выравнивание Север-Юг

Ось север-юг Великой пирамиды почти совпадает с истинным севером, отклонение составляет всего 2 фута 28 дюймов. Чтобы добиться такой точности, египтяне пришлось сделать точный осмотр и сделать контрольные замеры. Отто Нойгебауэр [1] предлагает простое решение этой проблемы.

Небольшая, но точно обработанная пирамидка (сделанная из дерева или камня) — это размещены как можно ближе к позиции север-юг на плоской земля, на которой будет построена пирамида. Затем проводят две линии, принимая края маленькой пирамидки и удлинение их на той стороне, которая лежит в тени. В течение дня инспектор отмечает, где именно кончик тени пирамиды прорезает эти две линии.Пирамидион точно выровнен с севера на юг, когда обе линии разрезаются одновременно расстояние до угла пирамидиона. Для этого пирамидион немного перемещается в течение нескольких дней, пока оба сегмента не будут точно такой же длины. Поскольку пирамидион можно перемещать, процесс можно повторяется в нескольких местах на плато пирамиды, таким образом проверяя и перепроверяя выравнивание север-юг. Даже при строительстве пирамиды при работе над усеченной пирамидой эту систему можно снова использовать для проверка, достаточно ли гладкая поверхность, например, на вершине пирамиды плато.

Как определить выравнивание пирамиды с севера на юг

Эти измерения легче проводить зимой месяцев, когда солнце находится ниже за горизонтом, потому что летом месяцами пирамиды не отбрасывают тени большую часть дня.

Для большей точности теперь вы можете построить небольшой, но точной формы пирамида.К югу от пирамиды Хуфу находится небольшая пирамида (G1d) размером 23 раза по 23 м и имеет угол 51-52 ° [2]. Эта пирамида или одна из пирамид королевы могли быть использованы для дальнейшей корректировки выравнивания север-юг, снова используя тот же процесс описано выше, но с небольшими изменениями.

Еще одно, более сложное предложение было сделано I.E.S. Эдвардс. Согласно его теории, египтяне построили круглую стену, вершина которой был тщательно выровнен, создав искусственный горизонт.С прямой шест с раздвоенным верхом в центре были сделаны наблюдения, чтобы определить, где именно восходила и заходила некая приполярная звезда. С использованием Отвесом позиции были отмечены внизу стены. Разделив пополам На этих позициях был обеспечен истинный север [3]. Иллюстрация

Источники

[1] О. Нойгебауэр Об ориентации пирамид
[2] Д.Арнольд Лексикон der Ägyptischen Baukunst
[3] I.E.S. Эдвардс Пирамиды Египта
[4] М. Ленер. Полные пирамиды. Египта
[5] Р. Штадельманн Die grossen Пирамида фон Гиза
[6] Это настоящая причина, а не то, как утверждают некоторые авторы, что Сенефру закончатся деньги до того, как пирамида будет завершена! Он действительно построил второй рядом — Красная пирамида.
[7] К. Росси Архитектура и математика в Древнем Египте
[8] Проект по картированию плато Гиза GPMP

Каир (Египет): Sun’s расположение / Обзор все месяцы
Самый короткий день (22. декабря):
Пиковая высота солнца (вершина) 36 °
Самая низкая высота солнца (нижняя точка кульминации) -83 °
Самый длинный день (21.Июнь):
Пиковая высота Солнца (вершина) 83 °
Самая низкая высота солнца (нижняя точка кульминации) -36 °
Пояснение:
Высота солнца указывается в градусах, ноль градусов означает положение солнца на горизонте и 90 градусов, что означает вертикаль положение солнца по отношению к наблюдателю.

Diese Seite auf Deutsch (Pyramidenform — Vermessungstechniken)

5.4 Тригонометрия прямоугольного треугольника — Precalculus

Мы ранее определили синус и косинус угла в терминах координат точки на единичной окружности, пересекаемой конечной стороной угла:

В этом разделе мы увидим еще один способ определения тригонометрических функций с использованием свойств прямоугольных треугольников.

Использование прямоугольных треугольников для вычисления тригонометрических функций

В предыдущих разделах мы использовали единичный круг для определения тригонометрических функций.В этом разделе мы расширим эти определения, чтобы применить их к прямоугольным треугольникам. Значение функции синуса или косинуса tt — это его значение в радианах tt. Во-первых, нам нужно создать наш прямоугольный треугольник. На рисунке 1 показана точка на единичной окружности радиуса 1. Если мы опустим вертикальный отрезок линии из точки (x, y) (x, y) на ось x , мы получим прямоугольный треугольник, вертикальная сторона которого длины yy, а горизонтальная сторона которого имеет длину xx Мы можем использовать этот прямоугольный треугольник, чтобы переопределить синус, косинус и другие тригонометрические функции как отношения сторон прямоугольного треугольника.

Рисунок 1

Мы знаем

Точно так же мы знаем

Эти соотношения по-прежнему применяются к сторонам прямоугольного треугольника, когда не используется единичный круг, и когда треугольник находится не в стандартном положении и не отображается на графике с использованием координат (x, y) (x, y). Чтобы иметь возможность свободно использовать эти соотношения, мы дадим сторонам более общие имена: вместо x, x мы будем называть сторону между заданным углом и прямым углом смежной стороной с углом t.t. (Соседний означает «рядом с.”) Вместо y, y назовем сторону, наиболее удаленную от данного угла, противоположной стороной от угла t.t. И вместо 1,1 назовем сторону прямоугольного треугольника, противоположную прямому углу, гипотенузой. Эти стороны обозначены на Рисунке 2.

Рисунок 2 Стороны прямоугольного треугольника в зависимости от угла t.t.

Понимание отношений правого треугольника

Дан прямоугольный треугольник с острым углом t, t,

sin (t) = противоположный гипотенузетан (t) = смежный гипотенузетан (t) = противоположныйаджаценцин (t) = противоположный гипотенуз (t) = смежный гипотенузетан (t) = противоположный смежный

Распространенным мнемоническим символом для запоминания этих отношений является SohCahToa, образованный из первых букв « S ine is o pposite over h ypotenuse, C osine is a djacent over h ypotenuse, Угол равен o pposite над a djacent.”

Как сделать

Зная длины сторон прямоугольного треугольника и один из острых углов, найдите синус, косинус и тангенс этого угла.

Найдите синус как отношение противоположной стороны к гипотенузе.
Найдите косинус как отношение смежной стороны к гипотенузе.
Найдите касательную как отношение противоположной стороны к прилегающей.

Пример 1

Вычисление тригонометрической функции прямоугольного треугольника

Для треугольника, показанного на рисунке 3, найдите значение cosα.cosα.

Рисунок 3

Решение

Сторона, прилегающая к углу, равна 15, а гипотенуза треугольника равна 17, поэтому:

cos (α) = смежная гипотенуза = 1517 cos (α) = смежная гипотенуза = 1517

Попробовать # 1

Для треугольника, показанного на рисунке 4, найдите значение sint.sint.

Рисунок 4

Взаимосвязь углов и их функций

При работе с прямоугольными треугольниками применяются одни и те же правила независимо от ориентации треугольника.Фактически, мы можем оценить шесть тригонометрических функций любого из двух острых углов в треугольнике на рисунке 5. Сторона, противоположная одному острому углу, является стороной, смежной с другим острым углом, и наоборот.

Рис. 5 Сторона, прилегающая к одному углу, противоположна другому.

Нас попросят найти все шесть тригонометрических функций для заданного угла в треугольнике. Наша стратегия — сначала найти синус, косинус и тангенс углов. Затем мы можем легко найти другие тригонометрические функции, потому что мы знаем, что величина, обратная синусу, является косекансной, обратная величина косинуса — секущей, а обратная величина касательной — котангенсом.

Как сделать

Учитывая длины сторон прямоугольного треугольника, вычислите шесть тригонометрических функций одного из острых углов.

При необходимости нарисуйте прямоугольный треугольник и обозначьте полученный угол.
Укажите угол, прилегающую сторону, сторону, противоположную углу, и гипотенузу прямоугольного треугольника.
Найдите нужную функцию:
- синус как отношение противоположной стороны к гипотенузе
- Косинус как отношение смежной стороны к гипотенузе
- касательная как отношение противоположной стороны к соседней
- секанс как отношение гипотенузы к прилегающей стороне
- косеканс как отношение гипотенузы к противоположной стороне
- котангенс как отношение соседней стороны к противоположной

Пример 2

Оценка тригонометрических функций углов, не находящихся в стандартном положении

Используя треугольник, показанный на рисунке 6, оцените sinα, sinα, cosα, cosα, tanα, tanα, secα, secα, cscα, cscα и cotα.cotα.

Рисунок 6

Решение

sinα = противоположный αгипотенуза = 45 cosα = прилегающий к αгипотенузе = 35tanα = противоположный α прилегающий к α = 43sec α = гипотенуза прилегающий к α = 53 cscα = гипотенуза напротив α = 54 cotα = смежный с αпротивоположным α = 34 sinα = противоположный ααгипотенуза = 45cosα = напротив αгипотенуза α рядом с α = 43 сек α = гипотенуза рядом с α = 53 csc α = гипотенуза напротив α = 54 cot α = рядом с α напротив α = 34

Попробовать # 2

Используя треугольник, показанный на рисунке 7, оцените sint, sint, cost, cost, tant, tant, sect, sect, csct, csct и cott.Котт.

Рисунок 7

Нахождение тригонометрических функций специальных углов с использованием длин сторон

Мы уже обсуждали тригонометрические функции, поскольку они связаны со специальными углами на единичной окружности. Теперь мы можем использовать эти отношения для оценки треугольников, содержащих эти особые углы. Мы делаем это, потому что, когда мы оцениваем специальные углы в тригонометрических функциях, они имеют относительно дружественные значения, значения, которые не содержат или содержат только один квадратный корень в соотношении.Поэтому эти углы часто используются в математических и научных задачах. Мы будем использовать кратные 30 °, 30 °, 60 °, 60 ° и 45 °, 45 °, однако помните, что при работе с прямоугольными треугольниками мы ограничены углами от 0 ° до 90 °, от 0,0 ° до 90 °.

Предположим, у нас есть треугольник 30 °, 60 °, 90 °, 30 °, 60 °, 90 °, который также можно описать как треугольник π6, π3, π2π6, π3, π2. Стороны имеют длины в соотношении s, 3s, 2s.s, 3s, 2s. Стороны треугольника 45 °, 45 °, 90 ° 45 °, 45 °, 90 °, который также можно описать как треугольник π4, π4, π2π4, π4, π2, имеют длины в соотношении s, s, 2s. .с, с, 2 с. Эти отношения показаны на рисунке 8.

Рис. 8 Длины сторон особых треугольников

Затем мы можем использовать отношения длин сторон для оценки тригонометрических функций специальных углов.

Как сделать

Даны тригонометрические функции особого угла, вычислить с помощью длин сторон.

Используйте длины сторон, показанные на рисунке 8, для особого угла, который вы хотите оценить.
Используйте соотношение длин сторон, соответствующее функции, которую вы хотите оценить.

Пример 3

Оценка тригонометрических функций специальных углов с использованием длин сторон

Найдите точное значение тригонометрических функций π3, π3, используя длины сторон.

Решение

sin (π3) = opphyp = 3s2s = 32cos (π3) = adjhyp = s2s = 12tan (π3) = oppadj = 3ss = 3sec (π3) = hypadj = 2ss = 2csc (π3) = hypopp = 2s3s = 23 = 233cot (π3 ) = adjopp = s3s = 13 = 33sin (π3) = opphyp = 3s2s = 32cos (π3) = adjhyp = s2s = 12tan (π3) = oppadj = 3ss = 3sec (π3) = hypadj = 2ss = 2csc (π3) = hypopp = 2s3s = 23 = 233cot (π3) = adjopp = s3s = 13 = 33

Попробовать # 3

Найдите точное значение тригонометрических функций π4, π4, используя длины сторон.

Использование равных функций дополнений

Если мы более внимательно посмотрим на соотношение между синусом и косинусом особых углов относительно единичной окружности, мы заметим закономерность. В прямоугольном треугольнике с углами π6π6 и π3, π3 мы видим, что синус π3, π3, а именно 32,32, также является косинусом π6, π6, а синус π6, π6, а именно 12,12, также является косинусом числа π3.π3.

sinπ3 = cosπ6 = 3s2s = 32sinπ6 = cosπ3 = s2s = 12sinπ3 = cosπ6 = 3s2s = 32sinπ6 = cosπ3 = s2s = 12

См. рисунок 9

Рис. 9 Синус числа π3π3 равен косинусу числа π6π6, и наоборот.

Этот результат не должен вызывать удивления, потому что, как мы видим из рисунка 9, сторона, противоположная углу π3π3, также является стороной, смежной с π6, π6, поэтому sin (π3) sin (π3) и cos (π6) cos (π6 ) имеют точно такое же соотношение тех же двух сторон, 3s3s и 2s.2s. Точно так же cos (π3) cos (π3) и sin (π6) sin (π6) также являются одинаковыми отношениями с использованием тех же двух сторон, ss и 2s.2s.

Взаимосвязь между синусами и косинусами π6π6 и π3π3 также сохраняется для двух острых углов в любом прямоугольном треугольнике, поскольку в любом случае отношение одних и тех же двух сторон будет составлять синус одного угла и косинус другого. .Поскольку три угла треугольника складываются с π, π, а прямой угол равен π2, π2, оставшиеся два угла также должны составлять π2.π2. Это означает, что прямоугольный треугольник может быть образован любыми двумя углами, которые складываются с π2π2, другими словами, любыми двумя дополнительными углами. Таким образом, мы можем сформулировать тождество кофункции : Если любые два угла дополняют друг друга, синус одного является косинусом другого, и наоборот. Эта идентичность проиллюстрирована на рисунке 10.

Рисунок 10 Тождество совместных функций синуса и косинуса дополнительных углов

Используя это равенство, мы можем утверждать, не вычисляя, например, что синус π12π12 равен косинусу 5π12,5π12, а синус 5π125π12 равен косинусу №12.№12. Мы также можем утверждать, что если для некоторого угла t, t, cost = 513, cost = 513, тогда также sin (π2 − t) = 513sin (π2 − t) = 513.

Идентификаторы совместных функций

Идентификаторы совместных функций в радианах перечислены в таблице 1.

стоимость = sin (π2 − t) стоимость = sin (π2 − t)	синт = соз (π2 − t) синт = соз (π2 − t)
tant = детская кроватка (π2 − t) tant = детская кроватка (π2 − t)	котт = загар (π2 − t) котт = загар (π2-t)
секция = csc (π2 − t) секция = csc (π2 − t)	csct = сек (π2 − t) csct = sec (π2 − t)

Таблица 1

Как сделать

Зная синус и косинус угла, найдите синус или косинус его дополнения.

Чтобы найти синус дополнительного угла, найдите косинус исходного угла.
Чтобы найти косинус дополнительного угла, найдите синус исходного угла.

Пример 4

Использование идентификаторов совместных функций

Если sint = 512, sint = 512, найти (cosπ2 − t). (Cosπ2 − t).

Решение

Согласно идентификаторам совместных функций для синуса и косинуса,

sint = cos (π2 − t). sin = cos (π2 − t).

Так

cos (π2 − t) = 512.cos (π2 − t) = 512.

Попробовать # 4

Если csc (π6) = 2, csc (π6) = 2, найти sec (π3) .sec (π3).

Использование тригонометрических функций

В предыдущих примерах мы вычисляли синус и косинус в треугольниках, где мы знали все три стороны. Но настоящая сила тригонометрии прямоугольного треугольника проявляется, когда мы смотрим на треугольники, в которых мы знаем угол, но не знаем всех сторон.

Как сделать

Дан прямоугольный треугольник, длина одной стороны и величина острого угла. Найдите остальные стороны.

Для каждой стороны выберите тригонометрическую функцию с неизвестной стороной в качестве числителя или знаменателя. Известная сторона, в свою очередь, будет знаменателем или числителем.
Напишите уравнение, устанавливающее значение функции известного угла, равное отношению соответствующих сторон.
Используя значение тригонометрической функции и известную длину стороны, найдите недостающую длину стороны.

Пример 5

Поиск недостающих длин сторон с использованием тригонометрических соотношений

Найдите неизвестные стороны треугольника на рисунке 11.

Рисунок 11

Решение

Мы знаем угол и противоположную сторону, поэтому мы можем использовать касательную, чтобы найти прилегающую сторону.

Переставляем решать для а.о.

a = 7tan (30 °) ≈12,1a = 7tan (30 °) ≈12,1

Мы можем использовать синус, чтобы найти гипотенузу.

Опять же, мы переставляем, чтобы решить для c.c.

c = 7sin (30 °) ≈14c = 7sin (30 °) ≈14

Попробовать # 5

В прямоугольном треугольнике один угол π3π3 и гипотенуза 20.Найдите неизвестные стороны и угол треугольника.

Использование тригонометрии прямоугольного треугольника для решения прикладных задач

Тригонометрия прямоугольного треугольника имеет множество практических применений. Например, способность вычислять длины сторон треугольника позволяет определить высоту высокого объекта, не взбираясь на вершину и не протягивая рулетку по его высоте. Мы делаем это, измеряя расстояние от основания объекта до точки на земле на некотором расстоянии, откуда мы можем смотреть на вершину высокого объекта под углом.Угол возвышения объекта над наблюдателем относительно наблюдателя — это угол между горизонталью и линией от объекта до глаза наблюдателя. Правый треугольник, создаваемый этим положением, имеет стороны, которые представляют неизвестную высоту, измеренное расстояние от основания и наклонную линию обзора от земли до вершины объекта. Зная измеренное расстояние до основания объекта и угол прямой видимости, мы можем использовать тригонометрические функции для вычисления неизвестной высоты.Точно так же мы можем сформировать треугольник из вершины высокого объекта, глядя вниз. Угол наклона объекта под наблюдателем относительно наблюдателя — это угол между горизонталью и линией от объекта до глаза наблюдателя. См. Рисунок 12.

Рисунок 12

Как сделать

Для высокого объекта измерьте его высоту косвенно.

Сделайте набросок проблемной ситуации, чтобы отслеживать известную и неизвестную информацию.
Разместите измеренное расстояние от основания объекта до точки, где верх объекта будет хорошо виден.
Посмотрите на верхнюю часть объекта на другом конце измеренного расстояния. Измерьте угол, под которым линия визирования образует горизонталь.
Напишите уравнение, связывающее неизвестную высоту, измеренное расстояние и тангенс угла линии визирования.
Решите уравнение для неизвестной высоты.

Пример 6

Косвенное измерение расстояния

Чтобы определить высоту дерева, человек подходит к точке в 30 футах от основания дерева.Она измеряет угол 57 ° 57 ° между линией обзора верхушки дерева и землей, как показано на рисунке 13. Найдите высоту дерева.

Рисунок 13

Решение

Мы знаем, что угол места 57 ° 57 °, а длина прилегающей стороны 30 футов. Противоположная сторона — неизвестная высота.

Тригонометрическая функция, связывающая сторону, противоположную углу, и сторону, прилегающую к углу, является касательной. Таким образом, мы представим нашу информацию в терминах тангенса 57 °, 57 °, пусть hh будет неизвестной высотой.

tanθ = противоположный соседний угол (57 °) = h40. Вычислить для hh = 30tan (57 °) Умножить. h≈46,2 С помощью калькулятора. tanθ = противоположный соседний край (57 °) = h40. Вычислить для hh = 30tan (57 °) Умножить. калькулятор.

Дерево примерно 46 футов в высоту.

Попробовать # 6

Какова длина лестницы, чтобы добраться до подоконника на высоте 50 футов над землей, если она упирается в здание под углом 5π125π12 к земле? Округлите до ближайшего фута.

Задачи со словами в правом треугольнике

Правый треугольник Проблемы со словами

Как только вы узнали о тригонометрии отношения (и их обратные), вы можете решать треугольники.Естественно, многие из этих треугольников будут представлены в контексте текстовых задач. Хороший первый шаг после прочтения всего упражнения — нарисовать правильный треугольник и попытайтесь придумать, как его обозначить. Как только у вас появится полезный диаграмма, математика обычно довольно проста.

Лестница длиной шесть метров прислоняется к зданию. Если лестница составляет угол 60 ° с на землю, как далеко до стены поднимается лестница? Как далеко от стена является основанием лестницы? Округлите ответы до двух знаков после запятой места по мере необходимости.

Сначала я нарисую картинку. Это не обязательно быть «хорошим»; это просто должно быть ясно достаточно, чтобы я мог отслеживать то, что делаю.

Моя фотография справа:

Мне нужно найти высоту х . Поскольку они дали мне угловую меру и «противоположное» и гипотенуза для этого угла, я буду использовать коэффициент синуса для находим высоту:

Вставив это в свой калькулятор, Я получаю приблизительное значение 5.196152423.

Для базы я использую косинусное отношение:

Лестница тянется примерно 5,20 м вверх по стене,
и его база находится в 3 метрах от стена.

Примечание. Если вас не попросят предоставить ответ в десятичной форме, или округлить, или иным образом , а не , чтобы дать «точный» ответ, вы, вероятно, должны предположить, что «точная» форма — вот чего они хотят.Например, если они не сказал мне округлить в упражнении выше, мое значение для роста должно было быть значение с радикалом.

Пятиметровая лестница прислоняется к стене так, чтобы верх лестницы был на четыре метра выше земля. Какой приблизительный угол образует лестница с земля?

Как обычно, начну с картинки:

Мне дали «противоположное» и гипотенуза, и спросил у меня значение угла.Для этого я необходимо использовать обратные триггерные отношения.

Угол между лестницей и землей около 53 ° .

Вы используете транзит до измерить угол падения солнца на небе; Солнце заполняет 34 фута дуги. Предполагая Солнце находится на расстоянии 92 919 800 миль, найдите диаметр Солнца. Круглый ваш ответ с точностью до ближайшей мили.

Сначала нарисую картинку:

Хм… Этот «рожок мороженого» картина не дает мне много работать, и нет права треугольник.

Две линии по бокам Мой треугольник измеряет лучи взгляда от Земли по сторонам солнца. Что, если я добавлю еще одну строку, будучи прямой линией от Земли до центра Солнца?

Теперь, когда у меня есть эта добавленная строка, У меня прямоугольный треугольник; на самом деле два прямоугольных треугольника, но я нужен только один.

Потому что Солнце так далеко, очевидно, эта картина не «в масштабе», и я буду игнорировать тот факт, что измеренное расстояние не совсем совпадает изображение. Но этого должно быть достаточно.

(Угол мера, «тридцать четыре угловые минуты», равна 34/60 градусов. Разделив это пополам, я получил 17/60 степени для меньшего угла.)

Мне нужно найти ширину Солнца. Эта ширина будет вдвое больше основания одного из прямоугольных треугольников. С Что касается моего угла, они дали мне «смежный» и попросил «противоположное», поэтому я буду использовать тангенциальное отношение: Авторские права © Элизабет Stapel 2010-2011 Все права защищены.

Это только половина ширины; несущий вычисления в моем калькуляторе (чтобы минимизировать ошибку округления), я получаю значение 919002.8129. Это больше, чем фактический диаметр, который ближе к 864 900 милям, но этого значения будет достаточно для целей данного упражнения.

Диаметр около 919 003 миль.

Летит частный самолет 1,3 часа на скорости 110 миль в час по азимуту 40 °. Потом поворачивается и продолжается еще 1,5 часа на той же скорости, но по пеленгу 130 °.В в конце этого времени, как далеко самолет от начальной точки? Каково его значение с этой отправной точки?

Подшипники говорят мне углы от «правильного севера» по часовой стрелке. Поскольку 130-40 = 90, эти два подшипника дадут мне прямоугольный треугольник. По времени и тарифам нахожу расстояния:

Теперь, когда у меня есть длины двух ножки, могу составить треугольник:

Я могу найти расстояние, используя теорему Пифагора:

165 находится напротив неизвестного угла, а 143 — рядом, поэтому я буду использовать обратное отношение тангенса, чтобы найти размер угла:

Но это не «подшипник», так как пеленг — это угол по отношению к «правильному северу».Мне нужно добавить исходный угол в сорок градусов, чтобы получить ответ:

Самолет находится на расстоянии примерно 218 миль с азимутом примерно 89 ° .

Другой основной класс слов в форме прямоугольного треугольника проблемы, с которыми вы, вероятно, столкнетесь, — это углы возвышение и депрессия ….

Вверх | Вернуться к индексу

Цитируйте эту статью как:

Стапель, Елизавета.»Задачи о прямоугольных словах». Пурпурная математика . Доступна с
https://www.purplemath.com/modules/rghtprob.htm . Доступ [Дата] [Месяц] 2016 г.

Дом без углов — ARTnews.com

В мастерской живет художник Виктор Мельников, сын архитектора.

HARF ZIMMERMAN

Дом с высеченной на фасаде надписью «Архитектор Константин Мельников» расположен в зеленом переулке в самом центре Москвы. Этой надписью сам Мельников превратил дом в памятник. Это редкая жемчужина прошлого века в России — дом, построенный для себя и своей семьи одним из самых блестящих и новаторских архитекторов.

Дом Мельникова — памятник в беде. Его ветхость слишком заметна. Его бетонные стены крошатся и заляпаны водой, а некоторые окна забиты. World Monuments Watch недавно включил его в список 100 наиболее находящихся под угрозой исчезновения мест 2006 года. Сын архитектора, Виктор Мельников, которому 90 лет, все еще живет в доме и заботится о его сохранении, но в Мельникове есть разногласия. семья поставила под сомнение будущее строения.

Константин Мельников (1890–1974) отказался от традиционных стилей и методов строительства в поисках нового пространства для нового мира. В начале ХХ века, когда русский авангард был в авангарде международного художественного мира, именно Мельников больше, чем кто-либо другой, воплотил инновации визуальных художников в архитектуре. Контррельефы Владимира Татлина, например, послужили источником вдохновения для русского павильона Мельникова на Международной выставке современного и декоративного искусства в Париже в 1925 году.

Мельников — наследник русской художественной традиции, подчеркивающей выразительность, эмоциональность в творчестве. Его формы намекают на образы и полны ассоциаций. Его знаменитый клуб «Русаков», построенный для Союза городских рабочих Москвы (1927–29), имеет три консольных клина, напоминающих зубья шестерни. Внутри они обеспечивают уклон для сидений театра.

Чтобы реализовать такие здания в эпоху, когда господствовали идеалы функционализма и рациональности, требовалась решимость.В период своего расцвета с 1927 по 1929 год Мельникову удалось построить в Москве шесть зданий, все они были рабочими клубами. Каждый из них уникален и поразительно оригинален. Он начал планировать построить дом для себя и своей семьи в начале 1920-х годов, но строительство не началось до 1927 года и не было завершено до 1929 года.

Строение дома необычное. Он состоит из двух взаимосвязанных вертикальных бетонных цилиндров, северный из которых выше, чтобы дать доступ к террасе на крыше южного.Входной фасад в южном цилиндре представляет собой стеклянную стену, обрамленную квадратными угловыми пилястрами, а северный цилиндр освещен 56 шестиугольными окнами, вставленными в диагональную кирпичную сетку рамы. Частью плана Мельникова было, чтобы эти окна можно было залить или в любой момент выбить новые из кирпичной сетки (он добавил окно, пока дом строился).

Построить дом без прямых углов было идеей фикс Мельникова. К счастью, его жена поддержала идею, хотя изначально ее беспокоило, что комнаты необычной формы вызовут у людей головокружение.Было сложно организовать внутреннее пространство для проживания и работы семьи, да и в доме есть свои неловкие места. В некоторых комнатах, как писал финский архитектор Юхани Палласмаа, «ориентация внутри двух цилиндров с диагональными и наклонными стенами действительно становится очень запутанной. Круглость, прямоугольность, диагональность и ось находятся в постоянном взаимодействии и напряжении ».

Кухня и столовая находятся на первом этаже, вместе с дневными комнатами для двоих детей, гардеробной, хозяйственной комнатой и ванной комнатой.Над ними, на втором этаже, расположены гостиная и спальная зона. Наверху более высокого цилиндра находится студия Мельникова, у которой есть балкон, выходящий на террасу на крыше.

Гостиная и студия Мельникова — самые большие и впечатляющие комнаты в доме. В высокой гостиной преобладает стеклянная стена фасада, четыре центральных стеклянных панели которой летом открываются в сад и на улицу. Я посетил этот дом с группой студентов МГУ, когда Мельников был еще жив, и он рассказал нам, что, когда из гостиной убрали леса, он стоял в центре комнаты и кричал так громко, как мог.Почему? Потому что «когда строительство базилики Святого Петра с ее уникальным гигантским куполом было завершено, великий итальянец стоял под ней и кричал». Впоследствии Микеланджело объяснил, что если бы купол рухнул, он бы похоронил только своего незадачливого создателя. К счастью, и Микеланджело, и Мельников были хорошими архитекторами, и их купола уцелели.

Спальная зона — это более интимное пространство, освещенное 12 шестиугольными окнами, с гораздо более низким потолком, чем в соседней гостиной.Здесь спала вся семья, потому что у Мельникова были сложные теории о сне — он считал его восстанавливающим почти чудесным образом. Единственными объектами в комнате были бетонная платформа для сна для архитектора и его жены и поменьше платформы для детей. (Их давно заменили на обычные кровати.) Платформа для родителей была отделена от детской диагональными перегородками с каждой стороны, которые не доходили до потолка. Эзотерические представления Мельникова о сне стояли за еще одной необычной особенностью этой комнаты.Он сказал нам, что изначально оно было золотым: стены, пол и потолок были выкрашены в золотой цвет, а все постельное белье было золотым. «Когда мы проснулись утром, — сказал он, — нам казалось, будто мы плывем в густом золотом воздухе. Это было необыкновенное чувство ».

Позже Мельников развил свои идеи о лечебной ценности сна в своей «Лаборатории сна», предложенной как составная часть его утопического Зеленого города. Это должно было быть общежитие для рабочих, которое во всех аспектах контролировалось командой технических специалистов.

Мастерская архитектора — еще одно большое общественное пространство, освещенное 38 шестигранными окнами. Первоначально он был окрашен в темно-фиолетовый фиолетовый цвет, что, по словам Палласмаа, придавало ему странную мистическую атмосферу. Сейчас студией пользуется Виктор Мельников, импрессионистические картины которого висят на стенах дома.

По иронии судьбы, этот самый современный и нетрадиционный дом был обставлен антиквариатом, купленным почти за бесценок в 1920-х годах. Но из-за того, что Мельников требовал чистоты и отсутствия пыли, мебель оставалась редкой.

С 1930 по 1950 год Мельников подвергался остракизму, и все его постройки, особенно его дом, подвергались резкой критике. Это чудо, что его не арестовали и не снесли дом. Только в 1965 году, когда ему неохотно была посвящена выставка в штаб-квартире Московского отделения Союза советских архитекторов — организации, разрушившей его карьеру много лет назад, — стало приемлемо ценить его. Хотя выставка закрылась через четыре дня и огласка была запрещена, интерес к Мельникову возродился.Дом в Кривоарбатском переулке получил мировую известность.

Конструкция долгое время разрушалась. Через несколько дней после немецкого вторжения в 1941 году поблизости упала бомба, и ударные волны разбили большую часть стекла. Вскоре после этого вышла из строя система отопления, в результате чего возникли проблемы с сыростью. Неудачная попытка реставрации в 1990-х годах привела к серьезному ущербу, причиненному водой. Теперь дом находится в еще большей опасности из-за безудержного бума застройки Москвы.
Его дренажная система была разрушена из-за строительства подземной автостоянки по соседству, и есть вероятность того, что он будет окружен со всех сторон новыми зданиями.Когда-то Кремль был виден с террасы, и солнечный свет заливал комнаты, но сегодня солнце больше не достигает большинства окон дома.

Судьба сооружения беспокоит всех, кто хочет сохранить памятники московского модерна. В марте Виктор Мельников провел пресс-конференцию, на которой объявил о своем завещании передать дом государству с условием, что он станет музеем, посвященным архитектору. Его поддерживает старшая дочь Екатерина, но младшая дочь Елена утверждает, что дом принадлежит ей.Согласно сообщению Михаила Ревзина в газете «Коммерсант », Виктор заявил, что Елена обманом заставила его подписать документ о предоставлении ей дома и что она хотела его продать, но его завещание аннулировало все предыдущие документы. Так что судьба дома может решиться в зале суда. Между тем, к сожалению, он продолжает разваливаться.

Как найти углы прямоугольного треугольника

Обновлено 3 ноября 2020 г.

Крис Дезил

Сложите значения трех углов в любом треугольнике, и вы получите 180 градусов.Если у вас прямоугольный треугольник, один из его углов по определению равен 90 градусам. Это означает, что сумма двух других углов должна составлять 90 градусов, и если вы знаете один из них, вы можете сразу найти другой. Но как найти углы, если вы тоже не знаете? Ответ заключается в том, чтобы полагаться на другое важное свойство треугольника — длину его сторон. Они связаны с величиной углов.

TL; DR (слишком длинный; не читал)

Найдите углы в прямоугольном треугольнике, вычислив их синус, косинус или тангенс, которые являются функциями длин сторон треугольника.

Синус, косинус и тангенс

Когда вы выбираете, какой из двух углов (ø) в прямоугольном треугольнике вы хотите найти, вы устанавливаете три стороны по отношению к нему. Линия, которая касается угла и продолжается до угла 90 градусов, называется стороной , прилегающей к , а сторона, противоположная углу, — это сторона , противоположная стороне . Гипотенуза всегда находится на стороне, противоположной прямому углу. Основываясь на этих определениях, математики используют три соотношения, которые определяют угол в терминах длин сторон:

Синус (sin) — это отношение противоположной стороны к гипотенузе:

\ sin ø = \ frac {\ text {напротив}} {\ text {hypotenuse}}

Косинус (cos) — это отношение смежной стороны к гипотенузе:

\ cos ø = \ frac {\ text {смежный} } {\ text {hypotenuse}}

Касательная (загар) — это отношение противоположной стороны к соседней стороне:

\ tan ø = \ frac {\ text {напротив}} {\ text {смежный }}

Каждое отношение каждой пары линий соответствует определенному углу, и эти отношения сведены в таблицу вместе с углами, которые они определяют.Если вы можете измерить длину хотя бы двух сторон прямоугольного треугольника, все, что вам нужно сделать, это вычислить синус, косинус или тангенс угла и использовать таблицу, чтобы найти его.

Лестница у стены

Одно из наиболее известных практических применений этих принципов — лестница, опирающаяся на вертикальную стену. Величины углов, которые лестница образует с землей и стеной, имеют решающее значение. Если угол относительно стены слишком мал, лестница упадет назад, а если угол на земле слишком мал, лестница соскользнет.Поскольку угол между стеной и землей составляет 90 градусов, вы можете рассчитать два угла, которые образует лестница, используя синус, косинус или тангенс, и таким образом вы можете предотвратить несчастный случай.

Лестница образует гипотенузу прямоугольного треугольника.

Это расстояние является соседней стороной при определении угла лестницы относительно земли.

Используйте таблицы косинусов, чтобы найти угол между лестницей и землей. Вычислите отношение соседней стороны к гипотенузе, а затем найдите это отношение в таблице косинусов, чтобы найти соответствующий угол.

Рассчитайте угол между лестницей и стеной, вычтя найденный угол из 90. Кроме того, вы можете найти значение этого угла с помощью таблицы синусов.

Пример

20-футовая лестница упирается в стенку дома, а расстояние от основания лестницы до фундамента составляет 12 футов. Каковы углы лестницы относительно земли и дома?

Вычислите косинус угла между лестницей и землей.Это

\ frac {12} {20} = 0,6

Используя таблицу косинусов (или научный калькулятор), вы обнаружите, что угол составляет почти точно 53 градуса. Таким образом, угол лестницы относительно стены составит

90 — 53 = 36 \ text {градусы}

Как выровнять опоры

При наличии фундамента на ровной поверхности возведение секции в квадрат довольно просто и может быть выполнено без наличия сложного геодезического оборудования на месте. Размещение опор на склоне становится немного сложнее, но если уклон находится в пределах разумного, и с использованием стремянки, прямого куска пиломатериала и уровня, это будет работать так же, как вы делаете это на ровной поверхности.

Я должен добавить, что заставить геодезиста выйти и закрепить все углы фундамента было бы неплохим планом. Особенно, если вы не привыкли заниматься такой работой. Попросите его поставить маркер (большой гвоздь с лентой) в углах фундаментной стены. Пусть он разметит столько углов фундамента, сколько вам нужно. Снимите внешнюю опору с досок с этих штифтов и вперед. Это сэкономит много времени и сэкономит хлопоты при строительстве фундамента. Не нужно искать булавки собственности, это само по себе может стать приключением.Нет необходимости проводить линию между выводами собственности, чтобы измерить неудачи. И нет необходимости читать дальше о том, как убедиться, что ваши опоры находятся в правильном месте и в правильном квадрате.

Подзаконные акты о зонировании — это набор правил, регулирующих то, для чего можно использовать землю, и одна из вещей, которые они охватывают, — это отступления от границ собственности до фундамента вашего дома.
В некоторых случаях, когда второй этаж имеет консоль, может потребоваться измерение требуемого отступа от линии собственности до внешней стороны верхнего этажа.Убедитесь, что вы это проверили!
Необходимые отступы должны быть на вашем плане здания. Когда у вас есть эта информация, вы готовы начать.
По крайней мере, вам нужно будет найти две передние штифты собственности и хотя бы одну из угловых штифтов задней части.

Всегда лучше найти все булавки собственности и измерить от булавки к булавке, чтобы убедиться, что они находятся в нужном месте в соответствии с вашим планом участка.

Затем вам нужно протянуть линию между задними и передними штифтами, чтобы можно было измерить ваши неудачи.Не всегда необходимо натягивать линию между выводами на передней стороне здания, но если эта линия свойств не проходит параллельно со зданием или у вас есть что-то, выступающее из передней части здания, вам, возможно, придется сделать это тоже. Имейте в виду, что требуемый откат происходит от границы участка до внешней стены фундамента, а не от фундамента.

Размещение опор и квадрат по диагонали

Начиная с угла A, найдите требуемые отступы спереди и сбоку.Если боковой отступ составляет 6 футов к фундаментной стене, то для 18-дюймовых опор (внутреннее измерение) и 8-дюймовой стены это будет 5 футов 7 дюймов к внутренней стороне внешней доски опор. Если передний требуемый отступ равен 20 ‘тогда это будет 19 футов 7 дюймов к внутренней стороне внешней доски опор. Закрепите этот угол на месте, чтобы он больше не мог двигаться. Сделайте то же самое для угла B. Получите необходимое смещение для стороны и сделайте разбивку. Проведите веревочную линию по внутренней стороне внешней доски от A до B немного выше доски и, выпрямив ее, сделайте накол с этой стороны.Теперь у вас есть один прямой участок в нужном месте. Постройте остальные опоры, если вы еще этого не сделали, как бы убедившись, что они находятся примерно в нужном месте. Следующий шаг перед возведением этого участка в квадрат — убедиться, что длины A — B и D — C идентичны. Проверьте то же самое для длин B-C и D-A. Если это не так, зафиксируйте их так, чтобы они были. Нет смысла возводить предметы в квадрат, если один или оба имеют разную длину. Теперь измерьте диагональ от внешнего угла A до угла C.Запомните это измерение. Сделайте то же самое для углов от B до D. Если длина AC больше, чем BD, скажем, на 2 дюйма, разделите разницу и переместите настенный CD на один дюйм вниз. Продолжайте повторять это до тех пор, пока длины диагоналей AC и BD не станут идентичными. при перемещении предметов вверх и вниз убедитесь, что секции опор, на которые повлияло перемещение, остаются достаточно прямыми. Здесь учитывается точность. У вас есть немного места для ошибки, но гораздо лучше начать с квадрата с самого начала!

После того, как вы будете довольны измерениями, сделайте колки по всем углам и с помощью бечевки от конца до конца распрямите секции, размещая дополнительные колья по бокам по мере необходимости.Если вы проделали безупречную работу с выемкой грунта, ее будет легко выровнять по высоте, прибивать колья по мере выравнивания опор с помощью лазера или строительного уровня.

Возведение сечения в квадрат методом 3 4 5

Вы не всегда можете пересечь квадрат, и тогда вам придется использовать метод 3 4 5 или его кратные .
В треугольнике, если длина A = 3 фута и длина B = 4 фута, размер диагонали = 5 футов
. Или кратно 6 ‘- 8’ — 10 ‘или 9’ — 12 ‘- 15’ и т. Д.. Легко запомнить.

Это основано на том, что 3 в квадрате плюс 4 в квадрате = 25 получают квадратный корень из этого = 5. Этот способ возведения в квадрат работает, и большинство людей смогут запомнить требуемые измерения.

Иногда будет эффективнее и точнее квадратить L-образную форму с использованием общей доступной длины. Не так просто, как использовать 3 4 5 в качестве измерений, и потребуется вычислить длину диагонали.

Разбивка углов фундамента »Небольшое домостроение

Основной урок по приблизительно

, где будет располагаться ваш дом

После того, как вы определили глубину промерзания и выбрали субподрядчика, который хорошо осведомлен о почве на вашем участке под застройку, теперь вы готовы разбить углы вашего фундамента и приблизительно определить местоположение вашего небольшого дома.

Используя измерительный инструмент (лучше всего подходит 100-футовая мерная лента), веревку, колья и молоток или кувалду, просто забейте колья примерно в углах фундамента и соедините веревкой. Это даст вам визуальное представление о том, где вы находитесь на участке.

Если ваш фундамент будет квадратным или прямоугольным, будет легко получить его относительно «квадратный» (прямые углы на всех углах), измерив угол до противоположного угла (есть также метод 3-4-5, который я ‘ Об этом расскажу позже).

Инструменты исследования говорят…

У геодезистов

есть очень точные… и дорогие… инструменты для точного измерения углов фундамента. Это определенно тот случай, когда наем профессионала для этого стоит потраченных не зря.

Представьте себе параллелограмм. А еще лучше сравнить квадрат и ромб. Если бы вы измеряли от угла до противоположного угла квадрата, ваши измерения были бы такими же. В то время как в ромбе вы можете видеть, что измерение в одном направлении всегда будет длиннее, чем в другом.

Итак, с вашими четырьмя кольями углов фундамента, вбитыми в землю, измерьте расстояние от угла до угла. На одно расстояние больше? Вы вышли из «квадрата». Продолжайте менять ставки и измерять, пока они не станут равными.

По общему признанию, это чрезмерное упрощение того, как разбивать ваш фундамент. Если бы все инструменты, которые у вас были, были точной измерительной лентой и кольями, вы, вероятно, могли бы потратить большую часть дня на точную разметку всех этих инструментов. К счастью, в вашем экскаваторе есть довольно изящные инструменты для измерения и съемки, позволяющие быстро и точно определить точки фундамента.

Построение прямых углов на местности сообщение: Ошибка 404 — Запрашиваемая страница на сайте отсутствует.

Построение прямых углов на местности. 5-й класс

Эккер и построение прямых углов на местности

Геометрия. 7 — 9 классы. Атанасян Л.С. и др.

Геометрия в геодезии

Геометрия в геодезии

Способы определения положения проектных точек на местности

Способы определения положения проектных точек на местности

Построение прямых углов на местности. 5-й класс > Мастера спешат на помощь!

Геометрия 7 Атанасян Учебник | 7 класс Онлайн

Геометрия 7 Атанасян Учебник

Глава I. Начальные геометрические сведения

Глава II. Треугольники

Глава III. Параллельные прямые.

Глава IV. Соотношения между сторонами и углами треугольника

Обследование и выравнивание пирамиды Хуфу

Выравнивание пирамид и контроль формы пирамиды

Обследование и контроллинг

Получение пирамиды

Определение прямых углов

Угол наклона и секед

Точное выравнивание Север-Юг

Источники

5.4 Тригонометрия прямоугольного треугольника — Precalculus

Использование прямоугольных треугольников для вычисления тригонометрических функций

Понимание отношений правого треугольника

Как сделать

Пример 1

Вычисление тригонометрической функции прямоугольного треугольника

Решение

Попробовать # 1

Взаимосвязь углов и их функций

Как сделать

Пример 2

Оценка тригонометрических функций углов, не находящихся в стандартном положении

Решение

Попробовать # 2

Нахождение тригонометрических функций специальных углов с использованием длин сторон

Как сделать

Пример 3

Оценка тригонометрических функций специальных углов с использованием длин сторон

Решение

Попробовать # 3

Использование равных функций дополнений

Идентификаторы совместных функций

Как сделать

Пример 4

Использование идентификаторов совместных функций

Решение

Попробовать # 4

Использование тригонометрических функций

Как сделать

Пример 5

Поиск недостающих длин сторон с использованием тригонометрических соотношений

Решение

Попробовать # 5

Использование тригонометрии прямоугольного треугольника для решения прикладных задач

Как сделать

Пример 6

Косвенное измерение расстояния

Решение

Попробовать # 6

Задачи со словами в правом треугольнике

Дом без углов — ARTnews.com

Как найти углы прямоугольного треугольника

TL; DR (слишком длинный; не читал)

Синус, косинус и тангенс

Лестница у стены

Пример

Как выровнять опоры

Размещение опор и квадрат по диагонали

Возведение сечения в квадрат методом 3 4 5

Разбивка углов фундамента »Небольшое домостроение

Основной урок по приблизительно

Инструменты исследования говорят…

Добавить комментарий Отменить ответ