Виды углов. Прямой угол. 2-й класс
Тип урока: объяснение нового материала.
Место урока в структуре по теме: данная тема изучается в разделе “Табличное сложение однозначных чисел с переходом через десяток”.
Цель урока: Познакомить учащихся с понятием “прямой угол” и научить применять полученные знания на практике.
Задачи урока:
1. Образовательные:
- Познакомить учащихся с понятием “прямой угол”;
- Сформировать практические навыки определения прямого угла при помощи треугольника и без него;
- Продолжить работу по совершенствованию навыка устного счёта в пределах 100;
2. Развивающие:
- Развитие логического мышления, внимания, памяти, пространственного воображения;
- Развитие творческих умений и навыков по теме для успешного выполнения заданий;
- Развитие культуры речи и эмоций учащихся.
3. Воспитательные:
- В целях решения задач нравственного воспитания содействовать воспитанию гуманности и коллективизма, наблюдательности и любознательности, развитию познавательной активности, формированию навыков самостоятельной работы;
- В целях решения задач эстетического воспитания содействовать развитию у учащихся чувства прекрасного.
ХОД УРОКА
I. Организационный момент.
Ну-ка проверь, дружок,
Ты готов начать урок?Все ль на месте
Все ль в порядке,
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Каждый хочет получать
Только лишь оценку “5”.
— Ребята, сегодня мы опять отправимся в путешествие по королевству Геометрия.
3. Устный счёт.
2 слайд
– У ворот нас встречают король Точка и его дочь – принцесса Прямая. Прежде чем король и принцесса познакомят нас с жителями своего королевства, они хотят вас испытать.
II. Устный счет.
1) Игра “Гусеница-растеряша”.
— Гусеница растеряла числа, посмотрите на оставшиеся, разгадайте по какому правилу можно продолжить ряд чисел. (Дети называют правило: это чётные числа; каждое последующее число на 2 больше предыдущего).
— Какие же числа растеряла гусеница? (2,4,6,8,10,12,14,16)
(Слайд 4)
2) Игра “Математический баскетбол”.
Баскетбол — командная спортивная игра, цель которой забросить руками мяч в подвешенную корзину.
— Любой из вас забьёт гол, если правильно решит пример. (Дети по цепочке решают примеры). 30 + 7 25 + 5 32 – 12 66 + 4 80 – 7 28 – 10 45 – 45 53 + 7 59 – 9 90 + 9
Слайд 5
Задание на логику
— Сколько пятачков у 15 поросят? (15)
— Когда гусь стоит на двух ногах, то весит 4 кг. Сколько будет весить гусь, когда встанет на одну ногу?
6 слайд
– Вы прошли все испытания. Король и принцесса очень довольны вами и готовы познакомить вас с жителями королевства “Геометрия”!
(По щелчку створки ворот открываются.)
(Слайд 7)
— Ребята, перед вами жители королевства “Геометрия”.
— Посмотрите на фигуры в каждой рамке. Какая из них лишняя? Почему?
(Учащиеся называют лишние фигуры, обосновывают свой выбор).
— Разделите все оставшиеся фигуры на две группы.
Как это можно сделать? (Оставшиеся фигуры можно
разделить на две группы: линии и многоугольники. )
)
— Назовите виды линий и многоугольников, известные вам. (Линии: прямая, ломаная, кривая. Многоугольники: квадрат, трапеция, прямоугольник, четырёхугольник, пятиугольник, шестиугольник, многоугольник).
IV. Работа над новым материалом.
(Слайд 8)
1) — Тему урока вам подскажет кроссворд. Кроссворд “Геометрический”.
1) Часть прямой, у которой есть начало, но нет конца. (Луч).
2) Геометрическая фигура, не имеющая углов. (Круг).
3) Самая маленькая геометрическая фигура. (Точка).
4) Геометрическая фигура, имеющая форму вытянутого круга. (Овал).
— Тема нашего урока спряталась по вертикали. Найдите её. (Угол). (щелчок вылетают геометрические фигуры).
— Сформулируйте пожалуйста тему нашего урока.
— Ребята, а зачем мы будем изучать углы?
— Как Вы думаете, вам эти знания пригодятся?
(Ответы детей)
— Углы окружают нас и в повседневной жизни. Приведите свои примеры, где можно найти углы вокруг нас.
— Ребята, а может, кто-то знает, что такое угол? (выслушиваются мнения детей)
Правильность нашей формулировки, мы проверим чуть позже.
— Люди, каких профессий чаще всего встречаются с углами? (конструктор, инженер, дизайнер, строитель, архитектор, моряк, астроном, архитектор, портной и т.д.)
Слайд 9.
Посмотрите на рисунки: уголок соединительный для труб и уголок канцелярский для бумаг; угольник плотника и угольник чертёжный; угловой стол и угловой диван.
— Ребята, а сейчас Король и Принцесса предлагают немного поиграть.
Слайд 10.
Игра “Им угол имя подарил”.
— Угол важная фигура. Многим фигурам он помог дать имя. Назовите фигуры.
— Что общего в названиях фигур? (что они имеют угольник – общая часть)
— Почему первая часть слов везде разная? (потому что углов разное количество)
Физминутка 11-16 слайды
Открываем тетради, записываем 18 января,
классная работа.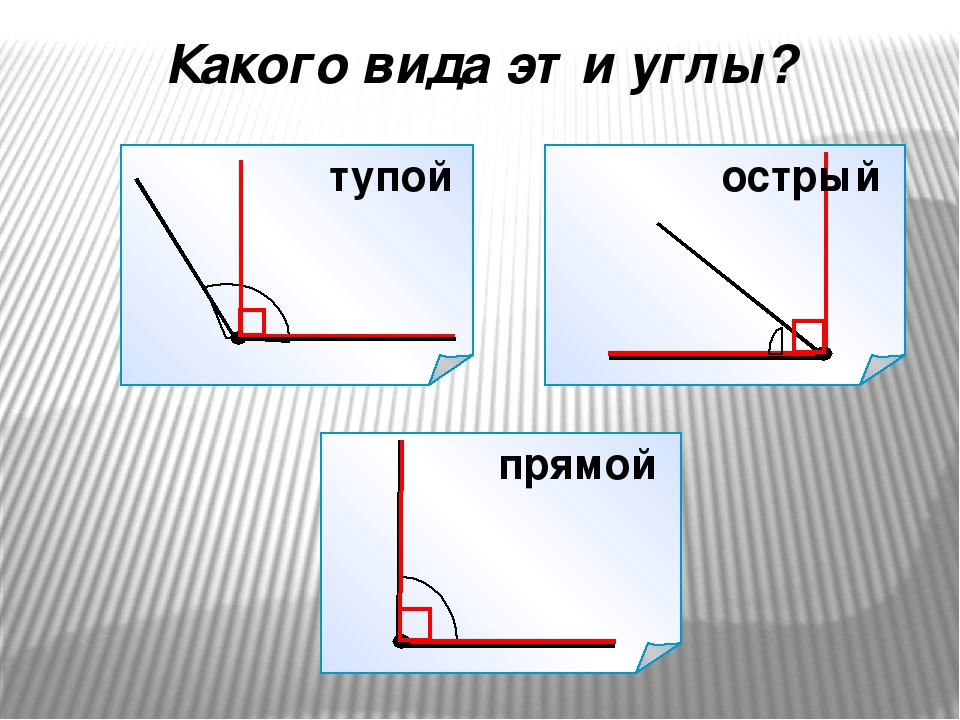 (слайд 17)
(слайд 17)
Слайд 18.
— Ребята, а теперь от красных полей отступите одну клеточку и поставьте точку О. От этой точки проведите два луча.
На доске заранее нарисовать точку О (4-5). Вызвать 4-5 детей, чтобы они провели лучи на доске.
— Что за фигуры у нас получилась? (угол)
— Посмотрите, какие разные эти углы.
— Ребята, а теперь соберите правило из слов.
Работа в парах.
(Вывод: угол — это геометрическая фигура, образованная двумя разными лучами
с общим началом).
— Ребята, а теперь посмотрите на фигуру, которую нарисовала я.
— Это угол, или нет.
(Дети говорят – нет, еще раз возвращаемся к правилу, после этого делаем вывод о том, что это тоже угол – развернутый)
Слайд 19. (вывод по углу)
Плакат на доске
Точка О – вершина угла. Угол можно назвать одной буквой, записанной около его вершины. Угол О. Но может быть несколько углов, имеющих одну вершину. Как быть тогда? (На листе чертеж таких углов)
Ответы детей.
— В таких случаях если называть разные углы одной буквой, то будет непонятно, о каком угле идёт речь. Что этого не произошло, на каждой стороне угла можно отметить по одной точке, поставить около неё букву и обозначить угол тремя буквами, при этом всегда в середине записывают букву, обозначающую вершину угла. Угол АОВ. Лучи АО и ОВ – стороны угла.
Плакат на доске
Слайд 20.
— Ребята, у вас на столах лежат разные виды углов. Найдите пожалуйста одинаковые виды углов.
— Как будете искать? (Ответы детей)
Один человек на моих моделях ищет одинаковые углы.
— Ребята, смотрите, номера 6 и 7 совпали
полностью, а 1 и 5 — нет. № 5 больше.
№ 5 больше.
— Какой можно сделать вывод? После ответа детей появляется слайд.
ВЫВОД: слайд 21
- Равные углы при наложении совпадают
- Если один угол наложить на другой и они совпадут, то эти углы равны
Слайд 22.
Изготовление модели прямого угла.
Слайд 23
Не всегда удобно определять прямой угол на глаз. Для этого используют линейку-угольник.
— Каким цветом выделен угол больше прямого? (Голубым).
— Меньше прямого? (Зелёным).
— Какой же угол из трёх предложенных прямой?
— Почему вы так решили? (Вершина и стороны угла совпали с прямым углом на линейке-угольнике).
— Как же определить вид угла?
ВЫВОД:
- Чтобы определить вид угла, надо совместить его вершину и сторону соответственно с вершиной и стороной прямого угла на угольнике.
Слайд 24
— Каждый из углов имеет своё название. Острый угол – это угол, который меньше прямого. Тупой угол – это угол, который больше прямого.
(На доске появляются таблички с названием углов)
— Какой угол мы будем считать главным?
Мама мой взяла листок,
И загнула уголок,
Угол вот такой у взрослых
Называется ПРЯМЫМ.
Если угол уже — ОСТРЫМ,
Если шире, то — ТУПЫМ.
Слайд 25.
— Ребята, а всегда возможно наложить углы?
— Нет. (Если начерчены в тетради…)
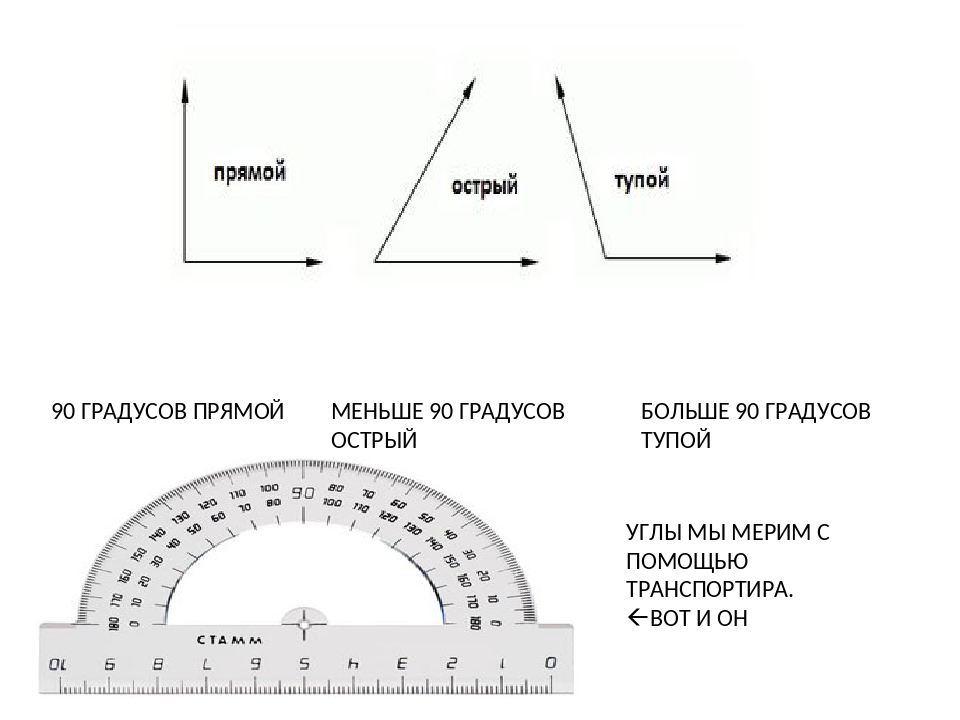
— Для этого существует транспортир, с помощью которого измеряют углы. Углы измеряют в градусах. Посмотрите на виды транспортиров.
Слайд 26.
Очень часто углы мы можем наблюдать на часах. Углы образуют часовые стрелки.
Работа по учебнику.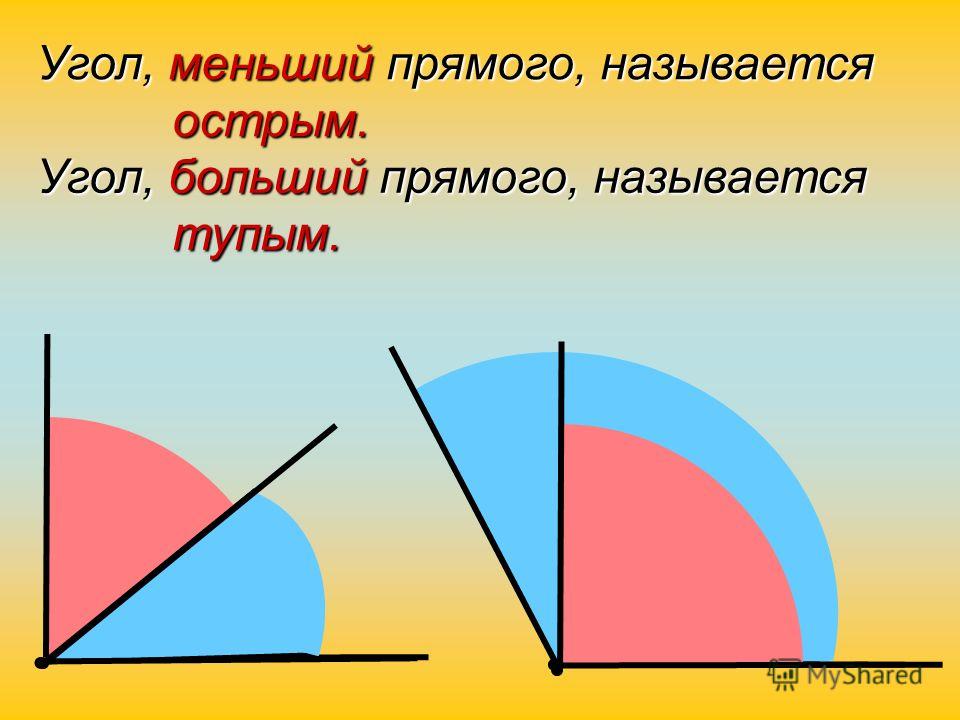
Задание: Используя модель прямого угла, найди прямые углы и выпиши их номера. (Дети выполняют задание самостоятельно, затем один ученик называет свой вариант ответа, все проверяют работу).
— С помощью угольника удобно не только определять прямые углы, но главное – строить их. Построим прямой угол, каждый сам назовёт его одной или тремя буквами.
Слайд 27-29 (Учитель на доске, а дети в тетрадях строят прямой угол. Выполняется взаимопроверка в парах).
Я ОСТРЫЙ — начертить хочу,
Сейчас возьму и начерчу.
Веду из точки две прямых,
Как будто два луча,
И видим ОСТРЫЙ УГОЛ мы,
как остриё меча.А для УГЛА ТУПОГО
Всё повторяем снова:
Из точки две прямых ведём,
Но их пошире разведём.
На чертёж мой посмотри,
Он, как ножницы внутри,
Если их за два кольца
Мы раздвинем до конца.
Практическая работа по закреплению изученного.
На партах у вас проволока. Сделайте из нее прямой угол и проверьте с помощью угольника, затем сделайте острый и тупой.
7. Итог урока.
— Расскажите мне по схеме о том, что вам дал сегодняшний урок математики?
8. Домашнее задание.
Касательная к окружности, почему прямой угол?
Когда я проходил эту тему в школе лет 40 назад, у меня вообще в этом месте вопросов не возникало. Все вроде по умолчанию понятно, на инстинктивном уровне. А тут, вишь ты, почему угол между касательной и радиусом именно прямой? Не 30, не 60, не 89,9, а именно 90°? Попробуй тут объясни.
— Вам что, на уроке не объясняли?
— Мы эту тему в прошлом году проходили. Я еще тогда ничего не поняла.
— Чего ж тогда не сказала?! Ладно, щас объясню.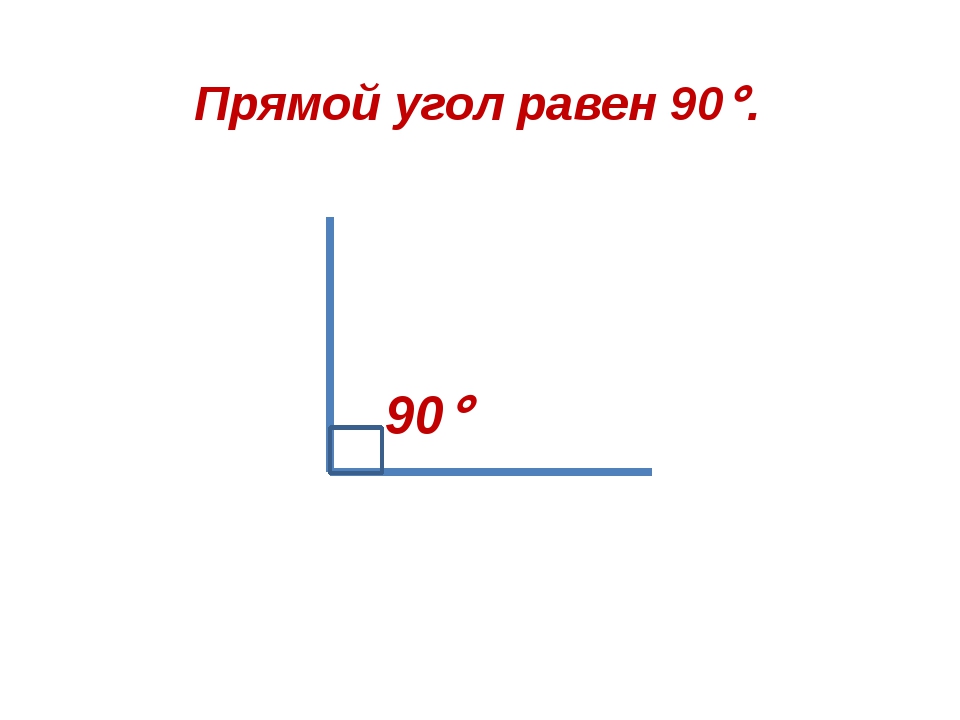
Дочка у меня звезд с неба не хватает, но учится в целом неплохо. На геометрию давно жалуется, но за помощью не подходит. Ей проще за 5 минут найти и списать ГДЗ, чем полчаса, а то и час слушать мои объяснения вперемешку с язвительными замечаниями по поводу знаний.
В этот вечер, а точнее ночь, началось все с того, что в начале одиннадцатого жена погнала детей спать, на что дочка ответила, что у нее еще геометрия не сделана. Дальше состоялся эмоциональный диалог, который меня и разбудил. Я вышел из спальни помочь ребенку решить задачу.
Задача такая: Наибольшая диагональ ромба равна 24 см, наименьший угол между сторонами — 60°. Определить радиус окружности, вписанной в ромб.
— Мда… Так сразу не решу. — Я зевнул, прощаясь с остатками сна. — Давай эти словесные формулировки трансформируем в зрительные образы, так оно понятнее будет.
Я потянулся за тетрадью, но был остановлен.
— Это у меня чистовик!
— Оба-на! А черновик где?
— У меня нет черновика, я сразу в чистовик делаю.
Блллллин!.. Получается ребенок настолько ничего не понимает в геометрии, что даже черновик себе не завел. Тупо копирует ГДЗ в чистовик, даже не пытаясь разобраться. Плохи дела!
— Ну, — говорю, — то, что ты циркуль не любишь, потому что он колется, это я еще могу понять, планшетное поколение все-таки. Но вот как можно разобраться в задачах по геометрии без черновика? Ведь восьмой класс уже.
В общем, нашли листок в клетку. Я нарисовал ромб, диагонали, окружность, вписанную в ромб, радиусы окружности, проведенные в точки касания. Все это без циркуля, транспортира (тоже давно в руках у дочери не видел) и линейки. Только простой карандаш. Получилось примерно так:
Рисунок 652,1.
— Во! Совсем другое дело! Ну, смотри. Так как АС = 24 см, то ОА = АС/2 = 24/2 = 12 см. При этом угол ОАВ= углу DАВ/2 = 60/2 = 30. Пока понятно?
— Не совсем.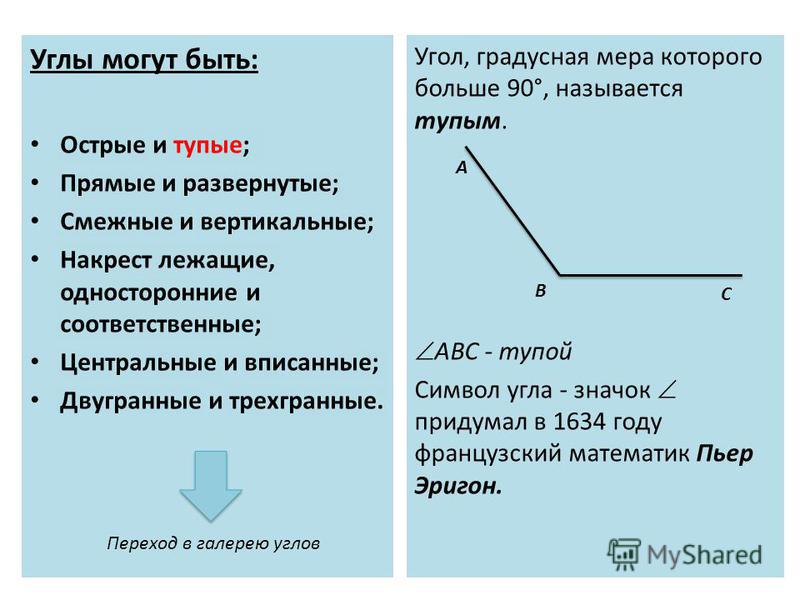
— Хорошо, попробуем поподробнее. Одна из особенностей ромбов в том, что между диагоналями ромба всегда образуются прямые углы, Т.е. угол АОВ — прямой. — Я добавил соответствующий значок на рисунок.
— Все потому, что любой ромб с одной диагональю можно рассматривать как два одинаковых равнобедренных треугольника с одной общей стороной. Например АDВ и DВС. Их общая сторона DВ — это и есть одна из диагоналей ромба. Далее, мы знаем, что у любого треугольника есть высота. Знаем, нет?
— Знаем.
— Уже хорошо. Высота — это прямая линия соединяющая вершину с основанием. Угол между высотой и основанием — 90°. У любого треугольника. Есть еще такое понятие, как биссектриса. Знаешь, что это?
— Да, такая крыса, которая бегает по углам и делит угол пополам.
— Правильно. Так вот у равнобедренного треугольника высота и биссектриса совпадают. Таким образом АО – это высота треугольника АDВ и одновременно его биссектриса. Ну то есть так как треугольник АDВ равнобедренный, то у него равные по значению 2 стороны и два угла, а когда мы опускаем высоту из вершины, то получаем два прямоугольных треугольника АDО и АОВ. Два угла АDО и АОВ изначально были одинаковыми, прямые углы у треугольников тоже одинаковые. Соответственно и неизвестные углы тоже одинаковые и составляют половину от угла, из которого проведена высота. Если мы проведем биссектрису или высоту, что в данном случае одно и тоже, для угла DСВ, то высоты треугольников АDВ и DВС соединятся в одной точке, точке О и таким образом станут второй диагональю ромба. Вот поэтому угол между диагоналями ромба всегда прямой. Понятно?
— Пока да.
— А значит мы имеем прямоугольный треугольник АОВ, у которого одна сторона равна половине диагонали ОА = АС/2 = 24/2 = 12 см, а угол ОАВ= углу DАВ/2 = 60/2 = 30. Соответственно сторона ОВ чему равна?
Дело в том, что не смотря на восьмой класс, ученикам еще не рассказывали про синусы-косинусы (похоже берегут психику современных детей). Их просто заставили выучить следующую аксиому: У прямоугольного треугольника сторона, противоположная углу 30 равна 1/2 гипотенузы. Поэтому и в условии задачи угол DАВ = 60°.
Их просто заставили выучить следующую аксиому: У прямоугольного треугольника сторона, противоположная углу 30 равна 1/2 гипотенузы. Поэтому и в условии задачи угол DАВ = 60°.
— АО/2?
— Правильно, 6 см. – Тут я спросонья тупанул, перепутал катет с гипотенузой. – Осталось найти радиус… Так, значит, вот радиусы, вот стороны ромба, они касательные к окружности. Значит угол между радиусом ОМ и касательной АВ прямой. Так… Тут через подобие треугольников АМО и МОВ решать надо. Сейчас-сейчас… Ясно, что меньше 6 см, где то 5,1-5.2, но придется повозиться. А что там в твоем ГДЗ пишут?
— 6 см.
— Как 6 см?! Они гонят, ведь тут же!.. А нет, это я гоню, катет с гипотенузой перепутал. Не тот прямоугольный треугольник рассматривал. — Я добавил знак прямого угла в углу АМО. — Ну да, задача совсем простая, так как треугольник АОМ прямоугольный, то при угле ОАВ = 30° и длине гипотенузы АО = 12 см ОМ = АО/2 = 12/2 = 6 см. Стоило меня из-за такой мелочи будить?
— Па, а почему угол между радиусом и касательной — прямой?
Тут я понял, что начинать нужно действительно издалека и рассказал то, что изложено в начале статьи. Дочь слушала, но понимания в ее глазах я не видел.
— Хорошо, давай от противного. Предположим, что угол между радиусом и касательной не прямой. Что это означает? Это означает, что если мы проведем окружность через эту точку, а для этого как раз и нужен циркуль, то увидим, что линия пересекает окружность еще в одной точке. При этом угол ОАВ = углу АВС. А как мы уже говорили, если прямая имеет с окружностью две общих точки, то такая прямая не является касательной, а пересекает окружность, понятно?
— Пока не очень.
— Хорошо, копнем еще глубже. Вот смотри, есть некая прямая DN и есть несколько точек, например А, О, С. Как определить расстояние от DN до любой из этих точек?
— Провести прямую! — подсказала из спальни жена.
— Правильно. Но не просто прямую, а прямую, перпендикулярную DN и проходящую через рассматриваемую точку, например О.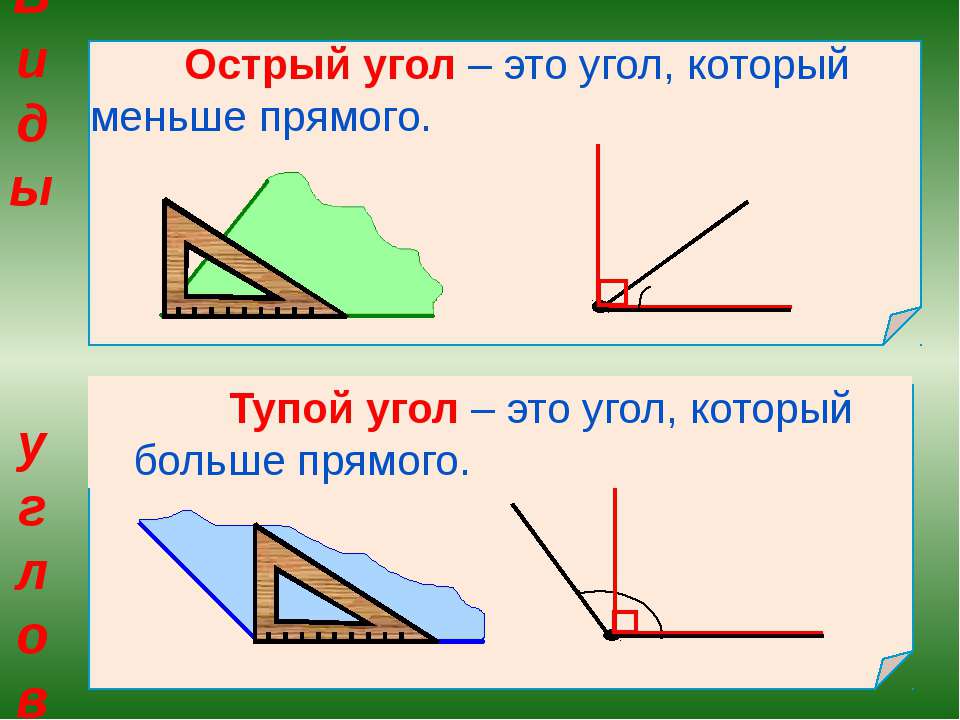 — Я нарисовал перпендикуляр и обозначения прямого угла. — Таким образом мы можем сказать, что линия ОN делит развернутый угол DMN (любую прямую мы можем рассматривать как развернутый угол) на два одинаковых угла и эти углы — прямые. Ну то есть линию DN мы можем соединить с точкой О любым количеством отрезков, но при этом все отрезки будут длиннее, чем отрезок ОМ. Вот смотри.
— Я нарисовал перпендикуляр и обозначения прямого угла. — Таким образом мы можем сказать, что линия ОN делит развернутый угол DMN (любую прямую мы можем рассматривать как развернутый угол) на два одинаковых угла и эти углы — прямые. Ну то есть линию DN мы можем соединить с точкой О любым количеством отрезков, но при этом все отрезки будут длиннее, чем отрезок ОМ. Вот смотри.
Я пририсовал отрезок NO.
— Таким образом мы получили прямоугольный треугольник MNO. Если мы представим, что ON — это радиус, то отрезок такой же длины будет у треугольника DMO. Тут мы как бы опять возвращаемся к особенностям равнобедренного треугольника, в данном случае треугольника DNO. То есть DM = DN, DO = ON, угол MDO = углу MNO, угол MOD = углу MON. И если мы теперь нарисуем окружность с радиусом ON, то увидим, что радиусы ON и DO — это не самые короткие расстояния до прямой DN. А самое короткое расстояние — это отрезок ОМ, который одновременно является высотой треугольника ODN и биссектрисой угла NOD. Так понятно?
— Вроде да. А почему любой треугольник, вписанный в окружность так, что его гипотенуза совпадает с диаметром окружности, является прямоугольным. Мы это недавно проходили, но я не поняла.
Было уже начало первого и я был не готов опять погружаться в глубины геометрии.
— Я тебе потом объясню. На синусах-косинусах, а сейчас уже время позднее, спи давай.
Тем не менее сам я заснуть не смог и начал крутить в полусонном уме эту задачку. Тут все не так наглядно, как с касательной, но тем не менее, должно же быть какое-то достаточно простое объяснение, понятное даже ученику восьмого класса?!
К 3 часам я нашел пару возможных объяснений.
1. Проведем радиус в точку В. Таким образом имеем 2 треугольника АВО и ВОС — оба равнобедренные, их бедра — радиусы окружности. Мы не знаем значения углов в этих треугольниках, но это не проблема! Например угол ВОА = х, то есть тупо нам неизвестен. Тогда угол ОВА = углу ОАВ = (180 -х)/2. По вышеизложенным причинам и потому, что сумма углов треугольника всегда равна 180°.
Тогда угол ОВА = углу ОАВ = (180 -х)/2. По вышеизложенным причинам и потому, что сумма углов треугольника всегда равна 180°.
АОС — это у нас развернутый угол, равный 180°. Соответственно угол ВОС = 180 — х. Тогда угол ОВС = углу ОСВ = (180 — угол ВОС)/2 = (180 — 180 + х)/2 = х/2.
Так как угол АВС = угол ОВА + угол ОВС = (180 -х)/2 + х/2 = 180/2 = 90°. Вне зависимости от того, какое значение имеет неизвестная величина х.
Вроде бы красивое решение, но спать еще не хотелось (проклятый мозг перевозбудился). Поэтому второй возможный вариант выглядел так:
2. Вернемся к рисунку . Если мы продлим сторону ОN так, чтобы она стала диаметром, т.е. АN = D = 2R = 2ON, а точку А соединим с точкой D, то получим треугольник ADN.
У треугольника MNO и DNA есть общий угол MNO, ON = NA/2, MN = DN/2. Т.е. эти треугольники — подобные. Отсюда следует, что угол DAN = углу МОА, а угол ADN = углу OMN и является прямоугольным.
Но тут опять же, я рассуждал, то ли сидя, то ли лежа на вершине своего жизненного опыта. Я ж не знаю, какую тему дети уже проходили в школе, а какую — нет. Возможно и подобные треугольники будут для моей дочери великим откровением. Как знать?..
А какой вариант можете предложить вы? Мне-то по-любому еще придется искать решение под синусы-косинусы. В общем ни хрена я не выспался. Заснул только под утро, часов в 5 или в 6. Будь она неладна эта геометрия, не дает нормальным людям спать! А особенно касательная с окружности, да еще и под прямым углом.
P.S. Дочка на следующий день принесла из школы отличную оценку по геометрии, а из предложенных мной двух вариантов объяснения, почему любой треугольник вписанный в окружность так, что его гипотенуза совпадает с диаметром, является прямоугольным, выбрала второй. И вроде бы можно порадоваться, но меня смутил ответ на вопрос:
— Ну так что, теперь все понятно?
— Кое-что начинает проясняться.
Такие дела.
Прямой угол, свойства и фигуры с прямыми углами
Прямой угол, свойства и фигуры с прямыми углами.

Прямой угол – это угол, градусная мера которого равна 90°.
Прямой угол (определение и понятие)
Геометрические фигуры с прямыми углами
Вертикальные углы, прямой угол, развернутый угол, смежные углы, тупой угол
Прямой угол (определение и понятие):
Прямой угол – это угол, градусная мера которого равна 90°.
Прямой угол – это угол, стороны которого перпендикулярны друг другу. При пересечении перпендикулярных прямых образуются прямые углы.
Прямой угол – это геометрическая фигура, которая состоит из двух перпендикулярных друг другу лучей (сторон), выходящих из одной точки (вершины).
Рис. 1. Прямой угол
Величина прямого угла может быть выражена в разных единицах измерения:
– 90°,
– π / 2 радиан,
– 100 град,
– 1/4 оборота или полного угла,
– 5400 угловых минут,
– 324000 угловых секунд.
Геометрические фигуры с прямыми углами:
У некоторых геометрических фигур имеется один или несколько прямых углов.
Например, прямой угол (или прямые углы ) имеются у прямоугольного треугольника, прямоугольника, квадрата, прямоугольной трапеции.
Прямоугольный треугольник – это треугольник, у которого один угол прямой.
Рис. 2. Прямоугольный треугольник и прямой угол
Прямоугольник – параллелограмм, у которого все углы прямые.
Рис. 3. Прямоугольник и прямые углы
Квадрат – это четырёхугольник, у которого все углы прямые, все углы и стороны равны между собой.
Рис. 4. Квадрат и прямые углы
Прямоугольная трапеция – это трапеция, хотя бы один из углов которой является прямым.
Рис. 5. Прямоугольная трапеция и прямые углы
Квадрат
Полукруг
Прямой угол
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Шестиугольник
Примечание: © Фото https://www. pexels.com, https://pixabay.com
pexels.com, https://pixabay.com
Найти что-нибудь еще?
Похожие записи:
карта сайта
Коэффициент востребованности 954
| Ç | Alt 128 | Латинская заглавная буква C с седилью |
|---|---|---|
| ü | Alt 129 | Латинская строчная буква u с диэризисом |
| é | Alt 130 | Латинская строчная буква e с акутом |
| â | Alt 131 | Латинская строчная буква a с циркумфлексом |
| ä | Alt 132 | Латинская строчная буква a с диэризисом |
| à | Alt 133 | Латинская строчная буква a с грависом |
| å | Alt 134 | Латинская строчная буква a с кружочком сверху |
| ç | Alt 135 | Латинская строчная буква c с седилью |
| ê | Alt 136 | Латинская строчная буква e с циркумфлексом |
| ë | Alt 137 | Латинская строчная буква e с диэризисом |
| è | Alt 138 | Латинская строчная буква e с грависом |
| ï | Alt 139 | Латинская строчная буква i с диэризисом (умляутом) |
| î | Alt 140 | Латинская строчная буква i с циркумфлексом сверху |
| ì | Alt 141 | Латинская строчная буква i с грависом |
| Ä | Alt 142 | Латинская заглавная буква A с диэризисом |
| Å | Alt 143 | Латинская заглавная буква A с кружочком сверху |
| É | Alt 144 | Латинская заглавная буква E с акутом |
| æ | Alt 145 | Латинская строчная лигатура ae |
| Æ | Alt 146 | Латинская заглавная буква AE |
| ô | Alt 147 | Латинская строчная буква o с циркумфлексом |
| ö | Alt 148 | Латинская строчная буква o с диэризисом |
| ò | Alt 149 | Латинская строчная буква o с грависом |
| û | Alt 150 | Латинская строчная буква u с циркумфлексом |
| ù | Alt 151 | Латинская строчная буква u с грависом |
| ÿ | Alt 152 | Латинская строчная буква y с диэризисом |
| Ö | Alt 153 | Латинская заглавная буква O с диэризисом |
| Ü | Alt 154 | Латинская заглавная буква U с диэризисом |
| ¢ | Alt 155 | Знак цента и сентаво |
| £ | Alt 156 | Знак фунта |
| ¥ | Alt 157 | Знак иены |
| ₧ | Alt 158 | Испанская песета |
| ƒ | Alt 159 | Латинская строчная буква «f» с хвостиком или знак флорина |
| á | Alt 160 | Латинская строчная буква a с акутом |
| í | Alt 161 | Латинская строчная буква i с акутом |
| ó | Alt 162 | Латинская строчная буква o с ударением |
| ú | Alt 163 | Латинская строчная буква u с акутом |
| ñ | Alt 164 | Латинская строчная буква n с тильдой |
| Ñ | Alt 165 | Латинская заглавная буква N с тильдой |
| ª | Alt 166 | Женский порядковый индикатор |
| º | Alt 167 | Мужской порядковый индикатор |
| ¿ | Alt 168 | Перевернутый вопросительный знак |
| ⌐ | Alt 169 | Обратный знак не |
| ¬ | Alt 170 | Знак отрицания |
| ½ | Alt 171 | Дробь – одна вторая |
| ¼ | Alt 172 | Дробь – одна четверть |
| ¡ | Alt 173 | Перевернутый восклицательный знак |
| « | Alt 174 | Открывающая левая кавычка «ёлочка» |
| » | Alt 175 | Закрывающая правая кавычка «ёлочка» |
| ░ | Alt 176 | Легкое затемнение |
| ▒ | Alt 177 | Среднее затемнение |
| ▓ | Alt 178 | Темное затемнение |
| │ | Alt 179 | Граница легкая вертикальная |
| ┤ | Alt 180 | Граница легкая вертикальная и налево |
| ╡ | Alt 181 | Граница вертикальная одинарная и двойная налево |
| ╢ | Alt 182 | Граница вертикальная двойная и одинарная налево |
| ╖ | Alt 183 | Граница двойная вниз и одинарная налево |
| ╕ | Alt 184 | Граница одинарная вниз и двойная налево |
| ╣ | Alt 185 | Граница двойная вертикальная и налево |
| ║ | Alt 186 | Граница двойная вертикальная |
| ╗ | Alt 187 | Граница двойная вниз и налево |
| ╝ | Alt 188 | Граница двойная вверх и налево |
| ╜ | Alt 189 | Граница двойная вверх и одинарная налево |
| ╛ | Alt 190 | Граница одинарная вверх и двойная налево |
| ┐ | Alt 191 | Граница легкая вниз и налево |
| └ | Alt 192 | Граница легкая вверх и направо |
| ┴ | Alt 193 | Граница легкая вверх и горизонтально |
| ┬ | Alt 194 | Граница легкая вниз и горизонтально |
| ├ | Alt 195 | Граница легкая вертикальная и направо |
| ─ | Alt 196 | Граница легкая горизонтальная |
| ┼ | Alt 197 | Граница легкая вертикальная и горизонтальная |
| ╞ | Alt 198 | Граница вертикальная одинарная и направо двойная |
| ╟ | Alt 199 | Граница вертикальная двойная и одинарная направо |
| ╚ | Alt 200 | Граница двойная вверх и направо |
| ╔ | Alt 201 | Граница двойная вниз и направо |
| ╩ | Alt 202 | Граница двойная вверх и горизонтально |
| ╦ | Alt 203 | Граница двойная вниз и горизонтально |
| ╠ | Alt 204 | Граница двойная вертикальная и направо |
| ═ | Alt 205 | Граница двойная горизонтальная |
| ╬ | Alt 206 | Граница двойная вертикально и горизонтально |
| ╧ | Alt 207 | Граница одинарная вверх и двойная горизонтально |
| ╨ | Alt 208 | Граница двойная вверх и одинарная горизонтально |
| ╤ | Alt 209 | Граница одинарная вниз и двойная горизонтально |
| ╥ | Alt 210 | Граница двойная вниз и одинарная горизонтально |
| ╙ | Alt 211 | Граница двойная вверх и одинарная направо |
| ╘ | Alt 212 | Граница одинарная вверх и двойная направо |
| ╒ | Alt 213 | Граница вниз одинарная и направо двойная |
| ╓ | Alt 214 | Граница двойная вниз и одинарная направо |
| ╫ | Alt 215 | Граница двойная вертикально и одинарная горизонтально |
| ╪ | Alt 216 | Граница одинарная вертикально и двойная горизонтально |
| ┘ | Alt 217 | Граница легкая вверх и налево |
| ┌ | Alt 218 | Граница легкая вниз в направо |
| █ | Alt 219 | Полный блок |
| ▄ | Alt 220 | Нижняя половина блока |
| ▌ | Alt 221 | Левая половина блока |
| ▐ | Alt 222 | Правая половина блока |
| ▀ | Alt 223 | Верхняя половина блока |
| α | Alt 224 | Греческая строчная буква альфа |
| ß | Alt 225 | Латинская строчная буква эсцет (S острое) |
| Γ | Alt 226 | Греческая заглавная буква гамма |
| π | Alt 227 | Греческая строчная буква пи |
| Σ | Alt 228 | Греческая заглавная буква сигма |
| σ | Alt 229 | Греческая строчная буква сигма |
| µ | Alt 230 | Знак микро |
| Τ | Alt 231 | Греческая заглавная буква тау |
| Φ | Alt 232 | Греческая заглавная буква фи |
| Θ | Alt 233 | Греческая заглавная буква тета |
| Ω | Alt 234 | Греческая заглавная буква омега |
| δ | Alt 235 | Греческая строчная буква дельта |
| ∞ | Alt 236 | Знак бесконечности |
| φ | Alt 237 | Греческая строчная буква фи |
| ε | Alt 238 | Греческая строчная буква эпсилон |
| ∩ | Alt 239 | Пересечение |
| ≡ | Alt 240 | Идентичный, тождество |
| ± | Alt 241 | Знак плюс-минус |
| ≥ | Alt 242 | Больше чем или равно |
| ≤ | Alt 243 | Меньше или равный |
| ⌠ | Alt 244 | Верхняя половина интеграла |
| ⌡ | Alt 245 | Нижняя половина интеграла |
| ÷ | Alt 246 | Знак деления |
| ≈ | Alt 247 | Почти равный |
| ° | Alt 248 | Знак градуса |
| ∙ | Alt 249 | Оператор точка маркер списка |
| · | Alt 250 | Точка по центру |
| √ | Alt 251 | Квадратный корень |
| ⁿ | Alt 252 | Верхний индекс латинская строчная буква n |
| ² | Alt 253 | Верхний индекс 2 |
| ■ | Alt 254 | Черный квадрат |
| Alt 255 | Неразрывный пробел | |
| € | Alt 0128 | Знак евро |
| ‚ | Alt 0130 | Нижняя одинарная открывающая кавычка |
| ƒ | Alt 0131 | Латинская строчная буква «f» с хвостиком или знак флорина |
| „ | Alt 0132 | Нижняя двойная открывающая кавычка |
| … | Alt 0133 | Многоточие |
| † | Alt 0134 | Крестик |
| ‡ | Alt 0135 | Двойной крестик |
| ˆ | Alt 0136 | Модификатор буквы циркумфлекс ударение |
| ‰ | Alt 0137 | Знак промилле |
| Š | Alt 0138 | Латинская заглавная буква «S» с гачеком |
| ‹ | Alt 0139 | Одинарная открывающая (левая) французская угловая кавычка |
| Œ | Alt 0140 | Латинская заглавная лигатура OE |
| Ž | Alt 0142 | Латинская заглавная буква «Z» с гачеком |
| ‘ | Alt 0145 | Открывающая одинарная кавычка |
| ’ | Alt 0146 | Закрывающая одинарная кавычка |
| “ | Alt 0147 | Закрывающая двойная кавычка |
| ” | Alt 0148 | Правая двойная кавычка |
| • | Alt 0149 | Точка маркер списка |
| – | Alt 0150 | Среднее тире |
| — | Alt 0151 | Длинное тире |
| ˜ | Alt 0152 | Строчная тильде |
| Alt 0153 | Знак торговой марки | |
| š | Alt 0154 | Латинская строчная буква «s» с гачеком |
| › | Alt 0155 | Одинарная закрывающая (правая) французская угловая кавычка |
| œ | Alt 0156 | Латинская строчная лигатура oe |
| ž | Alt 0158 | Латинская строчная буква «z» с гачеком |
| Ÿ | Alt 0159 | Латинская заглавная буква «Y» с диэрезисом |
| Alt 0160 | Неразрывный пробел | |
| ¡ | Alt 0161 | Перевернутый восклицательный знак |
| ¢ | Alt 0162 | Знак цента и сентаво |
| £ | Alt 0163 | Знак фунта |
| ¤ | Alt 0164 | Знак валюты |
| ¥ | Alt 0165 | Знак иены |
| ¦ | Alt 0166 | Изломанная вертикальная черта |
| § | Alt 0167 | Параграф |
| ¨ | Alt 0168 | Диэрезис |
| Alt 0169 | Знак авторского права | |
| ª | Alt 0170 | Женский порядковый индикатор |
| « | Alt 0171 | Открывающая левая кавычка «ёлочка» |
| ¬ | Alt 0172 | Знак отрицания |
| | Alt 0173 | Мягкий перенос |
| Alt 0174 | Зарегистрированный товарный знак | |
| ¯ | Alt 0175 | Макрон. Надчёркивание Надчёркивание |
| ° | Alt 0176 | Знак градуса |
| ± | Alt 0177 | Знак плюс-минус |
| ² | Alt 0178 | Верхний индекс 2 |
| ³ | Alt 0179 | Верхний индекс 3 |
| ´ | Alt 0180 | Знак ударения |
| µ | Alt 0181 | Знак микро |
| ¶ | Alt 0182 | Знак абзаца |
| · | Alt 0183 | Точка по центру |
| ¸ | Alt 0184 | Седиль |
| ¹ | Alt 0185 | Верхний индекс 1 |
| º | Alt 0186 | Мужской порядковый индикатор |
| » | Alt 0187 | Закрывающая правая кавычка «ёлочка» |
| ¼ | Alt 0188 | Дробь – одна четверть |
| ½ | Alt 0189 | Дробь – одна вторая |
| ¾ | Alt 0190 | Дробь – три четверти |
| ¿ | Alt 0191 | Перевернутый вопросительный знак |
| À | Alt 0192 | Латинская заглавная буква A с грависом |
| Á | Alt 0193 | Латинская заглавная буква A с акутом |
| Â | Alt 0194 | Латинская заглавная буква A с циркумфлексом |
| Ã | Alt 0195 | Латинская заглавная буква A с тильдой |
| Ä | Alt 0196 | Латинская заглавная буква A с диэризисом |
| Å | Alt 0197 | Латинская заглавная буква A с кружочком сверху |
| Æ | Alt 0198 | Латинская заглавная буква AE |
| Ç | Alt 0199 | Латинская заглавная буква C с седилью |
| È | Alt 0200 | Латинская заглавная буква E с грависом |
| É | Alt 0201 | Латинская заглавная буква E с акутом |
| Ê | Alt 0202 | Латинская заглавная буква E с циркумфлексом |
| Ë | Alt 0203 | Латинская заглавная буква E с диэрезисом |
| Ì | Alt 0204 | Латинская заглавная буква I с грависом |
| Í | Alt 0205 | Латинская заглавная буква I с акутом |
| Î | Alt 0206 | Латинская заглавная буква I с циркумфлексом |
| Ï | Alt 0207 | Латинская заглавная буква I с диэрезисом |
| Ð | Alt 0208 | Латинская заглавная буква ETH |
| Ñ | Alt 0209 | Латинская заглавная буква N с тильдой |
| Ò | Alt 0210 | Латинская заглавная буква O с грависом |
| Ó | Alt 0211 | Латинская заглавная буква O с акутом |
| Ô | Alt 0212 | Латинская заглавная буква O с циркумфлексом |
| Õ | Alt 0213 | Латинская заглавная буква O с тильдой |
| Ö | Alt 0214 | Латинская заглавная буква O с диэризисом |
| × | Alt 0215 | Знак умножения |
| Ø | Alt 0216 | Латинская заглавная буква O со штрихом |
| Ù | Alt 0217 | Латинская заглавная буква U с грависом |
| Ú | Alt 0218 | Латинская заглавная буква U с акутом |
| Û | Alt 0219 | Латинская заглавная буква U с циркумфлексом |
| Ü | Alt 0220 | Латинская заглавная буква U с диэризисом |
| Ý | Alt 0221 | Латинская заглавная буква Y с акутом |
| Þ | Alt 0222 | Латинская заглавная буква торн |
| ß | Alt 0223 | Латинская строчная буква эсцет (S острое) |
| à | Alt 0224 | Латинская строчная буква a с грависом |
| á | Alt 0225 | Латинская строчная буква a с акутом |
| â | Alt 0226 | Латинская строчная буква a с циркумфлексом |
| ã | Alt 0227 | Латинская строчная буква a с тильдой |
| ä | Alt 0228 | Латинская строчная буква a с диэризисом |
| å | Alt 0229 | Латинская строчная буква a с кружочком сверху |
| æ | Alt 0230 | Латинская строчная лигатура ae |
| ç | Alt 0231 | Латинская строчная буква c с седилью |
| è | Alt 0232 | Латинская строчная буква e с грависом |
| é | Alt 0233 | Латинская строчная буква e с акутом |
| ê | Alt 0234 | Латинская строчная буква e с циркумфлексом |
| ë | Alt 0235 | Латинская строчная буква e с диэризисом |
| ì | Alt 0236 | Латинская строчная буква i с грависом |
| í | Alt 0237 | Латинская строчная буква i с акутом |
| î | Alt 0238 | Латинская строчная буква i с циркумфлексом сверху |
| ï | Alt 0239 | Латинская строчная буква i с диэризисом (умляутом) |
| ð | Alt 0240 | Латинская строчная буква eth |
| ñ | Alt 0241 | Латинская строчная буква n с тильдой |
| ò | Alt 0242 | Латинская строчная буква o с грависом |
| ó | Alt 0243 | Латинская строчная буква o с ударением |
| ô | Alt 0244 | Латинская строчная буква o с циркумфлексом |
| õ | Alt 0245 | Латинская строчная буква o с тильдой |
| ö | Alt 0246 | Латинская строчная буква o с диэризисом |
| ÷ | Alt 0247 | Знак деления |
| ø | Alt 0248 | Латинская строчная буква o со штрихом |
| ù | Alt 0249 | Латинская строчная буква u с грависом |
| ú | Alt 0250 | Латинская строчная буква u с акутом |
| û | Alt 0251 | Латинская строчная буква u с циркумфлексом |
| ü | Alt 0252 | Латинская строчная буква u с диэризисом |
| ý | Alt 0253 | Латинская строчная буква y с акутом |
| þ | Alt 0254 | Латинская строчная буква торн |
| ÿ | Alt 0255 | Латинская строчная буква y с диэризисом |
Рассчитать прямой угол двух стен.
Тут появится ответ
О калькуляторе:
С помощью данного калькулятора можно построить прямой угол двух стен. Вам необходимо ввести в первое поле длину первой стены, во второе поле длину второй стены и нажать считать. Указывайте длину стен в миллиметрах. После вычисления вам станет известна длина линии, которая соединяет конечные точки стен. На рисунке изображены первая и вторая стена с начальными точками (А), и конечными точками (B). Получившийся отрезок с начальной и конечной точками (C) соединяет точки (B).
Просто разверните стены так, чтобы все точки соприкасались, но не меняйте указанные и вычисленную длину линий.
В интернете огромное количество статей на эту тему. В основном сайты предлагают один рабочий метод.
Выбирается последовательность трёх цифр [3, 4, 5]. Затем каждая цифра умножается например на 20. Получается новая последовательность [60, 80, 100], где 60 и 80 длина сторон с прямым углом, а 100 длина стороны с углами 45 градусов.
Но последовательность размеров сторон нельзя менять.
Давайте умножим последовательность [3, 4, 5] на любое другое число, например на 4. Получается [12, 16, 20], где 12 и 16 должны быть стороны с прямым углом, а 20 сторона с углами 45 градусов.
Вы можете рассчитать прямой угол популярным способом, но не всегда это удобно. Что если одна из стен будет короче или намного длинней. Какова будет погрешность. С данным способом вы всегда зависимы от трёх размеров.
Именно поэтому я предлагаю вам калькулятор, где вы просто укажете длину двух стен и получите длину третей линии.
Просто соедините все начальные и конечные точки линий и у вас получится прямой угол между двумя стенами.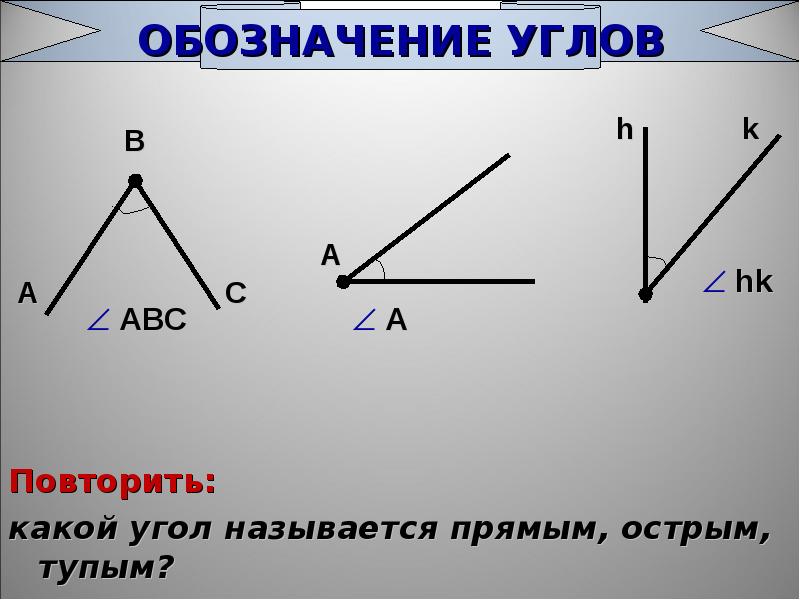
Конспект урока по математике на тему «Прямой угол»
Открытый урок математики во 2 классе по теме: «Угол. Прямой угол»
Цель:
1). Сформировать представление об угле и его элементах, способность к распознаванию и обозначению углов;
2).Познакомить с понятием «прямой угол»;
3).Учить находить прямой угол с помощью чертёжного угольника;
Задачи:
•Отрабатывать навыки анализа и решения задач;
•Пополнять активный запас детей; учить работать в паре;
•Развивать математическую речь, мыслительные операции;
•Формировать познавательный интерес;
•Способствовать здоровьесбережению детей;
•Соблюдать гигиенические требования к уроку;
Тип урока: ознакомление с новой темой.
План урока:
1.
2.
3.
4.
5.
6.
7.
Оборудование для урока:
демонстрационный материал: презетнация, картинка «Точки», угольник, карточки со словами: «Угол», «Прямой угол», «Вершина,стороны», «Перпендикулярные прямые», «Чертежный угольник».
раздаточный материал: чертежный угольник, лист бумаги (квадрат).
Ход урока:
I.Организационный момент.
Прозвенел для нас звонок,
Начинается урок.
II.Мотивация к учебной деятельности
Цель: создать условия для возникновения внутренней потребности включения в учебную деятельность.
Сказка-песня о зиме…
-О чём поётся в песенке о зиме.
-с чем ассоциируется у вас зима.
– Посмотрите, это … (Ёлочка.)
– Что необычного в изображении ёлочки? (Она составлена из геометрических фигур-треугольники и прямоугольников)
Почему вы решили что это треугольники (признаки 3 угла, 3 стороны)….
Прикатилось колесо,
Ведь похожее оно,
Как наглядная натура
Лишь на круглую фигуру.
Догадался, милый друг?
Ну, конечно, это … (круг). (дайте определение)
***
На фигуру посмотри
И в альбоме начерти
Три угла. Три стороны
Меж собой соедини.
Получился не угольник,
А красивый… (треугольник). (дайте определение)
***
Я фигура – хоть куда,
Очень ровная всегда,
Все углы во мне равны
И четыре стороны.
Кубик – мой любимый брат,
Потому что я…. (квадрат). (дайте определение)
***
Растянули мы квадрат
И представили на взгляд,
На кого он стал похожим
Или с чем-то очень схожим?
Не кирпич, не треугольник —
Стал квадрат… (прямоугольник). (дайте определение)
– Назовите эти фигуры одним словом. (Геометрические фигуры)
- Кто догадался из вас , какому разделу математики будет посвящён урок. (Геометрии.)
– Сегодня вам предстоит узнать новое из области геометрии.
III. Актуализация знаний и фиксация затруднения в деятельности.
Цель: активизировать представление о плоскости и луче; тренировать умения чертить, обозначать и называть лучи; активизировать мыслительные операции: анализ, синтез, обобщение;организовать самостоятельное выполнение учащимися индивидуального задания на применение нового знания, запланированного для изучения на данном уроке;организовать фиксацию учащимися возникшего затруднения в обосновании правильности полученного результата.
- Это что за фигура ? (угол)
Почему вы так решили? По каким признакам? – Как докажете, что данная фигура является углом?
Дети обосновывают своё мнение и приходят к выводу, что не могут доказать, что данная фигура является углом.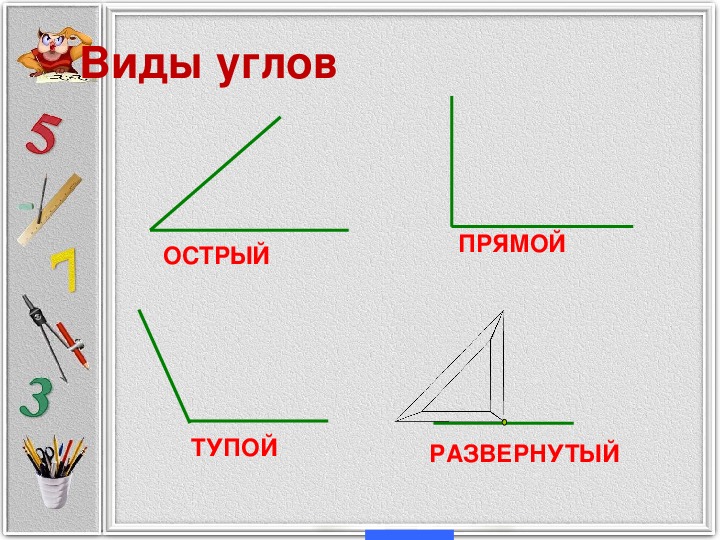
– Почему же возникло затруднение при доказательстве того, что выбранная вами фигура угол? (Нам неизвестно, что такое угол, каковы признаки этой геометрической фигуры.)
Как вы считаете какая цель нашего урока ,.чему мы хотим с вами научится ,что хотим узнать…
–Узнать, что такое угол, выявить его признаки.
IV. «Открытие» нового знания.
Цель организовать построение нового знания об угле; организовать фиксацию нового знания в речи; организовать выполнение задания, вызвавшего ранее затруднение; зафиксировать преодоление возникшего ранее затруднения.
— Углы окружают нас и в повседневной жизни. Приведите свои примеры, где можно найти углы вокруг нас. (слайд)
Посмотрите на рисунки: уголок соединительный для труб и уголок канцелярский для бумаг; угольник плотника и угольник чертёжный; угловой стол и угловой диван
Открываем тетради, записываем 28 ноября, классная работа.
— Ребята, а теперь от красных полей отступите одну клеточку и поставьте точку О. От этой точки проведите два луча.
– Покажите точку, общее начало лучей.
– Посмотрите, как называется общее начало лучей. (Это вершина угла)
– Покажите лучи, которые образуют угол.
– Как их называют? (Стороны угла.)
– Сколько вершин у угла? (1)
– Сколько сторон у угла? (2)
– Так из чего состоит угол? (Из точки – вершины и двух лучей – сторон, которые выходят из этой точки — вершины)
– Кто может сказать, что же такое угол? (Угол – это геометрическая фигура, которая состоит из точки — вершины и двух лучей — сторон, которые выходят из этой точки)
– Какие новые слова открыли для себя? (Угол, вершина угла, сторона угла).
– Вы конечно знаете, что у каждой геометрической фигуры есть имя, и у углов тоже есть имя.
– Яна, так тебя называет мама? А тебя Саша?
– Вас дома называют разными именами.
– И угол тоже можно назвать по-разному.
– Прочитайте его имя в учебнике на стр. …
- Что интересного заметили при чтении имён угла? (Буква, которая называет вершину читается в середине.
- У человека есть фамилия, имя и отчество, так и у угла есть сторона-это фамилия, имя-вершина, отчество-другая сторона).
– Записывают это так: слово «угол» заменяют специальным знаком:
– Запишем этот знак в тетради.
– Начинаем писать с верхнего правого угла клетки, ведём наклонную в нижний левый угол клетки и вправо по нижней стороне клетки в нижний правый угол. (Дети записывают знак в тетради)
– Как пишется ваше имя, фамилия и отчество? (С больших заглавных букв).
– А теперь обратите внимание на то, как пишется имя угла. (Все буквы заглавные)
– Как вы думаете, почему так записывают угол? (По названию вершины угла.)
- Правильно. Запишите имя угла в тетради.
V.Первичное закрепление с проговариванием во внешней речи
Цель: создать условия для выполнения учащимися нескольких типовых заданий на применение изученного знания с проговариванием во внешней речи.
- А теперь потренируемся в записи углов.
По-3 ученика возле доски , под диктовку….
Работа с учебником
– Выполним задание № с.
– Прочитайте задание.
Физминутка (проводят дежурные)
фиксики
– Продолжаем работу.
«Открытие» нового знания (продолжение)
Цели: организовать построение нового знания о прямом угле; организовать фиксацию нового знания в речи.
– Скажите, а можно ли угол сделать больше или меньше по размеру?
– Смоделируйте полученный угол так, чтобы он стал меньше, а теперь, чтобы он стал больше.
– Какой вывод можем сделать о размере углах? (Углы бывают разные по размеру)
Практическая работа с листком бумаги.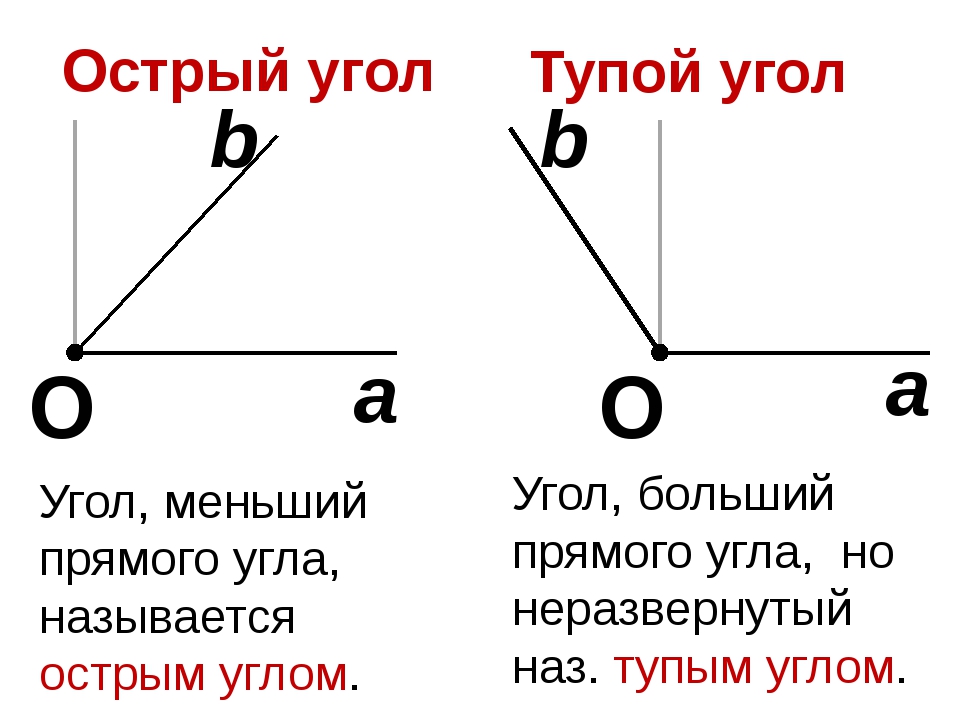
– Сложите лист бумаги пополам, а потом ещё раз пополам.
– Возьмите линейку и красный карандаш, проведите линии сгиба. Разверните лист.
- На сколько частей прямые разделили плоскость? (на 4 части)
– Что можете сказать о прямых? (Они пересекаются)
– Сколько углов образовали пересекающиеся прямые? (4)
– Эти пересекающиеся прямые образовали особенные углы.
– Может кто-нибудь знает названия этих углов?
– Это прямые углы (слайд 14)
– Покажите пальчиком каждый прямой угол.
- Раскрасьте прямые углы разными цветами.
– Поставьте точку на пересечении прямых.
– Чем будет являться эта точка для каждого из углов? (Вершиной угла)
Давайте на руках покажем уголки ( руки ровно-прямой , наклоняем –острый, отклоняем-тупой)
На партах салфетки, ( проволока). Сделайте из них прямой угол и проверьте с помощью угольника, затем сделайте острый и тупой.
На партах у вас проволока. Сделайте из нее прямой угол и проверьте с помощью угольника, затем сделайте острый и тупой
– Ребята, а вы обратили внимание, что у вас на партах лежит ещё один чертёжный инструмент.
– Кто знает, как он называется?
– Правильное его название чертёжный угольник.
– Прямые углы удобно находить и строить с помощью угольника.
– Рассмотрите его внимательно и подумайте, почему?
VI. Самостоятельная работа c самопроверкой.
Цель: организовать самостоятельное выполнение учащимися типовых заданий на применение новых знаний.
Работа по учебнику с. №
– А теперь самостоятельно найдите прямые углы с помощью чертёжного угольника.
Проверка работы с помощью доски (по эталону).
Самостоятельно проверьте, так ли вы нашли прямые углы, если так, поставьте «+».
Физминутка для глаз
Глазки видят всё вокруг,
Обведу я ими круг.
Глазком видеть всё дано-
Где окно, а где кино.
Обведу я ими круг
- Погляжу на мир вокруг
Повторение изученного (дополнительно).
– Решим задачу, в которой говорится о прямоугольнике .
Работа по учебнику с. №
Задача: Начерти прямоугольник со сторонами 6см и 2см и вычисли его периметр. .
– Прочитайте задачу про себя.
– А теперь прочитайте задачу вслух, чтобы узнать, что известно в задаче, а что надо найти.
– Что же нам известно в задаче?
– Что надо узнать?
– Прежде чем вычислить Р, что надо сделать? (Начертить прямоугольник)
– А потом? (Найти Р).
– Как найти Р прямоугольника? (Надо длину всех сторон сложить).
– Начертите прямоугольник и найдите его Р самостоятельно.
(Проверка: решение дети записывают на доске)
Домашнее задание ( с пояснением) тест 53 .стр100 работа с геометрическим материалом.( по заданию выбрать правильный ответ.)
Если осталось время дети рисуют с помощью геометрических фигур .( вывешиваем рисунки на доску.. Под музыку…
Вот такая интересная наука геометрия…
VII. Рефлексия учебной деятельности на уроке.
Цели:организовать фиксацию учащимися степени соответствия поставленной цели и полученного результата учебной деятельности;.организовать фиксацию затруднений, которые остались, и способов их преодоления; организовать самооценку учениками собственной учебной деятельности на уроке;
– Какую цель вы ставили перед собой на уроке? (Узнать, что такое угол, его признаки.)
– Достигли цели? Докажите.
– Что такое угол?
( Угол – это геометрическая фигура, образованная двумя разными лучами
с общим началом)
На слайде…
Сегодня я научился сам . ..
..
— Меня удивило…
— Было интересно …
— Было трудно …
— Я узнал, что …
— Я научился …
— У меня получилось …
- Мое настроение …
Выставление отметок с комментированием…
Просмотр содержимого документа
«Конспект урока по математике на тему «Прямой угол» »
Открытый урок математики во 2 классе по теме: «Угол. Прямой угол»
Цель:
1). Сформировать представление об угле и его элементах, способность к распознаванию и обозначению углов;
2).Познакомить с понятием «прямой угол»;
3).Учить находить прямой угол с помощью чертёжного угольника;
Задачи:
•Отрабатывать навыки анализа и решения задач;
•Пополнять активный запас детей; учить работать в паре;
•Развивать математическую речь, мыслительные операции;
•Формировать познавательный интерес;
•Способствовать здоровьесбережению детей;
•Соблюдать гигиенические требования к уроку;
Тип урока: ознакомление с новой темой.
План урока:
Орг.момент.
Мотивация к учебной деятельности.
Акуализация знаний, фиксация проблемы — затруднение в деятельности.
Открытие нового знания.
Первичное закрепление, составление алгоритма действий.
Самостоятельная работа с самопроверкой по эталону.
Рефлексия.
Оборудование для урока:
демонстрационный материал: презетнация, картинка «Точки», угольник, карточки со словами: «Угол», «Прямой угол», «Вершина,стороны», «Перпендикулярные прямые», «Чертежный угольник».
раздаточный материал: модели лучей (из картона), чертежный угольник, лист бумаги (квадрат).
Ход урока:
Организационный момент.
Прозвенел для нас звонок,
Начинается урок.
Мотивация к учебной деятельности.
Цель: создать условия для возникновения внутренней потребности включения в учебную деятельность.
Сказка-песня о зиме…
-О чём поётся в песенке о зиме.
-с чем ассоциируется у вас зима.
– Посмотрите, это … (Ёлочка.)
– Что необычного в изображении ёлочки? (Она составлена из геометрических фигур-треугольники и прямоугольников)
Почему вы решили что это треугольники (признаки 3 угла, 3 стороны)….
Прикатилось колесо,
Ведь похожее оно,
Как наглядная натура
Лишь на круглую фигуру.
Догадался, милый друг?
Ну, конечно, это … (круг). (дайте определение)
***
На фигуру посмотри
И в альбоме начерти
Три угла. Три стороны
Меж собой соедини.
Получился не угольник,
А красивый… (треугольник). (дайте определение)
***
Я фигура – хоть куда,
Очень ровная всегда,
Все углы во мне равны
И четыре стороны.
Кубик – мой любимый брат,
Потому что я…. (квадрат). (дайте определение)
***
Растянули мы квадрат
И представили на взгляд,
На кого он стал похожим
Или с чем-то очень схожим?
Не кирпич, не треугольник —
Стал квадрат… (прямоугольник). (дайте определение)
– Назовите эти фигуры одним словом. (Геометрические фигуры)
– Сегодня вам предстоит узнать новое из области геометрии.
III. Актуализация знаний и фиксация затруднения в деятельности.
Цель: активизировать представление о плоскости и луче; тренировать умения чертить, обозначать и называть лучи; активизировать мыслительные операции: анализ, синтез, обобщение;организовать самостоятельное выполнение учащимися индивидуального задания на применение нового знания, запланированного для изучения на данном уроке;организовать фиксацию учащимися возникшего затруднения в обосновании правильности полученного результата.
-Зимой с неба падают снежинки ,давайте нарисуем снежинку при помощи геометрических фигур!(учитель рисует на доске ,а дети называют признаки этих фигур)
1)точка, прямые, превращаем прямые в лучи, чертим круг, и украшаем снежинку вот такой фигурой…
Как она называется , почему так решили?
– Как докажете, что данная фигура является углом?
Дети обосновывают своё мнение и приходят к выводу, что не могут доказать, что данная фигура является углом.
– Почему же возникло затруднение при доказательстве того, что выбранная вами фигура угол? (Нам неизвестно, что такое угол, каковы признаки этой геометрической фигуры.)
Как вы считаете какая цель нашего урока ,.чему мы хотим с вами научится ,что хотим узнать…
–Узнать, что такое угол, выявить его признаки.
IV. «Открытие» нового знания.
Цель организовать построение нового знания об угле; организовать фиксацию нового знания в речи; организовать выполнение задания, вызвавшего ранее затруднение; зафиксировать преодоление возникшего ранее затруднения.
— Углы окружают нас и в повседневной жизни. Приведите свои примеры, где можно найти углы вокруг нас. (слайд)
Посмотрите на рисунки: уголок соединительный для труб и уголок канцелярский для бумаг; угольник плотника и угольник чертёжный; угловой стол и угловой диван
Открываем тетради, записываем 28 ноября, классная работа.
— Ребята, а теперь от красных полей отступите одну клеточку и поставьте точку О. От этой точки проведите два луча.
– Покажите точку, общее начало лучей.
– Посмотрите, как называется общее начало лучей. (Это вершина угла)
– Покажите лучи, которые образуют угол.
– Как их называют? (Стороны угла.)
– Сколько вершин у угла? (1)
– Сколько сторон у угла? (2)
– Так из чего состоит угол? (Из точки – вершины и двух лучей – сторон, которые выходят из этой точки — вершины)
– Кто может сказать, что же такое угол? (Угол – это геометрическая фигура, которая состоит из точки — вершины и двух лучей — сторон, которые выходят из этой точки)
– Какие новые слова открыли для себя? (Угол, вершина угла, сторона угла).
– Вы конечно знаете, что у каждой геометрической фигуры есть имя, и у углов тоже есть имя.
– Яна, как тебя называет мама? А тебя Саша?
– Вас дома называют разными именами.
– И угол тоже можно назвать по-разному.
– Прочитайте его имя в учебнике на стр. …
Что интересного заметили при чтении имён угла? (Буква, которая называет вершину читается в середине.
У человека есть фамилия, имя и отчество, так и у угла есть сторона-это фамилия, имя-вершина, отчество-другая сторона).
– Записывают это так: слово «угол» заменяют специальным знаком:
– Запишем этот знак в тетради.
– Начинаем писать с верхнего правого угла клетки, ведём наклонную в нижний левый угол клетки и вправо по нижней стороне клетки в нижний правый угол. (Дети записывают знак в тетради)
– Как пишется ваше имя, фамилия и отчество? (С больших заглавных букв).
– А теперь обратите внимание на то, как пишется имя угла. (Все буквы заглавные)
– Как вы думаете, почему так записывают угол? (По названию вершины угла.)
V.Первичное закрепление с проговариванием во внешней речи
Цель: создать условия для выполнения учащимися нескольких типовых заданий на применение изученного знания с проговариванием во внешней речи.
По-3 ученика возле доски , под диктовку….
Работа с учебником
– Выполним задание № с.
– Прочитайте задание.
Физминутка (проводят дежурные).
Под музыку.(выполняем движения-уголки)
– Продолжаем работу.
«Открытие» нового знания (продолжение)
Цели: организовать построение нового знания о прямом угле; организовать фиксацию нового знания в речи.
– Скажите, а можно ли угол сделать больше или меньше по размеру?
– Смоделируйте полученный угол так, чтобы он стал меньше, а теперь, чтобы он стал больше.
– Какой вывод можем сделать о размере углах? (Углы бывают разные по размеру)
Практическая работа с листком бумаги.
– Сложите лист бумаги пополам, а потом ещё раз пополам.
– Возьмите линейку и красный карандаш, проведите линии сгиба. Разверните лист.
– Что можете сказать о прямых? (Они пересекаются)
– Сколько углов образовали пересекающиеся прямые? (4)
– Эти пересекающиеся прямые образовали особенные углы.
– Может кто-нибудь знает названия этих углов?
– Это прямые углы (слайд 14)
– Покажите пальчиком каждый прямой угол.
– Поставьте точку на пересечении прямых.
– Чем будет являться эта точка для каждого из углов? (Вершиной угла)
На партах салфетки, ( проволока). Сделайте из них прямой угол и проверьте с помощью угольника, затем сделайте острый и тупой.
На партах у вас проволока. Сделайте из нее прямой угол и проверьте с помощью угольника, затем сделайте острый и тупой
– Ребята, а вы обратили внимание, что у вас на партах лежит ещё один чертёжный инструмент.
– Кто знает, как он называется?
– Правильное его название чертёжный угольник.
– Прямые углы удобно находить и строить с помощью угольника.
– Рассмотрите его внимательно и подумайте, почему?
VI. Самостоятельная работа c самопроверкой.
Цель: организовать самостоятельное выполнение учащимися типовых заданий на применение новых знаний.
Работа по учебнику с. №
– А теперь самостоятельно найдите прямые углы с помощью чертёжного угольника.
Проверка работы с помощью доски (по эталону).
Самостоятельно проверьте, так ли вы нашли прямые углы, если так, поставьте «+».
Физминутка для глаз
Глазки видят всё вокруг,
Обведу я ими круг.
Глазком видеть всё дано-
Где окно, а где кино.
Обведу я ими круг
Повторение изученного (дополнительно).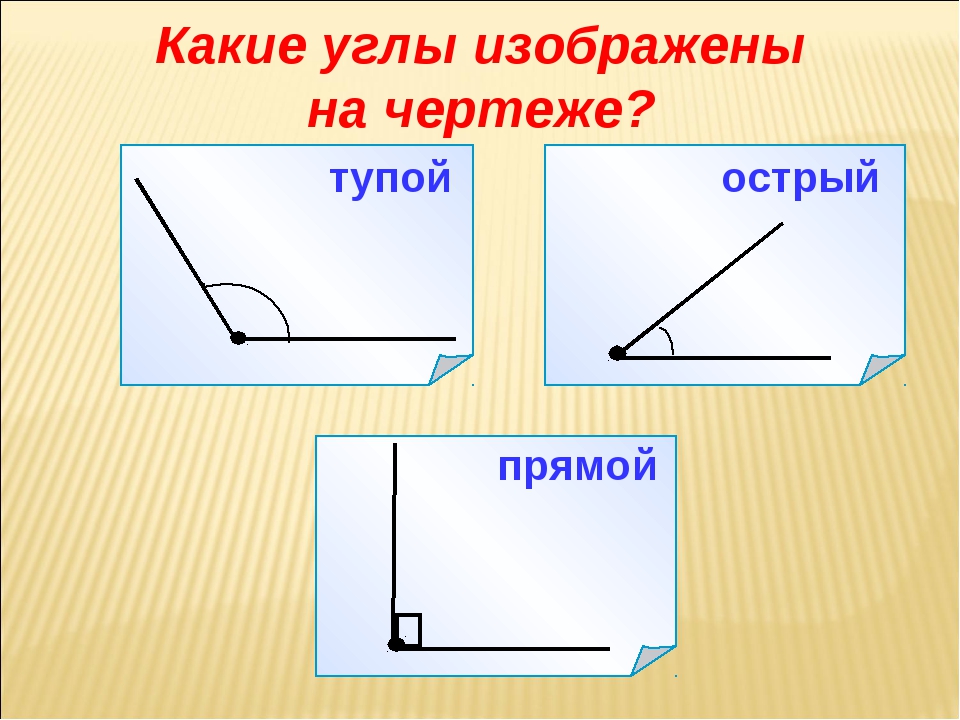
Игра «Им имя угол подарил»
Игра «Четвёртый лишний»
Назовите только те фигуры у которых есть прямой угол…
Что можно сделать, чтобы этих фигуры все углы стали прямыми? (обрезать угол или дочертить треугольник)
– Решим задачу, в которой говорится о прямоугольнике .
Работа по учебнику с. №
Задача: Начерти прямоугольник со сторонами 6см и 2см и вычисли его периметр. .
– Прочитайте задачу про себя.
– А теперь прочитайте задачу вслух, чтобы узнать, что известно в задаче, а что надо найти.
– Что же нам известно в задаче?
– Что надо узнать?
– Прежде чем вычислить Р, что надо сделать? (Начертить прямоугольник)
– А потом? (Найти Р).
– Как найти Р прямоугольника? (Надо длину всех сторон сложить).
– Начертите прямоугольник и найдите его Р самостоятельно.
(Проверка: решение дети записывают на доске)
Домашнее задание ( с пояснением) тест 53 .стр100 работа с геометрическим материалом.( по заданию выбрать правильный ответ.)
Если осталось время дети рисуют с помощью геометрических фигур.( вывешиваем рисунки на доску.. Под музыку…
Вот такая интересная наука геометрия…
VII. Рефлексия учебной деятельности на уроке.
Цели:организовать фиксацию учащимися степени соответствия поставленной цели и полученного результата учебной деятельности;.организовать фиксацию затруднений, которые остались, и способов их преодоления; организовать самооценку учениками собственной учебной деятельности на уроке;
– Какую цель вы ставили перед собой на уроке? (Узнать, что такое угол, его признаки.)
– Достигли цели? Докажите.
– Что такое угол?
( Угол – это геометрическая фигура, образованная двумя разными лучами
с общим началом)
– Углы бывают разные. С каким видом угла вы познакомились сегодня? (С прямым углом.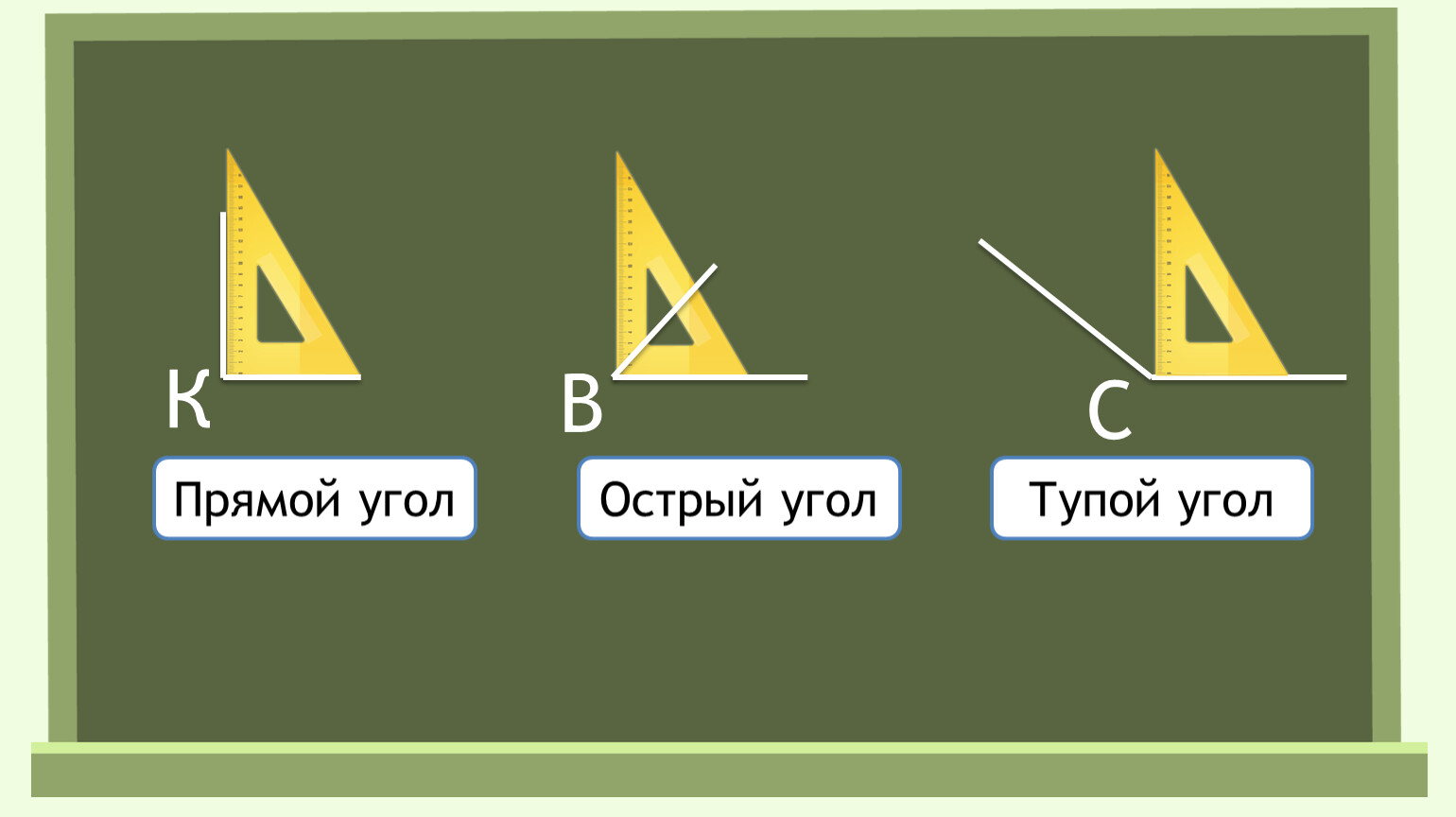 )
)
– Как вы находили прямой угол среди углов? (С помощью угольника: совмещали угол и одну из сторон угольника. Потом смотрели, совпадает ли другая сторона угла со стороной угольника.)
Выставление отметок с комментированием…
Презентация — Математика 5 класс «Углы — Развернутый угол
Слайды и текст этой презентации
Слайд 1
Углы. Развернутый угол. Прямой угол
Автор: Еремеева Марина Валерьевна,
учитель математики
МОУ «Средняя общеобразовательная школа №25» г. Бийска
Бийск, 2010
Слайд 2
Разгадайте кроссворд
1.
2
3
1
Единица измерения времени
2. Единица измерения массы
3. Сотая часть числа
4. Инструмент для измерения длины отрезков
М
И
Н
У
Т
А
Г
Р
А
М
М
П
Р
О
Ц
Е
Н
Т
Л
И
Н
Е
Й
К
А
Слайд 3
Как называются эти геометрические фигуры:
прямая
луч
отрезок
Слайд 4
Рассмотрим еще одну фигуру
Как образовалась эта фигура?
Слайд 5
Углом называют фигуру,
образованную двумя лучами, выходящими из одной точки.
О
А
В
Сторона угла
Вершина угла
Слайд 6
Назовите углы
Слайд 7
P
N
O
S
D
Какие точки лежат внутри угла?
M
H
R
А
F
Слайд 8
P
N
O
S
D
Какие точки лежат на сторонах угла?
M
H
R
А
F
Слайд 9
P
N
O
S
D
Какие точки лежат вне угла?
M
H
R
А
F
Слайд 10
Как сравнить углы?
Слайд 11
Вывод:
Равные углы при наложении
совпадают
Если один угол наложить на другой и
они совпадут, то эти углы равны
или
Слайд 12
Два дополнительных друг другу луча образуют развернутый угол
О
А
В
Слайд 13
Прямой угол – это половина развёрнутого угла
Слайд 14
Примеры:
Слайд 15
Чертежный треугольник
Слайд 16
Построение прямого угла
Для просмотра ролика — нажмите на квадрат
Слайд 17
Контрольные вопросы:
Что такое угол?
Какой угол называют развёрнутым?
Какие углы равны?
Какой угол называют прямым?
Как строят прямой угол с помощью чертежного треугольника?
Приведите примеры предметов, где есть углы
Прямой угол | Определение прямого угла на Dictionary.
 com
comсуществительное
угол, образованный двумя радиусами окружности, проведенными к концам дуги, равным одной четверти окружности; угол, образованный двумя пересекающимися перпендикулярными линиями; угол 90 °.
ВИКТОРИНА
БУДЕТ ЛИ ЭТА ВИКТОРИНА ВЫГОДНОЙ ПОБЕДОЙ ДЛЯ ВАС ТОРЖЕСТВЕННОЙ ПОБЕДЫ?
Думаете, вы отличите дефисы от дефисов? Вы стойкий приверженец em dash? Проверьте свою «лихую» силу духа с помощью этой викторины на всех рывках.
Вопрос 1 из 7
В то утро она проснулась ___ облачным, невзрачным утром ___ совершенно не подозревая, что ее жизнь вот-вот изменится с приходом письма от бабушки.
Происхождение прямого угла
Среднеанглийское слово, датируемое 1350–1400 гг.
ДРУГИЕ СЛОВА ОТ ПРЯМОГО угла
Прямоугольный, прилагательноеСлова рядом с прямым углом
Правый, правый, правый, правый, правый, правый и левый, правый угол, прямоугольный треугольник, прямое восхождение, правый как дождь, правый предсердно-желудочковый клапан, сразуСловарь.com Несокращенный На основе Несокращенного словаря Random House, © Random House, Inc. 2021
Примеры предложений из Интернета для прямого угла
.expandable-content {display: none;}. Css-12x6sdt.expandable.content-extended> .expandable- content {display: block;}]]>Глубоко внутри, в местах, где было невозможно протащить машины, были каменные проходы, которые, казалось, были вырезаны под прямым углом, а затем отполированы.
Сила захвата обычно проверяется с помощью динамометра, который человек берет так же, как держит стакан, при этом локоть загибается в сторону и располагается под прямым углом.
Я не одобряю то, что вы говорите, но я буду защищать до смерти ваше право сказать это.
Куда бы я ни пошел, «Эй, Картман, тебе должно понравиться Гриффины, верно?»
Изучить Dictionary.com
li {-webkit-flex -basis: 49%; — ms-flex-предпочтительный-размер: 49%; flex-base: 49%;} @ media only screen и (max-width: 769px) {. css-2jtp0r> li {-webkit-flex -basis: 49%; — ms-flex-предпочтительный размер: 49%; flex-base: 49%;}} @ media only screen and (max-width: 480px) {.css-2jtp0r> li {-webkit-flex-базис: 100%; — ms-flex-предпочтительный-размер: 100%; гибкий-базис: 100%;}}]]>Британский словарь определений для прямого угла
существительное
угол между двумя радиусами окружности, отсекающей по окружности дугу, равную по длине одной четверти окружности; угол 90 ° или π / 2 радиана
под прямым углом, перпендикулярно или перпендикулярно
Другие слова под прямым углом
Родственное прилагательное: ортогональныйПроизводные формы прямого угла
Прямоугольный, прилагательноеCollins English Dictionary — Полное и несокращенное цифровое издание 2012 г. © William Collins Sons & Co.Ltd. 1979, 1986 © HarperCollins Publishers 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012
Научные определения прямого угла
Угол с мерой 90 °.
Научный словарь американского наследия® Авторские права © 2011. Издано издательской компанией Houghton Mifflin Harcourt Publishing Company. Все права защищены.
Культурные определения для прямого угла
Новый словарь культурной грамотности, третье издание Авторские права © 2005 издательской компании Houghton Mifflin Harcourt.Опубликовано Houghton Mifflin Harcourt Publishing Company. Все права защищены.
Прочие — это Readingli {-webkit-flex-base: 100%; — ms-flex-предпочтительный размер: 100%; flex-base: 100%;} @ media only screen и (max-width: 769px) {. Css -1uttx60> li {-webkit-flex-базис: 100%; — ms-flex-предпочтительный-размер: 100%; гибкая-основа: 100%;}} @ экран только мультимедиа и (max-width: 480px) {. css-1uttx60> li {-webkit-flex-базис: 100%; — ms-flex-предпочтительный-размер: 100%; гибкий-базис: 100%;}}]]>Прямой угол — Cuemath
В этом разделе , мы исследуем мир прямых углов.Найдя ответы на вопрос, что такое сфера, как ее вычислить, и обнаружив интересные факты о прямых углах, тема станет ясной как кристалл.
Прежде чем мы начнем, давайте посмотрим, с чем недавно столкнулся Сэм.
После наблюдения угла, образованного стрелками часов в 15:00, одной четвертой части пиццы и углов комнаты, Сэм заметил, что в нескольких местах нас окружают прямые углы. Ты чувствуешь то же самое?
Наиболее распространенные прямые углы образуют вертикальная и горизонтальная линия.
Кроме того, диагональные линии, пересекающие друг друга, образуют прямой угол.
Давайте начнем наше путешествие и узнаем удивительные свойства прямых углов.
План урокаЧто такое прямой угол?
Определение прямого угла: Прямой угол — это угол со значением, равным 90 градусам.
Он играет важную роль в таких областях математики, как геометрия и тригонометрия.
Когда две прямые пересекаются друг с другом под углом 90 ° или перпендикулярны друг другу на пересечении, они образуют прямой угол. Все дело в определении прямого угла.
Прямой угол обозначается символом ∟.
Форма прямого угла
Прямой угол будет похож на алфавит L.
Воспользуйтесь данным интерактивным моделированием и посмотрите, как построить прямой угол с помощью транспортира или компаса.
Примеры прямого угла в реальной жизниПримеры прямых углов в формах, доступных вокруг нас:
- Кромки двери.
- Четыре края телевизора.
- 9:30 часов.
- Уголок стула.
Получите представление о прямых углах в формах вокруг нас из рисунка, приведенного ниже:
Эти формы чаще всего используются для получения примеров прямых углов.
Можете ли вы найти еще несколько примеров прямых углов в формах, доступных вокруг вас?
Калькулятор прямого угла
Некоторыми из устройств, используемых для измерения прямого угла, являются транспортир, заданные квадраты, угольники и т. Д. Поигравшись с моделированием, приведенным ниже, вы можете увидеть, как это делается.
Транспортир
Набор квадратов
Попробуйте Square
Типы углов
Существует шесть различных типов углов, а именно:
Есть еще одно место, где используется прямой угол, и это прямоугольный треугольник.
Если среди трех углов треугольника один угол равен 90 °, то этот треугольник называется прямоугольным.
Поскольку три внутренних угла прямоугольного треугольника в сумме составляют 180 градусов, и если один угол всегда равен 90 градусам, тогда два других угла всегда должны составлять в сумме 90 градусов, и они называются дополнительными углами.
Прямоугольный треугольник
Важные примечания
- Транспортир, заданные квадраты и пробный квадрат используются для измерения прямого угла в прямоугольном треугольнике.
- Существует шесть типов углов: острый угол, прямой угол, тупой угол, прямой угол, угол отражения и полный угол.
- Края двери, четыре края телевизора, 9:30 часов и угол стула — наиболее распространенные примеры прямого угла.
Тим нарисовал на бумаге несколько углов. Можете ли вы помочь ему определить правильный угол, не используя транспортир?
Раствор
С точки зрения прямого угла, прямой угол выглядит как алфавит L.
Среди заданных вариантов угол в левом нижнем углу является прямым
| \ (\ следовательно \) Угол в левом нижнем углу, который выглядит как L-образный угол алфавита, равен 90 |
Тревор хочет знать, какие типы углов больше прямого. Вы можете помочь ему разобраться с этой проблемой?
Раствор
Согласно определению прямого угла, любой угол, размер которого превышает 90 °, больше прямого угла.
Это:
(а) Тупой угол
(б) Уголок прямой
(c) Угол отражения
(d) Угол весь
| \ (\ следовательно \) Тупой угол, прямой угол, угол отражения и полный угол больше 90 ° |
Эй, вы можете написать название угла, показанного на картинке, это острый угол, тупой угол, прямой угол, угол рефлекса или весь угол?
Раствор
Название угла на картинке — прямой угол.
Маленькая Фиона видела часы в своем доме, и ей было любопытно узнать угол, сделанный двумя стрелками часов в 9:00 и 15:00. Вы знаете ответ на ее вопрос?
Раствор
мы можем видеть на картинке, что две стрелки часов образуют прямой угол.
| \ (\ следовательно \) Угол, образованный двумя стрелками часов в 9:00 и 15:00, равен -Прямому углу. |
Сложные вопросы
- Назовите возможный угол, сделанный стрелками часов в 12:00 и 10:00.
- Максимальный угол угла рефлекса?
Вот несколько занятий для вас.
Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Подведем итоги
Надеемся, вам понравилось узнать о прямоугольном треугольнике с помощью моделирования и практических вопросов. Теперь вы сможете легко решать задачи с острым углом, тупым углом, типом углов, прямым углом, определением прямого угла, прямоугольным треугольником, калькулятором прямого угла, прямыми углами в формах, примерами прямых углов и меньше прямого угла.
О компании CuemathВ Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу «обучение-обучение-обучение» учителя исследуют тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению.
Часто задаваемые вопросы (FAQ)
1.Каковы три угла прямоугольного треугольника?
Три угла прямоугольного треугольника равны:
Два острых угла и один прямой угол.
2. Напишите виды углов?
Вот разные типы углов:
Острый угол, прямой угол, тупой угол, прямой угол, угол отражения и угол полного вращения или нулевой градус.
3. Что такое тупой, острый и прямой угол?
Тупой угол — это угол между 90 ° и 180 °
Острый угол — это угол от 0 ° до 90 °
А прямой угол — это угол 180 °
4.Что такое прямой угол, угол отражения и угол полного поворота?
Прямой угол — это угол 90 °
Угол отражения — это угол от 180 ° до 270 °
А полный угол поворота составляет 360 ° или 0 °
Прямоугольные призмы— Учебное пособие по Java
Прямоугольные призмы— Учебное пособие по Java
Прямоугольная призма имеет простую геометрию прямоугольного треугольника с углом 45 градусов (см. Рисунок 1) и является одной из наиболее часто используемых призм. для перенаправления света и вращения изображений.В этом интерактивном руководстве рассматривается отражение света и вращение, инверсия и реверсирование изображения с помощью прямоугольной призмы в зависимости от ориентации призмы по отношению к падающему свету.
Учебное пособие инициализируется с прямоугольной призмой, расположенной так, чтобы действовать как призма Porro , свет, излучаемый меткой ориентации, попадает на грань гипотенузы. Метка ориентации содержит красную сферу вверху, синий блок на левой руке, заглушку внизу и желтый конус на правой руке.Свет, излучаемый меткой ориентации и отраженный призмой, представлен в учебном пособии одной красной линией. Инверсия, поворот и реверс метки ориентации могут происходить в результате прохождения света через прямоугольную призму и зависят от ориентации призмы. Для работы с учебным курсом используйте ползунок Prism Orientation , чтобы изменить ориентацию между прямоугольной призмой , Porro Prism или Dove Prism . Ползунок Orientation Mark можно использовать для поворота метки ориентации на любой угол от нуля до 360 градусов вокруг центральной оси.
В прямоугольной призме параллельный пучок световых волн, входящий в одну из меньших граней призмы (или опор ) под перпендикулярным углом, отражается от гипотенузы (самой длинной) грани и выходит через другую опору. При условии, что призма изготовлена из материала, имеющего показатель преломления больше квадратного корня из 2 (приблизительно 1,414), свет будет подвергаться полному внутреннему отражению на границе стекло / воздух, находясь внутри призмы.
Эта особенность делает призмы отличной заменой зеркалам, поскольку не требуется металлических или диэлектрических покрытий на отражающей поверхности, которая служит почти идеальным отражателем.Единственное возникающее рассеяние и потеря света (обычно всего несколько процентов) происходит из-за мелких дефектов поверхности, поглощения материалом призмы и отражений на входе и выходе призмы. Тщательная полировка поверхностей и нанесение подходящего антибликового покрытия на ножки минимизируют даже эти небольшие потери света. В этой ориентации прямоугольная призма действует как система инвертирования изображения, при этом верхняя грань выполняет функции плоского зеркала, создавая левосторонние изображения из правосторонних изображений и наоборот.Обратите внимание на рис. 1 (а), что заостренный конец маркера совмещения перевернут, но левая и правая стороны остаются в том же положении.
Изменение ориентации прямоугольной призмы так, чтобы свет теперь входил и выходил через поверхность гипотенузы, дает нереверсивное зеркало, как показано на рисунке 1 (b). Световой луч в этой конфигурации, который часто называют призмой Porro , подвергается двум внутренним отражениям после того, как входит в призму, и отклоняется на 180 градусов при выходе.В результате изображения инвертируются сверху вниз, но не переворачиваются справа налево. Когда призма используется таким образом, ее часто называют призмой с постоянным отклонением , потому что падающие и выходящие световые лучи будут параллельны, независимо от угла, под которым свет входит в призму. Призмы Порро часто используются в традиционных бинокулярных конфигурациях, где они перпендикулярно сложены вместе, чтобы сначала инвертировать, а затем реверсировать световые лучи для получения прямых или вертикальных изображений.Двойные призмы загибают световой путь оптической системы, а также смещают изображение как по горизонтали, так и по вертикали на половину длины гипотенузы в каждом направлении. Бинокулярные призмы обычно производятся с закругленными углами для уменьшения веса и размера и имеют небольшую прорезь, вырезанную на поверхности гипотенузы, чтобы препятствовать световым лучам, которые отражаются внутрь под углом взгляда.
Третья ориентация прямоугольной призмы по отношению к падающему световому лучу (рис. 1 (c)) обычно называется призмой голубя , которая полезна в качестве поворотного механизма изображения.У призм Dove часто удаляется ненужная треугольная вершина, как для экономии веса, так и для уменьшения паразитных внутренних отражений. Пучок световых лучей попадает в призму голубя параллельно грани гипотенузы и преломляется вниз на первой ноге к более длинной внутренней поверхности. После полного отражения от поверхности гипотенузы свет затем снова преломляется, поскольку он выходит из призмы через другую опору и движется в том же направлении, в котором он двигался перед входом в призму.Поскольку призма голубя вносит значительный астигматизм при прохождении сходящегося света, она используется почти исключительно с коллимированным светом. Призма голубя не отклоняет и не смещает изображение, но ее можно использовать для инвертирования или переворота изображения.
Хотя на первый взгляд призма голубя кажется хорошим кандидатом для рассеивания (из-за углового входа светового луча), пропускание света через призму фактически эквивалентно прохождению через пластину стекла с боковой выгодой в виде поворот изображения.Интересный эффект геометрии в виде голубя получается, когда призма вращается вдоль продольной оси. В ориентации, представленной на Рисунке 1 (c), свет, проходящий через призму голубя, формирует изображение, которое перевернуто сверху вниз и перевернуто справа налево. Однако, если призма повернута на 45 градусов, результирующее изображение поворачивается на 90 градусов, а когда призма поворачивается еще на 45 градусов (фактически на 90 градусов, когда она помещается «на бок»), изображение теперь повернут на 180 градусов.Таким образом, изображение поворачивается вдвое быстрее призмы. На практике две призмы типа «голубь» часто склеиваются вместе в гипотенузе (после размещения зеркальной поверхности на этих гранях), чтобы получить би-призму с возможностью изменения направления визирования для телескопов, перископов и других оптических инструментов.
Соавторы
Mortimer Abramowitz — Olympus America, Inc., Two Corporate Center Drive., Мелвилл, Нью-Йорк, 11747.
Мэтью Дж.Parry-Hill , Christopher A. Burdett и Michael W. Davidson — Национальная лаборатория сильных магнитных полей, 1800 East Paul Dirac Dr., Университет штата Флорида, Таллахасси, Флорида, 32310.
| Телефон : | 780-427-5318 | |
| (Composer d’abord le 310-0000 pour obtenir une ligne sans frais) | ||
| Телекопье: | 780-427-1179 | |
| Adresse de Courriel: | cshelpdesk @ gov.ab.ca | |
Знаете ли вы, что такое прямой угол?
Вы, наверное, уже имеете некоторое представление о том, что мы называем прямым углом. Но я все же рекомендую взглянуть на некоторые другие сообщения в нашем блоге, прежде чем продолжить, например, вы можете просмотреть этот пост о различных типах углов.
Вы готовы? Что ж, давайте расширим ваши знания о прямых углах.
Представьте себе, что…
… вы на углу футбольного поля. Теперь вы идете на другую сторону.
Чтобы продолжить, поверните на 90 ° и продолжайте идти по прямой до конца.
Наконец, вы снова поворачиваете, делая еще один прямой угол, и идете по прямой, пока не дойдете до конца.
Вы прибыли в другое место по сравнению с тем, с чего начали? Ответ очевиден, нет?
Итак, мы можем принять, что последовательность,
«Идите прямо + поверните на 90 ° + идите прямо + поверните на 90 ° + идите прямо»
всегда приводит нас в другое место, чем то, откуда мы начали.
А теперь представьте, что…
, вы — гигантский кемпинг по всей планете Земля, и вы следуете приведенной выше последовательности. Что случилось бы? Давайте взглянем!
Предположим, вы уезжаете с Северного полюса и идете на юг. Однако, достигнув экватора, вы поворачиваете, образуя прямой угол, и идете прямо по экватору. Затем вы снова поворачиваете на 90º в том же направлении, что и раньше, и продолжаете путешествие таким же образом. Посмотрите на изображение ниже!
Вы заметили, что произошло? Вы вернулись на Северный полюс, вашу отправную точку.Но что случилось? Мы могли бы задаться вопросом, являются ли эти углы 90º на поверхности Земли «прямыми» углами. Ответ, который мы ищем, таков, поэтому нам нужно искать объяснение в другом месте.
Если присмотреться, между двумя примерами нет ничего незначительного — первая поверхность плоская, а вторая изогнута. Таким образом, одна и та же последовательность движений «идти по прямой» и «повернуть на 90 °» может привести к разным местам.
Но интересно посмотреть на это задом наперед, другими словами, мы можем узнать кривизну поверхности, на которой мы находимся, без необходимости лететь на Луну, чтобы увидеть ее издалека.Аргументы такого рода используются астрономами, когда они изучают свойства Вселенной.
Я надеюсь, что вам понравился этот пост, и он воодушевил вас продолжить изучение интересных математических концепций с помощью Smartick. Войдите и зарегистрируйтесь, чтобы попробовать наш метод бесплатно!
Подробнее:
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.
Продажа не должна ощущаться как преодоление трудностей, связанных со слишком большим количеством неизвестных, неустойчивой опорой и отсутствием четкого плана достижения успеха. Мы даем вашей команде процесс, навыки и стратегию для поиска клиентов через успешный бизнес и построение прочных отношений.
из Луисвилля в Париж, из Стамбула в Ранчо Кукамонга, из Милуоки в Мюнхен, мы помогаем предприятиям, организациям и отделам продаж повышать эффективность, улучшать процессы и, в конечном итоге, увеличивать прибыль наших клиентов.
От зала заседаний до комнаты отдыха, от стратегии планирования до совершенствования процессов — мы даем компаниям и организациям новый взгляд на результаты бизнеса. Это больше, чем план … это действие, а затем результаты.
Прямой угол — элементарная математика
Значение
Неформальный: угол, соответствующий углу (прямоугольного) листа бумаги, или углу у основания заглавной L или вершины заглавной буквы T.
Это все примеры прямых углов:
Это не прямые углы: два слева тупые («шире» прямого угла), а два справа — острые («острее» прямого).
Математический фон
Построение прямого угла
Вы можете построить прямой угол, просто сложив бумагу, даже если она была разорвана так, чтобы не было прямых краев!
В любом направлении сложите лист бумаги.Например:
Результат будет выглядеть так:
Затем сделайте вторую складку, следя за тем, чтобы исходная складка лежала поверх самой себя.
Результат будет выглядеть так:
Когда вы развернете лист бумаги, две складки будут перпендикулярны друг другу. Все четыре угла — прямые.
Почему это работает? Первая складка образует прямую складку.Вторая складка складывает одну часть этой линии на другую. Если угол загнут через его вершину так, что одна сторона угла лежит прямо на другой, то складка делит угол пополам. Прямая линия исходной складки образует прямой угол (180 °) вокруг любой точки на ней. Складывание через эту точку делит угол пополам, поэтому каждый полученный угол составляет 90 °, и поэтому они прямые.
Факты о прямых углах
Четыре прямых угла подходят к точке. Как мы определяем градусы, «полный оборот» вокруг точки равен 360 °, поэтому размер каждого прямого угла составляет одну четвертую от этого значения: 90 °.В неформальной речи (не в математике) прямоугольные углы иногда называют квадратными, хотя, как и в приведенных выше фигурах, в форме нет ничего «квадратного». Две прямые, расположенные под прямым углом друг к другу, называются перпендикулярными друг другу.
Родственные математические идеи
перпендикуляр, угол, прямоугольник
«Правильно»: что одним словом?
Когда-то произносилось слово gh «правильно»; он произошел от латинского «rect-» с буквы «c». В английском языке слова с «rect-» в них часто имеют значение, относящееся к «right».”
Слово «право» имеет много значений. Одно из его значений — «правильно», противоположное «неправильному». (Когда мы получаем что-то не так, мы пытаемся исправить нашу ошибку). Другое значение — противоположное «левому». Еще одно значение — «прямо» или прямо, как в «После школы, пожалуйста, иди домой».
Почему все эти значения? Что у них общего?
Как и большинство слов, у правого есть великие… великие дедушка и бабушка. Самый ранний из известных нам предков мог звучать как рег, а многие кузены правых пишутся как рег или прямоугольник.Первоначальное значение было что-то вроде «двигаться по прямой». Когда мы что-то регулируем, мы держим это в нужном русле, не позволяя его изменяться, сохраняя контроль. Правила и предписания заставляют людей «идти прямым путем», поступать правильно. Слово «правитель» является двоюродным братом обычного и, следовательно, двоюродным братом права. Когда g в таком слове, как обычный, молчит (как в правильном, и во многих других словах), мы получаем линейку. Линейка помогает провести прямую линию. Король — это правитель, который устанавливает правила, регулирующие страну.Тираннозавр Рекс был «королем» динозавров; «Rex» на латыни означает «король» и связано с «reg» и «rect». Король — королевский просто царственен с другим молчаливым г — был самым богатым и могущественным человеком, который дал людям их права или отнял их! Когда мы называем детей Ричардом или Региной или, конечно же, Рексом — или Генри или Роем с еще одним молчаливым g — мы сравниваем их с королями и королевами!
Если «направо» означает что-то вроде «прямо», почему мы говорим «повернуть направо»?
Слово «право» предполагает силу — не только короля, но и правую руку — и поэтому поворот вправо — это поворот к этой правой руке.
Где прямой угол получил свое название? Есть ли еще «левые углы»?
Нет, прямой угол не имеет ничего общего с поворотами вправо или влево.
На этой карте мы говорим, что Уолнат-стрит составляет прямой угол с Мейн-стрит, потому что она идет как можно «прямо» от Мэйн-стрит. Корн-стрит поворачивает под другим углом.
.
