Как правильно выводить прямой угол фундамента на стройплощадке с применением теоремы Пифагора | Прораб Бывалый
Под моей статьёй «Как вывести прямой угол на фундаменте и для чего он нужен» появилось ряд комментариев, где утверждается что я иду сложным путем вместо того, чтобы просто применить теорему Пифагора.
Хочу сказать, что это довольно странные утверждения ведь я как раз и опираюсь на эту теорему. Видимо комментаторы, как обычно, просто не читают что написано в тексте публикации, а реагируют на заголовок.
Но всё равно хочу ответить на эти высказывания. Итак.
В комментариях утверждается что проще и точнее отмерить на одном из углов треугольник с катетами равными трём и четырем метрам соответственно. Гипотенуза должна составить пять метров.
В результате угол, составленный катетами, будет равен 90 градусам. То есть он будет прямым.
Казалось бы, всё просто. Но есть одна проблема. Всё просто, когда вы рисуете это на бумаге. То есть на плоскости. В полевых условиях выдержать шнурку в плоскости достаточно сложно. Причем желательно что бы строительная шнурка была натянута в горизонтальной плоскости. Почему я считаю это важным?
Причем желательно что бы строительная шнурка была натянута в горизонтальной плоскости. Почему я считаю это важным?
Давайте рассмотрим такой пример.
Допустим вы натянули шнурку с одной стороны выше горизонтальной плоскости, а с другой стороны – ниже.
Что получится, когда вы построите треугольник с нужной гипотенузой? Получится угол менее 90 градусов. Пусть это будет небольшая погрешность, но, например, при длине стен равной девяти и двенадцати метрам соответственно погрешность станет довольно существенной. И если допустить её на каждом из четырех углов, то в результате вы получите или ромб, или трапецию.
Поэтому в любом случае надо обязательно делать контрольный замер диагонали.
Только при равной длине диагоналей вы получите прямые углы.
Я как раз и предлагаю сразу опираться на это.
Поэтому предлагаю всем, кто легко и просто рисует треугольники на бумаге, пойти и сделать это в полевых условиях. Причем сделать это как они предлагают и как делаю я.
Потом уже высказываться.
Кстати, в видео я умышленно делаю не совсем правильно, но почему-то никто этого не замечает.
Что ещё раз говорит о знаниях моих критиков.
Что там неправильно я пока не буду говорить напишу об этом в другой раз.
Попутно хочу ответить на один комментарий что выводить прямые углы на фундаменте с помощью нивелира практически невозможно. Что там будут жуткие погрешности.
Как я уже писал выше погрешности могут быть при любом способе даже при использовании тахеометра. Всё зависит от того, кто это делает.
Поэтому оптический нивелир, на котором есть горизонтальный лимб вполне можно использовать для выведения прямых углов. Как это сделать я тоже напишу в дальнейшем.
Повторюсь ещё раз, самым точным методом будет вызов геодезиста со специальным оборудованием.
Я же предлагаю варианты выведения прямого угла, которые можно использовать если у вас по каким-то причинам нет возможности прибегнуть к услугам специалистов. Либо вы сами считаете себя вполне способным справиться с этой задачей.
Надеюсь, мои пояснения будут вам полезны.
Подписывайтесь на мой канал, будет ещё много познавательных материалов)
Египетский треугольник и качества
Египетский треугольник в строительстве. Общие сведения
Зарождение идеи
Идея у математика появилась после путешествия в Африку по просьбе Фалеса, который поставил задачу Пифагору изучить математику и астрономию тех мест. В Египте он среди бескрайней пустыни встретил величественные строения, поразившие его размером, изяществом и красотой.
Надо заметить, что более двух с половиной тысяч лет назад пирамиды были несколько другими – огромными, с четкими гранями. Тщательно изучив могущественные постройки, коих было не мало, так как рядом с великанами, стояли храмы поменьше, построенные для детей, жен и других родственных лиц фараона, это натолкнуло его на мысль.
Благодаря своим математическим способностям, Пифагор сумел определить закономерность в формах пирамиды, а умение анализировать и делать выводы привели к созданию одной из самых значимых теорий в истории геометрии.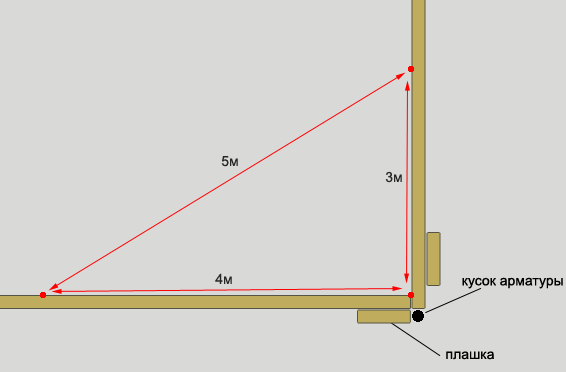
Из истории
Знали ли в древнем Египте о геометрии и математике? Конечно да. Жизнь египтян была тесно связана с наукой. Они регулярно пользовались знаниями при разметке полей, создании архитектурных шедевров. Даже существовала своя служба землемеров, которые применяли геометрические правила, занимаясь восстановлением границ.
Название треугольник получил благодаря эллинам, которые нередко бывали в Египте в VII-V вв. до н.э. Считается, что прообразом фигуры стала пирамида Хеопса, отличающаяся совершенными пропорциями. Ее место особенное в истории. Если посмотреть поперечное сечение, то можно отметить два треугольника, у которых угол внутри равняется 51о50’.
Строение
Сегодня это строение усеченной формы, приобретенной под воздействием времени, высота явно потерялась. Однако, восстановив ее геометричность, можно сделать вывод, что стороны треугольников равны. Получается в основе заложен золотой прямоугольный треугольник.
Однако, восстановив ее геометричность, можно сделать вывод, что стороны треугольников равны. Получается в основе заложен золотой прямоугольный треугольник.
Однако, следует рассмотреть другую пирамиду – Хефрена, у которой основа как раз-таки прямоугольный треугольник и где угол наклона боковых граней равен 53о12 с соотношением катетов 4:3. Это уже так называемый священный треугольник. Для египтян такая фигура сопоставлялась с семейным очагом: катет вертикального положения олицетворял мужчину, основание – представительницу прекрасного пола, а гипотенуза – рождение ребенка от обоих.
Стороны пирамиды Хефрена в соотношении равны 3:4:5, что точно соответствует теореме Пифагора. Значит, можно сделать вывод, что строители уже знали об этой теореме, но не могли ее сформулировать. Хотя, в исторических письменах встречаются следы использования египетского треугольника за много веков даже до Египта. До сегодняшнего дня это загадка, как могли такие знания получить древние египтяне. Понимали ли они чем обладают?
Особенность фигуры к тому же в том, что благодаря подобному соотношению, она является простым и первым Героновым треугольником, так как ее стороны и площадь целочисленные.
Обратное доказательство
Как доказать, что треугольник прямоугольный? Нужно порой исходить от обратного, то есть если сумма квадратов обеих сторон равна квадрату третьей, то треугольник прямоугольный, что подтверждает равенство 32х42=52 и значит он действительно прямоугольный.
Таким образом теорема Пифагора стала каноном и фундаментом развития математической науки. Со школьной скамьи каждый ученик знает, что означает выражение «Пифагоровы штаны во все стороны равны».
Интересно, что теорема Пифагора находится в Книге Гиннесса как теорема, обладающая самым большим количеством доказательств, которых примерно 500.
Особенности
Если рассмотреть более детально отличительные особенности египетского треугольника, то можно выделить следующие моменты:
- все стороны и площадь состоят из целых чисел, как говорилось выше;
- согласно теории великого математика, сумма квадратов катетов равна квадрату гипотенузе;
- такой фигурой возможно отмерить прямые углы в пространстве.
 Это используется в процессе строительства до сих пор;
Это используется в процессе строительства до сих пор; - не обязательно пользоваться специальными измерительными приборами, подойдут подручные средства, например, веревка.
Египетский треугольник в строительстве
Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.
Важно! Конечно, в идеале лучшим вариантом будет использование транспортира или угольника. Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы
Стороны конструкции имеют следующее соотношение друг к другу:
Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:
- 5,
- 4,
Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.
Внимание! Свойства египетского треугольника таковы, что квадрат гипотенузы равен квадратам двух катетов. Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример
Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять
Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.
Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.
Внимание! Длина каждого отрезка составит 4 и 3 см (при минимальных значениях). Пересечение этих прямых образует прямой угол, равняющийся 90 градусам
Альтернативные способы построить прямой угол на 90 градусов
Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.
Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.
Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.
Как получить египетский треугольник при помощи верёвки
Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.
Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.
Из них сложите фигуру с пропорциями 3, 4 и 5.
Как построить угол в 45, 30 и 60 градусов
Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.
Важно! Для получения нужного наклона вырвите лист бумаги из журнала и согните его. При этом линии изгиба будут проходить через угол
Края должны совпасть.
Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.
Внимание! Соотношение сторон на 30º нужно, чтобы сделать шестиугольники. Их свойства востребованы в столярных заготовках
Какие существуют альтернативные варианты
Как создать прямой угол
Лучшим вариантом смастерить прямой угол является применение угольника или транспортира. Это позволит с минимальными затратами найти необходимые пропорции. Но, основной момент египетского треугольника в его универсальности из-за возможности создать фигуру, не имея под рукой ничего.
Это позволит с минимальными затратами найти необходимые пропорции. Но, основной момент египетского треугольника в его универсальности из-за возможности создать фигуру, не имея под рукой ничего.
В этом деле может пригодиться все, даже печатные издания. Любая книга или даже журнал имеют всегда соотношение сторон, образующее прямой угол. Типографские станки работают всегда точно, чтобы рулон, заправленный в машину резался пропорциональными углами.
Древние инженеры придумывали много способов строительства египетского треугольника и всегда экономили ресурсы.
Поэтому, самым простым и широко применяемым был метод постройки геометрической фигуры с применением обычной веревки. Бралась бечевка и резалась на 12 ровных частей, из которых выкладывалась фигура с пропорциями 3,4 и 5.
Как создать другие углы?
Египетский треугольник в строительном мире нельзя недооценивать. Его свойства однозначно полезны, но без возможности построить углы другого градуса в строительстве невозможно. Чтобы образовался угол в 45 градусов, понадобится рамка или багет, которые распиливаются под углом в 45 градусов и соединяются между собой.
Его свойства однозначно полезны, но без возможности построить углы другого градуса в строительстве невозможно. Чтобы образовался угол в 45 градусов, понадобится рамка или багет, которые распиливаются под углом в 45 градусов и соединяются между собой.
Важно! Чтобы получить необходимый наклон, потребуется позаимствовать бумажный лист из печатного издания и согнуть его. Линии изгиба при этом будут проходить через угол
Края должны быть соединены.
Получить 60 градусов можно с применением двух треугольников по 30 градусов. Чаще всего используются для создания декоративных элементов.
Как треугольник используется в строительстве?
Треугольник используется в строительстве, чтобы убедиться, что что-то квадратное или что-то квадратное. Квадрат скорости представляет собой небольшой треугольный инструмент, используемый для обозначения углов стропила. Один из методов проверки квадрата комнаты или одной стены, перпендикулярной другой, состоит в том, чтобы измерить 3 фута вдоль одной стены и сделать отметку карандашом, чтобы они измеряли 4 фута вдоль другой стены и делали метку карандаша. Затем измерьте диагонально от метки карандаша до метки карандаша. Если число составляет 5 футов, две стены квадратные друг к другу.
Затем измерьте диагонально от метки карандаша до метки карандаша. Если число составляет 5 футов, две стены квадратные друг к другу.
Глаз в треугольнике
Символ, графически представляющий собой вписанный в треугольник глаз, называемый «глазом провидения» или «всевидящим оком», появился в Европе в XVII в. Считается, что он восходит к солярному глазу Гора древних египтян. Этот знак получил широкое распространение в барочной архитектуре, украшая фронтоны роскошных католических костелов.
В XIX в. он появился и на православных храмах, например, на фронтоне Казанского собора в Санкт-Петербурге. Христианство рассматривало его как символ Святой Троицы. Одновременно этот символ использовался и масонами, которые трактовали его как символ абсолюта, просвещения и высшего знания. У масонов «глаз провидения» располагается над стулом мастера ложи, чтобы таким образом напоминать о всепроникающей во все тайны мудрости Творца.
Декларация прав человека и гражданина, Франция, конец XVIII в.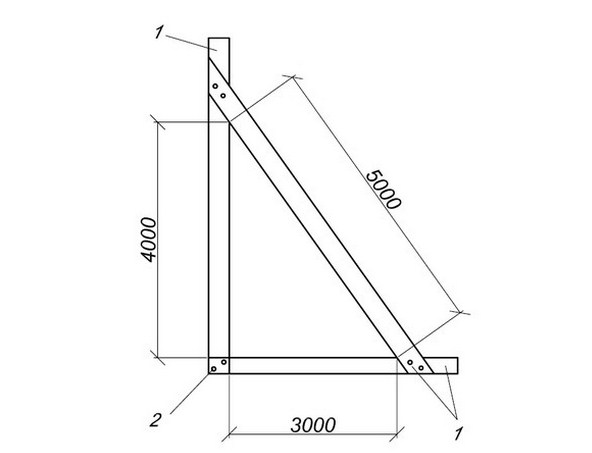
Герб белорусского города Браслав
Египетский треугольник и обратная теорема Пифагора
Математический лайфхак из обасти геометрии “Как при помощи простой верёвки получить треугольник с прямым углом”. Египтяне 4000 лет назад для строительства пирамид использовали метод получения прямоугольного треугольника при помощи верёвки разделенной на 12 равных частей.
Понятие “египетский треугольник”.
Почему треугольник со сторонами 3, 4, 5 называют египетским?
А всё дело в том, что строителям Древнего Египта пирамид нужен был простой и надежный метод построения треугольника с прямым углом. И вот как они это реализовывали. Верёвку разбивали на двеадцать равновеликих частей, обозначив границы между соседними частями; концы верёвки соединяли. После этого 3 человека натягивали верёвку таким образом, чтобы она образовала треугольник, причем расстояния между каждыми двумя египтянами, тянущими веревку, составляли соответственно три части, четыре части и пять частей. Получался треугольник с прямым углом с катетами в три и четыре части и гипотенузой в пять частей. Известно, прямым был угол между сторонами в три и четыре части. Как известно, древнеегипетских землемеров, которые кроме обмеривания земельных наделов занимались построениями на местности, в древнем Египте их называли гарпедонаптами (что буквально переводится как «натягивающие верёвки»). Гарпедонапты занимали 3 место в иерархии жрецоы Древнего Египта.
Известно, прямым был угол между сторонами в три и четыре части. Как известно, древнеегипетских землемеров, которые кроме обмеривания земельных наделов занимались построениями на местности, в древнем Египте их называли гарпедонаптами (что буквально переводится как «натягивающие верёвки»). Гарпедонапты занимали 3 место в иерархии жрецоы Древнего Египта.
Обратная теорема Пифагора.
Но из-за чего треугольник со сторонами 3, 4, 5 окажется прямоугольным? Большинство ответили бы на данный вопрос, что данный факт это теорема Пифагора: так как три в квадрате плюс четыре в квадрате равняется пяти в квадрате. Но теорема Пифагора говорит, что если треугольник с прямым углом, то тогда сумма квадратов 2-х его сторон равняется квадрату третьей. Здесь мы имеем дело с теоремой, обратной теореме Пифагора: если сумма квадратов 2-х сторон треугольника равна квадрату третьей, то тогда треугольник — прямоугольный.
Обрисованное практическое приложение обратной теоремы Пифагора относиться к далёкому прошлому. Едва ли кто-либо получает прямые углы таким методом сегодня. Но тем не менее данный способ является отличным математическим лайфхаком и может быть применён Вами в любой жизненной ситуации.
Едва ли кто-либо получает прямые углы таким методом сегодня. Но тем не менее данный способ является отличным математическим лайфхаком и может быть применён Вами в любой жизненной ситуации.
Стороны египетского треугольника обладают удивительным свойством. Этот удивительный египетский треугольник.
Ка-ж-дый, кто внимательно слушал в школе преподавателя геометрии, очень хорошо знаком с тем, что представляет собой египетский треугольник. От других видов подобных с углом в 90 градусов он отличается особым соотношением сторон. Когда человек впервые слышит словосочетание «египетский треугольник», на ум приходят картины величественных пирамид и фараонов. А что же говорит история?
У Апокалипсиса есть одержимость как ветхозаветными, так и новозаветными библейскими отрывками, фиксация, которая чаще встречается в масонстве, где объединены библейские и египетские идеи. Апокалипсис умирает, говоря «Все раскрывается», что не имеет смысла в фильме, но говорит с аудиторией, говоря, что скрытые знания или секреты масонов выходят из публики и больше не скрываются.
Боб говорит, что Апокалипсис создает пирамиду в современный день, используя свою способность перемещать материю. Способность укладывать материю на молекулярном уровне для формирования любой компоновки или конструкции материи в любой форме или форме, проявленной с помощью современных специальных эффектов, может быть секретом, который он утверждает, «раскрывается», когда он говорит «Все раскрыто». Пирамида и построение сознания Древних Строителей и Масонов должны представлять высший интеллект над звериной природой нормального человечества.
Как это всегда бывает, в отношении названия «египетский треугольник» есть несколько теорий. Согласно одной из них, известная теорема Пифагора увидела свет именно благодаря данной фигуре. В 535 году до н.э. Пифагор, следуя рекомендации Фалеса, отправился в Египет с целью восполнить некоторые пробелы в познаниях математики и астрономии
Там он обратил внимание на особенности работы египетских землемеров. Они очень необычным способом выполняли построение с прямым углом, стороны которой были взаимосвязаны одна с другой соотношением 3-4-5
Данный математический ряд позволял относительно легко связать квадраты всех трех сторон одним правилом.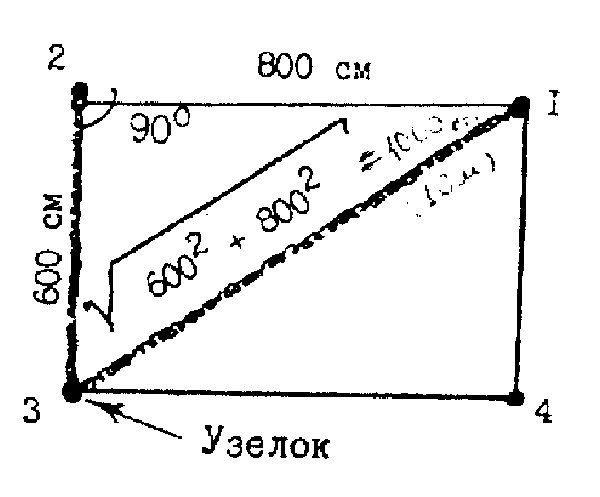 Именно так и возникла знаменитая теорема. А египетский треугольник как раз и есть та самая фигура, натолкнувшая Пифагора на гениальнейшее решение. Согласно другим историческим данным, фигуре дали название греки: в то время они часто гостили в Египте, где могли заинтересоваться работой землемеров. Существует вероятность, что, как это часто бывает с научными открытиями, обе истории произошли одновременно, поэтому нельзя с уверенностью утверждать, кто же придумал первым название «египетский треугольник». Свойства его удивительны и, разумеется, не исчерпываются одним лишь соотношением размеров сторон. Его площадь и стороны представлены целыми числами. Благодаря этому применение к нему теоремы Пифагора позволяет получить целые числа квадратов гипотенузы и катетов: 9-16-25. Конечно, это может быть простым совпадением. Но как в таком случае объяснить тот факт, что египтяне считали «свой» треугольник священным? Они верили в его взаимосвязь со всей Вселенной.
Именно так и возникла знаменитая теорема. А египетский треугольник как раз и есть та самая фигура, натолкнувшая Пифагора на гениальнейшее решение. Согласно другим историческим данным, фигуре дали название греки: в то время они часто гостили в Египте, где могли заинтересоваться работой землемеров. Существует вероятность, что, как это часто бывает с научными открытиями, обе истории произошли одновременно, поэтому нельзя с уверенностью утверждать, кто же придумал первым название «египетский треугольник». Свойства его удивительны и, разумеется, не исчерпываются одним лишь соотношением размеров сторон. Его площадь и стороны представлены целыми числами. Благодаря этому применение к нему теоремы Пифагора позволяет получить целые числа квадратов гипотенузы и катетов: 9-16-25. Конечно, это может быть простым совпадением. Но как в таком случае объяснить тот факт, что египтяне считали «свой» треугольник священным? Они верили в его взаимосвязь со всей Вселенной.
Концептуальное искусство Ральфа МакКуэрри для «Звездных войн» довольно простое, когда оно адаптировано к фильму, но есть одно изображение, которое, как представляется, является видом на землю Облачного города, с городом из трех основных пирамид, окруженных более мелкими пирамидами. Этот образ никогда не попадал в кино.
Этот образ никогда не попадал в кино.
Как вы можете встать, если вы не на коленях? Исаак Вайшаупт был на переднем крае теорий заговора, связанных с неуловимым «Иллюминатами» и его проникновением в индустрию развлечений. Это исследования теорий с использованием людей и событий в качестве демонстраций. Автор не знает, связаны ли эти люди с этими практиками, а изучает их поведение, чтобы получить теорию. Если кто-то здесь, как утверждается, является частью «Иллюминатов», пожалуйста, не принимайте его как факт, пока вы не выполните собственное исследование.
Правый треугольник имеет один угол, равный 90 градусам. Правый треугольник также может быть равнобедренным треугольником, что означает, что он имеет две стороны, которые равны. Правый равнобедренный треугольник имеет угол 90 градусов и два угла 45 градусов. Это единственный правильный треугольник, который является равнобедренным треугольником. Эта версия правого треугольника настолько популярна, что пластиковые модели из них изготавливаются и используются архитекторами, инженерами, плотниками и художниками-графиками в их проектных и строительных работах.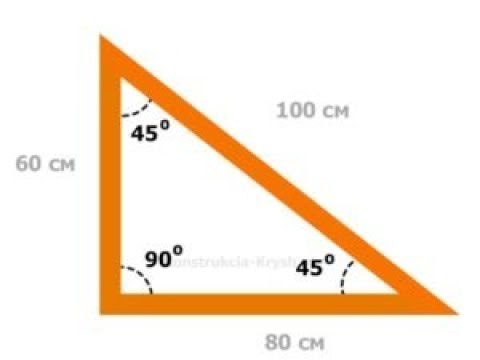
О египетском треугольнике и его свойствах хорошо известно ещё с древних времён. Эта фигура широко применялась в строительстве для разметки и построения правильных углов.
История египетского треугольника
Создателем этой геометрической конструкции является один из величайших математиков древности Пифагор. Именно благодаря его математическим изысканиям мы можем в полной мере использовать все свойства данного геометрического построения в строительстве.
Действительно, есть некоторые египетские рисунки, на которых найден такой инструмент. Имеются данные о том, что пифагорейская теорема была известна также и вавилонянам. Отсюда можно сделать вывод, что они также могли выполнять вычисления с прямоугольным треугольником, по крайней мере в некоторых случаях.
Основываясь на нынешнем уровне знаний об египетской и вавилонской математике и древних греческих источниках, Ван дер-Варден сделал следующий вывод. Достоинство первых греческих математиков, таких как Фалес, Пифагор и Пифагорейцы, – это не открытие математики, а ее систематизация и обоснование. В их руках вычислительные рецепты, основанные на смутных идеях, стали наукой.
В их руках вычислительные рецепты, основанные на смутных идеях, стали наукой.
Можно предположить, что математические навыки позволили Пифагору заметить закономерность в формах строения. Дальнейшее развитие событий можно легко представить. Базовый анализ и построение выводов создали одну из самых значимых фигур в истории. Скорее всего, в качестве прообраза была выбрана именно пирамида Хеопса из-за своих практически совершенных пропорций.
Геометрия у индейцев, а также у египтян и вавилонян была тесно связана с культами. Весьма вероятно, что квадрат гипотенузы был известен в Индии около 18 г. до н.э. Это разные фразы теоремы Пифагора в переводе с древнегреческого, латинского и немецкого языков.
В Евклиде эта теорема гласит. «В прямоугольном треугольнике квадрат стороны пролива над прямым углом равен квадратам сторон, которые фиксируют правый угол». Латинский перевод арабского текста ананиритов был сделан Герхардом Клемонским. «В каждом прямоугольном треугольнике квадрат, сформированный сбоку, нарисованный над прямым углом, равен сумме двух квадратов, сформированных с обеих сторон, покачиваясь под прямым углом».
Справочная информация
ДокументыЗаконыИзвещенияУтверждения документовДоговораЗапросы предложенийТехнические заданияПланы развитияДокументоведениеАналитикаМероприятияКонкурсыИтогиАдминистрации городовПриказыКонтрактыВыполнение работПротоколы рассмотрения заявокАукционыПроектыПротоколыБюджетные организацииМуниципалитетыРайоныОбразованияПрограммыОтчетыпо упоминаниямДокументная базаЦенные бумагиПоложенияФинансовые документыПостановленияРубрикатор по темамФинансыгорода Российской Федерациирегионыпо точным датамРегламентыТерминыНаучная терминологияФинансоваяЭкономическаяВремяДаты2015 год2016 годДокументы в финансовой сферев инвестиционной
Египетский треугольник
Египетский треугольник – прямоугольный треугольник с соотношением сторон 3:4:5. Сумма указанных чисел (3+4+5=12) с древних времен использовалась как единица кратности при построении прямых углов с помощью веревки, размеченной узлами на 3/12 и 7/12 ее длины. Применялся египетский треугольник в архитектуре средних веков для построения схем пропорциональности.
Итак, с чего же начать? Разве вот с этого: 3 + 5 = 8. а число 4 составляет половину числа 8. Стоп! Числа 3, 5, 8… Разве они не напоминают что-то очень знакомое? Ну конечно, они имеют прямое отношение к золотому сечению и входят в так называемый «золотой ряд»: 1, 1, 2, 3, 5, 8, 13, 21… В этом ряду каждый последующий член равен сумме двух предыдущих: 1 + 1= 2. 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8 и так далее. Выходит, что египетский треугольник имеет отношение к золотому сечению? И древние египтяне знали, с чем имели дело? Но не будем торопиться с выводами. Необходимо выяснить детали поточнее.
Выражение «золотое сечение», как считают некоторые, впервые ввел в XV веке Леонардо да Винчи. Но сам «золотой ряд» стал известен в 1202 году, когда его впервые опубликовал в своей «Книге о счете» итальянский математик Леонардо Пизанский. Прозванный Фибоначчи. Однако почти за две тысячи лет до них золотое сечение было известно Пифагору и его ученикам. Правда, называлось оно по-другому, как «деление в среднем и крайнем отношении». А вот египетский треугольник с его «золотым сечением» был известен еще в те далекие времена, когда строились пирамиды в Египте, когда процветала Атлантида.
Правда, называлось оно по-другому, как «деление в среднем и крайнем отношении». А вот египетский треугольник с его «золотым сечением» был известен еще в те далекие времена, когда строились пирамиды в Египте, когда процветала Атлантида.
Для доказательства теоремы о египетском треугольнике необходимо использовать отрезок прямой известной длины А-А1 (рис.). Он будет служить масштабом, единицей измерения, и позволит определить длину всех сторон треугольника. Три отрезка А-А1 равны по длине наименьшей из сторон треугольника ВС, у которой соотношение равно 3. А четыре отрезка А-А1 равны по длине второй стороне, у которой соотношение выражается числом 4. И, наконец, длина третьей стороны равна пяти отрезкам А-А1. А дальше, как говорится, дело техники. На бумаге проведем отрезок ВС, являющийся наименьшей стороной треугольника. Затем из точки В радиусом, равным отрезку с соотношением 5, проводим циркулем дугу окружности, а из точки С —дугу окружности радиусом, равным длине отрезка с соотношением 4. Если теперь точку пересечения дуг соединить линиями с точками В и С, то получим прямоугольный треугольнике соотношением сторон 3 : 4 : 5.
Если теперь точку пересечения дуг соединить линиями с точками В и С, то получим прямоугольный треугольнике соотношением сторон 3 : 4 : 5.
Что и требовалось доказать.
Глупая ошибка строителей
«Египетский треугольник» действительно может помочь в разметке периметра фундамента, однако применение этого метода требует сохранения чётких пропорций. Небольшое отклонение от них − и угол уже не будет прямым. А это приведёт к разнице длин стен. Не единичны случаи, когда при идеальном совпадении длин диагоналей стены получаются разными. Ведь если вдуматься, то трапеция также подходит под заданные параметры, её диагонали равны, в то время как верхняя и нижняя сторона имеют разные длины.
ФОТО: youc.irПравильная трапеция также имеет одинаковые длины диагоналей, однако на квадрат она явно не тянет
Место в строительном мире
С древнейших времен египетский треугольник нашел почетное место в архитектуре и строительстве. Конструкция пирамиды отличается тем, что позволяет создавать здание с совершенно правильными углами без каких-либо дополнительных инструментов.
Задача намного облегчается, если использовать транспортир или треугольник. Но, раньше применялись только шнуры и веревке, разделенные на отрезки. Благодаря отметкам на веревке можно было с точностью воссоздать прямоугольную фигуру. Строителям заменяла транспортир и угольник веревка, для чего отмечали узлами на ней 12 частей и складывали треугольник с отрезками 3,4,5. Прямой угол получался без затруднений. Эти знания помогли создать множество сооружений, в том числе пирамиды.
Интересно, что до древнего Египта, таким способом строили в Китае, Вавилоне, Месопотамии.
Свойства египетской треугольной фигуры подчиняются истине – квадрат гипотенузы равен квадратам двух катетов. Эта теорема Пифагора знакома каждому со школьной поры. Например, умножаем 5х5 и получаем гипотенузу равную числу 25. Квадраты обоих катетов равны 16 и 9, что в сумме дает цифру 25.
Благодаря таким свойствам, треугольник нашел применение в строительстве. Можно взять любую деталь, с целью провести линию прямого направления с условием, что ее длина должна быть кратной пяти. После этого заметить один край и прочертить от него линию кратную четырем, а от другого кратную трем. При этом каждый отрезок должен быть длиной минимум четыре и три. Пересекаясь, они образовывают один прямой угол в 90 градусов. Другие углы равны 53,13 и 36,87 градусам.
После этого заметить один край и прочертить от него линию кратную четырем, а от другого кратную трем. При этом каждый отрезок должен быть длиной минимум четыре и три. Пересекаясь, они образовывают один прямой угол в 90 градусов. Другие углы равны 53,13 и 36,87 градусам.
Прямой угол при строительстве. Нужна лишь веревка и помощь египтян.
При любой стройке часто сталкиваешься с проблемой разметки прямого угла на местности. Несомненно, что существуют всевозможные лазерные приборы, которые эту проблему решают на раз два. Они удобны и практичны. Но имеют один существенный недостаток — цена. Если вы профессионал — тогда — да, этот прибор незаменим. Ну а если любитель, и нужно всего пару раз построить прямой угол, то лишние расходы не к чему. Всегда можно обойтись веревкой, как делали с незапамятных времен. Даже египетские пирамиды строили с помощью этого способа и это до сих пор не потеряло актуальности.
Есть метод, который вполне рабочий и основан он на школьной геометрии.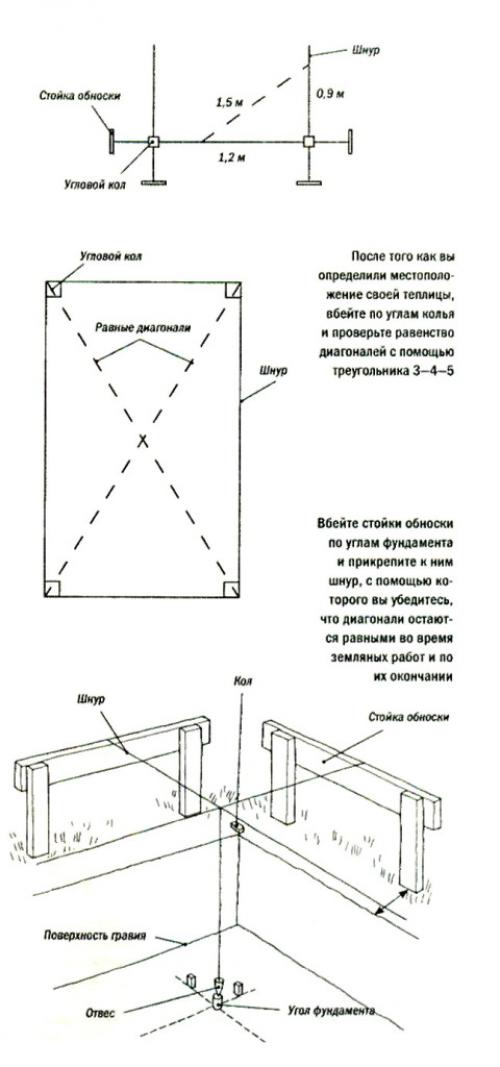 Допустим вам нужно поставить, грубо говоря, столбы под прямым углом друг к другу(угол забора). Этот способ я применял, когда делал на своем участке стол и вбивал трубы в землю. Конечно можно было и на глаз, но так как с этим у меня всегда была беда, то воспользовался обычной веревкой. Главное в этом, чтоб она не растягивалась, вот и все. У меня под рукой оказался мягкий тонкий провод, что вполне подходило под эти задачи.
Допустим вам нужно поставить, грубо говоря, столбы под прямым углом друг к другу(угол забора). Этот способ я применял, когда делал на своем участке стол и вбивал трубы в землю. Конечно можно было и на глаз, но так как с этим у меня всегда была беда, то воспользовался обычной веревкой. Главное в этом, чтоб она не растягивалась, вот и все. У меня под рукой оказался мягкий тонкий провод, что вполне подходило под эти задачи.
Суть основывается на, так называемых, египетских треугольниках. Их еще называют Героновыми, Евклидовыми, Пифагоровыми. Не будем вдаваться в подробности, отмечу лишь, что зачастую египетские — это частное от всех остальных. Лишь Пифагоровы тройки точно отвечают нашим требованиям.
Вот этот замечательный треугольник. Его стороны являются целым числом, что нам и нужно. Соответственно. Берем веревку и строим с помощью нее эту фигуру на земле. И не обязательно откладывать именно 3 метра, 4 и 5. Самое главное — соблюсти пропорции. За единицу измерения можно взять и полметра, а можно и любую другую удобную длину. Для примера — полуметровые соотношения — 1,5 м 2 м и 2,5 м. Просто, чем больше размеры — тем точнее наши построения.
Для примера — полуметровые соотношения — 1,5 м 2 м и 2,5 м. Просто, чем больше размеры — тем точнее наши построения.
Итак. Забиваем столб, от которого нам и надо построить прямой угол. От него отмечаем 3 метра и забиваем колышек на этом месте. К колышку привязываем веревку в пять метров а к столбу — четырехметровую. Связываем свободные концы друг с другом и натягиваем веревки, чтобы обе ни где не провисали. Когда найдем это место — туда колышек и все. Построения закончены — прямой угол у нас имеется. А дальше по линиям веревки забиваем столбы на нужном нам расстоянии.
Просто, дешево, быстро. Главное в этом деле — не спешить, и чем больше точность в отрезках веревки — тем ближе угол к 90 градусам.
Кстати, есть еще пару методов на основе треугольников и знаний геометрии, но об этом как нибудь в следующий раз. А на этом пока все.
Что такое Египетский треугольник на стройке? В чем его особенность +Фото и Видео
Строительство с применением египетского треугольника древний способ, активно используемый до сих пор современными строителями. Название получил благодаря древнеегипетским сооружениям, хотя известно, что история его начинается задолго до этого периода.
Название получил благодаря древнеегипетским сооружениям, хотя известно, что история его начинается задолго до этого периода.
Но, скорее всего, свойства уникальной фигуры не были оценены в те времена, пока не появился Пифагор, сумевший проанализировать и оценить изящные формы фигуры.
Египетский треугольник известен еще с древних времен. Он был и остается популярен в строительстве и архитектуре много веков.
Считается, что создал геометрическую конструкцию великий греческий математик Пифагор Самосский. Благодаря ему сегодня мы можем использовать все свойства геометрической постройки в области строения.
Египетский треугольник в строительстве. Общие сведения
Зарождение идеи
Идея у математика появилась после путешествия в Африку по просьбе Фалеса, который поставил задачу Пифагору изучить математику и астрономию тех мест. В Египте он среди бескрайней пустыни встретил величественные строения, поразившие его размером, изяществом и красотой.
Надо заметить, что более двух с половиной тысяч лет назад пирамиды были несколько другими – огромными, с четкими гранями. Тщательно изучив могущественные постройки, коих было не мало, так как рядом с великанами, стояли храмы поменьше, построенные для детей, жен и других родственных лиц фараона, это натолкнуло его на мысль.
Благодаря своим математическим способностям, Пифагор сумел определить закономерность в формах пирамиды, а умение анализировать и делать выводы привели к созданию одной из самых значимых теорий в истории геометрии.
Из истории
Знали ли в древнем Египте о геометрии и математике? Конечно да. Жизнь египтян была тесно связана с наукой. Они регулярно пользовались знаниями при разметке полей, создании архитектурных шедевров. Даже существовала своя служба землемеров, которые применяли геометрические правила, занимаясь восстановлением границ.
Название треугольник получил благодаря эллинам, которые нередко бывали в Египте в VII-V вв. до н.э. Считается, что прообразом фигуры стала
до н.э. Считается, что прообразом фигуры стала
Строение
Сегодня это строение усеченной формы, приобретенной под воздействием времени, высота явно потерялась. Однако, восстановив ее геометричность, можно сделать вывод, что стороны треугольников равны. Получается в основе заложен золотой прямоугольный треугольник.
Однако, следует рассмотреть другую пирамиду – Хефрена, у которой основа как раз-таки прямоугольный треугольник и где угол наклона боковых граней равен 53о12 с соотношением катетов 4:3. Это уже так называемый священный треугольник. Для египтян такая фигура сопоставлялась с семейным очагом: катет вертикального положения олицетворял мужчину, основание – представительницу прекрасного пола, а гипотенуза – рождение ребенка от обоих.
Стороны пирамиды Хефрена в соотношении равны 3:4:5, что точно соответствует теореме Пифагора. Значит, можно сделать вывод, что строители уже знали об этой теореме, но не могли ее сформулировать. Хотя, в исторических письменах встречаются следы использования египетского треугольника за много веков даже до Египта. До сегодняшнего дня это загадка, как могли такие знания получить древние египтяне. Понимали ли они чем обладают?
Особенность фигуры к тому же в том, что благодаря подобному соотношению, она является простым и первым Героновым треугольником, так как ее стороны и площадь целочисленные.
Обратное доказательство
Как доказать, что треугольник прямоугольный? Нужно порой исходить от обратного, то есть если сумма квадратов обеих сторон равна квадрату третьей, то треугольник прямоугольный, что подтверждает равенство 32
х42=52 и значит он действительно прямоугольный.
Таким образом теорема Пифагора стала каноном и фундаментом развития математической науки.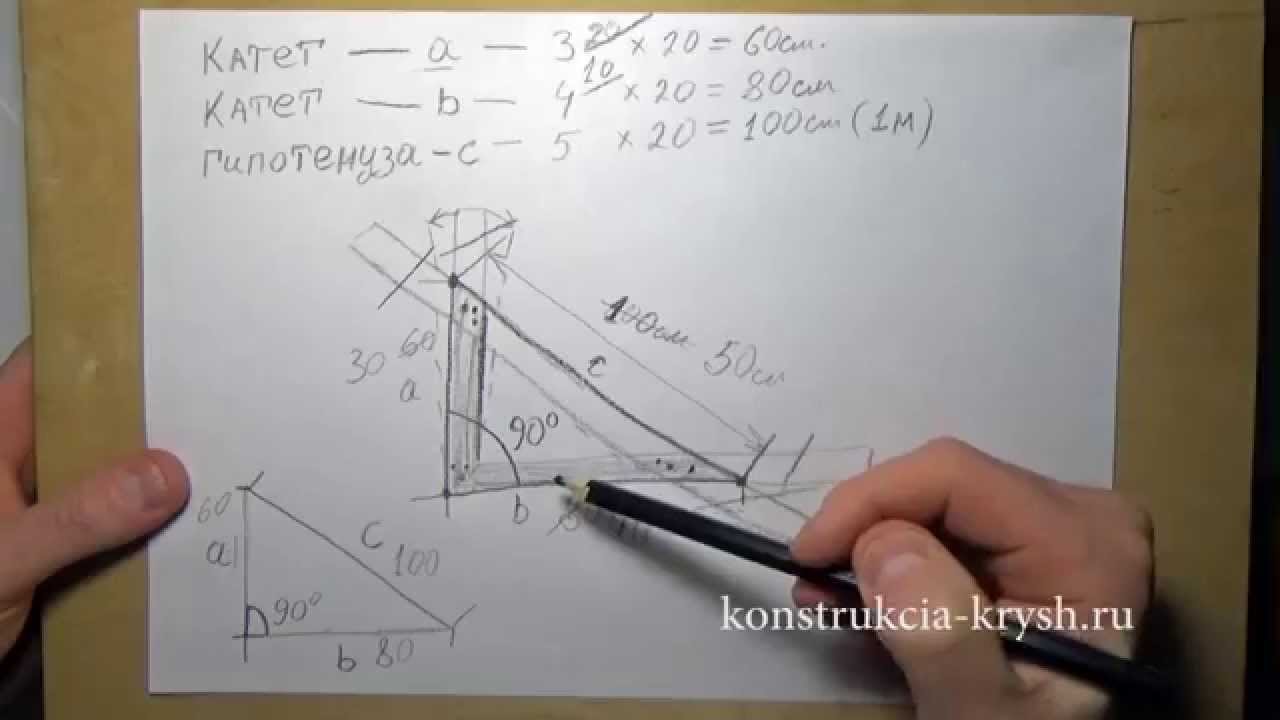 Со школьной скамьи каждый ученик знает, что означает выражение «Пифагоровы штаны во все стороны равны».
Со школьной скамьи каждый ученик знает, что означает выражение «Пифагоровы штаны во все стороны равны».
Интересно, что теорема Пифагора находится в Книге Гиннесса как теорема, обладающая самым большим количеством доказательств, которых примерно 500.
Особенности
Если рассмотреть более детально отличительные особенности египетского треугольника, то можно выделить следующие моменты:
- все стороны и площадь состоят из целых чисел, как говорилось выше;
- согласно теории великого математика, сумма квадратов катетов равна квадрату гипотенузе;
- такой фигурой возможно отмерить прямые углы в пространстве. Это используется в процессе строительства до сих пор;
- не обязательно пользоваться специальными измерительными приборами, подойдут подручные средства, например, веревка.
Место в строительном мире
С древнейших времен египетский треугольник нашел почетное место в архитектуре и строительстве. Конструкция пирамиды отличается тем, что позволяет создавать здание с совершенно правильными углами без каких-либо дополнительных инструментов.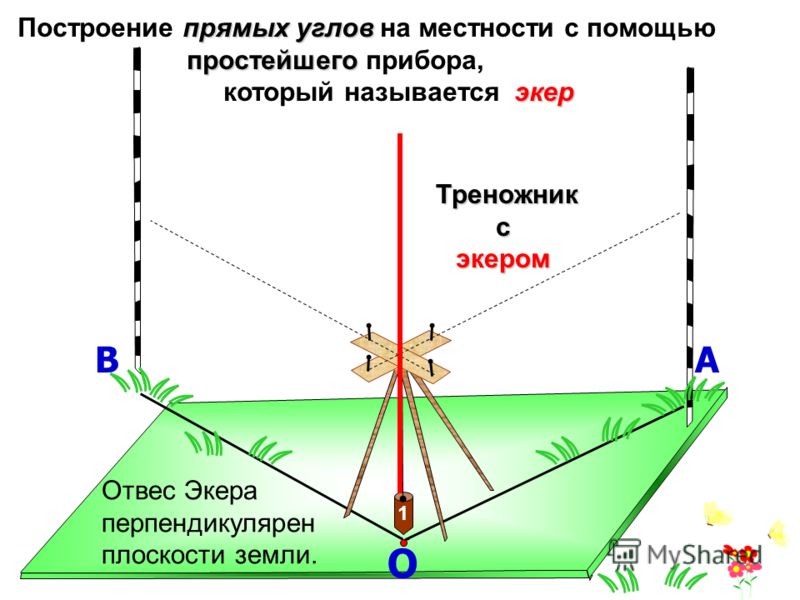
Задача намного облегчается, если использовать транспортир или треугольник. Но, раньше применялись только шнуры и веревке, разделенные на отрезки. Благодаря отметкам на веревке можно было с точностью воссоздать прямоугольную фигуру. Строителям заменяла транспортир и угольник веревка, для чего отмечали узлами на ней 12 частей и складывали треугольник с отрезками 3,4,5. Прямой угол получался без затруднений. Эти знания помогли создать множество сооружений, в том числе пирамиды.
Интересно, что до древнего Египта, таким способом строили в Китае, Вавилоне, Месопотамии.
Свойства египетской треугольной фигуры подчиняются истине – квадрат гипотенузы равен квадратам двух катетов. Эта теорема Пифагора знакома каждому со школьной поры. Например, умножаем 5х5 и получаем гипотенузу равную числу 25. Квадраты обоих катетов равны 16 и 9, что в сумме дает цифру 25.
Благодаря таким свойствам, треугольник нашел применение в строительстве. Можно взять любую деталь, с целью провести линию прямого направления с условием, что ее длина должна быть кратной пяти. После этого заметить один край и прочертить от него линию кратную четырем, а от другого кратную трем. При этом каждый отрезок должен быть длиной минимум четыре и три. Пересекаясь, они образовывают один прямой угол в 90 градусов. Другие углы равны 53,13 и 36,87 градусам.
После этого заметить один край и прочертить от него линию кратную четырем, а от другого кратную трем. При этом каждый отрезок должен быть длиной минимум четыре и три. Пересекаясь, они образовывают один прямой угол в 90 градусов. Другие углы равны 53,13 и 36,87 градусам.
Какие существуют альтернативные варианты
Как создать прямой угол
Лучшим вариантом смастерить прямой угол является применение угольника или транспортира. Это позволит с минимальными затратами найти необходимые пропорции. Но, основной момент египетского треугольника в его универсальности из-за возможности создать фигуру, не имея под рукой ничего.
В этом деле может пригодиться все, даже печатные издания. Любая книга или даже журнал имеют всегда соотношение сторон, образующее прямой угол. Типографские станки работают всегда точно, чтобы рулон, заправленный в машину резался пропорциональными углами.
Древние инженеры придумывали много способов строительства египетского треугольника и всегда экономили ресурсы.
Поэтому, самым простым и широко применяемым был метод постройки геометрической фигуры с применением обычной веревки. Бралась бечевка и резалась на 12 ровных частей, из которых выкладывалась фигура с пропорциями 3,4 и 5.
Как создать другие углы?
Египетский треугольник в строительном мире нельзя недооценивать. Его свойства однозначно полезны, но без возможности построить углы другого градуса в строительстве невозможно. Чтобы образовался угол в 45 градусов, понадобится рамка или багет, которые распиливаются под углом в 45 градусов и соединяются между собой.
Важно! Чтобы получить необходимый наклон, потребуется позаимствовать бумажный лист из печатного издания и согнуть его. Линии изгиба при этом будут проходить через угол. Края должны быть соединены.
Получить 60 градусов можно с применением двух треугольников по 30 градусов.
Чаще всего используются для создания декоративных элементов.
Небольшие хитрости
Египетский треугольник 3х4х5 актуален для маленьких домов. Но, что делать, если дом 12х15?
Для этого нужно построить прямоугольный треугольник, у которого катеты равняются 12 и 15 м. Гипотенуза находится как квадратный корень из суммы 12х12 и 15х15. В итоге получаем 19,2 м. С помощью чего-либо — веревки, шпагата, бечевки, тросика, военного кабеля, отмеряем 12, 15 и 19,2 м. Делаем узлы на этих местах и ставим жимки.
Затем треугольник нужно растянуть на нужном месте и установить 3 точки опоры, в которые вбить колышки. Четвертую точку можно получить, не трогая концы катетов. Для этого точка прямого угла перекидывается по диагонали и все готово.
Например, есть участок, где требуется прямой угол – для места под кухонный гарнитур, раскладки кафеля и других моментов. Хорошо бы такие вопросы учесть при кладке, но реальность другая и не всегда попадаются ровные стены и прямые углы. Здесь пригодится египетский треугольник с соотношением 3:4:5, либо при необходимости 1,5:2:2,5.
Здесь пригодится египетский треугольник с соотношением 3:4:5, либо при необходимости 1,5:2:2,5.
Обязательно учитывается толщина маяков, погрешность, бугры на стенах и т.д. Треугольник рисуется с помощью рулетки и мела. Если разметка небольшая, то можно воспользоваться листом гипсокартона, так как режутся они с правильными углами.
Египетский треугольник широко использовался в строительстве целых 2,5 века. И сегодня иногда приходится применять данную методику, при отсутствии необходимых инструментов, чтобы получить прямые углы. Свойства этой фигуры уникальны, что гарантирует точность в архитектуре и строительстве, без которой не обойтись. С ним легко работать, по форме он гармоничен и красив. До сих пор пытливые умы пытаются разгадать тайну египетского треугольника.
Разбивка фундамента
Для того чтобы начать строительство дома вы должны перенести его проект на участок, т. е. произвести так называемую разбивку дома.
е. произвести так называемую разбивку дома.
Разбивка должна выполняться очень точно и с большой тщательностью. Вероятно это одно из наиболее важных операций, т.к. неточная разбивка может привести к отклонениям в углах дома от прямого угла.
Даже если маленькие отклонения незаметны на глаз, однако это скажется при настиле полов. Придется при настиле использовать косые доски. Или при установке перекрытий придется подгонять балки. Если вы приобрели готовые крупномерные детали, дома изготовленные на заводе вы должны быть внимательны вдвойне.
Чтобы приступить к разбивке вам понадобятся геодезические инструменты для измерения углов – теодолит, мерная лента, вешки. Если вам нужна разбивка дома, который вы встраиваете между домами по улице можно обойтись веревочным треугольником со сторонами 3, 4 и 5 м. (теорему Пифагора помните?). Этого вполне достаточно для получения надежного результата.
Как сделать такой треугольник?
На крепком шпагате через 3, 4 и 5 м. делаете узлы и продеваете в них гвозди. Потом соединяете первый и последний узел. Между короткими сторонами должен получиться прямой угол.
делаете узлы и продеваете в них гвозди. Потом соединяете первый и последний узел. Между короткими сторонами должен получиться прямой угол.
Как же производят разбивку?
Сначала определяем сторону фасада. Для этого отмеряем расстояние от красной линии улицы, или провесив фасад относительно соседних домов. Для этого берем вешки и шнур, натягиваем по линии уличного фасада и привязываем к гвоздям, прибитым к кольям. Здесь следует иметь в виду, что колья прибиваются за пределами линий дома. Это делается, для того чтобы не повредить их при выкопке траншей для фундамента.
По этой линии нужно отметить первый угол дома. Получится точка, где вбивается кол. Эта точка будет вершиной нашего веревочного треугольника. Сторона равная 3 м идет вдоль линии фасада. Сторона в 4 м идет вдоль линии идущей внутрь участка и являющейся боковой. По этой стороне также вбиваем кол и натягиваем шпагат. От первой точки отмеряем две стороны дома – уличный и боковой фасады. В результате получаем еще две точки, куда вбиваем колья и натягиваем на них шпагат. Получили три угла четырехугольного плана дома.
Получили три угла четырехугольного плана дома.
Последнюю четвертую точку можно найти с помощью веревочного треугольника, приложив ко второй точке его вершину. Либо с помощью насечек отмерив на шпагате две стороны дома (циркуль помните?).
Как проверить правильно ли вы сделали разбивку?
Проведите диагонали. Они должны быть равны. Следует отметить, что высота кольев также играет роль, если участок неровный. Поэтому их высоты должны быть на одном уровне.
Колья, которые вы забили на углах дома, при земляных работах нужно передвинуть на 2-3 м за пределы дома и забить.
Шнур, натянутый при разбивке можно использовать и для расчета необходимой ширины траншеи для фундамента и размера цоколя. Делается это при помощи отвеса. Внутрь дома от шнура берем 50 см и за пределы 10 см. Только так стены попадут точно на середину фундамента и цоколя. Если вы отсчитаете равное расстояние по обе стороны шнура – стены окажутся за пределами уличного фасада.
Остальные пристройки (крыльцо, терраса, веранда) рассчитываются относительно основного контура дома.
Вот основные работы, которые вы должны произвести для разбивки дома. Хотя в них нет ничего сложного, однако, как было сказано выше расчеты и работы должны проводиться очень тщательно.
Построение прямого угла при помощи теодолита полным приемом (кп, кл)
Сущность работы сводится к построению разбивочного угла от исходной линии.
Построение угла с точностью, равной точности теодолита заключается в отложении от исходной линии МК (рис. 16) проектной величины угла при двух положениях вертикального круга теодолита КП и КЛ и производится в следующем порядке [5].
Рис. 16. Схема построения проектного угла
Устанавливают теодолит в вершине угла (точка М), приводят его в рабочее положение – центрируют над точкой, приводят в горизонтальное положение при помощи установочного уровня.

При открепленной алидаде, наблюдая в окуляр отсчетного микроскопа, устанавливают по горизонтальному кругу отсчет равный 000 при положении КП.
Закрепив алидаду и открепив лимб, визируют на цель (веха), установленную в точке К. Лимб закрепляют, алидаду открепляют.
Наблюдая в окуляр отсчетного микроскопа поворачивают алидаду до тех пор, пока не будет достигнуто значение проектного угла (в данном случае 90).
В створе линии на необходимом расстоянии точку С1 закрепляют шпилькой или колышком.
Повторно откладывают тот же угол при положении КЛ. В результате получают точку С2. Расстояние между точками С1 и С2 зависит, в основном, от коллимационной ошибки прибора.
Окончательное положение точки закрепляется в середине отрезка С1-С2 (точка С).
Построение разбивочного чертежа здания, вынос в натуру
основных осей здания
Вынос основных
осей здания в натуру производится от
пунктов строительной координатной
сетки или от геодезической опоры
(рис. 17). На практике в качестве геодезической
опоры следует принять красную линию
[5]. На красной линии через 6 метров на
длинной стороне здания закрепляют
кольями положения основных (1 и 4) и
вспомогательных (2 и 3) осей.
17). На практике в качестве геодезической
опоры следует принять красную линию
[5]. На красной линии через 6 метров на
длинной стороне здания закрепляют
кольями положения основных (1 и 4) и
вспомогательных (2 и 3) осей.
Установив теодолит в точку М, откладывают от линии МК прямой угол и в створе линии МС разбивают короткую сторону через 6 метров, закрепляя кольями. Теодолит перемещают в точку К, вновь откладывают угол 90. Далее производят окончательную разбивку – намечают основные и вспомогательные оси.
Рис. 17. Вынос в натуру основных осей здания
Контроль правильности построения осей здания производится сравниванием фактических длин диагоналей прямоугольников с их расчетными значениями. Расхождение не должно превышать 1/3000 длины диагонали.
Например:
После этого намечается обноска на расстоянии с и створный знак.
Расчет положения внутренней и внешней бровок котлована
Расчет положения
граней котлована и линий обноски ведется
от основных осей здания, закрепленных
в натуре кольями. Внутренняя грань
котлована (рис. 18) должна отстоять от
основной оси на 0,8 м. Внешняя грань должна
отстоять от внутренней на величину
Внутренняя грань
котлована (рис. 18) должна отстоять от
основной оси на 0,8 м. Внешняя грань должна
отстоять от внутренней на величину
d = i h, (46)
где d – заложение откосов;
i – уклон;
h – глубина котлована.
Линия обноски должна отстоять от внешней грани котлована на величину 3 – 5м.
Рис. 18. Расчет положения линии обноски
Таким образом, линии обноски должны отстоять от основных осей на расстояние:
c = a + d + b, (47)
где a – расстояние от основной оси до внутренней грани котлована;
b – расстояние от внешней грани котлована до линии обноски;
d – расстояние, равное заложению откосов.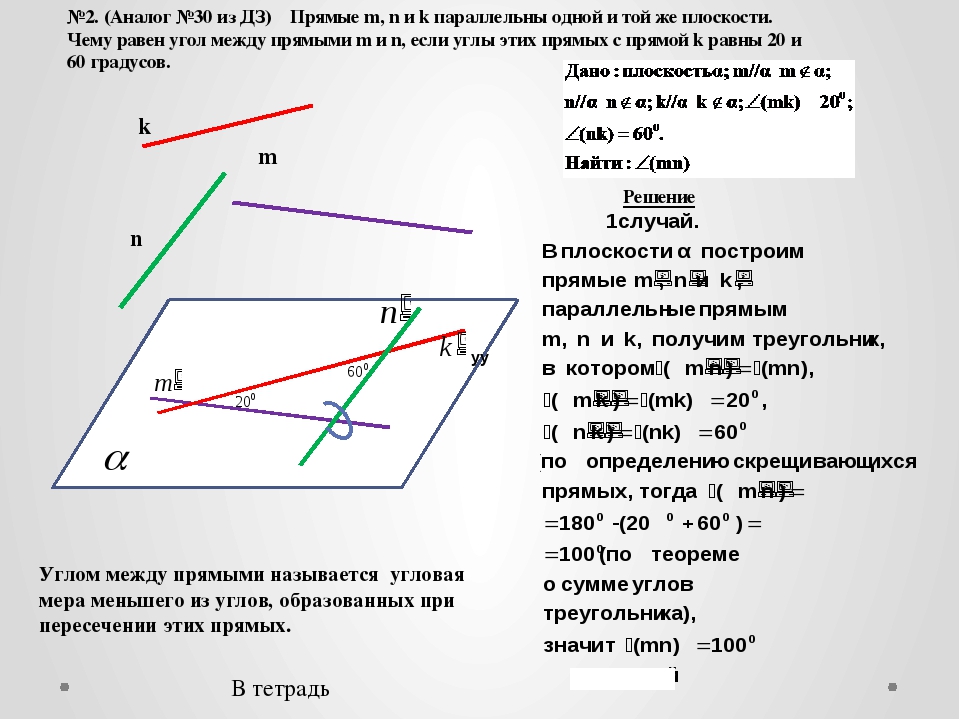
Вдоль основных осей, на их продолжении, откладывают расчетное расстояние с, закрепляя на местности линии обноски, параллельные основным осям. На готовую обноску основные оси переносят с помощью теодолита при двух положениях вертикального круга (КП и КЛ) и фиксируют среднее положение, забивая гвоздь на обноске. Между гвоздями, забитыми на противоположных линиях обноски, натягивают мягкую проволоку, обозначающую положение физической оси здания.
Правильная разметка под фундамент. Подробная пошаговая инструкция по разметке фундамента для дома
Кто занимается самостоятельным строительством знает, что до начала постройки сооружения надо своими руками разметить фундамент. Здесь рассмотрен случай начала работ по возведению свайного винтового фундамента на участке по ряду причин садоводческого характера не очищенного от полезных растений. Это затрудняло работы по разметке будущего фундамента, но эти трудности легко были преодолены с помощью простого приспособления по выставлению прямых углов.
Как сделать разметку фундамента своими руками
Обычно разметка фундамента в самостоятельном строительстве делается на глаз при помощи рулетки. Сначала выставляются столбики разметки углов стен на расстояниях длины и ширины будущей постройки. Потом делается замер диагоналей полученного прямоугольника и начинается процесс перестановки двух смежных столбов до выравнивания замеров диагоналей. По основам геометрии прямоугольником является фигура у которой две диагонали равны между собой. Но именно из за посадок замер диагоналей в процессе подгонки и был затруднен. Посадки мешали натянуть рулетку и затеняли лазер дальномера. Но эту трудность можно преодолеть.
1. До начала работ надо обладать минимальными знаниями геометрии и знать решение теоремы Пифагора:). Напомню теорему. Квадрат гипотенузы равен сумме квадратов катетов в прямоугольном треугольнике.
2. Натянем между двумя колышками шнур обозначающий первую стену фундамента. Если сторона фундамента, например, равна 6 метрам, то расстояние между колышками должно быть не меньше 8 метров.
3. Сделаем приспособление для выставления прямого угла на местности. Для этого надо приобрести упаковку обязательно нетянущегося шнура или применить стальной тросик. Всего потребуется около 13 метров шнура.
4. Связываем сложенные вместе концы шнура так, чтобы длина полученной петли равнялась 6 метрам. Точность завязывания и выставления размера важна.
5. Берем перманентный фломастер и от центра узла при помощи рулетки делаем отметки на расстоянии 3 метра в одну сторону и на расстоянии 4 метра в другую сторону. Так мы получили веревочный прямоугольный треугольник. Это изобретение позволит вычислить направление угла 90° простым растягиванием треугольника.
Разметка первой стены Набор для лайфхака Стороны треугольника
6. Для работы на местности нам потребуются тонкие деревянные колышки или куски тонкой арматуры.
7. Устанавливаем один колышек для обозначения угла фундамента на линии разметки сделанной ранее в п.2.
8. Берем веревочный лайфхак.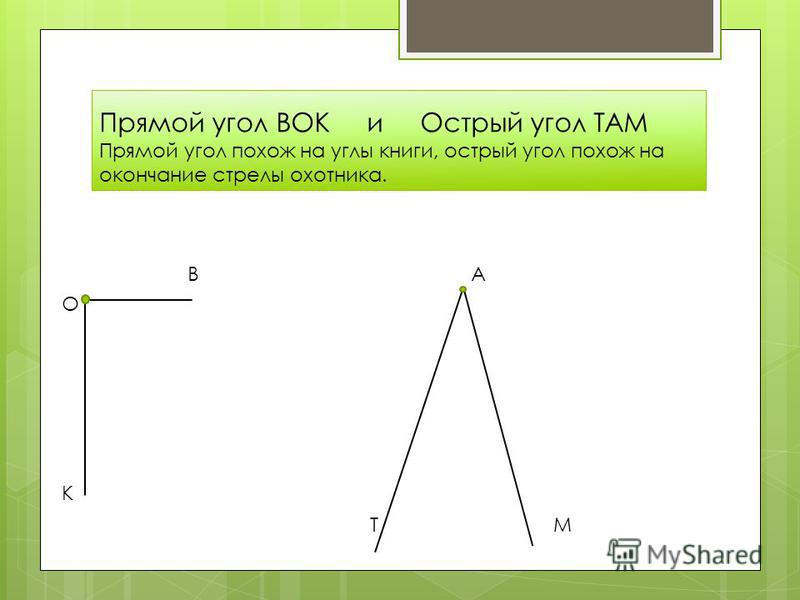 Узел помещаем на колышке обозначающем угол и растягиваем стороны веревочного треугольника вбивая первый колышек на расстоянии 4 метра в разметки стены п.2., перегиб шнура должен быть на метке фломастера 4 метра.
Узел помещаем на колышке обозначающем угол и растягиваем стороны веревочного треугольника вбивая первый колышек на расстоянии 4 метра в разметки стены п.2., перегиб шнура должен быть на метке фломастера 4 метра.
9. Выставляем колышек на метке 3 метра. Одна сторона прямоугольника параллельна разметке первой стены, а вторая сторона указывает направление разметки под углом 90° для второй стены. Теорема Пифагора в действии — смотри фото.
Куски арматуры Колышек основания прямого угла Веревочный треугольник10. Натягиваем разметочный шнур для второй стены, параллельно стороне треугольника.
11. Проводим аналогичные действия для разметки третьей стены.
12. Обозначаем на разметке длины второй и третьей стены и проводим контроль на одном из углов правильности направления четвертой стены. Если длина стены в разметке составила 6 метров и ее направление пересекло точки разметки стен два и три, то можно сказать, что замер диагоналей даст равный результат. Если схождения не получилось, проверьте еще раз правильность установки разметки.
Одним из самых дорогих и трудоемких этапов каждого из типов строительства является конструирование основы, базы под функциональное сооружение, неотъемлемым атрибутом которого есть разметка под фундамент своими руками. Понятно, что именно на это основание положена миссия нести большую ответственность за его будущую прочность, а также устойчивость здания, его прочность и функциональную состоятельность. Такая конструкция как фундамент выполняет роль той опоры, которая полностью принимает на себя всю нагрузку, оказываемую сооружением, распределяет ее по занимаемой зоне подстилающей поверхности.
Более того, именно грамотно сконструированное основание любого здания позволяет свести все нюансы рельефа грунта к единому однородному горизонту, в частности, с него и начинается сама по себе разметка участка под дом.
Этот процесс представляет собой определение всего периметра дома и также осуществление процедуры ориентировки фасада. Каким же образом правильно провести эту процедуру, не пользуясь услугами специалистов? Рассмотрим ниже.
Каким же образом правильно провести эту процедуру, не пользуясь услугами специалистов? Рассмотрим ниже.
Технология
Для начала стоит выделить базовые этапы процесса адекватной разметки участка под застройку. К их числу относят такие компоненты:
- определение привязки, степени ее правильности;
- фиксация таких параметров как ширина сооружения и его длина;
- измерение углов здания.
Сама вышеописанная процедура осуществляется обученными технологами – профессионалами – геодезистами. Конечно, когда вы непосредственно переходите к опции строительства, на руках к тому времени имеется грамотный утвержденный экспертами план застройки. Именно в этот момент стоит подробно изучить все особенности обрабатываемой почвы, а также то, на какой глубине находятся грунтовые воды на участке. Даже если речь идет об облегченном типе строения – бане, гараже – все равно разметка под фундамент своими руками очень важный компонент организованной деятельности.
Правильная геометрия – самый сложный элемент процесса. План стоит «наложить» на участок и соблюсти при этом все необходимые углы. Конечно, неточности расчета на качество и устойчивость фундамента никак не повлияют, но вот когда дело дойдет то процедуры возведения стен, доставят немало всякого рода неприятностей.
Для того чтобы правильно соблюсти все необходимые для адекватной разметки геометрические углы, стоит помнить о двух базовых геометрических правилах, известных все еще со школы:
- В пределах одного прямоугольника обе диагонали полностью одинаковы. Они также аналогичны и в другой фигуре – равнобедренной трапеции.
- Также стоит учитывать правило под названием «золотой треугольник». Так, прямоугольная фигура, стороны которой всегда кратны 3 и 4, в любом случае характеризуется наличием гипотенузы, величиной в пять единиц. Именно это принцип применим для строительства.
Условия и нюансы процесса
Для того чтобы разметка под ленточный фундамент была адекватной, для ее осуществления необходимо использовать такие инструменты:
- 20-метровая рулетка из металла;
- надежная толстая веревка;
- крепкие колышки из дерева и надежные прищепки, которые применимы для осуществления пометок локальных точек будущего сооружения.

Перед началом работы обязательно определяется точка, выполняющая роль угла здания. Сквозь то зону необходимо провести специальную длинную линию, ставшую основанием для первой стены (будет она фронтальной либо фасадного типа особого значения не имеет). Сам колышек стоит установить где-то на расстоянии в 50 см от первоначального угла, а вот последний помечаем с помощью прищепки.
При участии мерной рулетки откладываем необходимую длину от самой стены, после чего вбиваем другой колышек на том же расстоянии, что и первый, локализацию второго угла также фиксируем при помощи прищепки.
Сквозь отметку – точку следует внимательно провести ровную линию второй стены, так же, как это происходило и в первом случае, для начала происходит измерение необходимого угла:
- от первой стены откладываем четыре метра и маркируем эту точку;
- на второй и третей – и делаем тоже самое;
- измеряем полученное расстояние при помощи рулетки;
- если результат равен 5м – отлично, можно вбивать также следующий колышек очередной стены, измерять очередной угол;
- вымеряются другие геометрические показатели.

Следует сконцентрировать внимание – шнур, с помощью которого можно качественно разметить фундамент самостоятельно, обязательно должен располагаться на единой высоте во всех точках. Осуществлять измерения на самой почве более чем нецелесообразно, поскольку потенциально велика ошибка в расчетах из-за нюансов рельефа.
Сама по себе такая работа, в принципе, особой сложности не представляет. Но порой ее осуществление требует наличие опытного и умелого помощника. Завершить процедуру разметки можно осуществлением контроля за тем, одинаковы ли диагонали полученного прямоугольника. Если обнаружилось отклонение в пределах трех сантиметров, то такой показатель вполне допустим.
Внутренний контур размечают аналогичным способом. Углы контролируют так же. В случае если предполагается только залить траншею с применением фундамента, процедуру можно выполнить сразу, обязательно допуская опалубку. В целом, разметка участка под фундамент – это процедура довольно простая, гораздо проблематичнее соблюсти все геометрические параметры монтажа самой опалубки и оптимальной установки обязательного верхнего уровня, придерживаясь правильной высоты. С этой целью производится процедура тщательной расчистки строительной площадки и ее выравнивание еще до того, как была осуществлена разметка.
С этой целью производится процедура тщательной расчистки строительной площадки и ее выравнивание еще до того, как была осуществлена разметка.
Сам проект фундамента можно вымерять, применяя измерения технологической привязки к обрабатываемой местности, которые обозначены в его пределах. Тогда обычно фиксируется любой из потенциально возведенных углов сооружения с учетом выбранных расстояний от всех точек контроля. Это и будет непосредственно первый угол конструкции.
Помните о том, что сама по себе разметка участка под баню – это, в принципе, последний шанс трансформировать идею строительства. Существует возможность, что вы захотите изменить ориентацию по сторонам света, либо же выбрать иной материал для строительства стен сооружения, либо почувствуете, что стоит увеличить размер фундамента, поскольку кирпичная кладка в него так и не впишется.
Все эти факты очень важны для процесса строительства. Именно на этом этапе мы имеем возможность осуществить изменения уже утвержденного строительного плана, в которых возникла необходимость. Учитывать стоит только факт выдержки параметров для жилой застройки, например, такие как минимальная отдаленность от граничных пределов участка, а также трубопроводов магистрального типа.
Учитывать стоит только факт выдержки параметров для жилой застройки, например, такие как минимальная отдаленность от граничных пределов участка, а также трубопроводов магистрального типа.
Другой способ осуществления процедуры
В ответе на вопрос о том, как сделать разметку под фундамент, нет мелких нюансов. Важно учитывать каждую мелочь, конструкционные особенности основания повлияют на строительство всего сооружения в целом.
Опишем еще одну из наиболее оптимальных методик осуществления процедуры разметки, применимых в строительстве. Она характеризуется наличием таких структурных этапов:
- стоит для начала с определением местоположения основного либо же базисного угла, именно в него и вбивается специальный деревянный колышек;
- скамейки фиксируются на полутораметровом расстоянии от одной стороны возводимого фундамента и трехметровом – с его другого бока;
- шнур протягивается между досками и самим базисным углом; отмеряется длина самой стороны конструкции, колышек под номером два вбивается именно в этой точке;
- восстанавливаются все перпендикулярные линии из вбитых в землю кольев.
 мерной рулеткой выделяются одинаковые расстояния от них, фиксируются все маркеры. длина ее выставляется на 2, 1 м, чертятся дуги условных окружностей – там, где они впервые пересекутся, и будет крепиться строительная веревка к установленной на земле «скамейке».
мерной рулеткой выделяются одинаковые расстояния от них, фиксируются все маркеры. длина ее выставляется на 2, 1 м, чертятся дуги условных окружностей – там, где они впервые пересекутся, и будет крепиться строительная веревка к установленной на земле «скамейке». - далее от последней конструкции далее отмеряется необходимая величина, которая приравнивается к последующей длине возводимого фундамента, здесь обязательно устанавливается доска. стоит соединить их при помощи специальной веревки, представляющей собой высоту треугольника. очередная длина возводимого фундамента отмеряется от колышка и выделяется третий необходимый угол сооружения.
- другие расстояния и углы откладываются тем же способом.
- в конце стоит провести верификацию диагоналей прямоугольника. Если они равны, то процедуру разметки вы осуществили корректно.
По большому счету, правиться с такой работой можно за несколько часов, особенно тогда, когда есть хороший помощник.
Первым этапом любого строительства является создание плана. После данной процедуры, все то, что было в проекте, переносится на участок в соответствии с размерами и формами. Каждый шаг разметки фундамента зависит от того основания, которое обустраивается, но первый этап одинаков для всех видов фундамента. Данная статья расскажет о том, как правильно разметить фундамент в зависимости от его вида.
После данной процедуры, все то, что было в проекте, переносится на участок в соответствии с размерами и формами. Каждый шаг разметки фундамента зависит от того основания, которое обустраивается, но первый этап одинаков для всех видов фундамента. Данная статья расскажет о том, как правильно разметить фундамент в зависимости от его вида.
Подготовка участка под разметку
Перед тем, как будет произведена разметка фундамента своими руками на участке, нужно сделать его проект на бумаге с указанием размеров, площади, геометрии будущего строения и планировки внутреннего пространства. Каждый отдельный проект составляется на основе характеристик участка, на котором будет производиться строительство. Для того чтобы разметить участок, нужно подготовить следующие инструменты: колышки в достаточном количестве, рулетка и отвес, строительные уровни разного размера, лазерный дальномер и нивелир, крепкий шнур, доски для обустройства обноски.
Обязательно перед разметкой участок расчищается, удаляются старые постройки, и убирается весь мусор, который может помешать разметке и строительству.
Чистая площадка выравнивается так, чтобы она была максимально горизонтальной, без какого-либо рельефа.
Обязательно должен быть подготовлен проезд к участку для строительной техники. Лучше всего его присыпать гравием, чтобы во время осадков дорогу не размыло. Также расчищается место под строительные материалы и возводится забор, пусть и временный.
Общие данные о разметке участка под фундамент
Вне зависимости от выбранного типа фундамента и геометрии здания, первые работы по разметке основания для дома своими руками производятся одинаково. Здесь помогает правильно выстроить проект уже на участке теорема Пифагора или правило египетского треугольника.
Вот пошаговая технология универсального способа, как разметить фундамент:
- Для начала нужно определить размещение одной стены дома. Обычно она размещается вдоль забора или, если он еще не построен, параллельно границе участка. Если эта стена располагается вдоль забора, то от него отмеряются равные промежутки и прокладывается линия, равная длине соответствующей стены.
 Благодаря этой линии можно определить два угла здания, которые в обязательном порядке нужно отметить вбитыми в землю кольями. Далее линия закрепляется обноской. Она устанавливается на некотором расстоянии от предполагаемой траншеи или котлована и выполняется при помощи вертикальных и прибитых к ним горизонтальных досок.
Благодаря этой линии можно определить два угла здания, которые в обязательном порядке нужно отметить вбитыми в землю кольями. Далее линия закрепляется обноской. Она устанавливается на некотором расстоянии от предполагаемой траншеи или котлована и выполняется при помощи вертикальных и прибитых к ним горизонтальных досок. - Выбор угла на стороне дома, от которого будет произведена дальнейшая разметка. От колышка в данном углу нужно натянуть бечевку под углом 90 градусов в соответствующую сторону. Сделать такой угол на глаз не представляется возможным, но на данном этапе можно оставить и тот, который получился. Там, где бечевка будет пересекаться с первой вынесенной стороной, нужно сделать закрепление.
Важно! На первом этапе работы производятся только с использованием шнура.
- После того, как угол будет определен точно и его показатель станет равным 90 градусов, можно монтировать обноску второй стороны.
- На одной стороне отмечается 3 метра от места пересечения шнуров и 4 метра на другой.

- По прямой между этими двумя отметками измеряют расстояние. Это получается гипотенуза треугольника. Это нужно для того, чтобы проверить градусную меру угла. Если данное расстояние будет равно пяти, то такой угол верен и можно смело сооружать обноску под фундамент. Если же длина гипотенузы не равна значению 5, то нужно смещать один из катетов до того момента, пока не получиться прямой угол.
- Построение третьей стены идет таким образом: на первой прямой опять же берется точка и выстраивается прямой угол, в соответствии с которым нужно натянуть шнур.
- На обеих сторонах, которые построены от первой под прямым углом нужно отметить расстояние, которое равно длине стены и между этими точками под прямым углом закрепить четвертую бечевку.
- Последние две стороны измеряются и на них откладываются расстояния, которые равны габаритам здания. Если данные метки совпали, то разметка выполнена верно, если же нет, то нужно перемещать последнюю веревку до того момента, пока они не совпадут.

- Производится проверка правильности размеченного участка. Если все сделано верно, то диагональные измерения будут равны друг другу.
- Результат разметки — готовый прямоугольник, полученный из бечевки или обноски.
Разметка методом «паутина»
Выполнить разметку можно не только при помощи египетского треугольника, но и другим методом, который получил название «паутина». Данный вариант разметки потребует наличия бечевки, колышек и рулетки. Вот пошаговая инструкция такой разметки:
- Сделать заготовки из бечевки, длина каждой из которых равна стороне прямоугольника и его диагонали. Данные отрезки правильно соединить и скрепить места их пересечения.
- Одну сторону натянуть и закрепить при помощи колышков, которые вбиваются в грунт. Обычно за основу берется та сторона, которая идет в параллель забору.
- Натянуть шнур, который является диагональю, и закрепить колышками.
- Натянуть вторую диагональную веревку и также закрепить.
Важно!
Шнур по всем сторонам и диагоналям должен быть максимально натянут, без провисаний.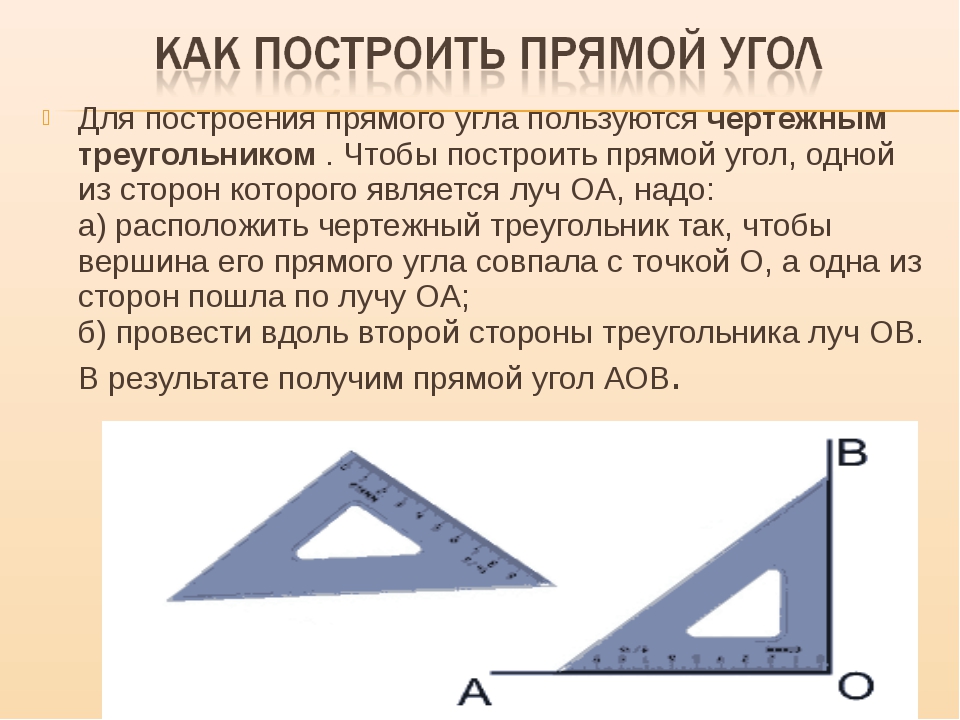
В данном методе нужно использовать только ту веревку, которая не будет растягиваться под влиянием силы. В противном случае измерения могут получиться неточными.
Разметка различных типов фундамента
Методы, приведенные ранее, являются универсальными и подходят для любого типа фундамента. А вот дальнейшие действия уже различаются для каждого из них.
Размечаем ленточный фундамент
Возведение ленточного основания может производиться в котловане или же в траншее. В зависимости от этого меняются способы для того, чтобы разметить фундамент под дом. Котлован нужен для того, чтобы организовать подвал дома. В первом случае обноску располагают только по внешнему контуру фундамента. Во втором же получается своеобразная лента, внутренние грани которой сначала нужно обозначить бечевкой, а потом произвести обноску, отступив от внутренних сторон ровно столько, сколько должна быть ширина ленты основания.
Размечаем столбчатый фундамент
Наружные грани определяются точно так же, как представлено ранее. Для того чтобы определить местоположение каждой сваи нужно монтировать обноску немного удаляя ее и натянуть веревку. Стойки обноски должны быть оборудованы дополнительными горизонтальными досками. Первая будет соответствовать уровню, по которому обрезается фундамент, вторая — верхней точке ростверка.
Для того чтобы определить местоположение каждой сваи нужно монтировать обноску немного удаляя ее и натянуть веревку. Стойки обноски должны быть оборудованы дополнительными горизонтальными досками. Первая будет соответствовать уровню, по которому обрезается фундамент, вторая — верхней точке ростверка.
Бечевки натягиваются в середине в соответствии с осями опор. Они располагаются на расстоянии, равном шагу опор здания. Для определения того места, куда необходимо установить сваю, нужно опустить отвес. После этого разметка перемещается к наружным краям опор.
Важно! Расположения свай должны отмечаться на обноске с помощью саморезов или гвоздей.
Ростверк отмечается также, как и ленточный фундамент. Можно сократить работу, отступив от каждой опоры половинчатое расстояние ширины ростверка в обе стороны и установить крепежи, на которые впоследствии натянуть бечевку.
Размечаем плитный фундамент
Разметка такого основания считается самой простой для проведения своими руками.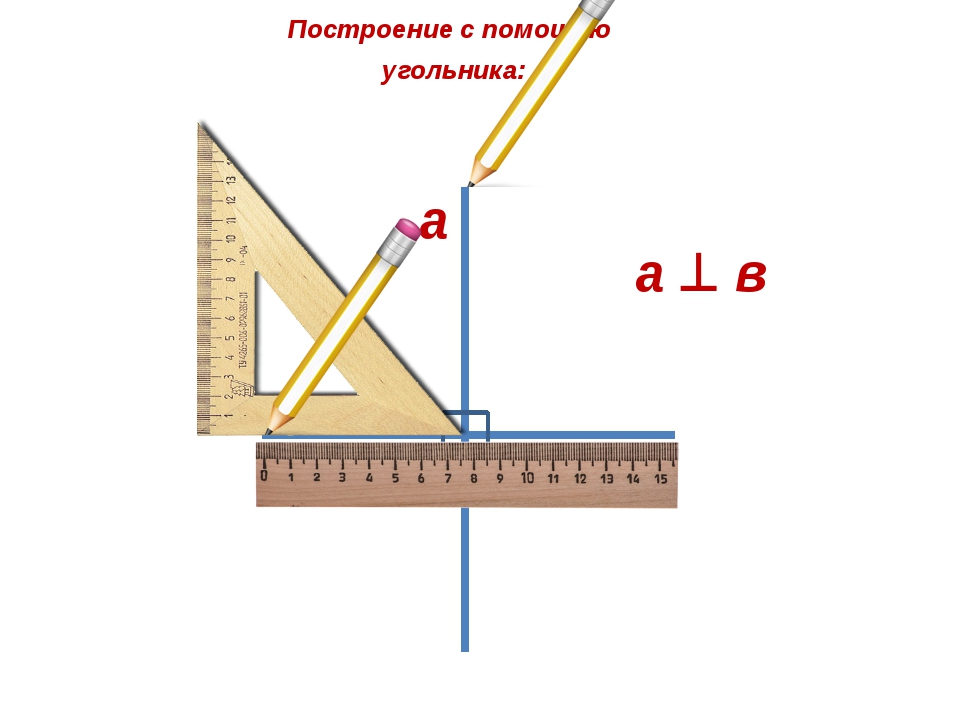 В этом случае отмечаются только внешние стороны фундамента, поэтому можно остановиться после выполнения основных пунктов по формированию прямоугольника на участке.
В этом случае отмечаются только внешние стороны фундамента, поэтому можно остановиться после выполнения основных пунктов по формированию прямоугольника на участке.
Сложность этой разметки заключается в том, что обязательно при разметке высчитывается площадь плит, чтобы они все вместились в фундамент, в противном случае, придется начинать работы сначала. Поэтому перед работой рассчитывается общая площадь фундамента и площадь каждой плиты и соотносятся друг с другом.
Заключение
Разметка фундамента — сложный процесс, который требует от мастера четкого следования инструкции и особой внимательности. Но и его можно выполнить самостоятельно, если заранее изучить все нюансы данного дела и правильно применить теоретические знания на практике. Конечно, можно обратиться к профессионалам, которые сделают все быстро и качественно, но, если бюджет на строительство строго ограничен, то вполне возможно сэкономить немалые средства на разметке, произведя ее самостоятельно.
После того как все подготовительные работы по сооружению фундамента сделаны, можно приступать к практике. А с чего же начинается строительство фундамента? Если речь идет о монолитном или ленточном фундаменте, то первое что нужно сделать — сконструировать разметку согласно плану. Благодаря разметке, вы сможете быстро и правильно выкопать траншею под основание.
А с чего же начинается строительство фундамента? Если речь идет о монолитном или ленточном фундаменте, то первое что нужно сделать — сконструировать разметку согласно плану. Благодаря разметке, вы сможете быстро и правильно выкопать траншею под основание.
Но возникает вопрос, как правильно выполнить разметку под фундамент своими руками? Что потребуется для работы? Как сделать все правильно, чтобы фундамент простоял долго. Ответы на эти и другие вопросы мы узнаем из данной статьи. Кроме того, мы рассмотрим несколько методов сооружение разметки.
Разметка фундамента под дом — инструменты
Для того чтобы выполнить разметку под фундамент своими руками, вам нужно запастись подходящим инструментами. Какие они?
- Рулетка. Но, не берите маленькие рулетки на 3 или 6 м. Вам понадобится большая, на 15-25 м.
- Шнур или веревка в большом количестве. Леску лучше не брать, так как ее плохо видно.
- Гидроуровень и ответ отвес (как вариант лазерный нивелир).
- Деревянные или металлические колышки.

- Доски в качестве обноски.
- Гвозди и молоток.
Как видите, список простой, а инструменты легко найти у себя дома. Но, как из этого набора соорудить качественную разметку? Давайте узнаем.
Начинаем конструировать разметку
Итак, что нужно делать дальше? Первым делом определите две исходные точки, обозначив их колышками. Достаточно просто забить их на углах будущего здания. При этом важно разместить их на одной прямой линии по длине. Небольшую схему вы можете видеть на фото ниже.
Способ №1 — египетский треугольник
Его можно назвать самым простым методом. Этот способ еще называют методом золотого треугольника, который имеет соотношение длины сторон 5×3×4. Весь процесс можно разделить на несколько шагов:
Обратите внимание! Для надежности проверьте все замеры еще раз, чтобы не ошибиться. Измеряйте диагонали, они должны сходиться по длине.
Способ №2 — две дуги
Тоже простой вариант, без использования высокотехнологичных инструментов.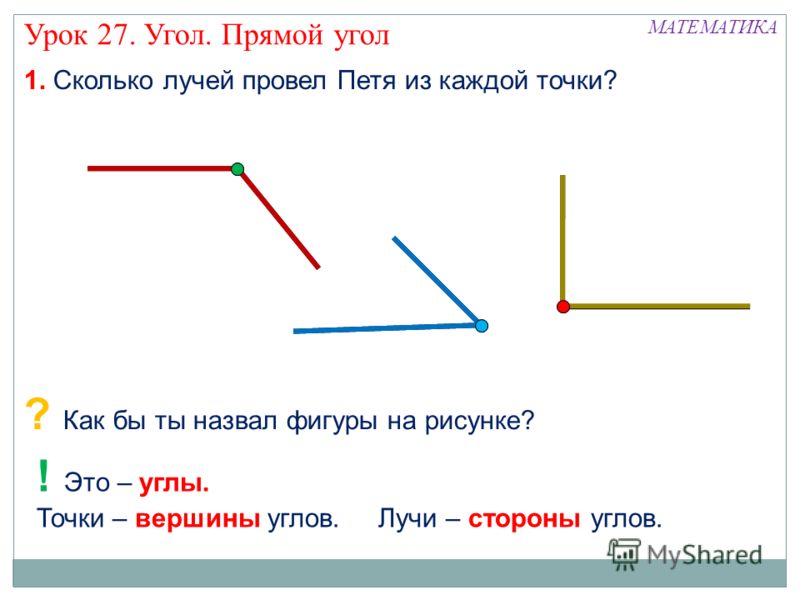 Разметка под фундамент включает себя использование простой веревки. Заранее вбейте один колышек в землю. От него измеряйте по прямой линии два одинаковых расстояния и сделайте там пометки. Можно просто вбить колышки. Дальше к каждому из крайних колышков по очереди нужно привязать веревку. Начнем с одной стороны. На конце веревки должен быть гвоздь. Теперь натяните веревкой и проведите дугу напротив колышка посередине. Точно также сделайте с другой стороны. У вас образуется пересечение двух дуг напротив центрального колышка. Если соединить точку пересечения дуг с центральным колышком, то образуется прямой угол в 90˚.
Разметка под фундамент включает себя использование простой веревки. Заранее вбейте один колышек в землю. От него измеряйте по прямой линии два одинаковых расстояния и сделайте там пометки. Можно просто вбить колышки. Дальше к каждому из крайних колышков по очереди нужно привязать веревку. Начнем с одной стороны. На конце веревки должен быть гвоздь. Теперь натяните веревкой и проведите дугу напротив колышка посередине. Точно также сделайте с другой стороны. У вас образуется пересечение двух дуг напротив центрального колышка. Если соединить точку пересечения дуг с центральным колышком, то образуется прямой угол в 90˚.
В конце осталось к колышкам на высоте будущего основания привязать веревку, проверить горизонтальность всех четырех сторон при помощи строительного уровня. Но, одного квадрата нам недостаточно. Если говорить о ленточном фундаменте, то нужно сделать внутренний контур, соответствующий ширине ленты.
Совет!
Если вы планируете копать траншею не лопатами, а с привлечением специальной техники, то лучше использовать для разметки не веревку, а песок. Дело в том, что веревку при рытье ковшом можно порвать, да и видно ее плохо. А вот песок будет четко выделять границы.
Дело в том, что веревку при рытье ковшом можно порвать, да и видно ее плохо. А вот песок будет четко выделять границы.
Благодаря этим простым способам, вы сможете добиться ровности разметки без лазерного уровня и т. д.
Делаем разметку своими руками
Теперь от теории давайте перейдем к практике. Мы узнаем, как сделать разметку под ленточный фундамент, имея запас знаний. Процесс следующий:
В работе потребуется сдвинуть веревку в ту или иную сторону, чтобы довести угол до идеала. После всех расчетов можно выполнять разметку второй половины постройки и дополнительных помещений.
Обратите внимание! Дополнительные помещения, такие как баня, веранда или балкон, нужно размещать по стене жилого помещения.
Так как речь идет о ленточном фундаменте, то нужно натянуть не одну линию, а сделать их две, чтобы образовалась лента. Достаточно отступить от исходной линии расстояние, равное ширине будущей ленте. Так, вы сделаете внутренний контур. Повторимся, что после того, как вы полностью сделали разметку под фундамент, нужно все еще раз проверить рулеткой. Все должно быть ровно и сходиться с планом фундамента.
Все должно быть ровно и сходиться с планом фундамента.
Вот и все, согласно этой разметке можно приступать к земельным работам, начиная рытье котлована. Много людей считают разметку под фундамент мелочью, которой не стоит уделять особого внимания. Но, если ее сделать неправильно, или не сделать вовсе, то 100% гарантируем вам то, что добиться идеально ровного и правильного фундамента под дом будет невозможно. Поэтому нужно быть особо внимательными и осторожными. А чтобы вам было легче, мы подготовили специальный материал, из которого вы наглядно увидите процесс сооружения. Разметка фундамента своими руками видео:
Подведем итоги
Сегодня вы узнали два простых способа, благодаря которым можно выполнить разметку под фундамент. Если делать все правильно, то у вас все получится. Не стоит тратить деньги на то, чтобы привлекать специалистов. Но, если вы сомневаетесь в своих силах, ведь фундамент дело серьезное, то лучше попросить помощи. Лучше заплатить и получить отличное качество готового фундамента.
Схематическое изображение формирования разметки фундамента
От правильности сделанной разметки будет зависеть долговечность здания. Чтобы сделать разметку не потребуется особых усилий и наличия различных инструментов. Всю работу могут выполнить два человека с минимальным набором инструментов:
- строительный шнур;
- рулетка;
- угольник;
- колышки;
- гидроуровень.
Разметка выполняется после выравнивания стройплощадки. Чем лучше будет подготовлено место, тем легче и удобнее будет переносить проектные схемы с бумаги на саму площадку. Сам процесс можно разделить на разметку внешнего периметра и разметку самого фундамента, включая внутренние перегородки и пристройки к будущему зданию.
Схема разметки фундамента с указанием ширины
Первую сторону фундаментной основы привязывают к какому-либо объекту на площадке. Ориентиром для привязки может служить ограждение участка или соседние постройки. Стоит учитывать и расположение солнца.
Согласно выбранному ориентиру, натягивают первый шнур на нужное расстояние и забивают два колышка. Чтобы колышки не провалились во время копания траншеи, их устанавливают дальше угла фундамента. Места пересечения шнуров будут обозначать углы. Такой способ размещения шнуров позволит сохранить первоначальную разметку при выемке грунта.
Разметка внешнего контура и формирование угла фундамента
Изображение сформированного угла фундамента
Например, будет строиться дом 6 х 8. После разметки стороны, которая будет служить его длиной, размечают вторую сторону. Для этого забивают еще колышек, привязывают к нему шнур и натягивают перпендикулярно первому. Точку пересечения шнуров скрепляют. Это и будет угол фундамента. На втором шнуре нужно сделать отметку, которая должна равняться ширине 6 м.
Для формирования угла применяется теорема Пифагора. Чтобы не заниматься глубокими геометрическими расчетами, берут два отрезка 3 м и 4 м. На первом шнуре, который обозначает длину фундамента, от угла отмеряют 4 м и ставят отметку.
На втором шнуре наносят отметку на расстоянии 3 м. Далее рулеткой соединяют одну отметку с другой так, чтобы на рулетке было отделено 5 м. Если расстояние между отметками будет равно 5 м, все нормально. Если нет, то конец второго шнура с отметкой 3 м перемещают, пока рулетка не установится на нужное расстояние.
Построение прямоугольника
Пошаговая инструкция определения прямого угла
После выравнивания угла в 90 градусов, на шнуре длины делают отметку 8 м, а на шнуре ширины 6 м. Дальше переходят к третьей стороне. Натягивают третий шнур перпендикулярно первому и скрепляют на отметке 8 м.
Четвертый шнур натягивают перпендикулярно второму и скрепляют на отметке 6 м. Чтобы получить четырехугольник с прямыми углами необходимо, чтобы обе отметки на третьем и четвертом шнурах совпали.
Если длины диагоналей четырехугольника одинаковые, то получен прямоугольник. Но диагонали могут быть одинаковые и в равнобедренной трапеции. Поэтому главным условием построения правильного прямоугольника является наличие угла 90º, а в равнобедренной трапеции таких углов нет.
Этот способ является внешней разметкой. Она подходит для плитного фундамента. При изготовлении фундаментной основы ленточного типа производят разметку по внутреннему периметру, с учетом ширины ленты.
После того, как первоначальная разбивка сделана, переходят ко второму этапу — обноски территории. Это позволит сохранить натянутые шнуры, обозначающие контуры основы до конца строительства.
Обноски устанавливают за пределами траншей. Они состоят из попарно вбитых столбиков, соединенных планкой. Установка обноски является ответственным моментом. Их монтируют так, чтобы верхние части планок были на одном уровне. Для этого и требуется гидроуровень. Шнуры, натянутые на верхние планки, будут служить нулевой горизонтальной отметкой опоры.
Разметка под фундамент
После того как все подготовительные работы по сооружению фундамента сделаны, можно приступать к практике. А с чего же начинается строительство фундамента? Если речь идет о монолитном или ленточном фундаменте, то первое что нужно сделать – сконструировать разметку согласно плану. Благодаря разметке, вы сможете быстро и правильно выкопать траншею под основание.
Благодаря разметке, вы сможете быстро и правильно выкопать траншею под основание.
Но возникает вопрос, как правильно выполнить разметку под фундамент своими руками? Что потребуется для работы? Как сделать все правильно, чтобы фундамент простоял долго. Ответы на эти и другие вопросы мы узнаем из данной статьи. Кроме того, мы рассмотрим несколько методов сооружение разметки.
Разметка фундамента под дом – инструменты
Для того чтобы выполнить разметку под фундамент своими руками, вам нужно запастись подходящим инструментами. Какие они?
- Рулетка. Но, не берите маленькие рулетки на 3 или 6 м. Вам понадобится большая, на 15–25 м.
- Шнур или веревка в большом количестве. Леску лучше не брать, так как ее плохо видно.
- Гидроуровень и ответ отвес (как вариант лазерный нивелир).
- Деревянные или металлические колышки.
- Доски в качестве обноски.
- Гвозди и молоток.
Как видите, список простой, а инструменты легко найти у себя дома. Но, как из этого набора соорудить качественную разметку? Давайте узнаем.
Но, как из этого набора соорудить качественную разметку? Давайте узнаем.
Начинаем конструировать разметку
Итак, что нужно делать дальше? Первым делом определите две исходные точки, обозначив их колышками. Достаточно просто забить их на углах будущего здания. При этом важно разместить их на одной прямой линии по длине. Небольшую схему вы можете видеть на фото ниже.
Способ №1 – египетский треугольник
Его можно назвать самым простым методом. Этот способ еще называют методом золотого треугольника, который имеет соотношение длины сторон 5×3×4. Весь процесс можно разделить на несколько шагов:
Способ №2 – две дуги
Тоже простой вариант, без использования высокотехнологичных инструментов. Разметка под фундамент включает себя использование простой веревки. Заранее вбейте один колышек в землю. От него измеряйте по прямой линии два одинаковых расстояния и сделайте там пометки. Можно просто вбить колышки. Дальше к каждому из крайних колышков по очереди нужно привязать веревку. Начнем с одной стороны. На конце веревки должен быть гвоздь. Теперь натяните веревкой и проведите дугу напротив колышка посередине. Точно также сделайте с другой стороны. У вас образуется пересечение двух дуг напротив центрального колышка. Если соединить точку пересечения дуг с центральным колышком, то образуется прямой угол в 90˚.
Начнем с одной стороны. На конце веревки должен быть гвоздь. Теперь натяните веревкой и проведите дугу напротив колышка посередине. Точно также сделайте с другой стороны. У вас образуется пересечение двух дуг напротив центрального колышка. Если соединить точку пересечения дуг с центральным колышком, то образуется прямой угол в 90˚.
В конце осталось к колышкам на высоте будущего основания привязать веревку, проверить горизонтальность всех четырех сторон при помощи строительного уровня. Но, одного квадрата нам недостаточно. Если говорить о ленточном фундаменте, то нужно сделать внутренний контур, соответствующий ширине ленты.
Благодаря этим простым способам, вы сможете добиться ровности разметки без лазерного уровня и т. д.
Делаем разметку своими руками
Теперь от теории давайте перейдем к практике. Мы узнаем, как сделать разметку под ленточный фундамент, имея запас знаний. Процесс следующий:
В работе потребуется сдвинуть веревку в ту или иную сторону, чтобы довести угол до идеала. После всех расчетов можно выполнять разметку второй половины постройки и дополнительных помещений.
После всех расчетов можно выполнять разметку второй половины постройки и дополнительных помещений.
Так как речь идет о ленточном фундаменте, то нужно натянуть не одну линию, а сделать их две, чтобы образовалась лента. Достаточно отступить от исходной линии расстояние, равное ширине будущей ленте. Так, вы сделаете внутренний контур. Повторимся, что после того, как вы полностью сделали разметку под фундамент, нужно все еще раз проверить рулеткой. Все должно быть ровно и сходиться с планом фундамента.
Вот и все, согласно этой разметке можно приступать к земельным работам, начиная рытье котлована. Много людей считают разметку под фундамент мелочью, которой не стоит уделять особого внимания. Но, если ее сделать неправильно, или не сделать вовсе, то 100% гарантируем вам то, что добиться идеально ровного и правильного фундамента под дом будет невозможно. Поэтому нужно быть особо внимательными и осторожными. А чтобы вам было легче, мы подготовили специальный материал, из которого вы наглядно увидите процесс сооружения. Разметка фундамента своими руками видео:
Разметка фундамента своими руками видео:
Подведем итоги
Сегодня вы узнали два простых способа, благодаря которым можно выполнить разметку под фундамент. Если делать все правильно, то у вас все получится. Не стоит тратить деньги на то, чтобы привлекать специалистов. Но, если вы сомневаетесь в своих силах, ведь фундамент дело серьезное, то лучше попросить помощи. Лучше заплатить и получить отличное качество готового фундамента.
Технология разметки участка под фундамент
Любой дом должен обладать надежным и устойчивым фундаментом. При строительстве загородного дома, необходимо знать, как разметить фундамент, ведь от качества опоры зависит эксплуатационный срок здания и уровень комфортности при проживании в нём.
Разметка для дома позволит ориентироваться в точном расположении объекта на участке. Ошибок в этой работе быть не должно. Это влияет на устойчивость и прочность фундаментной основы. Процесс разметки предполагает распределение всех величин с составленного плана на участок . То есть на земле осуществляется разделение с учетом формы дома и его размеров.
То есть на земле осуществляется разделение с учетом формы дома и его размеров.
Подготовка к разметке фундамента
Перед тем как разметить фундамент своими руками составляется проект будущего здания . При этом определяется площадь объекта, внешний вид строения и планировка отдельных помещений. Проект привязывается к участку, где будет проводиться строительство. Сначала проводятся работы по исследованию грунта, а затем осуществляется разметка основания.
Для проведения разметки потребуются следующие инструменты:
- Колышки из металла или дерева.
- Строительные уровни.
Перед тем как сделать разметку под фундамент, необходимо произвести подготовительные работы:
- Демонтируются старые строения , убирается мусор и лишние насаждения на участке.
Разметка начинается с любой стороны строения . Это может быть фасад или боковая часть постройки. При использовании рулетки стоит отдать предпочтение изделиям из металла, которые имеют длину более 10 м. Модели из ткани не гарантируют точность измерений и провисают при замерах.
Участок выбирается с учетом следующих факторов:
- Перспектива проведения всех коммуникаций.
- Состояние дорог.
- Географическая привязка к сторонам света .

Важнейшим предназначением разметки является осуществление правильной ориентации будущего строения, относительно местности. Это позволит возвести строение с учетом стандартных технологических правил.
Этапы выполнения замеров
Правильная разметка под фундамент состоит из нескольких этапов. Прежде всего, определяется основная точка , которой является правый угол постройки. Он устанавливается с учетом проектного задания. В данную точку монтируется первый колышек.
Начало разметки
От колышка откладывается расстояние, которое равняется размеру фундамента. Проведенный отрезок должен быть параллельным фронтальной линии . Внутрь промеряется перпендикулярная направляющая. При этом полученный угол должен составлять 90 градусов. Угол выверяется нивелиром.
Обозначение внешних границ выполняется следующим образом:
- Берется шнур размером 12 метров .
 Отметина фиксируется брусом.
Отметина фиксируется брусом.Таким же способом размечаются другие элементы . Если диагонали полученного прямоугольника одинаковые, то углы прямые.
Внутренние границы
После выполнения разметки, все значения поверяются еще раз и в нужных местах устанавливаются колышки. Данная работа должна проводиться с ответственностью, а замеры тщательно поверяться. Даже небольшая погрешность при расчетах повлияет на качество опоры . Правильная разметка углов помогает в дальнейшем минимизировать давление на грунт.
Выполнение обноски
После завершения работ по разметке производится обноска. Данный этап процесса считается необходимым для контрольных замеров. Все контуры будущей конструкции выносятся на поверхность земли . Верхний слой убирается и выполняется углубление на размер штыка лопаты.
Верхний слой убирается и выполняется углубление на размер штыка лопаты.
Обноска — это монтаж столбиков из дерева, которые попарно вбиваются в почву на расстоянии 1,5-2 метра от угла основания. Обноска позволяет создать правильный контур вертикальных плоскостей . При этом плоскости имеют по паре столбиков. Горизонтальные детали столбов должны располагаться на одном уровне.
Высота обноски равняется высоте основанию строения. Разметка глубины траншеи выполняется от обносков. При этом периметр независимо от характера рельефа должен быть одинаковым.
Использование нивелира
Лазерный нивелир представляет собой уровень для произведения разметки . Внутренний пузырьковый уровень позволяет проконтролировать, ровно ли установлен нивелир. В современных моделях присутствуют автоматические механизмы, настраивающие уровень положения. Решая, как разметить фундамент своими силами, можно применить данный прибор.
При этом выполняются следующие действия:
- От отметки угла здания, с помощью нивелира вычисляется и проводится линия, которая должна совпадать с одной из стен будущего здания.

- Все замеры производятся из одной отправной точки. Это позволит повысить точность выполняемых замеров.
- Нулевая отметка выполняется на каком-либо видимом элементе.
Особенности разметки ленточного фундамента
Создание ленточного фундамента своими руками начинается с правильной разметки. Подобное основание выполняется из непрерывных лент из железобетона , которые укладываются в траншею. Ширина опоры зависит от качества грунта. Фундамент не должен быть тоньше стен. Его толщина должны быть более 50 см, если здание будет возводиться из кирпича или блоков.
Глубина заложения основания зависит от уровня промерзания почвы . Подобные конструкции возводятся на прочных грунтах и отличаются простотой монтажа, а также позволяют обустроить цокольный этаж и подвальное помещение.
Выполняя разметку, следует учитывать, что здание от забора и соседской территории должно располагаться на следующих расстояниях:
- По правилам пожарной безопасности расстояние от окон до стен другого здания должно быть не менее 6 метров.
 Не менее 3 метров от строения до соседского участка.
Не менее 3 метров от строения до соседского участка. - По санитарно-бытовым нормам не менее 3 метров.
Разметка для ленточного фундамента выполняется по общим правилам разметки участка под строительство. Ровно также выполняется обноска.
На верхней детали обноски забиваются гвозди для отметок :
- В центральной части метка для оси стен фундамента.
- Слева и справа от осевой — метка для ширины основы;
- Дальше обозначается ширина подушки под основу.
Как разметить столбчатый фундамент?
Столбчатый фундамент представляет собой более простой вариант свайного основания. Под столбчатый фундамент по осям постройки монтируются прямоугольные или круглые опоры в вертикальном положении . Их необходимо установить в самых нагруженных участках здания: в будущих углах здания, а также в местах пересечения несущих конструкций.
Разметка подобного фундамента требует сооружения обноски. Размер элементов зависит от высоты будущей основы . Обноска выполняется при помощи досок. Каждая пара должна располагаться друг против друга. Каждая из них ограничивается шнуром. При этом получается прямоугольник или квадрат. Все углы должны быть прямыми.
Размер элементов зависит от высоты будущей основы . Обноска выполняется при помощи досок. Каждая пара должна располагаться друг против друга. Каждая из них ограничивается шнуром. При этом получается прямоугольник или квадрат. Все углы должны быть прямыми.
Столбы нужно располагать на одном уровне. Контрольные веревки выполняются по отметкам, которые делаются при помощи гидроуровня. В местах пересечения шнура монтируются колышки, которые обозначают места под бурение углублений для опор .
Затем убираются шнуры. На местах колышек выкапываются выемки. В углубления монтируются сваи и заливаются цементным раствором. После этого выполняется разметка основной части фундамента. Она выполняется в соответствии с общими правилами разметочных работ.
Разметка плитного фундамента
Плитные виды фундамента применяются на участках с проблемным грунтом . Они считаются самыми надежными из всех видов оснований. Применяются на почвах с близким расположением грунтовых вод, на заболоченных или торфяных участках.
Данный вид основы называется плавающим, так как при движении грунта, он как бы перемещается по волнам. Фундамент представляет собой монолитную плиту из железобетона. При любых изменениях грунта нагрузка равномерно распределяется по всей плите, что предотвращает любые нарушения в постройке.
В этом случае разметка фундамента под дом мало чем отличается от обычной разметки . Также определяются углы, расставляются колышки и натягиваются веревки.
Перед работами нужно точно знать общую площадь фундамента и площадь каждой плиты. Площадь всех элементов складывается и сравнивается с общей площадью.
Если знать, как правильно разметить фундамент, а также придерживаться технологии проведения разметки то можно выполнить точные замеры и возвести прочный и качественный фундамент. При самостоятельном выполнении работ необходимо четко следовать инструкции.
Разметка фундамента под дом своими руками: пошаговая инструкция +Видео
Проектные документы
Перед началом разметочных работ, Вы должны уладить вопрос с проектными документами, чтобы:
- не возникло сложностей при строительстве стен;
- строительные материалы обошлись дешевле;
- не сталкиваться с не очень приятными неожиданностями.

При составлении документации и проекта дома, важна не только фактура материалов для строительства, но и соблюдение параметров. При малейших неточностях при произведении разметки фундамента, вероятность возведения конструкции отличной от проекта возрастает.
Предварительные мероприятия:
- Для начала определите планируемое место для конструкции, по возможности на ровном участке.
- Определитесь с видом фундамента и его размерами. Выбор зависит от климатических условий и массивности будущего дома.
Как сделать разметку углов?
Существует несколько способов построения прямого угла. Мы рассмотрим два основных.
Правило золотого треугольника
Для того, чтобы построить прямой угол вспомним теорему Пифагора.
Для того, чтобы между отрезками A и B сделать прямой угол нужно сложить квадраты их длин и вычислить корень из их суммы. Полученное число будет являться длиной диагонали соединяющей эти два отрезка. Это достаточно просто вычислить при помощи калькулятора.
Как правило, для разметки фундамента берут такую длину сторон, чтобы при вычислении корня получалось целое число. Например: 3 х 4 х 5; 6 х 8х 10.
Сейчас попробуем сделать это практически.
Первый вариант: Правило золотого треугольника
Для примера рассмотрим, как разметить прямоугольный фундамент с размерами 6 х 8 м.
- При разметке первой стороны фундамента нужно помнить, что если Вы хотите, например, чтобы фундамент был параллелен какой-либо стороне забора, то первую его линию нужно делать равноудаленной от выбранной стороны. Для цели размещения первой бечевки можете использовать обноску. Расстояние между обносками для этой стороны сделайте 14 м (добавляем по 3 м между обносками и будущими углами). Первый шнур натянули.
- Теперь необходимо натянуть второй шнур перпендикулярно этому. Для этого скрепляем их скотчем или скобкой в точке их пересечения.
- Начинаем формировать прямой угол по теореме Пифагора. Для этого построим прямоугольный треугольник с катетами 3 м и 4 м и гипотенузой 5 метров.
 Для этого отмеряем на первой бечевке 4 м от места их пересечения, а на второй 3 м. Ставим пометки в этих местах любым способом. Соединяем пометки и измеряем полученную гипотенузу рулеткой.
Для этого отмеряем на первой бечевке 4 м от места их пересечения, а на второй 3 м. Ставим пометки в этих местах любым способом. Соединяем пометки и измеряем полученную гипотенузу рулеткой. - Если треугольник действительно прямоугольный, то пометки сойдутся на расстоянии 5 м.
- Далее достроим прямоугольник. Отложим на шнурах длины сторон будущего фундамента 6 м и 8 м, и поставим пометки.
- Теперь нужно постараться натянуть третий шнур перпендикулярно к первому и скрепить их на пометке 8 м.
- Также натянем четвертый шнур перпендикулярно ко второму. Скрепим их на отметке 6 м.
- Сделаем пометки на третьем шнуре 6 м и на четвертом 8 м.
- Для получения прямоугольника нужно, чтобы пометки на третьем и четвертом шнурах совпали. Для этого мы будем перемещать их до совпадения.
- Проверяем наш прямоугольник, измерив его диагонали. Если они равны, значит, мы получили желаемый прямоугольник
Второй вариант. Паутина.
- Для начала нужно нарезать куски бечевки, по длине сторон фундамента.
 Напоминаю, что мы решили разметить фундамент со сторонами 6 м на 8 м. Также нам нужны две диагонали, которые в нашем случае равняются 10 м. Оставьте на бечевках запас длины на их закрепление.
Напоминаю, что мы решили разметить фундамент со сторонами 6 м на 8 м. Также нам нужны две диагонали, которые в нашем случае равняются 10 м. Оставьте на бечевках запас длины на их закрепление. - Соедините Вашу «паутину», скрепив стороны и диагонали по углам. Диагонали в точке пересечения скреплять не обязательно.
- Натяните первую бечевку и создайте первый и второй угол. Закрепите ее при помощи колышков.
- Натягиваем диагональную бечевку к третьему углу. Постарайтесь, чтобы бечевки не провисали и были максимально натянутыми. Фиксируем третий угол, при помощи колышка, и первый угол становится прямым
- По аналогии натягиваем четвертый угол и фиксируем колышком.
Способы разметки под различные фундаменты
Для ленточного фундамента
При проведении разметки для ленточного фундамента обязательно нужно делать запас от длины стен около 1 м, Так как закладывание фундамента предусматривает рытье котлована, и при установке кольев по точным размерам, они упадут при копании.
Для свайного и столбчатого фундамента
При разметке этого фундамента вышеуказанный запас длины не нужен, и выполнить его монтаж намного труднее.
Разметка делается при помощи двухъярусной обноски, где нижний ярус – это уровень столбов, а верхний ярус – уровень ростверка.
Для плитного фундамента
Делается простейшим способом — строим прямоугольник по размерам фундамента по вышеуказанной теореме
В целом ничего сложного в проведении разметки для плитного фундамента своими руками нет. Цена вопроса – это стоимость шнура, доски для обноски, или колышков.
Разметка фундамента под дом. Рассказывают форумчане
С чего начинается разметка разметка дома на участке, как избежать ошибок и проверить геометрию – вспоминаем теорему Пифагора и слушаем советы форумчан!
Любой, кто регулярно читает forumhouse.ru, хорошо знает, что от надёжности основания дома во многом зависит срок эксплуатации дома и комфортность проживания в нём.
Одним из самых главных этапов строительства, напрямую влияющих на качество основания, становится правильная разметка фундамента.
В последнее время для этого всё чаще используются современные измерительные приборы.
Теодолит, лазерный нивелир или лазерный уровень существенно облегчают проведение строительных работ.
Каждому застройщику пригодятся базовые навыки по ручной разметке фундамента.
С чего начинается разметка фундамента
Первое, что приходит в голову – настрогать колышков, запастись прочным шнуром, рулеткой, понять, как работает гидроуровень, и можно приступать к разметке.
Как выставить разметку под фундамент
Для качественной разметки основания здания необходимо составить план, включающий в себя два последовательных шага:
1. Независимо от того, какой фундамент требуется по проекту – ленточный, свайный или плитный, сначала необходимо выяснить точные границы участка.
2. Затем на листке бумаги фундамент правильно привязывают к территории. Необходимо заранее учесть расположение предполагаемых хозяйственных построек, расстояние до соседского забора, септика, колодца или скважины. И только после этого можно приступить к разметке «в натуре».
Необходимо заранее учесть расположение предполагаемых хозяйственных построек, расстояние до соседского забора, септика, колодца или скважины. И только после этого можно приступить к разметке «в натуре».
Узнать о минимально допустимых расстояниях между соседними домами можно в этой теме.
– Разметку я начал с того, что отступил 5 метров от красной линии по границе участка.
Для разметки вам потребуется:
- рулетка;
- шнурка – моток прочного шнура или лески;
Лучшая веревка для разметки фундамента – это шнур. На фоне травы или земли леска визуально теряется, в то время как шнур белого цвета хорошо заметен.
- колышки;
- деревянная рамка, или, как её ещё называют, – «скамеечка».
Почти профи:
– В качестве шнурки лучше использовать капроновую нить толщиной в 1.5-2 мм, т.к. она хорошо натягивается и не провисает.
Виталяля:
– При разметке фундамента я использовал полипропиленовая нить толщиной в 1 мм. Она отличается повышенной прочностью.
Она отличается повышенной прочностью.
Как размечать со «скамеечкой»
«Скамеечка» существенно упрощает и ускоряет разметку. Этот инструмент легко сделать своими руками: его сколачивают из двух деревянных столбиков. Нижние концы заостряют, а сверху и посередине прибивают две горизонтальные перекладины. Для большей устойчивости под углом к столбикам прибивают две упорные дощечки. Получается треугольная основа. В перекладину вворачивают два самореза, на которых потом крепится шнурка.
Простой и небольшой фундамент можно правильно разметить, забив только лишь колышки. Но если речь заходит о сложной конструкции – под большой дом, то «скамеечка», при помощи которой делается разноска фундамента, просто необходима.
Количество «скамеечек» увеличивается прямо пропорционально сложности фундамента.
Вворачивая или выворачивая саморезы в перекладину, на разном расстоянии друг от друга можно регулировать ширину между шнуром, которая должно соответствовать ширине подушки основания дома.
Проверка геометрии
Мы определились, где будет возводиться фундамент на участке. Подготовили все необходимые инструменты и материалы. Теперь нужно определить базисный угол, который задаст направление будущей стены. В этом месте ставим и вбиваем колышек. Затем, отступив от колышка на 1- 2 метра, устанавливаем «скамеечку».
Выставить этот отступ необходимо для того, чтобы при выемке грунта (под ленточный фундамент и т.п.), рамка не мешала копать, маневрировать технике и не упала в вырытую траншею. Ширина траншеи также выкапывается с запасом по отношению к ширине ленты фундамента для беспрепятственной установки опалубки!
После установки скамеечки на саморезе закрепляется шнур. После этого от колышка отмеряем необходимое нам расстояние. Его длина обычно равна самой длинной стене дома. В этом месте ставим и вбиваем второй колышек, устанавливаем вторую «скамеечку» на том же самом расстоянии от колышка, что и первую, и натягиваем веревку.
Виталяля:
– Установленная разноска оставляется до окончания всех фундаментных работ. Благодаря отступу от фундамента, веревку можно снимать и натягивать по мере необходимости.
Благодаря отступу от фундамента, веревку можно снимать и натягивать по мере необходимости.
Дятька, Москва:
– Если скамеечек много, то выносить сразу все точки не следует. Из-за большого количества шнурок это только мешает работе.
В самом начале разметки важно выставить прямой угол между предполагаемыми стенами. Если не выполнить это сразу, то упущение может привести к плачевным результатам.
EvgeniyT79:
– Перед тем как начать копать траншею, мы тщательно перемерили все диагонали фундамента . Размеры сошлись. Но после установки опалубки оказалось, что одна из сторон фундамента меньше другой на 40 см!
– Это называется равнобедренная трапеция. При такой фигуре, даже если все диагонали сошлись, то фундамент всё равно получится кривой.
Трапеция, боковые стороны которой равны, называется равнобедренной или равнобокой. У равнобедренной трапеции диагонали одинаковы, а вот углы не равны 90 градусам.
Как добиться прямого угла
Для этого вспоминаем теорему Пифагора: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
Для нахождения прямого угла при разметке следует воспользоваться формулой: 3² + 4² = 5².
Суть формулы заключается в следующем:
Если отмерить по одной стороне фундамента – 3 метра, а по другой – 4 метра, то при угле в 90 градусов диагональ между ними равна – 5 метрам.
Используя эту пропорцию, можно разметить прямые углы всех сторон.
– Я пробовал выставлять прямые углы лазерным нивелиром, но по диагоналям получилось проще и точнее.
Чтобы упростить разметку прямого угла, можно заранее сколотить треугольник с нужными сторонами из досок или сварить друг с другом отрезки арматуры.
Главное – семь раз отмерить и один раз выкопать!
Читайте на FORUMHOUSE о том, как как правильно разметить фундамент и избежать ошибок. Всё, что вы хотели узнать о разметке котлована разметке котлована под цоколь, находится в этой теме.
Читайте о том, как исправить «подводные камни» у купленного дома, а из нашего видео вы узнаете, как переделать проблемный фундамент под старым домом.
под дом, беседку, гараж, забор своими руками
Строительные работы отличаются своими сложностями и нюансами. Состоят они из многочисленных операций, имеющий в отдельности важное значение для будущего результата. Первое, что выполняется на площадке, отведенной под застройку – подготовка территории и разметка фундамента. Правильность ее выполнения влияет на качество дальнейших мероприятий.
С чего начать
Разметка относится к начальному этапу строительных работ, и важность ее переоценивать не стоит. Особенность состоит в том, что при выполнении большего количество построений потребуется знать правила прямоугольной разметки. Практически в любом случае можно использовать только эти сведения, и качество при этом останется на должном уровне.
Перед тем, как разметить фундамент, выполняем подготовку. Важнейшим мероприятием является уборка территории – удаление мусора и растительности, выравнивание поверхности.
Разметка ленточного фундамента имеет определенные правила, и все построения должны выполняться в соответствии с ними.
В противном случае, основание получится неровным или перекошенным. Сложней всего выполнять разметку уклонного или неровного участка. Здесь придется правильно выбрать тип основания, чтобы стены дома получились прямыми.
Разметка фундамента под дом своими руками считается сложной работой, которую рекомендуется доверить профессиональным специалистам, способным учесть все особенности ее выполнения.
Материалы и инструменты
Перед тем, как разметить фундамент для дома, следует подготовить все необходимое для работы.
Разбивка выполняется с применением специальных инструментов, которые должны быть у вас под рукой. К такому набору относятся:
- рулетка. Длина ее должна соответствовать или превышать аналогичный параметр диагонали. Разрешается использовать и короткие приспособления, но в работе это создаст определенные неудобства;
- деревянные колышки. С их помощью крепится бечевка по земле, как только вы перенесете разметку осей в нижнюю плоскость;
- угольник.
 Необходим для того, чтобы проверять угловые участки в девяносто градусов. Будет неплохо, если такие инструменты вы заготовите для проверки углов на тридцать и шестьдесят градусов;
Необходим для того, чтобы проверять угловые участки в девяносто градусов. Будет неплохо, если такие инструменты вы заготовите для проверки углов на тридцать и шестьдесят градусов; - разметочный шнур;
- крепеж. С его помощью шнур фиксируется на кольях. С этой целью используют гвозди, прищепки, зажимы;
- разметка выполняется теодолитом, но лазерный уровень в этом вопросе будет более удобен. Допускается применять недорогой вариант – ватерпас.
Как найти прямой угол
Первая сторона фундаментного основания привязывается к одному из объектов, имеющихся на площадке. Как правило, многие берут ориентир «под забор», рекомендуется также учитывать и солнечную сторону.
Определив основной ориентир, натягиваем первый шнурок на необходимое расстояние, забиваем пару кольев.
Чтобы колышки не проваливались в процессе подготовки траншеи, их рекомендуется вбивать немного подальше от фундаментных углов.
В точках пересечений бечевок находятся предполагаемые углы. Этот вариант расположения разметочного шнура позволяет сохранять начальную разметку.
Этот вариант расположения разметочного шнура позволяет сохранять начальную разметку.
Разберемся, как найти прямой угол. Предположим, мы решили строить здание 6 на 6. Разметив одну из сторон, приступаем к разметке второй. Для этого следует вбить дополнительный колышек, привязать к нему бечевку и протянуть ее перпендикулярно первой, скрепив в месте пересечения. Таким образом можно найти угол в 90 градусов. На отрезке второй веревки отсекается шестиметровая длина для второй стороны объекта.
Формируется угол с помощью теоремы Пифагора. Чтобы не выполнять глубокие геометрические вычисления, рекомендуется взять отрезки трех- и четырехметровой длины. На одном из шнуров, обозначающем длину основания, откладывается длина в четыре метра, наносится отметка. Для второго шнура выполняются аналогичные действия на трехметровую длину. Остается рулеткой соединить две точки, чтобы длина ленты была равна пяти метрам. Если все получилось – действуете правильно. В том случае, если есть отклонения, конец шнурка с отметкой в три метра смещают, пока не образуется требуемое расстояние.
Получив прямой угол, на бечевках отмеряют стороны будущего фундамента (по шесть метров). После этого можно размечать третью фундаментную сторону. Для этого очередной шнурок натягивается строго перпендикулярно первой бечевке и скрепляется в точке, совпадающей с отметкой в шесть метров.
Четвертую веревку протягиваем перпендикулярно второму отрезку шнура, находим шестиметровую длину, скрепляем. Если все отметки на вновь натянутых шнурах совпали – вы построили прямоугольный четырехугольник, а в нашем случае – квадрат.
Если диагонали совпадают по длине, то разметка по осям выполнена правильно.
Такая внешняя разметка применяется для устройства плитного фундамента. При изготовлении ленточной основы разметка выполняется по внутреннему периметру, при этом учитывается ширина железобетонной ленты.
Закончив первоначальную разбивку, необходимо выполнить обноску территории, чтобы сохранить натянутые шнуры до окончания строительных работ.
Обноска выполняется за границами фундаментной траншеи и состоит из парных колышков, соединенных планками. Момент ответственный, так как планки должны располагаться по одному уровню. Лучше всего при выносе разметки использовать гидроуровень.
Технология разметки
Приведем пошаговые инструкции, с помощью которых можно выполнить разметку участка под разные типы фундаментов.
Под столбчатый фундамент
Следует заметить, что разметка столбчатого фундамента особых сложностей не вызывает, так как такое основание представляет собой наиболее простой вариант свайного фундамента.
При установке такого фундамента под оси сооружения монтируют опорные элементы прямоугольной или круглой формы, установленные вертикально.
Установка их выполняется в наиболее загруженных местах – по углам, в точках пересечений несущих и межкомнатных стен.
Как правило, шаг установки опор составляет полтора – два метра, верхние их участки соединяются балками, свободное пространство заполняется песчано-щебеночной смесью.
Размеры элементов определяются с учетом высоты будущего основания. Чтобы разметить подобный фундамент, необходимо соорудить обноску. Для этого потребуются доски, расположенные попарно друг напротив друга и ограниченные шнуром, чтобы получился квадрат либо прямоугольник.
Опорные столбы располагают по уровню, веревки натягиваются по отметкам, нанесенным с помощью гидроуровня. В точках пересечений бечевок устанавливаются колышки, обозначающие места для бурения скважин.
Теперь веревки разрешается снять, вместо каждого колышка устроить приямок, в углубление вставить сваю, залить свободное пространство бетонным раствором.
Затем проводится основная разметка будущего фундамента, действия соответствуют общепринятым правилам подобных работ.
Под ленточный фундамент
Мы знаем, как выполняется разметка под свайный фундамент. Теперь предлагаем вашему вниманию последовательность действий о том, как правильно сделать разметку под ленточный фундамент своими руками.
Теперь предлагаем вашему вниманию последовательность действий о том, как правильно сделать разметку под ленточный фундамент своими руками.
Возведению ленточного основания предшествует правильно исполненная разметка. Такой тип фундамента представляет собой непрерывную железобетонную ленту, уложенную в траншею. Параметр ширины ее опорной части определяется с учетом качества грунтового состава и используемыми для возведения стен материалами. К примеру, ширина ленты под кирпичную кладку или под блоки должна быть минимум пятьдесят сантиметров.
Уровень заглубленности определяется по точке промерзания почвенного состава. Ленточные конструкции заливаются по прочному грунту, монтируются легко, дают возможность для обустройства подвала или цокольного этажа.
Проводя разметку на местности, необходимо учитывать, что ваше сооружение должно быть удалено от ограждения и соседней территории на определенные расстояния:
- оконные проемы до стен соседнего здания должны быть удалены на шесть метров, сам объект возводится не ближе трех метров от территории соседа;
- санитарно-бытовые правила определяют, что удаления должны быть минимум по три метра.

Размечают ленточное основание по общепринятым правилам разбивки участка для строительных работ, по такому же принципу делается обноска.
В верхние части элементов обноски вбиваются гвоздики для выполнения отметок:
- в центре – оси фундаментных стен;
- по бокам от осевой – метка под ширину фундамента;
- ширина опорной подушки.
Под плитный фундамент
Если нет возможности разместить свайное поле под фундамент или забетонировать ленту, устраивают основание из плит. Такой вариант считается наиболее надежным, применяется на участках с проблемным грунтом, по торфяной или заболоченной местности.
Разметить устройство плитного фундамента можно самому, так как порядок определения углов с расстановкой колышков и натягивание бечевки нам уже знаком.
Есть одна особенность в устройстве такого основания – приходится принимать во внимание площадь фундаментных плит. Если какая-то из них не войдет в размеченный контур, все придется переделывать заново.
Если нет возможности проверить диагональ, придется уточнять общую площадь фундаментного основания и аналогичные параметры каждой плиты, после всего значения всех плит складываются, и выполняется сравнение с проектным решением.
Фундамент произвольной формы
Естественно, разметка прямоугольных фундаментов 10 на 10 для дома, 4 на 4 под беседку, 3 на 6 под гараж 3 на 3 и т. п. выполнять просто. Но порой возникает необходимость залить основание под конструкцию с многочисленными углами. Возникают определенные сложности, но процесс вполне решаемый. Алгоритм действий следующий:
- в первую очередь придется самому разметить общий контур объекта, отметить расстояния от крайних точек и построить большой прямоугольник;
- затем все углы корректируются, снова проверяются диагонали и размеры сторон;
- начинается сложный этап – разметка изломных участков.
 Заметим, что каждый такой отрезок представляет собой дополнительный прямоугольник, который тоже приходится строить. В завершении выставляются и перепроверяются угловые участки;
Заметим, что каждый такой отрезок представляет собой дополнительный прямоугольник, который тоже приходится строить. В завершении выставляются и перепроверяются угловые участки; - отвесами определяются места пересечений, которые формируют контур объекта.
Такой фундамент не рекомендуется размечать на неровном участке.
Тонкости разметки
Теперь вы знаете, как разместить столбчатый фундамент или разметить плитное основание, как закрепить шнур, чтобы сохранить данные разметки до окончания строительства.
В обязательном порядке принимайте в расчет отсчетную точку, располагайте один из угловых участков с привязкой к какому-то сооружению. Это необходимо, чтобы легко исправить допущенные ошибки. При выполнении разметки пользуйтесь тахеометром.
Как рассчитать углы крыши | Home Guides
Расчеты для определения углов крыши основаны на ширине и высоте крыши. Это потому, что часть крыши здания можно сравнить с треугольником с шириной основания, высотой посередине и двумя наклонными сторонами. Используя основные измерения и некоторую тригонометрию, можно рассчитать углы любой крыши.
Используя основные измерения и некоторую тригонометрию, можно рассчитать углы любой крыши.
Определите расстояние от края крыши до точки в той же плоскости непосредственно под самой высокой точкой.Запишите это как ширину крыши. Например, если крыша идет вверх от фасада дома к центральному коньку, измерьте расстояние от передней стены до точки непосредственно под центральным коньком. Если расстояние между стеной и точкой под коньком составляет 15 футов, запишите это как ширину крыши.
Определите высоту по вертикали между основанием крыши и самой высокой точкой. Это можно прочитать на чертежах архитектора или получить путем прямого измерения. Запишите это как высоту крыши.Например, если расстояние от чердачного этажа до вершины крыши составляет 7,5 футов, запишите это как высоту крыши.
Рассчитайте тангенс угла крыши, разделив высоту крыши на ширину крыши. Например, если высота составляет 7,5 футов, а ширина — 15 футов, тангенс угла крыши составляет 0,5, потому что 7,5, разделенное на 15, равняется 0,5.
Преобразуйте тангенс угла в фактический угол, установив арктангенс значения, полученного на шаге 3. Используйте для этого функцию арктангенса на калькуляторе или онлайн-калькулятор тригонометрии.Например, арктангенс 0,5 равен 26,57, поэтому угол наклона крыши или угол наклона составляет 26,57 градуса.
Округлите вычисленное значение до ближайшего целого градуса. Чтобы завершить пример, ближайший к 26,57 градус равен 27, поэтому угол наклона крыши равен 27 градусам.
Ссылки
Ресурсы
Советы
- Дважды проверьте все свои измерения; если вы используете неправильные размеры, вы найдете неправильный угол.
- Преобразуйте измерения в футах и дюймах в десятичные значения перед определением угла крыши.Расчеты будут намного проще.
Предупреждения
- Если необходимо определить ширину и высоту крыши путем прямых измерений существующей конструкции, примите соответствующие меры перед тем, как получить доступ к зоне крыши.
 Как отмечает британский исполнительный орган по здравоохранению и безопасности, работа на крышах является одной из основных причин смертельных исходов в строительной отрасли. Падения с высоты часто заканчиваются смертельным исходом.
Как отмечает британский исполнительный орган по здравоохранению и безопасности, работа на крышах является одной из основных причин смертельных исходов в строительной отрасли. Падения с высоты часто заканчиваются смертельным исходом.
Биография писателя
Дэвид Робинсон профессионально пишет с 2000 года.Он является членом Королевского географического общества и Королевского метеорологического общества. Он писал статьи для газет «Telegraph» и «Guardian» в Великобритании, правительственных изданий, веб-сайтов, журналов и школьных учебников. Он имеет диплом бакалавра искусств в области географии и образования с отличием, а также сертификат преподавателя Даремского университета в Англии.
Теорема Пифагора и плотницкое дело
Современные столярные работы намного проще, если применить теорему Пифагора к поставленной задаче.Обрамление крыш, возведение стен и фундаменты основываются на этом основном математическом принципе.
Основы теоремы
В геометрии эта теорема утверждает, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадраты двух других сторон. В прямоугольном треугольнике один угол равен 90 градусам. Гипотенуза находится на противоположной стороне прямоугольного треугольника.
Вот формула теоремы Пифагора. a в квадрате + b в квадрате = c в квадрате В этой формуле c представляет длину гипотенузы, a и b — длины двух других сторон. Если известны две стороны прямоугольного треугольника, вы можете подставить эти значения в формулу, чтобы найти недостающую сторону.
Если известны две стороны прямоугольного треугольника, вы можете подставить эти значения в формулу, чтобы найти недостающую сторону.
Возведение зданий в квадрат с помощью теоремы Пифагора
При закладке бетонных оснований для нового здания метод Пифагора Теорема — наиболее точный метод получения квадратных углов в 90 градусов. Это то же самое, что и старый столярный трюк 3–4–5, только более точный, потому что можно определить точные углы.
Обычно в плотницких работах известны точки a и b , поэтому все, что вам нужно сделать, это решить для c . Вот небольшой изящный калькулятор, который можно использовать для упрощения математических расчетов.
Вот небольшой изящный калькулятор, который можно использовать для упрощения математических расчетов.
2 + 2 =
Допустим, у вас есть размер 16 x 14 футов, который вам нужно возвести в квадрат. если ты
введите 16 и 14 в калькулятор и нажмите «Решить», вы получите ответ 21.2602
если ты
введите 16 и 14 в калькулятор и нажмите «Решить», вы получите ответ 21.2602
4693 . Это число бесполезно, пока мы не переведем его в футы и дюймы.
Ниже приведены шаги, необходимые для преобразования этого числа в футы и дюймы с помощью обычного калькулятора .
- Бросьте 21 , который представляет 21 фут .

- Округлите десятичную точку до четырех разрядов, так что .2602
4693 станет .2603 .
- Введите в калькулятор ,2603 и умножьте на 12 — 0,2603 x 12 = 3,1236 дюйма .
- Введите в калькулятор .
 1236 и умножьте на 16-. 1236 x 16 = 1,9776 16-дюймовые доли дюйма .
1236 и умножьте на 16-. 1236 x 16 = 1,9776 16-дюймовые доли дюйма .- Круглый 1,9776 до 2/16 или 1/8 «.
Итак, ответ: 21 ‘3 1/8 «.
Использование обычного калькулятора
Теорема Пифагора также может использоваться с обычным калькулятором, если она
оснащен функциональной клавишей извлечения квадратного корня. Ниже приведена последовательность нажатий клавиш с использованием
пример 16 ‘x 14’.
Ниже приведена последовательность нажатий клавиш с использованием
пример 16 ‘x 14’.
16 x = 256 MS (сохранение в памяти) 14 x = 196 + MR (вызов из памяти) = 452 sqrt (квадратный корень) 21,2602
4693
Вот несколько практических задач, хотите ли вы попробовать свои силы?
32 ‘x 42’ = Ответ
44 ‘x 24’ = Ответ
62 ‘x 28’ = Ответ
Если вы все поняли правильно, поздравляю, теперь у вас в рукаве новый столярный трюк.
Construction Master Calculator
Этот калькулятор значительно упрощает этот процесс по сравнению с двумя ранее упомянутыми методы. Вот единственные нажатия клавиш, необходимые для тех же результатов. 16 Feet Rise (подъем на 16 футов) Бег на 14 футов Диаграмма 21 ‘3 1/8 «.
Вот как теория применяется к конструкции крыши.
Происхождение теоремы Пифагора
Примерно в 2000 году до нашей эры древним египтянам понадобился способ планировки квадратных углов
для своих полей.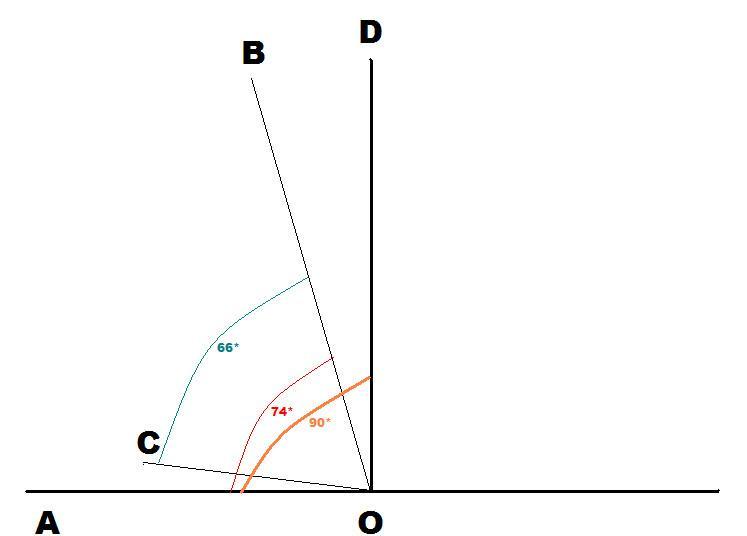 Они взяли веревку, завязанную на 12 равных частей, и натянули ее вокруг
три ставки, расположенные в виде треугольника. Когда у них было 3 длины между двумя кольями, 4 длины
между следующими двумя, и 5 длин назад до начальной точки гипотенуза справа
образовался треугольник.
Они взяли веревку, завязанную на 12 равных частей, и натянули ее вокруг
три ставки, расположенные в виде треугольника. Когда у них было 3 длины между двумя кольями, 4 длины
между следующими двумя, и 5 длин назад до начальной точки гипотенуза справа
образовался треугольник.
Человек по имени Пифагор прославился формулировкой теоремы, однако это наверняка было известно раньше. Он был греческим философом и математиком. около 530 г. до н. э. Он основал братство пифагорейцев в Кротоне, Италия. среди аристократов этого города.Горожане с подозрением отнеслись к братству и убил большинство его членов в ходе политического восстания. Неизвестно, сбежал ли он из город до восстания или погиб в нем.
Ссылки на связанные страницы Carpentry Pro Framer
Правые треугольники
Правые треугольники Давайте снова согласимся со стандартным условием обозначения частей прямоугольного треугольника. Обозначим прямой угол C , а гипотенузу c. Пусть A и B обозначают два других угла, а a и b стороны, противоположные им, соответственно.
Обозначим прямой угол C , а гипотенузу c. Пусть A и B обозначают два других угла, а a и b стороны, противоположные им, соответственно.
Решение прямоугольных треугольников
Мы можем использовать теорему Пифагора и свойства синусов, косинусов и касательных, чтобы решить треугольник, то есть найти неизвестные части в терминах известных частей.- Теорема Пифагора: a 2 + b 2 = c 2 .
- Синусы: sin A = a / c, sin B = b / c.
- Косинусы: cos A = b / c, cos B = a / c.
- Касательные: tan A = a / b, tan B = b / a.
 Например, если a = 10 и b = 24, то c 2 = a 2 + b 2 = 10 2 + 24 2 = 100 + 576 = 676. Квадратный корень из 676 равен 26, поэтому c = 26. (Приятно привести примеры, когда квадратные корни получаются из целых чисел; в жизни обычно этого не происходит.)
Например, если a = 10 и b = 24, то c 2 = a 2 + b 2 = 10 2 + 24 2 = 100 + 576 = 676. Квадратный корень из 676 равен 26, поэтому c = 26. (Приятно привести примеры, когда квадратные корни получаются из целых чисел; в жизни обычно этого не происходит.)Теперь предположим, что мы знаем гипотенузу и одну сторону, но должны найти другую.Например, если b = 119 и c = 169, то a 2 = c 2 — b 2 = 169 2 — 119 2 = 28561 — 14161 = 14400, а квадратный корень из 14400 равен 120, поэтому a = 120.
Мы можем знать только одну сторону, но мы также знаем угол. Например, если сторона a = 15 и угол A = 41 °, мы можем использовать синус и касательную, чтобы найти гипотенузу и другую сторону.Поскольку sin A = a / c, мы знаем, что c = a / sin A = 15 / sin 41.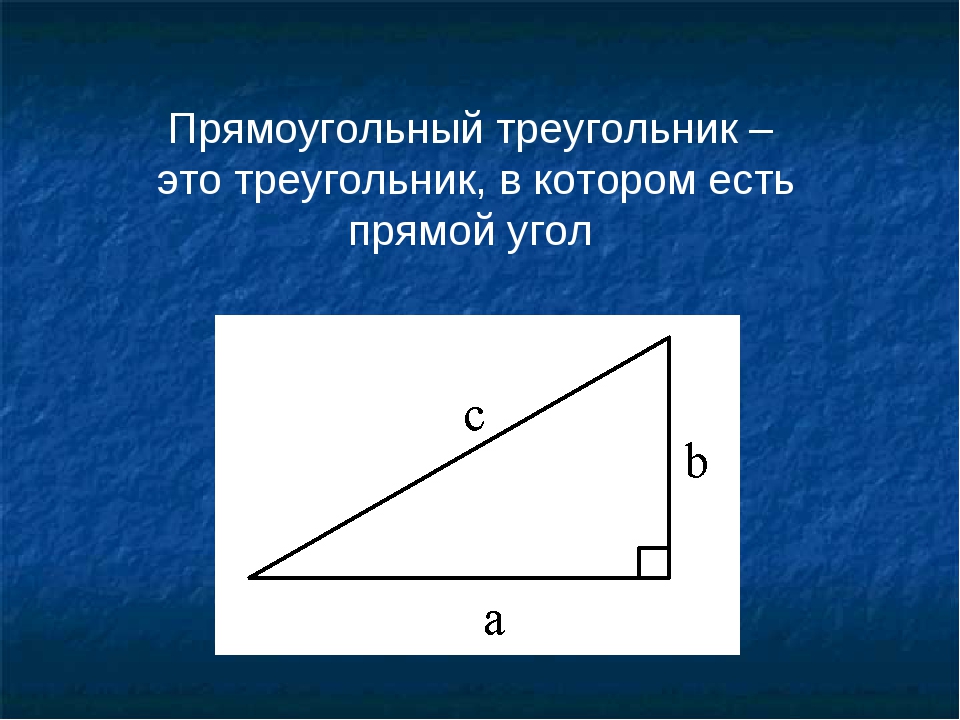 Используя калькулятор, это 15 / 0,6561 = 22,864. Кроме того, tan A = a / b, , поэтому b = a / tan A = 15 / tan 41 = 15 / 0,8693 = 17,256. Используете ли вы синус, косинус или тангенс, зависит от того, какую сторону и угол вы знаете.
Используя калькулятор, это 15 / 0,6561 = 22,864. Кроме того, tan A = a / b, , поэтому b = a / tan A = 15 / tan 41 = 15 / 0,8693 = 17,256. Используете ли вы синус, косинус или тангенс, зависит от того, какую сторону и угол вы знаете.
Обратные триггерные функции: арксинус, арккосинус и арктангенс
Теперь давайте посмотрим на проблему нахождения углов, если вы знаете стороны.Опять же, вы используете триггерные функции, но в обратном порядке. Вот пример. Предположим, a = 12,3 и b = 50,1. Тогда tan A = a / b = 12,3 / 50,1 = 0,2455. Раньше, когда люди использовали таблицы тригонометрических функций, они просто смотрели в таблицу касательных, чтобы увидеть, какой угол имеет тангенс 0,2455. В калькуляторе мы используем обратные триггерные функции с именами арктангенс, арксинус и арккосинус. Обычно на калькуляторе есть кнопка с надписью «inv» или «arc», которую вы нажимаете перед нажатием соответствующей триггерной кнопки. Арктангенс 0,2455 равен 13,79, поэтому угол A равен 13,79 °. (Если хотите, можете преобразовать 0,79 градуса в минуты и секунды.)
Арктангенс 0,2455 равен 13,79, поэтому угол A равен 13,79 °. (Если хотите, можете преобразовать 0,79 градуса в минуты и секунды.)Вот и все.
Остальные три тригонометрические функции: котангенс, секанс и косеканс
Для большинства целей достаточно трех триггерных функций: синуса, косинуса и тангенса. Однако бывают случаи, когда нужны другие. В исчислении часто используется секанс. Вы можете спросить: «Почему шесть триггерных функций?» Это своего рода симметрия.Есть шесть способов соотношения двух сторон прямоугольного треугольника, и это дает шесть функций:- sin A = кондиционер (opp / hyp)
- cos A = b / c (прил / гип)
- желто-коричневый A = a / b (opp / adj)
- детская кроватка A = b / a (adj / opp)
- сек A = c / b (hyp / adj)
- csc A = c / a (hyp / opp)
 Они в значительной степени избыточны, но стоит знать, что они из себя представляют, на случай, если вы с ними столкнетесь. Обратите внимание, что котангенсы — это касательные к дополнительным углам, что означает, что кроватка A = tan B, и косеканс являются секущими дополнительных углов, и это означает, что csc A = sec B.
Они в значительной степени избыточны, но стоит знать, что они из себя представляют, на случай, если вы с ними столкнетесь. Обратите внимание, что котангенсы — это касательные к дополнительным углам, что означает, что кроватка A = tan B, и косеканс являются секущими дополнительных углов, и это означает, что csc A = sec B. Эти три другие функции также можно интерпретировать с помощью круговой диаграммы.
Мы рассматриваем угол AOB. Напомним, что его касательной является прямая AC. По симметрии тангенс угла FOB является линией FG, , но FOB является дополнительным углом AOB, , следовательно, котангенс AOB равен FG.
Затем, чтобы интерпретировать секущие геометрически. Угол AOB появляется в треугольнике COA как угол AOC, , поэтому sec AOB = sec AOC = hyp / adj = OC / OA = OC. Вот и все — секущая — это прямая от центра окружности к касательной AC. Причина, по которой он называется секущей, состоит в том, что она разрезает круг, а слово «секанс» происходит от латинского слова, означающего «разрезание».
Причина, по которой он называется секущей, состоит в том, что она разрезает круг, а слово «секанс» происходит от латинского слова, означающего «разрезание».
Аналогично, косеканс угла AOB — это линия OG от центра окружности до линии котангенса FG.
Упражнения
Примечание: как обычно, во всех упражнениях на прямоугольные треугольники c обозначает гипотенузу, a и b для перпендикулярных сторон и A и B для углов, противоположных a и b соответственно. 26. В каждом из следующих прямоугольных треугольников, у которых даны две стороны, вычислите sin, cos и tan углов A, и B. Выразите результаты в виде общих дробей.
(я). c = 41, a = 9.
(ii). c = 37, a = 35.
(iii). a = 24, b = 7.
31. В прямоугольном треугольнике c = 6 футов 3 дюйма и загар B = 1. 2. Найдите a, и b.
2. Найдите a, и b.
34. a = 1,2, b = 2,3. Найдите A, и c.
42. a = 10,11, b = 5,14. Найдите B, и c.
В следующих нескольких задачах треугольники не являются прямоугольными, но вы можете решить их, используя то, что вы знаете о прямоугольных треугольниках.
61. В наклонном треугольнике ABC, A = 30 °, B = 45 °, а длина перпендикуляра от C до AB составляет 12 дюймов. Найдите длину AB.
67. Если сторона равностороннего треугольника равна a, найдите высоту и радиусы описанных и вписанных окружностей.
202. От вершины здания высотой 50 футов углы подъема и понижения верха и низа другого здания составляют 19 ° 41 ‘и 26 ° 34’ соответственно.Какая высота и расстояние до второго дома.
207. От вершины маяка высотой 175 футов углы падения верха и низа флагштока составляют 23 ° 17 ‘и 42 ° 38’ соответственно. Какой высоты у шеста?
Какой высоты у шеста?
214. В двух точках на расстоянии 65 футов на одной стороне дерева и на одной линии с ним углы подъема вершины дерева составляют 21 ° 19 ‘и 16 ° 20’. Найдите высоту дерева.
215. Когда воздушный шар проходит между двумя точками A, и B, на расстоянии 2 миль, углы подъема воздушного шара в этих точках составляют 27 ° 19 ‘и 41 ° 45’ соответственно. Найдите высоту воздушного шара. Возьмите A и B на одном уровне.
233. Вершина маяка находится на высоте 230 футов над уровнем моря. Как далеко находится объект, который находится только «на горизонте»? [Предположим, что Земля — это сфера радиусом 3956 миль.]
234. Какая должна быть высота наблюдателя, чтобы он мог видеть объект на земле в тридцати милях от него? Предположим, что Земля представляет собой гладкую сферу.
На каждом из рисунков, упомянутых в следующих нескольких задачах, объект должен выразить свою площадь (i) через радиус R, то есть радиус описанной окружности, (ii) через apothem r, , то есть радиус вписанной окружности, и (iii) относительно стороны a.
251. Равносторонний треугольник. [См. Проблему 67 выше.]
252. пл.
253. Правильный пятиугольник.
254. Правильный шестигранник.
255. Правильный восьмиугольник.
Подсказки
26. Вам нужны только sin, cos и tan углов A и B ; сами углы не нужны.Итак, вам нужна только третья сторона, которую вы можете вычислить с помощью теоремы Пифагора, а затем вычислить отношения двух сторон.
31. Вы знаете c и tan B. К сожалению, tan B — это соотношение двух сторон, о которых вы не знаете, а именно b / a. Эту проблему можно решить несколькими способами. Вот два.
Метод 1. Возьмите уравнение 1.2 = tan B = b / a, , чтобы получить связь между a и b, а именно b = 1.2 а. Теорема Пифагора тогда дает 6,25 2 = a 2 + 1,44 a 2 , из которых вы можете определить a, и затем найти b.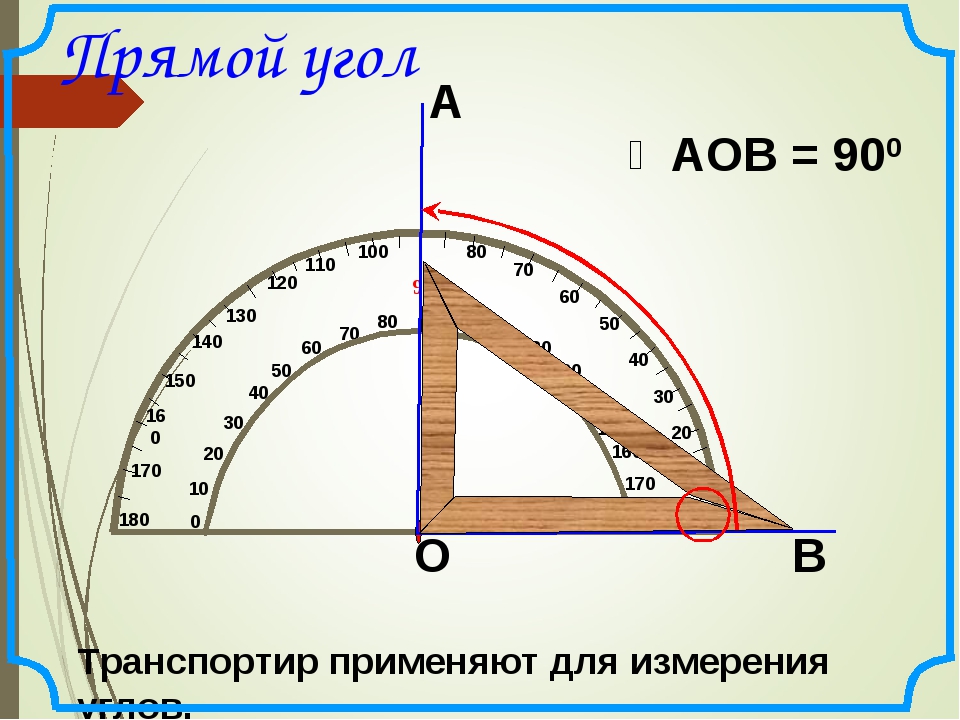
Метод 2. Из tan B, вы можете определить угол B (используйте arctan). Отсюда вы можете найти cos B, , а затем a, , и вы можете найти sin B, , а затем b.
34. Поскольку у вас есть a и b, , вы можете использовать касательные, чтобы найти A , и теорему Пифагора, чтобы найти c.
42. Найдите B по касательным и c по теореме Пифагора.
61. Начните с рисования рисунка. Хотя треугольник ABC не является прямоугольным, он разбивается на два прямоугольных треугольника. Вы можете использовать касательные, чтобы найти две части стороны AB и сложить их.
67. Равносторонний треугольник ABC имеет три угла при вершине 60 °. Отбросьте перпендикуляр из одной вершины, скажем, вершины C, , и вы получите два конгруэнтных прямоугольных треугольника ACF и BCF, , и вы можете найти длину этого перпендикуляра, и это высота равностороннего треугольника. Описанный круг — это круг, проходящий через три вершины, а вписанный круг — это круг, касающийся всех трех сторон.Отбрасывая перпендикуляры из другой вершины равностороннего треугольника и используя триггер на полученных маленьких треугольниках, вы можете найти радиусы этих двух окружностей.
Описанный круг — это круг, проходящий через три вершины, а вписанный круг — это круг, касающийся всех трех сторон.Отбрасывая перпендикуляры из другой вершины равностороннего треугольника и используя триггер на полученных маленьких треугольниках, вы можете найти радиусы этих двух окружностей.
202. Поскольку вам известна высота вашего здания и угол наклона основания другого здания, вы можете определить, как далеко оно находится. Тогда угол подъема к вершине другого здания покажет вам, насколько оно выше вашего.
207. Подсказка, похожая на 202. Видите ли, триггер может быть полезен, если вы одинокий смотритель маяка и не знаете, что делать!
214. Это полезная задача. Вы можете использовать его, чтобы найти высоты недоступных вещей. Нарисуйте фигуру. Есть два неизвестных: высота дерева x и расстояние x ближайшей точки к дереву. Дальнейшая точка будет x + 65 футов от дерева. Используя тангенсы известных углов, вы можете составить два уравнения, которые можно решить, чтобы определить y, и x.
215. Это похоже на 214, но в этой задаче баллон находится между двумя точками. Нарисуйте фигуру. Определитесь с вашими переменными. Составьте уравнения и решите их.
233. Очень интересная задача. На протяжении веков для вычисления радиуса Земли использовались различные обратные величины. В этой задаче мы предполагаем, что знаем о Земле. Все, что вам здесь нужно, это теорема Пифагора. Одна сторона прямоугольного треугольника равна r, — радиус Земли, а гипотенуза — r + h , где h — высота маяка.Теорема Пифагора о третьей стороне треугольника.
234. Задайте эту задачу аналогично 233, но известны разные переменные.
251–255. Вы можете сделать все это сразу, оставив вычисления напоследок. Пусть n — количество сторон правильного многоугольника. Проведите линии от центра фигуры к вершинам и серединам сторон. У вас получится 2 n маленьких треугольников. Каждый из них представляет собой прямоугольный треугольник с гипотенузой R, один катет r, и другой катет a /2. Угол в центре составляет 360 ° / (2 n ) = 180 ° / n. Используя тригонометрию, вы можете легко написать уравнения, связывающие площадь правильного многоугольника, как требуется.
Угол в центре составляет 360 ° / (2 n ) = 180 ° / n. Используя тригонометрию, вы можете легко написать уравнения, связывающие площадь правильного многоугольника, как требуется.
ответы
26. (i). b = 40. Таким образом sin A = cos B = 9/41, cos A = sin B = 40/41, tan A = 9/40, tan B = 40 / 9.(ii). b = 12. Итак sin A = cos B = 35/37, cos A = sin B = 12/37, tan A = 35/12, tan B = 12 / 37.
(iii). c = 25. Итак sin A = cos B = 24/25, cos A = sin B = 7/25, tan A = 24/7, tan B = 7 / 24.
31. a = 4 фута, b = 4,8 фута, около 4 футов 10 дюймов.
34. A = 27,55 °, около 28 °. с = 2,6.
42. B = 26,95 ° или 26 ° 57 ‘. с = 11.3.
61.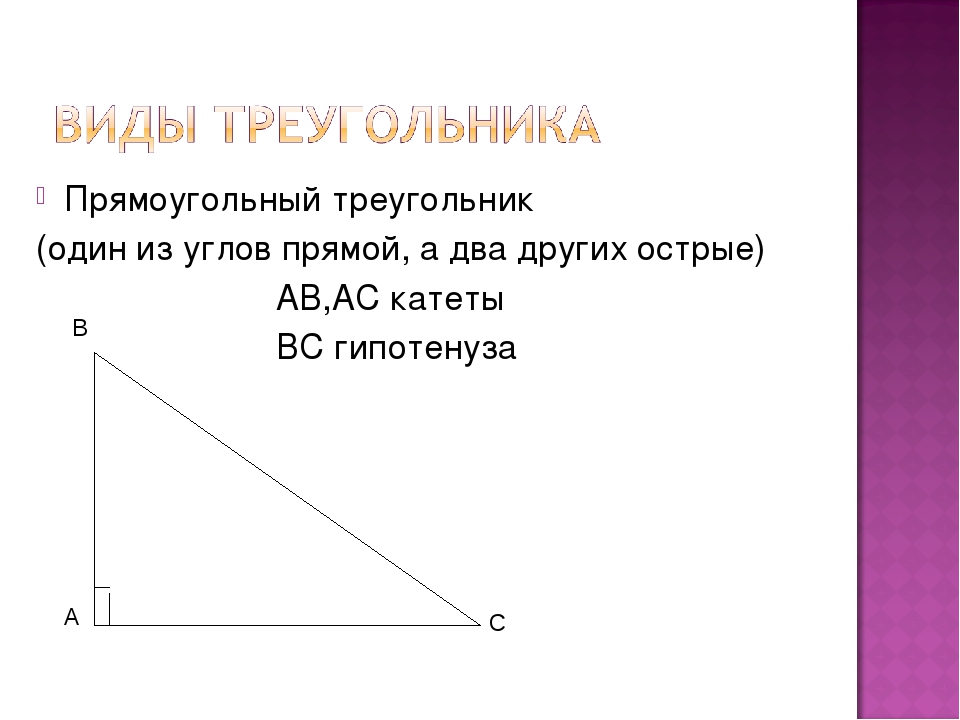 AB = 12 / tan A + 12 / tan B = 12 (√3 + 1) дюймов, около 33 дюймов.
AB = 12 / tan A + 12 / tan B = 12 (√3 + 1) дюймов, около 33 дюймов.
67. ( a √3) / 2, ( a √3) / 3 и ( a √3) / 6 соответственно.
202. Расстояние = 50 / тангаж 26 ° 34 ‘= 100 футов. Высота = 50 + 100 см. 19 ° 41 ‘= 85,8’ = 85’9 дюймов.
207. Расстояние = 175 / тангенс угла 42 ° 38 ‘= 190 футов. Рост = 175 — 190, загар 23 ° 17 ‘= 93.23 ‘= 9’3 «.
214. Два уравнения:
- 0,293052 = загар 16 ° 20 ‘= h / (65 + x ), и
0,3 = загар 21 ° 19 ‘= h / x .
Расстояние x = 196 футов. Высота х = 76,5 футов.
215. Если h — высота воздушного шара, а x — расстояние по земле от A до точки непосредственно под воздушным шаром, то два уравнения равны
- tan 27 ° 19 ‘= h / x , и
tan 41 ° 45 ‘= h / (2 — x )

Высота = 0,654 мили = 3455 футов.
233. Мелочь больше 18.5 миль.
234 600 футов.
251–255. Площадь обычного n -угольника равна A = nra /2. Чтобы найти A в терминах R, r, или a, , используйте отношения
- cos 180 ° / n = r / R, и
tan 180 & deg / n = a / (2 r ).
- (i) в единицах R, площадь A = nR 2 cos 180 ° / n sin 180 ° / n ,
(ii) в терминах r, площадь A = nr 2 tan 180 & deg / n , и
(iii) в терминах a, площадь A = na 2 / (4tan 180 & deg / n ).
| Проблема | форма | (i) R | (ii) r | (iii) a |
|---|---|---|---|---|
| 251 | треугольник | (3 R 2 √3) / 4 | 3 r 2 √3 | ( a 2 √3) / 4 |
| 252 | квадрат | 2 R 2 | 4 r 2 | a 2 |
| 253 | пятиугольник | (5 R 2 sin 108 °) / 2 | 5 r 2 tan 36 ° | (5 a 2 загар 54 °) / 4 |
| 254 | шестигранник | (3 R 2 √3) / 2 | 2 r 2 √3 | (3 a 2 √3) / 2 |
| 255 | восьмиугольник | 2 R 2 √2 | 8 r 2 tan 22 ° 30 ‘ | 2 a 2 tan 67 ° 30 ‘ |
Отступление на пифагоровы тройки
Это не имеет ничего общего с тригонометрией, но интересно. Вы, наверное, заметили, как Кроули часто выбирал две стороны прямоугольного треугольника как целые числа, а третья также оказывается целым числом. Как и в задаче 26, где стороны всех трех прямоугольных треугольников имеют целые числа, а именно 9:40:41, 12:35:37 и 7:24:25. Кроме того, в начале этой страницы был треугольник 5:12:13 (на самом деле 10:24:26, но он похож на треугольник 5:12:13). И, без сомнения, вы уже знаете о прямоугольном треугольнике 3: 4: 5.
Вы, наверное, заметили, как Кроули часто выбирал две стороны прямоугольного треугольника как целые числа, а третья также оказывается целым числом. Как и в задаче 26, где стороны всех трех прямоугольных треугольников имеют целые числа, а именно 9:40:41, 12:35:37 и 7:24:25. Кроме того, в начале этой страницы был треугольник 5:12:13 (на самом деле 10:24:26, но он похож на треугольник 5:12:13). И, без сомнения, вы уже знаете о прямоугольном треугольнике 3: 4: 5. Итак, существуют ли другие специальные прямоугольные треугольники, все стороны которых представляют собой целые числа? Да, и их давно изучают.Три числа a, b, и c такие, что a 2 + b 2 = c 2 , как говорят, образуют тройку Пифагора , в честь Пифагора. Он жил около 550 г. до н. Э. и наверное знаю немало из них. Но древние вавилоняне примерно 1800 г. до н. Э. знал их всех, и многие из них были известны в других древних цивилизациях, таких как Китай и Индия.
Прежде чем читать абзац, посмотрите, сможете ли вы найти еще несколько троек Пифагора.Не считайте те, у которых есть общий множитель, как новые, например 6: 8: 10, поскольку они будут похожи на меньшие.
В книге Евклида « Элементы » есть описание всех возможных пифагоровых троек. Вот современный пересказ Евклида. Возьмем любые два нечетных числа: m, и n, с m, n и взаимно простое (то есть без общих множителей). Пусть a = mn, let b = ( n 2 — m 2 ) / 2, и пусть c = ( n 2 + m 2 ) / 2.Тогда a : b : c — тройка Пифагора. Например, если взять m = 1 и n = 3, то получится наименьшая тройка Пифагора 3: 4: 5.
открытых учебников | Сиявула
Математика
Наука
- Читать онлайн
Учебники
Английский
Класс 7A
Марка 7Б
7 класс (A и B вместе)
Африкаанс
Граад 7А
Граад 7Б
Граад 7 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 8A
Сорт 8Б
8 класс (A и B вместе)
Африкаанс
Граад 8А
Граад 8Б
Граад 8 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 9А
Марка 9Б
9 класс (A и B вместе)
Африкаанс
Граад 9А
Граад 9Б
Граад 9 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Класс 4A
Класс 4Б
Класс 4 (вместе A и B)
Африкаанс
Граад 4А
Граад 4Б
Граад 4 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 5А
Марка 5Б
Оценка 5 (вместе A и B)
Африкаанс
Граад 5А
Граад 5Б
Граад 5 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 6А
Марка 6Б
6 класс (A и B вместе)
Африкаанс
Граад 6А
Граад 6Б
Граад 6 (A en B saam)
Пособия для учителя
Наша книга лицензионная
Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий. Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки каким-либо образом, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки каким-либо образом, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Узнайте больше о спонсорстве и партнерстве с другими организациями, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без бренда)
Эти небрендовые версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, трансформировать, изменять или дополнять их любым способом, с единственным требованием — предоставить соответствующую информацию Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
The Теорема Пифагора (стр. 2 из 2)
«Вершины» — модное слово для «углов», так что это просит меня выяснить, точки — это три угла прямоугольного треугольника. Из быстрого графика Я вижу, что точки — это углы какого-то треугольника типа : Я могу использовать расстояние
Формула для определения длин каждой из сторон треугольника,
эти длины представляют собой расстояния между парами точек. Думаю баллы (2, 3) и (5, 2) отметить гипотенузу, полагая этот треугольник оказывается правильным, поэтому я проверю расстояния, которые путь первый. (2, 3) и (2, 1): (2, 1) и (5, 2): (2, 3) и (5, 2): проверка теоремы (используя квадраты
расстояний): Поскольку квадраты двух меньших расстояния равны квадрату наибольшего расстояния, тогда этих точки — это вершины прямоугольного треугольника.
Ширина (по горизонтали), высота (идущий вертикально), и провод (идущий по диагонали) для ворота образуют прямоугольный треугольник.Когда ворота квадратные, диагональ будет подчиняться теореме Пифагора. Авторские права Элизабет Стапель 2010-2011 Все права защищены Таким образом, растяжка будет девяти футов длинный плюс еще 0,43389 футов или около того. В одном футе двенадцать дюймов, поэтому: Будет еще около 5.2 дюймы; 0,2 ближе к 0,25 чем до 0,0, итак: Длина провода будет 9 футов, 5 1 / 4 дюйма.
Обратите внимание, что для того, чтобы ответ был правильным,
отображаемая картинка никак не может быть «в масштабе». Вам следует
Разумеется, предполагаем, что рисунки для геометрии и тригонометрии
упражнения а не «в масштабе». << Предыдущая Вверх | 1 | 2 | Вернуться к индексу
|
Гипотенуза — используйте ее для квадрата вашей работы — Steadman’s Ace Hardware
Дэмиен Эндрюс
Проблема
Весна. В этом году вы решили залить бетонную подушку для нового гриля для барбекю, который вы купили в прошлом году, а также для стола для семейного пикника.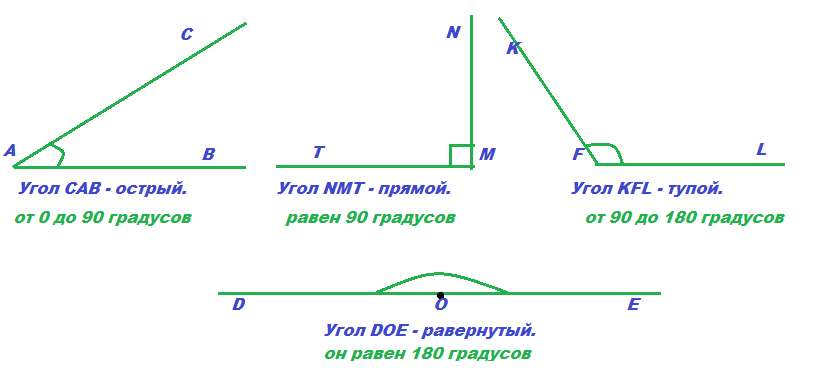 Вы решили, что идеальный размер для нового пэда — 10 x 14 футов. Это довольно амбициозный проект «сделай сам», но, как вы знаете, он принесет результат, которым вся семья будет наслаждаться долгие годы.
Вы решили, что идеальный размер для нового пэда — 10 x 14 футов. Это довольно амбициозный проект «сделай сам», но, как вы знаете, он принесет результат, которым вся семья будет наслаждаться долгие годы.
В субботу утром с первыми лучами солнца, и вы на улице с 4 деревянными кольями, кувалдой 3 # и веревкой. Вы забиваете первую ставку в известном угловом положении. Затем вы измеряете 14 футов и вбиваете еще одну ставку. Оттуда вы отмеряете 10 футов и вбиваете еще одну ставку. Наконец, вы снова измеряете 14 футов и делаете еще одну ставку.Затем вы проводите веревочную линию между всеми ставками.
Вы берете свою любимую лопату и начинаете копать снаружи веревки. Вы копаете примерно на 6 дюймов за пределами строковой линии, чтобы оставалось достаточно места для установки форм размером 2 x 4 дюйма. Выкопав внешнее кольцо, вы удалите грязь внутри кольца, чтобы освободить место для бетона. Но после того, как вы выкопали внешнее кольцо, прямоугольник не будет казаться квадратным. Вы дважды проверяете свои измерения между кольями — все в порядке.Но вы уверены, что работа не квадратная, поэтому вы берете квадрат кровельщика, кладете его на угловую стойку и проверяете линию веревки. Вы были правы, даже с относительно небольшим квадратом кровельщика видно, что работа не квадратная.
Вы дважды проверяете свои измерения между кольями — все в порядке.Но вы уверены, что работа не квадратная, поэтому вы берете квадрат кровельщика, кладете его на угловую стойку и проверяете линию веревки. Вы были правы, даже с относительно небольшим квадратом кровельщика видно, что работа не квадратная.
Гипотенуза спешит на помощь
Проще говоря: гипотенуза — это самая длинная сторона прямоугольного треугольника (также называемого прямоугольным треугольником). Если вы забыли геометрию начальной школы, прямоугольный треугольник должен иметь угол 90 ° — см. Иллюстрацию A.Гипотенуза противоположна углу 90 °. Углы 90 ° — это именно то, что вам нужно на углах вашей новой бетонной подушки. Итак, как мы можем использовать гипотенузу, чтобы помочь нам получить идеальные углы 90 ° во всех наших углах…
Формула для вычисления гипотенузы: Гипотенуза сумма квадратов длин катетов равна квадрату длины гипотенузы. Ссылаясь на иллюстрацию B, формула будет записана: a² + b² = c². Но это несколько вводит в заблуждение — особенно для тех из нас, кто бросает вызов геометрии.Нам не нужно знать длину квадрата гипотенузы, нам нужна гипотенуза. Итак, мы берем решение вышеуказанного уравнения (c²) и находим его квадратный корень (√ c). Еще не запутались? Не волнуйтесь — читайте дальше, и мы все упростим.
Но это несколько вводит в заблуждение — особенно для тех из нас, кто бросает вызов геометрии.Нам не нужно знать длину квадрата гипотенузы, нам нужна гипотенуза. Итак, мы берем решение вышеуказанного уравнения (c²) и находим его квадратный корень (√ c). Еще не запутались? Не волнуйтесь — читайте дальше, и мы все упростим.
Прежде, чем мы перейдем к действительно простому способу использования гипотенузы для квадрирования вашей работы, давайте решим проблему: какова гипотенуза вашей бетонной площадки 10х14 футов (иллюстрация C). 10² = 100. 14² = 196. Теперь мы знаем, что квадрат гипотенузы равен 196 ′.Это не принесет нам много пользы для нового пэда, поэтому нам нужно найти квадратный корень из 196, что составляет 17,2 ′. Если мы продолжим идти по этому пути, нам нужно будет выяснить, что такое 0,2 фута, а затем, что такое 0,4 дюйма, чтобы мы могли точно измерить расстояние от одного угла площадки до другого. Все становится слишком сложно.
Вот простой способ использовать гипотенузу для вычисления квадрата вашей работы. Гипотенуза К счастью для нас, старых мастеров, гипотенуза прямоугольного треугольника с одним катетом 3 и другим катетом равняется 4.Гипотенуза вышеупомянутого всегда равна 5 (иллюстрация D). Неважно, какую единицу измерения вы используете: дюймы, футы, метры, ярды, миллиметры — все, что лучше всего подходит для работы, которую вы выполняете. Если вы делаете музыкальную шкатулку, возможно, вы захотите использовать дюймы. Ноги отлично подойдут для бетонной площадки. Дворы являются предпочтительными единицами измерения для ограждений углов.
Гипотенуза К счастью для нас, старых мастеров, гипотенуза прямоугольного треугольника с одним катетом 3 и другим катетом равняется 4.Гипотенуза вышеупомянутого всегда равна 5 (иллюстрация D). Неважно, какую единицу измерения вы используете: дюймы, футы, метры, ярды, миллиметры — все, что лучше всего подходит для работы, которую вы выполняете. Если вы делаете музыкальную шкатулку, возможно, вы захотите использовать дюймы. Ноги отлично подойдут для бетонной площадки. Дворы являются предпочтительными единицами измерения для ограждений углов.
Теперь давайте снова натянем нашу бетонную площадку, на этот раз используя гипотенузу, чтобы обеспечить идеально квадратную площадку… Гипотенуза
(См. Иллюстрацию E) Забейте кол №1.Отмерьте 14 ′ и забейте кол №2. Плотно пропустите шнур между двумя кольями. Сделайте небольшую отметку на веревке 4 ′ от второй стойки. Откройте линейку до высоты примерно 11 футов и поместите начало линейки под второй столб — приблизьте его к квадрату. Теперь, используя вторую линейку, поместите один конец линейки на отметку 4 ′ и отрегулируйте обе линейки так, чтобы линейка 1 оказалась на отметке 5 ′ на линейке 2.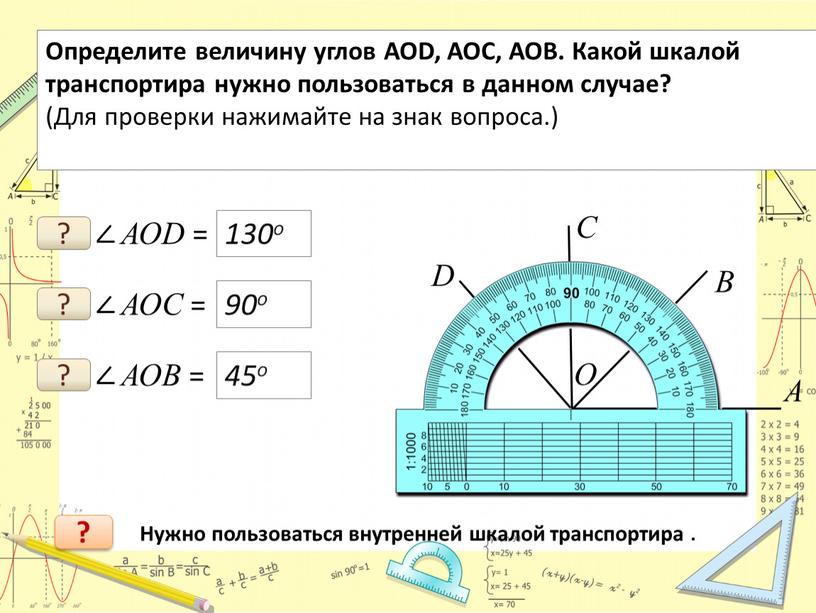 Выйдите на отметку 10 ′ на этой линии и забейте третью колышек. Проведите тугую веревочную линию между №2 и №3.Повторите этот процесс для 3-го и 4-го кольев — только на этот раз откройте линейку на земле примерно на 15 футов перед началом измерения. Затем вы можете провести линию между ставками №1 и №4, поскольку они уже должны быть возведены в квадрат, но дважды проверьте!
Выйдите на отметку 10 ′ на этой линии и забейте третью колышек. Проведите тугую веревочную линию между №2 и №3.Повторите этот процесс для 3-го и 4-го кольев — только на этот раз откройте линейку на земле примерно на 15 футов перед началом измерения. Затем вы можете провести линию между ставками №1 и №4, поскольку они уже должны быть возведены в квадрат, но дважды проверьте!
Вы также можете использовать кратные этой удобной формулы для удовлетворения конкретных требований к работе. Гипотенуза 3 × 4 = 5, или 6 × 8 = 10, или 12 × 16 = 20 — и так далее. Помните, что чем больше задание, тем больше должна быть гипотенуза, используемая для возведения в квадрат, чтобы обеспечить максимальную точность.
Советы профессионалов : Лучше всего измерять гипотенузу вдвоем. Это необходимо для того, чтобы линия струны не выходила за линию во время измерения. Попросите одного человека держать конец линейки чуть ниже линии струны, а второй отмеряет гипотенузу. При квадратном брусе каркаса 2 ″ x4 ″ обязательно измеряйте гипотенузу изнутри древесины, то есть там, где будет находиться бетон, а не снаружи дерева, и уж тем более не снаружи одной стороны к стене. внутри другого.Это даст вам неточную гипотенузу.
внутри другого.Это даст вам неточную гипотенузу.
Как найти квадрат с помощью лазерного уровня
Важнейшей частью каждой задачи по планировке является разметка квадратных углов под углом 90 градусов для внешних фундаментов или внутренних стен. Для очень небольших площадей квадрат подрядчика может помочь, но для укладки под углом 90 градусов на большей площади требуется немного больше точности. Большинство подрядчиков изучают 3-4-5 или метод Пифагора для разметки квадрата.
Разметка квадрата с помощью метода Пифагора
Шаги метода Пифагора следующие:
- Измерьте 3 фута от точки в одном направлении.
- Измерьте 4 ‘от той же точки на 90 ° в другом направлении.
- Измерьте поперек двух точек и отрегулируйте угол так, чтобы расстояние на третьей стороне треугольника составляло 5 футов.
- Вы также можете использовать числа, кратные 3-4-5, в том же соотношении (например, 6, 8, 10) для образования больших или меньших прямых углов
Для этого метода обычно требуется как минимум два человека, и он менее точен. Если угол отклонен от нескольких градусов, ошибка усугубляется только по мере того, как вы продлеваете линию уровня дальше.В итоге, метод не такой точный, занимает больше времени и его трудно сделать в одиночку.
Если угол отклонен от нескольких градусов, ошибка усугубляется только по мере того, как вы продлеваете линию уровня дальше.В итоге, метод не такой точный, занимает больше времени и его трудно сделать в одиночку.
Использование 5-точечного лазера PLS для разметки квадрата
Лазерный точечный извещатель PLS-60545 HVD 500 предназначен для крепления к маятниковой мишени и поставляется с конфигурацией системы PLS 5 для использования на больших расстояниях, на открытом воздухе или в условиях яркого освещения.
PLS 5 имеет левую, правую, верхнюю и нижнюю точки, выровненные под углом 90 градусов к обращенной вперед точке. Вы можете быстро пометить квадрат от любой базовой линии, выполнив следующую процедуру:
- Поместите PLS 5 на пол (при необходимости используйте напольную стойку PLS-20844) и совместите точку вниз с точкой поворота.
- Совместите точку, обращенную вперед, по базовой линии, будь то геодезический маркер на новом фундаменте или общий край основной стены или край фундамента.

- Используя маятниковую мишень PLS-10090, найдите точку под углом 90 градусов от PLS 5 и легко перенесите отметку на пол. Делайте это с разной длиной, и затем вы можете щелкнуть мелом или использовать уровень подрядчика, чтобы нарисовать прямой край вдоль линии.
- При использовании на открытом воздухе, в условиях яркого освещения или на больших расстояниях лазерный точечный извещатель PLS-60545 HVD 500 предназначен для крепления к маятниковой мишени и поставляется с конфигурацией системы PLS 5.
Этот метод может быть выполнен одним человеком за меньшее время, как метод 3-4-5. Практический результат: использование лазерного уровня обеспечивает большую точность за меньшее время, и это может легко сделать один рабочий. PLS 5 имеет точность до 1/8 дюйма на расстоянии 50 футов, что означает, что это ценный инструмент, когда вам нужно разметить квадрат на большом расстоянии. Для достижения еще большей точности на больших расстояниях вы также можете использовать PLS HVR 505, вращающийся вертикально, чтобы обеспечить точность 1/8 дюйма на 100 футов.

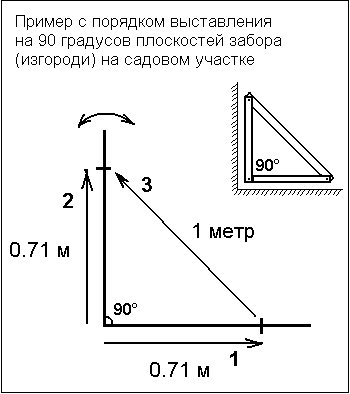 Это используется в процессе строительства до сих пор;
Это используется в процессе строительства до сих пор;
 Чаще всего используются для создания декоративных элементов.
Чаще всего используются для создания декоративных элементов.


 мерной рулеткой выделяются одинаковые расстояния от них, фиксируются все маркеры. длина ее выставляется на 2, 1 м, чертятся дуги условных окружностей – там, где они впервые пересекутся, и будет крепиться строительная веревка к установленной на земле «скамейке».
мерной рулеткой выделяются одинаковые расстояния от них, фиксируются все маркеры. длина ее выставляется на 2, 1 м, чертятся дуги условных окружностей – там, где они впервые пересекутся, и будет крепиться строительная веревка к установленной на земле «скамейке». Благодаря этой линии можно определить два угла здания, которые в обязательном порядке нужно отметить вбитыми в землю кольями. Далее линия закрепляется обноской. Она устанавливается на некотором расстоянии от предполагаемой траншеи или котлована и выполняется при помощи вертикальных и прибитых к ним горизонтальных досок.
Благодаря этой линии можно определить два угла здания, которые в обязательном порядке нужно отметить вбитыми в землю кольями. Далее линия закрепляется обноской. Она устанавливается на некотором расстоянии от предполагаемой траншеи или котлована и выполняется при помощи вертикальных и прибитых к ним горизонтальных досок.



 Не менее 3 метров от строения до соседского участка.
Не менее 3 метров от строения до соседского участка.
 Для этого отмеряем на первой бечевке 4 м от места их пересечения, а на второй 3 м. Ставим пометки в этих местах любым способом. Соединяем пометки и измеряем полученную гипотенузу рулеткой.
Для этого отмеряем на первой бечевке 4 м от места их пересечения, а на второй 3 м. Ставим пометки в этих местах любым способом. Соединяем пометки и измеряем полученную гипотенузу рулеткой. Напоминаю, что мы решили разметить фундамент со сторонами 6 м на 8 м. Также нам нужны две диагонали, которые в нашем случае равняются 10 м. Оставьте на бечевках запас длины на их закрепление.
Напоминаю, что мы решили разметить фундамент со сторонами 6 м на 8 м. Также нам нужны две диагонали, которые в нашем случае равняются 10 м. Оставьте на бечевках запас длины на их закрепление.
 Необходим для того, чтобы проверять угловые участки в девяносто градусов. Будет неплохо, если такие инструменты вы заготовите для проверки углов на тридцать и шестьдесят градусов;
Необходим для того, чтобы проверять угловые участки в девяносто градусов. Будет неплохо, если такие инструменты вы заготовите для проверки углов на тридцать и шестьдесят градусов;
 Заметим, что каждый такой отрезок представляет собой дополнительный прямоугольник, который тоже приходится строить. В завершении выставляются и перепроверяются угловые участки;
Заметим, что каждый такой отрезок представляет собой дополнительный прямоугольник, который тоже приходится строить. В завершении выставляются и перепроверяются угловые участки; Как отмечает британский исполнительный орган по здравоохранению и безопасности, работа на крышах является одной из основных причин смертельных исходов в строительной отрасли. Падения с высоты часто заканчиваются смертельным исходом.
Как отмечает британский исполнительный орган по здравоохранению и безопасности, работа на крышах является одной из основных причин смертельных исходов в строительной отрасли. Падения с высоты часто заканчиваются смертельным исходом. потом
Я могу добавить эти расстояния в теорему, чтобы увидеть,
— прямоугольный треугольник.
потом
Я могу добавить эти расстояния в теорему, чтобы увидеть,
— прямоугольный треугольник. Если ворота
является «квадратным» (то есть, если стороны пересекаются в углах, чтобы
образуют прямые углы), какой будет длина диагональной связи
провод? Округлите до ближайшей четверти дюйма.
Если ворота
является «квадратным» (то есть, если стороны пересекаются в углах, чтобы
образуют прямые углы), какой будет длина диагональной связи
провод? Округлите до ближайшей четверти дюйма.  Он провел измерения до точки R от точек P и Q на любом
стороне пруда, и уверен, что угол при P правильный,
как показано:
Он провел измерения до точки R от точек P и Q на любом
стороне пруда, и уверен, что угол при P правильный,
как показано:  Не , а не ошибка попытки угадать ответы по картинкам!
Не , а не ошибка попытки угадать ответы по картинкам!