Как упрощать схемы в электротехнике: Преобразования в линейных электрических схемах

Содержание

Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Главная → Примеры решения задач ТОЭ → Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Основными законами, определяющими расчет электрической цепи, являются законы Кирхгофа.

На основе законов Кирхгофа разработан ряд практических методов расчета электрических цепей постоянного тока, позволяющих сократить вычисления при расчете сложных схем.

Существенно упростить вычисления, а в некоторых случаях и снизить трудоемкость расчета, возможно с помощью эквивалентных преобразований схемы.

Преобразуют параллельные и последовательные соединения элементов, соединение «звезда» в эквивалентный «треугольник» и наоборот. Осуществляют замену источника тока эквивалентным источником ЭДС. Методом эквивалентных преобразований теоретически можно рассчитать любую цепь, и при этом использовать простые вычислительные средства.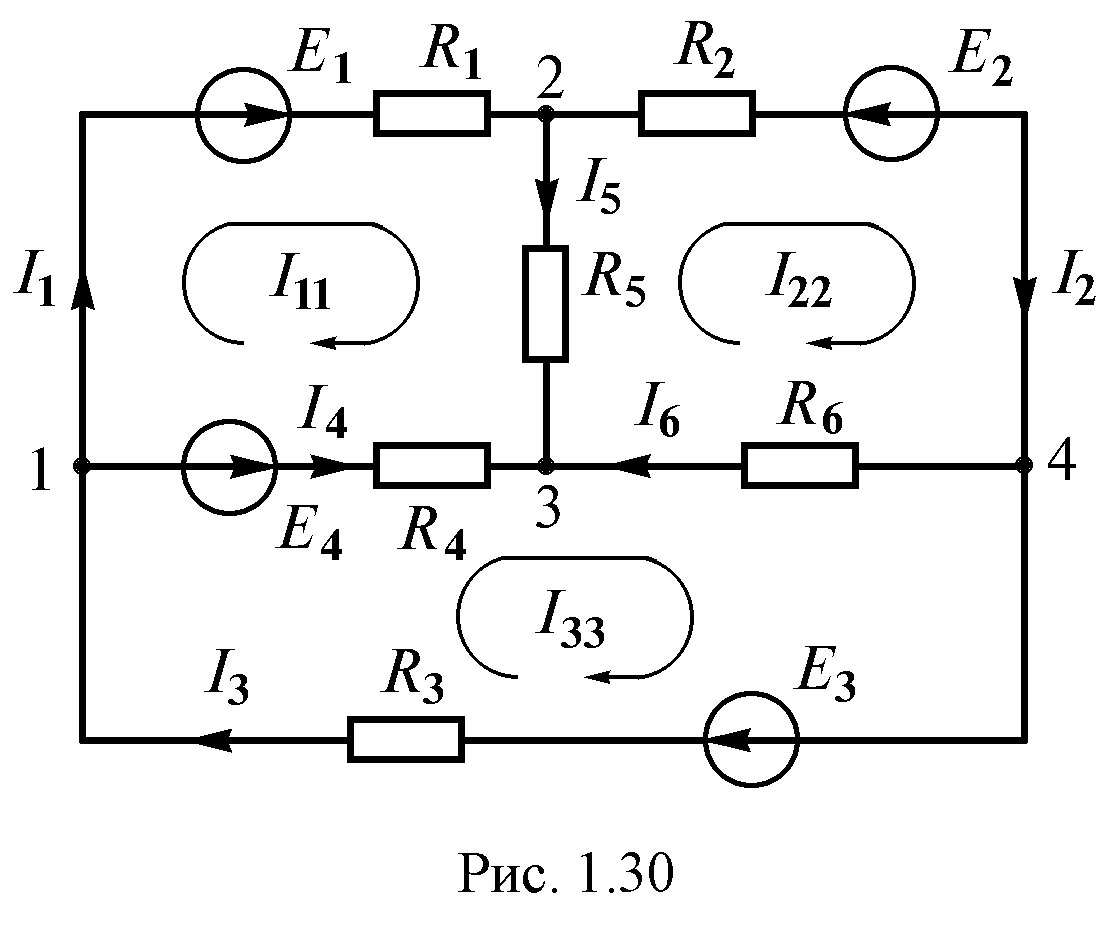

Или же определить ток в какой-либо одной ветви, без расчета токов других участков цепи.

В данной статье по теоретическим основам электротехники рассмотрены примеры расчета линейных электрических цепей постоянного тока с использованием метода эквивалентных преобразований типовых схем соединения источников и потребителей энергии, приведены расчетные формулы.

Решение задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Задача 1. Для цепи (рис. 1), определить эквивалентное сопротивление

относительно входных зажимов a−g, если известно: R₁ = R₂ = 0,5 Ом, R₃ = 8 Ом, R₄ = R₅ = 1 Ом, R₆ = 12 Ом, R₇ = 15 Ом, R₈ = 2 Ом, R₉ = 10 Ом, R₁₀= 20 Ом.

Рис. 1

Решение

Начнем эквивалентные преобразования схемы с ветви наиболее удаленной от источника, т.е. от зажимов a−g:

Задача 2. Для цепи (рис. 2,

а), определить входное сопротивление если известно: R₁ = R₂ = R₃ = R₄= 40 Ом.

Рис. 2

Решение

Исходную схему можно перечертить относительно входных зажимов (рис. 2, б), из чего видно, что все сопротивления включены параллельно. Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивленияможно воспользоваться формулой:

где R – величина сопротивления, Ом;

n – количество параллельно соединенных сопротивлений.

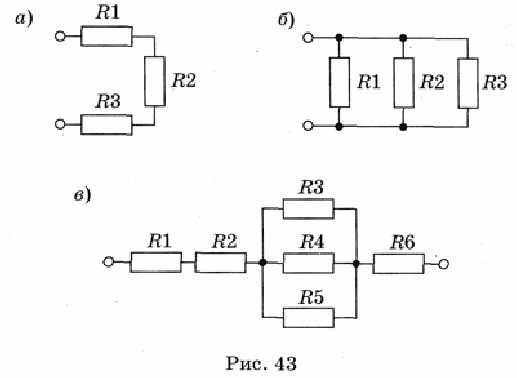
Задача 3. Определить эквивалентное сопротивление

относительно зажимов a–b, если R₁ = R₂ = R₃ = R₄ = R₅ = R₆ = 10 Ом (рис.

3, а).

Рис. 3

Решение

Преобразуем соединение «треугольник» f−d−c в эквивалентную «звезду». Определяем величины преобразованных сопротивлений (рис. 3, б):

По условию задачи величины всех сопротивлений равны, а значит:

На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда

эквивалентное сопротивление равно:

И тогда эквивалентное сопротивление исходной схемы представляет последовательное соединение сопротивлений:

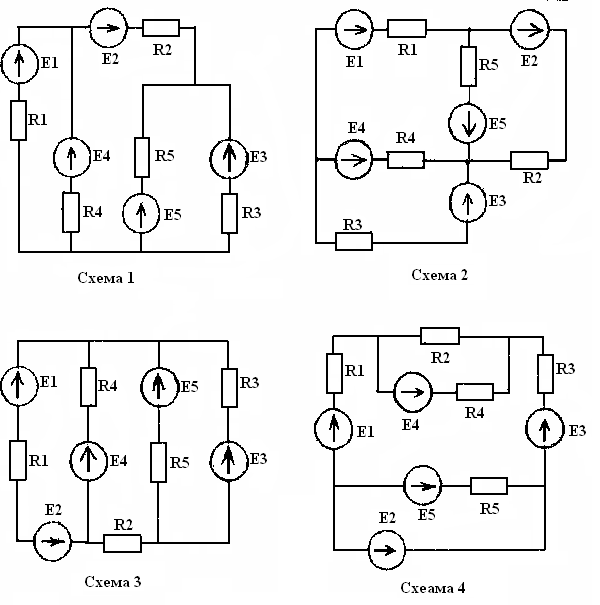
Задача 4. В заданной цепи (рис. 4, а) определить методом эквивалентных преобразований входные сопротивления ветвей a−b, c–d и f−b, если известно, что: R₁ = 4 Ом, R₂ = 8 Ом, R₃ =4 Ом, R₄ = 8 Ом, R₅ = 2 Ом, R₆ = 8 Ом, R₇ = 6 Ом, R₈ =8 Ом.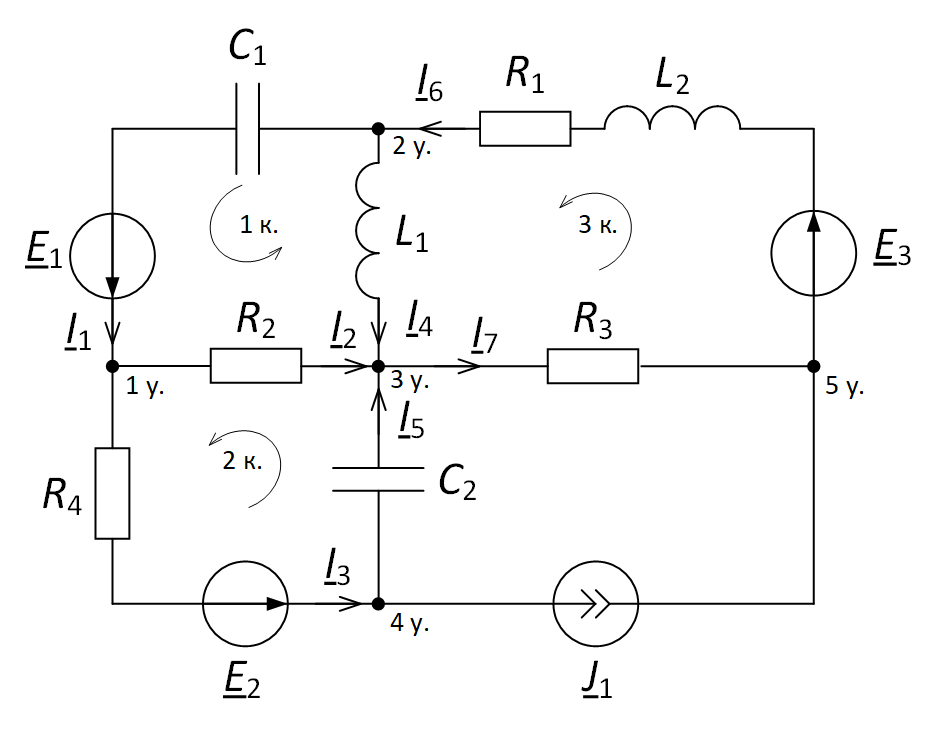

Решение

Для определения входного сопротивления ветвей исключают из схемы все источники ЭДС. При этом точки c и d, а также b и f соединяются накоротко, т.к. внутренние сопротивления идеальных источников напряжения равны нулю.

Рис. 4

Ветвь a−b разрывают, и т.к. сопротивление R_a_–b = 0, то входное сопротивление ветви равно эквивалентному сопротивлению схемы относительно точек a и b (рис. 4, б):

Аналогично методом эквивалентных преобразований определяются входные сопротивления ветвей R_cd и R_bf. Причем, при вычислении сопротивлений учтено, что соединение накоротко точек

a и b исключает ( «закорачивает») из схемы сопротивления R₁, R₂, R₃, R₄ в первом случае, и R₅, R₆, R₇, R₈ во втором случае.

Задача 5. В цепи (рис. 5) определить методом эквивалентных преобразований токи I₁, I₂, I₃ и составить баланс мощностей

, если известно: R₁ = 12 Ом, R₂ = 20 Ом, R₃ = 30 Ом, U = 120 В.

Рис. 5

Решение

Эквивалентное сопротивлениедля параллельно включенных сопротивлений:

Эквивалентное сопротивление всей цепи:

Ток в неразветвленной части схемы:

Напряжение на параллельных сопротивлениях:

Токи в параллельных ветвях:

Баланс мощностей:

Задача 6. В цепи (рис. 6, а), определить методом эквивалентных преобразований

показания амперметра, если известно: R₁ = 2 Ом, R₂ = 20 Ом, R₃ = 30 Ом, R₄ = 40 Ом, R₅ = 10 Ом, R₆ = 20 Ом, E = 48 В.

Сопротивление амперметра можно считать равным нулю.

Рис. 6

Решение

Если сопротивления R₂, R₃, R₄, R₅ заменить одним эквивалентным сопротивлением R_Э, то исходную схему можно представить в упрощенном виде (рис. 6,

б).

Величина эквивалентного сопротивления:

Преобразовав параллельное соединение сопротивлений R_Э и R₆ схемы (рис. 6, б), получим замкнутый контур, для которого по второму закону Кирхгофа можно записать уравнение:

откуда ток I₁:

Напряжение на зажимах параллельных ветвей U_ab выразим из уравнения по закону Ома для пассивной ветви, полученной преобразованием R_Э и R₆:

Тогда амперметр покажет ток:

Задача 7.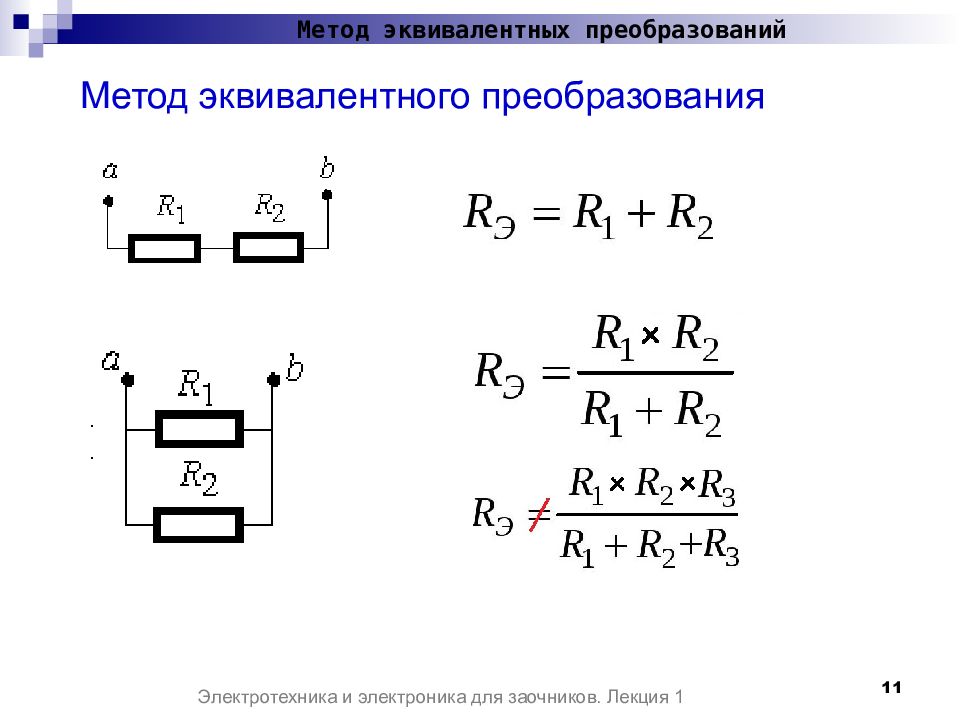

Определить токи ветвей схемы методом эквивалентных преобразований (рис. 7, а), если R₁ = R₂ = R₃ = R₄ = 3 Ом, J = 5 А, R₅ = 5 Ом.

Рис. 7

Решение

Преобразуем «треугольник» сопротивлений R₁, R₂, R₃ в эквивалентную «звезду» R₆, R₇, R₈ (рис. 7, б) и определим величины полученных сопротивлений:

Преобразуем параллельное соединение ветвей между узлами 4 и 5

Ток в контуре, полученном в результате преобразований, считаем равным току источника тока J, и тогда напряжение:

И теперь можно определить токи I₄ и I₅:

Возвращаясь к исходной схеме, определим напряжение U₃₂ из уравнения по второму закону Кирхгофа:

Тогда ток в ветви с сопротивлением R₃ определится:

Величины оставшихся неизвестными токов можно определить из уравнений по первому закону Кирхгофа для узлов 3 и 1:

Электронная версия статьи Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Примеры решения задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Метод эквивалентных преобразований

02. 09.2011, 291354 просмотра.

Электротехника. Методы расчёта электрических цепей. (лекция 4)

1. Конспект лекций по электротехнике Подготовлен: Степановым К.С., Беловой Л.В., Кралиным А.А., Панковой Н.Г. Кафедра теоретической и общей элект

Конспект лекций по
электротехнике
Подготовлен:
Степановым К.С., Беловой Л.В.,
Кралиным А.А., Панковой Н.Г.
Кафедра теоретической и общей
электротехники.
Лекция 4

2. Методы расчёта электрических цепей

• 1. По закону Ома.
• 2. По методу суперпозиции.
• 3. По уравнениям Кирхгофа.
• 4. По методу контурных токов.
• 5. По методу узловых потенциалов.
• 6. По методу эквивалентного
двухполюсника.
• 7. По методу компенсации.
• 8. Топологический метод расчёта.

4. Расчёт простых цепей

• Простая цепь – это цепь,
содержащая один и только один
источник энергии.
• Простые цепи рассчитываются при
помощи метода свертывания и
развертывания.

Расчёт идёт по
закону Ома.

5. Пусть требуется определить все токи в такой цепи.

1
R4
R6
R2
R7
R1
R5
R3
E
2
R8

6. Для этого будем упрощать схему в следующей последовательности.

1
R4
R678
R2
R1
E
R5
R3
2
R678=R6(R7+R8)/(R6+R7+R8)

7. R(4-8)= R678(R4+R5)/(R4+R5+R876)

1
R2
R4-8
R1
R3
E
2
R(4-8)= R678(R4+R5)/(R4+R5+R876)
1
R2-8
R1
E
2
R2-8= R(4-8)(R2+R3)/(R2+R3+R(4-8))
E
Rэкв
Rэкв=R1+R2-8
• Тогда токи в ветвях определяются по
следующим формулам:
• I1=E/Rэкв ,
U12=I1 R12
• I2=U12/(R2+R3),
• I3=U12/(R4+R5),
• I5=U12/(R7+R8),
I4=U12/R6

11. Метод наложения или суперпозиции

12. Метод наложения или суперпозиции

• Применяется, когда цепь содержит
несколько источников питания.
• Разветвленная электрическая цепь
с несколькими источниками
питания и все процессы
происходящие в этой цепи можно
рассматривать как совокупность
нескольких цепей в каждой из
которых содержится один и только
один источник питания.

13. Метод наложения или суперпозиции

• При составлении цепей учитывается
правило:
• Если есть идеальный ЭДС (E) с Rвн=0,
то ЭДС заменяется голым проводом.
• Если есть источник тока (J) с Rвн= ,
то он заменяется разрывом цепи.
• Число составных частей ровно числу
источников питания.
• Тогда, общий ток определится как
сумма токов в вышеприведенных
цепях.

14. Пусть требуется определить токи в такой цепи

R2
J5
R3
R5
R1
R4
R6
E1
E4

15. Преобразуем схему к виду 1 и определим токи в ветвях I’1,I’2,I’3,I’4,I’5.

R2
R3
R5
R1
R4
R6
E1

16. Преобразуем схему к виду 2 и определим токи в ветвях I»1,I»2,I»3,I»4,I»5.

R2
R3
R5
R1
R4
R6
E4

17. Преобразуем схему к виду 3 и определим токи в ветвях I»’1,I»’2,I»’3,I»’4,I»’5.

R2
J5
R3
R5
R1
R4
R6
Тогда общие токи в ветвях определятся
как суммы вышерасчитанных частных
токов.

• I1 = I’1+I»1+I»’1;
• I2 = I’2+I»2+I»’2;
• I3 = I’3+I»3+I»’3;
• I4 = I’4+I»4+I»’4;
• I5 = I’5+I»5+I»’5.

19. Расчёт разветвлённых цепей с помощью законов Кирхгофа.

20. Алгоритм расчёта

• 1. Упрощение элементарных
цепей.
• 2. Произвольный выбор
направления и обозначение
токов в ветвях.
• 3. Выбор и расставление
направления обхода
независимых контуров.
(Независимый контур – такой, который
содержит хотя бы одну ветвь,
которая не рассмотрена в других
контурах.)

21. Алгоритм расчёта

• 4. Запись уравнений по первому
закону Кирхгофа. (Число этих урав-
нений на 1 меньше числа узлов. Использовать
все Y уравнений невозможно, т.к. одно из них
обязательно будет зависимым. Это связано с
тем, что токи ветвей войдут в уравнения,
составленные для всех Y узлов, дважды,
причем с разными знаками, т.к. один и тот же
ток направлен от одного узла к другому.

При
сложении всех уравнений левая и правая
части будут равны нулю, а это означает, что
одно из уравнений можно получить
суммированием (Y-1) уравнений и заменой
знаков всех токов на противоположные.
Таким образом Y-е уравнение всегда будет
зависимым).

22. Алгоритм расчёта

• 5. Запись уравнений по 2 закону
Кирхгофа для независимых
контуров.
(Для определения неизвестных токов в
ветвях необходимо составить
уравнения Кирхгофа, количество
которых должно быть равно
количеству неизвестных токов).
• 6. Решение системы уравнений
относительно токов.

23. Пример. Определить токи в ветвях схемы по законам Кирхгофа.

R2
J5
R3
R5
R1
R4
R6
E1
E4

24. 1. Упрощаем элементарные цепи. Для этого преобразуем схему.

R2
J5
R3
R5
R1
R4
R6
E1
E4

25. В этой схеме источник тока J5 заменён на источник эквивалентной ЭДС E5экв (см.

лек.3) 1
I2
R2
2
E5экв
к
кон
R3
R5
R1
I3
I5
кон
I4
R4
R6
E4
E1
I1
3

26. Составим уравнения по первому и второму законам Кирхгофа

• Уравнения по первому закону
Кирхгофа для независимых узлов:
1) I1 – I2 – I5 = 0
2) I2 – I3 – I4 = 0
Уравнения по второму закону
Кирхгофа для независимых
контуров:
3) I1R1 + I5(R5+R6) = E1 + E5экв
4) I2R2 + I3R3 — I5(R5+R6) = -E5экв
5) -I3R3 -I4R4 = -E4

27. Запишем матрицу коэффициентов и столбец свободных членов

|1 –1 0 0 –1
|
|0
|0 1 –1 –1 0
|
|0
|R1 0 0 0 (R5+R6)| =
|E1+E5экв|
|0 R2 R3 0 (R5+R6)| | -E5экв
|0 0 R3 R4 0
| | -E4
Решая эту систему, определим токи
во всех ветвях.
|
|
|
|

28. Благодарю за внимание

Расчет сопротивления цепи

Расчет сопротивления цепи необходим при решении различных задач по электротехнике. Суть заключается в приведении сложной разветвленной электрической цепи к цепи с единственным эквивалентным сопротивлением, которую называют простой электрической цепью.

Пример 1

Цепь в данном примере состоит из двух последовательно соединенных сопротивлений, следовательно, их общее сопротивление будет равно сумме их сопротивлений. Подробнее о видах соединений тут.

Допустим, что R₁=10 Ом R₂=20 Ом, тогда

Пример 2

Два сопротивления соединены параллельно, значит при сворачивании схемы, общее сопротивление будет равно (значения R₁,R₂ такие же как и в примере 1)

Можно заметить, что при параллельном соединении общее сопротивление меньше, чем при последовательном в несколько раз.

Пример 3

В данном примере ситуация аналогична примеру 2, за тем лишь исключением, что сопротивлений три.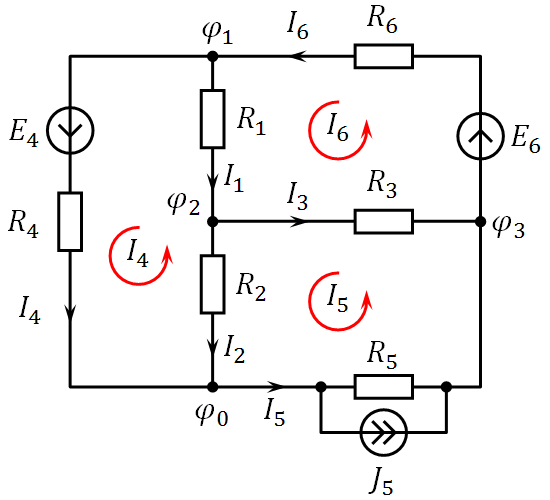 Тогда общее сопротивление будет равно (R₁,R₂ прежние, R₃=105 Ом)

Пример 4

Чтобы рассчитать общее сопротивление смешанного соединения проводников, необходимо для начала найти общее сопротивление резисторов R₁ и R₂ соединенных параллельно, а затем общее сопротивление, как сумму R₁₂ и R₃ соединенных последовательно.

Пример 5

Данная электрическая цепь сложнее, чем предыдущие, но как можно увидеть, она также состоит из последовательно или параллельно соединенных сопротивлений, которые можно постепенно сворачивать, приводя цепь к единственному эквивалентному сопротивлению R.

R₄=20 Ом, R₅=40 Ом, R₆=15 Ом

Путем сворачивания цепи с помощью преобразований последовательно и параллельно соединенных проводников, можно максимально упростить для дальнейшего расчета сколь угодно сложную схему. Исключением служат цепи содержащие сопротивления, соединенные по схеме звезда и треугольник.

2. Схемы электрических цепей и их элементы

На любую машину, в состав которой входят электрические устройства, кроме конструкторских чертежей имеется электродокументация, состоящая из различных электрических схем. Электрические функциональные схемы раскрывают принцип действия устройства. Существуют электромонтажные схемы, в которых раскрывается монтаж (соединение) электрических элементов цепи.

Электрические принципиальные схемы раскрывают электрические связи всех отдельных элементов электрической цепи между собой.

Все схемы вычерчиваются по определенным стандартам- ГОСТам.

Кроме основных электрических схем существуют схемы замещения, по которым наиболее удобно составлять математические уравнения, описания электрических и энергетических процессов. Такие схемы являются эквивалентными моделями электрической цепи. Схемы максимально упрощены и по ним удобнее провести анализ отображаемых ими сложных электрических цепей.

Все элементы электрических цепей можно разделить на три группы: источники (активные элементы), потребители и элементы для передачи электроэнергии от источников к потребителю (пассивные элементы).

Источником электрической энергии (генератором) называют устройство, преобразующее в электроэнергию какой-либо другой вид энергии (электромашинный генератор — механическую, гальванический элемент или аккумулятор — химическую, фотоэлектрическая батарея — лучистую и т.п.). Источники делятся на источники напряжения (Е,U=соnst, при изменении I) и источники тока (I=соnst, при изменении U). Все источники имеют внутреннее сопротивление Rвн, значение которого невелико по сравнению с сопротивлением других элементов электрической цепи.

Приемником электрической энергии (потребителем) называют устройство, преобразующее электроэнергию в какой-либо другой вид энергии (электродвигатель — в механическую, электронагреватель — в тепловую, источник света — в световую (лучистую) и т. п.).

Элементами передачи электроэнергии от источника питания к приемнику служат провода, устройства, обеспечивающие уровень и качество напряжения и др.

Условные обозначения элементов электрической цепи на схеме стандартизованы. Примеры:

контур, схема, расчет, разветвленные и линейные цепи

На чтение 9 мин Просмотров 686 Опубликовано 02.09.2019 Обновлено 29.08.2019

При обустройстве новой квартиры или дома, обновлении или ремонте жилья приходится сталкиваться с элементами, предназначенными для протекания электрического тока. Важно знать, что представляет собой электрическая цепь, из чего она состоит, зачем нужна схема, и какие расчеты необходимо выполнить.

Что такое электрические цепи

Электрической цепью называют совокупность устройств, необходимых для прохождения по ним электрического тока

Электрическая цепь – это комплекс различных элементов, соединенных между собой. Она предназначена для протекания электрического тока, где происходят переходные процессы. Движение электронов обеспечивается наличием разности потенциалов и может быть описано при помощи таких терминов, как напряжение и сила тока.

Внутренняя цепь обеспечивается подключением напряжения, как источника питания. Остальные элементы образуют внешнюю сеть. Для движения зарядов в источнике питания поля потребуется приложение сторонней силы. Это может быть обмотка генератора, трансформатора или гальванический источник.

Чтобы такая система правильно функционировала, ее контур должен быть замкнутый, иначе ток протекать не будет. Это обязательное условие для согласованной работы всех устройств. Не всякий контур может быть электрической цепью. Например, линии заземления или защиты не являются таковыми, поскольку в обычном режиме по ним не проходит ток. Назвать их электрическими можно по принципу действия. В аварийной ситуации по ним проходит ток, а контур замыкается, уходя в грунт.

В зависимости от источника питания напряжение в цепи может быть постоянным или переменным. Батарея элементов дает постоянное напряжение, а обмотки генераторов или трансформаторов – переменное.

Основные компоненты

Инвентор электрического тока

Все составные части в цепи участвуют в одном электромагнитном процессе. Условно их разделяют на три группы.

Первичные источники электрической энергии и сигналов могут преобразовывать энергию неэлектромагнитной природы в электрическую. Например, гальванический элемент, аккумулятор, электромеханический генератор.
Вторичный тип, как на входе, так и на выходе имеет электрическую энергию. Изменяются только ее параметры – напряжение и ток, их форма, величина и частота. Примером могут быть выпрямители, инверторы, трансформаторы.
Потребители активной энергии преобразовывают электрический ток в освещение или тепло. Это электротермические устройства, лампы, резисторы, электродвигатели.
К вспомогательным компонентам относят коммутационные устройства, измерительные приборы, соединительные элементы и провод.

Основой электрической сети является схема. Это графический рисунок, который содержит условные изображения и обозначения элементов и их соединение. Они выполняются согласно ГОСТу 2.721-74 – 2.758-81

Схема простейшей линии включает в себя гальванический элемент. С помощью проводов к нему через выключатель подсоединена лампа накаливания. Для измерения силы тока и напряжения в нее включен вольтметр и амперметр.

Классификация цепей

Электроцепи классифицируют по типу сложности: простые (неразветвленные) и сложные (разветвленные). Есть разделение на цепи постоянного тока и переменного, а также синусоидального и несинусоидального. Исходя из характера элементов, они бывают линейные и нелинейные. Линии переменного тока могут быть однофазными и трехфазными.

Разветвленные и неразветвленные

Во всех элементах неразветвленной цепи течет один и тот же ток. Простейшая разветвленная линия включает в себя три ветви и два узла. В каждой ветви течет свой ток. Ветвь определяют как участок цепи, который образован последовательно соединенными элементами, заключенными между двух узлов. Узел – это точка, в которой сходятся три ветви.

Если на схеме при пересечении двух прямых поставлена точка, в этом месте есть электрическое соединение двух линий. Если узел не обозначен – цепь неразветвленная.

Линейные и нелинейные

Электрическая цепь, в которой потребители не зависят от значения напряжения и направления токов, а все компоненты линейные, называется линейной. К элементам такой цепи относятся зависимые и независимые источники токов и напряжений. В линейной сопротивление элемента не зависит от тока, например, электропечь.

В нелинейной, пассивные элементы зависят от значений направления токов и напряжения, имеют хотя бы один нелинейный элемент. Например, сопротивление лампы накаливания зависит от скачков напряжения и силы тока.

Обозначения элементов на схеме

Прежде чем приступить к монтажу оборудования необходимо изучить нормативные сопровождающие документы. Схема позволяет донести до пользователя полную характеристику изделия с помощью буквенных и графических обозначений, занесенных в единый реестр конструкторской документации.

К чертежу прилагаются дополнительные документы. Их перечень может быть указан в алфавитном порядке с цифровой сортировкой на самом чертеже, либо отдельным листом. Классифицируют десять видов схем, в электротехнике обычно используют три основные схемы.

Функциональная имеет минимальную детализацию. Основные функции узлов изображают прямоугольником с буквенными обозначениями.
Принципиальная схема подробно отображает конструкцию использованных элементов, а также их связи и контакты. Необходимые параметры могут быть отображены непосредственно на схеме или в отдельном документе. Если указана только часть установки, это однолинейная схема, когда указаны все элементы – полная.
В монтажной электрической схеме используют позиционные обозначения элементов, их месторасположение, способ монтажа и очередность.

Для чтения электросхем нужно знать условные графические обозначения. Провода, которые соединяют элементы, изображаются линиями. Сплошная линия – это общее обозначение проводки. Над ней могут быть указаны данные о способе прокладки, материале, напряжении, токе. Для однолинейной схемы группа проводников изображается пунктирной линией. В начале и в конце указывают маркировку провода и место его подключения.

Вертикальные засечки на линии проводки говорят о количестве проводников. Если их более трех, выполняют цифровое обозначение. Прерывистой линией обозначают управляющие цепи, сеть охранного, эвакуационного, аварийного освещения.

Выключатель на схеме выглядит как кружок с наклоненной вправо чертой. По виду и количеству черточек определяют параметры устройства.

Кроме основных чертежей есть схемы замещения.

Трехфазные электрические цепи

Трехфазная цепь в рабочем режиме

Среди электрических цепей распространены как однофазные, так и многофазные системы. Каждая часть многофазной цепи характеризуется одинаковым значением тока и называется фазой. Электротехника различает два понятия этого термина. Первое – непосредственная составляющая трехфазной системы. Второе – величина, изменяющаяся синусоидально.

Трехфазная цепь – это одна из многофазных систем переменного тока, где действуют синусоидальные ЭДС (электродвижущая сила) одинаковой частоты, которые сдвинуты во времени относительно друг друга на определенный фазовый угол. Она образована обмотками трехфазного генератора, тремя приемниками электроэнергии и соединительными проводами.

Такие цепи служат для обеспечения генерации электрической энергии, для ее передачи, распределения, и имеет следующие преимущества:

экономичность выработки и транспортировки электроэнергии в сравнении с однофазной системой;
простое генерирование магнитного поля, которое необходимо для работы трехфазного асинхронного электродвигателя;
одна и та же генераторная установка выдает два эксплуатационных напряжения – линейное и фазное.

Трехфазная система выгодна при передаче электроэнергии на большие расстояния. К тому же материалоемкость значительно ниже, чем однофазных. Основные потребители – трансформаторы, асинхронные электродвигатели, преобразователи, индукционные печи, мощные нагревательные и силовые установки. Среди однофазных маломощных устройств можно отметить электроинструменты, лампы накаливания, бытовые приборы, блоки питания.

Трехфазная схема отличается значительной уравновешенностью системы. Способы соединения фаз получили структуру «звезда» и «треугольник». Обычно «звездой» соединяются фазы генерирующих электромашин, а фазы потребителей «звездой» и «треугольником».

Законы, действующие в электрических цепях

На схемах направление токов указывают стрелками. Для расчета нужно принять направления для напряжений, токов, ЭДС. При расчетах в электротехнике используют следующие основные законы:

Закон Ома для прямолинейного участка цепи, который определяет связь между электродвижущей силой, напряжением источника с протекающей в проводнике силой тока и сопротивлением самого проводника.
Чтобы найти все токи и напряжения, используют правила Кирхгофа, которые действуют между токами и напряжениями любого участка электрической цепи.
Закон Джоуля–Ленца дает количественную оценку теплового действия электрического тока.

В цепях постоянного тока направление действия электродвижущей силы указывают от отрицательного потенциала к положительному. За направление принимают движение положительных зарядов. При этом стрелка направлена от большего потенциала к меньшему. Напряжение всегда направлено в ту сторону, что и ток.

В синусоидальных цепях ЭДС, напряжение и ток обозначают, используя полупериод тока, при этом он не изменяет свое направление. Чтобы подчеркнуть разницу потенциалов, их обозначают знаками «+» и «–».

Как производится расчет электрических цепей

Путь вычисления делится на множество способов, которые используются на практике:

метод, основанный на законе Ома и правилах Кирхгофа;
способ определения контурных токов;
прием эквивалентных преобразований;
методика измерений сопротивлений защитных проводников;
расчет узловых потенциалов;
метод идентичного генератора, и другие.

Основа расчета простой электрической цепи по закону Ома – это определение силы тока в отдельном участке при известном сопротивлении проводников и заданном напряжении.

По условию задачи известны сопротивления подсоединенных к цепи резисторов R1, R2, R3, R4, R5, R6 (без учета сопротивления амперметра). Необходимо вычислить силу токов J1, J2…J6.

На схеме есть три последовательных участка. Причем второй и третий имеют разветвления. Сопротивления этих участков обозначим, как R1, R’, R”. Тогда общее сопротивление равно сумме сопротивлений:

R = R1 + R’ + R”, где

R’ – общее сопротивление параллельно подключенных резисторов R2, R3, R4.

R” – общее сопротивление резисторов R5 и R6.

Используя закон параллельного соединения, вычисляем сопротивления R’ и R”.

1/R’ = 1/R2 + 1/R3 + 1/R4

1/R” = 1/R5 + 1/R6

Определить силу тока в неразветвленной цепи, зная общее сопротивление при заданном напряжении, можно по следующей формуле:

I = U/R, тогда I = I1

Для вычисления силы тока в отдельно взятых ветвях, нужно определить напряжение на участках последовательных цепей по закону Ома:

U1 = IR1; U2 = IR’; U3 = IR”;

Зная напряжение конкретных участков, можно вычислить силу тока на отдельных ветвях:

I2 = U2/R2; I3 = U2/R3; I4 = U2/R4; I5 = U3/R5; I6 = U3/R6

Иногда необходимо узнать сопротивление участков по известным параметрам напряжения, силы токов, сопротивления других участков или сделать расчет напряжения по имеющимся данным сопротивления и силе тока.

Основная часть методик направлена на упрощение расчетов. Это достигается адаптацией систем уравнений, либо самой схемы. Расчет электрических цепей производится различными способами, в зависимости от класса их сложности.

Литература по ТОЭ, учебники по ТОЭ, методички по ТОЭ, задачники по ТОЭ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ к контрольным работам по дисциплине: «Электротехника и электроника» для студентов неэлектрических специальностей очной и заочной форм обучения

ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ ИНСТИТУТ КИБЕРНЕТИКИ, ИНФОРМАТИКИ И СВЯЗИ

КАФЕДРА ЭЛЕКТРОЭНЕРГЕТИКИ

Тюмень 2011

ЗАДАНИЯ ДЛЯ РАСЧЕТНО-ГРАФИЧЕСКИХ РАБОТ

3.1. Расчетно-графическая работа №1

Расчет разветвленных электрических цепей

Задание 1 Решить методом эквивалентных преобразований

Задание 2 Решить методом применения законов Кирхгофа

Задание 3 Решить методом контурных токов

Задание 4 Решить методом узловых напряжений

3.2. Расчетно-графическая работа №2

Расчет электрических цепей переменного тока

Задание 1 Рассчитать однофазную электрическую цепь с последовательным соединением элементов

Задание 2 Рассчитать однофазную электрическую цепь с параллельным соединением элементов

Задание 3 Рассчитать трехфазную электрическую цепь при соединении фаз приемника треугольником

Задание 4 Рассчитать трехфазную электрическую цепь при соединении фаз приемника звездой

3.3. Расчетно-графическая работа №3

Расчет режимов работы электрических машин

Задание 1 Рассчитать параметры трехфазного трансформатора

Задание 2 Рассчитать режимы работы двигателя постоянного тока

Задание 3 Рассчитать режимы работы трехфазного асинхронного двигателя

Задание 4 Рассчитать режимы работы синхронного электродвигателя

Скачать МЕТОДИЧЕСКИЕ УКАЗАНИЯ к контрольным работам по дисциплине: «Электротехника и электроника» для студентов неэлектрических специальностей очной и заочной форм обучения Тюмень 2011 eie-muk-i-kz-tyumgngu-2011.pdf [631,22 Kb] (cкачиваний: 446)

Электротехника КР

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное

учреждение высшего профессионального образования

«Ивановский государственный энергетический университет

имени В.И. Ленина»

Кафедра ТОЭЭ

Контрольная работа

«Технические Основы Электротехники»

Вариант №02

Выполнил: студент гр. 3-75^х

Беляев А.Н.

Иваново 2015.

Содержание

Задача 1. Методы расчета электрических цепей постоянного тока.	3
Задача 2. Расчет однофазных линейных электрических цепей переменного тока.	8
Задача 3. Расчет линейных электрических цепей при несинусоидальных токах и напряжениях.	15
Задача 4. Расчет трехфазных электрических цепей.	24

Задача 1. Методы расчета электрических цепей постоянного тока.

Задание:

Упростить схему до двухконтурной.
Рассчитать потенциал независимого узла относительно узла 0 по методу узловых потенциалов.
Заменить источник тока эквивалентным источником напряжения.
Рассчитать токи в преобразованной схеме методом контурных токов.
Определить ток в ветви, не содержащей активных элементов по методу эквивалентного генератора.
Проверить решение по балансу мощностей.

Исходные данные:

R₁,

Ом

R₂,

Ом

R₃,

Ом

R₄,

Ом

R₅,

Ом

R₆,

Ом

Решение:

Для того чтобы преобразовать эту схему в двухконтурную, заменим треугольник, состоящий из резисторов R₁, R₂, R₃ эквивалентной звездой (R₁₂, R₂₃, R₁₃).

По известным формулам преобразования треугольника в звезду определим:

В данной схеме независимым принимаем узел 4.

Уравнение, составленное по методу узловых потенциалов, будет следующим:

Из этого уравнения после расчетов получаем потенциал

Преобразование источника ток в источник напряжения проводится по формуле

Для решения задачи методом контурных токов необходимо выбрать (произвольно) направления токов в ветвях (I₁, I₂, I₃) и направления контурных токов (I₁₁ и I₂₂).

Система уравнений по методу контурных токов составляется по второму закону Киргофа и выглядит следующим образом:

Решая систему относительно I₁₁ и I₂₂, получаем I₁₁= 1.6 А, I₂₂ = 0.776 А.

Определяем токи в ветвях:

I₁ = I₁₁ = 1.6 А

I₂ = I₁₁ – I₂₂ = 1.6 – 0.776 = 0.824 А

I₃ = I₂₂ = 0.776 А

Для определения тока в ветви, содержащей резисторы R₆ и R₁₂, необходимо всю схему по отношению к данной ветви представить в виде эквивалентного генератора, содержащего эквивалентную ЭДС – E_э и эквивалентное сопротивление – R_э.

В этом случае ток I₁ можно определить как:

Для расчета E_э проведем опыт холостого хода. Уберем исследуемую цепь и определим напряжение холостого хода U_хх.

Определим сопротивление по отношению к точкам 0 – 1. Это будет R_э.

Получаем:

Проверка решения по балансу мощностей сводится к решению уравнения вида:

В правой части уравнения необходимо цчитывать режим работы источника ЭДС. Если источник работает в режиме потребителя, он учитывается со знаком (-), в генераторном режиме знак – (+).

При решении баланса мощностей:

Таким образом, баланс мощностей сошелся, что указывает о правильности проведенного решения задачи.

Задача 2. Расчет однофазных линейных электрических цепей переменного тока.

Задание:

Определить сопротивления элементов электрической цепи.
По заданному напряжению между двумя точками рассчитать действующее значение тока.
Определить напряжение на всех элементах электрической цепи.
Рассчитать ЭДС источника электрической энергии.
Включить в схему электрической цепи вольтметр электромагнитной системы и рассчитать его показания.
Построить временные зависимости e(t) и i(t).
Проверить расчет по балансу мощности.
Построить потенциальную (топографическую) диаграмму напряжений.

Исходные данные:

R₁,

Ом

R₂,

Ом

R₃,

Ом

L₃,

мГн

C₂,

мкФ

Гц

U_mn,

9,7

6,8

95,5

9,1

100

U₃₅ = 75 В

Решение:

Определим активные и реактивные сопротивления схемы замещения.

Для резисторов:

R₁ = 9,7 Ом, R₂ = 6,8 Ом, R₃ = 12 Ом.

Сопротивление катушки индуктивности и конденсатора рассчитываются по формулам:

Комплексное сопротивление катушки индуктивности всегда мнимое положительное:

Комплексное сопротивление конденсатора также мнимое, но отрицательное:

Для расчета тока найдем сопротивление Z₃₅, к которому приложено напряжение U₃₅:

Поскольку начальная фаза напряжения не задана, то примем ее равной нулю. То есть комплекс действующего напряжения между точками 3-5:

По закону Ома ток, протекающий по R₂ и C₂,

При последовательном соединении всех элементов электрической цепи ток во всех ее элементах будет один и тот же, т.е.

Используя закон Ома, рассчитаем напряжения на всех элементах электрической цепи и представим их в показательной и алгебраической формах:

По второму закону Киргофа алгебраическая сумма напряжений на всех пассивных элементах замкнутого контура электрической цепи равна алгебраической сумме ЭДС источников в этом контуре. Поскольку у нас один контур, ток направлен во всех элементах электрической цепи в одном направлении и имеется один источник ЭДС, то ее величина будет равна просто сумме напряжений на всех участках цепи. Удобнее суммировать комплексные числа в алгебраической форме. Тогда:

ЭДС источника в электрической цепи с последовательным соединением элементов может быть также найдена по закону Ома как произведение суммарного сопротивления цепи и протекающего по ней тока. Суммарное сопротивление электрической цепи:

Тогда

Рассчитаем показание вольтметра, подключенного к точкам 4 – 6. Поскольку вольтметр электромагнитной системы показывает действующее значение напряжения, то оно может быть определено по закону Ома как произведение полного сопротивления участка цепи между точками 4 – 6 и протекающего тока. Полное сопротивление этого участка цепи определяется формулой:

Действующее значение тока равно I = 0,43 А. Тогда показание вольтметра :

Для построения временных зависимостей e(t) и i(t) перейдем от комплексов действующих значений этих величин к их мгновенным значениям. Амплитуда синусоид в раз больше действующего значения. Найдем амплитуды ЭДС и тока:

Угловая частота синусоид связана с частотой переменного тока f соотношением:

Мгновенные значения ЭДС источника и ток будут изменяться синусоидально во времени в соответствии с формулами:

где и — начальные фазы ЭДС и тока, рассчитанные ранее для комплексных значений этих величин.

Графики изменения мгновенных значений ЭДС и тока в функции времени:

Баланс мощности в электрических цепях заключается в равенстве сумм активной и реактивной мощностей всех источников и приемников электрической энергии:

где и — сумма активных и реактивных мощностей всех источников энергии электрической цепи;

и — сумма активных и реактивных мощностей всех приемников энергии электрической цепи.

Для источника активная мощность определяется формулой:

Поскольку в задаче один источник, то его мощность:

Активную мощность потребляют только резисторы, поэтому

Погрешность баланса активной мощности:

Реактивная мощность источника определяется формулой:

Реактивную мощность потребляют реактивные элементы электрической цепи – катушки индуктивности и конденсаторы. Для каждого реактивного элемента реактивная мощность определяется формулой:

при этом сопротивление реактивного элемента (X_К) берется положительным для катушек индуктивности и отрицательным для конденсаторов.

В нашем случае:

Полученные значения показывают, что проведенный ранее расчет выполнен достаточно точно.

Потенциальная (топографическая) диаграмма напряжений – это совокупность точек на комплексной плоскости, каждая из которых соответствует потенциалу точки электрической цепи относительно точки, потенциал которой равен нулю. То есть необходимо принять потенциал одной из точек электрической цепи равным нулю. Выбор этой точки произволен. Однако для того, чтобы иметь всю диаграмму, сориентированную по току, при расчёте потенциалов надо двигаться против тока. Поэтому в нашей задаче рационально приравнять к нулю потенциал точки 6 (. Тогда потенциал точки 5 будет выше потенциала точки 6 на величину напряжения на резисторе R₃(ток течет от большего потенциала к меньшему). То есть

Аналогично потенциал точки 4 будет выше потенциала точки 5 на величину напряжения на конденсаторе C₂:

Расчет потенциалов остальных точек электрической цепи аналогичен:

Потенциальную диаграмму можно строить и не рассчитывая потенциалы всех точек. Для этого необходимо к потенциалу предыдущей точки прибавлять в масштабе отрезок, соответствующий комплексному значению напряжения на последующем элементе схемы электрической цепи.

При этом следует сначала построить на комплексной плоскости в своем масштабе вектор тока и затем откладывать отрезки, пропорциональные напряжениям на элементах электрической цепи, с учетом их сдвига относительно тока.

Векторная диаграмма тока и потенциальная диаграмма напряжений электрической цепи.

Удобство потенциальной диаграммы в том, что с ее помощью можно определить напряжение между любыми двумя точками электрической цепи. Например, измерив отрезок между точками 4 и 6, можно, использовав масштаб, определить напряжение на зажимах вольтметра V.

Задача 3. Расчет линейных электрических цепей при несинусоидальных токах и напряжениях.

К электрической цепи приложено несинусоидальное напряжение, представленное в виде гармонического ряда:

Исходные данные:

U₀,

U_m1,

U_m3,

ψ_U1

ψ_U3

f₍₁₎,

Гц

R₁,

Ом

R₃,

Ом

L₃,

мГн

C₁,

мкФ

C₂,

мкФ

300

10 º

70 º

100

95,5

30,04

25,28

Задание:

Записать выражение для приложенного к электрической цепи напряжения в соответствии с исходными данными.
Определить сопротивления пассивных двухполюсников электрической цепи для каждой из гармоник.
Рассчитать комплексные сопротивления всех ветвей электрической цепи для каждой из гармоник.
По заданному напряжению и сопротивлению элементов рассчитать мгновенные значения токов во всех ветвях i₁(t), i₂(t), i₃(t) и общий ток i(t).
Построить графики мгновенных значений напряжения u(t) и тока i(t).
Рассчитать показания амперметра и вольтметра электромагнитной системы и ваттметра электродинамической системы.

Решение:

Рассчитаем угловую частоту для первой гармоники:

Угловая частота третьей гармоники напряжения

Приложенное к электрической цепи напряжение будет иметь вид:

То есть приложенное к электрической цепи напряжение содержит:

третью гармонику с частотой, в три раза большей, f₍₃₎ = 300 Гц (3 = 1884 1/с),

Определение сопротивлений элементов электрической цепи для каждой из гармоник проводится в соответствии со следующими положениями:

R₁ = 50 Ом, R₃ = 55 Ом;

поскольку частота постоянного тока равна нулю (f = 0), то и сопротивление катушки индуктивности постоянному току также рано нулю:

сопротивление катушки индуктивности:

сопротивления конденсаторов:

сопротивление катушки индуктивности:

сопротивления конденсаторов:

Все приведенные расчеты сведем в таблицу:

Элемент цепи	Единица измерения	Постоянная составляющая f = 0	Первая гармоника f = 100 Гц	Третья гармоника f = 300 Гц
R₁	Ом	50	50	50
R₃	Ом	55	55	55
X_L3	Ом	0	60	180
X_C1	Ом		53	17,7
X_C2	Ом		63	21

Упростите резистивные сети | Прядильные числа

Сложные резистивные схемы можно упростить, найдя последовательные и параллельные комбинации резисторов в контексте более крупной схемы.

Содержание

Вот пример схемы, над которой мы будем работать вместе,

Мы видим источник напряжения, подключенный к сети резисторов. Два маленьких кружка у левого края представляют порт резисторной сети.

Выясните, какой ток $ (i) $ требуется источнику напряжения для подачи в сеть резисторов.

Ответ очевиден не сразу. Но в нашем распоряжении есть несколько инструментов: мы знаем, как вычислить эквивалентное сопротивление последовательных и параллельных резисторов. С помощью этих инструментов мы можем упростить схему резисторов до тех пор, пока проблема не станет легко решаемой.

На этом этапе попробуйте решить проблему самостоятельно. Попробовав, продолжайте читать, чтобы увидеть, как разворачивается решение.

Обновите свои представления о последовательных и параллельных резисторах.

Стратегия

Вот общая стратегия упрощения любой сети резисторов,

Начните как можно дальше от рассматриваемого участка цепи.
Определите и замените комбинации последовательно или параллельно подключенных резисторов их эквивалентными резисторами.
Продолжайте движение, пока один эквивалентный резистор не представит всю сеть резисторов.

Пошаговое решение к примеру

Исходный вопрос задан про ток от источника напряжения.Таким образом, «рассматриваемое место» находится рядом с источником напряжения на дальнем левом конце цепи. Поэтому мы начинаем процесс упрощения с крайнего правого угла и возвращаемся к источнику.

Упрощение схемы — это процесс, состоящий из множества небольших шагов. Рассмотрите небольшой фрагмент схемы, упростите его и перейдите к следующему фрагменту. Совет: перерисовывайте схему после каждого шага, чтобы не упустить возможность упростить.

Шаг 1. Закрашенные резисторы $ 2 \, \ Omega $ и $ 8 \, \ Omega $ включены последовательно.

Если посмотреть на заштрихованную область со стороны стрелок, два последовательных резистора эквивалентны одному резистору с сопротивлением ______ $ \ Omega $.

подсказка

Эти два резистора включены последовательно, поэтому мы складываем их два сопротивления, чтобы получить эквивалентное последовательное сопротивление.

показать ответ

$ 2 \, \ Omega + 8 \, \ Omega = 10 \, \ Omega $

Два резистора можно заменить эквивалентным сопротивлением

Ключевые выводы: С внешней стороны заштрихованной рамки два исходных последовательных резистора и эквивалентный резистор неотличимы друг от друга.В обеих версиях одинаковы ток и напряжение.

Шаг 2. Теперь мы находим два резистора $ 10 \, \ Omega $, включенных параллельно в новом крайнем правом углу схемы.

Эти два резистора можно заменить их параллельной комбинацией.

Результирующий эквивалентный резистор: ______ $ \ Omega $.

показать ответ

$ 10 \, \ Omega \ parallel 10 \, \ Omega = \ dfrac {10 \ cdot 10} {10 + 10} = 5 \, \ Omega $

Обозначение $ \ parallel $ означает «параллельно с».

Опять же, если посмотреть в заштрихованный прямоугольник слева, ток и напряжение с эквивалентным резистором $ 5 \, \ Omega $ по-прежнему неотличимы от всего оригинала.

Шаг 3. Вы видите, как возникает закономерность? Мы прорабатываем схему справа налево, упрощая и перерисовывая по мере продвижения. Далее мы находим два последовательных резистора, $ 1 \, \ Omega $ и $ 5 \, \ Omega $.

Резисторы этой серии можно заменить эквивалентным сопротивлением: ______ $ \ Omega $.

показать ответ

$ 1 \, \ Omega + 5 \, \ Omega = 6 \, \ Omega $

Шаг 4. Этот шаг немного сложнее. У нас есть три резистора параллельно.

Эти три резистора можно заменить их параллельной комбинацией.

Результирующий эквивалентный резистор: ______ $ \ Omega $.

подсказка

Поскольку у нас есть три параллельных резистора, используйте уравнение полного параллельного резистора,

$ \ dfrac {1} {\ text R _ {\ text {parallel}}} = \ dfrac {1} {\ text {R1}} + \ dfrac {1} {\ text {R2}} + \ dfrac {1 } {\ text {R3}}

долл. США покажи ответ

$ \ dfrac {1} {\ text R _ {\ text {parallel}}} = \ left (\ dfrac {1} {12 \, \ Omega} + \ dfrac {1} {4 \, \ Omega} + \ dfrac {1} {6 \, \ Omega} \ right) = \ left (\ dfrac {1} {12} + \ dfrac {3} {12} + \ dfrac {2} {12} \ right) = \ dfrac {1} {2}

долл. США

Таким образом, эквивалентное сопротивление является обратной величиной $ \ dfrac {1} {2} $ или $ 2 \, \ Omega $.

Шаг 5. Мы подошли к двум последним резисторам серии,

Вы можете сделать это в уме,

Остался единственный резистор $ 3 \, \ Omega $. Насколько может судить источник напряжения, этот резистор эквивалентен всей сети резисторов.

Чтобы ответить на вопрос: Источник напряжения должен обеспечивать ток

$ i = \ dfrac {\ text V} {3 \, \ Omega}

Вы начали с резисторов за 7 долларов и упростили до 1 доллара, что значительно снижает сложность.Отличная работа.

Не все упрощения сводятся к одному резистору в конце. (Схема не может состоять полностью из резисторов.) Но всегда пользуйтесь возможностью упростить, если представится такая возможность.

Ради удовольствия, вот анимация процесса упрощения,

Исключения

Определенные конфигурации резисторов нельзя упростить, используя описанную выше стратегию. Мы относимся к ним как к особому случаю.Примеры описаны в следующей статье о преобразовании Delta Wye).

Сводка

Ключевая идея: Стратегия упрощения состоит в том, чтобы начать в точке цепи, наиболее удаленной от интересующего компонента .

В этом примере нас спросили о токовой нагрузке на источник напряжения в крайнем левом углу, поэтому мы начали с дальнего правого конца схемы и пошли «назад» влево.

Работа в этом «обратном» направлении может поначалу казаться неловкой, учитывая, что у многих из нас есть укоренившаяся привычка читать слева направо.В электронике принято начинать анализ, начиная с выходного конца схемы (который обычно отображается в правой части страницы), и возвращаться к входу. Наше предвзятое чтение слева направо может мешать. Вы можете сказать, что «превращаетесь в инженера», когда вам станет комфортно работать в этом обратном направлении.

Определение анализа эквивалентных цепей | Chegg.com

Анализ эквивалентной схемы — это «анализ, упрощающий сложную электрическую схему до эквивалентной упрощенной схемы».
В общем, электрическая цепь состоит из нескольких компонентов, таких как активные элементы (источники напряжения и тока), пассивные элементы (конденсатор, катушка индуктивности и резистор), линейные или нелинейные элементы, односторонние или двусторонние элементы и т. Д. Если электрическая схема состоит из нелинейных компонентов, анализ схемы становится сложным. Поэтому нелинейные компоненты обычно рассматриваются как эквивалентные линейные компоненты при анализе эквивалентной схемы, чтобы упростить сложную схему.
Анализ эквивалентной схемы помогает понять и проанализировать сложную электрическую схему простым и легким способом. Анализ эквивалентной схемы используется для анализа характеристик электрических машин, таких как машины постоянного тока (двигатели постоянного тока и генераторы постоянного тока) и машины переменного тока (трансформаторы, двигатели переменного тока и генераторы переменного тока).
Анализ эквивалентной схемы используется для определения требуемых параметров в цепи, таких как ток в конкретной ветви, напряжение в конкретном узле, падение напряжения на любом компоненте, а также подача или потеря мощности любым компонентом.Сложные электрические схемы упрощаются различными теоремами, такими как теорема Тевенина, теорема Нортона, теорема замещения и теорема Миллмана.
В анализе эквивалентной схемы Нортона вся схема упрощается до эквивалентной эквивалентной схемы Нортона. Эквивалентная схема Нортона состоит из тока Нортона (тока короткого замыкания через нагрузку), параллельного эквивалентному сопротивлению Нортона.
Для чего нужна схема замещения?
Анализ эквивалентной схемы играет жизненно важную роль в упрощении сложной электрической схемы.Эквивалентная схема используется для различных целей в электротехнике следующим образом:

Эквивалентная схема очень полезна для анализа электрических устройств или сложных электрических цепей.
Он используется для прогнозирования поведения электрического устройства.
Используется для понимания работы электрической схемы.
Он используется для понимания характеристик цепей и электрических машин.
Анализ эквивалентной схемы помогает узнать поведение электрической схемы без использования компонентов в реальном времени.То есть помогает теоретически анализировать схемы.
Анализ эквивалентной схемы экономит время и усилия при выполнении схемы в системах реального времени.

Поскольку анализ эквивалентной схемы во многом помогает при анализе схем, он наиболее часто используется в электротехнике.
Как сделать эквивалентную схему?
Эквивалентная упрощенная схема может быть получена из исходной сложной схемы, рассмотрев определенные процедуры следующим образом:
Считайте, что резисторы соединены последовательно.Выражение для эквивалентного сопротивления резисторов N получается следующим образом:

Здесь
— сопротивления отдельных резисторов, а
— эквивалентное сопротивление.
Считайте, что индукторы соединены последовательно. Выражение для эквивалентной индуктивности индукторов N получается следующим образом:

Здесь
— индуктивности отдельных индукторов, а
— эквивалентная индуктивность.
Считайте, что конденсаторы включены последовательно.Выражение для эквивалентной емкости конденсаторов N получается следующим образом:

Здесь
— емкости отдельных конденсаторов, а
— эквивалентная емкость.
Считайте, что резисторы включены параллельно. Выражение для эквивалентного сопротивления резисторов Н, получается следующим образом:

Рассмотрим, катушки индуктивности соединены параллельно. Выражение для эквивалентной индуктивности индукторов Н, получается следующим образом:

Рассмотрим конденсаторы, соединенные последовательно.Выражение для эквивалентной емкости конденсаторов Н, получается следующим образом:

Процедура преобразования звезды в треугольник или из треугольника в звезду используется для упрощения сопротивления в сложной цепи. Теоремы Тевенина и Нортона также используются для упрощения схемы.
Что такое эквивалентная схема Тевенина?
При анализе эквивалентной схемы Тевенина вся схема упрощается до эквивалентной эквивалентной схемы Тевенина. Эквивалентная схема Тевенина состоит из напряжения Тевенина, включенного последовательно с эквивалентным сопротивлением Тевенина.Напряжение Тевенина — это напряжение холостого хода на нагрузке.
Процедура расчета сопротивления Тевенина следующая:

Разомкните источники тока в цепи.
Замкните накоротко источники напряжения в цепи.
Найдите эквивалентное сопротивление нагрузки, которое является сопротивлением Тевенина.

Рассмотрим пример, чтобы понять эквивалентную схему Тевенина следующим образом:
Рассмотрим схему, показанную на рисунке 1.

Считайте сопротивление сопротивлением нагрузки и найдите эквивалентное сопротивление Тевенина следующим образом:
Измените схему, открыв цепь источника тока 2 А и замкнув накоротко источник напряжения 20 В, чтобы найти сопротивление Тевенина, как показано на рисунке 2.

Из На рис. 2 сопротивление Тевенина получается следующим образом:

В данной схеме, чтобы найти напряжение Тевенина, снимите нагрузочный резистор на клеммах ab.
Модифицированная схема показана на рисунке 3.

На рисунке 3 напряжение на резисторе 5 Ом рассчитывается с использованием закона Ома следующим образом:

На рисунке 3 напряжение на резисторе 10 Ом рассчитывается с использованием принципа деления напряжения следующим образом:

На рисунке 3 применяется Закон напряжения Кирхгофа и запишите выражение в терминах напряжения Тевенина следующим образом:

Замените на и для, чтобы найти напряжение Тевенина в вольтах.

Согласно анализу, напряжение Тевенина равно 0 В, а сопротивление Тевенина равно.

Таким образом, эквивалентная схема Тевенина для схемы на Рисунке 1 изображена, как показано на Рисунке 4.

Как использовать теорему Тевенина | ОРЕЛ

Существует множество методов, доступных для анализа сложных электрических цепей, например, анализ сетки, узловой анализ или законы Кирхгофа для цепей. Проблема в том, что при проектировании сети постоянного тока у вас будет нагрузка, значение которой будет меняться по мере развития процесса проектирования. Вместо того, чтобы пересчитывать ток и напряжение всей вашей цепи каждый раз при изменении нагрузки, вы можете упростить этот процесс с помощью теоремы Тевенина.В этом блоге мы рассмотрим, как упростить любую сложную линейную схему до единого источника напряжения и последовательного сопротивления. Оттуда мы можем использовать нашу эквивалентную схему Тевенина для быстрого расчета тока и напряжения. Давайте начнем.

Что такое теорема Тевенина?

Как и все другие математические и научные теории / законы, теорема Тевенина была изобретена самим человеком, Леоном Шарлем Тевенином, французским телеграфным инженером, родившимся в Мо, Франция. После службы в корпусе инженеров-телеграфистов Тевенин был назначен инспектором по обучению в Высшей школе телеграфии в 1882 году.Именно здесь он заинтересовался измерением электрических цепей двумя доступными в то время методами — Законом Кирхгофа и Законом Ома.

Леон Шарль Тевенин (Источник изображения)

Стремясь упростить анализ сложных схем для каждого инженера, Тевенин разработал свою теперь известную теорему Тевенина, которая сводит сложные схемы к упрощенным эквивалентным схемам Тевенина.

Эта теорема утверждает, что вы можете взять любую линейную схему, которая может содержать несколько ЭДС и резистивных компонентов, и упростить схему до одного источника напряжения и последовательного сопротивления, подключенного к нагрузке.

Упрощенная эквивалентная схема Тевенина с одним источником напряжения и сопротивлением. (Источник изображения)

В данном случае линейная цепь — это цепь, которая включает в себя пассивные компоненты, такие как резисторы, катушки индуктивности и конденсаторы. Однако если вы работаете со схемой, которая включает газоразрядные или полупроводниковые компоненты, то у вас нелинейная схема. Теорема Тевенина не для этого годилась. Так зачем использовать эту теорему для анализа линейных цепей?

КПД .Теорема Тевенина обеспечивает простой метод анализа силовых цепей, в которых обычно есть нагрузка, которая меняет значение в процессе анализа. Эта теорема обеспечивает эффективный способ вычисления напряжения и тока, протекающих через нагрузку, без необходимости заново рассчитывать всю схему.
Фокус . Теорема Тевенина также предоставляет эффективный способ сосредоточить анализ на определенной части схемы. Это позволяет вам рассчитать напряжение и ток на конкретном терминале, упростив остальную часть схемы с помощью эквивалента Тевенина.

Посмотрите на приведенный ниже пример схемы. Здесь у нас есть резистор R2 в качестве нагрузки. Мы хотим рассчитать напряжение и ток, протекающие через этот резистор, без необходимости использовать трудоемкие методы анализа, такие как Branch Current, Mesh Current и т. Д., Каждый раз, когда изменяется значение резистора нагрузки.

(Источник изображения)

Чтобы упростить эту задачу, мы можем использовать теорему Тевенина, чтобы удалить сопротивление нагрузки и напряжения. Затем мы упрощаем остальную часть схемы как единый источник напряжения и последовательное сопротивление.В этой упрощенной схеме Тевенина два резистора R1 и R3 вместе с вторичным напряжением B2 упрощены до единого источника напряжения и последовательного сопротивления. Что касается нагрузочного резистора, то упрощенные напряжение и сопротивление будут работать так же, как и наша оригинальная схема. Теперь у нас есть только две простые переменные, с которыми мы будем работать в наших расчетах.

(Источник изображения)

Теорема Тевенина в действии

Давайте посмотрим на пример схемы и вычислим ток, протекающий через нагрузочный резистор между двумя выводами.Процесс анализа цепи постоянного тока с использованием теоремы Тевенина требует следующих шагов:

Найдите сопротивление Тевенину, отключив все источники напряжения и нагрузочный резистор.
Найдите напряжение Thevenin, подключив напряжение.
Используйте сопротивление и напряжение Тевенина, чтобы найти ток, протекающий через нагрузку.

Вот пример схемы, с которой мы будем работать:

(Источник изображения)

Шаг 1 — Thevenin Resistance

Сначала нам нужно снять нагрузочный резистор 40 Ом, соединяющий клеммы A и B, вместе со всеми источниками напряжения.Это даст нам разомкнутую цепь при нулевом напряжении, в результате чего останется только два резистора, подключенных последовательно.

(Источник изображения)

Чтобы рассчитать общее сопротивление тевенину, мы можем использовать следующий процесс:

Шаг 2 — Напряжение Thevenin

Затем мы можем использовать закон Ома для вычисления полного тока, протекающего по цепи, следующим образом:

Поскольку эти резисторы соединены последовательно, они будут иметь одинаковый 0.33 ампера. Мы можем использовать эти значения резисторов и наш ток для расчета падения напряжения, которое составляет:

Шаг 3 — Ток нагрузки

Теперь, когда у нас есть сопротивление и напряжение Тевенина, мы можем соединить эквивалентную схему Тевенина с нашим исходным нагрузочным резистором, как показано ниже.

Отсюда мы можем использовать закон Ома для расчета полного тока, протекающего через нагрузочный резистор, следующим образом:

Готовы проверить свои навыки? Используйте теорему Тевенина, чтобы найти iload и vload для схемы ниже!

Запомните трехэтапный процесс:

Найдите сопротивление Тевенину, отключив все источники напряжения и нагрузку.
Найдите напряжение Thevenin, повторно подключив источники напряжения.
Используйте сопротивление и напряжение Тевенина, чтобы найти полный ток, протекающий через нагрузку.

Сохраняйте простоту

Планируете разработать схему питания постоянного тока? Скорее всего, вы включите нагрузку, значение которой изменится во время анализа схемы. Вместо того, чтобы пересчитывать всю схему каждый раз, когда вы меняете значение этой нагрузки, теперь у вас есть теорема Тевенина, которая упрощает вашу работу.

Эта теорема позволяет вам взять любую сложную линейную схему с множеством резистивных компонентов и ЭДС и упростить ее до эквивалентной схемы Тевенина. С помощью этой упрощенной схемы вы можете легко рассчитать общий ток и напряжение, протекающие через нагрузку. Это огромная экономия времени для любого инженера, которому необходимо эффективно анализировать схемы для силовых схем и других сложных приложений.

Тем из вас, кто изучает визуальное и кинестетическое мышление, обязательно посмотрите видео ниже, в котором показано, как использовать теорему Тевенина шаг за шагом.

Готовы спроектировать свою первую силовую цепь? Попробуйте Autodesk EAGLE бесплатно сегодня!

Программное обеспечение для электротехники — математическое программное обеспечение для инженеров-электриков

Capture Design Intent

Документ Maple объединяет в себе живую математику, текст, изображения и графики в одном документе. Фактически, Maple фиксирует внутренние допущения и мыслительный процесс, стоящий за анализом, а также вычислениями.

Подробнее Среда технической документации Maple

Символьная и числовая математика высокого уровня

Maple предлагает практичные высокоуровневые инструменты для числовой и символьной математики, анализа данных и программирования.Эти инструменты предназначены как для простых, так и для сложных инженерных задач.

Численное решение уравнений для согласования заглушек
Символическое манипулирование передаточными функциями, возникающими в результате анализа цепей

Символьные и числовые математические механизмы полностью связаны; параметры, уравнения и вычисления могут плавно перемещаться между ними. Это означает, что вы можете выводить и численно оценивать свои уравнения в рамках единого согласованного рабочего процесса.

Кроме того, язык программирования Maple обладает преимуществами интерактивной среды разработки и может использовать любые математические инструменты высокого уровня Maple.

Код быстрее разрабатывать, отлаживать и проверять
Может использовать математические функции высокого уровня Maple, а
Люди легче читают

Снизьте расчетный риск с помощью единиц измерения

Почти каждая величина, с которой сталкивается инженер-электрик — будь то сопротивление, напряжение или длина — имеет единицу измерения.Единицы плавно интегрированы в Maple и могут использоваться в простых вычислениях, а также для решения числовых уравнений, оптимизации и визуализации.

вольт: = 5,2 В:
ток: = 3,2 А:
мощность: = ток вольт = 16,64 Вт

Использование единиц измерения в вычислениях устраняет риск появления ошибок преобразования единиц измерения, а также действует как проверка физической достоверности уравнений.

2 подхода к анализу и решению последовательных параллельных сетей

Последовательные параллельные сети

Твердое понимание основных принципов, связанных с последовательными и параллельными цепями, является достаточным основанием для начала исследования любой сети постоянного тока с одним источником, имеющей комбинацию последовательных цепей. и параллельные элементы или ответвления. В общем, последовательно-параллельные сети — это сети, которые содержат конфигурации как последовательных, так и параллельных цепей.

2 подхода к анализу и решению последовательно-параллельных сетей

Специалисты в анализе последовательно-параллельных сетей могут стать специалистами только при наличии опыта, практики и опыта .Со временем путь к желаемому неизвестному становится более очевидным, если вспомнить похожие конфигурации и разочарование, вызванное неправильным подходом.

Начало работы //

Есть несколько шагов , которые могут быть полезны для начала работы на первых нескольких упражнениях, хотя ценность каждого станет очевидной только с опытом.

Шаг № 1 Найдите минутку, чтобы изучить проблему «в целом» и сделать краткий мысленный набросок общего подхода, который вы планируете использовать.В результате могут быть сокращены время и энергия.

Шаг № 2 Затем исследуйте каждую область сети независимо, прежде чем связывать их вместе в последовательно-параллельные комбинации. Обычно это упрощает сеть и, возможно, открывает прямой подход к получению одного или нескольких желаемых неизвестных.

Он также устраняет многие ошибки , которые могут возникнуть из-за отсутствия систематического подхода.

Шаг № 3 Перерисовывайте сеть как можно чаще с уменьшенными ветвями и неизменными неизвестными величинами, чтобы сохранить ясность и обеспечить сокращенные сети для возврата к неизвестным величинам от источника.

Шаг № 4 Когда у вас есть решение, проверьте его разумность, учитывая величины источника энергии и элементов в сети. Если это не кажется разумным, либо решите схему, используя другой подход, либо очень внимательно проверьте свою работу.

Подход с уменьшением и возвратом //

Для многих последовательных параллельных сетей с одним источником используется анализ, который возвращается к источнику, определяет ток источника, а затем находит путь к желаемому неизвестному.

Рисунок 1 — Представление подхода уменьшения и возврата

На рисунке 1 (a), например, желательно напряжение V ₄. Отсутствие единственного последовательного или параллельного пути к V ₄ от источника сразу показывает, что методы, представленные в последних двух главах, здесь не применимы. Во-первых, необходимо объединить последовательные и параллельные элементы, чтобы получить сокращенную схему на рис. 1 (b). Затем элементы серии объединяются, образуя простейшую конфигурацию, показанную на рис.1 (в).

Теперь ток источника можно определить с помощью закона Ома, и мы можем вернуться через сеть, как показано на рис. 1 (d) справа.

Напряжение V ₂ может быть определено, а затем исходная сеть может быть перерисована, как показано на Рис. 1 (e). Поскольку теперь известно V ₂, можно использовать правило делителя напряжения , чтобы найти желаемое напряжение V ₄ . Из-за сходства между сетями на рисунках 1 (a) и 1 (e), а также между схемами 1 (b) и 1 (d), сети, нарисованные во время фазы сокращения, часто используются для обратного пути.

Хотя все детали анализа не были описаны выше, общая процедура для ряда проблем последовательно-параллельной сети использует процедуру, описанную выше: Неизвестно .

Не все проблемы пойдут по этому пути. У некоторых найдутся более простые и прямые решения. Однако подход с уменьшением и возвратом решает один тип проблем, которые возникают снова и снова.

Подход с блок-схемой //

Для решения последовательно-параллельных сетей будет использоваться подход блок-схемы, чтобы подчеркнуть тот факт, что комбинации элементов, а не просто отдельные резистивные элементы, могут быть включены последовательно или параллельно . Этот подход также позволит выявить количество, казалось бы, разных сетей, которые имеют одинаковую базовую структуру и, следовательно, могут включать аналогичные методы анализа.

Рисунок 2 — Представление подхода на основе блок-схемы

Первоначально будет некоторая озабоченность по поводу того, что идентифицирует последовательные и параллельные элементы и ветви и выберет наилучшую процедуру для решения.

Однако по мере того, как вы продвигаетесь по примерам и пробуете несколько проблем, вы обнаружите общий путь к большинству решений, которые действительно могут сделать анализ таких систем интересным и приятным занятием 🙂

На рисунке 2, блоки B и C подключены параллельно (точки b и c общие), а источник напряжения E включен последовательно с блоком A (точка a общая). Параллельная комбинация B и C также включена последовательно с A и источником напряжения E из-за общих точек b и c соответственно.

Чтобы последующий анализ был как можно более ясным и лаконичным, будут использоваться следующие обозначения для последовательных и параллельных комбинаций элементов .

Для резисторов серии R ₁ и R ₂ , запятая будет вставлена между их нижними индексами, как показано здесь //

Для параллельных резисторов R ₁ и R ₂ , параллельный символ будет вставлен между их нижними индексами, как показано ниже //

Анализ параллельных и последовательных цепей резисторов

Эта процедура утомительна, но требует очень мало математических вычислений, а это концептуально красиво .Вы должны иметь возможность взглянуть на готовый продукт и объяснить, ПОЧЕМУ значения падений напряжения и токов для каждого резистора и комбинации резисторов имеют такие отношения.

Ура! Теперь вы можете упростить любую схему , используя всего одну батарею и набор резисторов !

Ссылка // Основы электротехники Джорджио Риццони (получите на Amazon)

(PDF) Упрощение схем для символьного анализа аналоговых интегральных схем

DAEMS ET AL.: УПРОЩЕНИЕ СИМВОЛИЧЕСКОГО АНАЛИЗА АНАЛОГОВЫХ ИНТЕГРИРОВАННЫХ ЦЕПЕЙ 13

параметр num expr rel-error [dec]

AVLF 79,91 дБ 80,69 дБ 0,039 дес. dec

fz1 591,1 МГц 437,9 МГц -0,13 dec

ТАБЛИЦА II

Сравнение значений числовых параметров, полученных с помощью прямого численного моделирования

(num), со значениями, полученными

путем оценки выражений (expr) и относительной погрешности

в количестве декад (rel-error)

труднее извлечь из поддиапазона 3, чем из поддиапазона 2.

Точность выражений сравнивается с результатами, полученными численным расчетом в таблице Таблицы II. Также указана относительная погрешность, которая составляет

очень мала.

VII. Выводы

В этой статье был представлен метод упрощения линеаризованных аналоговых схем

с учетом сложности графа потоков сигналов

схемы. Такой подход позволяет сократить время упрощения схемы

.Это также позволяет генерировать

структурных потоков сигналов, которые очень эффективно описывают поведение схемы. Эти графики можно использовать

для генерации символьных уравнений для требуемых характеристик схемы и даже полюсов и нулей. Методы декомпозиции графов

позволяют эффективно анализировать графы и генерировать

информацию о локализации полюсов замкнутого контура и

нулей. Таким образом, мы можем избежать генерации длинных, не интерпретируемых

выражений, которые генерируются традиционными методами символьного анализа

ﬂ.

Благодарности

Авторы хотели бы поблагодарить

Европейского Союза за поддержку проекта ESPRIT № 21812

«AMADEUS» и поблагодарить анонимных рецензентов за

комментариев, которые позволили улучшить эту рукопись.

Ссылки

[1] Л. О. Чуа и П. М. Лин, Компьютерный анализ электронных схем

: алгоритмы и вычислительные методы. Prentice-

Hall, 1975.

[2] S.J. Seda, GR Degrauwe и W. Fichtner, «Инструмент символьного анализа

ysis для автоматизации проектирования аналоговых схем», в Proceedings

IEEE / ACM International Conference on Computer Aided De-

sign, pp. 488– 491, 1988.

[3] Дж. Гилен, Х. Уолшартс и В. Сансен, «ISAAC: симулятор

для аналоговых интегральных схем», IEEE Journal of Solid —

State Circuits, vol. 24, pp. 1587–1597, Dec. 1989.

[4] П. М. Линь, Анализ символьных сетей.Elsevier, 1991.

[5] FV Fern´andez-Fernand´ez, A. Rodr´ıguez-V´azquez, JL Huer-

tas и G. Gielen, Символьные методы анализа — Приложения

to Analog Design Автоматизация. IEEE Press, 1998.

[6] П. Вамбак, Ф. В. Ферн’андес-Фернандес, Г. Гилен, В. Сансен,

и А. Родригес-Васкес, «Энергичные символьные вычисления

». приближенных характеристик слабого сигнала », IEEE Journal of

Solid-State Circuits, vol.30, стр. 327–330, март 1995 г.

[7] Ф. В. Ферн’андес-Фернандез и А. Родригес-Васкес, «Моделирование активного переменного тока Inter-

и определение характеристик аналоговых цепей с помощью

символьный анализ, Журнал аналоговых интегральных схем и

Обработка сигналов, вып. 1, pp. 183–208, Nov. 1991.

[8] Q. Yu и C. Sechen, «Эффективное приближение символьных сетевых

рабочих функций с использованием алгоритмов пересечения матроидов», Pro-

ceedings Symbolic Methods Применение в схемотехнике

Workshop, стр.261–227, Oct. 1994.

[9] X.-D. Тан и К.-Дж. Р. Ши, «Канонический символьный анализ больших аналоговых схем

с определяющими диаграммами решений», IEEE

Транзакции по автоматизированному проектированию интегральных схем

и системы, т. 19, pp. 1–18, Jan. 2000.

[10] Q. Yu и C. Sechen, «Приближенный символьный анализ больших аналоговых интегральных схем

», in Proceedings IEEE / ACM Inter-

national Conference on Компьютерный дизайн, стр.664–671,

1994.

[11] Р. Зоммер, Э. Хенниг, Г. Дрёге и Э.-Х. Хорнебер,

«Символьная аппроксимация на основе уравнений путем матричной редукции

с количественным прогнозированием ошибок», Alta Frequenza — Rivista Di

Elettronica, vol. 5, pp. 317–325, Dec. 1993.

[12] X.-D. Тан и К.-Дж. Р. Ши, «Интерпретируемая символьная характеристика малых сигналов

больших аналоговых схем с использованием детерминантных решающих диаграмм

», в Proceedings Design Automation and Test in

Europe Conference, 1999.

[13] Дж. Дж. Хсу и К. Сечен, «Полностью символьный анализ больших аналоговых интегральных схем

», Proceedings Custom Integrated Circuits

Conference, pp. 21.4.1–21.4.4, 1994.

[14 ] О. Герра, Дж. Д. Родригес-Гарсия, Э. Рока, Ф. В. Ферн’андес-

Фернандес, и А. Родригес-Васкес, «Упрощение до

и методология генерации. для символьного анализа больших схем

», в Proceedings International Conference on Electronic

Circuits and Systems, vol.3, pp. 81–84, Sept. 1998.

[15] JJ Hsu и C. Sechen, «Точное извлечение упрощенных символьных выражений полюс / ноль сим-

для больших аналоговых ИС», Proceed-

ings IEEE International Symposium on Circuits and Systems,

pp. 2083–2087, 1995.

[16] JD Rodr´ıguez-Garc´ıa, O. Guerra, FV Fern´andez-Fernand´ez,

and A. Родригес-Васкес, «Методика символического извлечения полюса / нуля

, основанная на анализе постоянных времени схемы», в Pro-

ceedings Design of Circuits and Integrated Systems, стр.327–332,

1999.

[17] W. Daems, G. Gielen и W. Sansen, «Снижение сложности схемы

для символьного анализа аналоговых интегральных схем», в

Proceedings Design Automation Conference , pp. 958–963, June

1999.

[18] С. Мейсон, «Теория обратной связи — некоторые свойства графиков потока сигналов

», Proceedings IRE, pp. 1144–1156, сентябрь 1953.

[19] К.Л. Коутс, «Решения линейных алгебраических уравнений в виде потоковых графов», в IRE Transactions on Circuit Theory, vol.6, pp. 170–

187, июнь 1959.

[20] Ф. Лейн, У. Дэмс, Г. Гилен и В. Сансен, «Поведенческая методология моделирования пути сигнала

для качественного понимания и

эффективный выбор размера CMOS операционных усилителей », в материалах IEEE / ACM In-

Международная конференция

по автоматизированному проектированию, стр. 374–381,

ноябрь 1997 г.

[21] Р.К. Рой, Введение в метод Тагучи. . Нью-Йорк: Van

Nostrand Reinhold, 1990.

[22] W.Daems, W. Verhaegen, P. Wambacq, G. Gielen и

W. Sansen, «Оценка стратегий контроля ошибок для линейного символьного анализа

аналоговых интегральных схем», IEEE Trans-

, действия по схемам и схемам. Системы-I: фундаментальная теория и приложения

, т. 46, pp. 594–606, May 1999.

[23] Б. У. Джонсон, Проектирование и анализ отказоустойчивых цифровых систем

. Addison-Wesley, 1989.

Чем занимается инженер-электрик?

Электротехника восходит к концу 19 века и является одной из новейших отраслей машиностроения.Область электроники зародилась с изобретением в 1904 году Джоном Амброузом Флемингом термоэмиссионной ламповой диодной лампы и была основой всей электроники, включая радиоприемники, телевидение и радары, до середины 20-го века.

Некоторые из наиболее важных пионеров в области электротехники включают Томаса Эдисона (электрическая лампочка), Джорджа Вестингауза (переменный ток), Николы Тесла (асинхронный двигатель), Гульельмо Маркони (радио) и Фило Т. Фарнсворта (телевидение). Инновационные идеи и концепции были превращены в практические устройства и системы, проложившие путь к тому, что мы имеем и используем сегодня.

Инженеры-электрики работают над различными проектами, такими как компьютеры, роботы, сотовые телефоны, карты, радары, навигационные системы, проводка и освещение в зданиях и другие виды электрических систем.

Инженеры-электрики все больше и больше полагаются на системы автоматизированного проектирования (САПР) для создания схем и компоновки цепей, и они используют компьютеры для моделирования работы электрических устройств и систем.

Инженеры-электрики работают в разных отраслях, и требуемые навыки также различаются.Эти навыки могут варьироваться от базовой теории схем до навыков, необходимых для работы менеджером проекта. Инструменты и оборудование, которые могут понадобиться инженеру-электрику, также разнообразны и могут варьироваться от простого вольтметра до анализатора верхнего уровня и до передового программного обеспечения для проектирования и производства.

Должностные обязанности инженера-электрика могут требовать:

Оценка электрических систем, продуктов, компонентов и приложений
Разработка и проведение исследовательских программ
Применение знаний в области электричества и материалов
Подтверждение возможностей системы и компонентов путем разработки методов и свойств испытаний
Разработка электротехнической продукции на основе изучения требований клиентов
Исследования и испытания методов производства и сборки и материалов
Разработка производственных процессов путем проектирования и модификации оборудования
Обеспечение качества продукции путем разработки методов электрических испытаний
Тестирование готовой продукции и возможностей системы
Подготовка отчетов о продуктах путем сбора, анализа и обобщения информации и тенденций
Предоставление инженерной информации путем ответов на вопросы и запросы
Поддержание репутации продукции и компании путем соблюдения федеральных и государственных нормативных требований
Ведение базы данных о продукции путем написания компьютерных программ и ввода данных

Электротехника включает множество дисциплин.Некоторые инженеры-электрики специализируются исключительно на одной дисциплине, в то время как другие специализируются на комбинации дисциплин.

Наиболее популярные дисциплины:

Инженер-электронщик
Инженеры-электронщики исследуют, проектируют, создают и тестируют электронные системы и компоненты, которые будут использоваться в таких областях, как телекоммуникации, акустика, аэрокосмическое наведение и управление движением, или приборы и средства управления. Эта карьера очень похожа на карьеру инженера-электрика — обе профессии в США взаимозаменяемы.Основное отличие — специализация. В то время как инженеры-электрики заботятся обо всех электрических системах, инженеры-электронщики оттачивают более мелкие детали, такие как отдельные компьютеры, электронные схемы, резисторы, конденсаторы, катушки индуктивности, транзисторы и диоды, и используют свои знания теории электроники и свойств материалов.

Инженер по микроэлектронике
Микроэлектроника — это подраздел электроники, относящийся к изучению и микроизготовлению очень малых электронных конструкций и компонентов схем, обычно изготавливаемых из полупроводниковых материалов.Многие компоненты нормальной электронной конструкции также доступны в микроэлектронном эквиваленте, который может включать транзисторы, конденсаторы, индукторы, резисторы, диоды, изоляторы и проводники. Инженеры в области микроэлектроники используют специализированное оборудование и уникальные методы подключения, такие как соединение проводов, из-за необычно малого размера компонентов, выводов и контактных площадок. По мере совершенствования технологий масштаб микроэлектронных компонентов продолжает уменьшаться, поэтому влияние свойств схемы, таких как межсоединения, может стать более интересным.Задача инженера по микроэлектронике — найти способы минимизировать эти «паразитные» эффекты, создавая при этом устройства меньшего размера, более быстрые и дешевые.

Инженер по обработке сигналов
Инженер по обработке сигналов анализирует и изменяет цифровые сигналы, чтобы сделать их более точными и надежными. В обязанности входит разработка, управление и обновление цифровых сигналов, а также создание алгоритмов для их более эффективной обработки. Инженер по обработке сигналов может работать в таких областях, как обработка изображений, обработка речи, распознавание образов, проектирование микросхем, разработка радиочастот, обработка биомедицинских сигналов, а также космические и военные приложения, включая спутниковую и мобильную связь.Эффективное использование сигналов достигается за счет реализации точных алгоритмов, закодированных в программных пакетах, с краткими шагами и выводами в реальном времени. Инженеры должны разработать необходимые этапы, предоставить спецификации, спроектировать процессор, который действует как машина, и смоделировать систему перед изготовлением.

Инженер-энергетик
Инженер-энергетик, также называемый инженером по энергетическим системам, имеет дело с подобластью электротехники, которая включает в себя производство, передачу, распределение и использование электроэнергии, а также электрического оборудования, связанного с этими системами (например, трансформаторы, генераторы, двигатели и силовая электроника).Хотя большая часть внимания энергетиков сосредоточена на вопросах, связанных с трехфазным питанием переменного тока, другая область внимания связана с преобразованием между мощностью переменного и постоянного тока и развитием конкретных систем питания, таких как те, которые используются в самолетах или на электрических железных дорогах. сети. Энергетики большую часть своей теоретической базы черпают из электротехники.

Инженер по контролю
Инженерия управления, или разработка систем управления, обычно преподается вместе с электротехникой во многих университетах, и особое внимание уделяется реализации систем управления, полученных путем математического моделирования широкого диапазона систем.Этот тип инженерной дисциплины использует теорию автоматического управления для разработки контроллеров, которые заставляют системы вести себя определенным образом, используя микроконтроллеры, программируемые логические контроллеры, процессоры цифровых сигналов и электрические схемы. Используя детекторы и датчики для измерения выходной производительности управляемого процесса и обеспечения корректирующей обратной связи, можно достичь желаемой производительности.

Инженер по телекоммуникациям
Телекоммуникационная инженерия — это дисциплина, сосредоточенная на электротехнике и компьютерной инженерии, которая пытается помочь и улучшить телекоммуникационные системы.Работа инженера по телекоммуникациям будет варьироваться от проектирования базовой схемы до предоставления услуг высокоскоростной передачи данных и надзора за установкой телекоммуникационного оборудования (такого как системы электронной коммутации, оптоволоконные кабели, IP-сети и системы микроволновой передачи). Они используют ассортимент оборудования и транспортных средств для проектирования сетевой инфраструктуры (такой как витая пара, коаксиальные кабели и оптические волокна) и предоставляют решения для беспроводных режимов связи и передачи информации, таких как услуги беспроводной телефонной связи, радио и спутниковая связь. связь, Интернет и широкополосные технологии.

Инженер по КИП
Приборостроение берет свое начало как в электротехнике, так и в электронике и занимается разработкой измерительных устройств для измерения давления, расхода и температуры. Короче говоря, эта область имеет дело с процессами измерения, автоматизации и управления, что требует глубокого понимания физики. Инженеры по КИП разрабатывают новые интеллектуальные датчики, интеллектуальные преобразователи, технологию MEMS и технологию Blue Tooth. Можно найти инженеров по КИП, работающих практически во всех обрабатывающих отраслях промышленности, включая сталелитейную, нефтяную, нефтехимическую, энергетическую и оборонную промышленность.

Инженер-компьютерщик
Большинство университетов предлагают компьютерную инженерию либо в качестве степени, субдисциплины электротехники, либо предлагают двойную степень в области электротехники и вычислительной техники. Компьютерные инженеры исследуют, проектируют, разрабатывают и тестируют компьютерные системы и компоненты, такие как процессоры, компьютерные платы, устройства памяти, сети и маршрутизаторы, микрочипы и другие электронные компоненты.

Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Электротехника. Методы расчёта электрических цепей. (лекция 4)

1. Конспект лекций по электротехнике Подготовлен: Степановым К.С., Беловой Л.В., Кралиным А.А., Панковой Н.Г. Кафедра теоретической и общей элект

2. Методы расчёта электрических цепей

4. Расчёт простых цепей

5. Пусть требуется определить все токи в такой цепи.

6. Для этого будем упрощать схему в следующей последовательности.

7. R(4-8)= R678(R4+R5)/(R4+R5+R876)

11. Метод наложения или суперпозиции

12. Метод наложения или суперпозиции

13. Метод наложения или суперпозиции

14. Пусть требуется определить токи в такой цепи

15. Преобразуем схему к виду 1 и определим токи в ветвях I’1,I’2,I’3,I’4,I’5.

16. Преобразуем схему к виду 2 и определим токи в ветвях I»1,I»2,I»3,I»4,I»5.

17. Преобразуем схему к виду 3 и определим токи в ветвях I»’1,I»’2,I»’3,I»’4,I»’5.

19. Расчёт разветвлённых цепей с помощью законов Кирхгофа.

20. Алгоритм расчёта

21. Алгоритм расчёта

22. Алгоритм расчёта

23. Пример. Определить токи в ветвях схемы по законам Кирхгофа.

24. 1. Упрощаем элементарные цепи. Для этого преобразуем схему.

25. В этой схеме источник тока J5 заменён на источник эквивалентной ЭДС E5экв (см.

26. Составим уравнения по первому и второму законам Кирхгофа

27. Запишем матрицу коэффициентов и столбец свободных членов

28. Благодарю за внимание

Расчет сопротивления цепи

Пример 1

Пример 2

Пример 3

Пример 4

Пример 5

2. Схемы электрических цепей и их элементы

контур, схема, расчет, разветвленные и линейные цепи

Что такое электрические цепи

Основные компоненты

Классификация цепей

Разветвленные и неразветвленные

Линейные и нелинейные

Обозначения элементов на схеме

Трехфазные электрические цепи

Законы, действующие в электрических цепях

Как производится расчет электрических цепей

Литература по ТОЭ, учебники по ТОЭ, методички по ТОЭ, задачники по ТОЭ

Электротехника КР

Упростите резистивные сети | Прядильные числа

Содержание

Стратегия

Пошаговое решение к примеру

Исключения

Сводка

Определение анализа эквивалентных цепей | Chegg.com

Как использовать теорему Тевенина | ОРЕЛ

Что такое теорема Тевенина?

Теорема Тевенина в действии

Шаг 1 — Thevenin Resistance

Шаг 2 — Напряжение Thevenin

Шаг 3 — Ток нагрузки

Сохраняйте простоту

Программное обеспечение для электротехники — математическое программное обеспечение для инженеров-электриков

Capture Design Intent

Символьная и числовая математика высокого уровня

Снизьте расчетный риск с помощью единиц измерения

2 подхода к анализу и решению последовательных параллельных сетей

Последовательные параллельные сети

Начало работы //

Подход с уменьшением и возвратом //

Подход с блок-схемой //

Анализ параллельных и последовательных цепей резисторов

(PDF) Упрощение схем для символьного анализа аналоговых интегральных схем

Чем занимается инженер-электрик?

Чем занимается инженер-электрик?

Добавить комментарий Отменить ответ