Лимб и алидада теодолита — Морской флот
Теодолит — середины 20 го века Теодолит измерительный прибор для измерения горизонтальных и вертикальных углов при геодезических работах, топографических, геодезических и маркшейдерских съёмках, в строительстве и т. п. Основной рабоч … Википедия
Лимб (инструмент) — Эта статья слишком короткая. Пожалуйста … Википедия
Корпус военных топографов — Основание Указ императора Александра I 28 января 1822 года Ликвидация Постановление СНК СССР 1918 год Корпус военных топографов (КВТ) (до 1866 Корпус топографов) был организован в 1822 году для централизов … Википедия
Теодолит — геодезический инструмент (См. Геодезические инструменты) для определения направлений и измерения горизонтальных и вертикальных углов при геодезических работах, топографических и маркшейдерских съёмках, в строительстве и т. п. (см.… … Большая советская энциклопедия
Магнитные приборы* — для наблюдения земного магнетизма: I) для абсолютных наблюдений, II) для вариационных и III) магнитограф. I. М. приборы для абсолютных измерений элементов земного магнетизма (см.). Простейший прибор для определения склонения буссоль склонения,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
I. М. приборы для абсолютных измерений элементов земного магнетизма (см.). Простейший прибор для определения склонения буссоль склонения,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Магнитные приборы — для наблюдения земного магнетизма: I) для абсолютных наблюдений, II) для вариационных и III) магнитограф. I. М. приборы для абсолютных измерений элементов земного магнетизма (см.). Простейший прибор для определения склонения буссоль склонения,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ГЕОДЕЗИЯ — (греч. geodaisia, от ge Земля и daio делю, разделяю), наука об определении положения объектов на земной поверхности, о размерах, форме и гравитационном поле Земли и других планет. Это отрасль прикладной математики, тесно связанная с геометрией,… … Энциклопедия Кольера
геодезия — наука, изучающая форму, размеры и гравитационное поле Земли, а также технические средства и методы измерений на местности. Геодезия зародилась в странах Древнего Востока и в Египте, где задолго до н. э. были известны методы измерения земельных… … Географическая энциклопедия
Геодезия зародилась в странах Древнего Востока и в Египте, где задолго до н. э. были известны методы измерения земельных… … Географическая энциклопедия
Универсальный инструмент — универсал в астрономии и геодезии, переносный угломерный инструмент, служащий для измерения углов в вертикальной и горизонтальной плоскостях. С помощью У. и. по наблюдениям звёзд и Солнца определяют географические координаты места,… … Большая советская энциклопедия
Теодолит состоит из (рис. 5 а, б): подставки с тремя подъемными винтами, которая крепится к головке штатива становым (закрепительным) винтом через трегер, представляющий собой пластину со втулкой, в которой имеется резьба. В подставке вращается алидадная часть теодолита, состоящая из лимба, цилиндрическая ось которого входит в полость подставки и собственно алидады, ось которой, в свою очередь, входит в цилиндрическую полость лимба. Между стойками закреплена на оси и может вращаться зрительная труба, состоящая из объектива, окуляра и расположенной между ними фокусирующей линзы, которая может перемещаться в небольших пределах с помощью винта фокусировки.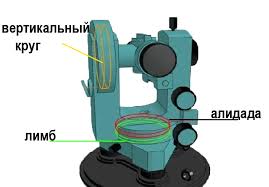 В окулярном колене зрительной трубы расположена, заключенная в оправу, стеклянная пластина, закрепленная четырьмя юстировочными винтами, на которой методом гравировки нанесена сетка нитей. Окулярное кольцо при вращении перемещает линзу, заключенную в обойму, и позволяет фокусировать изображение сетки нитей зрительной трубы в соответствии со зрением. На корпусе зрительной трубы закреплены оптические визиры, позволяющие осуществлять грубое наведение теодолита на цель.
В окулярном колене зрительной трубы расположена, заключенная в оправу, стеклянная пластина, закрепленная четырьмя юстировочными винтами, на которой методом гравировки нанесена сетка нитей. Окулярное кольцо при вращении перемещает линзу, заключенную в обойму, и позволяет фокусировать изображение сетки нитей зрительной трубы в соответствии со зрением. На корпусе зрительной трубы закреплены оптические визиры, позволяющие осуществлять грубое наведение теодолита на цель.
На одной из стоек расположен установочный цилиндрический уровень, один конец которого заделан шарнирно, а дугой закреплен между двумя юстировочными винтами (или винтом и пружиной).
На другой стойке закреплен вертикальный круг, состоящий из лимба, скрепленного со зрительной трубой и алидады, скрепленной со стойкой, линия нулей которой перпендикулярна оси вращения теодолита или устанавливается горизонтально автоматически с помощью компенсатора.
Горизонтальный и вертикальный угломерные круги теодолита одинаковые по размерам и изготовлены в виде колец из стекла. На посеребренном крае угломерного круга нанесены градусные деления. Изображения горизонтального и вертикального угломерных кругов с помощью оптической системы теодолита предается в поле зрения оптического шкалового микроскопа, расположенного рядом с окуляром зрительной трубы. В поле зрения шкалового микроскопа видны изображения горизонтального и вертикального угломерных кругов, а также шкалы верньеров, с помощью которых производится отсчет. Окулярное кольцо шкалового микроскопа позволяет фокусировать изображения делений лимба и алидады и их оцифровку.
На посеребренном крае угломерного круга нанесены градусные деления. Изображения горизонтального и вертикального угломерных кругов с помощью оптической системы теодолита предается в поле зрения оптического шкалового микроскопа, расположенного рядом с окуляром зрительной трубы. В поле зрения шкалового микроскопа видны изображения горизонтального и вертикального угломерных кругов, а также шкалы верньеров, с помощью которых производится отсчет. Окулярное кольцо шкалового микроскопа позволяет фокусировать изображения делений лимба и алидады и их оцифровку.
Теодолит имеет ряд закрепительных и наводящих винтов: лимба, алидады, зрительной трубы. Обычно, перпендикулярно закрепительному винту расположен наводящий винт. Центрирование теодолита над вершиной измеряемого угла осуществляется с помощью нитяного отвеса, который крепится к специальному крючку станового винта или с помощью оптического отвеса, вмонтированного в подставку.
Рис. 5 а. Теодолит 4Т30П. 1 – трегер, 2 – подъемные винты подставки, 3 – оптический центрир, 4 – подставка, 5 – алидадная часть теодолита, 6 – винт вращения лимба, совмещения нулей лимба и алидады, 7 – цилиндрический, установочный уровень, 8 – юстировочные винты цилиндрического уровня, 9 – стойки, 10 – зеркало подсветки оптической системы, 11 –наводящий винт зрительной трубы, 12 – оптический визир, 13 – вертикальный круг, 14 – винт фокусировки, 15 – зрительная труба (объектив), 16 – зажимной винт зрительной трубы, 17 – цилиндрический уровень при зрительной трубе, 18 – закрепительный винт ориентир – буссоли, 19 – ориентир – буссоль, 20 – зеркало
Рис. 5 б. Теодолит 3Т15П. 1 – трегер, 2 – подъемные винты подставки, 3 – подставка, 4 – закрепительный винт лимба, 5 – наводящий винт алидады, 6 – закрепительный винт алидады, 7 – винт вращения лимба, совмещения нулей лимба и алидады, 8 – цилиндрический уровень, 9 – юстировочные винты цилиндрического уровня, 10 – микрометренный винт шкалового микроскопа, 11 –наводящий винт зрительной трубы, 12 – стойки, 13 – зеркало подсветки оптической системы, 14 – оптический визир, 15 – вертикальный круг, 16 – винт фокусировки, 17 – ось зрительной трубы, 18 – зрительная труба (объектив), 19 – зажимной винт зрительной трубы, 20 – цилиндрический уровень при зрительной трубе
5 б. Теодолит 3Т15П. 1 – трегер, 2 – подъемные винты подставки, 3 – подставка, 4 – закрепительный винт лимба, 5 – наводящий винт алидады, 6 – закрепительный винт алидады, 7 – винт вращения лимба, совмещения нулей лимба и алидады, 8 – цилиндрический уровень, 9 – юстировочные винты цилиндрического уровня, 10 – микрометренный винт шкалового микроскопа, 11 –наводящий винт зрительной трубы, 12 – стойки, 13 – зеркало подсветки оптической системы, 14 – оптический визир, 15 – вертикальный круг, 16 – винт фокусировки, 17 – ось зрительной трубы, 18 – зрительная труба (объектив), 19 – зажимной винт зрительной трубы, 20 – цилиндрический уровень при зрительной трубе
Лимб горизонтального круга представляет собой стеклянный угломерный круг. Стеклянные лимбы выполняются обычно в виде колец, на которые нанесены деления от 0 до 360°. Размеры лимба зависят от требуемой точности измерения углов. Чем выше требуемая точность, тем больше диаметр лимба.Деления на лимбе наносятся с помощью специальной делительной машины.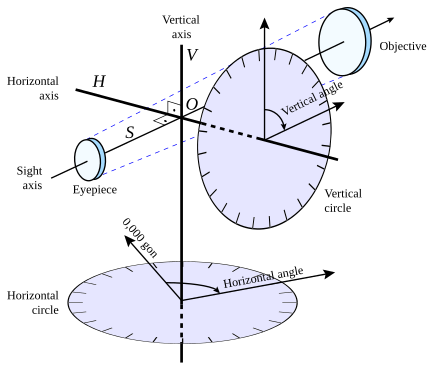 Цифры наносятся на шкале, как правило через 1°. Количество делений, содержащихся в одном градусе, определяет цену деления лимба.
Цифры наносятся на шкале, как правило через 1°. Количество делений, содержащихся в одном градусе, определяет цену деления лимба.
Подставка предназначена для крепления теодолита к штативу и состоит из следующих основных частей: собственно подставки с цилиндрической полостью, трех подъемных винтов, трегера и пружины (современные теодолиты пружины не имеют). Подъемные винты служат для установки оси вращения теодолита в отвесное положение. В центре трегера укреплена втулка с резьбой для станового винта, которым подставка крепится к головке штатива.
Алидада горизонтального круга представляет собой круг или два диаметрально противоположных сектора, центры которых должны совпадать с центром лимба. Один из диаметров алидады принимается за начальный и обозначается «». От нуля по ходу часовой стрелки нанесена специальная шкала – верньер, разделяющая один градус на определенное количество делений, определяемое точностью прибора.
Отсчитывание углов по лимбу и алидаде производится с помощью специального оптического отсчетного устройства – шкалового микроскопа.
Алидада горизонтального круга имеет меньший диаметр, чем лимб, и расположена в конической полости оси лимба. Теодолиты, конструкция осей которых позволяет независимо вращать алидаду и лимб, называются повторительными.
Цилиндрический уровень (рис. 6) служит для точной установки осей прибора в горизонтальное или вертикальное положение. Основным элементом уровня является стеклянная трубка 1, называемая ампулой. Ампулу заполняют разогретым эфиром. При остывании эфир уменьшается в объеме, и в ампуле образуется пространство 4, заполненное парами эфира, которое называют пузырьком уровня. Внутреннюю поверхность ампулы уровня тщательно шлифуют под определенным радиусом кривизны R. Наивысшая точка поверхности ампулы называется нуль-пунктом (точка О на рис. 6). На наружной поверхности ампулы нанесены деления 5, по которым определяется положение пузырька уровня. Когда концы пузырька располагаются симметрично относительно нуль-пункта, принято говорить, что пузырек находится в нуль-пункте.
6). На наружной поверхности ампулы нанесены деления 5, по которым определяется положение пузырька уровня. Когда концы пузырька располагаются симметрично относительно нуль-пункта, принято говорить, что пузырек находится в нуль-пункте.
Касательная UU1 к дуге АОВпродольного сечения внутренней поверхности ампулы в нуль-пункте (рис. 6, в) называется осью цилиндрического уровня. Когда пузырек уровня находится в нуль-пункте, ось уровня занимает горизонтальное положение.
Рис. 6. Цилиндрический уровень: а – вертикальный разрез: 1 – ампула; 2 – корпус; 3 – юстировочные гайки; 4 – пузырек уровня: 5 – верх ампулы с делениями; 6 – оправа уровня; б – вид сверху: в – принцип работы цилиндрического уровня.
Угол τ, на который наклоняется ось уровня при перемещении пузырька на одно деление ампулы, называется ценой деления уровня. Цена деления уровня служит мерой чувствительности уровня.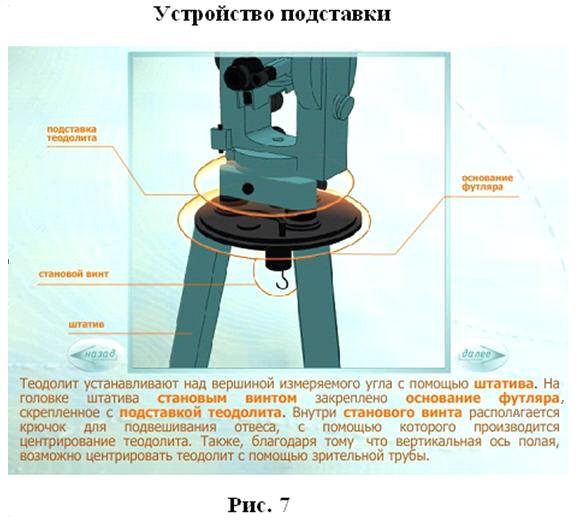 Чем меньше цена деления, тем выше его чувствительность. Ампула уровня помещается в специальную оправу 6, один конец которой шарнирно соединен с корпусом2 уровня, а другой закреплен двумя юстировочнымигайками (или винтами) 3, с помощью которых можно изменять наклон оси уровня относительно его корпуса.
Чем меньше цена деления, тем выше его чувствительность. Ампула уровня помещается в специальную оправу 6, один конец которой шарнирно соединен с корпусом2 уровня, а другой закреплен двумя юстировочнымигайками (или винтами) 3, с помощью которых можно изменять наклон оси уровня относительно его корпуса.
Зрительная труба (рис. 7а) служит для наведения теодолита на удаленные точки местности, построения направления и проектирования его на горизонтальный круг. Зрительная труба состоитизобъектива и окуляра, заключенных в общий корпус. Для получения отчетливого изображения при различных удалениях наблюдаемого предмета между объективом и окуляром помещается фокусирующая линза, которая может перемещаться в небольших пределах. Процесс получения отчетливого изображения путем перемещения фокусирующей линзы называется фокусированием.
| Рис. 7. Устройство зрительной трубы с внутренним фокусированием | Диафрагма и сетка нитей |
В зрительной трубе различают геометрическую, оптическую, визирную оси и ось вращения.Зрительные трубы геодезических приборов обеспечивают точность наведения на предметы, расположенные на расстоянии, которое в 2 раза больше фокусного расстояния объектива. У современных оптических теодолитов зрительные трубы имеют внутреннее фокусирование и увеличение 20 – 25 крат.
Поскольку геометрическая и оптическая оси (геометрической осью называют прямую, соединяющую центры входного и выходного отверстий, оптической осью называют прямую, соединяющую оптические центры объектива и окуляра) не совпадают и, кроме того, ничем не зафиксированы, пользоваться ими для точного наведения трубы на точки местности практически невозможно. Для получения в поле зрения трубы постоянной фиксированной точки, служащей для наведения трубы на предмет, перед окуляром с помощью винтов крепится диафрагма 4со стекломна котором выгравировано несколько пересекающихся прямых линий. Средние из них, пересекаясь, образуют крест сетки нитей К. Пластина заключена в специальную оправу-диафрагму, которая может перемещаться в небольших пределах с помощью винтов(рис. 7 б).
Для получения в поле зрения трубы постоянной фиксированной точки, служащей для наведения трубы на предмет, перед окуляром с помощью винтов крепится диафрагма 4со стекломна котором выгравировано несколько пересекающихся прямых линий. Средние из них, пересекаясь, образуют крест сетки нитей К. Пластина заключена в специальную оправу-диафрагму, которая может перемещаться в небольших пределах с помощью винтов(рис. 7 б).
Визирной осью трубы называется прямая, соединяющая оптический центр объектива с крестом сетки нитей. При наведении креста сетки нитей на изображение точки местности, видимой в поле зрения (этот процесс называется визированием), происходит построение направления от исходной точки на искомую.
Для того чтобы спроектировать это направление на горизонтальный круг, труба должна вращаться в плоскости, перпендикулярной к плоскости штрихов лимба и проходящей через центр угломерного круга (лимба). При повороте трубы вокруг оси вращения визирная ось описывает плоскость, которая носит название коллимационной. Коллимационная плоскость должна проходить через нуль горизонтального круга. Поворот трубы вокруг оси вращения, в результате которого окуляр становится в положение, занимаемое до этого объективом, называется переводом зрительной трубы через зенит.
При повороте трубы вокруг оси вращения визирная ось описывает плоскость, которая носит название коллимационной. Коллимационная плоскость должна проходить через нуль горизонтального круга. Поворот трубы вокруг оси вращения, в результате которого окуляр становится в положение, занимаемое до этого объективом, называется переводом зрительной трубы через зенит.
Вертикальный круг служит для измерения углов наклона. Он состоит из лимба вертикального круга, скрепленного со зрительной трубой и алидады вертикального круга, скрепленной со стойкой.Современные теодолиты снабжены устройствами – компенсаторами – (взамен уровня) для автоматической установки горизонтально линии нулей верньера вертикального круга. При отсутствии компенсатора горизонтальность линии нулей обеспечивается конструкцией теодолита.
Если визирную ось трубы установить горизонтально, то нули лимба должны совместиться с нулями верньера алидады. Отсчет по лимбу вертикального круга при горизонтальном положении визирной оси называется местом нуля вертикального круга и обозначается МО. В процессе измерения вертикальных углов этот угол должен оставаться постоянным.
Отсчет по лимбу вертикального круга при горизонтальном положении визирной оси называется местом нуля вертикального круга и обозначается МО. В процессе измерения вертикальных углов этот угол должен оставаться постоянным.
Штативслужит для установки теодолита (или любого другого геодезического прибора) над точкой местности. Основными частями штатива являются:
головка, на которой устанавливается инструмент при измерении;
ножки (металлические или деревянные), которые крепятся шарнирно к головке штатива с помощью болтов с гайками.
Верхние части ножек оправлены металлом, на нижние концы набиваются металлические наконечники. Ножки штатива могут быть постоянной длины или раздвижными. Раздвижные ножки позволяют быстро устанавливать инструмент над точкой при работе на наклонных участках местности и на нужной высоте над точкой местности. В центре головки штатива имеется отверстие, через которое с помощью станового винта крепится подставка теодолита. Ось симметрии станового винта совпадает с осью вращения теодолита. Соблюдение этого условия необходимо для центрирования теодолита над точкой местности. Центрирование осуществляется с помощью нитяного или оптического отвеса.
Ось симметрии станового винта совпадает с осью вращения теодолита. Соблюдение этого условия необходимо для центрирования теодолита над точкой местности. Центрирование осуществляется с помощью нитяного или оптического отвеса.
Нитяной отвес подвешивается за крючок станового винта на шнуре. Отвес представляет собой цилиндр с коническим окончанием, причем вершина конуса совпадает с осью симметрии станового винта.
Оптический отвес (рис. 8) состоит из окуляра1, в поле зрения которого на сетку нитей 2 через призму 3 передается изображение точки местности 4. Оптический отвес с помощью специальных винтов 5 крепится либо к подставке, либо к нижней поверхности цилиндрической оси вращения теодолита. Он устанавливается так, чтобы ось, проходящая через перекрестие сетки нитей 6, была перпендикулярна к оси 7вращения прибора. Установка сетки нитей производится с помощью юстировочных винтов 8.
Рис.8. Оптический отвес: 1 – окуляр; 2 – сетка нитей; 3 – призма; 4 – закрепленная точка местности; 5 – винт; 6 – перекрестие сетки нитей:7 – ось вращения прибора; 8 – юстировочные винты
С точки зрения входящих в комплект частей, устройство теодолита простое. Трудности возникают в процессе настройки прибора. Дело это тонкое и требуют постоянные проверки. Однако в строительстве и проектировании прибор просто незаменим. Геодезисты знают об этом, мы же попробуем описать, так сказать, строение теодолита и его работу более популярным языком.
Основные части теодолита
Приспособление позволяет с высокой точностью замерять углы в пространстве и работать в горизонтальной или вертикальной плоскости. Как правило, выбирается относительный метод, когда за основу принимается эталонный объект, а по нему уже отсчитывается искомый угол. Измерение таким способом известно с XIX века, но сегодняшние теодолиты — это усовершенствованные приспособления, которых существует несколько разновидностей.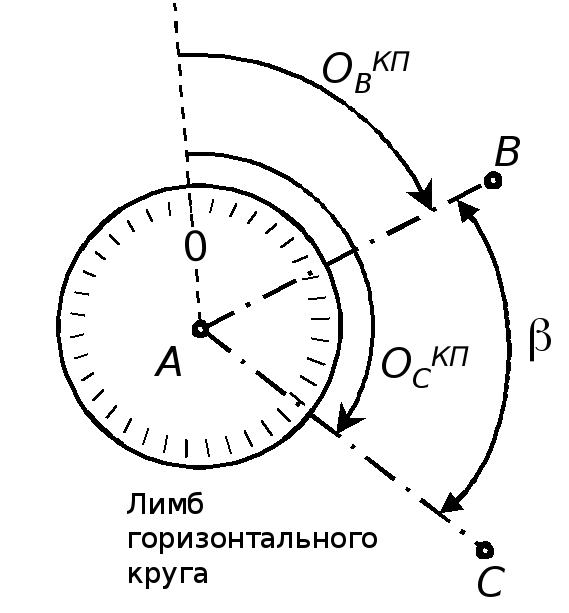
Шкала. Этот элемент, представленный горизонтально или вертикально расположенным кругом, показывает результат. Находится на подставке, имеющей регулировочные винты для управления главными узлами. Измеритель смотрит в окуляр, управляемый винтами, которые позволяют навести окуляр на объект и закрепить его, когда найдена контрольная точка.
Лимб и алидада. Части горизонтального круга, активно использующиеся при измерении горизонтальных углов.
- Лимб — это стационарное стеклянное кольцо с делениями на 360°.
- Алидада — элемент, вращающийся с примыкающей частью прибора и выставляющий отсчет.
Для фиксации отсчета и дальнейшего проведения измерений относительно него закрепляется специальный винт и отпускается лимб, корпус в этом случае останется неподвижным, двигаться же будут лимб и алидада.
Это и есть главные части теодолита. Но снимать показания помогают и другие устройства, с которыми тоже будет полезно познакомиться. Степень горизонтальности установки теодолита контролируется с помощью цилиндрического уровня, а точку отсчета потерять не дает оптический центрир. Отсчеты снимаются по микроскопу, и это финальная стадия работы замерщика.
Степень горизонтальности установки теодолита контролируется с помощью цилиндрического уровня, а точку отсчета потерять не дает оптический центрир. Отсчеты снимаются по микроскопу, и это финальная стадия работы замерщика.
Виды устройств
Имеются следующие виды устройств:
- Механические. Наиболее простой по конструкции и самый дешевый тип, однако у него и самая низкая точность, поэтому для серьезной работы он не подходит.
- Электронные. Электронный теодолит удобен, потому что оснащен устройством для считывания и обработки результатов, геодезисту остается правильно выставить его, а остальное прибор сделает сам.
- Оптические. Наиболее широкое распространение получил теодолит оптический. Он не производит расчеты, как электронный, но стоимость устройства и качество измерения привлекают.
- Лазерные. Эти теодолиты самые дорогие, но и более совершенные устройства. Позволяют делать измерения с большой точностью и удобны в использовании, но приобретать их имеет смысл лишь для постоянных работ, где высоки требования к результату.

Два принципиально разных вида теодолитов отличаются по подвижности алидады и лимба. В повторительных типах данные элементы могут закреплять поочередно, а показания снимать методом последовательных повторений. Обыкновенные варианты этого не допускают, так как алидада с осью представляют в них единое неподвижное целое, и для каждого измерения требуется отдельная настройка.
Маркировка
Марка теодолита — это совокупность букв и цифр. В каждой есть связка литеры «Т» с какой-либо цифрой. Буква указывает на то, что прибор — теодолит, цифры показывают погрешность измерения в секундах, чем они больше, тем больше и погрешность.
- Цифрой 1 маркируются высокоточные приборы.
- Цифрами 2 и 5 маркируются точные теодолиты.
- Цифрами 15 и 30 маркируются технические приборы.
Стоит цифра точности после литеры «Т», а если перед буквой есть другая цифра, она служит для обозначения поколения прибора или его модификации в категории марки.
Требования перед работой
Перед измерением углов теодолит проверяется. Нужно проверять специальную отметку или пломбу, а также периодически — геометрические параметры, так как ошибка в пару градусов со временем может привести к катастрофе!
- Важна абсолютная вертикальность оси алидады и ее перпендикулярность цилиндрическому уровню.
- Визирная ось зрительной трубы должна быть перпендикулярна ей, не выполнив этого коллимационного условия, четкая система отсчета невозможна.
- Оси трубы и алидады должны быть перпендикулярными.
- Проверяем, насколько измерительная сетка расположена в вертикальной коллимационной плоскости.
Использование теодолита
Приемов профессионального использования приборов много, и им учат на специальных курсах, здесь же приведем основные из них.
- Установка теодолита. Первым шагом станет нахождение точки отсчета.
 На местности находим ровную поверхность, по которой центрируем прибор на подставке уровнями и зажимными винтами. В итоге положение прибора должно получиться строго горизонтальным.
На местности находим ровную поверхность, по которой центрируем прибор на подставке уровнями и зажимными винтами. В итоге положение прибора должно получиться строго горизонтальным. - Ловим объект. Визиром отыскиваем цель и точнее наводим винтами измерительную сетку, чтобы установить центр объекта. На это смотрим через окуляр, а если света недостаточно, улучшить ситуацию поможет специальное зеркальце (как в случае с микроскопом). После выставления центра окуляром фиксируется его значение.
- Обработка результатов. Лучше сделать не одно, а несколько измерений. Новый отсчет рекомендуется на известную величину, к примеру, 90°. Если новые измерения отличаются от предыдущих на 90°, то результат можно фиксировать, если нет — производится еще пара подобных измерений с разным отсчетом и вычисляется среднее значение.
История приборов
Первые теодолиты в центре угломерного круга на острие иголки имели линейку, способную вращаться на этом острие свободно (подобно стрелке компаса).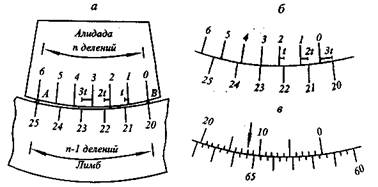 В линейке делались вырезы, в которых натягивались нити, служащие отсчетными индексами. Центр угломерного круга помещался в вершину измеряемого угла, где и закреплялся.
В линейке делались вырезы, в которых натягивались нити, служащие отсчетными индексами. Центр угломерного круга помещался в вершину измеряемого угла, где и закреплялся.
Поворачивая линейку, ее совмещали с первой стороной угла и по шкале круга брали отсчет N1. Потом линейку совмещали со второй стороной угла и брали отсчет N2. Разность N2 и N1 равнялась значению угла. Подвижную линейку назвали алидадой, а угломерный круг — лимбом. Совмещение линейки-алидады со сторонами угла осуществлялось с помощью примитивных визиров.
Современные теодолиты существенно отличаются от предшественников.
- Совмещение алидады со сторонами угла производится с помощью зрительной трубы, которая может вращаться по высоте и азимуту.
- Для отсчета по шкале лимба применяется отсчетное приспособление.
- Конструкцию покрывает прочный металлический кожух.
- Прочее.
Плавное вращение алидады и лимба обеспечивает система осей, а регулируются вращения наводящими и зажимными винтами.
Установки теодолита производятся с помощью специального штатива. Центр лимба с отвесной линией, которая проходит через вершину измеряемого угла, осуществляется оптическим центриром или нитяным отвесом.
Коллимационная плоскость образуется визирной осью окуляра при вращении зрительной трубы вокруг собственной оси. Стороны угла проектируются на лимб подвижной вертикальной плоскостью, называющейся коллимационной плоскостью. Плоскость эта образуется визирной осью зрительной трубы, когда труба вращается вокруг своей оси.
Визирной осью трубы (визирной линией) называется воображаемая линия, которая проходит через центр сетки нитей и оптический центр объектива трубы.
ТЕОДОЛИТ | МобиСтрой
Теодолитом называют геодезический оптический прибор для измерения и построения на местности горизонтальных углов. Конструкции многих теодолитов позволяют измерять и вертикальные углы, но с меньшей точностью, чем горизонтальные. Различают теодолит ы высокоточные, точные и технические (малой точности).
Конструкции многих теодолитов позволяют измерять и вертикальные углы, но с меньшей точностью, чем горизонтальные. Различают теодолит ы высокоточные, точные и технические (малой точности).
Схема устройства и основные элементы теодолита: 1 — исходная станция {вершина угла), 2 — подставка, 3 — подъемный винт, 4 и 5 — лимб и алидада горизонтального круга, 6 — подставка трубы, 7 и 8 — вертикальный круг, 9 — зрительная труба, 10 — визирная ось трубы, 11 — ось вращения трубы, 12 — цилиндрический уровень, 13 — ось уровня, 14 — зажимные винты горизонтального круга, 15 — штатив, 16 — становой винт, 17 — нитяной отвес
Конструктивные ‘элементы теодолита: подставка-треножник (трегер) 2 с тремя подъемными винтами, горизонтальный круг (лимб 4 и алидада 5), подставка трубы (колонки) 6, вертикальный круг (алидада 7 и лимб 8), зрительная труба 9, цилиндрический уровень 12 при горизонтальном круге. Прибор крепится к штативу 15 с помощью станового винта 16. Для крепления частей прибора в нужном положении служат зажимные винты 14.
Зрительная труба 9 имеет три оси: геометрическую (ось цилиндра трубы), оптическую (линия, соединяющая оптические центры объектива и окуляра) и визирную 10 (линия, связывающая оптический центр объектива и точку пересечения нитей сетки).
Горизонтальный круг состоит из двух частей: лимба 4 и алидады 5. Лимб — это металлическое или стеклянное кольцо, по внешнему краю которого нанесены градусные и минутные деления. Деления отсчитываются по ходу часовой стрелки. Наименьшее расстояние между двумя делениями — цена деления лимба. Алидада — это концентрически связанный с лимбом круг или двойной сектор, на котором расположены отсчетные приспособления. На кожухе алидады крепится подставка 6 зрительной трубы. При измерении горизонтальных углов лимб остается неподвижным, а трубу вместе с алидадой устанавливают в заданном направлении.
Вертикальный круг, служащий для измерения вертикальных углов, состоит из лимба 8, наглухо соединенного со зрительной трубой, и алидады 7, жестко связанной с осью 11 вращения трубы. В рабочее положение круг часто устанавливается с помощью специального уровня или маятникового компенсатора.
Измерение горизонтальных углов. | Инженерная геодезия. Часть 1.
Измерение горизонтального угла выполняют способом приемов. При измерении нескольких углов, имеющих общую вершину, применяют способ круговых приемов.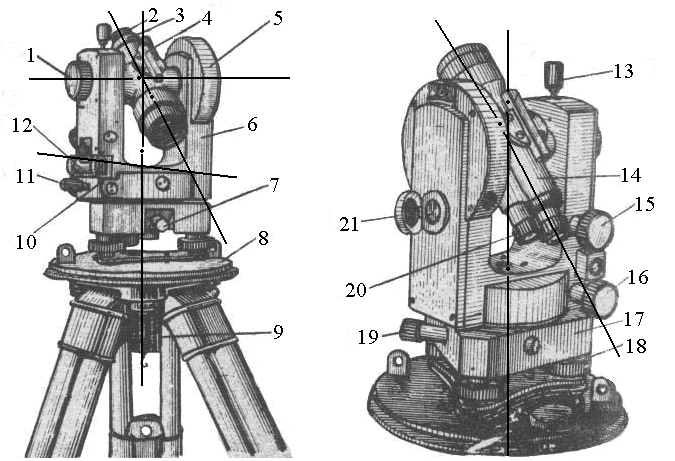
Работу начинают с установки теодолита над центром знака (например, колышка), закрепляющим вершину угла, и визирных целей (вех, специальных марок на штативах) на концах сторон угла.
Установка теодолита в рабочее положение состоит из центрирования прибора, горизонтирования его и фокусирования зрительной трубы.
Центрирование выполняют с помощью отвеса. Устанавливают штатив над колышком так, чтобы плоскость его головки была горизонтальна, а высота соответствовала росту наблюдателя. Закрепляют теодолит на штативе, подвешивают отвес на крючке станового винта и, ослабив его, перемещают теодолит по головке штатива до совмещения острия отвеса с центром колышка. Точность центрирования нитяным отвесом 3 – 5 мм.
Пользуясь оптическим центриром, теодолита (если такой у теодолита имеется), сначала надо выполнить горизонтирование, а затем центрирование. Точность центрирования оптическим центриром 1 – 2 мм.
Горизонтирование теодолита выполняют в следующем порядке. Поворачивая алидаду, устанавливают ее уровень по направлению двух подъемных винтов, и, вращая их в разные стороны, приводят пузырёк уровня в нуль-пункт. Затем поворачивают алидаду на 90º и третьим подъёмным винтом снова приводят пузырёк в нуль-пункт.
Поворачивая алидаду, устанавливают ее уровень по направлению двух подъемных винтов, и, вращая их в разные стороны, приводят пузырёк уровня в нуль-пункт. Затем поворачивают алидаду на 90º и третьим подъёмным винтом снова приводят пузырёк в нуль-пункт.
Фокусирование зрительной трубы выполняют “по глазу” и “по предмету”. Фокусируя “по глазу”, вращением диоптрийного кольца окуляра добиваются четкого изображения сетки нитей. Фокусируя “по предмету”, вращая рукоятку кремальеры, добиваются четкого изображения наблюдаемого предмета. Фокусирование должно быть выполнено так, чтобы при покачивании головы наблюдателя изображение не перемещалось относительно штрихов сетки нитей.
Измерение угла способом приемов. Прием состоит из двух полуприемов. Первый полуприем выполняют при положении вертикального круга слева от зрительной трубы. Закрепив лимб и открепив алидаду, наводят зрительную трубу на правую визирную цель. После того как наблюдаемый знак попал в поле зрения трубы, зажимают закрепительные винты алидады и зрительной трубы и, действуя наводящими винтами алидады и трубы, наводят центр сетки нитей на изображение знака и берут отсчёт по горизонтальному кругу.
Второй полуприем выполняют при положении вертикального круга справа, для чего переводят трубу через зенит. Чтобы отсчёты отличались от взятых в первом полуприеме, смещают лимб на несколько градусов. Затем измерения выполняют в той же последовательности, как в первом полуприеме.
Если результаты измерения угла в полуприёмах различаются не более двойной точности прибора (то есть 1¢ для теодолита Т30), вычисляют среднее, которое и принимают за окончательный результат.
Понятие об измерении способом круговых приемов нескольких углов, имеющих общую вершину. Одно из направлений принимают за начальное. Поочередно, по ходу часовой стрелки, при круге слева наводят трубу на все визирные цели и берут отсчеты. Последнее наведение вновь делают на начальное направление. Затем, переведя трубу через зенит, вновь наблюдают все направления, но в обратном порядке – против часовой стрелки. Из отсчетов при круге слева и круге справа находят средние и вычитают из них среднее значение начального направления. Получают список направлений – углов, отсчитываемых от начального направления.
Затем, переведя трубу через зенит, вновь наблюдают все направления, но в обратном порядке – против часовой стрелки. Из отсчетов при круге слева и круге справа находят средние и вычитают из них среднее значение начального направления. Получают список направлений – углов, отсчитываемых от начального направления.
Схема устройства теодолита — ГЕОЛОГ
В своей работе мы используем только высококачественное профессиональное геологическое оборудование. Благодаря развитию цифровой и компьютерной техники значительно увеличилась скорость обработки информации, улучшилось качество выполнения работ, а еще сократилась стоимость. К примеру, при помощи роботизированных геодезических измерителей на строительной площадке уже не нужно несколько геологов, достаточно одного специалиста.
Очень важную роль в геодезических работах продолжает оказывать устройство, предназначенное для измерения горизонтальных и вертикальных углов в проведение топографических съемок – теодолит.
Конструктивные особенности
Схема устройства теодолита конструктивно состоит из вертикального и горизонтального кругов, цилиндрического уровня, микроскопа для снятия отсчетов, цилиндрического отвеса и подставки, зрительной трубы.
Горизонтальный круг представляет собой вращающуюся часть прибора, на котором расположены лимб (стеклянное кольцо с автоматическими делениями) и алидада. Лимб, как мы уже поняли, является шкалой деления. Лимб неподвижен, а алидада вращается вокруг него, изменяя отсчет горизонтального круга.
Основная его функция — измерение проекции вертикальных плоскостей. При измерениях получившиеся углы относят к двум группам: положительные (расположенные над горизонтом) и отрицательные (расположенные под ним).
Рассмотрим два варианта измерения углов (горизонтальный круг), в которых лимб с алидадой:
используются отдельно друг от друга.

используются вместе со зрительной трубой. Измерение угла производится следующим образом: размещается центр горизонтального круг над углом при помощи оптического центрира.
Перед проведением исследования следует проверить общее состояние прибора, зачистить оптические поверхности, если это требуется, убедиться в его исправности. Затем проверяется вращение алидады и зрительной трубы.
Далее проверяется работа переключателя отсчетной системы. И наконец, следует проверка плавности вращения подъемных винтов. После того как было осуществлено выполнение предварительных проверочных мероприятий теодолит устанавливается на треногу. Потом выбираются две точки (например, A и B). Опорные точки выбираются так, чтобы осуществить наведение зрительной трубы на них. Труба наводится на первую точку, далее устанавливается прибор и измеряются данные с помощью вертикальной нити. Далее отслеживаем точку В (проводим ту же операцию). Затем переводим трубу через зенит, соответственно, изменяем положение круга. Снова наводим зрительную трубу на точку. Все измерения записываем в журнал.
Далее отслеживаем точку В (проводим ту же операцию). Затем переводим трубу через зенит, соответственно, изменяем положение круга. Снова наводим зрительную трубу на точку. Все измерения записываем в журнал.
Схема устройства теодолита как видно не особенно сложна. Подразделяются они на два вида: оптические и электронные. В целом, если изучить схему устройства теодолита, то можно использовать как оптический, так и электронный теодолит.
Мы работаем с любыми из описанных измерителей. Заказать проведение изысканий вы можете уже сегодня, цена на работы невысока, а качество и скорость вас приятно удивят. Смета может быть составлена нашими специалистами сразу после того как будет представлено техническое задание. Стоимость всех работ рассчитаем. Ждем ваших обращений.
«Способы измерения горизонтальных углов теодолитом» — Информио
Дисциплина: Прикладная геодезия и экологическое картографированиеСпециальность: 20.02.01 Рациональное использование природохозяйственных комплексов, 3 курс
На практике в зависимости от решаемых задач применяют различные способы измерения горизонтального угла:
- способ одного полного приема;
- способом круговых приемов;
- способом повторений.

Вспомним, что такое горизонтальный угол. Горизонтальный угол – это горизонтальная проекция угла, образованного точками местности, на уровенную поверхность.
Для того чтобы измерить горизонтальный угол необходимо:
- на вершине угла установить теодолит;
- провести операцию центрирования;
- провести операцию горизонтирования прибора;
- на точках, фиксирующих стороны угла, установить визирные цели.
Измерение горизонтального угла способом одного полного приема.
Способ измерения угла одним полным приемом применяют в том случае, если точка является вершиной двух направлений. Принципиальная схема измерения горизонтального угла данным способом изображена на рисунке 1.
Пусть АСВ – угол β, который необходимо измерить. Для
этого теодолит устанавливают на точке С (точка
стояния), а на точках А и В (точки
визирования) – визирные цели (вехи). Одну из точек, например А, считают передней, а другую, в нашем случае В, – задней. Тогда если в точке стояния С стоять
по направлению к передней точке, то угол β можно считать левым, а его дополнение до 360°, угол β¢, – правым. Далее необходимо последовательно
произвести следующие действия:
Тогда если в точке стояния С стоять
по направлению к передней точке, то угол β можно считать левым, а его дополнение до 360°, угол β¢, – правым. Далее необходимо последовательно
произвести следующие действия:
- Операция не является обязательной, но в дальнейшем облегчает вычисления: Вращая алидаду относительно лимба (например, при круге лево) устанавливают отсчет, близкий к нулю, алидаду закрепляют.
- Вращая лимб вокруг вертикальной оси, а зрительную трубу – вокруг её горизонтальной оси, наводят оптический визир на заднюю точку, закрепительные винты лимба и зрительной трубы закрепляют и с помощью диоптрийного кольца и винта кремальеры устанавливают трубу «по глазу» и «по предмету», добиваясь резкого изображения сетки нитей и визирной цели. Затем наводящими винтами лимба и трубы точно наводят биссектор вблизи перекрестия сетки на низ вехи и берут отсчет по горизонтальному кругу. Отсчет записывают в журнал измерений (табл. 1, столбец 4).
- Ослабив закрепительные винты алидады
(лимб должен быть неподвижен) и зрительной трубы, визируют и берут отсчет на переднюю
точку, действуя, как в пункте 2.
 Отсчет записывают в журнал измерений (табл. 1,
столбец 4). Указанные действия составляют первый полуприем.
Отсчет записывают в журнал измерений (табл. 1,
столбец 4). Указанные действия составляют первый полуприем. - Открепляют лимб, поворачивают его примерно на 90° и вновь закрепляют. Эта операция делает отсчеты в полуприемах независимыми друг от друга и уменьшает ошибки делений лимба. Открепляют алидаду, зрительную трубу и меняют круг. Далее выполняют действия, изложенные в пунктах 2 и 3, при круге право (второй полуприем).
- Производят вычисления угла. Необходимо отметить, что в процессе
вычислений может быть получен как левый угол β, если
от отсчета на переднюю точку отнять отсчет на заднюю (табл. 1, столбец 5), так
и правый β¢, при вычитании
наоборот. В любом случае получаем два значения угла, которые при измерении
теодолитом 2Т30 не должны отличаться более чем на 1¢(полевой
контроль, выполняемый на точке стояния сразу после измерений).
Среднее значение (табл. 1, столбец 6) вычисляют с точностью до 0,1¢,
округляя в сторону четной цифры.
Таблица 1.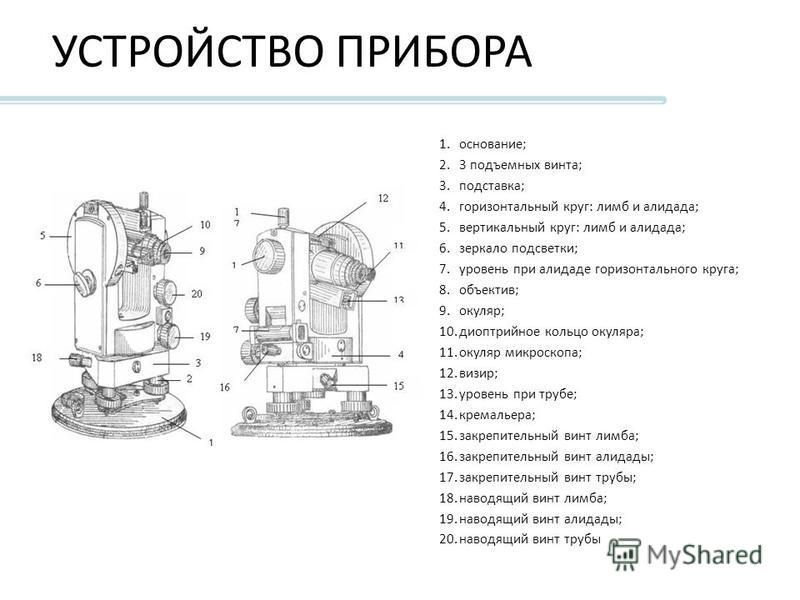 Журнал измерения горизонтального угла способом одного полного приема.
Журнал измерения горизонтального угла способом одного полного приема.
Название точек | Положение круга | Отсчет | Горизонтальный угол | Среднее значение | |
Стояния | Визирования | ||||
1 | 2 | 3 | 4 | 5 | 6 |
С | А | КЛ | 0°01,5¢ | 39°13,5¢ | 39°13,8¢ |
В | 39°15,0¢ | ||||
А | КП | 90°09,0¢ | 39°14,0¢ | ||
В | 129°23,0¢ | ||||
Измерение горизонтального угла способом
круговых приемов.
Способ измерения угла круговыми приемами применяют в том случае, если точка является вершиной более чем двух направлений. Принципиальная схема измерения горизонтального угла данным способом изображена на рисунке 2. Угол получают как разность двух направлений. Направление с наиболее благоприятными условиями для визирования принимают в качестве начального (например, DC на рисунке 2). Далее действуют в следующей последовательности:
- При круге лево на лимбе устанавливают отсчет, близкий к нулю, закрепляют алидаду и, вращая лимб, визируют на точку С. Установленный отсчет записывают в журнал измерений (табл. 2, столбец 3).
- При неподвижном лимбе вращают алидаду по часовой стрелке, наводят
зрительную трубу на точки А, В
и опять на С. После каждого визирования берут и записывают в журнал отсчеты (табл.
2, столбец 3). Их значения, полученные при визировании на начальное
направление, должны быть равны (полевой
контроль). При измерении техническим теодолитом разность между ними (незамыкание горизонта) не должна быть
больше 1′.
 Указанные действия составляют первый полуприём.
Указанные действия составляют первый полуприём. - Не изменяя положения лимба, переводят зрительную трубу через зенит и при круге право выполняют второй полуприём. При этом вращение алидады осуществляют против хода часовой стрелки. Если незамыкание горизонта отвечает допуску, вычисляют (табл. 2, столбец 4) средние из отсчетов (при этом усредняют только минуты, а градусы берут из первого полуприема) и по средним на начальное направление вычисляют незамыкание горизонта ω (табл. 2, столбец 5).
- Затем в средние направления вводят поправки Δ (табл. 2, столбец 4), которые вычисляют по формуле , где i – номер направления; n – число направлений (n= 3). Поправка – это часть невязки с противоположным знаком. Их суммируют высчитанными средними направлениями и записывают в столбец 5 таблицы 2. В заключение направления приводят к общему нулю, вычитая из всех направлений начальное.
Таблица 2.
Журнал измерения горизонтального угла способом круговых приемов.
Название Направления | Положение круга | Отсчет | Среднее направление | Исправленное направление | Приведенное направление |
1 | 2 | 3 | 4 | 5 | 6 |
С | КЛ | 0°01,5¢ | 0°02,0¢ | 0°02,0¢ | 0°00,0¢ |
КП | 180°02,5¢ | ||||
А | КЛ | 278°11,5¢ | +0,2¢ 278°12,0¢ | 278°12,2¢ | 278°10,2¢ |
КП | 98°12,5¢ | ||||
В | КЛ | 322°13,0¢ | +0,3¢ 322°13,2¢ | 322°13,5¢ | 322°11,5¢ |
КП | 142°13,5¢ | ||||
С | КЛ | 0°01,0¢ | 0°01,5¢ | ω = -0,5¢ | — |
КП | 180°02,0¢ |
Измерение горизонтального угла способом повторений.
Данный способ иногда используют для уменьшения ошибки отсчитывания горизонтальных углов. Суть его состоит в последовательном откладывании измеряемого угла на лимбе k раз при круге лево и столько же раз при круге право. При этом на заднюю точку наводят, вращая лимб, а на переднюю – вращая алидаду. Если n1 – отсчет, полученный при первом наведении на заднюю точку, а n2k – последний отсчет при наведении на переднюю, то . К результату следует добавлять 0; 90; 180 или 270° в зависимости от значения самого угла, например β <90°, 90° < β < 180° и т.д., при условии, что k=2.
Самостоятельная работа студентов
Задание. Заполните журналы измерения горизонтальных углов теодолитом.
Журнал измерения горизонтального угла одним полным приемом
Вариант 1
Название точек | Положение круга | Отсчет | Горизонтальный угол | Среднее значение | |
Стояния | Визирования | ||||
С | А | КЛ | 0°01,0¢ |
|
|
В | 39°14,5¢ | ||||
А | КП | 90°08,5¢ |
| ||
В | 129°22,5¢ | ||||
Вариант 2
Название точек | Положение круга | Отсчет | Горизонтальный угол | Среднее значение | |
Стояния | Визирования | ||||
С | А | КЛ | 0°00,5¢ |
|
|
В | 39°14,0¢ | ||||
А | КП | 90°08,0¢ |
| ||
В | 129°22,0¢ | ||||
Вариант 3
Название точек | Положение круга | Отсчет | Горизонтальный угол | Среднее значение | |
Стояния | Визирования | ||||
С | А | КЛ | 0°02,0¢ |
|
|
В | 39°15,5¢ | ||||
А | КП | 90°09,5¢ |
| ||
В | 129°23,5¢ | ||||
Журнал измерения горизонтальных углов круговыми приёмами
Вариант 1
Название направления | Положение круга | Отсчет | Среднее направление | Исправленное направление | Приведенное направление |
С | КЛ | 0°01,0¢ |
|
|
|
КП | 180°02,0¢ | ||||
А | КЛ | 278°11,0¢ |
|
|
|
КП | 98°12,0¢ | ||||
В | КЛ | 322°12,5¢ |
|
|
|
КП | 142°13,0¢ | ||||
С | КЛ | 0°00,5¢ |
|
|
|
КП | 180°01,5¢ |
Вариант 2
Название направления | Положение круга | Отсчет | Среднее направление | Исправленное направление | Приведенное направление |
С | КЛ | 0°00,5¢ |
|
|
|
КП | 180°01,5¢ | ||||
А | КЛ | 278°10,5¢ |
|
|
|
КП | 98°11,5¢ | ||||
В | КЛ | 322°12,0¢ |
|
|
|
КП | 142°12,5¢ | ||||
С | КЛ | 0°01,0¢ |
|
|
|
КП | 180°02,0¢ |
Вариант 3
Название направления | Положение круга | Отсчет | Среднее направление | Исправленное направление | Приведенное направление |
С | КЛ | 0°02,0¢ |
|
|
|
КП | 180°03,0¢ | ||||
А | КЛ | 278°12,0¢ |
|
|
|
КП | 98°13,0¢ | ||||
В | КЛ | 322°13,5¢ |
|
|
|
КП | 142°14,0¢ | ||||
С | КЛ | 0°01,5¢ |
|
|
|
КП | 180°02,5¢ |
Список использованной литературы
- Корнилов Ю.
 Н. Геодезия. Топографические съемки: Учебное пособие/Ю.Н. Корнилов.
Санкт-Петербургский государственный горный институт (технический университет).
СПб, 2008. – 145 с.
Н. Геодезия. Топографические съемки: Учебное пособие/Ю.Н. Корнилов.
Санкт-Петербургский государственный горный институт (технический университет).
СПб, 2008. – 145 с. - Чекалин С.И. Топографические и специальные карты: Учебное пособие по курсу «Картография» (для студентов дневного отделения специальности «Геоэкология»). М.: Российский госуд. геологоразв. ун-т., 2007. – 126 с.
- Ерилова И.И. Геодезия и маркшейдерия. Часть I: Задание и методические указания по выполнению лабораторных работ по курсу «Геодезия и маркшейдерия». М.: Темплан, 2011. – 37 с.
Угловые измерения | Геодезия | Студенту
Прибор, используемый для измерения горизонтальных и вертикальных углов называется:А) нивелиром;
В) тахеометром;
С) дальномером;
Д) теодолитом;
Е) мензулой.
Для установки теодолитов на местности используют:
А) столы;
В) штативы;
С) подставки;
Д) уровень;
Е) башмаки.
Принцип измерения горизонтального угла следующий :
А) Вершине А измеряемого угла ВАС устанавливают нивелир, круг с делениями прибора располагают горизонтально т. е. параллельно уровенной поверхности, его центр совмещают с точкой А, проекции направлении АВ и АС, угол между которыми измеряют, пересекут шкалу круга прибора по отсчетам В и С. Разность этих отсчетов дает искомый угол;
е. параллельно уровенной поверхности, его центр совмещают с точкой А, проекции направлении АВ и АС, угол между которыми измеряют, пересекут шкалу круга прибора по отсчетам В и С. Разность этих отсчетов дает искомый угол;
В) Вершине А измеряемого угла ВАС устанавливают теодолит, круг с делениями прибора располагают горизонтально т.е. параллельно уровенной поверхности, его центр совмещают с точкой А, проекции направлении АВ и АС, угол между которыми измеряют, пересекут шкалу круга прибора по отсчетам В и С. Разность этих отсчетов дает искомый угол;
С) Вершине А измеряемого угла ВАС устанавливают угольник, круг с делениями прибора располагают горизонтально т.е. параллельно уровенной поверхности, его центр совмещают с точкой А, проекции направлении АВ и АС, угол между которыми измеряют, пересекут шкалу круга прибора по отсчетам В и С. Разность этих отсчетов дает искомый угол;
D) Вершине А измеряемого угла ВАС устанавливают дальноиер, круг с делениями прибора располагают горизонтально т.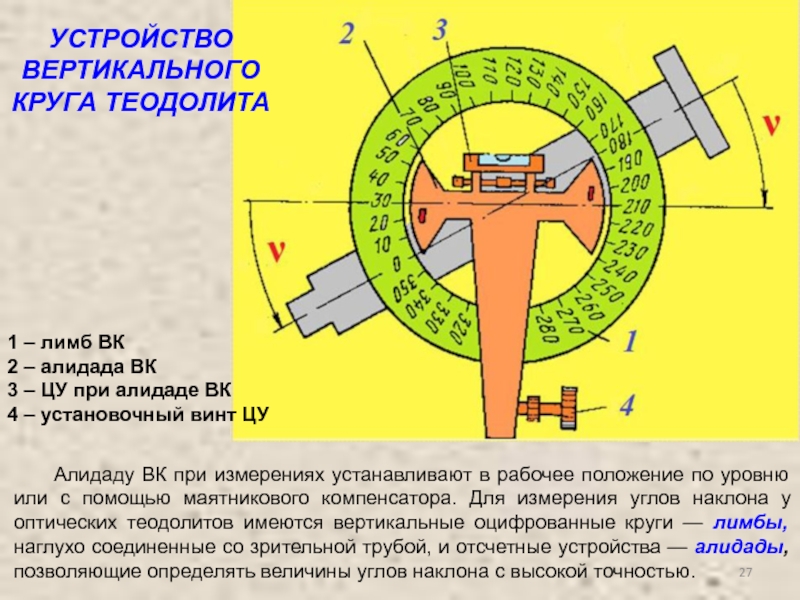 е. параллельно уровенной поверхности, его центр совмещают с точкой А, проекции направлении АВ и АС, угол между которыми измеряют, пересекут шкалу круга прибора по отсчетам В и С. Разность этих отсчетов дает искомый угол;
е. параллельно уровенной поверхности, его центр совмещают с точкой А, проекции направлении АВ и АС, угол между которыми измеряют, пересекут шкалу круга прибора по отсчетам В и С. Разность этих отсчетов дает искомый угол;
Е) Вершине А измеряемого угла ВАС устанавливают нивелир, круг с делениями прибора располагают горизонтально т.е. параллельно уровенной поверхности, его центр совмещают с точкой А, проекции направлении АВ и АС, угол между которыми измеряют, пересекут шкалу круга прибора по отсчетам В и С. Разность этих отсчетов дает искомый угол;
Принципиальная схема устройства теодолитов следующие :
А) три подъемных винта, алидада, штатив, рейка, экер;
В) три подъемных винта, лимб, алидада, оси;
С) подставка, зрительная труба, уровень ;
D) подставка, зрительная труба, экер, колышки;
Е) правильный ответ В и С.
Зрительная труба в геодезических приборах предназначены::
А) для получения угломерного отсчета;
В) для визирования на удаленные предметы;
С) для приведения частей или осей прибора горизонтальное или отвесное положение;
Д) для отсчитывания делений лимба теодолита;
Е) основанием теодолита и предназначена для приведения вертикальной оси вращения теодолита в отвесное положения.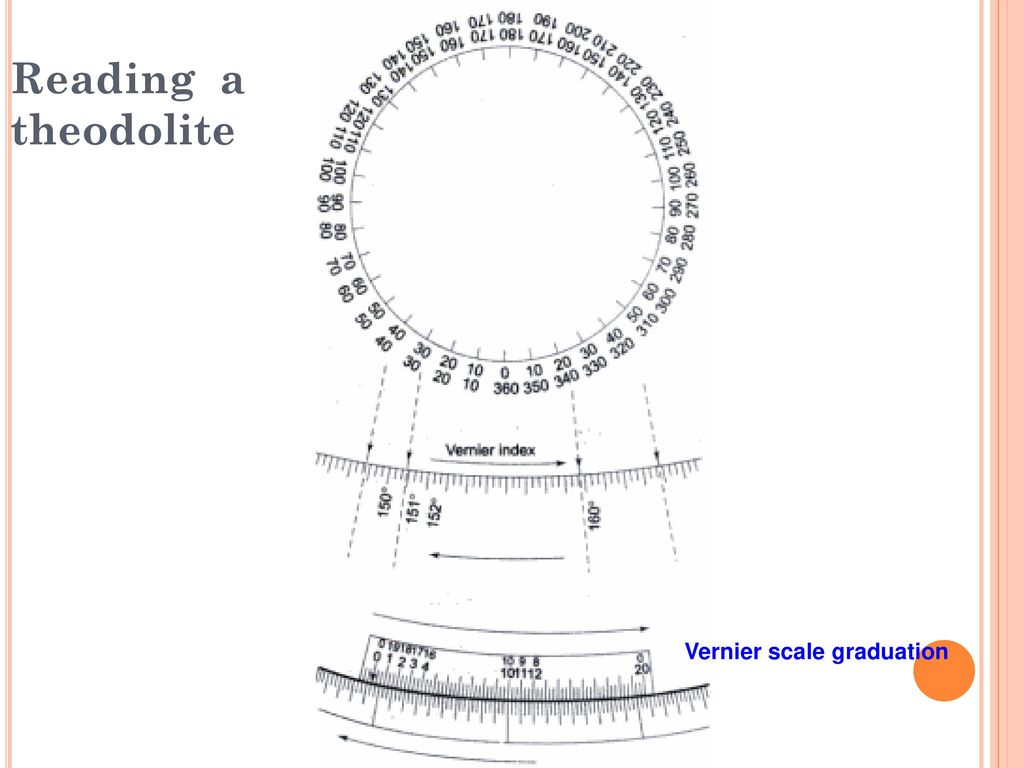
Уровни в геодезических приборах служат:
А) для получения угломерного отсчета;
В) для визирования на удаленные предметы;
С) для приведения частей или осей прибора горизонтальное или отвесное положение;
Д) для отсчитывания делений лимба теодолита;
Е) основанием теодолита и предназначена для приведения вертикальной оси вращения теодолита в отвесное положения.
Лимб и алидада теодолита предназначены::
А) для получения угломерного отсчета;
В) для визирования на удаленные предметы;
С) для приведения частей или осей прибора горизонтальное или отвесное положение;
Д) для отсчитывания делений лимба теодолита;
Е) основанием теодолита и предназначена для приведения вертикальной оси вращения теодолита в отвесное положения.
Лимб теодолита представляет:
А) горизонтальный и вертикальный круг с делениями градусной или градовой градуировки:
В) устройство, которое фиксирует положение подвижной визирной коллимационной плоскости трубы;
С) устройство, для визирования на удаленные предметы;
Д) устройство, для приведения частей или осей прибора горизонтальное или отвесное положение;
Алидада теодолита служит:
А) для фиксации положение подвижной визирной коллимационной плоскости трубы и для производства отсчета по лимбу с высокой точностью ;
В) для измерения расстояний по нитяному дальномеру и для визирования на удаленные предметы;
С) для перемещения двояковогнутой фокусирующей линзы зрительной трубы;
Д) для приведения с помощью подъемных винтов вертикальную ось теодолита в отвесное положение;
Е) основанием теодолита и позволяет получать мнимое и увеличенное изображения.
Отсчетные устройства теодолита предназначены:
А) для получения линейного отсчета;
В) для визирования на удаленные предметы;
С) для приведения частей или осей прибора горизонтальное или отвесное положение;
Д) для отсчитывания делений лимба теодолита;
Е) основанием теодолита и предназначена для приведения вертикальной оси вращения теодолита в отвесное положения.
Подставка теодолита с подъемными винтами служат:
А) для получения угломерного отсчета;
В) для визирования на удаленные предметы;
С) для приведения частей или осей прибора горизонтальное или отвесное положение;
Д) для отсчитывания делений лимба теодолита;
Е) основанием теодолита и предназначена для приведения вертикальной оси вращения теодолита в отвесное положения.
Кремальера теодолита служит:
А) для фиксации положение подвижной визирной коллимационной плоскости трубы и для производства отсчета по лимбу с высокой точностью ;
В) для измерения расстояний по нитяному дальномеру и для визирования на удаленные предметы;
С) для перемещения двояковогнутой фокусирующей линзы зрительной трубы;
Д) для приведения с помощью подъемных винтов вертикальную ось теодолита в отвесное положение;
Е) основанием теодолита и позволяет получать мнимое и увеличенное изображения.
В процессе поверок теодолита удостоверяются :
А) в правильном закрепление теодолита в штатив;
В) в правильном взаимном положении осей прибора;
С) в правильном расположении прибора на местности;
D) в правильном взятии отсчетов по микроскопу;
Е) в правильном хранение прибора;
Первая поверка теодолита :
А) Ось цилиндрического уровня горизонтального круга должна быть перпендикулярна оси вращения прибора;
В) Визирная ось трубы должна быть перпендикулярна оси вращения трубы;
С) Ось вращения трубы должна быть перпендикулярна оси вращения прибора;
D) Вертикальная нить сетки зрительной трубы должна быть перпендикулярно оси её вращения;
Е) компенсатор вертикального круга должен обеспечит неизменный отсчет по вертикальному кругу, при наклонах вертикальной оси теодолита в пределах ±2/
Вторая проверка теодолита:
А) Ось цилиндрического уровня горизонтального круга должна быть перпендикулярна оси вращения прибора;
В) Визирная ось трубы должна быть перпендикулярна оси вращения трубы;
С) Ось вращения трубы должна быть перпендикулярна оси вращения прибора;
D) Вертикальная ось сетки зрительной трубы должна быть перпендикулярно оси её вращения;
Е) компенсатор вертикального круга должен обеспечит неизменный отсчет по вертикальному кругу, при наклонах вертикальной оси теодолита в пределах ±2/.
Третья проверка теодолита:
А) Ось цилиндрического уровня горизонтального круга должна быть перпендикулярна оси вращения прибора;
В) Визирная ось трубы должна быть перпендикулярна оси вращения трубы;
С) Ось вращения трубы должна быть перпендикулярна оси вращения прибора;
D) Вертикальная ось сетки зрительной трубы должна быть перпендикулярно оси её вращения;
Е) компенсатор вертикального круга должен обеспечит неизменный отсчет по вертикальному кругу, при наклонах вертикальной оси теодолита в пределах ±2/.
Четвертая поверка теодолита:
А) Ось цилиндрического уровня горизонтального круга должна быть перпендикулярна оси вращения прибора;
В) Визирная ось трубы должна быть перпендикулярна оси вращения трубы;
С) Ось вращения трубы должна быть перпендикулярна оси вращения прибора;
D) Вертикальная нить сетки зрительной трубы должна быть перпендикулярно оси её вращения;
Е) компенсатор вертикального круга должен обеспечит неизменный отсчет по вертикальному кругу, при наклонах вертикальной оси теодолита в пределах ±2/.
Поверка теодолита с индексами К:
А) Ось цилиндрического уровня горизонтального круга должна быть перпендикулярна оси вращения прибора;
В) Визирная ось трубы должна быть перпендикулярна оси вращения трубы;
С) Ось вращения трубы должна быть перпендикулярна оси вращения прибора;
D) Вертикальная ось сетки зрительной трубы должна быть перпендикулярно оси её вращения;
Е) компенсатор вертикального круга должен обеспечит неизменный отсчет по вертикальному кругу, при наклонах вертикальной оси теодолита в пределах ±2/.
Место нуля это:
А) отсчет по вертикальному кругу, соответствующий горизонтальному положению визирной оси и уровня при алидаде в нуль-пункте;
В) отсчет по горизонтальному кругу, соответствующий горизонтальному положению визирной оси и уровня при алидаде в нуль-пункте;
С) горизонтальность отчетного индекса у теодолитов с компенсатором при вертикальном круге;
Д) ответ А и С;
Е) ответ В и С;
Место нуля при работе теодолитом 3Т30 вычисляют:
МО=(П+Л)/2;
МО=(П+Л+1800)/2;
МО=(Л-П-1800)/2;
МО=(Л-П)/2;
МО=(П-Л)/2;
Место нуля при работе теодолитом 3Т5КП вычисляют:
МО=(П+Л)/2;
МО=(П+Л+1800)/2;
МО=(Л-П-1800)/2;
МО=(Л-П)/2;
МО=(П-Л)/2;
Для автономного определения истинных азимутов направлений применяют:
А) кодовые теодолиты;
В) гиротеодолиты;
С) теодолиты 3Т30;
D) теодолиты 3Т5КП;
Е) теодолиты 2Т30.
Для автоматизаций процесса измерения углов применяют:
А) гидравлические теодолиты;
В) аэродинамические теодолиты;
С) кодовые теодолиты;
D) теодолиты 3Т5КП;
Е) теодолиты 2Т30КП.
Лазерный теодолит конструктивно характерен тем, что обычном теодолите:
А) зрительная труба заменена визирной осью;
В) зрительная труба заменена лазерным излучателем;
С) зрительная труба заменена лазерной оптической осью;
D) зрительная труба заменена геометрической осью;
Е) алидада заменена лазерным лучом.
Лазерные геодезические приборы конструируют таким образом чтобы;
А) лазер был установлен параллельно визирной оси;
В) лазер был установлен вертикально визирной оси;
С) лазерный пучок направлялся через зрительную трубу прибора;
D) ответ А и С;
Е) ответ В и С;
Поверками лазерных теодолитов определяют соответствие;
А) геометрических условий взаимного положения всех частей прибора;
В) взаимного положения визирных осей и вертикальной оси прибора;
С) взаимного положения зрительной трубы, излучателя и других частей
прибора;
D) ответ А и С;
Е) ответ В и С.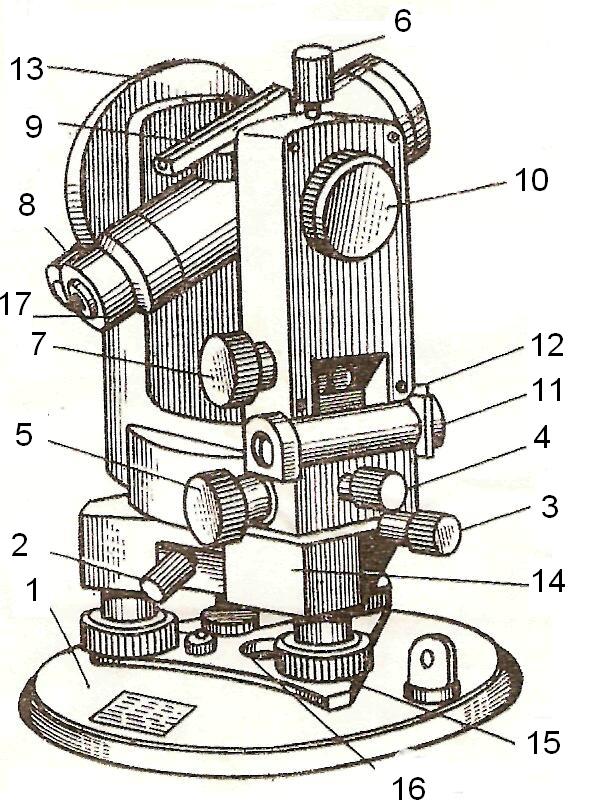
4. Определение места нуля – вертикального круга — Документ
4. Определение места нуля – вертикального круга.
Местом нуля (МО) называется отсчет по вертикальному кругу при горизонтальном положении трубы. МО определяют так: теодолитом приводят в горизонт.положение, трубу теодолита центром сетки нитей наводят на точку, удаленную от теодолита на 50м и находящуюся примерно на одном уровне с лучом визирования. Берут отсчет по вертикальному кругу Акп. Далее трубу переводят через зенит, вторично наводят ее на ту же точку и берут отсчет на Акл. Место нуля определяют по формуле МО= акл+ акп/2 ; МО ≤ 1I
(угол наклона ) = акл— акп/2 а0КЛ= +МО
Этот
отсчет а0КЛ устанавливают наводящим винтом трубы.
При этом центр сетки уходит с наблюдаемой
точки. Работая вертикальными юстировычными
винтами при сетке, центр сетки наводят
на точку.
Измерение угла наклона. Трубу теодолита наводит на высоту прибора и берем отсчет по вертикальному кругу. Этот отсчет и равен углу наклона, если МО=0, если нет, тогда = аКЛ – МО;
=МО- акп
5. Измерение вертикальных углов.
Вертикальным углом называется угол наклона составленный визирной осью зрительной трубы направленной на определенную точку. С гор. плоскостью измерение верт.углов производится с помощью верт.круга прикрепленного на оси вращения зрительной трубы (гориз.оси)
Лимб вертикального круга жестко связан со зрительной трубой, при чем нулевой диаметр лимба параллелен визирной оси трубы. При изменении верт.углов лимб вращается вместе с трубой относительно неподвижной алидады.
При гор.положении трубы отсчет по верт.кругу должен быть равен 0, однако бывает что этот отсчет отличный от поля, он называется местом нуля МО.
6. Нивелир. Классификация. Устройство нивелира
Нивелир – инструмент для определения разности
высот
между несколькими точками земной
поверхности относительно условного
уровня т. е определение превышения.
е определение превышения.
Нивелирование – работы, связанные с определением высот точек земной поверхности. Под высотой точки понимают расстояние по вертикали от данной точки земной поверхности до поверхности, взятой за начало отсчета высот. Высоты бывают абсолютными и относительными. Отсчет абс.высот в нашей стране ведется от среднего уровня воды Балтийского моря. Отсчет отн.(условных) высот ведется от некоторой поверхности условно применяемой за начало отсчета высот. В строительстве, как правило, за такую поверхность принимается чистый пол первого этажа.
Способы нивелирования: геометрическое(нивелир), тригонометрическое(теодолит, h=d*tgV+i-v-f, где i-высота наведения пи измерений игла наклона, f-поправка за кривизну Земли), гидростатическое(основывается на свойстве жидкостей находиться в сообщающихся сосудах на одном уровне), барометрические (основано на свойстве разности воздушного давления в различных по высоте на уровенной поверхностью точках; барометр-анероид; микробарометр)
При нивелировании из середины нивелир устанавливают между нивелирными точками, одна из которых называется задней (относительно нее определяется превышение), другая передней(точка, для которой определяют превышение)
В
точках А и В ставят рейки, ноль рейки
внизу. Трубу нивелира, после приведения
ее в гор.положение, наводят сначала на
заднюю рейку и берут отсчет а3,
затем переднюю(отсчет вП).
h=a3-вП.
Превышение равно: отсчет на заднюю
рейку, минус отсчет на переднюю рейку.
При нивелировании вперед нивелир
устанавливают над задней точкой, над
передней ставится рейка. Превышение
равно: высота прибора минус отсчет на
переднюю рейку h=I—
вП
Трубу нивелира, после приведения
ее в гор.положение, наводят сначала на
заднюю рейку и берут отсчет а3,
затем переднюю(отсчет вП).
h=a3-вП.
Превышение равно: отсчет на заднюю
рейку, минус отсчет на переднюю рейку.
При нивелировании вперед нивелир
устанавливают над задней точкой, над
передней ставится рейка. Превышение
равно: высота прибора минус отсчет на
переднюю рейку h=I—
вП
Станция – место установки прибора. Нивелирование с одной станцией называется простым, с несколькими – сложным
a1-b1=h1
a2-b2=h2
a3-b3=h3
hAB=h1+h2+h3=(a1-b1)+(a2-b2)+(a3-b3)=
Устройство:
зрительная труба; цилиндрический
уровень при трубе; элевационный винт;
установочный круглый уровень;
закрепительный и микрометренный винты,
подставка с тремя подъемными винтами.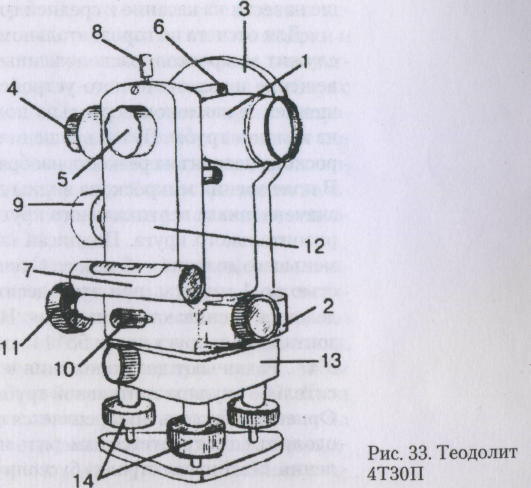
3.Измерение горизонтального угла способом полного приема
Лимб закрепляем. Вращением алидады например при КП наводим трубу теодолита на правую точку и берем отсчет по горизонтальному кругу. Далее открепляем алидаду(лимб не трогаем) вращением трубы наводим на левую точку и берм отсчет. Далее трубу переводят через зенит. Лимб смещаю на произвольный угол , после чего его закрепляют. И снова наводят трубу теодолита на правую и левую точки. Каждый раз беря отсчеты по горизонтальному кругу. Если отсчет на правую точку меньше отсчета на левую точку, то необходимо к отсчету на правую точку прибавить 360° и отнять отсчет на левую точку. Угол считается правильно измеренным, если расхождение между углами не превышает двойной точности теодолита. За окончательное значение берут среднее.
7. Поверки и юстировка нивелира.
1.
Ось круглого
уровня должна быть параллельна оси
вращения нивелира.
Круглый уровень устанавливают параллельно
линии двух подъемных винтов и, действуя
тремя винтами, приводят пузырек в
нуль-пункт. Затем поворачивают верхнюю
часть нивелира на 180гр относительно
исходного положения. Если после этого
пузырек уровня остался в нуль-пункте,
то условие выполнено. В противном случае,
действуя исправительными винтами
уровня, перемещают пузырек в нуль-пункт
на половину дуги его отклонения. Затем
подъемными винтами вновь выводят пузырек
уровня в нуль-пункт и повторяют те же
действия до выполнения условия.
Затем поворачивают верхнюю
часть нивелира на 180гр относительно
исходного положения. Если после этого
пузырек уровня остался в нуль-пункте,
то условие выполнено. В противном случае,
действуя исправительными винтами
уровня, перемещают пузырек в нуль-пункт
на половину дуги его отклонения. Затем
подъемными винтами вновь выводят пузырек
уровня в нуль-пункт и повторяют те же
действия до выполнения условия.
2. Горизонтальный
штрих сетки нитей должен быть
перпендикулярен, а вертикальный
параллелен оси вращения нивелира.
Перпенд икулярность горизонтального
и вертикального штрихов гарантируется
заводом-производителем. Поэтому поверку
можно выполныть несколькими способами.
Первый – на расстоянии 20-25 м от нивелира
подвешивают отвес. По кругому уровню
приводят ось вращения в отвесное
положение. Зрительной трубой визируют
на отвес и совмещают один из концов
вертикального штриха с нитью. Если
другое конечно отходит от нмтм более
чем на 0,5 мм, то проводят исправление
положеня сетки нитей. Второй способ –
нивелир наводят на рейку так, чтобы ее
изображнеие в трубе оказалось в левой
части поля зрения, и берут отсчет по
горизонтальной нити сетки. Поворотом
нивелира переводят изображение в правую
часть и вновь берут отсчет по рейке.
Взятые отсчеты не должны различаться
более чем на 1 мм.
Второй способ –
нивелир наводят на рейку так, чтобы ее
изображнеие в трубе оказалось в левой
части поля зрения, и берут отсчет по
горизонтальной нити сетки. Поворотом
нивелира переводят изображение в правую
часть и вновь берут отсчет по рейке.
Взятые отсчеты не должны различаться
более чем на 1 мм.
3. Ось
цилиндрического уровня должна быть
параллельна визирной оси зрительной
трубы. Поверка
выполнятеся двойным нивелированием
вперед одной и той же линии длиной 40-60
м с разных ее концов. Для это концы линии
AB
закрепляют на местности кольями. Нивелир
располагают над точкой A,
производят предварительную установку
нивелира по круглому уровню и измеряют
высоту прибора i
с точностью до мм. В точке B
устанавливают рейку, с помощью
элевационного винта приводят пузырек
цилиндрического уровня в нуль-пункт и
делают отсчет b1
по рейке.
Если визирная ось и ось цилиндрического
уровня непараллельны, то вместо
правильного отсчета с по рейке будет
взят отсчет b1,
содержащий погрешность x. Тогда превышение точки B
над A
будет h
= i1
– с = i1
– (b1
– x).
Затем меняют мастами нивелир и рейку,
измеряют высоту прибора i2
по рейке b2.
Отсчет b2
будет ошибочным на ту же величину x,
тогда h
= c2
– i2
= b2
– x
– i2.
Решая уравнение относительно x
получим,
Тогда превышение точки B
над A
будет h
= i1
– с = i1
– (b1
– x).
Затем меняют мастами нивелир и рейку,
измеряют высоту прибора i2
по рейке b2.
Отсчет b2
будет ошибочным на ту же величину x,
тогда h
= c2
– i2
= b2
– x
– i2.
Решая уравнение относительно x
получим,
9. Для технического нивелирования используют нивелиры и рейки. Работу на станции выполняют в следующей последовательности:
1. На крайние точки A и В нивелируемой линии устанавливают рейки, и примерно на равном удалении от них — нивелир. Неравенство плеч на станции не должно превышать 10 м;
2. Нивелир приводят в рабочее положение, наводят трубу на заднюю рейку и берут отсчет по черной ее стороне ач;
3. Наводят трубу на переднюю рейку и берут отсчеты сначала по черной, а затем по красной стороне bч и bк;
4. Наводят трубу на заднюю рейку и берут отсчет по красной стороне ак;
5.
Если кроме крайних точек A и B необходимо
определить высоты точек C1, C2,…, Cn
промежуточных точек, то заднюю рейку
последовательно устанавливают на эти
точки и берут отсчеты C1, C2,. .., Cn по черной
стороне. При выполнении ответственных
работ отсчеты на промежуточных точках
производят по обеим сторонам рейки. При
использовании уровенных нивелиров
перед каждым отсчетом пузырек приводят
в нуль-пункт;
.., Cn по черной
стороне. При выполнении ответственных
работ отсчеты на промежуточных точках
производят по обеим сторонам рейки. При
использовании уровенных нивелиров
перед каждым отсчетом пузырек приводят
в нуль-пункт;
6. Для контроля вычисляют разность нулей передней РОп=ак-ач и задней РОз=bк-bч. Расхождение разности нулей по абсолютной величине не должно превышать 5 мм;
7. На каждой станции вычисляют значения превышений, определяемых по черным и красным сторонам реек: hч=ач-bч, hк=ак-bк. Измерения считают выполненными правильно, если hч-hк
В техническом нивелировании расстояние от нивелира д реек не должно превышать 120 м. Высоту передней точки вычисляют по формуле НB=НA+h. Высоты промежуточных точек удобно вычислять через горизонт прибора (ГП). ГП — высота визирного луча над исходной уровенной поверхностью. ГП=НA+а=НB+b. Высоты промежуточных точек НCi=ГП-Ci.
Случайные
и систематические погрешности при
нивелировании возникают вследствие
недостаточной точности нивелира и
реек, неполной юстировки нивелира,
влияния внешней среды и нарушении
методики измерений.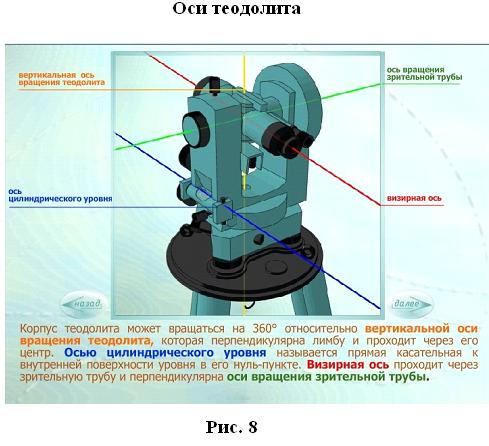
Для уменьшения приборных погрешностей превышения рекомендуется измерять способом из середины по двум сторонам реек, а рейки удерживать отвесно на устойчивых предметах. Предельные расстояния от нивелира до реек ограничивают 100-120 м, погрешности измерений превышений на станции в этом случае не превысят 5 мм.
16.Классификация условных знаков.
Топографические условные знаки принято разделять на масштабные, внемасштабные, линейные и пояснительные.
Масштабные условные знаки служат для изображения топографических объектов, которые в плане могут быть выражены в масштабе данной карты или плана.
Внемасштабные условные знаки используются для передачи объектов, не выражающихся в масштабе карты. Эти знаки не позволяют судить о размерах изображаемых местных предметов.
Линейные условные
знаки предназначены для изображения
протяженных объектов на местности,
например железные и автомобильные
дороги, линии электропередач и другие.
Пояснительные условные знаки применяются в целях дополнительной характеристики показываемых на карте местных предметов. Например, длина, ширина и грузоподъемность моста, ширина и характер покрытия дорог, средняя толщина и высота деревьев в лесу, глубина и характер грунта брода и т. д. Различные надписи и собственные названия объектов на картах также носят пояснительный характер; каждая из них выполняется установленным шрифтом и буквами определенного размера.
8. Нивелированием называется совокупность измерений на местности, в результате которых определяют превышения между точками местности с последующим вычислением их высот относительно принятой исходной поверхности.
Различают два способа геометрического нивелирования: вперед и из середины.
При нивелировании
вперед прибор
устанавливают над точкой А, измеряют
его высоту V и
берут отсчет П по
рейке в точке В. Превышение определяют
вычитанием из высоты прибора V отсчета П.
h = V – П.
Высоту передней точки В вычисляется по формуле:
Высоту визирного луча на уровенной поверхностью называют горизонтом инструмента HГИ и вычисляют
НГИ = НА + З = НА + V.
При
нивелировании из середины нивелир
располагают между двумя точками примерно
на одинаковых расстояниях (рис.61, а). В
точках устанавливают отвесно рейки с
сантиметровыми делениями. Их ставят на
колышек, вбитый вровень с землей, или
на специальный костыль, так как рейка
под собственной тяжестью будет давить
на землю и отсчет по ней будет меняться.
Визирный луч зрительной трубы нивелира
последовательно наводят на рейки и
берут отсчеты З и П,
которые записывают в миллиметрах в
журнал нивелирования. Отсчет по рейке
производят по средней нити нивелира,
т. е. по месту, где проекция средней нити
пересекает рейку. Превышение между
точками определяют по формуле
е. по месту, где проекция средней нити
пересекает рейку. Превышение между
точками определяют по формуле
h = З – П
где З – отсчет назад на заднюю точку А; П – отсчет вперед на переднюю точку B.
Если же превышение между точками определяют только после нескольких установок нивелира, такое нивелирование называют сложным или последовательным.
Рис. 62. Последовательное нивелирование.
В этом случае точки С и D называют связующими. Превышение между ними определяют как при простом нивелировании:
; ;
h = ∑З – ∑П
17. Горизонтали и их свойства.
Горизонталь-линия, соединяющая точки равных высот.
Дополнительные горизонтали — проводятся прерывистой линией , их высота сечения равна половине основной оси сечения.
Бергштрихи —
указатели направления скатов ( на картах
и планах — короткие черточки на горизонталях
( перпендикулярно им ) по направлению
покатостей ).
Свойства горизонталей: все точки горизонтали имеют одну и ту же высоту; горизонтали никогда не пересекаются; расстояние между горизонталями характеризует крутизну склона; водораздельные линии и оси лощин пересекаются горизонталями под прямым углом; горизонтали прерываются у водоемов, но с последующим продолжением.
При высоте сечения рельефа 1,2, 5 м утолщается каждая 5-я горизонталь, с отметками кратными 5, 10, 25 м соответственно. При высоте сечения рельефа 0,25,0,5,2,5 м утолщается каждая 4-я горизонталь, с отметками кратными 1, 2, 10 м соответственно.
Заложение(d)-расстояние между соседними горизонталями в горизонтальной плоскости. Оно характеризует крутизну склонов; чем заложение меньше, тем склон круче; чем заложение больше, тем крутизна ската меньше.
Высота сечения (h)-расстояние между горизонталями в вертикальной плоскости.
12.Измерение длин линий 20-ти метровой лентой
Линейные
измерения выполняются непосредственно
с помощью специальных мерных приборов(лент,
рулеток) и косвенно с помощью дальномеров
и других величин(углов) по определенным
формулам вычисляют расстояния.
Наиболее
большое применение в практике получила
20-ти метровая стальная лента. На концах
ее есть вырезы, в которые при измерениях
вставляются металлические шпильки.
Напротив вырезов нанесены штрихи
,расстояние между которыми и определяет
длину ленты. Метровые деления обозначены
бляшками, на которых выдавлен номер
метра. Полуметры отмечены заклепками.
Дециметровые деления обозначены
сквозными отверстиями. К концам ленты
крепятся ручки, которые служат для
натяжения ленты в процессе измерения.
К каждой ленте прилагается набор шпилек:
6 или 11 штук. Измерение линии выполняет
бригада из 2 человек. Ленту разматывают
с кольца. Передний мерщик (МП) с десятью
(пятью) шпильками протягивает передний
конец ленты и по указанию заднего мерщика
(МЗ) укладывает ее в створ измеряемой
линии. МЗ совмещает начальный штрих
заднего конца ленты с начала линии,
выставляя в вырез ленты шпильку. МП
встряхивает ленту, натягивает ее и в
вырез на переднем конце вставляет
шпильку, МП снимает со шпильки ленту, и
оба переносят ее вперед вдоль линии. Дойдя до первой шпильки, МЗ закрепляет
на ней ленту, ориентирует МП по передней
вехе. Затем работа продолжается в том
же порядке, что и на первом уложении
ленты. Целое уложение ленты называется
пролетом. Когда все 11(6) шпилек окажутся
выставлены у МЗ окажется 10(5) шпилек. МЗ
передает МП все собранные шпильки.
D=100*a+20*b+
r, где а-число передач, b-число
шпилек у МЗ по окончанию измерений,
r-остаток.
Для контроля линию измеряют вторично.
Дойдя до первой шпильки, МЗ закрепляет
на ней ленту, ориентирует МП по передней
вехе. Затем работа продолжается в том
же порядке, что и на первом уложении
ленты. Целое уложение ленты называется
пролетом. Когда все 11(6) шпилек окажутся
выставлены у МЗ окажется 10(5) шпилек. МЗ
передает МП все собранные шпильки.
D=100*a+20*b+
r, где а-число передач, b-число
шпилек у МЗ по окончанию измерений,
r-остаток.
Для контроля линию измеряют вторично.
11. Тригонометрическое нивелирование
Тригонометрическое нивелирование выполняют с помощью теодолита и нивелирной рейки. Для определения превышения измеряют угол наклона υ и горизонтальное проложение d или наклонное расстояние до наблюдаемой точки D.
Устанавливают
теодолит на штатив, центрируют его над
точкой А (как
показано на рисунке), приводят основную
ось прибора в отвесное положение
и при помощи металлической рулетки как
можно более
тщательно измеряют высоту in прибора
от верха колышка А до
горизонтальной оси вращения трубы. Измеренное значение
высоты iп записывают
в журнале тригонометрического
нивелирования
и отмечают повязкой на нивелирной рейке,
которую ставят затем на наблюдаемую
точку В.
Измеренное значение
высоты iп записывают
в журнале тригонометрического
нивелирования
и отмечают повязкой на нивелирной рейке,
которую ставят затем на наблюдаемую
точку В.
Наводят трубу на точку В; после примерного наведения на нее в горизонтальной плоскости проверяют положение пузырька цилиндрического уровня при алидаде горизонтального круга. Если он отклонился, то одним из подъемных винтов возвращают его в нуль-пункт. Только после этого наводят среднюю горизонтальную нить сетки на повязку, укрепленную на рейке на высоте прибора. Если по условиям местности повязка не видна, то наводят на верх рейки и производят отсчеты по нитяному дальномеру и по вертикальному кругу.
Переводят трубу через зенит и повторяют наведение при другом положении вертикального круга теодолита. Постоянно следят за положением пузырька уровня; если возникает необходимость, приводят его в нуль-пункт.
Отсчеты
по вертикальному кругу используют для
вычисления
значения места нуля МО и угла наклона
v.
Вычисляют превышение точки В над станцией А, используя следующие формулы.
При визировании на верх рейки
h = D’/2*sin2v + in — l
где D‘ — наклонное расстояние, определенное при помощи нитяного дальномера теодолита по формуле D’=Kn+c ; v— угол наклона линии визирования; / — высота визирования; К — коэффициент нитяного дальномера; п — количество делений рейки, уместившихся в поле зрения трубы между крайними дальномерными нитями сетки; с≈0 представляет собой постоянное слагаемое нитяного дальномера.
При визировании на повязку, фиксирующую высоту прибора на рейке (l=in), определяют
h = h‘ = D’/2*sin2v.
От известной высоты станции hA через вычисленное превышение h легко вычисляют высоту наблюдаемой точки
HB=HA+ h
2. Поверки
теодолита
Поверки
теодолита
Первая поверка
Ось цилиндрического уровня должна быть перпендикулярна оси вращения прибора. Поверку делают так: устанавливают уровень по направлению 2-х подъёмных винтов, работая которыми приводят пузырёк уровня в нуль-пункт. Далее, разворачивают алидаду на 90° и устанавливают уровень по направлению одного винта. Затем снова устанавливают уровень по направлению 2-х винтов, при необходимости приводят пузырёк в нуль-пункт. Далее,поворотом алидады, разворачивают уровень на 180°. Если при этом пузырёк остался в нуль пункте — поверка выполнена.В противном случае приступают к юстировке(исправлению осей).Юстировка: работая подъёмными винтами, по направлению которых находится уровень, перемещают пузырёк уровня к нуль — пункту на половину отклонения. Окончательно пузырёк приводят в нуль-пункт, работая исправительными винтами при уровне. Для контроля поверку повторяют.
Вторая поверка
Ось
визирования трубы должна быть
перпендикулярна горизонтальной оси
вращения трубы. Теодолит приводят в горизонтальное
положение. Трубу теодолита центром
сетки нитей наводят на удалённую
точку(40-60м) и берут отсчет по горизонтальному
кругу при КП. Затем трубу переводят
через зенит и наводят на ту же точку.
Берут отсчет по горизонтальному кругу
при КЛ. Если отсчет при КП=КЛ±180° или
отличаются не более чем на двойную
точность прибора, то условие выполнено.В
противном случае вычисляют калимационную
погрешность по формуле С=КП-(КЛ±180)/2. Для
устранения калимационной погрешности
вычисляют отсчет соответствующий
правильному положению оси визирования.
Теодолит приводят в горизонтальное
положение. Трубу теодолита центром
сетки нитей наводят на удалённую
точку(40-60м) и берут отсчет по горизонтальному
кругу при КП. Затем трубу переводят
через зенит и наводят на ту же точку.
Берут отсчет по горизонтальному кругу
при КЛ. Если отсчет при КП=КЛ±180° или
отличаются не более чем на двойную
точность прибора, то условие выполнено.В
противном случае вычисляют калимационную
погрешность по формуле С=КП-(КЛ±180)/2. Для
устранения калимационной погрешности
вычисляют отсчет соответствующий
правильному положению оси визирования.
акл=КЛ-С
акп=КП-С
Работая наводящим винтом алидады по горизонтальному кругу устанавливаем отсчет акл или акп , при этом центр сетки уйдет с наблюдаемой точки. Работая горизонтальными исправительными винтами при сетке наводим центр сетки на наблюдаемую точку. Для контроля поверку повторяют.
Третья поверка
Вертикальная
нить сетки должна быть вертикальна,
горизонтальная – горизонтальна. Взаимную перпендикулярность этих двух
нитей гарантирует завод. Проверяется
или вертикальность, или горизонтальность
нитей. Вертикальность вертикальных
нитей проверяют так: на расстоянии 8-10
м от теодолита закрепляют отвес. После
приведения инструмента в горизонтальное
положение трубу наводят на нить отвеса.
Если нить сетки совпала с нитью отвеса,
то условие выполнено.В противном случае
приступают к юстировке: ослабив
винты, скрепляющие окулярную часть с
объективной, рукой поворачивают окулярную
часть до совпадения вертикальной нити
с нитью отвеса. После чего винты
закрепляют, поверку повторяют.
Взаимную перпендикулярность этих двух
нитей гарантирует завод. Проверяется
или вертикальность, или горизонтальность
нитей. Вертикальность вертикальных
нитей проверяют так: на расстоянии 8-10
м от теодолита закрепляют отвес. После
приведения инструмента в горизонтальное
положение трубу наводят на нить отвеса.
Если нить сетки совпала с нитью отвеса,
то условие выполнено.В противном случае
приступают к юстировке: ослабив
винты, скрепляющие окулярную часть с
объективной, рукой поворачивают окулярную
часть до совпадения вертикальной нити
с нитью отвеса. После чего винты
закрепляют, поверку повторяют.
Четвертая поверка
Горизонтальная
ось вращения трубы должна быть
перпендикулярна оси вращения теодолита. Инструмент устанавливают на расстоянии
20-30м от высокого предмета, приводят в
горизонтальное положение. Трубу теодолита
центром сетки наводят на высокую
выбранную точку. Затем трубу опускают
вниз(до верхней части цоколя здания) и
находим проекцию точки внизу. Трубу
переводят через зенит и повторяют
предыдущее действие. Если расхождение
между проекциями не превышает 3 мм,то
условие выполнено. Юстировка производится
в мастерской.
Трубу
переводят через зенит и повторяют
предыдущее действие. Если расхождение
между проекциями не превышает 3 мм,то
условие выполнено. Юстировка производится
в мастерской.
1.Теодолит, основные его части и их назначения, классификация теодолитов.
Теодолит – геодезический прибор, предназначенный для измерения горизонтальных и вертикальных углов, расстояний и углов ориентирования.
Теодолиты классифицируют по разным признакам: точности, конструктивным особенностям, назначению. По точности теодолиты различают на:
1)высокоточные(Т0,5 , Т1)обеспечивающие точность измерения угла до 1й секунды.
2)точные(Т2,Т5)
3)технические(Т15,Т30,Т60)
Устройство теодолита
Теодолит состоит из нижнего круга-лимба К центральной части лимба крепится ось. Края лимба скошены, на них нанесены штрихи(деления).
По
кругу лимба нанесены градусные деления
в виде штрихов. Каждый штрих соответствует
определённой градусной мере. Деления
возрастают по часовой стрелке. Над
лимбом, не касаясь его, помещён второй
круг – алидада. Алидада имеет отсчетные
приспособления или в виде штриха, или
в виде шкалы. При лимбе и алидаде имеются
зажимные и наводящие винты. К верхней
части алидады крепятся колонки, которые
несут ось вращения трубы. Кремальера
служит для четкого изображения
наблюдаемого предмета(фокусировки).
При трубы имеются зажимной и наводящий
винты. Труба состоит из окулярной и
объективной частей. В окулярной части
трубы помещена стеклянная пластинка,
на которой нанесены штрихи: вертикальный
и 3 горизонтальных. Стекло взято в оправу
и удерживается в трубе с помощью
исправительных винтов при сетке.
Окулярная часть соединена с объективной
с помощью 4х винтов. Нижняя часть теодолита
называется подставкой ,в центральной
части которой имеется место для установки
теодолита на штатив. Подставка имеет
три подъёмных винта, с помощью которых
прибор приводится в горизонтальное
положение. О горизонтальности судят по
положению пузырька цилиндрического
уровня, находящегося на алидаде
горизонтального круга.
Деления
возрастают по часовой стрелке. Над
лимбом, не касаясь его, помещён второй
круг – алидада. Алидада имеет отсчетные
приспособления или в виде штриха, или
в виде шкалы. При лимбе и алидаде имеются
зажимные и наводящие винты. К верхней
части алидады крепятся колонки, которые
несут ось вращения трубы. Кремальера
служит для четкого изображения
наблюдаемого предмета(фокусировки).
При трубы имеются зажимной и наводящий
винты. Труба состоит из окулярной и
объективной частей. В окулярной части
трубы помещена стеклянная пластинка,
на которой нанесены штрихи: вертикальный
и 3 горизонтальных. Стекло взято в оправу
и удерживается в трубе с помощью
исправительных винтов при сетке.
Окулярная часть соединена с объективной
с помощью 4х винтов. Нижняя часть теодолита
называется подставкой ,в центральной
части которой имеется место для установки
теодолита на штатив. Подставка имеет
три подъёмных винта, с помощью которых
прибор приводится в горизонтальное
положение. О горизонтальности судят по
положению пузырька цилиндрического
уровня, находящегося на алидаде
горизонтального круга.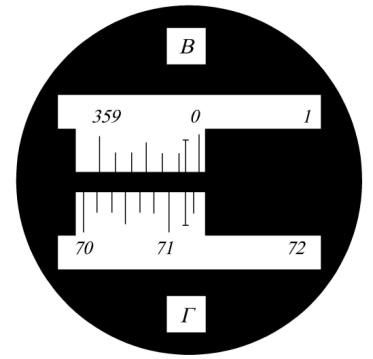
3 Требования к геодезии для наук о Земле | Точная геодезическая инфраструктура: национальные требования к общему ресурсу
Эпохав гидрологии суши, открывающая важные новые перспективы для исследований земного водного цикла, прогнозирования наводнений и водных ресурсов.
ПОГОДА Спутниковые изображения, показываемые по телевидению, могут создать впечатление, что прогнозы погоды основаны на этих изображениях, но на самом деле прогнозы основаны на физических моделях тропосферы , самых нижних 14 километров атмосферы.Эти модели должны постоянно получать измерения состояния атмосферы (давления, температуры, влажности и ветра) на разных высотах вокруг планеты, чтобы соответствовать реальным атмосферным условиям. Способность предсказывать как серьезность, так и временную и пространственную протяженность погодных изменений, особенно осадков, имеет решающее значение для общественной безопасности и сельского хозяйства, и правительства всего мира сотрудничают для сбора данных, используемых в прогнозах. На протяжении десятилетий исходные данные для этих моделей предоставлялись радиозондами, более известными как метеозонды.К сожалению, пространственное распределение пунктов радиозондов ограничено как из-за отсутствия покрытия над океанами, так и из-за значительного сокращения числа пунктов в южном полушарии. Увеличение количества запусков радиозондов в день сдерживается стоимостью оборудования, которое нельзя использовать повторно. Геодезисты, ориентированные на точное позиционирование, используют поправки для устранения атмосферных эффектов, которые считаются источником шума в их измерениях. И наоборот, эти же поправки могут быть использованы метеорологами для лучшего понимания атмосферы.Таким образом, улучшение геодезической инфраструктуры приносит пользу обеим областям науки.
На протяжении десятилетий исходные данные для этих моделей предоставлялись радиозондами, более известными как метеозонды.К сожалению, пространственное распределение пунктов радиозондов ограничено как из-за отсутствия покрытия над океанами, так и из-за значительного сокращения числа пунктов в южном полушарии. Увеличение количества запусков радиозондов в день сдерживается стоимостью оборудования, которое нельзя использовать повторно. Геодезисты, ориентированные на точное позиционирование, используют поправки для устранения атмосферных эффектов, которые считаются источником шума в их измерениях. И наоборот, эти же поправки могут быть использованы метеорологами для лучшего понимания атмосферы.Таким образом, улучшение геодезической инфраструктуры приносит пользу обеим областям науки.
Эффекты атмосферной рефракции уже давно признаны важным источником ошибок в геодезии. Вместо того, чтобы полагаться на неопределенные модели, методы космической геодезии, такие как GNSS / GPS, оценивают тропосферные вариации вместе с интересующими параметрами позиционирования. В конце концов, проблему удалось обратить вспять; предполагая, что положение станции точно определено, ученые могли бы использовать «мешающий» сигнал в оценках GNSS / GPS, чтобы восстановить изменяющееся во времени поведение атмосферы (Ware et al., 2000). В отличие от радиозондов, которые измеряют атмосферные условия на нескольких высотах, наземные GNSS / GPS измеряют только «интегрированное» влияние атмосферы, то есть насколько атмосфера задерживает измерение в целом. Примерно 80 процентов задержки (известной как «сухая тропосфера») можно предсказать, если измерить приземное давление. После устранения задержки в сухой тропосфере можно восстановить задержку из-за водяного пара, которая может быть масштабирована до так называемого осажденного водяного пара (PWV).Измерения PWV оценивают модели переноса влаги и скрытого тепла, которые имеют решающее значение для прогнозов погоды. Однако, чтобы быть полезными для прогнозирования погоды, данные должны быть доступны практически в реальном времени.
В конце концов, проблему удалось обратить вспять; предполагая, что положение станции точно определено, ученые могли бы использовать «мешающий» сигнал в оценках GNSS / GPS, чтобы восстановить изменяющееся во времени поведение атмосферы (Ware et al., 2000). В отличие от радиозондов, которые измеряют атмосферные условия на нескольких высотах, наземные GNSS / GPS измеряют только «интегрированное» влияние атмосферы, то есть насколько атмосфера задерживает измерение в целом. Примерно 80 процентов задержки (известной как «сухая тропосфера») можно предсказать, если измерить приземное давление. После устранения задержки в сухой тропосфере можно восстановить задержку из-за водяного пара, которая может быть масштабирована до так называемого осажденного водяного пара (PWV).Измерения PWV оценивают модели переноса влаги и скрытого тепла, которые имеют решающее значение для прогнозов погоды. Однако, чтобы быть полезными для прогнозирования погоды, данные должны быть доступны практически в реальном времени.
Поскольку PWV варьируется как в пространстве, так и во времени, необходимы глобально распределенные и часто собираемые данные. Для текущего созвездия примерно из 30 спутников один приемник GNSS / GPS обычно принимает сигналы от 6 до 12 спутников. Эти данные в основном используются для оценки PWV в воздушном столбе над приемником GNSS / GPS.Но, в принципе, наличие измерений с более чем одного направления означает, что GNSS / GPS имеет азимутальную, а также вертикальную чувствительность. Чем больше спутников передают сигналы с заданного направления, тем выше будет чувствительность. Это также означает, что комбинация сигналов от нескольких систем, таких как Galileo, ГЛОНАСС и КОМПАС, даст еще более чувствительные возможности атмосферного мониторинга, чем те, которые доступны только с помощью GPS Соединенных Штатов. Кроме того, поскольку приемники GNSS / GPS работают непрерывно, зондирование атмосферы GNSS / GPS имеет исключительную временную чувствительность, что особенно важно для мониторинга и прогнозирования поведения сильных погодных явлений.
Поскольку атмосферная задержка неразрывно связана с тем, насколько хорошо может быть определено положение, для исследований тропосферы GNSS / GPS требуется такая же инфраструктура: точное определение орбиты вдоль
Применение методов космической геодезии к погоде и климату
Абстрактные
С появлением крупномасштабных геодезических наземных сетей, как региональных, так и глобальных, и доступных космических научных приемников GPS, методы космической геодезии находят разнообразные и неожиданные новые применения во многих областях дистанционного зондирования Земли.Базовые приемники GPS-навигации теперь практически незаменимы для всех видов полетов на низкую околоземную орбиту. Научные приложения космической GPS сегодня включают определение орбиты с точностью до сантиметра для картографирования силы тяжести, альтиметрии океана, обнаружения геоцентра и расширенной глобальной геодезии; трехмерное изображение глобальной ионосферы с высоким разрешением; зондирование границ затмения для восстановления точных профилей рефракции атмосферы, плотности, давления, температуры, водяного пара и геопотенциальных высот; и экспериментальное обнаружение отражений океана с помощью GPS для прямой альтиметрии и рефлектометрии океана. За последние пять лет произошел взрывной рост использования как наземных, так и космических геодезических приемников для прямого зондирования атмосферы с целью получения данных для прогнозирования погоды и исследований глобального изменения климата. Атмосферные приложения космической геодезии вызывают растущий научный интерес. Плотные сети GPS в Японии, Северной Америке, Скандинавии, Европе и других странах теперь регулярно предоставляют данные для использования в ежедневных прогнозах погоды. Созвездие из шести орбитальных приемников затмения, таких как миссия COSMIC, которая будет запущена в 2005 году, может измерять атмосферную рефракцию с точностью, эквивалентной 0.1 К при температуре в климатическом регионе, соответствующем 1/30 земной поверхности, всего за несколько недель данных. Вертикальное разрешение может достигать менее ста метров. Это предлагает, пожалуй, наиболее многообещающий подход к обнаружению и различению едва уловимых вынужденных климатических сигналов, которые могут составлять всего несколько десятых среднего изменения температуры по Кельвину за десятилетие.
За последние пять лет произошел взрывной рост использования как наземных, так и космических геодезических приемников для прямого зондирования атмосферы с целью получения данных для прогнозирования погоды и исследований глобального изменения климата. Атмосферные приложения космической геодезии вызывают растущий научный интерес. Плотные сети GPS в Японии, Северной Америке, Скандинавии, Европе и других странах теперь регулярно предоставляют данные для использования в ежедневных прогнозах погоды. Созвездие из шести орбитальных приемников затмения, таких как миссия COSMIC, которая будет запущена в 2005 году, может измерять атмосферную рефракцию с точностью, эквивалентной 0.1 К при температуре в климатическом регионе, соответствующем 1/30 земной поверхности, всего за несколько недель данных. Вертикальное разрешение может достигать менее ста метров. Это предлагает, пожалуй, наиболее многообещающий подход к обнаружению и различению едва уловимых вынужденных климатических сигналов, которые могут составлять всего несколько десятых среднего изменения температуры по Кельвину за десятилетие. В этой презентации будут рассмотрены методы и приложения GPS-зондирования атмосферы с земли и из космоса, а также описаны перспективные разработки на будущее.
В этой презентации будут рассмотрены методы и приложения GPS-зондирования атмосферы с земли и из космоса, а также описаны перспективные разработки на будущее.
РСДБ Геодезия: наблюдения, анализ и результаты
2. Метод РСДБ
Систему РСДБ можно описать следующими компонентами:
астрономический объект, радиоисточник,
распространение радиоволн, среда распространения электромагнитной волны, в частности атмосфера Земли,
антенно-приемная система, механическое и электронное оборудование,
Земля как носитель базовых линий интерферометра, образованных парами антенн ,
коррелятор и
анализ РСДБ наблюдений, т.е.е. применение физически мотивированных математических моделей с помощью программного обеспечения на основе объективных и субъективных решений оператора (ов).
Несмотря на большое количество общих для анализа частей, научные цели астрометрических и геодезических и астрофизических РСДБ существенно различаются. В то время как радиоастрономия направлена на исследование большого разнообразия астрономических объектов и их астрофизических характеристик, геодезические и астрометрические РСДБ сосредоточены на точном позиционировании точек и их производных, таких как точное определение очень больших расстояний на Земле, движения плит или ориентации Земли.В следующих разделах я опишу различные компоненты системы более подробно, что необходимо для понимания научных результатов, полученных с помощью геодезических и астрометрических РСДБ.
В то время как радиоастрономия направлена на исследование большого разнообразия астрономических объектов и их астрофизических характеристик, геодезические и астрометрические РСДБ сосредоточены на точном позиционировании точек и их производных, таких как точное определение очень больших расстояний на Земле, движения плит или ориентации Земли.В следующих разделах я опишу различные компоненты системы более подробно, что необходимо для понимания научных результатов, полученных с помощью геодезических и астрометрических РСДБ.
2.1. Космический сегмент: радиоисточники
В то время как астрономический РСДБ имеет дело с большим разнообразием объектов, таких как сверхновые, пульсары, блазары, вспышки, области звездообразования, такие как глобулы, OH- и H 2 O-мазерные источники, близко и далекие галактики, гравитационные линзы, звездообразования-галактики и активные галактические ядра (AGN), геодезические и астрометрические РСДБ предпочитают внегалактические, радиогромкие и компактные объекты, такие как квазары (квазизвездный радиоисточник), радиогалактики (см.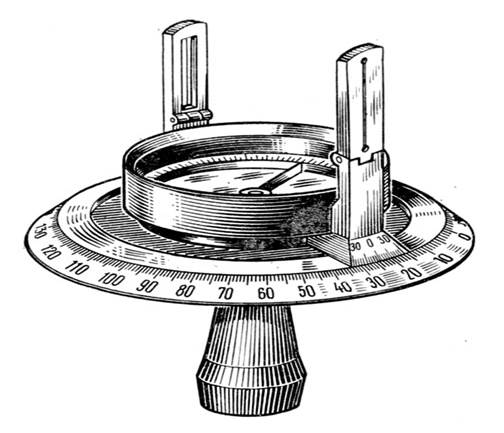 рис. .), а также предметы типа BL Lac (ertae). Радиоизлучение квазаров вызвано аккрецией вещества в черную дыру в центре так называемой родительской галактики, где в спектре обычно преобладает оптическое, ультрафиолетовое или рентгеновское излучение. При их попадании в черную дыру вещество и электроны релятивистски ускоряются. Таким образом, помимо меньшего количества теплового излучения естественное излучение радиоисточников обусловлено синхротронным эффектом. Это излучение имеет ряд полезных характеристик, таких как высокая интенсивность и непрерывность, т.е.е. излучаются не отдельные отдельные спектральные линии, а шум в широкой полосе частот. Квазары содержат чрезвычайно громкие радиоактивные галактики, доминирующие в излучении родительских галактик. Радиогалактики содержат или, по крайней мере, также содержат AGN, поскольку без существования такого центра невозможно объяснить образование наблюдаемого истечения материи (струй) и радиопузырьков (лепестков). Вокруг гравитирующего центра этих объектов обычно находится пылевой тор.
рис. .), а также предметы типа BL Lac (ertae). Радиоизлучение квазаров вызвано аккрецией вещества в черную дыру в центре так называемой родительской галактики, где в спектре обычно преобладает оптическое, ультрафиолетовое или рентгеновское излучение. При их попадании в черную дыру вещество и электроны релятивистски ускоряются. Таким образом, помимо меньшего количества теплового излучения естественное излучение радиоисточников обусловлено синхротронным эффектом. Это излучение имеет ряд полезных характеристик, таких как высокая интенсивность и непрерывность, т.е.е. излучаются не отдельные отдельные спектральные линии, а шум в широкой полосе частот. Квазары содержат чрезвычайно громкие радиоактивные галактики, доминирующие в излучении родительских галактик. Радиогалактики содержат или, по крайней мере, также содержат AGN, поскольку без существования такого центра невозможно объяснить образование наблюдаемого истечения материи (струй) и радиопузырьков (лепестков). Вокруг гравитирующего центра этих объектов обычно находится пылевой тор. Различие между квазаром и радиогалактикой связано с геометрией наблюдения.Квазары — это радиогалактики, у которых край пылевого тора закрывает AGN на луче зрения наблюдателя (Haas & Meisenheimer, 2003). Объекты типа BL Lac также относятся к радиогалактикам (Tateyama et al., 1998). Для этого типа объектов угол между линией взгляда и направлением струи очень мал, то есть человек смотрит в струю. Хотя физические характеристики астрономических объектов все еще являются предметом научных дискуссий, их сильное шумовое излучение в широком радиодиапазоне — факт.Для геодезии радиоисточник должен соответствовать ряду критериев, чтобы быть полезным в качестве небесной точки отсчета.
Различие между квазаром и радиогалактикой связано с геометрией наблюдения.Квазары — это радиогалактики, у которых край пылевого тора закрывает AGN на луче зрения наблюдателя (Haas & Meisenheimer, 2003). Объекты типа BL Lac также относятся к радиогалактикам (Tateyama et al., 1998). Для этого типа объектов угол между линией взгляда и направлением струи очень мал, то есть человек смотрит в струю. Хотя физические характеристики астрономических объектов все еще являются предметом научных дискуссий, их сильное шумовое излучение в широком радиодиапазоне — факт.Для геодезии радиоисточник должен соответствовать ряду критериев, чтобы быть полезным в качестве небесной точки отсчета.
Рис. 1.
Негативное черно-белое изображение радиогалактики 3C219 (0917 + 458) из суперпозиции радио и оптических изображений (NRAO / AUI / NSF). Черная точка в середине показывает AGN.
Яркость, то есть интенсивность излучения должна быть достаточно сильной в наблюдаемых диапазонах частот. В зависимости от характеристик антенны минимум находится в районе 0. 01 Ян (Янский; 1 Ян = 10 -26 Дж м -2 ). Это условие должно быть выполнено для достижения подходящего отношения сигнал / шум (SNR). Средняя интенсивность составляет 0,38 Ян в X-диапазоне и 0,47 Ян в S-диапазоне, двух так называемых частотах геодезических РСДБ НАСА (Национальное управление по аэронавтике и исследованию космического пространства, США). Максимальная интенсивность радиоисточника может достигать 20 Ян в обоих диапазонах. К настоящему времени с помощью геодезических РСДБ было обнаружено около 4500 источников. Количество компактных ярких (интенсивность> 0.06 Янв) ожидается около 25 000 радиоисточников (Preuss, 1982), и, таким образом, количество наблюдаемых астрометрических радиоисточников пока не используется. Кроме того, интенсивность радиопотока не должна сильно меняться во времени, чтобы можно было вести непрерывное наблюдение.
01 Ян (Янский; 1 Ян = 10 -26 Дж м -2 ). Это условие должно быть выполнено для достижения подходящего отношения сигнал / шум (SNR). Средняя интенсивность составляет 0,38 Ян в X-диапазоне и 0,47 Ян в S-диапазоне, двух так называемых частотах геодезических РСДБ НАСА (Национальное управление по аэронавтике и исследованию космического пространства, США). Максимальная интенсивность радиоисточника может достигать 20 Ян в обоих диапазонах. К настоящему времени с помощью геодезических РСДБ было обнаружено около 4500 источников. Количество компактных ярких (интенсивность> 0.06 Янв) ожидается около 25 000 радиоисточников (Preuss, 1982), и, таким образом, количество наблюдаемых астрометрических радиоисточников пока не используется. Кроме того, интенсивность радиопотока не должна сильно меняться во времени, чтобы можно было вести непрерывное наблюдение.
Компактность, то есть пространственное распространение максимума интенсивности, определяемое через угловой диаметр сердцевины радиоисточника, должна быть меньше предполагаемой точности координаты, склонения и прямого восхождения. Поскольку только очень небольшое количество радиоисточников идеально компактно в X- и, в частности, в S-диапазонах, источники демонстрируют внутреннюю структуру в пределах углового диаметра, и, следовательно, необходимо учитывать структурные поправки наблюдений (Charlot, 1990). ). Пренебрежение структурой приведет к средней ошибке около 8 пс (2,4 мм) при наблюдении групповой задержки (Sovers et al., 2002).
Поскольку только очень небольшое количество радиоисточников идеально компактно в X- и, в частности, в S-диапазонах, источники демонстрируют внутреннюю структуру в пределах углового диаметра, и, следовательно, необходимо учитывать структурные поправки наблюдений (Charlot, 1990). ). Пренебрежение структурой приведет к средней ошибке около 8 пс (2,4 мм) при наблюдении групповой задержки (Sovers et al., 2002).
В идеале максимум интенсивности внутри радиоисточника не должен сдвигаться между наблюдаемыми частотами.Однако этот эффект, как правило, не выполняется, и наблюдаемое положение колеблется до 700 мкс в источнике в зависимости от частоты. Для геодезии / астрометрии не имеет значения, вызван ли сдвиг основной частоты фактически разными местоположениями излучения или самопоглощением объекта. Коррекция структуры должна быть оценена в зависимости от наблюдаемых частот; в нашем случае — двухчастотная структурная коррекция (Charlot, 2002). Для сравнения и ссылки на каталоги в других странах, например. грамм. оптических частот, включение радиооптических аналогов — еще один критерий выбора опорных источников. Таким образом, некоторые источники радио наблюдаются для этой цели, когда положение оптического аналога, как известно, даже если другие характеристики референтной точки не являются оптимальными.
грамм. оптических частот, включение радиооптических аналогов — еще один критерий выбора опорных источников. Таким образом, некоторые источники радио наблюдаются для этой цели, когда положение оптического аналога, как известно, даже если другие характеристики референтной точки не являются оптимальными.
Стабильность, т. Е. Временная неизменность положения максимума интенсивности, должна быть придана определенной величине, и радиоисточник не должен проявлять значительных собственных движений или параллаксов.Принимая во внимание очень большие расстояния от привязанных к Земле или околоземных базовых линий до внегалактических объектов, очевидно, что два более поздних условия выполняются в достаточной степени. Тем не менее, некоторые радиоисточники демонстрируют существенные вариации топологии максимума их интенсивности. Области излучения большинства радиоисточников не идеально симметричны и центрированы в ядре, а вытянуты с яркой составляющей в начале диффузного хвоста: структура ядра-джета. К счастью, лишь некоторые радиоисточники демонстрируют значительные деформации своей топологии до 300 мкс.Помимо радиоизображений, которые позволяют астрофизическое моделирование изменений структуры, математическое моделирование временных рядов координат источника достигается с помощью статистических методов, таких как дисперсия Аллана или проверка гипотез. В то время как утверждения о конкретной структуре зависят от количества и качества радиоизображений и астрофизических предположений, статистические методы полагаются на количество и качество наблюдений за задержкой и декорреляцию источника и других параметров.Было обнаружено, что в некоторых случаях два критерия стабильности противоречат друг другу (Moor et al., 2011).
К счастью, лишь некоторые радиоисточники демонстрируют значительные деформации своей топологии до 300 мкс.Помимо радиоизображений, которые позволяют астрофизическое моделирование изменений структуры, математическое моделирование временных рядов координат источника достигается с помощью статистических методов, таких как дисперсия Аллана или проверка гипотез. В то время как утверждения о конкретной структуре зависят от количества и качества радиоизображений и астрофизических предположений, статистические методы полагаются на количество и качество наблюдений за задержкой и декорреляцию источника и других параметров.Было обнаружено, что в некоторых случаях два критерия стабильности противоречат друг другу (Moor et al., 2011).
Для реализации радиокаталогов необходимы повторные наблюдения радиоисточников и, следовательно, соответствующая видимость с привязанных к Земле базовых линий. Этот критерий конкурирует с желаемым геометрическим распределением радиоисточников, которое в идеале направлено на равномерное и постоянное покрытие неба.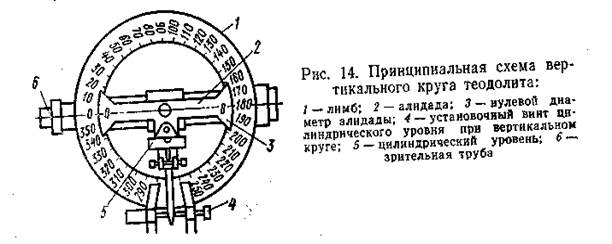
2.2. Среда распространения: пространство-время, частицы и электроны
На своем пути через пространство-время радиоволна может подвергаться воздействию не только кривизны пространства, но также заряженных и нейтральных частиц.В зависимости от расстояния от Земли эти эффекты можно разделить на межзвездные эффекты, которые в значительной степени представляют собой ионизирующие эффекты, гравитационные эффекты через тела нашей солнечной системы, а также эффекты ионизации и задержки через атмосферу, ионосферу и нейтросферу Земли.
Мало что известно о межзвездном воздействии на задержки групп РСДБ. Поскольку РСДБ — это интерферометрический метод, все эффекты, которые являются общими для обоих сигналов помех, поглощаются моделью часов и, следовательно, не видны при наблюдении.Предполагается, что большая часть сред межзвездного распространения имеет большую пространственную протяженность с небольшими вариациями в пространственных масштабах базовых линий Земли примерно до 12 000 км.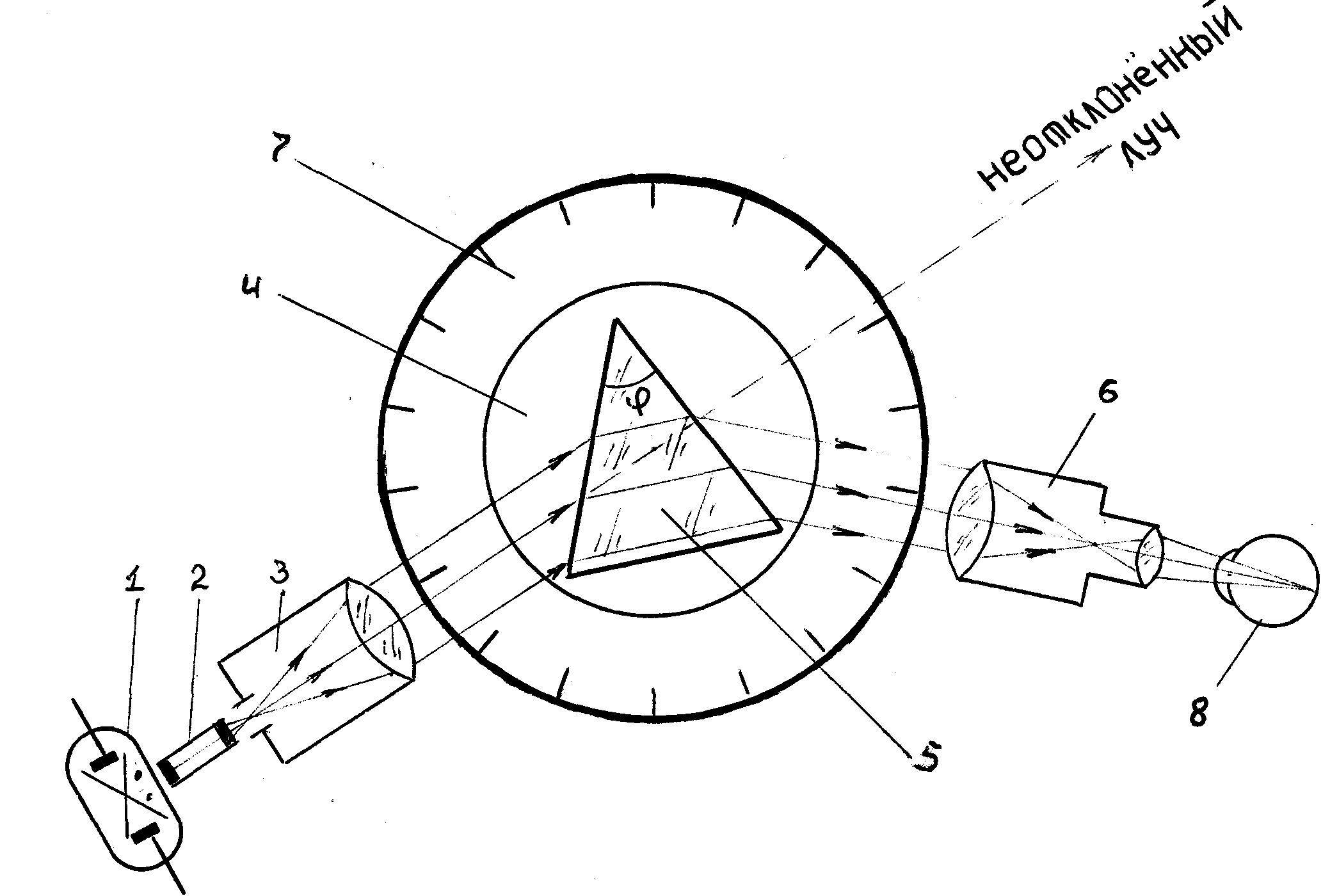 Тем не менее, если наблюдения РСДБ будут ионизированы через межзвездную среду, сравнение ионосферных задержек, полученных из РСДБ, с данными, полученными другими методами космической геодезии, например GNSS подойдет для расследования. В наших сравнениях (Dettmering et al., 2011a) в течение двух недель и другого отдельного дня мы не обнаружили никаких доказательств дополнительной ионизации, кроме той, которая вызывается ионосферой Земли.Конечно, сравнения следует распространить на все доступные данные.
Тем не менее, если наблюдения РСДБ будут ионизированы через межзвездную среду, сравнение ионосферных задержек, полученных из РСДБ, с данными, полученными другими методами космической геодезии, например GNSS подойдет для расследования. В наших сравнениях (Dettmering et al., 2011a) в течение двух недель и другого отдельного дня мы не обнаружили никаких доказательств дополнительной ионизации, кроме той, которая вызывается ионосферой Земли.Конечно, сравнения следует распространить на все доступные данные.
В то время как радиоволны распространяются через нашу Солнечную систему, расстояния до массивных объектов могут стать очень маленькими, а кривизна пространства может существенно повлиять на два сигнала по-разному. Для истории наблюдений РСДБ и точности в 1 пс текущей теоретической модели групповой задержки РСДБ, называемой консенсусной моделью, влияние Солнца, Земли и в некоторых случаях Юпитера сказалось на результатах.Для Солнца и Земли влияние кривизны пространства на групповые задержки, так называемая задержка Шапиро, следует учитывать не только для конкретной геометрии наблюдения.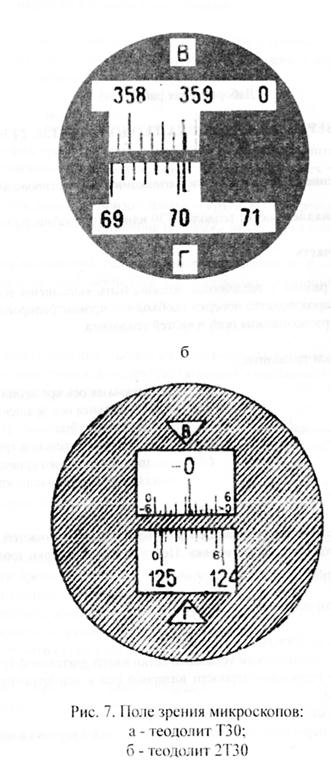 В случае Земли гравитационная задержка становится теоретически максимальной, если одна антенна ведет наблюдение в зените, а другая — в нулевом градусе места. Из-за самой большой массы в Солнечной системе гравитационная задержка вблизи Солнца должна включать еще один постньютоновский термин. На краю Солнца задержка может достигать 169 нс (если смотреть с базовой линии 6000 км) и все еще составляет около 17 пс почти в противоположном направлении (175 градусов от луча зрения с базовой линии 6000 км).Член более высокого порядка в окрестности Солнца составляет около 307 пс на лимбе и 6 пс все еще значимы на расстоянии в один градус от гелиоцентра; но затем он падает значительно быстрее. Для Юпитера и других планет солнечной системы поправки будут необходимы только в том случае, если путь луча почти в направлении объекта, то есть задевая конечность объекта. Гравитационные задержки различных массивных тел могут быть добавлены суперпозицией и обычно рассматриваются в теоретической модели задержки.
В случае Земли гравитационная задержка становится теоретически максимальной, если одна антенна ведет наблюдение в зените, а другая — в нулевом градусе места. Из-за самой большой массы в Солнечной системе гравитационная задержка вблизи Солнца должна включать еще один постньютоновский термин. На краю Солнца задержка может достигать 169 нс (если смотреть с базовой линии 6000 км) и все еще составляет около 17 пс почти в противоположном направлении (175 градусов от луча зрения с базовой линии 6000 км).Член более высокого порядка в окрестности Солнца составляет около 307 пс на лимбе и 6 пс все еще значимы на расстоянии в один градус от гелиоцентра; но затем он падает значительно быстрее. Для Юпитера и других планет солнечной системы поправки будут необходимы только в том случае, если путь луча почти в направлении объекта, то есть задевая конечность объекта. Гравитационные задержки различных массивных тел могут быть добавлены суперпозицией и обычно рассматриваются в теоретической модели задержки.
На сегодняшний день наибольший вклад в наблюдаемую задержку из-за эффектов распространения дает атмосфера Земли. Для электромагнитных волн моделирование эффектов удобно разделить на дисперсионную (частотно-зависимую) и недисперсионную (частотно-независимую) части. Дисперсионные характеристики ионосферы являются основной причиной двухчастотных наблюдений в геодезических РСДБ. Радионаблюдения задерживаются ионосферой на несколько десятков метров, а вклад нейтросферы составляет около 15 метров.Оба в основном зависят от угла места наблюдения, поскольку длина пути через сферическую оболочку приблизительно пропорциональна синусу угла места. Разница между атмосферами заключается в том, что ионосферные эффекты могут быть уменьшены до миллиметровой точности с помощью двухчастотной калибровки, в то время как только гидростатическая часть нейтросферы, около 90% задержки нейтросферы, может быть эффективно уменьшена, если давление приземного воздуха Расположение обсерваторий точно известно. Остающаяся негидростатическая часть требует оценки (Dettmering et al., 2010).
Остающаяся негидростатическая часть требует оценки (Dettmering et al., 2010).
2.3. Наземный сегмент: радиотелескопы и другое оборудование
Для радиотелескопов можно в первую очередь различать антенны с одной тарелкой и антенные решетки с несколькими тарелками или группу, которые расположены в определенной конфигурации, например по прямой, в звездообразовании, Y- или Т-образной форме. В то время как решетки, соединенные с помощью фазостабильных кабелей, обычно используются для реконструкции изображений в астрономических РСДБ, антенны с одной тарелкой широко распространены для геодезических и астрометрических целей.Тем не менее, применение антенных решеток было исследовано также для геодезических целей (Saosao & Morimoto, 1991). Геодезические РСДБ-антенны (см. Рисунок 2) обычно представляют собой полностью управляемые конструкции из стали с бетонным фундаментом, прикрепленным к фиксированной геометрической точке отсчета. В 80-х и 90-х годах прошлого века действовал ряд мобильных РСДБ-станций: американские системы MV1, MV2 и MV3 (Clark et al. , 1987), которые эксцентрично устанавливались над одной из примерно 40 платформ (Ma и другие., 1990). Немецкая передвижная интегрированная геодезическая система наблюдений (TIGO, Hase, 1999), которая после фазы тестирования в Веттцелле, Германия, была постоянно установлена в Консепсьоне, Чили, для улучшения наземной сети основных РСДБ-объектов IVS. С появлением GNSS применение мобильных РСДБ было прекращено, поскольку оно стало экономически невыгодным.
, 1987), которые эксцентрично устанавливались над одной из примерно 40 платформ (Ma и другие., 1990). Немецкая передвижная интегрированная геодезическая система наблюдений (TIGO, Hase, 1999), которая после фазы тестирования в Веттцелле, Германия, была постоянно установлена в Консепсьоне, Чили, для улучшения наземной сети основных РСДБ-объектов IVS. С появлением GNSS применение мобильных РСДБ было прекращено, поскольку оно стало экономически невыгодным.
Большинство отражателей РСДБ антенн относятся к типу Кассегрена. В дополнение к параболическому основному рефлектору антенна Кассегрена имеет вспомогательный рефлектор в фокусе главного рефлектора, который имеет выпуклую гиперболическую форму.Одна из фокусных точек вспомогательного рефлектора находится в середине основного рефлектора. После того, как радиосигнал сфокусирован в отверстии основного отражателя, закрытом рупором, он не принимается сразу, а подвергается нескольким электронным преобразованиям, так называемому гетеродинному приему. Положение вспомогательного рефлектора может привести к затенению основного рефлектора. Однако вызванная потеря сигнала ничтожно мала (Rogers, 1991). Для получения достаточного отношения сигнал / шум существенную роль играют диаметр и направленность антенны.Дополнительные источники радиошума, такие как атмосферный шум и шум, излучаемый температурой электронных компонентов, должны подавляться. Принимаемый сигнал может быть нарушен переходными сигналами, например от радио- или телевещания, так называемые радиочастотные помехи (RFI), в частности в S-диапазоне, которые в конечном итоге могут привести к полной потере одного или нескольких каналов. О таких случаях все чаще сообщалось в зависимости от окружающей среды, например Авторы Sorgente & Petrov (1999) в Матере, Италия.Чтобы тепловой шум был как можно меньше, детали электроники охлаждаются до нескольких градусов Кельвина, например на радиотелескопе Веттцелль, Германия, с использованием жидкого гелия. Для фокусировки напряжения с малыми потерями поверхность антенны должна быть изготовлена с очень высокой точностью.
Положение вспомогательного рефлектора может привести к затенению основного рефлектора. Однако вызванная потеря сигнала ничтожно мала (Rogers, 1991). Для получения достаточного отношения сигнал / шум существенную роль играют диаметр и направленность антенны.Дополнительные источники радиошума, такие как атмосферный шум и шум, излучаемый температурой электронных компонентов, должны подавляться. Принимаемый сигнал может быть нарушен переходными сигналами, например от радио- или телевещания, так называемые радиочастотные помехи (RFI), в частности в S-диапазоне, которые в конечном итоге могут привести к полной потере одного или нескольких каналов. О таких случаях все чаще сообщалось в зависимости от окружающей среды, например Авторы Sorgente & Petrov (1999) в Матере, Италия.Чтобы тепловой шум был как можно меньше, детали электроники охлаждаются до нескольких градусов Кельвина, например на радиотелескопе Веттцелль, Германия, с использованием жидкого гелия. Для фокусировки напряжения с малыми потерями поверхность антенны должна быть изготовлена с очень высокой точностью. Требуемая точность составляет около 0,05 длины волны (Nottarp & Kilger, 1982).
Требуемая точность составляет около 0,05 длины волны (Nottarp & Kilger, 1982).
Рис. 2.
RTW (Радиотелескоп Веттцелля), геодезическая РСДБ-антенна диаметром 20 м в Геодезической обсерватории Веттцелль, Германия (BKG / FESG), провела наибольшее количество наблюдений в рамках кампаний IVS
Азимут-высота XY, полярные или экваториальные крепления можно найти для геодезических РСДБ-систем.Большинство полярных антенн принадлежали другим программам и раньше использовались для других целей. Антенна сети дальнего космоса в Хартебистуке, Южная Африка, например, была построена НАСА для отслеживания космических кораблей, но позже была оснащена геодезическими приемниками и устройством точной синхронизации и, таким образом, перестроена для геодезических целей. Геодезические графики требуют относительно больших вращений телескопов при переключении между удаленными радиоисточниками, покрывающими большие расстояния по азимуту и углу места.Поэтому и для достижения достаточного отношения сигнал / шум, среднего размера, диаметром около 20 м, телескопы оказались оптимальными для геодезических графиков. Посуда с такими размерами, конечно, значительно деформируется в зависимости от тепловых и ветровых условий окружающей среды, а также из-за гравитационного мешкования под различными углами подъема. Изменения геометрии телескопа могут вызвать расфокусировку и, как следствие, потерю сигнала. В частности, для больших управляемых телескопов, таких как Effelsberg, Германия, необходимо перемещать рупор, а вместе с ним и фокальную точку рефлектора в соответствии с углом места наблюдения, чтобы оставаться сфокусированным.С меньшими телескопами деформации могут не привести к полной потере сигнала, но влияние окружающей среды может значительно исказить наблюдаемую РСДБ. Существуют эмпирические модели, материальные константы и данные, зависящие от антенны, доступные для тепловых деформаций (Nothnagel, 2008), так что для большинства геодезических антенн этот эффект можно исправить. Только те антенны, которые закрыты обтекателем, требуют индивидуальной обработки, поскольку внутренняя температура обтекателя обычно недоступна через IVS.
Посуда с такими размерами, конечно, значительно деформируется в зависимости от тепловых и ветровых условий окружающей среды, а также из-за гравитационного мешкования под различными углами подъема. Изменения геометрии телескопа могут вызвать расфокусировку и, как следствие, потерю сигнала. В частности, для больших управляемых телескопов, таких как Effelsberg, Германия, необходимо перемещать рупор, а вместе с ним и фокальную точку рефлектора в соответствии с углом места наблюдения, чтобы оставаться сфокусированным.С меньшими телескопами деформации могут не привести к полной потере сигнала, но влияние окружающей среды может значительно исказить наблюдаемую РСДБ. Существуют эмпирические модели, материальные константы и данные, зависящие от антенны, доступные для тепловых деформаций (Nothnagel, 2008), так что для большинства геодезических антенн этот эффект можно исправить. Только те антенны, которые закрыты обтекателем, требуют индивидуальной обработки, поскольку внутренняя температура обтекателя обычно недоступна через IVS. Для гравитационной деформации также доступны модели, например опубликовано Sarti et al. (2010), но для согласованного приложения собраны не все соответствующие антенно-зависимые данные. Гравитационные деформации больше для антенн с первичным фокусом, то есть для тех антенн, где приемник относительно вертикальной волны расположен в фокусе основного отражателя, и это, скорее, меньшинство геодезических антенн. Нет доступных моделей деформаций, вызванных ветром. В случае сильного ветра телескоп обычно прекращает наблюдение и перемещается в безопасное положение.
Для гравитационной деформации также доступны модели, например опубликовано Sarti et al. (2010), но для согласованного приложения собраны не все соответствующие антенно-зависимые данные. Гравитационные деформации больше для антенн с первичным фокусом, то есть для тех антенн, где приемник относительно вертикальной волны расположен в фокусе основного отражателя, и это, скорее, меньшинство геодезических антенн. Нет доступных моделей деформаций, вызванных ветром. В случае сильного ветра телескоп обычно прекращает наблюдение и перемещается в безопасное положение.
Опорная точка РСДБ, к которой на самом деле относятся измерения РСДБ, обычно представляет собой нематериальную инвариантную точку, расположенную на пересечении осей телескопа. Поскольку эта точка обычно недоступна напрямую, ее необходимо реализовать эксцентрично, например посредством косвенных измерений с помощью внешних эталонных маркеров (Vittuari et al., 2001; Dawson et al., 2007). Эти эксцентричные опорные маркеры позволяют доступ и обслуживание опорной точки РСДБА для других космических геодезических или инженер съемочных методов. Последние обычно применяются для определения расстояний между опорными точками с помощью различных космических геодезических приемов, называемых локальными связями. Локальные связи после преобразования в декартову геоцентрическую систему космических геодезических методов являются одним из наиболее важных вопросов для реализации многотехнических наземных систем отсчета, таких как текущая традиционная международная наземная система отсчета, ITRF2008 (Altamimi et al. др., 2011). Основные оси телескопов практически не пересекаются.Размер смещения оси антенны может составлять всего несколько миллиметров или достигать нескольких метров (Nothnagel & Steinforth, 2005). Для его определения в лучшем случае доступны измерения точными инженерными изыскательскими методами; в противном случае это должно быть оценено на основе наблюдений РСДБ.
Последние обычно применяются для определения расстояний между опорными точками с помощью различных космических геодезических приемов, называемых локальными связями. Локальные связи после преобразования в декартову геоцентрическую систему космических геодезических методов являются одним из наиболее важных вопросов для реализации многотехнических наземных систем отсчета, таких как текущая традиционная международная наземная система отсчета, ITRF2008 (Altamimi et al. др., 2011). Основные оси телескопов практически не пересекаются.Размер смещения оси антенны может составлять всего несколько миллиметров или достигать нескольких метров (Nothnagel & Steinforth, 2005). Для его определения в лучшем случае доступны измерения точными инженерными изыскательскими методами; в противном случае это должно быть оценено на основе наблюдений РСДБ.
Антенны приводятся в действие и контролируются полевой системой, программным обеспечением на основе LINUX для движения радиоантенн (Himwich, 2000), которое позволяет автоматически управлять во время заранее запланированного эксперимента VLBI. Также необходимо учитывать намотку кабеля, поскольку антенна может только ограниченно поворачиваться в одном направлении. Также изучаются новые подходы к автоматизированному полуавтономному управлению антенной (Neidhardt et al., 2011).
Также необходимо учитывать намотку кабеля, поскольку антенна может только ограниченно поворачиваться в одном направлении. Также изучаются новые подходы к автоматизированному полуавтономному управлению антенной (Neidhardt et al., 2011).
С помощью вышеупомянутых антенн в принципе можно принимать частоты от 0,4 до 22 ГГц. Для геодезических и астрометрических РСДБ стало принято применение так называемых частот НАСА около 8,4 ГГц (X-диапазон) и 2,3 ГГц (S-диапазон).При двухчастотном приеме каналы от нескольких до нескольких сотен МГц вокруг средних частот пропускаются полосовой фильтрацией от континуального шума радиоисточника, а затем обрабатываются индивидуально. Входящий радиосигнал, так называемая принимаемая частота, сначала поляризуется, а затем усиливается. После этого он преобразуется с понижением частоты до промежуточной частоты около 300 МГц на переднем конце антенны (Whitney et al., 1976). Чтобы сохранить небольшую скорость передачи данных, обрабатывается не вся полоса пропускания, а несколько каналов в несколько МГц. Позже отдельные каналы синтезируются для получения большей эффективной полосы пропускания, применяя синтез полосы пропускания (Rogers, 1970; Hinteregger et al., 1972). По коаксиальному кабелю сигнал передается в близлежащее здание управления, так называемый задний конец, где выполняются дальнейшие этапы обработки данных, пока сигнал не будет окончательно записан. После преобразования в частоту основной полосы сигнал проходит через форматер, на который накладываются временные метки гетеродина. Затем этот видеосигнал дискретизируется и квантуется, так что цифровое значение представлено буквой e.грамм. 1-битная выборка. Также возможно оцифровывать сигнал с более высоким назначением битов. До РСДБ системы Mark III полученные цифровые сигналы записывались на магнитные ленты. После этого, используя Mark IV или более новые VLBI-системы, данные сохраняются на жестких дисках. Требования к скорости записи данных были и остаются очень сложными.
Позже отдельные каналы синтезируются для получения большей эффективной полосы пропускания, применяя синтез полосы пропускания (Rogers, 1970; Hinteregger et al., 1972). По коаксиальному кабелю сигнал передается в близлежащее здание управления, так называемый задний конец, где выполняются дальнейшие этапы обработки данных, пока сигнал не будет окончательно записан. После преобразования в частоту основной полосы сигнал проходит через форматер, на который накладываются временные метки гетеродина. Затем этот видеосигнал дискретизируется и квантуется, так что цифровое значение представлено буквой e.грамм. 1-битная выборка. Также возможно оцифровывать сигнал с более высоким назначением битов. До РСДБ системы Mark III полученные цифровые сигналы записывались на магнитные ленты. После этого, используя Mark IV или более новые VLBI-системы, данные сохраняются на жестких дисках. Требования к скорости записи данных были и остаются очень сложными.
Носители данных, магнитные ленты или жесткие диски, затем отправляются в центральный процессор, так называемый коррелятор, для дальнейшей обработки и определения наблюдаемых.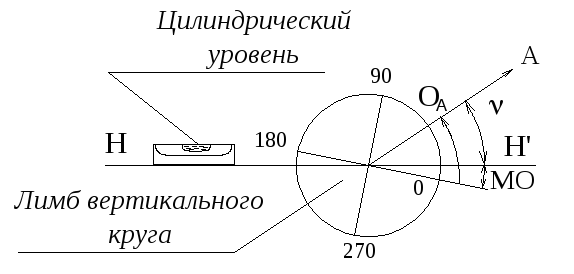 Еще в стадии разработки находится шаг от носителей информации к e-VLBI, то есть VLBI в реальном времени с передачей данных по широкополосным кабелям (Whitney & Ruszczyk, 2006), например через Интернет. К сожалению, этот метод обмена данными должен конкурировать с коммерческими пользователями и поэтому может стать очень дорогим. Кроме того, многие РСДБ-антенны были намеренно построены в довольно удаленных местах, поэтому кабели, в частности, на последних нескольких километрах, часто недоступны, и их придется прокладывать только для этой цели.Вот почему e-VLBI был успешно протестирован, но часто не применяется для рутинных экспериментов IVS VLBI на всех участвующих сайтах.
Еще в стадии разработки находится шаг от носителей информации к e-VLBI, то есть VLBI в реальном времени с передачей данных по широкополосным кабелям (Whitney & Ruszczyk, 2006), например через Интернет. К сожалению, этот метод обмена данными должен конкурировать с коммерческими пользователями и поэтому может стать очень дорогим. Кроме того, многие РСДБ-антенны были намеренно построены в довольно удаленных местах, поэтому кабели, в частности, на последних нескольких километрах, часто недоступны, и их придется прокладывать только для этой цели.Вот почему e-VLBI был успешно протестирован, но часто не применяется для рутинных экспериментов IVS VLBI на всех участвующих сайтах.
Для измерения эффектов с помощью электронных компонентов и приборов на каждую антенную систему вводится искусственный сигнал, с помощью которого можно обнаруживать изменения фазы сигнала, так называемая фазовая калибровка. Калибровочный сигнал индуцируется гетеродином на переднем конце в виде равномерно разнесенных импульсов с интервалом 1 мкс. Искусственный сигнал проходит тот же путь сигнала, что и принятый сигнал.Поскольку амплитуда, фаза и частота искусственного сигнала известны, можно восстановить влияние на принятый сигнал. Для обнаружения частотно-зависимых характеристик инструментальных эффектов калибровка фазы выполняется для каждого частотного канала отдельно (Whitney et al., 1976; Corey, 1999). Помимо калибровки фазы, также калибруется задержка в кабеле, то есть задержка сигнала между эпохами, прохождением сигнала через эталонную точку VLBI и эпохой, в которой он фактически записывается.Другой источник ошибки в наблюдаемой РСДБ связан с утечкой поляризации. Утечка поляризации возникает из-за неизбежных недостатков конструкции поляризатора. Он искажает наблюдаемую фазу таким образом, который может зависеть от частоты. До сих пор было показано, что поляризация влияет на геодезические наблюдаемые порядка 1,6 пс для 90% наблюдений, эффект, которым все еще можно пренебречь (Бертарини и др. ., 2011). Тем не менее, для системы наблюдений VLBI2010 поляризация станет проблемой.
Искусственный сигнал проходит тот же путь сигнала, что и принятый сигнал.Поскольку амплитуда, фаза и частота искусственного сигнала известны, можно восстановить влияние на принятый сигнал. Для обнаружения частотно-зависимых характеристик инструментальных эффектов калибровка фазы выполняется для каждого частотного канала отдельно (Whitney et al., 1976; Corey, 1999). Помимо калибровки фазы, также калибруется задержка в кабеле, то есть задержка сигнала между эпохами, прохождением сигнала через эталонную точку VLBI и эпохой, в которой он фактически записывается.Другой источник ошибки в наблюдаемой РСДБ связан с утечкой поляризации. Утечка поляризации возникает из-за неизбежных недостатков конструкции поляризатора. Он искажает наблюдаемую фазу таким образом, который может зависеть от частоты. До сих пор было показано, что поляризация влияет на геодезические наблюдаемые порядка 1,6 пс для 90% наблюдений, эффект, которым все еще можно пренебречь (Бертарини и др. ., 2011). Тем не менее, для системы наблюдений VLBI2010 поляризация станет проблемой.
2.4. Интерферометр и принцип интерферометрии
Длина волны центральных частот, то есть среднее геометрическое значение нижней и верхней граничных частот, в X- и S-диапазоне составляет примерно λ X = 3,6 см и λ S = 13. см. Поскольку ширина полосы частот довольно мала по сравнению с центральными частотами, полосы частот достаточно представлены своими центральными частотами. Если бы наблюдения были ограничены одной антенной, можно было бы достичь углового разрешения около 100 ас (угловых секунд).Соединяя две или более антенн одного типа на базовой линии (рис. 3), можно синтезировать антенну гораздо большего диаметра. Угловое разрешение на средней базе около 6000 км, например От Вестфорда, США до Веттцелля, Германия, уже достигает 1,2 мсек (миллисекунды дуги) и, таким образом, на несколько порядков выше, чем разрешение, полученное с помощью одной антенны. Однако благодаря такому соединению антенн, называемому интерферометром, передаются не радиоизображения, а диаграммы помех. Помехи возбуждаются, если принятые сигналы удовлетворяют условию когерентности. Временная когерентность одинаково поляризованного излучения, выраженная упрощенно, означает, что фаза временно инвариантна. Помимо временной когерентности, которая зависит от разной длины путей прохождения сигнала, пространственная когерентность также играет важную роль. При соблюдении пространственной когерентности диаметр радиоисточника должен быть довольно маленьким, оптимально точечным. Вариации помех, вызванных пространственным расширением радиоисточника, являются основой для исследований структуры источника в радиоастрономии.Чтобы разделить пространственную и временную когерентность, ширина полосы частот должна быть намного меньше наблюдаемой частоты.
Помехи возбуждаются, если принятые сигналы удовлетворяют условию когерентности. Временная когерентность одинаково поляризованного излучения, выраженная упрощенно, означает, что фаза временно инвариантна. Помимо временной когерентности, которая зависит от разной длины путей прохождения сигнала, пространственная когерентность также играет важную роль. При соблюдении пространственной когерентности диаметр радиоисточника должен быть довольно маленьким, оптимально точечным. Вариации помех, вызванных пространственным расширением радиоисточника, являются основой для исследований структуры источника в радиоастрономии.Чтобы разделить пространственную и временную когерентность, ширина полосы частот должна быть намного меньше наблюдаемой частоты.
Рис. 3.
Размах задержки VLBI и основные инструментальные компоненты системы Mark III VLBI взяты из брошюры NASA / GSFC «РСДБ — измерение нашей изменяющейся Земли»
Учитывая зарегистрированные полосы пропускания в несколько сотен МГц по сравнению с наблюдаемыми частотами 2,3 и 8,4 ГГц разделение в принципе возможно. Для РСДБ-наблюдений когерентность должна быть реализована через местные частотные нормали.Синхронизация нормалей может быть приблизительно достигнута посредством передачи времени, например системой GPS. Однако с местными частотными нормами невозможно поддерживать когерентность в течение всего сеанса наблюдения, но в течение меньших промежутков времени в несколько минут. Этого короткого когерентного промежутка времени обычно достаточно для интегрирования одного наблюдения, называемого сканированием (Thompson et al., 2001). Требования VLBI к стабильности частоты очень высоки, но только в течение этих коротких промежутков времени, примерно до 1000 с (17 минут).Нормали водородных мазеров доказали, что обеспечивают наивысшую стабильность частоты в течение необходимого когерентного промежутка времени и поэтому устанавливаются в геодезических РСДБ обсерваториях. Неточность из-за синхронизации и дрейфа различных мазеров обычно параметризуется и оценивается вместе с другими астрометрическими, геодезическими и вспомогательными параметрами (см.
Для РСДБ-наблюдений когерентность должна быть реализована через местные частотные нормали.Синхронизация нормалей может быть приблизительно достигнута посредством передачи времени, например системой GPS. Однако с местными частотными нормами невозможно поддерживать когерентность в течение всего сеанса наблюдения, но в течение меньших промежутков времени в несколько минут. Этого короткого когерентного промежутка времени обычно достаточно для интегрирования одного наблюдения, называемого сканированием (Thompson et al., 2001). Требования VLBI к стабильности частоты очень высоки, но только в течение этих коротких промежутков времени, примерно до 1000 с (17 минут).Нормали водородных мазеров доказали, что обеспечивают наивысшую стабильность частоты в течение необходимого когерентного промежутка времени и поэтому устанавливаются в геодезических РСДБ обсерваториях. Неточность из-за синхронизации и дрейфа различных мазеров обычно параметризуется и оценивается вместе с другими астрометрическими, геодезическими и вспомогательными параметрами (см. Раздел 3). Характерной чертой интерферометрической техники является то, что при наблюдении видны только те величины, которые по-разному влияют на мешающие сигналы, т.е.е. интерферометр не зависит от эффектов, общих для обоих сигналов.
Раздел 3). Характерной чертой интерферометрической техники является то, что при наблюдении видны только те величины, которые по-разному влияют на мешающие сигналы, т.е.е. интерферометр не зависит от эффектов, общих для обоих сигналов.
2.5. Земля: Носитель баз интерферометра
Условие временной когерентности обычно не выполняется из-за движения Земли во время наблюдения. Геометрия базовой линии и радиоисточника постоянно меняется, например из-за вращения Земли. Поэтому фаза принимаемого сигнала медленно меняется со временем. Как следствие, в течение конечной продолжительности наблюдения наблюдается не постоянная частота помех, а медленно меняющаяся частота полос, в основном вызванная дифференциальным эффектом Доплера вращения Земли.
Радиотелескопы, образующие опорные линии, довольно устойчиво прикреплены к нижележащему горному дну с помощью своей опоры, конструкции в основном из стали и бетона. Однако поверхность Земли нестабильна. Напротив, литосфера подвержена множеству деформаций. Некоторые деформации скорее постоянные, вековые или периодические. Другие бывают индивидуальными, эпизодическими и прерывистыми, например во время и после сейсмического события. Иногда требуется серьезный ремонт антенны, когда антенна снимается с направляющей.Несмотря на обычно очень тщательно выполняемую процедуру, такой ремонт обычно приводит к смещению реперной точки РСДБ на несколько миллиметров. На некоторых участках наблюдались локальные деформации, например за счет увеличения водозабора или орошения в зависимости от сезона. Вековые вариации, такие как медленная геодинамика литосферы, в частности, недавние движения земной коры, движения плит и послеледниковый отскок, являются предметом моделей движения плит, таких как Фактическая кинематическая модель плит APKIM (Drewes, 2009).Эти вековые дрейфы плит почти точно линейны в масштабе времени в тысячи лет и, как полагают, вызваны непрерывным процессом расширения морского дна (Campbell et al., 1992). Таким образом, модель координат станции текущих наземных систем отсчета содержит, по крайней мере, координаты положения и линейной скорости для каждого участка.
Некоторые деформации скорее постоянные, вековые или периодические. Другие бывают индивидуальными, эпизодическими и прерывистыми, например во время и после сейсмического события. Иногда требуется серьезный ремонт антенны, когда антенна снимается с направляющей.Несмотря на обычно очень тщательно выполняемую процедуру, такой ремонт обычно приводит к смещению реперной точки РСДБ на несколько миллиметров. На некоторых участках наблюдались локальные деформации, например за счет увеличения водозабора или орошения в зависимости от сезона. Вековые вариации, такие как медленная геодинамика литосферы, в частности, недавние движения земной коры, движения плит и послеледниковый отскок, являются предметом моделей движения плит, таких как Фактическая кинематическая модель плит APKIM (Drewes, 2009).Эти вековые дрейфы плит почти точно линейны в масштабе времени в тысячи лет и, как полагают, вызваны непрерывным процессом расширения морского дна (Campbell et al., 1992). Таким образом, модель координат станции текущих наземных систем отсчета содержит, по крайней мере, координаты положения и линейной скорости для каждого участка.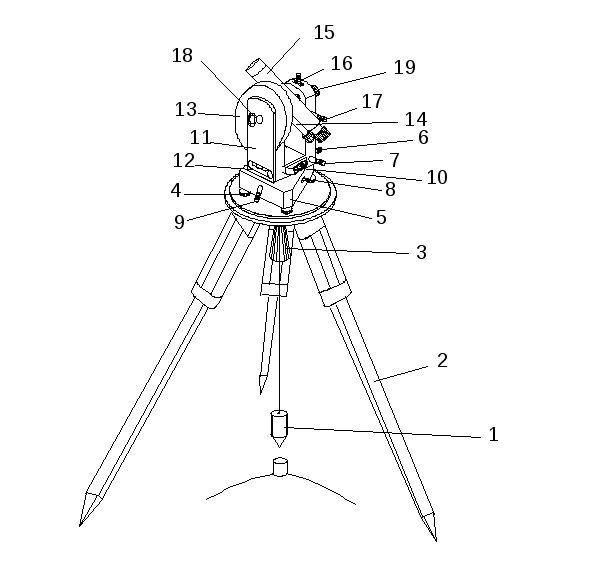 Тем не менее, на границах между пластинами, границах пластин могут быть обнаружены значительные аномалии по отношению к линейным скоростям. Снятие напряжений и деформаций на границах плит также является основной причиной землетрясений.Ко- и постсейсмические деформации литосферы можно объяснить только индивидуально в зависимости от механизма землетрясения. Для очень хорошо наблюдаемого землетрясения М7.9 Денали с эпицентром недалеко от Фэрбенкса, Аляска, в ноябре 2002 г. нелинейные движения РСДБ станции в Гилмор-Крик были успешно аппроксимированы комбинированной логарифмически-экспоненциальной моделью. Экспоненциальная деформация сохранялась в течение нескольких лет после косейсмического позиционного скачка (Heinkelmann et al., 2008).
Тем не менее, на границах между пластинами, границах пластин могут быть обнаружены значительные аномалии по отношению к линейным скоростям. Снятие напряжений и деформаций на границах плит также является основной причиной землетрясений.Ко- и постсейсмические деформации литосферы можно объяснить только индивидуально в зависимости от механизма землетрясения. Для очень хорошо наблюдаемого землетрясения М7.9 Денали с эпицентром недалеко от Фэрбенкса, Аляска, в ноябре 2002 г. нелинейные движения РСДБ станции в Гилмор-Крик были успешно аппроксимированы комбинированной логарифмически-экспоненциальной моделью. Экспоненциальная деформация сохранялась в течение нескольких лет после косейсмического позиционного скачка (Heinkelmann et al., 2008).
Смещения реперных точек из-за приливных и нагрузочных деформаций происходят в гораздо более коротких временных масштабах, таких как часы, дни, месяцы или годы.Эта группа эффектов до такой степени достаточно понятна и описана геофизическими моделями, что обычно напрямую сокращается из наблюдений, и поэтому никакие вклады не появляются в остаточных временных рядах координат станции. К этой группе принадлежат следующие деформации:
К этой группе принадлежат следующие деформации:
Приливы на твердой Земле, вызванные, в основном, внешними моментами Луны и Солнца, где деформации связаны с моментами посредством набора констант, зависящих от времени и частоты, называемых Любовью и Числа Шида.
Нагрузочные деформации, которые также включают вторичные воздействия на твердую Землю из-за взаимодействий между сферами земной системы, в основном вызванные океаническими приливами и атмосферным давлением, а также сезонные гидрологические и вызванные снегом деформации нагрузки.
Помимо деформаций твердой Земли и смещения прикрепленных опорных точек, ось вращения Земли перемещается из-за наклона оси вращения относительно оси фигуры.Движение оси может быть выражено относительно поверхности Земли, то есть Международной наземной системы отсчета (ITRS), или относительно квазиинерциального пространства, реализуемого геоцентрической системой отсчета неба (GCRS). Эффекты, выраженные по отношению к поверхности Земли, отделены от эффектов по отношению к небесной системе отсчета в зависимости от частоты. По соглашению все термины, относящиеся к ретроградному суточному диапазону, относятся к GCRS, а другие термины, выходящие за пределы ретроградного суточного диапазона, относятся к ITRS.Наконец, между ITRS и GCRS имеет место суточное вращение Земли. Термины, относящиеся к ITRS, называются полярным движением. Помимо основных периодических сигналов с 430 днями (колебание Чендлера) и годовыми периодами, полярное движение показывает вековые дрейфы, называемые полярным блужданием. Полярное блуждание объясняется большими долгосрочными изменениями массы внутри земной системы. Такое большое изменение массы произошло, например, в результате наступления и последующего таяния ледников во время последнего ледникового периода в конце плейстоцена, когда ледяные щиты толщиной до 3 км покрывали большие части Скандинавии, Гренландии и Канады.С тех пор, например, Скандинавия поднялась вверх примерно на 300 м, а мировой уровень моря поднялся примерно на 120–130 м. Полярное движение вызывает другую группу смещений опорных точек:
По соглашению все термины, относящиеся к ретроградному суточному диапазону, относятся к GCRS, а другие термины, выходящие за пределы ретроградного суточного диапазона, относятся к ITRS.Наконец, между ITRS и GCRS имеет место суточное вращение Земли. Термины, относящиеся к ITRS, называются полярным движением. Помимо основных периодических сигналов с 430 днями (колебание Чендлера) и годовыми периодами, полярное движение показывает вековые дрейфы, называемые полярным блужданием. Полярное блуждание объясняется большими долгосрочными изменениями массы внутри земной системы. Такое большое изменение массы произошло, например, в результате наступления и последующего таяния ледников во время последнего ледникового периода в конце плейстоцена, когда ледяные щиты толщиной до 3 км покрывали большие части Скандинавии, Гренландии и Канады.С тех пор, например, Скандинавия поднялась вверх примерно на 300 м, а мировой уровень моря поднялся примерно на 120–130 м. Полярное движение вызывает другую группу смещений опорных точек:
Полюсные приливы, центробежный эффект из-за векового движения среднего полюса оси вращения Земли относительно земной коры и приливы на полюсах океана, эффект второго порядка на твердой Земле из-за равновесной реакции океанов по отношению к основным периодическим сигналам в пределах полярного движения, чендлеровского колебания и годового члена.

РСДБ — необычный метод определения вариаций скорости вращения Земли. Скорость вращения Земли показывает, например, колебания, вызванные приливом, и вековое замедление из-за приливного трения в системе из двух тел Земля-Луна. Относительно GCRS меняется и ориентация Земли, что называется прецессией-нутацией. Непрерывный мониторинг этих величин позволяет улучшить модели земных недр. Модели нутации свободных кернов были получены по параметрам ориентации Земли, определенным из РСДБ-наблюдений.До сих пор для свободной нутации ядра предполагался период около 430 дней, хотя некоторые авторы считают интерференцию двух сигналов с периодами около 410 и 450 дней (Malkin & Miller, 2007). Для определения таких моделей всегда прибегают к косвенным методам, так как самое глубокое бурение земной коры достигало всего около 15 км.
Даже во время короткой задержки между приемами радиосигналов двумя РСДБ-антеннами около 20 мс, если смотреть с точки отсчета 6000 км, интерферометр значительно перемещается из-за вращения Земли и движения эклиптики. Следовательно, базовая линия изначально определяется в этих двух эпохах, что называется эффектом запаздывающей базовой линии, и ее следует относить к одной эпохе. Движение второй антенны после приема сигнала первой антенной учитывается в теоретической модели задержки VLBI.
Следовательно, базовая линия изначально определяется в этих двух эпохах, что называется эффектом запаздывающей базовой линии, и ее следует относить к одной эпохе. Движение второй антенны после приема сигнала первой антенной учитывается в теоретической модели задержки VLBI.
Все эти эффекты имеют общие последствия: каждая базовая линия, образованная парой антенн, непостоянна, а меняется со временем. Длины и направления векторов базовой линии могут изменяться относительно поверхности Земли и относительно системы отсчета радиоисточников.
2.6. Корреляция: определение наблюдаемых
Во время корреляции индивидуально записанные цифровые сигналы накладываются друг на друга для достижения помех, в результате чего получаются наблюдаемые. Оборудование, с помощью которого выполняется этот процесс, называется коррелятором. В принципе, можно различать аппаратные и программные корреляторы. Хотя аппаратный коррелятор ограничен количеством магнитных лент или дисков, которые могут обрабатываться параллельно, производительность программного коррелятора зависит только от доступной вычислительной мощности. Применяя современные концепции, такие как компьютерные кластеры или распределенные системы, а также из-за постоянных улучшений и развития компьютерного оборудования, технические границы корреляторов еще не достигнуты (Кондо и др., 2004; Мачида и др., 2006).
Применяя современные концепции, такие как компьютерные кластеры или распределенные системы, а также из-за постоянных улучшений и развития компьютерного оборудования, технические границы корреляторов еще не достигнуты (Кондо и др., 2004; Мачида и др., 2006).
В зависимости от цели приложения можно получить множество наблюдаемых. Астрономический РСДБ в первую очередь предназначен для восстановления изображений с высоким разрешением. Следовательно, желаемыми наблюдаемыми являются амплитуды и фазы полос. Вклад каждого телескопа складывается таким образом, как если бы вся решетка была одной антенной.Для геодезических и астрометрических РСДБ требуются точные данные о групповой задержке и скорости задержки. Групповую задержку можно получить, сдвигая мешающие сигналы во временной области до тех пор, пока не будет достигнута максимальная взаимная корреляция. В дополнение к взаимной корреляции битовых потоков необходимо устранить вращение полос, в основном вызванное эффектом Доплера из-за вращения Земли, так называемую остановку полос.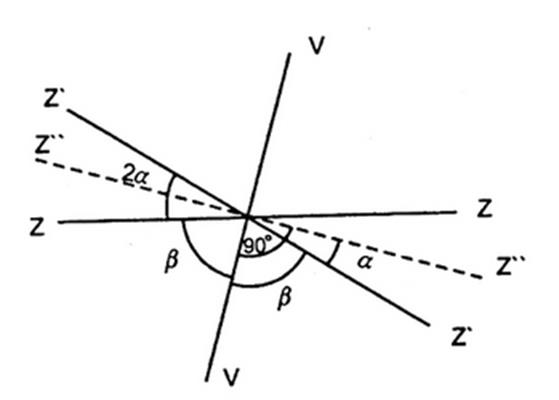 Это может быть достигнуто путем умножения на синус и косинус, так называемого квадратурного смешения, когда сигнал взаимной корреляции с вращающейся полосой, который колеблется в диапазоне кГц, доводится до частоты, близкой к нулю.Амплитуда и фаза границы могут быть получены путем суммирования или деления (тангенса) синуса и косинуса соответственно. Периферийную частоту, частную производную фазовой задержки по времени, можно отслеживать в течение нескольких минут, пока один радиоисточник непрерывно сканируется. Однако переключение между радиоисточниками приводит к неоднозначности, которую необходимо решить для измерения фазы, называемой решением неоднозначности. Проблемной неоднозначности можно избежать, если использовать групповую задержку как наблюдаемую, поскольку функция взаимной корреляции обычно показывает уникальный максимум.Скорость задержки — еще одна наблюдаемая величина, используемая в геодезической РСДБ для устранения неоднозначностей, вносимых широкополосным синтезом, до анализа групповых задержек.
Это может быть достигнуто путем умножения на синус и косинус, так называемого квадратурного смешения, когда сигнал взаимной корреляции с вращающейся полосой, который колеблется в диапазоне кГц, доводится до частоты, близкой к нулю.Амплитуда и фаза границы могут быть получены путем суммирования или деления (тангенса) синуса и косинуса соответственно. Периферийную частоту, частную производную фазовой задержки по времени, можно отслеживать в течение нескольких минут, пока один радиоисточник непрерывно сканируется. Однако переключение между радиоисточниками приводит к неоднозначности, которую необходимо решить для измерения фазы, называемой решением неоднозначности. Проблемной неоднозначности можно избежать, если использовать групповую задержку как наблюдаемую, поскольку функция взаимной корреляции обычно показывает уникальный максимум.Скорость задержки — еще одна наблюдаемая величина, используемая в геодезической РСДБ для устранения неоднозначностей, вносимых широкополосным синтезом, до анализа групповых задержек.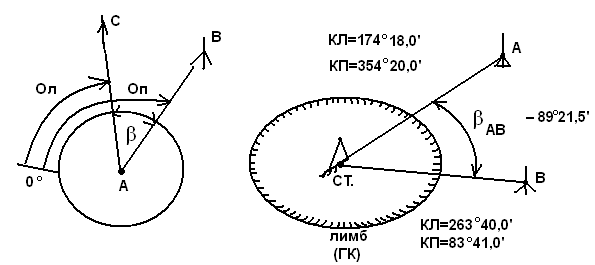 Его можно получить из интерференционной частоты, описывающей фазовый дрейф из-за вращения Земли. Поскольку точность скорости задержки по параметрам геодезической цели значительно хуже по сравнению с групповой задержкой, она обычно не используется сама по себе для определения параметров.
Его можно получить из интерференционной частоты, описывающей фазовый дрейф из-за вращения Земли. Поскольку точность скорости задержки по параметрам геодезической цели значительно хуже по сравнению с групповой задержкой, она обычно не используется сама по себе для определения параметров.
Процедура корреляции может быть математически описана с помощью взаимной корреляции и преобразования Фурье.Если сигналы сначала взаимно коррелированы, а затем преобразованы Фурье, тип коррелятора называется XF-коррелятором, например Марка VLBI-системы. В противном случае, если две математические процедуры применяются наоборот, это называется FX-коррелятором, например VLBA-системы. Оба типа корреляторов имеют свои преимущества и недостатки (Moran, 1989; Alef, 1989; Whitney, 2000).
2.7. Точность наблюдаемой групповой задержки
Инструментальная точность групповой задержки из корреляционного анализа
στ = 12π ∙ Beff ∙ SNR E1
\ n \ t \ t \ t \ tв первую очередь зависит от отношения сигнал / шум SNR и эффективная ширина полосы B eff , полученные путем синтеза реальных наблюдаемых и коррелированных каналов
Beff = ∑fi-f2N E2
, где fi — частоты каналов ( i = 1,2,… , N ) и f — их средняя частота. Отношение сигнал / шум
Отношение сигнал / шум
SNR = η2 ∙ Beff ∙ tintI2kA1 ∙ A2TR, 1 ∙ TR, 2b E3
является критерием успешного наблюдения с η ≈ 0,73 (1-битная выборка) инструментальным коэффициентом потерь, t int = от 60 до 1000 с время когерентного интегрирования, I поток радиоизлучения или интенсивность радиоисточника, k постоянная Больцмана; A 1,2 обозначают эффективные площади антенны, а T R, 1 и T R, 2 — шумовые температуры электронных устройств (Whitney et al., 1976). Приведенные выше уравнения (1-3) описывают чувствительность точности измерения в первую очередь к эффективной ширине полосы, но также и к интенсивности радиоисточника. Чтобы наблюдать радиоисточники с меньшей интенсивностью, время когерентной интеграции необходимо увеличивать в квадрате, чтобы сохранить точность измерений с использованием того же оборудования. Термины предполагают, что общий системный шум присутствует неявно, независимо на каждом канале и одинакового размера. Однако существует ряд инструментальных отрицательных эффектов, влияющих только на отдельные каналы.Поэтому Ray и Corey (1991) обсуждают расширение вышеупомянутой модели с помощью двух эмпирических переменных: масштабного коэффициента и аддитивной константы.
Термины предполагают, что общий системный шум присутствует неявно, независимо на каждом канале и одинакового размера. Однако существует ряд инструментальных отрицательных эффектов, влияющих только на отдельные каналы.Поэтому Ray и Corey (1991) обсуждают расширение вышеупомянутой модели с помощью двух эмпирических переменных: масштабного коэффициента и аддитивной константы.
Помимо инструментальной точности, связанной с одиночным наблюдением, стохастическая модель ансамблей РСДБ-наблюдений может быть описана не только диагональными элементами, но также недиагональными элементами в весовой или ковариационной матрице, соответственно. В принципе возможно большое разнообразие ковариационных моделей для описания корреляции наблюдений между собой (Tesmer, 2004).Среди них моделирование шума, зависящего от станции, показало, что оно значительно улучшает стохастику систем уравнений РСДБ (Gipson, 2007).
3. Анализ групповых задержек
После того, как неоднозначности от широкополосного синтеза были устранены с учетом наблюдаемой скорости задержки, математическая модель анализа групповых задержек имеет дело с
функциональной моделью, то есть созданием теоретических расчетов.
 Смоделированные наблюдения рассчитываются для каждого реального наблюдения с применением теоретической модели групповой задержки VLBI и различных моделей коррекции.Теоретическая модель РСДБ, используемая сегодня, называется консенсусной моделью и включает все необходимые условия для достижения точности 1 пс (около 0,3 мм). Как было представлено на Генеральной ассамблее МАС в 2012 году, Комиссия 52 МАС по теории относительности в фундаментальной астрономии вскоре представит новую модель с точностью 0,1 пс. Текущие традиционно применяемые модели коррекции определены Конвенциями IERS (2010).
Смоделированные наблюдения рассчитываются для каждого реального наблюдения с применением теоретической модели групповой задержки VLBI и различных моделей коррекции.Теоретическая модель РСДБ, используемая сегодня, называется консенсусной моделью и включает все необходимые условия для достижения точности 1 пс (около 0,3 мм). Как было представлено на Генеральной ассамблее МАС в 2012 году, Комиссия 52 МАС по теории относительности в фундаментальной астрономии вскоре представит новую модель с точностью 0,1 пс. Текущие традиционно применяемые модели коррекции определены Конвенциями IERS (2010).Определение параметров, которое также включает стохастику переопределенной проблемы путем моделирования допущенных ошибок и пренебречь детерминированной систематикой.В геодезической РСДБ для определения параметров были применены несколько методов: в первую очередь оценка методом наименьших квадратов (Koch, 1997), затем коллокация методом наименьших квадратов (Titov & Schuh, 2000), фильтрация Калмана (Herring et al.
 , 1990) и фильтрация информации с использованием квадратного корня (Bierman, 1977).
, 1990) и фильтрация информации с использованием квадратного корня (Bierman, 1977).
Детерминированная часть математической модели, функциональная модель наблюдения групповой задержки τ gd , может быть условно записана как
τgd = -1cb \ ‘WRQk + δτrel + δτiono + δτneut + δτcable +… E4
Он содержит скорость света c , вектор базовой линии b ‘, матрицу полярного движения W , матрицу суточного вращения R , смещение кадра, матрицу прецессии-нутации Q , и вектор положения радиоисточника k, , который зависит от склонения и прямого восхождения в эпоху J2000.0. Первое выражение в правой части перед коррекцией релятивистской задержки δτ rel называется геометрической задержкой. Вместе с релятивистской коррекцией задержки геометрическая задержка называется теоретической моделью задержки; указано например с помощью модели консенсуса (Eubanks, 1991) в ее нынешней традиционной форме (IERS Conventions, 2010).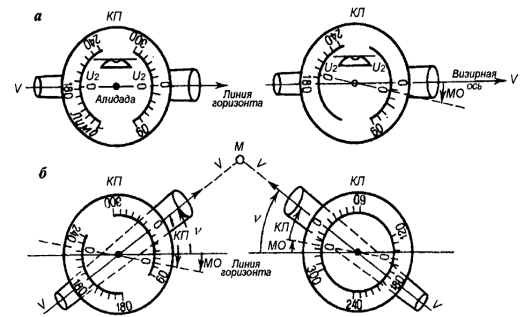 С текущей точностью достаточно смоделировать групповую задержку ньютоновским способом и добавить релятивистские последствия, запаздывающую базовую линию и другие специальные и общие релятивистские эффекты в форме поправок к ньютоновской задержке.Поправка на ионосферу первого порядка
С текущей точностью достаточно смоделировать групповую задержку ньютоновским способом и добавить релятивистские последствия, запаздывающую базовую линию и другие специальные и общие релятивистские эффекты в форме поправок к ньютоновской задержке.Поправка на ионосферу первого порядка
δτiono = fS2fX2-fS2τX-τS E5
получается линейной комбинацией задержек одной полосы в X- и S-полосах, умноженной на коэффициент, отношение квадрата частоты нижней полосы к разделению квадратов частот. Членами более высокого порядка можно пренебречь для достижения желаемой точности (Hawarey et al., 2005). По аналогии с этим термином ошибка измерения в S-диапазоне, которая возникает из-за более низкого разрешения, обычно большего, чем разрешение в X-диапазоне, распространяется на групповую задержку X-диапазона.Чем меньше коэффициент, тем меньше вклад ошибок от S-диапазона в групповую задержку X-диапазона. Широкое частотное разделение снижает коэффициент и, таким образом, способствует точности.
Дополнительно явно упоминаются поправки на задержку нейтросферы δτ нейтрон и задержку в кабеле δτ , кабель . Три точки в конце приведенного выше уравнения означают, что могут быть рассмотрены дальнейшие исправления.Каждая из этих задержек содержит два члена, один вклад от первой и один от второй станции, образующих базовую линию. Если радиосигнал сначала достигает первой антенны, вклад в групповую задержку будет положительным для второй антенны и отрицательным для первой антенны и наоборот. Поправка нейтросферы i-й станции равна
δτneut, i = 1c ∙ mfhe ∙ zhd + mfgecosaGN + sinaGE E6
, где mf — картографические функции гидростатической задержки (индекс h ), или градиенты (индекс g ) в зависимости от угла места e .Горизонтальная асимметрия моделируется двумя градиентами в направлениях север-юг G N и восток-запад G E в зависимости от азимутального угла a . Вышеупомянутый член умножается на коэффициент -1, если i = 1. Современные функции картографии выводятся путем трассировки лучей с помощью численных моделей погоды, например VMF1 (Böhm et al., 2006). Гидростатическая задержка в направлении зенитного ZHD прямо пропорциональна давление воздуха на поверхность в опорной точке РСДБА конкретного инструмента.Соответствующая априорная модель градиента должна применяться для геодезических РСДБ-анализов, поскольку расчетные параметры градиента обычно ограничены и, таким образом, могут зависеть от априорных значений. Помимо априорной модели градиента, указанной в IERS Conventions (2010), можно использовать априорную градиентную модель, определенную из погодной модели Data Assimilation Office, предоставленной Центром анализа IVS в Центре космических полетов имени Годдарда НАСА (MacMillan & Ma, 1998). рекомендуемые. Задержка в кабеле измеряется на каждой антенне и может применяться напрямую, как взято из базы данных IVS.Теоретические значения, вычисленные описанным выше способом, вычитаются из наблюдаемых групповых задержек, формируя вектор o-c (наблюдаемое минус вычисленное).
Вышеупомянутый член умножается на коэффициент -1, если i = 1. Современные функции картографии выводятся путем трассировки лучей с помощью численных моделей погоды, например VMF1 (Böhm et al., 2006). Гидростатическая задержка в направлении зенитного ZHD прямо пропорциональна давление воздуха на поверхность в опорной точке РСДБА конкретного инструмента.Соответствующая априорная модель градиента должна применяться для геодезических РСДБ-анализов, поскольку расчетные параметры градиента обычно ограничены и, таким образом, могут зависеть от априорных значений. Помимо априорной модели градиента, указанной в IERS Conventions (2010), можно использовать априорную градиентную модель, определенную из погодной модели Data Assimilation Office, предоставленной Центром анализа IVS в Центре космических полетов имени Годдарда НАСА (MacMillan & Ma, 1998). рекомендуемые. Задержка в кабеле измеряется на каждой антенне и может применяться напрямую, как взято из базы данных IVS.Теоретические значения, вычисленные описанным выше способом, вычитаются из наблюдаемых групповых задержек, формируя вектор o-c (наблюдаемое минус вычисленное).
Перед процессом оценки параметров аналитик должен принять решение о параметризации, т. Е. Определении параметров, которые должны быть определены. Согласно этому решению, конструкция или матрица Якоби, связывающая наблюдения с параметрами, фиксируется в ее общей структуре. Записи матрицы плана — это частные производные наблюдений по отдельным параметрам.Большое разнообразие частных производных геодезических и астрометрических параметров можно найти у Nothnagel (1991) или у Sovers & Jacobs (1996). Ряды строк и столбцов системы уравнений расширяются за счет геодезических данных и псевдонаблюдений соответственно. Псевдонаблюдения — это ограничения на вспомогательные параметры, которые могут быть необходимы для предотвращения сингулярностей. Воздействие ограничения определяется его весом, который выбирает аналитик. С точностью групповой задержки в качестве основы для весовой матрицы математическая модель завершена, и параметры могут быть определены.
Целью анализа является получение нормально распределенных остатков.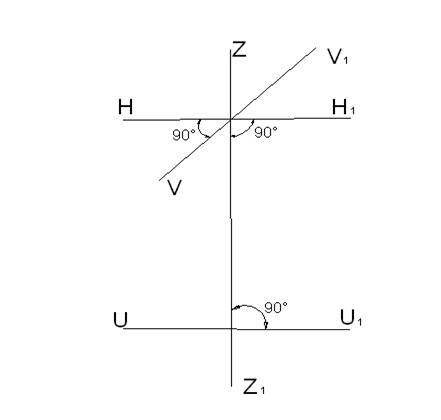 Это означает, что все существующие существенные систематики идентифицированы и достаточно смоделированы, и что стохастическая часть содержит чистый белый шум, предположение методов оценки. С помощью робастной оценки нормальное распределение может быть в определенной степени принудительным. Однако этот метод практически отбрасывает наблюдения, нарушающие определенные критерии устойчивости, и тем самым снижает избыточность проблемы. Это также требует некоторых дополнительных операций, что увеличивает время выполнения.Тем не менее, оба недостатка обычно принимаются с учетом преимуществ робастной оценки (Kutterer et al., 2003). Полученные формальные ошибки параметров являются результатом наблюдения и ошибок модели, проецируемых в пространство параметров путем распространения ошибок. Не все возможные источники ошибок обязательно включены, и поэтому можно предположить существование других игнорируемых ошибок, называемых пропущенными ошибками. Следовательно, чтобы получить значимую точность, необходимо оценить тип и размер пропущенных ошибок и добавить их к формальным ошибкам.
Это означает, что все существующие существенные систематики идентифицированы и достаточно смоделированы, и что стохастическая часть содержит чистый белый шум, предположение методов оценки. С помощью робастной оценки нормальное распределение может быть в определенной степени принудительным. Однако этот метод практически отбрасывает наблюдения, нарушающие определенные критерии устойчивости, и тем самым снижает избыточность проблемы. Это также требует некоторых дополнительных операций, что увеличивает время выполнения.Тем не менее, оба недостатка обычно принимаются с учетом преимуществ робастной оценки (Kutterer et al., 2003). Полученные формальные ошибки параметров являются результатом наблюдения и ошибок модели, проецируемых в пространство параметров путем распространения ошибок. Не все возможные источники ошибок обязательно включены, и поэтому можно предположить существование других игнорируемых ошибок, называемых пропущенными ошибками. Следовательно, чтобы получить значимую точность, необходимо оценить тип и размер пропущенных ошибок и добавить их к формальным ошибкам. Если значительный источник ошибок известен, но не учитывается, формальные ошибки, которые в этом случае фактически меньше реальных ошибок, не должны быть завышены, например на коэффициент или постоянную величину в зависимости от предполагаемых характеристик пропущенных ошибок. Из-за присущих РСДБ характеристик повторяемость базовой линии представляет собой надежный и часто используемый критерий качества для выполнения оценки параметров, поскольку он не зависит от геодезических данных. Более подробный обзор геодезического РСДБ-анализа представлен Schuh (2000).
Если значительный источник ошибок известен, но не учитывается, формальные ошибки, которые в этом случае фактически меньше реальных ошибок, не должны быть завышены, например на коэффициент или постоянную величину в зависимости от предполагаемых характеристик пропущенных ошибок. Из-за присущих РСДБ характеристик повторяемость базовой линии представляет собой надежный и часто используемый критерий качества для выполнения оценки параметров, поскольку он не зависит от геодезических данных. Более подробный обзор геодезического РСДБ-анализа представлен Schuh (2000).
3.1. Координаты и параметры ориентации Земли
VLBI для геодезических и астрометрических анализов групповой задержки в первую очередь предназначены для определения наземных базовых линий (см. Рисунок 4.), положений радиоисточников и параметров ориентации Земли (EOP). Эти группы параметров можно оценивать одновременно. Тем не менее, при планировании сеансов наблюдений, которые выполняются в геодезическом или астрометрическом режиме, обычно оптимизируется одна или две из этих трех групп параметров.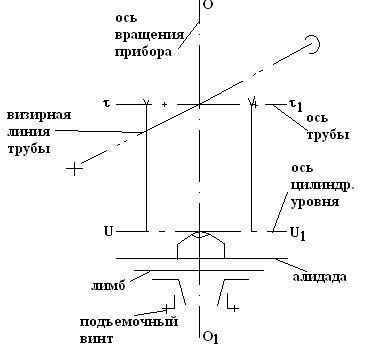 При стандартном подходе к оценке для одного 24-часового сеанса ИВС вспомогательные параметры для синхронизации часов и моделирования задержки нейтросферы и градиента оцениваются одновременно. Часы уже синхронизированы, например. через системное время GPS. Во время эксперимента нормали водородного мазера демонстрируют некоторый дрейф, а иногда и скачки друг относительно друга. Необходимо определить эталонные часы, а дрейф других часов обычно можно аппроксимировать полиномом второго порядка по отношению к эталонным часам.Дополнительные вспомогательные устройства параметризуются как кусочно-линейные функции с временным разрешением около 30 минут для стохастических флуктуаций часов и задержек нейтросферы и нескольких часов для градиентов нейтросферы, соответственно. Чтобы различать общие вращения радиоисточников и параметры ориентации Земли, необходимо включать уравнения условия отсутствия чистого вращения (NNR) для небесных координат. Кроме того, многогранник наземных базовых линий может подвергаться общим поворотам, которые по соглашению должны выражаться EOP, и, таким образом, условия NNR должны применяться также и на наземной стороне.
При стандартном подходе к оценке для одного 24-часового сеанса ИВС вспомогательные параметры для синхронизации часов и моделирования задержки нейтросферы и градиента оцениваются одновременно. Часы уже синхронизированы, например. через системное время GPS. Во время эксперимента нормали водородного мазера демонстрируют некоторый дрейф, а иногда и скачки друг относительно друга. Необходимо определить эталонные часы, а дрейф других часов обычно можно аппроксимировать полиномом второго порядка по отношению к эталонным часам.Дополнительные вспомогательные устройства параметризуются как кусочно-линейные функции с временным разрешением около 30 минут для стохастических флуктуаций часов и задержек нейтросферы и нескольких часов для градиентов нейтросферы, соответственно. Чтобы различать общие вращения радиоисточников и параметры ориентации Земли, необходимо включать уравнения условия отсутствия чистого вращения (NNR) для небесных координат. Кроме того, многогранник наземных базовых линий может подвергаться общим поворотам, которые по соглашению должны выражаться EOP, и, таким образом, условия NNR должны применяться также и на наземной стороне. Чтобы получить координаты сетевой станции вместо базовых линий, необходимо предоставить априорный набор координат и другую геодезическую базу. Для получения геоцентрических координат априорные значения должны относиться к геоцентру. Это справедливо для обычных наземных опорных кадров, таких как версия ITRF. Данные должны ограничивать корректировки априорных значений, по крайней мере, таким образом, чтобы присущие трансляционные неоднозначности были надлежащим образом зафиксированы, и тогда в системе уравнений не появлялись сингулярности.
Чтобы получить координаты сетевой станции вместо базовых линий, необходимо предоставить априорный набор координат и другую геодезическую базу. Для получения геоцентрических координат априорные значения должны относиться к геоцентру. Это справедливо для обычных наземных опорных кадров, таких как версия ITRF. Данные должны ограничивать корректировки априорных значений, по крайней мере, таким образом, чтобы присущие трансляционные неоднозначности были надлежащим образом зафиксированы, и тогда в системе уравнений не появлялись сингулярности.
Рис. 4.
При длине почти 6000 км базовая линия WESTFORD (Вестфорд, США) — WETTZELL (Веттцелль, Германия) показывает постоянный линейный рост примерно 1,7 см в год, что связано с движением Северной Америки wrt Евразийская плита. Небольшой годовой сигнал связан с немоделированными геофизическими эффектами. Цифра предоставлена IVS (http://vlbi.geod.uni-bonn.de/baseline-project/) и сделана на основе результатов IVS AC NASA / GSFC.
Этот набор условных уравнений называется отсутствием чистого перевода (NNT). Уравнения NNR и NNT в настоящее время являются лучшими недеформируемыми условиями базы данных, потому что в отличие от фиксации определенных наборов координат, все координаты регулируются с помощью этого подхода, называемого настройкой свободной сети. Происхождение и ориентация априорных рамок сохраняются, но только в кинематическом смысле. Следовательно, из-за несовершенного представления системы через координаты измеряемых объектов все еще могут присутствовать некоторые повороты кадра, которые нельзя подавить с помощью этого подхода.Недостатки кинематического невращающегося подхода могут привести к небольшим различиям между кинематически и динамически невращающимся режимом, которые, возможно, придется учесть путем корректировки.
Уравнения NNR и NNT в настоящее время являются лучшими недеформируемыми условиями базы данных, потому что в отличие от фиксации определенных наборов координат, все координаты регулируются с помощью этого подхода, называемого настройкой свободной сети. Происхождение и ориентация априорных рамок сохраняются, но только в кинематическом смысле. Следовательно, из-за несовершенного представления системы через координаты измеряемых объектов все еще могут присутствовать некоторые повороты кадра, которые нельзя подавить с помощью этого подхода.Недостатки кинематического невращающегося подхода могут привести к небольшим различиям между кинематически и динамически невращающимся режимом, которые, возможно, придется учесть путем корректировки.
3.2. Базовые кадры
В отличие от анализа одного сеанса VLBI, полная история данных VLBI обычно анализируется для определения опорных кадров и временных рядов EOP. Если анализируются более длительные интервалы времени, скорости станций наземной сети также должны быть параметризованы. Следовательно, необходимо включить дополнительные исходные условия для временной эволюции как наземных NNR, так и NNT условий. В принципе, чем больше базовых точек включается, тем надежнее становится датум (Baarda, 1968). Для определения кадра выбор опорных станций или опорных радиоисточников, соответственно, является одной из основных задач. Станции обычно используются в качестве эталонов, если они в достаточной степени соответствуют линейной модели станции. Если станция демонстрирует значительное отклонение от линейности, например.грамм. после сейсмического события он обычно исключается из набора опорных точек. На данный момент лучшей реализацией наземной системы отсчета является ITRF2008 (см. Рисунок 5.). Для небесных реперных точек рассматриваются астрометрические и астрофизические критерии устойчивости, если таковые имеются (Heinkelmann et al., 2007a). Поскольку количество наблюдаемых радиоисточников намного превышает количество доступных сетевых станций, этот набор опорных точек может быть выбран с применением более строгих критериев.
Следовательно, необходимо включить дополнительные исходные условия для временной эволюции как наземных NNR, так и NNT условий. В принципе, чем больше базовых точек включается, тем надежнее становится датум (Baarda, 1968). Для определения кадра выбор опорных станций или опорных радиоисточников, соответственно, является одной из основных задач. Станции обычно используются в качестве эталонов, если они в достаточной степени соответствуют линейной модели станции. Если станция демонстрирует значительное отклонение от линейности, например.грамм. после сейсмического события он обычно исключается из набора опорных точек. На данный момент лучшей реализацией наземной системы отсчета является ITRF2008 (см. Рисунок 5.). Для небесных реперных точек рассматриваются астрометрические и астрофизические критерии устойчивости, если таковые имеются (Heinkelmann et al., 2007a). Поскольку количество наблюдаемых радиоисточников намного превышает количество доступных сетевых станций, этот набор опорных точек может быть выбран с применением более строгих критериев. Для текущей стандартной реализации ICRF2 (см. Рисунок 6.), помимо устойчивости, учитывалось также геометрическое распределение опорных радиоисточников (IERS, 2009). Метрика базовых линий VLBI зависит только от введенной шкалы времени и скорости света, которая является одной из наиболее точно известных естественных констант. Точная сетевая шкала наземных координат — действительно сильная сторона метода РСДБ. Если временные масштабы модели VLBI правильно обрабатываются, в частности, во время преобразования Лоренца из барицентрического координатного времени (TCB) в геоцентрическое координатное время (TCG), результирующая геоцентрическая метрика VLBI является одной из самых точных среди методов космической геодезии.Масштаб космических геодезических методов с использованием спутников, таких как GNSS и SLR, дополнительно зависит от несовершенства моделей гравитационного поля Земли и неопределенности геоцентрической гравитационной постоянной GM. Однако эти методы необходимы для реализации геоцентра, в частности SLR.
Для текущей стандартной реализации ICRF2 (см. Рисунок 6.), помимо устойчивости, учитывалось также геометрическое распределение опорных радиоисточников (IERS, 2009). Метрика базовых линий VLBI зависит только от введенной шкалы времени и скорости света, которая является одной из наиболее точно известных естественных констант. Точная сетевая шкала наземных координат — действительно сильная сторона метода РСДБ. Если временные масштабы модели VLBI правильно обрабатываются, в частности, во время преобразования Лоренца из барицентрического координатного времени (TCB) в геоцентрическое координатное время (TCG), результирующая геоцентрическая метрика VLBI является одной из самых точных среди методов космической геодезии.Масштаб космических геодезических методов с использованием спутников, таких как GNSS и SLR, дополнительно зависит от несовершенства моделей гравитационного поля Земли и неопределенности геоцентрической гравитационной постоянной GM. Однако эти методы необходимы для реализации геоцентра, в частности SLR. В то время как конфигурации орбиты спутника напрямую относятся к центру масс системы Земли, РСДБ не зависит от этой динамики, и поэтому невозможно отнести к центру масс только РСДБ.
В то время как конфигурации орбиты спутника напрямую относятся к центру масс системы Земли, РСДБ не зависит от этой динамики, и поэтому невозможно отнести к центру масс только РСДБ.
Рис. 5.
Кинематика обсерваторий с различными космическими геодезическими методами, включая РСДБ (оранжевый), как дано решением наземной системы отсчета ITRF2008, определенным в DGFI (http://www.dgfi.badw.de/), любезно предоставлено M. Seitz
EOP определяются как параметры вращения между GCRS и ITRS. VLBI обеспечивает прямой доступ к обеим системам. Таким образом, РСДБ — единственный метод прямого определения EOP. Спутниковые методы требуют дополнительного преобразования их динамических конфигураций спутниковой орбиты в GCRS, подвержены ряду источников ошибок, и, таким образом, только производные от некоторых EOP достигают достаточной точности.Поскольку для поворота определены пять углов (EOP), этого можно достичь только с помощью трех независимых углов, например Углы Эйлера, ЭОП по определению коррелируют друг с другом. Параметры ориентации Земли, определенные с помощью РСДБ, использовались для определения множества величин, таких как нутация свободного ядра (IERS Conventions, 2010) или условия океанических приливов (Englich et al., 2008).
Параметры ориентации Земли, определенные с помощью РСДБ, использовались для определения множества величин, таких как нутация свободного ядра (IERS Conventions, 2010) или условия океанических приливов (Englich et al., 2008).
Рисунок 6.
Средние позиционные ошибки мультисессионных радиоисточников ICRF2, наблюдаемые IVS.Более крупные позиционные ошибки (> 1000 мксек) могут быть обнаружены почти только вблизи галактической плоскости (омега-образная линия). Рисунок взят из IERS Tech. Примечание 35, любезно предоставлено C. Jacobs
3.3. Атмосферные величины
Основная цель атмосферных анализов — определение содержания водяного пара в атмосфере. Атмосферный водяной пар, например описываемая осаждаемой водой, может быть получена путем умножения коэффициента на расчетную зенитную задержку во влажном состоянии (Heinkelmann et al., 2007b). В принципе, параметры нейтросферы оптимально декоррелированы на малых высотах.Однако, если угол места наблюдения слишком мал, разброс становится слишком большим, и наблюдение может быть потеряно. В качестве компромисса применяется угол отсечки по высоте, который в случае РСДБ обычно составляет 5 °. Для РСДБ возможны малые углы отсечки возвышения, поскольку РСДБ-антенны являются направленными и отсутствуют эффекты многолучевого распространения, сравнимые с теми, которые присутствуют в случае ненаправленных, например Антенны GNSS. Еще один критерий для определения оптимального параметра нейтросферы — это пространственно-временной отбор проб.Примерно с начала 1990-х годов геодезические VLBI-графики требуют, чтобы антенны указывали в самых разных направлениях в течение относительно коротких интервалов времени. При такой пространственно-временной выборке нейтросфера наблюдается с хорошим геометрическим распределением в течение относительно короткого времени. Следовательно, параметры нейтросферы могут быть успешно оценены с высоким временным разрешением.
В качестве компромисса применяется угол отсечки по высоте, который в случае РСДБ обычно составляет 5 °. Для РСДБ возможны малые углы отсечки возвышения, поскольку РСДБ-антенны являются направленными и отсутствуют эффекты многолучевого распространения, сравнимые с теми, которые присутствуют в случае ненаправленных, например Антенны GNSS. Еще один критерий для определения оптимального параметра нейтросферы — это пространственно-временной отбор проб.Примерно с начала 1990-х годов геодезические VLBI-графики требуют, чтобы антенны указывали в самых разных направлениях в течение относительно коротких интервалов времени. При такой пространственно-временной выборке нейтросфера наблюдается с хорошим геометрическим распределением в течение относительно короткого времени. Следовательно, параметры нейтросферы могут быть успешно оценены с высоким временным разрешением.
Помимо стандартных моделей анализа и графиков наблюдений, точное определение зенитных задержек с повышенной влажностью зависит от точных значений приземного давления воздуха в местах расположения станций сети во время наблюдений. Влияние на определение зенитных задержек было количественно оценено и исследовано. В частности, наземная система отсчета, если она также не скорректирована, может внести большие систематические поправки в оценки зенитной задержки. Например, слабые места в определении происхождения по оси z ITRF2000 могут вызывать очевидные тенденции в климатологии водяного пара в атмосфере (Heinkelmann, 2008). Измерения атмосферного давления на месте показали, что они могут быть наилучшими имеющимися данными для этой цели.Однако в течение более чем 30 лет наблюдений временные ряды измерений давления воздуха на месте часто подвержены неоднородностям, вызванным множеством возможных эффектов. Если эти неоднородности гомогенизируются соответствующими процедурами (Heinkelmann et al., 2005), временные ряды зенитной влажной задержки можно использовать для надежной оценки тенденций атмосферного водяного пара и других климатических величин. Кроме того, зенитные «мокрые» задержки могут использоваться в качестве критерия качества для внутренней согласованности (сравнение внутри техники) и внешней проверки (сравнение между методами).
Влияние на определение зенитных задержек было количественно оценено и исследовано. В частности, наземная система отсчета, если она также не скорректирована, может внести большие систематические поправки в оценки зенитной задержки. Например, слабые места в определении происхождения по оси z ITRF2000 могут вызывать очевидные тенденции в климатологии водяного пара в атмосфере (Heinkelmann, 2008). Измерения атмосферного давления на месте показали, что они могут быть наилучшими имеющимися данными для этой цели.Однако в течение более чем 30 лет наблюдений временные ряды измерений давления воздуха на месте часто подвержены неоднородностям, вызванным множеством возможных эффектов. Если эти неоднородности гомогенизируются соответствующими процедурами (Heinkelmann et al., 2005), временные ряды зенитной влажной задержки можно использовать для надежной оценки тенденций атмосферного водяного пара и других климатических величин. Кроме того, зенитные «мокрые» задержки могут использоваться в качестве критерия качества для внутренней согласованности (сравнение внутри техники) и внешней проверки (сравнение между методами). Межтехнические сравнения с другими методами космической геодезии на радиоволнах были выполнены и опубликованы большим количеством авторов. Задержки нейтросферы, определяемые этими методами, должны в принципе равняться друг другу, если реперные точки локальных приборов расположены на одной высоте. Чтобы скорректировать задержки нейтросферы по высоте, необходима поправка, которая должна учитывать зависимость симметричной модели нейтросферы от высоты. Помимо вышеупомянутых гидростатических и негидростатических (влажных) зенитных задержек, также функции картирования меняются с высотой и вносят свой вклад в нейтросферную связь.Другой тип параметра нейтросферы, градиенты должны равняться друг другу без поправки. На самом деле, однако, параметры нейтросферы для различных методов космической геодезии различаются (Teke et al., 2011), даже если применяются связи. Причины могут заключаться в внутреннем упрощении модели нейтросферы и пренебрежении обстоятельствами, например обтекатели над приборами, которые не рассматриваются в модели нейтросферы.
Межтехнические сравнения с другими методами космической геодезии на радиоволнах были выполнены и опубликованы большим количеством авторов. Задержки нейтросферы, определяемые этими методами, должны в принципе равняться друг другу, если реперные точки локальных приборов расположены на одной высоте. Чтобы скорректировать задержки нейтросферы по высоте, необходима поправка, которая должна учитывать зависимость симметричной модели нейтросферы от высоты. Помимо вышеупомянутых гидростатических и негидростатических (влажных) зенитных задержек, также функции картирования меняются с высотой и вносят свой вклад в нейтросферную связь.Другой тип параметра нейтросферы, градиенты должны равняться друг другу без поправки. На самом деле, однако, параметры нейтросферы для различных методов космической геодезии различаются (Teke et al., 2011), даже если применяются связи. Причины могут заключаться в внутреннем упрощении модели нейтросферы и пренебрежении обстоятельствами, например обтекатели над приборами, которые не рассматриваются в модели нейтросферы.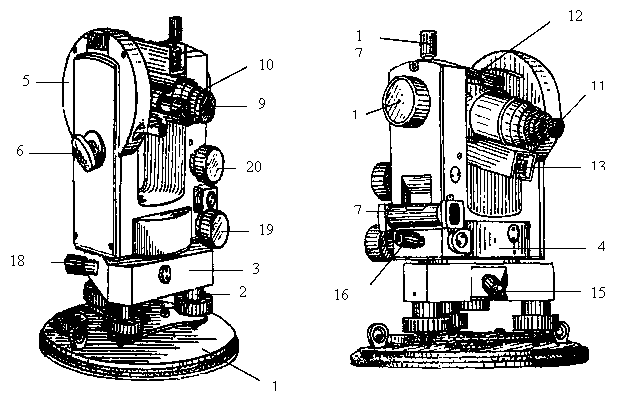 Кроме того, оценки запаздывания во влажном зените, к сожалению, не только описывают состояние нейтросферы, но также и дополнительный шум и систематику от неучтенных эффектов вне модели нейтросферы, которые показывают сопоставимые характеристики, зависящие от высоты.
Кроме того, оценки запаздывания во влажном зените, к сожалению, не только описывают состояние нейтросферы, но также и дополнительный шум и систематику от неучтенных эффектов вне модели нейтросферы, которые показывают сопоставимые характеристики, зависящие от высоты.
Другие примеры атмосферных величин, полученных с помощью геодезических РСДБ, менее популярны: Jin et al. (2008) показали, что гидростатическая составляющая внутри общей задержки нейтросферы может быть использована для определения амплитуд атмосферных приливов и отливов, а Tesmer et al. (2008) оценили коэффициенты модели нагрузочных деформаций атмосферного давления с помощью подхода, основанного на временных рядах высоты станции.
3.4. Дополнительные параметры, полученные из групповых задержек
Помимо вышеупомянутых величин, геодезическая РСДБ показала свою способность точно определять другие параметры.Эти параметры обычно оцениваются с помощью индивидуально оптимизированного анализа, разработанного для конкретной цели, в то время как другие параметры не рассматриваются и не ограничиваются. Следующие параметры, полученные с помощью геодезических РСДБ, — это
Следующие параметры, полученные с помощью геодезических РСДБ, — это
числа Лява и Шида. Числа Лява и Шида были недавно оценены Центром анализа IVS Института геодезии и геофизики (IGG), Венский технический университет, Австрия (Spicakova et al., 2010). Значения очень хорошо согласуются со значениями, указанными в соглашениях IERS (2004), и могут рассматриваться как улучшение по сравнению с теми значениями, которые ранее были оценены VLBI (Haas & Schuh, 1996).
Эксцентриситет сетевых станций. Для определения эксцентриситетов геодезист обычно предпочитает измерение, например получены инженерно-геодезическими методами. Тем не менее, когда такие измерения недоступны, в пространство параметров можно вставить эксцентриситет. Наибольшие эксцентриситеты для геодезических РСДБ-антенн были измерены в мобильных обсерваториях примерно в 1990-х годах. Если на одной и той же платформе установлено различное оборудование, эксцентриситет на площадке может измениться между двумя мобильными занятиями.
 На стационарных антеннах обычно избегают больших эксцентриситетов. Когда доступны точно измеренные эксцентриситеты, в принципе возможно сравнить измеренные эксцентриситет с расчетными. Однако преобразование локальной системы измерения в геоцентрическую декартову систему априорного каталога может значительно ухудшить точность измеренного эксцентриситета и, следовательно, сравнения.
На стационарных антеннах обычно избегают больших эксцентриситетов. Когда доступны точно измеренные эксцентриситеты, в принципе возможно сравнить измеренные эксцентриситет с расчетными. Однако преобразование локальной системы измерения в геоцентрическую декартову систему априорного каталога может значительно ухудшить точность измеренного эксцентриситета и, следовательно, сравнения.γ-параметр параметризованной постньютоновской теории.Параметр γ описывает, насколько единица массы деформирует пространство-время и равна единице в теории гравитации Эйнштейна. В определении γ-параметра РСДБ конкурирует с дальномерными измерениями космических аппаратов, которые в настоящее время показывают, что они дают оценки с несколько лучшей повторяемостью. Однако измерения дальности с помощью космических аппаратов выполняются в гораздо меньшее количество эпох и почти в одном направлении Вселенной. РСДБ, с его более чем 30-летними непрерывными наблюдениями в квази-всех направлениях Вселенной, может дополнительно доказать, что эта универсальная постоянная действительно инвариантна для эпохи измерений и направлений в нашей Вселенной.
 Обзор последних оценок и более ранних результатов РСДБ можно найти в Heinkelmann & Schuh (2010).
Обзор последних оценок и более ранних результатов РСДБ можно найти в Heinkelmann & Schuh (2010).Скорости радиоисточников и другие расширенные астрометрические параметры. Внегалактические радиоисточники в принципе должны подвергаться галактическому вращению со скоростью около 5,4 мкс в год (Ковалевский, 2003). Однако точное определение величины этого эффекта очень сложно. Одной из трудностей является корреляция со скоростью прецессии, которая составляет около 50 в год.Модели прецессии также корректируются с помощью VLBI (Capitaine et al., 2003). Несмотря на то, что галактическое вращение происходит в галактической плоскости, а прецессия определяется вдоль небесного экватора, галактическая аберрация может перерасти в скорость прецессии, оцененную РСДБ (Малкин, 2011). Кроме того, исследование скоростей радиоисточников привело к тому, что Титов и др. (2011) к оценке постоянной Хаббла, описывающей анизотропное расширение Вселенной или низкочастотные гравитационные волны, и, таким образом, космология стала проблемой также для геодезических и астрометрических РСДБ.

4. Выводы
\ nМы очень надеемся, что посткризисный кризис станет импульсом для радикальных изменений в обществе во всем мире. Мы также предлагаем, чтобы люди обращались к экспертным рекомендациям не только от своих национальных и региональных правительств, но и от Всемирной организации здравоохранения, а также для стран с низким и средним уровнем доходов.
\ nКризис COVID-19 предполагает, что последствия делятся на экономический рост, медицину и устойчивость.Так как же распределить эффект и усилия по восстановлению между этими измерениями? Как распределить время и человеческие ресурсы, не говоря уже о том, какие испытания и какие пациенты?
\ nВ этой главе мы не хотели давать специализированные ответы с экономической, медицинской или экологической точки зрения, а скорее связать эти ответы с другими темами, представляющими интерес для общества.
\ n Существует множество руководств для обсуждения вопросов экономики и адаптации ее к окружающей среде и с экономической точки зрения, а также суровой налогово-бюджетной политики, которая ставит во главу угла занятость и возобновление деятельности за счет оптимизации ресурсов и усилий.
Нам нужно изменить приоритеты. Главное, что важно, а что не важно, и именно поэтому нам также необходимо столкнуться с изменениями в человеческом поведении. Мы хотим утверждать, что одна из вещей, которые кажутся очень важными, — это идея солидарности. Это просто вопрос поиска медицинских отходов, потому что уже много написано, и просто необходимо, чтобы люди имели доступ к тому, что подходит для данной ситуации. Мы можем накапливать все эти знания в этой новой ситуации, каждый из нас.
\ nОтвет правительства должен касаться трех вопросов. Во-первых, чтобы обеспечить бесперебойное предоставление основных услуг. Во-вторых, чтобы обеспечить безопасность работников превыше любых других мер, потому что нам нужны эти команды, нам нужны эти люди, и нам нужны эти герои на улицах, и, в-третьих, мы должны обеспечить частую и легкую связь с гражданами, чтобы остановить фальшивые новости и чтобы избежать распространения недоразумений.
\ n Наконец, хороший способ противостоять кризису — это выиграть небольшие битвы, в области здоровья, за счет территориального управления инфекциями, в окружающей среде, избегая очень долгосрочных целей и вместо этого ставя более краткосрочные и среднесрочные цели.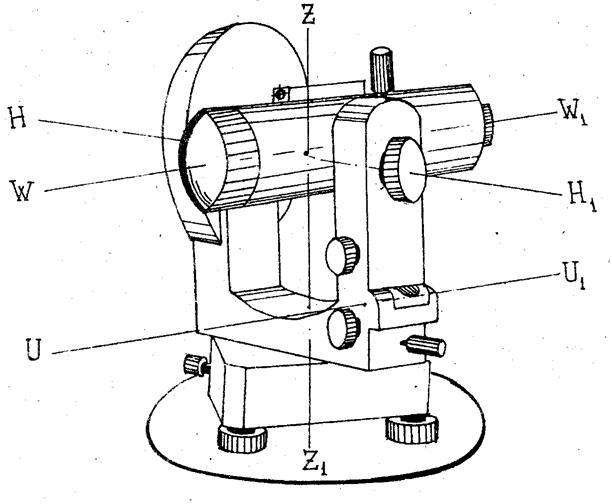 .
.
Команда научных консультантов IntechOpen поддерживает команду издателей, предоставляя редакционные и академические материалы и обеспечивая высочайшее качество бесплатных рецензируемых статей. Совет директоров состоит из независимых внешних сотрудников, которые помогают нам на добровольной основе. Их вклад включает консультирование по новым темам в своей области, предложение потенциальных экспертов-соавторов и рассмотрение предложений по изданию книг, если это необходимо. Члены совета являются экспертами, которые работают в основных областях STEM и HSS.Все они являются доверенными сотрудниками IntechOpen и академическими редакторами, что гарантирует удовлетворение потребностей научного сообщества.
Глоссарий
ГлоссарийГлоссарий
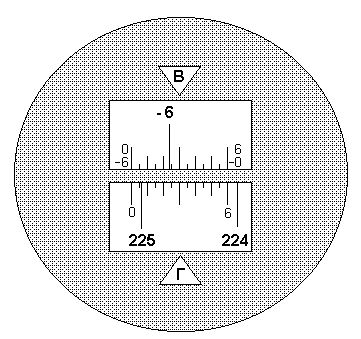


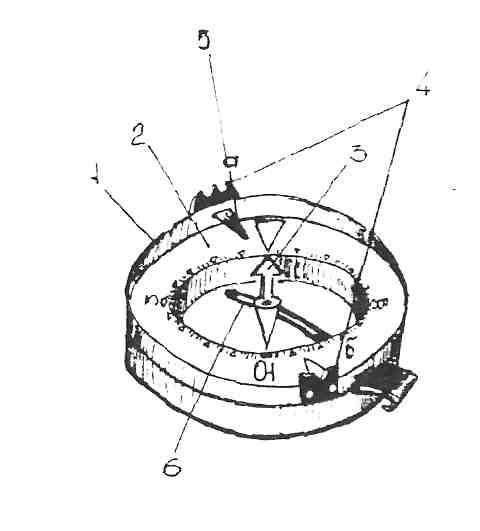 Когда вы нажимаете на ссылку аннотированного глоссария, в этом окне появляется определение термина.
Когда вы нажимаете на ссылку аннотированного глоссария, в этом окне появляется определение термина.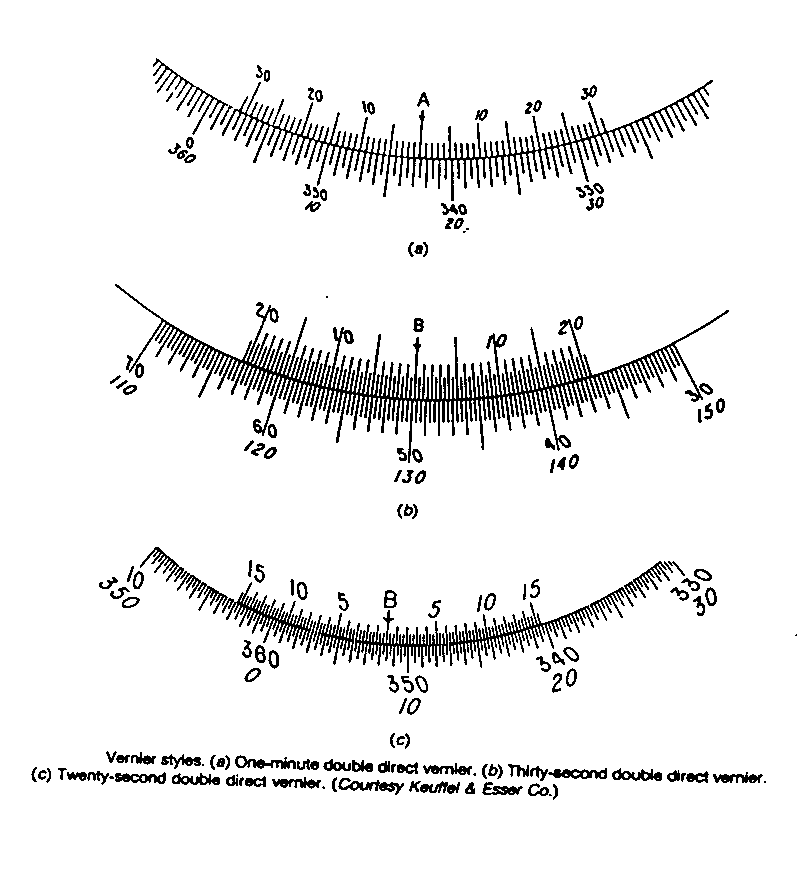
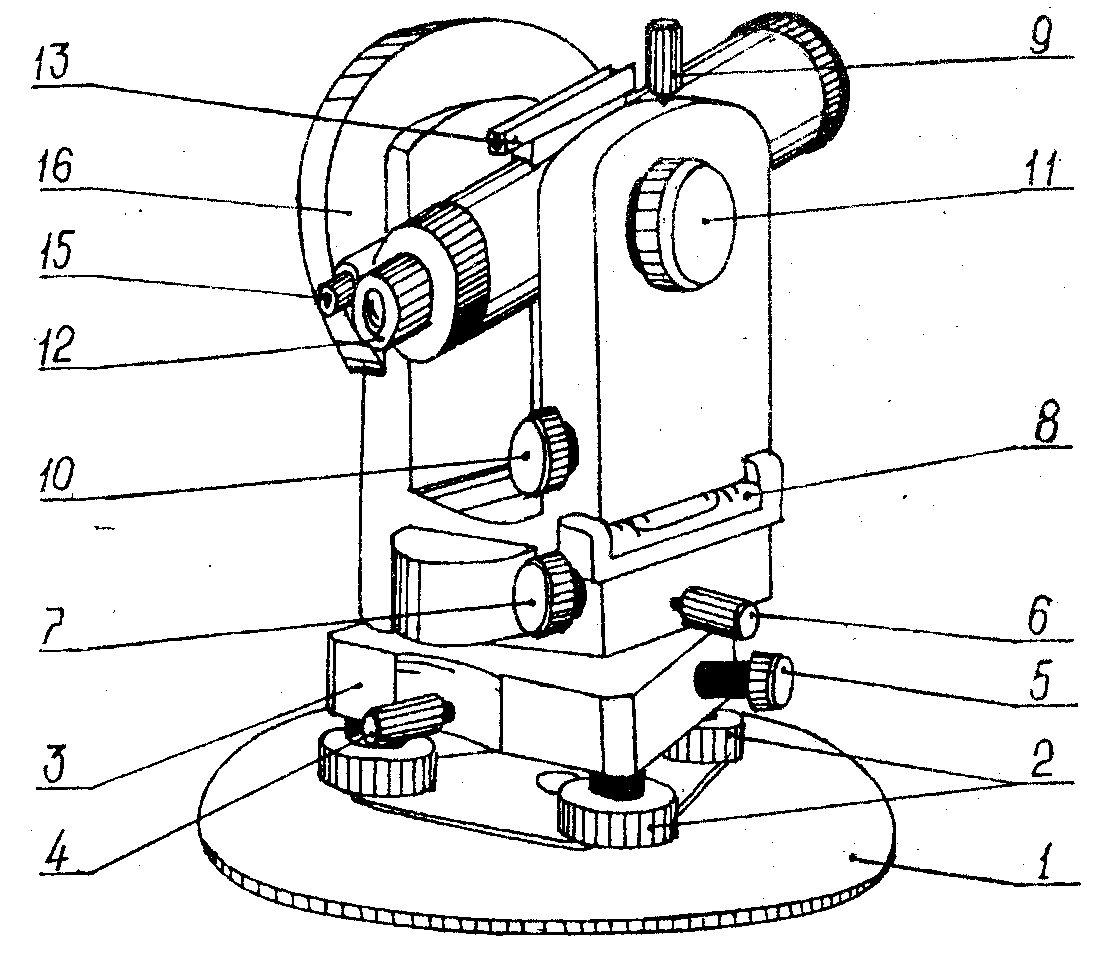
 Смещение увеличивается по мере того, как океанские волны становятся выше, а ветер сильнее.
Смещение увеличивается по мере того, как океанские волны становятся выше, а ветер сильнее.
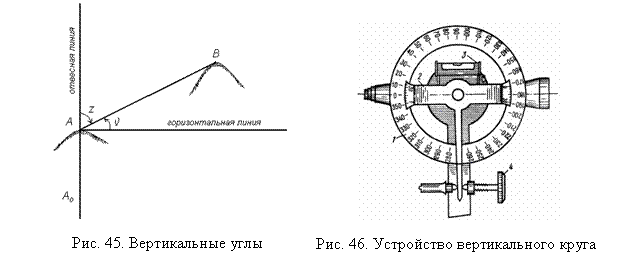
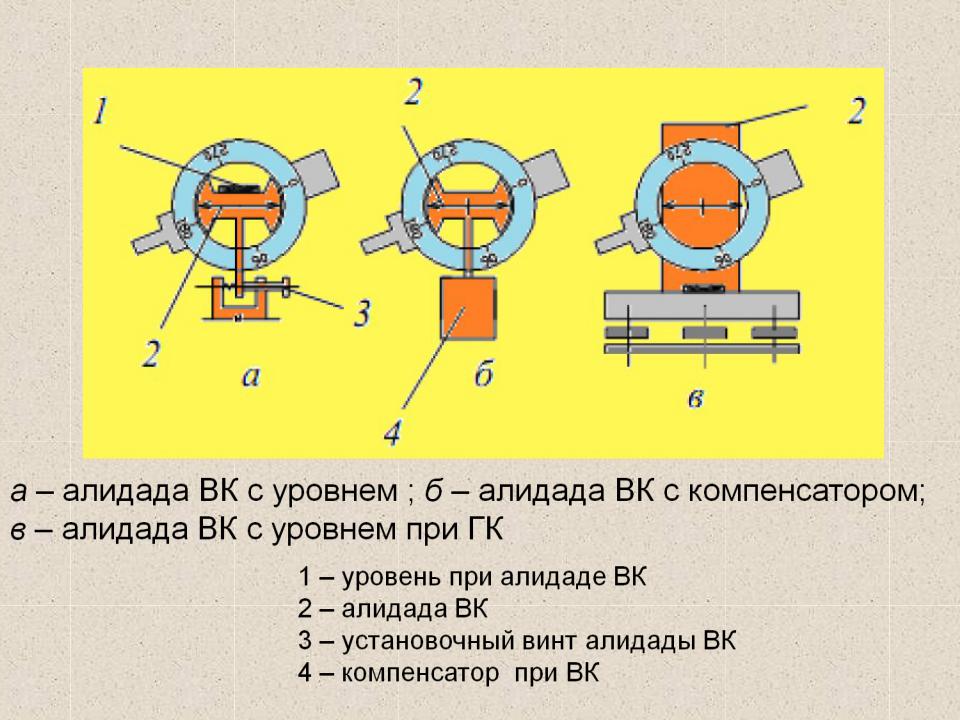
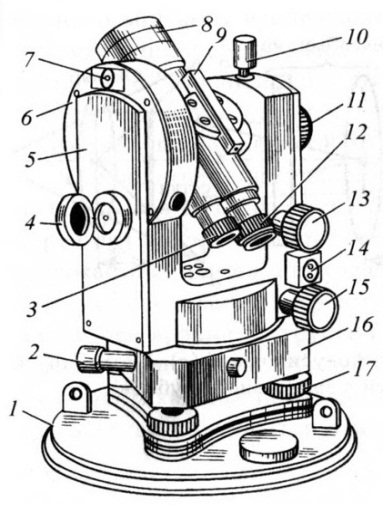
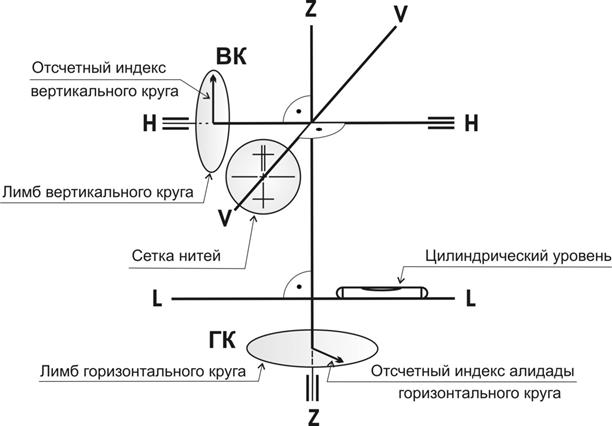


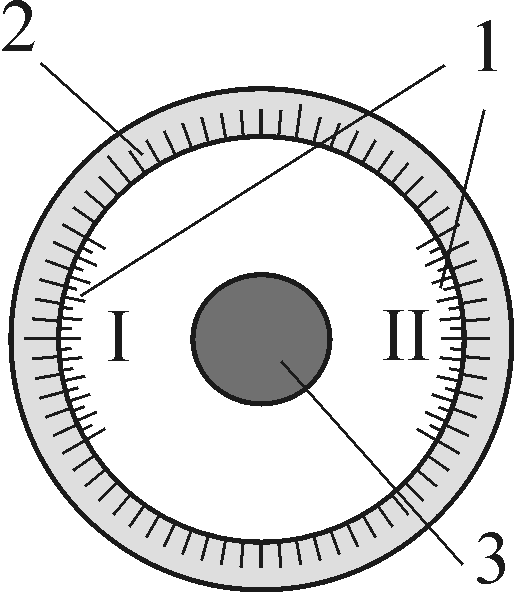


typhon.geodesy — документация Typhon 0.8.0dev
# - * - кодировка: utf-8 - * -
"" "Функции для работы с географическими системами координат
и справочные эллипсоиды.
Если не указано иное, функции перенесены из atmlab-2-3-181.
"" "
импортировать numpy как np
из констант импорта typhon
__all__ = [
'эллипсоидные модели',
'ellipsoid_r_geodetic',
'ellipsoid_r_geocentric',
'ellipsoid2d',
'ellipsoidcurvradius',
'синд',
'cosd',
'танд',
'asind',
'в диапазоне',
'cart2geocentric',
'geocentric2cart',
'cart2geodetic',
'geodetic2cart',
'geodetic2geocentric',
'geocentric2geodetic',
'great_circle_distance',
'geographic_mean',
'cartposlos2geocentric',
'geocentricposlos2cart',
'сфера_плоскость_пересечение',
'tunnel_distance',
]
[документы] def sind (x):
"" "Синус аргумента в градусах. "" "
вернуть np.sin (np.deg2rad (x))
[документы] def cosd (x):
"" "Косинус аргумента в градусах." ""
вернуть np.cos (np.deg2rad (x))
[документы] def tand (x):
"" "Тангенс аргумента в градусах." ""
вернуть np.tan (np.deg2rad (x))
[документы] def asind (x):
"" "Обратный синус в градусах." ""
вернуть np.arcsin (np.deg2rad (x))
[документы] def inrange (x, minx, maxx, exclude = 'none', text = None):
"" "Проверить, находится ли x в заданных пределах.
Параметры:
x: переменная для тестирования.
minx: нижняя граница.
maxx: верхняя граница.exclude (str): исключить границы. Возможные значения:
"нет", "нижний", "верхний" и "оба"
text (str): Дополнительный текст предупреждения.
Повышает:
Исключение: если значение выходит за допустимые пределы.
"" "
compare = {'none': (np.greater_equal, np.less_equal),
'нижний': (np.greater, np.less_equal),
'верхний': (np.greater_equal, np.
"" "
вернуть np.sin (np.deg2rad (x))
[документы] def cosd (x):
"" "Косинус аргумента в градусах." ""
вернуть np.cos (np.deg2rad (x))
[документы] def tand (x):
"" "Тангенс аргумента в градусах." ""
вернуть np.tan (np.deg2rad (x))
[документы] def asind (x):
"" "Обратный синус в градусах." ""
вернуть np.arcsin (np.deg2rad (x))
[документы] def inrange (x, minx, maxx, exclude = 'none', text = None):
"" "Проверить, находится ли x в заданных пределах.
Параметры:
x: переменная для тестирования.
minx: нижняя граница.
maxx: верхняя граница.exclude (str): исключить границы. Возможные значения:
"нет", "нижний", "верхний" и "оба"
text (str): Дополнительный текст предупреждения.
Повышает:
Исключение: если значение выходит за допустимые пределы.
"" "
compare = {'none': (np.greater_equal, np.less_equal),
'нижний': (np.greater, np.less_equal),
'верхний': (np.greater_equal, np. less),
'оба': (np.greater, np.less),
}
больше, меньше = сравнить [исключить]
если меньше (x, minx) или больше (x, maxx):
если текст None:
Raise Exception ('Диапазон вне пределов [{}, {}]'.формат (minx, maxx))
еще:
поднять исключение (
'Диапазон вне границы [{}, {}]: {}'. Формат (minx, maxx, текст)
)
[документы] класс ellipsoidmodels ():
"" "Предоставьте данные для различных справочных эллипсоидов.
Охватываются следующие модели:
* SphericalEarth (радиус установлен как constants.earth_radius)
* WGS84
* SphericalVenus (радиус такой же, как в ARTS)
* SphericalMars (радиус такой же, как в ARTS)
* EllipsoidMars
* Сферический Юпитер (радиус такой же, как в ARTS)
Примеры:
>>> e = эллипсоидные модели ()
.. Портировано из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
[документы] def __init __ (self):
self.
less),
'оба': (np.greater, np.less),
}
больше, меньше = сравнить [исключить]
если меньше (x, minx) или больше (x, maxx):
если текст None:
Raise Exception ('Диапазон вне пределов [{}, {}]'.формат (minx, maxx))
еще:
поднять исключение (
'Диапазон вне границы [{}, {}]: {}'. Формат (minx, maxx, текст)
)
[документы] класс ellipsoidmodels ():
"" "Предоставьте данные для различных справочных эллипсоидов.
Охватываются следующие модели:
* SphericalEarth (радиус установлен как constants.earth_radius)
* WGS84
* SphericalVenus (радиус такой же, как в ARTS)
* SphericalMars (радиус такой же, как в ARTS)
* EllipsoidMars
* Сферический Юпитер (радиус такой же, как в ARTS)
Примеры:
>>> e = эллипсоидные модели ()
.. Портировано из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
[документы] def __init __ (self):
self. _data = {
"SphericalEarth": (constants.earth_radius, 0),
«WGS84»: (6378137, 0,08181916),
"SphericalVenus": (6051800.0, 0),
«СферикалМарс»: (3389500.0, 0),
«ЭллипсоидМарс»: (3396190.0, 0.1083),
«Сферический Юпитер»: (690.0, 0),
}
def __getitem __ (я, модель):
вернуть self.get (модель)
[документы] def get (self, model = 'WGS84'):
"" "Возвращает данные для различных справочных эллипсоидов.Параметры:
model (str): Модель эллипсоида.
Возврат:
кортеж: Экваториальный радиус (r), эксцентриситет (e)
Примеры:
>>> e ['WGS84']
(6378137, 0,08181916)
>>> e.get ('WGS84')
(6378137, 0,08181916)
>>> ellipsoidmodel () ['WGS84']
(6378137, 0,08181916)
"" "
если модель в self._data:
вернуть self._data .__ getitem __ (модель)
еще:
Raise Exception ('Неизвестная модель эллипсоида "{}".
_data = {
"SphericalEarth": (constants.earth_radius, 0),
«WGS84»: (6378137, 0,08181916),
"SphericalVenus": (6051800.0, 0),
«СферикалМарс»: (3389500.0, 0),
«ЭллипсоидМарс»: (3396190.0, 0.1083),
«Сферический Юпитер»: (690.0, 0),
}
def __getitem __ (я, модель):
вернуть self.get (модель)
[документы] def get (self, model = 'WGS84'):
"" "Возвращает данные для различных справочных эллипсоидов.Параметры:
model (str): Модель эллипсоида.
Возврат:
кортеж: Экваториальный радиус (r), эксцентриситет (e)
Примеры:
>>> e ['WGS84']
(6378137, 0,08181916)
>>> e.get ('WGS84')
(6378137, 0,08181916)
>>> ellipsoidmodel () ['WGS84']
(6378137, 0,08181916)
"" "
если модель в self._data:
вернуть self._data .__ getitem __ (модель)
еще:
Raise Exception ('Неизвестная модель эллипсоида "{}". '.format (модель))
@свойство
def модели (self):
"" "Список доступных моделей.
Примеры:
>>> e.models
['SphericalVenus',
«Сферический Марс»,
'WGS84',
'Сферический Юпитер',
"Эллипсоид Марс",
'SphericalEarth']
"" "
список возврата (self._data.keys ())
[документы] def ellipsoid_r_geocentric (эллипсоид, широта):
«» "Геоцентрической радиус эллипсоида.
Дает расстояние от центра Земли и эллипсоида
как функция гео \ ** центрической ** широты.Примечание:
Чтобы получить радиусы для ** геодезической ** широты,
используйте: func: `ellipsoid_r_geodetic`.
Параметры:
эллипсоид (кортеж): эллипсоид модели, возвращенный
Автор: class: `ellipsoidmodels`.
lat (float или ndarray): геоцентрические широты.
Возврат:
float или ndarray: Радиусы.
.. Портировал из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.
'.format (модель))
@свойство
def модели (self):
"" "Список доступных моделей.
Примеры:
>>> e.models
['SphericalVenus',
«Сферический Марс»,
'WGS84',
'Сферический Юпитер',
"Эллипсоид Марс",
'SphericalEarth']
"" "
список возврата (self._data.keys ())
[документы] def ellipsoid_r_geocentric (эллипсоид, широта):
«» "Геоцентрической радиус эллипсоида.
Дает расстояние от центра Земли и эллипсоида
как функция гео \ ** центрической ** широты.Примечание:
Чтобы получить радиусы для ** геодезической ** широты,
используйте: func: `ellipsoid_r_geodetic`.
Параметры:
эллипсоид (кортеж): эллипсоид модели, возвращенный
Автор: class: `ellipsoidmodels`.
lat (float или ndarray): геоцентрические широты.
Возврат:
float или ndarray: Радиусы.
.. Портировал из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида. '
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
если эллипсоид [1] == 0:
г = нп.единицы (np.shape (lat)) * эллипсоид [0]
еще:
c = 1 - эллипсоид [1] ** 2
b = эллипсоид [0] * np.sqrt (c)
r = b / np.sqrt (c * cosd (лат) ** 2 + sind (лат) ** 2)
вернуть г
[документы] def ellipsoid_r_geodetic (эллипсоид, широта):
«» "Геодезический радиус эллипсоид.
Дает расстояние от центра Земли и эллипсоида
как функция гео \ ** детической ** широты.
Примечание:
Чтобы получить радиусы для ** геоцентрической ** широты,
используйте: func: `ellipsoid_r_geocentric`.Параметры:
эллипсоид (кортеж): эллипсоид модели, возвращенный
Автор: class: `ellipsoidmodels`.
lat (float или ndarray): геодезические широты.
Возврат:
float или ndarray: Радиусы.
.. Портировал из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.
'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
если эллипсоид [1] == 0:
г = нп.единицы (np.shape (lat)) * эллипсоид [0]
еще:
c = 1 - эллипсоид [1] ** 2
b = эллипсоид [0] * np.sqrt (c)
r = b / np.sqrt (c * cosd (лат) ** 2 + sind (лат) ** 2)
вернуть г
[документы] def ellipsoid_r_geodetic (эллипсоид, широта):
«» "Геодезический радиус эллипсоид.
Дает расстояние от центра Земли и эллипсоида
как функция гео \ ** детической ** широты.
Примечание:
Чтобы получить радиусы для ** геоцентрической ** широты,
используйте: func: `ellipsoid_r_geocentric`.Параметры:
эллипсоид (кортеж): эллипсоид модели, возвращенный
Автор: class: `ellipsoidmodels`.
lat (float или ndarray): геодезические широты.
Возврат:
float или ndarray: Радиусы.
.. Портировал из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида. '
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
если эллипсоид [1] == 0:
r = np.ones (np.shape (lat)) * эллипсоид [0]
еще:
e2 = эллипсоид [1] ** 2
sin2 = синд (лат) ** 2
r = (эллипсоид [0] * np.sqrt ((1 - e2) ** 2 * sin2 +
cosd (лат) ** 2) / np.sqrt (1 - e2 * sin2))
вернуть г
[документы] def ellipsoid2d (эллипсоид, orbitinc):
"" "Приближенный эллипсоид для 2D расчетов.
Определяет приблизительный опорный эллипсоид, следующий по орбитальному пути.
Новый эллипсоид определяется просто, определяя радиус в точке
максимальная широта и по этому значению вычисляется новый эксцентриситет.
Орбита задается наклонением орбиты, т. Е.
обычно значение около 100 градусов для полярных солнечно-синхронных орбит.Параметры:
эллипсоид (кортеж): эллипсоид модели, возвращенный
Автор: class: `ellipsoidmodels`.
orbitinc (float): Наклон орбиты.
Возврат:
кортеж: измененный вектор эллипсоида.
'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
если эллипсоид [1] == 0:
r = np.ones (np.shape (lat)) * эллипсоид [0]
еще:
e2 = эллипсоид [1] ** 2
sin2 = синд (лат) ** 2
r = (эллипсоид [0] * np.sqrt ((1 - e2) ** 2 * sin2 +
cosd (лат) ** 2) / np.sqrt (1 - e2 * sin2))
вернуть г
[документы] def ellipsoid2d (эллипсоид, orbitinc):
"" "Приближенный эллипсоид для 2D расчетов.
Определяет приблизительный опорный эллипсоид, следующий по орбитальному пути.
Новый эллипсоид определяется просто, определяя радиус в точке
максимальная широта и по этому значению вычисляется новый эксцентриситет.
Орбита задается наклонением орбиты, т. Е.
обычно значение около 100 градусов для полярных солнечно-синхронных орбит.Параметры:
эллипсоид (кортеж): эллипсоид модели, возвращенный
Автор: class: `ellipsoidmodels`.
orbitinc (float): Наклон орбиты.
Возврат:
кортеж: измененный вектор эллипсоида. .. Портировал из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
inrange (орбитинк, 0, 180,
exclude = 'оба',
text = 'Недействительный наклон орбиты.')
rp = ellipsoid_r_geocentric (эллипсоид, орбитинк)
вернуть эллипсоид [0], np.sqrt (1 - (rp / ellipsoid [0]) ** 2)
[docs] def ellipsoidcurvradius (эллипсоид, широта_гр, азимут):
"" "Устанавливает эллиспоид на локальный радиус кривизны
Вычисляет радиус кривизны для заданной широты и азимута.
угол, и использует это, чтобы установить сферический опорный эллипсоид
подходит для одномерных расчетов. Радиус кривизны лучше
локальное приближение, чем использование локального радиуса эллипсоида.
Для точного результата следует использовать * геодезическую * широту.Параметры:
lat_gd: Геодезическая широта.
азимут: Азимутальный угол (угол от плоскости NS).
.. Портировал из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
inrange (орбитинк, 0, 180,
exclude = 'оба',
text = 'Недействительный наклон орбиты.')
rp = ellipsoid_r_geocentric (эллипсоид, орбитинк)
вернуть эллипсоид [0], np.sqrt (1 - (rp / ellipsoid [0]) ** 2)
[docs] def ellipsoidcurvradius (эллипсоид, широта_гр, азимут):
"" "Устанавливает эллиспоид на локальный радиус кривизны
Вычисляет радиус кривизны для заданной широты и азимута.
угол, и использует это, чтобы установить сферический опорный эллипсоид
подходит для одномерных расчетов. Радиус кривизны лучше
локальное приближение, чем использование локального радиуса эллипсоида.
Для точного результата следует использовать * геодезическую * широту.Параметры:
lat_gd: Геодезическая широта.
азимут: Азимутальный угол (угол от плоскости NS). Если возвращаются заданные радиусы кривизны, см. Выше.
Возврат:
кортеж: измененный эллипсоид.
.. Портировал из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
aterm = 1 - эллипсоид [1] ** 2 * sind (lat_gd) ** 2
rn = 1 / np.sqrt (aterm)
rm = (1 - эллипсоид [1] ** 2) * (rn / aterm)
e0 = (эллипсоид [0] / (cosd (азимут) ** 2.0 / пог. + Синд (азимут) ** 2,0 / пог.))
e1 = 0
вернуть e0, e1
[docs] def cart2geocentric (x, y, z, lat0 = None, lon0 = None, za0 = None, aa0 = None):
"" "Преобразование декартовых координат в сферические координаты.
Геоцентрическая декартова система координат фиксирована относительно
Земля с центром в центре эллипсоида и ее координатами X-, Y-,
и оси Z, пересекающие поверхность в следующих точках:
* Ось X: экватор на нулевом меридиане (0 °, 0 °)
* Ось Y: экватор на 90 градусов восточной долготы (0 °, 90 °)
* Ось Z: Северный полюс (90 °, 0 °)
Распространенным синонимом являются координаты по центру Земли, координаты с фиксированной землей или ECEF.
Если возвращаются заданные радиусы кривизны, см. Выше.
Возврат:
кортеж: измененный эллипсоид.
.. Портировал из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
aterm = 1 - эллипсоид [1] ** 2 * sind (lat_gd) ** 2
rn = 1 / np.sqrt (aterm)
rm = (1 - эллипсоид [1] ** 2) * (rn / aterm)
e0 = (эллипсоид [0] / (cosd (азимут) ** 2.0 / пог. + Синд (азимут) ** 2,0 / пог.))
e1 = 0
вернуть e0, e1
[docs] def cart2geocentric (x, y, z, lat0 = None, lon0 = None, za0 = None, aa0 = None):
"" "Преобразование декартовых координат в сферические координаты.
Геоцентрическая декартова система координат фиксирована относительно
Земля с центром в центре эллипсоида и ее координатами X-, Y-,
и оси Z, пересекающие поверхность в следующих точках:
* Ось X: экватор на нулевом меридиане (0 °, 0 °)
* Ось Y: экватор на 90 градусов восточной долготы (0 °, 90 °)
* Ось Z: Северный полюс (90 °, 0 °)
Распространенным синонимом являются координаты по центру Земли, координаты с фиксированной землей или ECEF. Если указаны необязательные аргументы, гарантируется, что широта и
долгота остается постоянной для случаев зенита или надира, а долгота
для случаев N-S. Необязательный ввод должен интерпретироваться как [x, y, z]
получается перемещением от [lat0, lon0] в направлении [za0, aa0].
Параметры:
x: координата в измерении x.
y: Координата по оси y.
z: координата по оси z.
lat0: исходная широта.
lon0: Исходная долгота.
za0: исходный зенитный угол.aa0: Исходный азимутальный угол.
Возврат:
кортеж: Радиус, Широта, Долгота
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
r = np.sqrt (x ** 2 + y ** 2 + z ** 2)
если np.any (r == 0):
Raise Exception («Этот набор функций не обрабатывает r = 0»)
широта = np.rad2deg (np.arcsin (z / r))
lon = np.rad2deg (np.arctan2 (y, x))
если все (x не равно None для x в [lat0, lon0, za0, aa0]):
для i в диапазоне (np.size (r)):
если za0 [i] <1e-06 или za0 [i]> 180 - 1e-06:
lat [i] = lat0 [i]
lon [i] = lon0 [i]
if (abs (lat0 [i]) <90 - 1e-08 и
(abs (aa0 [i]) <1e-06 или abs (aa0 [i] - 180) <1e-06)):
если abs (lon [i] - lon0 [i]) <1:
lon [i] = lon0 [i]
еще:
если lon0 [i]> 0:
lon [i] = lon0 [i] - 180
еще:
lon [i] = lon0 [i] + 180
вернуть r, lat, lon
[документы] def geocentric2cart (r, lat, lon):
"" "Преобразование из сферической координаты в декартову позицию.
Если указаны необязательные аргументы, гарантируется, что широта и
долгота остается постоянной для случаев зенита или надира, а долгота
для случаев N-S. Необязательный ввод должен интерпретироваться как [x, y, z]
получается перемещением от [lat0, lon0] в направлении [za0, aa0].
Параметры:
x: координата в измерении x.
y: Координата по оси y.
z: координата по оси z.
lat0: исходная широта.
lon0: Исходная долгота.
za0: исходный зенитный угол.aa0: Исходный азимутальный угол.
Возврат:
кортеж: Радиус, Широта, Долгота
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
r = np.sqrt (x ** 2 + y ** 2 + z ** 2)
если np.any (r == 0):
Raise Exception («Этот набор функций не обрабатывает r = 0»)
широта = np.rad2deg (np.arcsin (z / r))
lon = np.rad2deg (np.arctan2 (y, x))
если все (x не равно None для x в [lat0, lon0, za0, aa0]):
для i в диапазоне (np.size (r)):
если za0 [i] <1e-06 или za0 [i]> 180 - 1e-06:
lat [i] = lat0 [i]
lon [i] = lon0 [i]
if (abs (lat0 [i]) <90 - 1e-08 и
(abs (aa0 [i]) <1e-06 или abs (aa0 [i] - 180) <1e-06)):
если abs (lon [i] - lon0 [i]) <1:
lon [i] = lon0 [i]
еще:
если lon0 [i]> 0:
lon [i] = lon0 [i] - 180
еще:
lon [i] = lon0 [i] + 180
вернуть r, lat, lon
[документы] def geocentric2cart (r, lat, lon):
"" "Преобразование из сферической координаты в декартову позицию. См .: func: `cart2geocentric` для определения геоцентрического
система координат.
Параметры:
r: Радиус.
lat: Широта в градусах.
lon Долгота в градусах.
Возврат:
кортеж: координаты в измерениях x, y, z.
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если np.any (r == 0):
Raise Exception («Этот набор функций не обрабатывает r = 0»)
latrad = np.deg2rad (лат)
lonrad = np.deg2rad (долг)
х = г * нп.cos (латрад)
y = x * np.sin (лонрад)
х = х * np.cos (лонрад)
z = r * np.sin (латрад)
вернуть x, y, z
[docs] def cart2geodetic (x, y, z, ellipsoid = None):
"" "Преобразование декартовых координат в геодезические.
Геодезические координаты относятся к эталонному эллипсоид
заданный входным эллипсоидом.
См. Раздел документации модуля для определения геоцентрической системы координат.
Параметры:
x: координаты в измерении x.
y: координаты в измерении y.
См .: func: `cart2geocentric` для определения геоцентрического
система координат.
Параметры:
r: Радиус.
lat: Широта в градусах.
lon Долгота в градусах.
Возврат:
кортеж: координаты в измерениях x, y, z.
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если np.any (r == 0):
Raise Exception («Этот набор функций не обрабатывает r = 0»)
latrad = np.deg2rad (лат)
lonrad = np.deg2rad (долг)
х = г * нп.cos (латрад)
y = x * np.sin (лонрад)
х = х * np.cos (лонрад)
z = r * np.sin (латрад)
вернуть x, y, z
[docs] def cart2geodetic (x, y, z, ellipsoid = None):
"" "Преобразование декартовых координат в геодезические.
Геодезические координаты относятся к эталонному эллипсоид
заданный входным эллипсоидом.
См. Раздел документации модуля для определения геоцентрической системы координат.
Параметры:
x: координаты в измерении x.
y: координаты в измерении y. z: координаты в измерении z.эллипсоид: кортеж с формой (большая полуось, эксцентриситет).
По умолчанию - 'WGS84' из: class: `ellipsoidmodels`.
Возврат:
кортеж: геодезическая высота, широта и долгота
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если эллипсоид None:
ellipsoid = ellipsoidmodels () ['WGS84']
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
lon = np.rad2deg (np.arctan2 (y, x))
B0 = np.arctan2 (z, np.hypot (x, y))
B = np.ones (B0.shape)
e2 = эллипсоид [1] ** 2
если e2 == 0.0:
h, lat, lon = cart2geocentric (x, y, z)
h - = эллипсоид [0]
еще:
while (np.any (np.abs (B - B0)> 1e-10)):
N = эллипсоид [0] / np.sqrt (1 - e2 * np.sin (B0) ** 2)
h = np.hypot (x, y) / np.cos (B0) - N
B = B0.copy ()
B0 = np.arctan (z / np.hypot (x, y) * ((1-e2 * N / (N + h)) ** (- 1)))
широта = np.
z: координаты в измерении z.эллипсоид: кортеж с формой (большая полуось, эксцентриситет).
По умолчанию - 'WGS84' из: class: `ellipsoidmodels`.
Возврат:
кортеж: геодезическая высота, широта и долгота
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если эллипсоид None:
ellipsoid = ellipsoidmodels () ['WGS84']
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
lon = np.rad2deg (np.arctan2 (y, x))
B0 = np.arctan2 (z, np.hypot (x, y))
B = np.ones (B0.shape)
e2 = эллипсоид [1] ** 2
если e2 == 0.0:
h, lat, lon = cart2geocentric (x, y, z)
h - = эллипсоид [0]
еще:
while (np.any (np.abs (B - B0)> 1e-10)):
N = эллипсоид [0] / np.sqrt (1 - e2 * np.sin (B0) ** 2)
h = np.hypot (x, y) / np.cos (B0) - N
B = B0.copy ()
B0 = np.arctan (z / np.hypot (x, y) * ((1-e2 * N / (N + h)) ** (- 1)))
широта = np. rad2deg (B)
вернуть ч, лат, долг
[docs] def geodetic2cart (h, lat, lon, ellipsoid = None):
"" "Преобразование из геодезических в геоцентрические декартовы координаты.Геодезические координаты относятся к эталонному эллипсоид
заданный входным эллипсоидом.
См. Раздел документации модуля для определения геоцентрической системы координат.
Параметры:
h: Геодезическая высота (высота над опорным эллипсоидом).
lat: Геодезическая широта.
lon: Геодезическая долгота.
эллипсоид: кортеж с формой (большая полуось, эксцентриситет).
По умолчанию - 'WGS84' из: class: `ellipsoidmodels`.
Возврат:
кортеж: координаты x, y, z... Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если эллипсоид None:
ellipsoid = ellipsoidmodels () ['WGS84']
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
а = эллипсоид [0]
e2 = эллипсоид [1] ** 2
N = a / np.
rad2deg (B)
вернуть ч, лат, долг
[docs] def geodetic2cart (h, lat, lon, ellipsoid = None):
"" "Преобразование из геодезических в геоцентрические декартовы координаты.Геодезические координаты относятся к эталонному эллипсоид
заданный входным эллипсоидом.
См. Раздел документации модуля для определения геоцентрической системы координат.
Параметры:
h: Геодезическая высота (высота над опорным эллипсоидом).
lat: Геодезическая широта.
lon: Геодезическая долгота.
эллипсоид: кортеж с формой (большая полуось, эксцентриситет).
По умолчанию - 'WGS84' из: class: `ellipsoidmodels`.
Возврат:
кортеж: координаты x, y, z... Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если эллипсоид None:
ellipsoid = ellipsoidmodels () ['WGS84']
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
а = эллипсоид [0]
e2 = эллипсоид [1] ** 2
N = a / np. sqrt (1 - e2 * sind (лат) ** 2)
x = (N + h) * (cosd (долг)) * (cosd (долг))
y = (N + h) * (cosd (lat)) * (sind (долг))
# np.ones (np.shape (lon)): Обеспечьте одинаковую форму x, y, z.z = (N * (1 - e2) + h) * (sind (лат)) * np.ones (np.shape (долг))
вернуть x, y, z
[docs] def geodetic2geocentric (h, lat, lon, ellipsoid = None, ** kwargs):
"" "Преобразование геодезических координат в геоцентрические.
Геодезические координаты относятся к эталонному эллипсоид
заданный входным эллипсоидом.
См. Раздел документации модуля для определения геоцентрической системы координат.
Параметры:
h: Геодезическая высота (высота над опорным эллипсоидом).
lat: Геодезическая широта.lon: Геодезическая долгота.
kwargs: Дополнительные аргументы ключевого слова для: func: `cart2geocentric`.
эллипсоид: кортеж с формой (большая полуось, эксцентриситет).
По умолчанию - 'WGS84' из: class: `ellipsoidmodels`.
Возврат:
кортеж: радиус, геоцентрическая широта, геоцентрическая долгота
.
sqrt (1 - e2 * sind (лат) ** 2)
x = (N + h) * (cosd (долг)) * (cosd (долг))
y = (N + h) * (cosd (lat)) * (sind (долг))
# np.ones (np.shape (lon)): Обеспечьте одинаковую форму x, y, z.z = (N * (1 - e2) + h) * (sind (лат)) * np.ones (np.shape (долг))
вернуть x, y, z
[docs] def geodetic2geocentric (h, lat, lon, ellipsoid = None, ** kwargs):
"" "Преобразование геодезических координат в геоцентрические.
Геодезические координаты относятся к эталонному эллипсоид
заданный входным эллипсоидом.
См. Раздел документации модуля для определения геоцентрической системы координат.
Параметры:
h: Геодезическая высота (высота над опорным эллипсоидом).
lat: Геодезическая широта.lon: Геодезическая долгота.
kwargs: Дополнительные аргументы ключевого слова для: func: `cart2geocentric`.
эллипсоид: кортеж с формой (большая полуось, эксцентриситет).
По умолчанию - 'WGS84' из: class: `ellipsoidmodels`.
Возврат:
кортеж: радиус, геоцентрическая широта, геоцентрическая долгота
. . Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если эллипсоид None:
ellipsoid = ellipsoidmodels () ['WGS84']
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
cart = geodetic2cart (ч, широта, долгота, эллипсоид)
возврат cart2geocentric (* cart, ** kwargs)
[docs] def geocentric2geodetic (r, lat, lon, ellipsoid = None):
"" "Преобразование геоцентрических координат в геодезические.
Геодезические координаты относятся к эталонному эллипсоид
заданный входным эллипсоидом.
См. Раздел документации модуля для определения геоцентрической системы координат.
Возврат:
кортеж: геодезическая высота, широта и долгота
Параметры:
r: Радиус:
lat: геоцентрическая широта.lon: геоцентрическая долгота.
эллипсоид: кортеж с формой (большая полуось, эксцентриситет).
По умолчанию - 'WGS84' из: class: `ellipsoidmodels`.
. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если эллипсоид None:
ellipsoid = ellipsoidmodels () ['WGS84']
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
cart = geodetic2cart (ч, широта, долгота, эллипсоид)
возврат cart2geocentric (* cart, ** kwargs)
[docs] def geocentric2geodetic (r, lat, lon, ellipsoid = None):
"" "Преобразование геоцентрических координат в геодезические.
Геодезические координаты относятся к эталонному эллипсоид
заданный входным эллипсоидом.
См. Раздел документации модуля для определения геоцентрической системы координат.
Возврат:
кортеж: геодезическая высота, широта и долгота
Параметры:
r: Радиус:
lat: геоцентрическая широта.lon: геоцентрическая долгота.
эллипсоид: кортеж с формой (большая полуось, эксцентриситет).
По умолчанию - 'WGS84' из: class: `ellipsoidmodels`. .. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если эллипсоид None:
ellipsoid = ellipsoidmodels () ['WGS84']
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
тележка = geocentric2cart (r, lat, lon)
return cart2geodetic (* тележка, эллипсоид)
[документы] def great_circle_distance (lat1, lon1, lat2, lon2, r = None):
r "" "Рассчитать расстояние между двумя географическими положениями
Это расстояние по прямой между двумя точками, определяемое
их широта и долгота.2} \ справа)
Аргументы:
lat1: Широта позиции 1.
lon1: долгота позиции 1.
lat2: Широта позиции 2.
lon2: долгота позиции 2.
r (float): радиус (общий для обеих точек).
Возврат:
Если указан необязательный аргумент * r *, возвращается расстояние в метрах.
В противном случае возвращается угловое расстояние в градусах.
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если эллипсоид None:
ellipsoid = ellipsoidmodels () ['WGS84']
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
тележка = geocentric2cart (r, lat, lon)
return cart2geodetic (* тележка, эллипсоид)
[документы] def great_circle_distance (lat1, lon1, lat2, lon2, r = None):
r "" "Рассчитать расстояние между двумя географическими положениями
Это расстояние по прямой между двумя точками, определяемое
их широта и долгота.2} \ справа)
Аргументы:
lat1: Широта позиции 1.
lon1: долгота позиции 1.
lat2: Широта позиции 2.
lon2: долгота позиции 2.
r (float): радиус (общий для обеих точек).
Возврат:
Если указан необязательный аргумент * r *, возвращается расстояние в метрах.
В противном случае возвращается угловое расстояние в градусах. .. Взято с https://stackoverflow.com/a/29546836/
.. Взято с https://stackoverflow.com/a/29546836/
90
"" "
lon1, lat1, lon2, lat2 = map (np.radians, [lon1, lat1, lon2, lat2])
dlon = lon2 - lon1
dlat = lat2 - lat1
а = нп.sin (dlat / 2.0) ** 2 + np.cos (lat1) * np.cos (lat2) * np.sin (
dlon / 2,0) ** 2
c = 2 * np.arcsin (np.sqrt (а))
если r равно None:
вернуть np.rad2deg (c)
еще:
вернуть r * c
[docs] def geographic_mean (lat, lon, h = 0, ellipsoid = None):
"" "Вычислить среднее положение для набора координат.
Параметры:
lat (float или ndarray): широта в градусах.
lon (float или ndarray): долгота в градусах.
h (float или ndarray): оптимальная высота для
каждая координата (по умолчанию).эллипсоид: кортеж с формой (большая полуось, эксцентриситет).
По умолчанию - 'WGS84' из: class: `ellipsoidmodels`.
Возврат:
кортеж: средние значения широты и долготы в градусах.
"" "
если эллипсоид None:
ellipsoid = ellipsoidmodels () ['WGS84']
x, y, z = geodetic2cart (
час,
лат,
лон
эллипсоид = эллипсоид)
mh, mlat, mlon = cart2geodetic (
np. mean (x),
np.mean (y),
np.mean (z),
эллипсоид = эллипсоид)
возврат млат, млон
[docs] def cartposlos2geocentric (x, y, z, dx, dy, dz, ppc = None,
lat0 = Нет, lon0 = Нет, za0 = Нет, aa0 = Нет):
"" "Преобразование декартовых координат POS / LOS в сферические координаты.Положение задается как (x, y, z), а линия прямой видимости задается как (dx, dy, dz).
Соответствующие величины в полярных координатах: (r, lat, lon)
и (za, aa) соответственно.
См. * Содержание * для определения систем координат.
Если указаны необязательные аргументы, гарантируется, что широта и
долгота остается постоянной для случаев зенита или надира, а долгота
и азимутальный угол для случаев с севера на юг. Необязательный ввод должен интерпретироваться
поскольку [x, y, z] получается перемещением из [r0, lat0, lon0] в направлении
из [za0, aa0].Эта версия отличается от версии atmlab тем, что нормализует потери.
vector и требует все или ничего для работы необязательных аргументов.
mean (x),
np.mean (y),
np.mean (z),
эллипсоид = эллипсоид)
возврат млат, млон
[docs] def cartposlos2geocentric (x, y, z, dx, dy, dz, ppc = None,
lat0 = Нет, lon0 = Нет, za0 = Нет, aa0 = Нет):
"" "Преобразование декартовых координат POS / LOS в сферические координаты.Положение задается как (x, y, z), а линия прямой видимости задается как (dx, dy, dz).
Соответствующие величины в полярных координатах: (r, lat, lon)
и (za, aa) соответственно.
См. * Содержание * для определения систем координат.
Если указаны необязательные аргументы, гарантируется, что широта и
долгота остается постоянной для случаев зенита или надира, а долгота
и азимутальный угол для случаев с севера на юг. Необязательный ввод должен интерпретироваться
поскольку [x, y, z] получается перемещением из [r0, lat0, lon0] в направлении
из [za0, aa0].Эта версия отличается от версии atmlab тем, что нормализует потери.
vector и требует все или ничего для работы необязательных аргументов. Параметры:
x: координата в измерении x.
y: Координата по оси y.
z: координата по оси z.
dx: компонент LOS в измерении x.
dy: компонент LOS в измерении y.
dz: компонент LOS в измерении z.
ppc: Константа пути распространения = r0 * sin (za0).
lat0: исходная широта.
lon0: Исходная долгота.za0: исходный зенитный угол.
aa0: Исходный азимутальный угол.
Возврат:
кортеж (ndarray): радиус, широта, долгота,
Зенитный угол, Азимутальный угол
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
# Вот драконы!
# Трансляция всех входных переменных в одну и ту же форму. По крайней мере (1)
if (ppc не равно None и za0 не равно None, а lat0 не равно None и
aa0 не равно None, а lon0 не равно None):
x, y, z, dx, dy, dz, ppc, lat0, lon0, za0, aa0 = _broadcast (
x, y, z, dx, dy, dz, ppc, lat0, lon0, za0, aa0)
elif ppc не равно None:
x, y, z, dx, dy, dz, ppc = _broadcast (x, y, z, dx, dy, dz, ppc)
еще:
x, y, z, dx, dy, dz = _broadcast (x, y, z, dx, dy, dz)
r, lat, lon = cart2geocentric (x, y, z, lat0, lon0, za0, aa0)
# Перенормировать длину переменных (не в atmlab)
norm_r = np.
Параметры:
x: координата в измерении x.
y: Координата по оси y.
z: координата по оси z.
dx: компонент LOS в измерении x.
dy: компонент LOS в измерении y.
dz: компонент LOS в измерении z.
ppc: Константа пути распространения = r0 * sin (za0).
lat0: исходная широта.
lon0: Исходная долгота.za0: исходный зенитный угол.
aa0: Исходный азимутальный угол.
Возврат:
кортеж (ndarray): радиус, широта, долгота,
Зенитный угол, Азимутальный угол
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
# Вот драконы!
# Трансляция всех входных переменных в одну и ту же форму. По крайней мере (1)
if (ppc не равно None и za0 не равно None, а lat0 не равно None и
aa0 не равно None, а lon0 не равно None):
x, y, z, dx, dy, dz, ppc, lat0, lon0, za0, aa0 = _broadcast (
x, y, z, dx, dy, dz, ppc, lat0, lon0, za0, aa0)
elif ppc не равно None:
x, y, z, dx, dy, dz, ppc = _broadcast (x, y, z, dx, dy, dz, ppc)
еще:
x, y, z, dx, dy, dz = _broadcast (x, y, z, dx, dy, dz)
r, lat, lon = cart2geocentric (x, y, z, lat0, lon0, za0, aa0)
# Перенормировать длину переменных (не в atmlab)
norm_r = np. sqrt (dx ** 2 + dy ** 2 + dz ** 2)
dx = dx / norm_r
dy = dy / norm_r
dz = dz / norm_r
coslat = np.cos (np.deg2rad (широта))
sinlat = np.sin (np.deg2rad (лат))
coslon = np.cos (np.deg2rad (долг))
sinlon = np.sin (np.deg2rad (долг))
dr = np.clip (coslat * coslon * dx + sinlat * dz + coslat * sinlon * dy,
-1., 1.)
# Получить угол LOS
если ppc равно None:
za = np.rad2deg (np.arccos (dr))
еще:
za = np.rad2deg (np.arcsin (ppc / r))
aa = np.zeros (za.shape)
# Исправить зенит и азимутальный угол с дополнительным вводом, только когда все существует
если (za0 не равно None и lat0 не равно None и
aa0 не равно None, а lon0 не равно None):
# Определить тип для зенита
noz = np.логическая_ор (za0 <1e-06, za0> 180 - 1e-06)
nan = np.isnan (za)
pre = np.logical_and (~ noz, nan)
# Либо установить, либо нет
za [noz] = za0 [noz]
za [pre] = 90.
# NB: удалена проверка на dr <0, поскольку установка dr == 1 более разумна
# Определить тип по азимуту
cir1 = abs (aa0) <1e-06
cir2 = np.
sqrt (dx ** 2 + dy ** 2 + dz ** 2)
dx = dx / norm_r
dy = dy / norm_r
dz = dz / norm_r
coslat = np.cos (np.deg2rad (широта))
sinlat = np.sin (np.deg2rad (лат))
coslon = np.cos (np.deg2rad (долг))
sinlon = np.sin (np.deg2rad (долг))
dr = np.clip (coslat * coslon * dx + sinlat * dz + coslat * sinlon * dy,
-1., 1.)
# Получить угол LOS
если ppc равно None:
za = np.rad2deg (np.arccos (dr))
еще:
za = np.rad2deg (np.arcsin (ppc / r))
aa = np.zeros (za.shape)
# Исправить зенит и азимутальный угол с дополнительным вводом, только когда все существует
если (za0 не равно None и lat0 не равно None и
aa0 не равно None, а lon0 не равно None):
# Определить тип для зенита
noz = np.логическая_ор (za0 <1e-06, za0> 180 - 1e-06)
nan = np.isnan (za)
pre = np.logical_and (~ noz, nan)
# Либо установить, либо нет
za [noz] = za0 [noz]
za [pre] = 90.
# NB: удалена проверка на dr <0, поскольку установка dr == 1 более разумна
# Определить тип по азимуту
cir1 = abs (aa0) <1e-06
cir2 = np. logical_or (cir1, abs (aa0 - 180) <1e-06)
то же = np.equal (lon, lon0)
circ = np.logical_and (cir2, то же самое)
left = np.логическое_и (cir1, ~ то же)
right = np.logical_and (~ cir1, ~ то же)
# Это должно установить все случаи
aa [circ] = aa0 [circ]
аа [слева] = 180.
аа [справа] = 0.
еще:
# Определить тип выполняемых расчетов
noz = np.logical_or (za <1e-06, za> 180 - 1e-06)
pol = abs (широта)> 90 - 1e-08
pre = np.logical_and (~ noz, pol)
non = np.logical_and (~ noz, ~ pol)
аа [noz] = 0.
aa [pre] = np.rad2deg (np.arctan2 (dy [pre], dx [pre]))
dlat = (- sinlat [non] * coslon [non] / r [non] * dx [non] + coslat [non] /
r [non] * dz [non] - sinlat [non] * sinlon [non] / r [non] * dy [non]
)
dlon = (- sinlon [non] / coslat [non] / r [non] * dx [non] + coslon [non] /
coslat [non] / r [non] * dy [non])
aa [non] = (np.
logical_or (cir1, abs (aa0 - 180) <1e-06)
то же = np.equal (lon, lon0)
circ = np.logical_and (cir2, то же самое)
left = np.логическое_и (cir1, ~ то же)
right = np.logical_and (~ cir1, ~ то же)
# Это должно установить все случаи
aa [circ] = aa0 [circ]
аа [слева] = 180.
аа [справа] = 0.
еще:
# Определить тип выполняемых расчетов
noz = np.logical_or (za <1e-06, za> 180 - 1e-06)
pol = abs (широта)> 90 - 1e-08
pre = np.logical_and (~ noz, pol)
non = np.logical_and (~ noz, ~ pol)
аа [noz] = 0.
aa [pre] = np.rad2deg (np.arctan2 (dy [pre], dx [pre]))
dlat = (- sinlat [non] * coslon [non] / r [non] * dx [non] + coslat [non] /
r [non] * dz [non] - sinlat [non] * sinlon [non] / r [non] * dy [non]
)
dlon = (- sinlon [non] / coslat [non] / r [non] * dx [non] + coslon [non] /
coslat [non] / r [non] * dy [non])
aa [non] = (np. rad2deg (np.arccos (r [не] *
dlat / np.sin (np.deg2rad (za [non])))))
fix = np.logical_or (np.isnan (aa), ~ np.isreal (aa))
aa [np.logical_and (fix, dlat> = 0)] = 0
aa [np.logical_and (fix, dlat <0)] = 180
aa [np.logical_and (~ fix, dlon <0)] * = -1
вернуть r, lat, lon, za, aa
[docs] def geocentricposlos2cart (r, lat, lon, za, aa):
"" "
Преобразование из сферической POS / LOS в декартовую POS / LOS
См. Раздел Содержание для определения геоцентрической системы координат.Локальные углы прямой видимости определяются по системе ВОСТОК-СЕВЕР-ВВЕРХ:
за аа
90 0 указывает на север
90 90 очков на восток
0 аа баллов вверх
FORMAT [x, y, z, dx, dy, dz] = geocentricposlos2cart (r, lat, lon, za, az)
ИЗ
Координата x в измерении x
Координата y в измерении y
Координата z по оси z
dx компонент LOS в измерении x
dy Компонент LOS в измерении y
dz LOS
В
r Радиус
широта Широта
долгота
зенитный угол
азимутальный угол
Портировано из атмлаба.
rad2deg (np.arccos (r [не] *
dlat / np.sin (np.deg2rad (za [non])))))
fix = np.logical_or (np.isnan (aa), ~ np.isreal (aa))
aa [np.logical_and (fix, dlat> = 0)] = 0
aa [np.logical_and (fix, dlat <0)] = 180
aa [np.logical_and (~ fix, dlon <0)] * = -1
вернуть r, lat, lon, za, aa
[docs] def geocentricposlos2cart (r, lat, lon, za, aa):
"" "
Преобразование из сферической POS / LOS в декартовую POS / LOS
См. Раздел Содержание для определения геоцентрической системы координат.Локальные углы прямой видимости определяются по системе ВОСТОК-СЕВЕР-ВВЕРХ:
за аа
90 0 указывает на север
90 90 очков на восток
0 аа баллов вверх
FORMAT [x, y, z, dx, dy, dz] = geocentricposlos2cart (r, lat, lon, za, az)
ИЗ
Координата x в измерении x
Координата y в измерении y
Координата z по оси z
dx компонент LOS в измерении x
dy Компонент LOS в измерении y
dz LOS
В
r Радиус
широта Широта
долгота
зенитный угол
азимутальный угол
Портировано из атмлаба. Оригинальный автор: Бенгт Ридберг 2011-10-31
"" "
r, lat, lon, za, aa = _broadcast (r, lat, lon, za, aa)
если есть (r == 0):
Raise Exception ("Эта функция не обрабатывает случай r = 0")
если есть (lat <-90) или любые (lat> 90):
Raise RuntimeError ("Широта вне допустимого диапазона")
если есть (lon <-180) или любое (lon> 180):
Raise RuntimeError («Долгота вне допустимого диапазона»)
если есть (za <0) или любое (za> 180):
Raise RuntimeError («Зенитный угол вне допустимого диапазона»)
deg2rad = np.град2рад (1)
x = np.empty (r.shape)
y = np.empty (r.shape)
z = np. пусто (r.shape)
dx = np.empty (r.shape)
dy = np.empty (r.shape)
dz = np.empty (r.shape)
at_pole = abs (широта)> (90 - 1e-8)
если есть (at_pole):
s = np.sign (широта [at_pole])
х [at_pole] = 0.
y [at_pole] = 0.
z [at_pole] = s * r [at_pole]
dz [at_pole] = s * np.cos (deg2rad * (za [at_pole]))
dx [at_pole] = np.
Оригинальный автор: Бенгт Ридберг 2011-10-31
"" "
r, lat, lon, za, aa = _broadcast (r, lat, lon, za, aa)
если есть (r == 0):
Raise Exception ("Эта функция не обрабатывает случай r = 0")
если есть (lat <-90) или любые (lat> 90):
Raise RuntimeError ("Широта вне допустимого диапазона")
если есть (lon <-180) или любое (lon> 180):
Raise RuntimeError («Долгота вне допустимого диапазона»)
если есть (za <0) или любое (za> 180):
Raise RuntimeError («Зенитный угол вне допустимого диапазона»)
deg2rad = np.град2рад (1)
x = np.empty (r.shape)
y = np.empty (r.shape)
z = np. пусто (r.shape)
dx = np.empty (r.shape)
dy = np.empty (r.shape)
dz = np.empty (r.shape)
at_pole = abs (широта)> (90 - 1e-8)
если есть (at_pole):
s = np.sign (широта [at_pole])
х [at_pole] = 0.
y [at_pole] = 0.
z [at_pole] = s * r [at_pole]
dz [at_pole] = s * np.cos (deg2rad * (za [at_pole]))
dx [at_pole] = np. sin (deg2rad * (za))
dy [at_pole] = dx [at_pole] * np.sin (deg2rad * (aa))
dx [at_pole] * = np.cos (deg2rad * (aa))
not_pole = np.logical_not (at_pole)
если есть (not_pole):
latrad = deg2rad * lat [not_pole]
lonrad = deg2rad * lon [not_pole]
zarad = deg2rad * za [not_pole]
aarad = deg2rad * aa [not_pole]
coslat = np.cos (латрад)
sinlat = np.sin (латрад)
coslon = np.cos (лонрад)
sinlon = np.sin (лонрад)
cosza = np.cos (zarad)
sinza = np.sin (зарад)
cosaa = np.cos (aarad)
sinaa = np.sin (аарад)
x [not_pole] = r [not_pole] * coslat
y [not_pole] = x [not_pole] * sinlon
x [not_pole] * = кослон
z [not_pole] = r [not_pole] * sinlat
dr = cosza
dlat = sinza * cosaa
dlon = sinza * sinaa / coslat
dx [not_pole] = (coslat * coslon * dr - sinlat * coslon * dlat -
coslat * sinlon * dlon)
dz [not_pole] = sinlat * dr + coslat * dlat
dy [not_pole] = (coslat * sinlon * dr - sinlat * sinlon * dlat +
coslat * coslon * dlon)
вернуть x, y, z, dx, dy, dz
def get_ellipsoid_semiminor_axis (эллипсоид):
"" "Возвращает малую полуось эллипсоида.
sin (deg2rad * (za))
dy [at_pole] = dx [at_pole] * np.sin (deg2rad * (aa))
dx [at_pole] * = np.cos (deg2rad * (aa))
not_pole = np.logical_not (at_pole)
если есть (not_pole):
latrad = deg2rad * lat [not_pole]
lonrad = deg2rad * lon [not_pole]
zarad = deg2rad * za [not_pole]
aarad = deg2rad * aa [not_pole]
coslat = np.cos (латрад)
sinlat = np.sin (латрад)
coslon = np.cos (лонрад)
sinlon = np.sin (лонрад)
cosza = np.cos (zarad)
sinza = np.sin (зарад)
cosaa = np.cos (aarad)
sinaa = np.sin (аарад)
x [not_pole] = r [not_pole] * coslat
y [not_pole] = x [not_pole] * sinlon
x [not_pole] * = кослон
z [not_pole] = r [not_pole] * sinlat
dr = cosza
dlat = sinza * cosaa
dlon = sinza * sinaa / coslat
dx [not_pole] = (coslat * coslon * dr - sinlat * coslon * dlat -
coslat * sinlon * dlon)
dz [not_pole] = sinlat * dr + coslat * dlat
dy [not_pole] = (coslat * sinlon * dr - sinlat * sinlon * dlat +
coslat * coslon * dlon)
вернуть x, y, z, dx, dy, dz
def get_ellipsoid_semiminor_axis (эллипсоид):
"" "Возвращает малую полуось эллипсоида. "" "
вернуть эллипсоид [0] * np.sqrt (1.0 - эллипсоид [1] ** 2)
def line_ellipsoid_intersect (x, y, z, dx, dy, dz,
эллипсоид, высота = 0,0):
"" "Находит точки пересечения прямой с эллипсоидом
Решает относительно d:
$$ (X / a) ** 2 + (Y / a) ** 2 + (Z / b) ** 2 - 1 = 0 $$
$$ X = x + d * dx $$
$$ Y = y + d * dy $$
$$ Z = z + d * dz $$
где d - множитель sqrt (dx ** 2 + dy ** 2 + dz ** 2), a -
Большая полуось, b - малая полуось. X, Y, Z дает
точка пересечения.Если dx, dy, dz нормализованы, d - расстояние
в единицах размера эллипсоида. Если пересечения нет, код возвращает расстояние np.nan
Для действительного d точка на полпути между точками - это точка касания,
хотя он ниже эллипсоида + высота поверхности
Возврат:
d: массив параметров расстояния, последнее измерение дает 2 решения
Параметры:
x: геоцентрическая декартова координата x
y: геоцентрическая декартова координата y
z: геоцентрическая декартова координата z.
"" "
вернуть эллипсоид [0] * np.sqrt (1.0 - эллипсоид [1] ** 2)
def line_ellipsoid_intersect (x, y, z, dx, dy, dz,
эллипсоид, высота = 0,0):
"" "Находит точки пересечения прямой с эллипсоидом
Решает относительно d:
$$ (X / a) ** 2 + (Y / a) ** 2 + (Z / b) ** 2 - 1 = 0 $$
$$ X = x + d * dx $$
$$ Y = y + d * dy $$
$$ Z = z + d * dz $$
где d - множитель sqrt (dx ** 2 + dy ** 2 + dz ** 2), a -
Большая полуось, b - малая полуось. X, Y, Z дает
точка пересечения.Если dx, dy, dz нормализованы, d - расстояние
в единицах размера эллипсоида. Если пересечения нет, код возвращает расстояние np.nan
Для действительного d точка на полпути между точками - это точка касания,
хотя он ниже эллипсоида + высота поверхности
Возврат:
d: массив параметров расстояния, последнее измерение дает 2 решения
Параметры:
x: геоцентрическая декартова координата x
y: геоцентрическая декартова координата y
z: геоцентрическая декартова координата z. dx: геоцентрическое декартово представление в формате dx
dy: геоцентрическое декартово отображение
dz: геоцентрический декартово вид dz
эллипозид: модель эллипсоида [a, e]
высота: высота над эллипсоидом до точки пересечения [по умолчанию ноль]
Сделать:
Обратитесь к line_sphere_intersect, если эллипсоид является сферой
"" "
# большая полуось
a = эллипсоид [0] + высота
# малая полуось
b = get_ellipsoid_semiminor_axis (эллипсоид) + высота
# Если это скаляры, сделайте их массивами
x, y, z, dx, dy, dz = _broadcast (x, y, z, dx, dy, dz)
# A * d ** 2 + B * d + C = 0, решить относительно d
А = ((dx ** 2 + dy ** 2) / a ** 2 + dz ** 2 / b ** 2).сплющить ()
B = (2 * ((x * dx + y * dy) / a ** 2 + z * dz / b ** 2)). Flatten ()
C = ((y ** 2 + x ** 2) / a ** 2 + z ** 2 / b ** 2 - 1.0) .flatten ()
d = np.zeros ((len (A), 2))
для i в диапазоне (len (A)):
корни = np.roots ([A [i], B [i], C [i]])
если есть (np.
dx: геоцентрическое декартово представление в формате dx
dy: геоцентрическое декартово отображение
dz: геоцентрический декартово вид dz
эллипозид: модель эллипсоида [a, e]
высота: высота над эллипсоидом до точки пересечения [по умолчанию ноль]
Сделать:
Обратитесь к line_sphere_intersect, если эллипсоид является сферой
"" "
# большая полуось
a = эллипсоид [0] + высота
# малая полуось
b = get_ellipsoid_semiminor_axis (эллипсоид) + высота
# Если это скаляры, сделайте их массивами
x, y, z, dx, dy, dz = _broadcast (x, y, z, dx, dy, dz)
# A * d ** 2 + B * d + C = 0, решить относительно d
А = ((dx ** 2 + dy ** 2) / a ** 2 + dz ** 2 / b ** 2).сплющить ()
B = (2 * ((x * dx + y * dy) / a ** 2 + z * dz / b ** 2)). Flatten ()
C = ((y ** 2 + x ** 2) / a ** 2 + z ** 2 / b ** 2 - 1.0) .flatten ()
d = np.zeros ((len (A), 2))
для i в диапазоне (len (A)):
корни = np.roots ([A [i], B [i], C [i]])
если есть (np. isreal (корни)):
d [i, 0] = корни [0]
d [i, 1] = корни [1]
еще:
d [i, 0] = np.nan
d [i, 1] = np.nan
sh = []
для i в x.shape:
sh.append (я)
sh.append (2)
вернуть d.reshape (кортеж (sh))
def geometry_limb_zenith_angle (эллипсоид, r, широта, долгота,
аа = 0.0, alt = 0.0, za_acc = 1e-10):
"" "Численный метод вычисления геометрического зенитного угла лимба, зная
другие параметры спутника
Предполагает, что планета представляет собой эллипсоид, и вычисляет конечность численно
минимизация расстояния между соседними пересечениями эллипсоида.
Скорость сближения с прямым зенитным углом должна составлять 180/30 ** N,
хотя численные ошибки очень точной точности не защищены.
Параметры:
эллипсоид: эллипсоид [a, e]
r: геоцентрический радиус спутника
lat: геоцентрическая широта спутника
lon: геоцентрическая долгота спутника
aa: азимутальный угол спутника
alt: касательная высота
za_acc: точность зенитного угла.
isreal (корни)):
d [i, 0] = корни [0]
d [i, 1] = корни [1]
еще:
d [i, 0] = np.nan
d [i, 1] = np.nan
sh = []
для i в x.shape:
sh.append (я)
sh.append (2)
вернуть d.reshape (кортеж (sh))
def geometry_limb_zenith_angle (эллипсоид, r, широта, долгота,
аа = 0.0, alt = 0.0, za_acc = 1e-10):
"" "Численный метод вычисления геометрического зенитного угла лимба, зная
другие параметры спутника
Предполагает, что планета представляет собой эллипсоид, и вычисляет конечность численно
минимизация расстояния между соседними пересечениями эллипсоида.
Скорость сближения с прямым зенитным углом должна составлять 180/30 ** N,
хотя численные ошибки очень точной точности не защищены.
Параметры:
эллипсоид: эллипсоид [a, e]
r: геоцентрический радиус спутника
lat: геоцентрическая широта спутника
lon: геоцентрическая долгота спутника
aa: азимутальный угол спутника
alt: касательная высота
za_acc: точность зенитного угла. Предупреждение: бесконечный цикл, если он слишком мал
Возврат:
za: зенитный угол спутника для геометрии обзора конечностей. Форма как вход
"" "
если (za_acc == 0):
поднять RuntimeError («Точность зенита не может быть 0»)
r, lat, lon, aa, alt = _broadcast (r, lat, lon, aa, alt)
# Запомните форму, потому что мы сгладим эти массивы для упрощения цикла
sh = r.shape
r = r.flatten ()
lat = lat.flatten ()
lon = lon.flatten ()
aa = aa.flatten ()
alt = alt.flatten ()
za = np.empty_like (r)
для i в диапазоне (len (r)):
za_min = 0.0
za_max = 180,0
while True: # Пока не будет достигнута зенитная точность
# num = 31 означает 180/30 ** N - количество петель для достижения точности
zenith_angles = np.linspace (za_min, za_max, число = 31)
# Получите декартовы представления для зенитной точности зондирования
x, y, z, dx, dy, dz = geocentricposlos2cart (r [i], lat [i], lon [i],
zenith_angles, aa [i])
# Получите пересечения с эллипсоидом на касательной высоте
d = line_ellipsoid_intersect (x, y, z, dx, dy, dz,
эллипсоид, alt [i])
# Если мы каким-то образом разработали сценарий, который невозможен или плох
если нп.
Предупреждение: бесконечный цикл, если он слишком мал
Возврат:
za: зенитный угол спутника для геометрии обзора конечностей. Форма как вход
"" "
если (za_acc == 0):
поднять RuntimeError («Точность зенита не может быть 0»)
r, lat, lon, aa, alt = _broadcast (r, lat, lon, aa, alt)
# Запомните форму, потому что мы сгладим эти массивы для упрощения цикла
sh = r.shape
r = r.flatten ()
lat = lat.flatten ()
lon = lon.flatten ()
aa = aa.flatten ()
alt = alt.flatten ()
za = np.empty_like (r)
для i в диапазоне (len (r)):
za_min = 0.0
za_max = 180,0
while True: # Пока не будет достигнута зенитная точность
# num = 31 означает 180/30 ** N - количество петель для достижения точности
zenith_angles = np.linspace (za_min, za_max, число = 31)
# Получите декартовы представления для зенитной точности зондирования
x, y, z, dx, dy, dz = geocentricposlos2cart (r [i], lat [i], lon [i],
zenith_angles, aa [i])
# Получите пересечения с эллипсоидом на касательной высоте
d = line_ellipsoid_intersect (x, y, z, dx, dy, dz,
эллипсоид, alt [i])
# Если мы каким-то образом разработали сценарий, который невозможен или плох
если нп. isnan (d) .all ():
Raise RuntimeError ("Невозможно получить точку касания." +
«Все попытки упускают из виду эллипсоид».)
Элиф не np.isnan (d) .any ():
Raise RuntimeError ("Невозможно получить точку касания." +
«Внутри эллипсоида или атмосферы»).
# Зенит конечностей от минимизации расстояния между перекрестками
D = d [:, 0] - d [:, 1]
# Вот достопримечательности
эти = np.nan_to_num (D)> 0
# Обновлен первый из зенитных углов, попадающих в атмосферу.
za_max = zenith_angles [эти] [0]
# Обновлен последний зенитный угол без атмосферы
za_min = zenith_angles [np.logical_not (эти)] [- 1]
# Мы уже на месте?
если (za_max-za_min)
isnan (d) .all ():
Raise RuntimeError ("Невозможно получить точку касания." +
«Все попытки упускают из виду эллипсоид».)
Элиф не np.isnan (d) .any ():
Raise RuntimeError ("Невозможно получить точку касания." +
«Внутри эллипсоида или атмосферы»).
# Зенит конечностей от минимизации расстояния между перекрестками
D = d [:, 0] - d [:, 1]
# Вот достопримечательности
эти = np.nan_to_num (D)> 0
# Обновлен первый из зенитных углов, попадающих в атмосферу.
za_max = zenith_angles [эти] [0]
# Обновлен последний зенитный угол без атмосферы
za_min = zenith_angles [np.logical_not (эти)] [- 1]
# Мы уже на месте?
если (za_max-za_min)  , 30.)
>>> sat = сфера_плоскость_пересечение (np.массив ([x, y, z]), 6978e3)
"" "
assert r> 0.0, "Невозможно работать со сферой нулевого радиуса"
assert len (pos.shape) == 2, "Требуется (N, 3) как pos-shape"
d = np.linalg.norm (pos, axis = 1)
assert all (d> 0.0), «Невозможно работать с 0-вектором для позиции»
число_углов = лен (тета)
number_of_positions = pos.shape [0]
points = np.empty ((число_углов, число_позиций, 3))
если number_of_angles == 0:
точки возврата
# Если сфера находится под плоскостью или по касательной к плоскости
для ii в диапазоне (число_позиций):
если d [ii]> r:
для i в диапазоне (число_углов):
точки [i, ii,:] = np.массив ([np.nan, np.nan, np.nan])
Продолжить
elif d [ii] == r:
для i в диапазоне (число_углов):
точки [i, ii,:] = pos [ii,:]
Продолжить
# Вектор плоскости (нормализованный / единичный)
n = pos [ii] / d [ii]
# Южный вектор
единицы, широта, долгота = cart2geocentric (n [0], n [1], n [2])
если (широта == 90,0):
v1 = np.
, 30.)
>>> sat = сфера_плоскость_пересечение (np.массив ([x, y, z]), 6978e3)
"" "
assert r> 0.0, "Невозможно работать со сферой нулевого радиуса"
assert len (pos.shape) == 2, "Требуется (N, 3) как pos-shape"
d = np.linalg.norm (pos, axis = 1)
assert all (d> 0.0), «Невозможно работать с 0-вектором для позиции»
число_углов = лен (тета)
number_of_positions = pos.shape [0]
points = np.empty ((число_углов, число_позиций, 3))
если number_of_angles == 0:
точки возврата
# Если сфера находится под плоскостью или по касательной к плоскости
для ii в диапазоне (число_позиций):
если d [ii]> r:
для i в диапазоне (число_углов):
точки [i, ii,:] = np.массив ([np.nan, np.nan, np.nan])
Продолжить
elif d [ii] == r:
для i в диапазоне (число_углов):
точки [i, ii,:] = pos [ii,:]
Продолжить
# Вектор плоскости (нормализованный / единичный)
n = pos [ii] / d [ii]
# Южный вектор
единицы, широта, долгота = cart2geocentric (n [0], n [1], n [2])
если (широта == 90,0):
v1 = np. array ([cosd (lon), sind (lon), 0.]) * sind (лат)
еще:
v1 = np.array ([cosd (долг) * синд (лат),
синд (долг) * синд (лат),
cosd (лат-180.0)])
# Восточный вектор
v2 = -np.cross (n, v1) # указывает на восток
# Радиус круга
rc = np.sqrt (r ** 2 - d [ii] ** 2)
для i в диапазоне (число_углов):
точки [i, ii,:] = pos [ii,:] + rc * (cosd (theta [i]) * v1 +
синд (тета [я]) * v2)
точки возврата
def tunnel_distance (lat1, lon1, lat2, lon2):
"" "Рассчитайте туннельное расстояние между двумя точками на поверхности Земли.
Аргументы:
lat1: одно число или массив чисел с широтой в градусах.lon1: одиночное число или массив numpy с долготой в градусах.
lat2: одиночное число или массив numpy с широтой в градусах.
lon2: одиночное число или массив numpy с долготой в градусах.
Возврат:
Расстояние туннеля в метрах
"" "
points1 = np.
array ([cosd (lon), sind (lon), 0.]) * sind (лат)
еще:
v1 = np.array ([cosd (долг) * синд (лат),
синд (долг) * синд (лат),
cosd (лат-180.0)])
# Восточный вектор
v2 = -np.cross (n, v1) # указывает на восток
# Радиус круга
rc = np.sqrt (r ** 2 - d [ii] ** 2)
для i в диапазоне (число_углов):
точки [i, ii,:] = pos [ii,:] + rc * (cosd (theta [i]) * v1 +
синд (тета [я]) * v2)
точки возврата
def tunnel_distance (lat1, lon1, lat2, lon2):
"" "Рассчитайте туннельное расстояние между двумя точками на поверхности Земли.
Аргументы:
lat1: одно число или массив чисел с широтой в градусах.lon1: одиночное число или массив numpy с долготой в градусах.
lat2: одиночное число или массив numpy с широтой в градусах.
lon2: одиночное число или массив numpy с долготой в градусах.
Возврат:
Расстояние туннеля в метрах
"" "
points1 = np. column_stack (
geocentric2cart (constants.earth_radius, lat1, lon1)
)
points2 = np.column_stack (
geocentric2cart (constants.earth_radius, lat2, lon2)
)
вернуть np.sqrt (np.sum ((points2 - points1) ** 2, axis = 1))
def _broadcast (* args):
"" "Аналогично broadcast_arrays в numpy, но с минимальным размером вывода (1,)
"" "
shape = np.трансляция (* args) .shape
если не форма:
shape = (1,)
return [np.broadcast_to (array, shape) for array in args]
column_stack (
geocentric2cart (constants.earth_radius, lat1, lon1)
)
points2 = np.column_stack (
geocentric2cart (constants.earth_radius, lat2, lon2)
)
вернуть np.sqrt (np.sum ((points2 - points1) ** 2, axis = 1))
def _broadcast (* args):
"" "Аналогично broadcast_arrays в numpy, но с минимальным размером вывода (1,)
"" "
shape = np.трансляция (* args) .shape
если не форма:
shape = (1,)
return [np.broadcast_to (array, shape) for array in args]
Перейти к основному содержанию
Поиск Поиск
- Где угодно
- Быстрый поиск где угодно
Поиск Поиск
- Войти | регистр
- Подписка / продление
- Учреждения
- Индивидуальные подписки
- Индивидуальные продления
- Библиотекари
- Тарифы и полные платежи Пакет для Чикаго
- Полный цикл и охват содержимого
- Файлы KBART и RSS-каналы
- Разрешения и перепечатка
- Инициатива развивающихся стран Чикаго
- Даты отправки и претензии
- Часто задаваемые вопросы библиотекарей
- Тарифы, заказы, и платежи
- Полный пакет Chicago
- Полный охват и содержание
- Даты отправки и претензии
- Часто задаваемые вопросы об агенте
- О нас
- Публикуйте у нас
- Недавно приобретенные журналы
- Издательская стоимость tners
- Подпишитесь на уведомления eTOC
- Пресс-релизы
- Медиа
- Книги издательства Чикагского университета
- Распределительный центр в Чикаго
- Чикагский университет
- Положения и условия
- Заявление об издательской этике
- Уведомление о конфиденциальности
- Доступность Chicago Journals
- Доступность университета
- Следуйте за нами на facebook
- Следуйте за нами в Twitter
- Свяжитесь с нами
- Запросы СМИ и рекламы
- Открытый доступ в Чикаго
- Следуйте за нами на facebook
- Следуйте за нами в Twitter
SMILE — Сенсорно-моторный интерфейс для экзоскелетов нижних конечностей
- Дом
- Общественные проекты
- Моделирование
SMILE — Сенсорно-моторный интерфейс для экзоскелетов нижних конечностей
Разработка экзоскелетов нижних конечностей (LEE), адаптированных для отдельных пациентов, с учетом их физиологических и клинических потребностей.
Партнеры проекта
Лондонский Имперский колледж
Продолжительность
01.10.2020 — 30.09.2024
Финансирующий орган
TUM Международная высшая школа науки и техники (IGSSE)
Мотивация
Потеря подвижности или равновесия в результате нервной травмы или старения является критически важным фактором в общественном здравоохранении.Носимые роботы (например, экзоскелеты) признаны решениями для реабилитации и помощи при движении. Хотя исследования экзоскелетов обширны, полной реализации экзоскелетов мешают два препятствия: соотношение мощности и веса конструкции экзоскелета и машинный интеллект, позволяющий адаптироваться к конкретному пациенту. Проект направлен на разработку полностью автоматизированной структуры от оптимизации топологии структурных частей до быстрого прототипирования на основе роботов, чтобы производить индивидуальные LEE для пациентов с инсультом менее чем за 24 часа.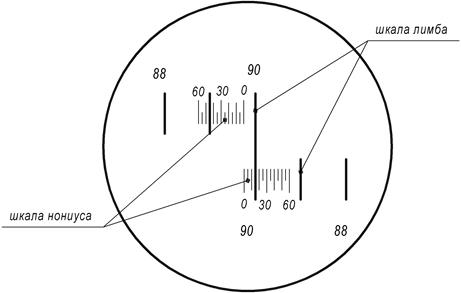
Method
Чтобы разработать экзоскелет, специально адаптированный для отдельных пациентов, как топология, так и функциональность оптимизировали структуры LEE (т.е.е. оптимизация соотношения мощности / веса) и искусственный интеллект для бесперебойного взаимодействия человека с машиной. Настройка геометрии в сочетании с настройкой жесткости — задача, которая будет решена в этом проекте. Это будет реализовано с использованием специальных алгоритмов оптимизации топологии, адаптированных к процессам быстрого прототипирования на основе роботов с локальным армированием волокон. В результате можно производить индивидуальные легкие детали в полностью автоматизированном процессе.Кроме того, алгоритмы машинного обучения будут использоваться для получения параметров дизайна для каждого пользователя на основе моделирования ходьбы, ограниченного медицинскими потребностями пациента. Это позволяет настраивать нейромеханику суставов жесткости, размера, веса и размещения датчиков для оптимального использования.
Это позволяет настраивать нейромеханику суставов жесткости, размера, веса и размещения датчиков для оптимального использования.
Благодарность
Кафедра с благодарностью отмечает финансирование, поддержанное Международной высшей школой науки и инженерии TUM (IGSSE) через программу Объединенной академии докторских исследований (JADS).

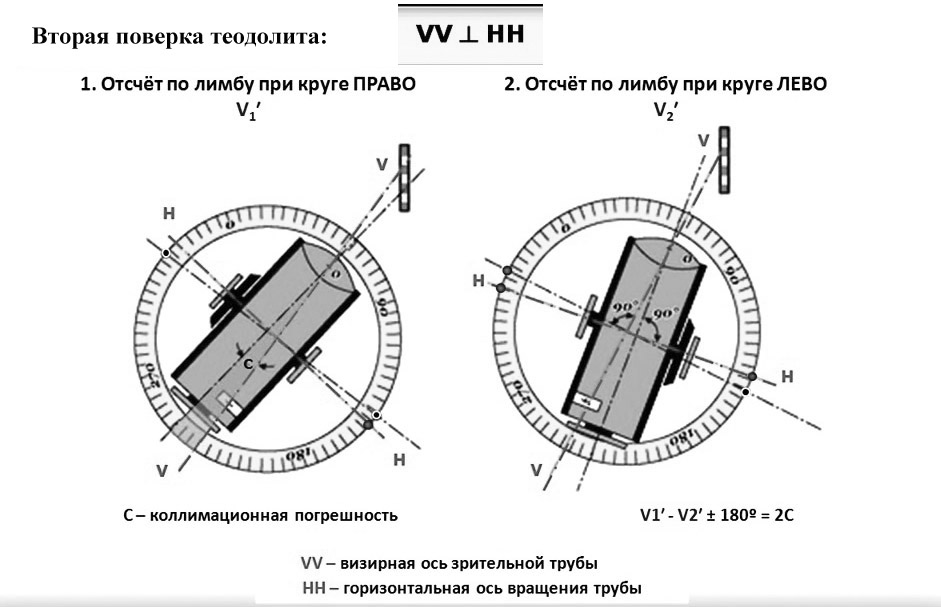
 На местности находим ровную поверхность, по которой центрируем прибор на подставке уровнями и зажимными винтами. В итоге положение прибора должно получиться строго горизонтальным.
На местности находим ровную поверхность, по которой центрируем прибор на подставке уровнями и зажимными винтами. В итоге положение прибора должно получиться строго горизонтальным.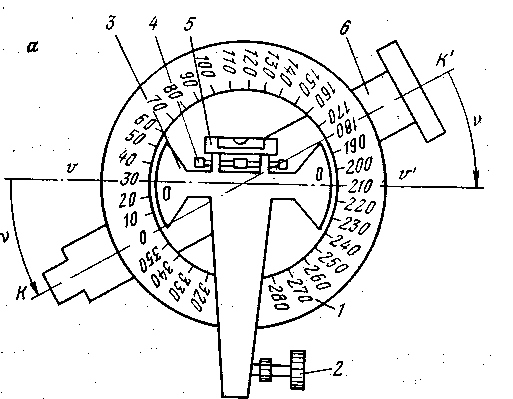

 Отсчет записывают в журнал измерений (табл. 1,
столбец 4). Указанные действия составляют первый полуприем.
Отсчет записывают в журнал измерений (табл. 1,
столбец 4). Указанные действия составляют первый полуприем. Указанные действия составляют первый полуприём.
Указанные действия составляют первый полуприём. Н. Геодезия. Топографические съемки: Учебное пособие/Ю.Н. Корнилов.
Санкт-Петербургский государственный горный институт (технический университет).
СПб, 2008. – 145 с.
Н. Геодезия. Топографические съемки: Учебное пособие/Ю.Н. Корнилов.
Санкт-Петербургский государственный горный институт (технический университет).
СПб, 2008. – 145 с.
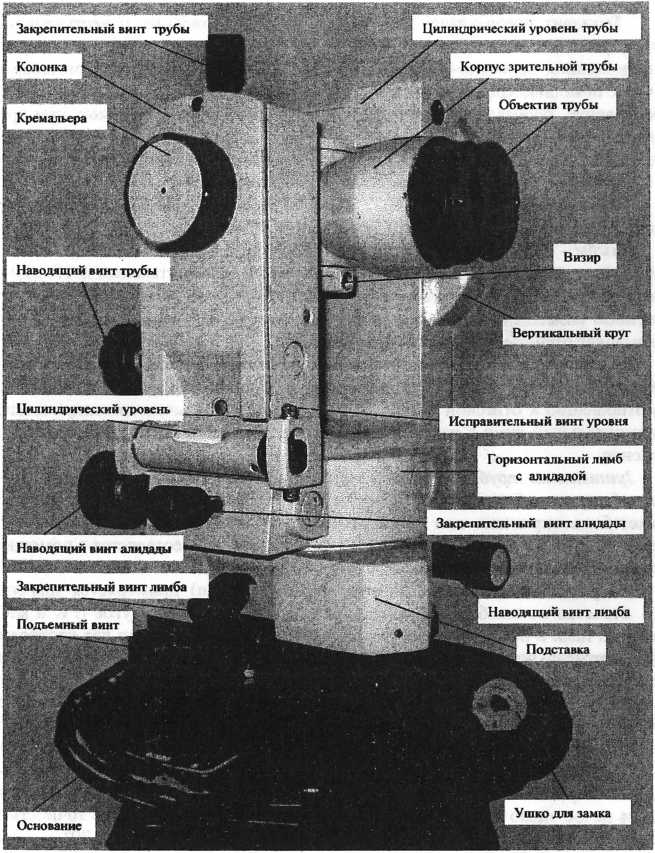 Смоделированные наблюдения рассчитываются для каждого реального наблюдения с применением теоретической модели групповой задержки VLBI и различных моделей коррекции.Теоретическая модель РСДБ, используемая сегодня, называется консенсусной моделью и включает все необходимые условия для достижения точности 1 пс (около 0,3 мм). Как было представлено на Генеральной ассамблее МАС в 2012 году, Комиссия 52 МАС по теории относительности в фундаментальной астрономии вскоре представит новую модель с точностью 0,1 пс. Текущие традиционно применяемые модели коррекции определены Конвенциями IERS (2010).
Смоделированные наблюдения рассчитываются для каждого реального наблюдения с применением теоретической модели групповой задержки VLBI и различных моделей коррекции.Теоретическая модель РСДБ, используемая сегодня, называется консенсусной моделью и включает все необходимые условия для достижения точности 1 пс (около 0,3 мм). Как было представлено на Генеральной ассамблее МАС в 2012 году, Комиссия 52 МАС по теории относительности в фундаментальной астрономии вскоре представит новую модель с точностью 0,1 пс. Текущие традиционно применяемые модели коррекции определены Конвенциями IERS (2010). , 1990) и фильтрация информации с использованием квадратного корня (Bierman, 1977).
, 1990) и фильтрация информации с использованием квадратного корня (Bierman, 1977).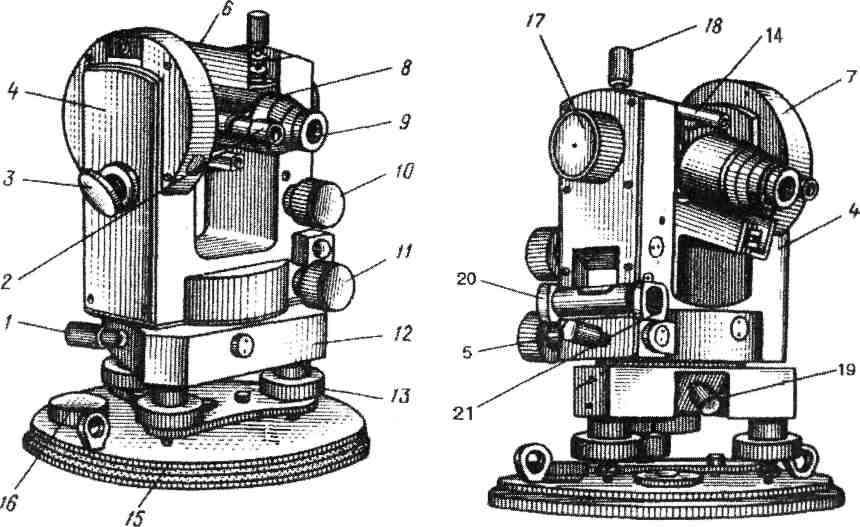 На стационарных антеннах обычно избегают больших эксцентриситетов. Когда доступны точно измеренные эксцентриситеты, в принципе возможно сравнить измеренные эксцентриситет с расчетными. Однако преобразование локальной системы измерения в геоцентрическую декартову систему априорного каталога может значительно ухудшить точность измеренного эксцентриситета и, следовательно, сравнения.
На стационарных антеннах обычно избегают больших эксцентриситетов. Когда доступны точно измеренные эксцентриситеты, в принципе возможно сравнить измеренные эксцентриситет с расчетными. Однако преобразование локальной системы измерения в геоцентрическую декартову систему априорного каталога может значительно ухудшить точность измеренного эксцентриситета и, следовательно, сравнения.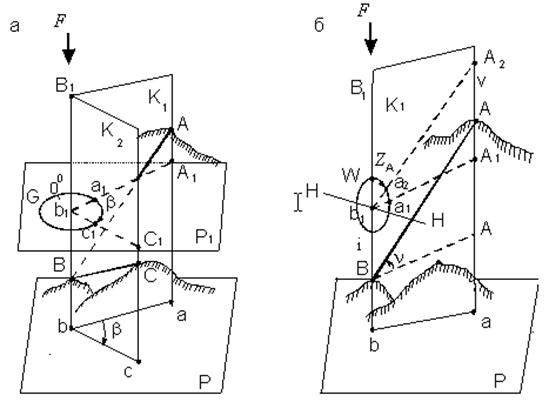 Обзор последних оценок и более ранних результатов РСДБ можно найти в Heinkelmann & Schuh (2010).
Обзор последних оценок и более ранних результатов РСДБ можно найти в Heinkelmann & Schuh (2010).
 "" "
вернуть np.sin (np.deg2rad (x))
[документы] def cosd (x):
"" "Косинус аргумента в градусах." ""
вернуть np.cos (np.deg2rad (x))
[документы] def tand (x):
"" "Тангенс аргумента в градусах." ""
вернуть np.tan (np.deg2rad (x))
[документы] def asind (x):
"" "Обратный синус в градусах." ""
вернуть np.arcsin (np.deg2rad (x))
[документы] def inrange (x, minx, maxx, exclude = 'none', text = None):
"" "Проверить, находится ли x в заданных пределах.
Параметры:
x: переменная для тестирования.
minx: нижняя граница.
maxx: верхняя граница.exclude (str): исключить границы. Возможные значения:
"нет", "нижний", "верхний" и "оба"
text (str): Дополнительный текст предупреждения.
Повышает:
Исключение: если значение выходит за допустимые пределы.
"" "
compare = {'none': (np.greater_equal, np.less_equal),
'нижний': (np.greater, np.less_equal),
'верхний': (np.greater_equal, np.
"" "
вернуть np.sin (np.deg2rad (x))
[документы] def cosd (x):
"" "Косинус аргумента в градусах." ""
вернуть np.cos (np.deg2rad (x))
[документы] def tand (x):
"" "Тангенс аргумента в градусах." ""
вернуть np.tan (np.deg2rad (x))
[документы] def asind (x):
"" "Обратный синус в градусах." ""
вернуть np.arcsin (np.deg2rad (x))
[документы] def inrange (x, minx, maxx, exclude = 'none', text = None):
"" "Проверить, находится ли x в заданных пределах.
Параметры:
x: переменная для тестирования.
minx: нижняя граница.
maxx: верхняя граница.exclude (str): исключить границы. Возможные значения:
"нет", "нижний", "верхний" и "оба"
text (str): Дополнительный текст предупреждения.
Повышает:
Исключение: если значение выходит за допустимые пределы.
"" "
compare = {'none': (np.greater_equal, np.less_equal),
'нижний': (np.greater, np.less_equal),
'верхний': (np.greater_equal, np. less),
'оба': (np.greater, np.less),
}
больше, меньше = сравнить [исключить]
если меньше (x, minx) или больше (x, maxx):
если текст None:
Raise Exception ('Диапазон вне пределов [{}, {}]'.формат (minx, maxx))
еще:
поднять исключение (
'Диапазон вне границы [{}, {}]: {}'. Формат (minx, maxx, текст)
)
[документы] класс ellipsoidmodels ():
"" "Предоставьте данные для различных справочных эллипсоидов.
Охватываются следующие модели:
* SphericalEarth (радиус установлен как constants.earth_radius)
* WGS84
* SphericalVenus (радиус такой же, как в ARTS)
* SphericalMars (радиус такой же, как в ARTS)
* EllipsoidMars
* Сферический Юпитер (радиус такой же, как в ARTS)
Примеры:
>>> e = эллипсоидные модели ()
.. Портировано из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
[документы] def __init __ (self):
self.
less),
'оба': (np.greater, np.less),
}
больше, меньше = сравнить [исключить]
если меньше (x, minx) или больше (x, maxx):
если текст None:
Raise Exception ('Диапазон вне пределов [{}, {}]'.формат (minx, maxx))
еще:
поднять исключение (
'Диапазон вне границы [{}, {}]: {}'. Формат (minx, maxx, текст)
)
[документы] класс ellipsoidmodels ():
"" "Предоставьте данные для различных справочных эллипсоидов.
Охватываются следующие модели:
* SphericalEarth (радиус установлен как constants.earth_radius)
* WGS84
* SphericalVenus (радиус такой же, как в ARTS)
* SphericalMars (радиус такой же, как в ARTS)
* EllipsoidMars
* Сферический Юпитер (радиус такой же, как в ARTS)
Примеры:
>>> e = эллипсоидные модели ()
.. Портировано из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
[документы] def __init __ (self):
self. _data = {
"SphericalEarth": (constants.earth_radius, 0),
«WGS84»: (6378137, 0,08181916),
"SphericalVenus": (6051800.0, 0),
«СферикалМарс»: (3389500.0, 0),
«ЭллипсоидМарс»: (3396190.0, 0.1083),
«Сферический Юпитер»: (690.0, 0),
}
def __getitem __ (я, модель):
вернуть self.get (модель)
[документы] def get (self, model = 'WGS84'):
"" "Возвращает данные для различных справочных эллипсоидов.Параметры:
model (str): Модель эллипсоида.
Возврат:
кортеж: Экваториальный радиус (r), эксцентриситет (e)
Примеры:
>>> e ['WGS84']
(6378137, 0,08181916)
>>> e.get ('WGS84')
(6378137, 0,08181916)
>>> ellipsoidmodel () ['WGS84']
(6378137, 0,08181916)
"" "
если модель в self._data:
вернуть self._data .__ getitem __ (модель)
еще:
Raise Exception ('Неизвестная модель эллипсоида "{}".
_data = {
"SphericalEarth": (constants.earth_radius, 0),
«WGS84»: (6378137, 0,08181916),
"SphericalVenus": (6051800.0, 0),
«СферикалМарс»: (3389500.0, 0),
«ЭллипсоидМарс»: (3396190.0, 0.1083),
«Сферический Юпитер»: (690.0, 0),
}
def __getitem __ (я, модель):
вернуть self.get (модель)
[документы] def get (self, model = 'WGS84'):
"" "Возвращает данные для различных справочных эллипсоидов.Параметры:
model (str): Модель эллипсоида.
Возврат:
кортеж: Экваториальный радиус (r), эксцентриситет (e)
Примеры:
>>> e ['WGS84']
(6378137, 0,08181916)
>>> e.get ('WGS84')
(6378137, 0,08181916)
>>> ellipsoidmodel () ['WGS84']
(6378137, 0,08181916)
"" "
если модель в self._data:
вернуть self._data .__ getitem __ (модель)
еще:
Raise Exception ('Неизвестная модель эллипсоида "{}".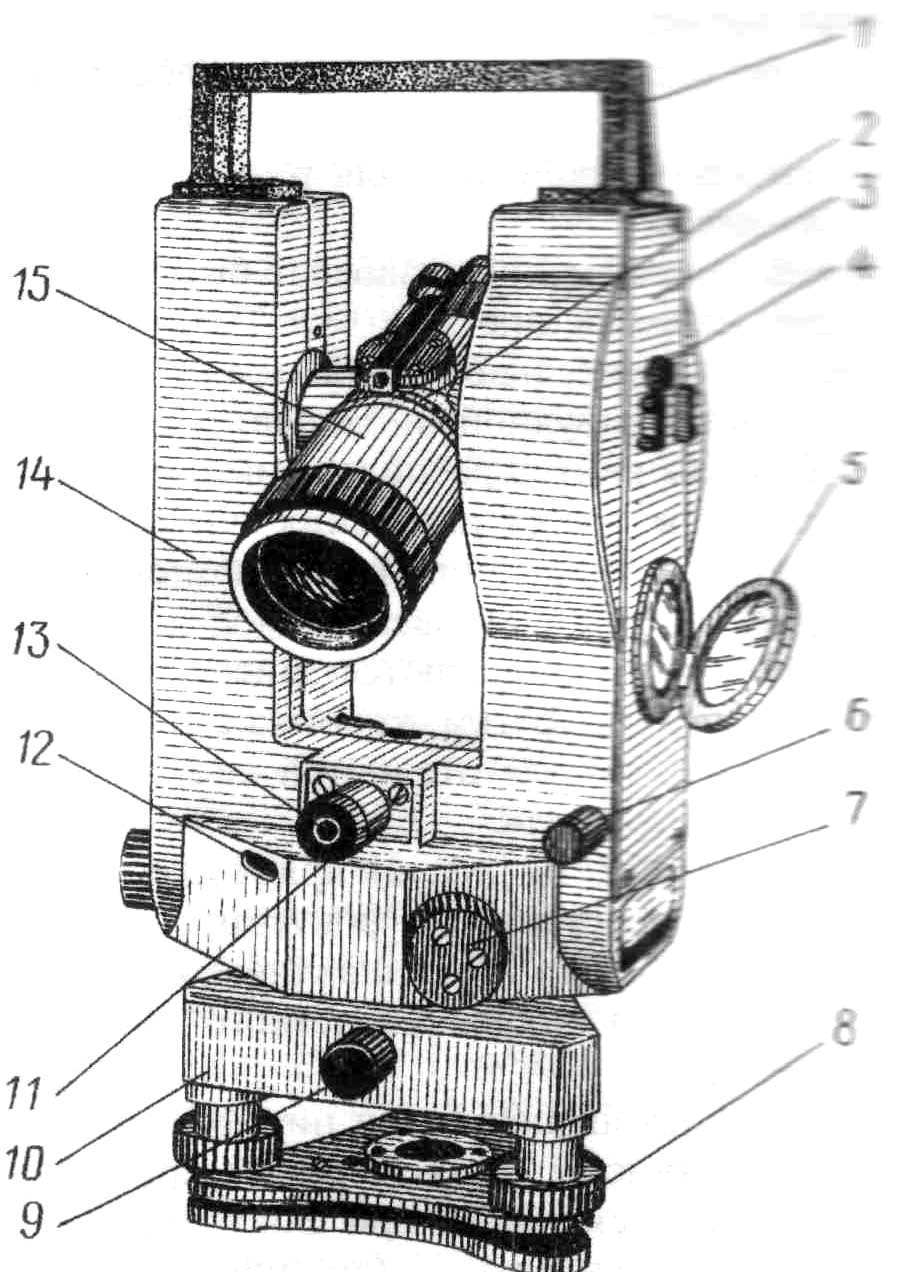 '.format (модель))
@свойство
def модели (self):
"" "Список доступных моделей.
Примеры:
>>> e.models
['SphericalVenus',
«Сферический Марс»,
'WGS84',
'Сферический Юпитер',
"Эллипсоид Марс",
'SphericalEarth']
"" "
список возврата (self._data.keys ())
[документы] def ellipsoid_r_geocentric (эллипсоид, широта):
«» "Геоцентрической радиус эллипсоида.
Дает расстояние от центра Земли и эллипсоида
как функция гео \ ** центрической ** широты.Примечание:
Чтобы получить радиусы для ** геодезической ** широты,
используйте: func: `ellipsoid_r_geodetic`.
Параметры:
эллипсоид (кортеж): эллипсоид модели, возвращенный
Автор: class: `ellipsoidmodels`.
lat (float или ndarray): геоцентрические широты.
Возврат:
float или ndarray: Радиусы.
.. Портировал из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.
'.format (модель))
@свойство
def модели (self):
"" "Список доступных моделей.
Примеры:
>>> e.models
['SphericalVenus',
«Сферический Марс»,
'WGS84',
'Сферический Юпитер',
"Эллипсоид Марс",
'SphericalEarth']
"" "
список возврата (self._data.keys ())
[документы] def ellipsoid_r_geocentric (эллипсоид, широта):
«» "Геоцентрической радиус эллипсоида.
Дает расстояние от центра Земли и эллипсоида
как функция гео \ ** центрической ** широты.Примечание:
Чтобы получить радиусы для ** геодезической ** широты,
используйте: func: `ellipsoid_r_geodetic`.
Параметры:
эллипсоид (кортеж): эллипсоид модели, возвращенный
Автор: class: `ellipsoidmodels`.
lat (float или ndarray): геоцентрические широты.
Возврат:
float или ndarray: Радиусы.
.. Портировал из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида. '
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
если эллипсоид [1] == 0:
г = нп.единицы (np.shape (lat)) * эллипсоид [0]
еще:
c = 1 - эллипсоид [1] ** 2
b = эллипсоид [0] * np.sqrt (c)
r = b / np.sqrt (c * cosd (лат) ** 2 + sind (лат) ** 2)
вернуть г
[документы] def ellipsoid_r_geodetic (эллипсоид, широта):
«» "Геодезический радиус эллипсоид.
Дает расстояние от центра Земли и эллипсоида
как функция гео \ ** детической ** широты.
Примечание:
Чтобы получить радиусы для ** геоцентрической ** широты,
используйте: func: `ellipsoid_r_geocentric`.Параметры:
эллипсоид (кортеж): эллипсоид модели, возвращенный
Автор: class: `ellipsoidmodels`.
lat (float или ndarray): геодезические широты.
Возврат:
float или ndarray: Радиусы.
.. Портировал из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.
'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
если эллипсоид [1] == 0:
г = нп.единицы (np.shape (lat)) * эллипсоид [0]
еще:
c = 1 - эллипсоид [1] ** 2
b = эллипсоид [0] * np.sqrt (c)
r = b / np.sqrt (c * cosd (лат) ** 2 + sind (лат) ** 2)
вернуть г
[документы] def ellipsoid_r_geodetic (эллипсоид, широта):
«» "Геодезический радиус эллипсоид.
Дает расстояние от центра Земли и эллипсоида
как функция гео \ ** детической ** широты.
Примечание:
Чтобы получить радиусы для ** геоцентрической ** широты,
используйте: func: `ellipsoid_r_geocentric`.Параметры:
эллипсоид (кортеж): эллипсоид модели, возвращенный
Автор: class: `ellipsoidmodels`.
lat (float или ndarray): геодезические широты.
Возврат:
float или ndarray: Радиусы.
.. Портировал из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида. '
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
если эллипсоид [1] == 0:
r = np.ones (np.shape (lat)) * эллипсоид [0]
еще:
e2 = эллипсоид [1] ** 2
sin2 = синд (лат) ** 2
r = (эллипсоид [0] * np.sqrt ((1 - e2) ** 2 * sin2 +
cosd (лат) ** 2) / np.sqrt (1 - e2 * sin2))
вернуть г
[документы] def ellipsoid2d (эллипсоид, orbitinc):
"" "Приближенный эллипсоид для 2D расчетов.
Определяет приблизительный опорный эллипсоид, следующий по орбитальному пути.
Новый эллипсоид определяется просто, определяя радиус в точке
максимальная широта и по этому значению вычисляется новый эксцентриситет.
Орбита задается наклонением орбиты, т. Е.
обычно значение около 100 градусов для полярных солнечно-синхронных орбит.Параметры:
эллипсоид (кортеж): эллипсоид модели, возвращенный
Автор: class: `ellipsoidmodels`.
orbitinc (float): Наклон орбиты.
Возврат:
кортеж: измененный вектор эллипсоида.
'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
если эллипсоид [1] == 0:
r = np.ones (np.shape (lat)) * эллипсоид [0]
еще:
e2 = эллипсоид [1] ** 2
sin2 = синд (лат) ** 2
r = (эллипсоид [0] * np.sqrt ((1 - e2) ** 2 * sin2 +
cosd (лат) ** 2) / np.sqrt (1 - e2 * sin2))
вернуть г
[документы] def ellipsoid2d (эллипсоид, orbitinc):
"" "Приближенный эллипсоид для 2D расчетов.
Определяет приблизительный опорный эллипсоид, следующий по орбитальному пути.
Новый эллипсоид определяется просто, определяя радиус в точке
максимальная широта и по этому значению вычисляется новый эксцентриситет.
Орбита задается наклонением орбиты, т. Е.
обычно значение около 100 градусов для полярных солнечно-синхронных орбит.Параметры:
эллипсоид (кортеж): эллипсоид модели, возвращенный
Автор: class: `ellipsoidmodels`.
orbitinc (float): Наклон орбиты.
Возврат:
кортеж: измененный вектор эллипсоида. .. Портировал из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
inrange (орбитинк, 0, 180,
exclude = 'оба',
text = 'Недействительный наклон орбиты.')
rp = ellipsoid_r_geocentric (эллипсоид, орбитинк)
вернуть эллипсоид [0], np.sqrt (1 - (rp / ellipsoid [0]) ** 2)
[docs] def ellipsoidcurvradius (эллипсоид, широта_гр, азимут):
"" "Устанавливает эллиспоид на локальный радиус кривизны
Вычисляет радиус кривизны для заданной широты и азимута.
угол, и использует это, чтобы установить сферический опорный эллипсоид
подходит для одномерных расчетов. Радиус кривизны лучше
локальное приближение, чем использование локального радиуса эллипсоида.
Для точного результата следует использовать * геодезическую * широту.Параметры:
lat_gd: Геодезическая широта.
азимут: Азимутальный угол (угол от плоскости NS).
.. Портировал из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
inrange (орбитинк, 0, 180,
exclude = 'оба',
text = 'Недействительный наклон орбиты.')
rp = ellipsoid_r_geocentric (эллипсоид, орбитинк)
вернуть эллипсоид [0], np.sqrt (1 - (rp / ellipsoid [0]) ** 2)
[docs] def ellipsoidcurvradius (эллипсоид, широта_гр, азимут):
"" "Устанавливает эллиспоид на локальный радиус кривизны
Вычисляет радиус кривизны для заданной широты и азимута.
угол, и использует это, чтобы установить сферический опорный эллипсоид
подходит для одномерных расчетов. Радиус кривизны лучше
локальное приближение, чем использование локального радиуса эллипсоида.
Для точного результата следует использовать * геодезическую * широту.Параметры:
lat_gd: Геодезическая широта.
азимут: Азимутальный угол (угол от плоскости NS). Если возвращаются заданные радиусы кривизны, см. Выше.
Возврат:
кортеж: измененный эллипсоид.
.. Портировал из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
aterm = 1 - эллипсоид [1] ** 2 * sind (lat_gd) ** 2
rn = 1 / np.sqrt (aterm)
rm = (1 - эллипсоид [1] ** 2) * (rn / aterm)
e0 = (эллипсоид [0] / (cosd (азимут) ** 2.0 / пог. + Синд (азимут) ** 2,0 / пог.))
e1 = 0
вернуть e0, e1
[docs] def cart2geocentric (x, y, z, lat0 = None, lon0 = None, za0 = None, aa0 = None):
"" "Преобразование декартовых координат в сферические координаты.
Геоцентрическая декартова система координат фиксирована относительно
Земля с центром в центре эллипсоида и ее координатами X-, Y-,
и оси Z, пересекающие поверхность в следующих точках:
* Ось X: экватор на нулевом меридиане (0 °, 0 °)
* Ось Y: экватор на 90 градусов восточной долготы (0 °, 90 °)
* Ось Z: Северный полюс (90 °, 0 °)
Распространенным синонимом являются координаты по центру Земли, координаты с фиксированной землей или ECEF.
Если возвращаются заданные радиусы кривизны, см. Выше.
Возврат:
кортеж: измененный эллипсоид.
.. Портировал из атмлаба. Оригинальный автор: Патрик Эрикссон
"" "
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
aterm = 1 - эллипсоид [1] ** 2 * sind (lat_gd) ** 2
rn = 1 / np.sqrt (aterm)
rm = (1 - эллипсоид [1] ** 2) * (rn / aterm)
e0 = (эллипсоид [0] / (cosd (азимут) ** 2.0 / пог. + Синд (азимут) ** 2,0 / пог.))
e1 = 0
вернуть e0, e1
[docs] def cart2geocentric (x, y, z, lat0 = None, lon0 = None, za0 = None, aa0 = None):
"" "Преобразование декартовых координат в сферические координаты.
Геоцентрическая декартова система координат фиксирована относительно
Земля с центром в центре эллипсоида и ее координатами X-, Y-,
и оси Z, пересекающие поверхность в следующих точках:
* Ось X: экватор на нулевом меридиане (0 °, 0 °)
* Ось Y: экватор на 90 градусов восточной долготы (0 °, 90 °)
* Ось Z: Северный полюс (90 °, 0 °)
Распространенным синонимом являются координаты по центру Земли, координаты с фиксированной землей или ECEF. Если указаны необязательные аргументы, гарантируется, что широта и
долгота остается постоянной для случаев зенита или надира, а долгота
для случаев N-S. Необязательный ввод должен интерпретироваться как [x, y, z]
получается перемещением от [lat0, lon0] в направлении [za0, aa0].
Параметры:
x: координата в измерении x.
y: Координата по оси y.
z: координата по оси z.
lat0: исходная широта.
lon0: Исходная долгота.
za0: исходный зенитный угол.aa0: Исходный азимутальный угол.
Возврат:
кортеж: Радиус, Широта, Долгота
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
r = np.sqrt (x ** 2 + y ** 2 + z ** 2)
если np.any (r == 0):
Raise Exception («Этот набор функций не обрабатывает r = 0»)
широта = np.rad2deg (np.arcsin (z / r))
lon = np.rad2deg (np.arctan2 (y, x))
если все (x не равно None для x в [lat0, lon0, za0, aa0]):
для i в диапазоне (np.size (r)):
если za0 [i] <1e-06 или za0 [i]> 180 - 1e-06:
lat [i] = lat0 [i]
lon [i] = lon0 [i]
if (abs (lat0 [i]) <90 - 1e-08 и
(abs (aa0 [i]) <1e-06 или abs (aa0 [i] - 180) <1e-06)):
если abs (lon [i] - lon0 [i]) <1:
lon [i] = lon0 [i]
еще:
если lon0 [i]> 0:
lon [i] = lon0 [i] - 180
еще:
lon [i] = lon0 [i] + 180
вернуть r, lat, lon
[документы] def geocentric2cart (r, lat, lon):
"" "Преобразование из сферической координаты в декартову позицию.
Если указаны необязательные аргументы, гарантируется, что широта и
долгота остается постоянной для случаев зенита или надира, а долгота
для случаев N-S. Необязательный ввод должен интерпретироваться как [x, y, z]
получается перемещением от [lat0, lon0] в направлении [za0, aa0].
Параметры:
x: координата в измерении x.
y: Координата по оси y.
z: координата по оси z.
lat0: исходная широта.
lon0: Исходная долгота.
za0: исходный зенитный угол.aa0: Исходный азимутальный угол.
Возврат:
кортеж: Радиус, Широта, Долгота
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
r = np.sqrt (x ** 2 + y ** 2 + z ** 2)
если np.any (r == 0):
Raise Exception («Этот набор функций не обрабатывает r = 0»)
широта = np.rad2deg (np.arcsin (z / r))
lon = np.rad2deg (np.arctan2 (y, x))
если все (x не равно None для x в [lat0, lon0, za0, aa0]):
для i в диапазоне (np.size (r)):
если za0 [i] <1e-06 или za0 [i]> 180 - 1e-06:
lat [i] = lat0 [i]
lon [i] = lon0 [i]
if (abs (lat0 [i]) <90 - 1e-08 и
(abs (aa0 [i]) <1e-06 или abs (aa0 [i] - 180) <1e-06)):
если abs (lon [i] - lon0 [i]) <1:
lon [i] = lon0 [i]
еще:
если lon0 [i]> 0:
lon [i] = lon0 [i] - 180
еще:
lon [i] = lon0 [i] + 180
вернуть r, lat, lon
[документы] def geocentric2cart (r, lat, lon):
"" "Преобразование из сферической координаты в декартову позицию. См .: func: `cart2geocentric` для определения геоцентрического
система координат.
Параметры:
r: Радиус.
lat: Широта в градусах.
lon Долгота в градусах.
Возврат:
кортеж: координаты в измерениях x, y, z.
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если np.any (r == 0):
Raise Exception («Этот набор функций не обрабатывает r = 0»)
latrad = np.deg2rad (лат)
lonrad = np.deg2rad (долг)
х = г * нп.cos (латрад)
y = x * np.sin (лонрад)
х = х * np.cos (лонрад)
z = r * np.sin (латрад)
вернуть x, y, z
[docs] def cart2geodetic (x, y, z, ellipsoid = None):
"" "Преобразование декартовых координат в геодезические.
Геодезические координаты относятся к эталонному эллипсоид
заданный входным эллипсоидом.
См. Раздел документации модуля для определения геоцентрической системы координат.
Параметры:
x: координаты в измерении x.
y: координаты в измерении y.
См .: func: `cart2geocentric` для определения геоцентрического
система координат.
Параметры:
r: Радиус.
lat: Широта в градусах.
lon Долгота в градусах.
Возврат:
кортеж: координаты в измерениях x, y, z.
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если np.any (r == 0):
Raise Exception («Этот набор функций не обрабатывает r = 0»)
latrad = np.deg2rad (лат)
lonrad = np.deg2rad (долг)
х = г * нп.cos (латрад)
y = x * np.sin (лонрад)
х = х * np.cos (лонрад)
z = r * np.sin (латрад)
вернуть x, y, z
[docs] def cart2geodetic (x, y, z, ellipsoid = None):
"" "Преобразование декартовых координат в геодезические.
Геодезические координаты относятся к эталонному эллипсоид
заданный входным эллипсоидом.
См. Раздел документации модуля для определения геоцентрической системы координат.
Параметры:
x: координаты в измерении x.
y: координаты в измерении y. z: координаты в измерении z.эллипсоид: кортеж с формой (большая полуось, эксцентриситет).
По умолчанию - 'WGS84' из: class: `ellipsoidmodels`.
Возврат:
кортеж: геодезическая высота, широта и долгота
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если эллипсоид None:
ellipsoid = ellipsoidmodels () ['WGS84']
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
lon = np.rad2deg (np.arctan2 (y, x))
B0 = np.arctan2 (z, np.hypot (x, y))
B = np.ones (B0.shape)
e2 = эллипсоид [1] ** 2
если e2 == 0.0:
h, lat, lon = cart2geocentric (x, y, z)
h - = эллипсоид [0]
еще:
while (np.any (np.abs (B - B0)> 1e-10)):
N = эллипсоид [0] / np.sqrt (1 - e2 * np.sin (B0) ** 2)
h = np.hypot (x, y) / np.cos (B0) - N
B = B0.copy ()
B0 = np.arctan (z / np.hypot (x, y) * ((1-e2 * N / (N + h)) ** (- 1)))
широта = np.
z: координаты в измерении z.эллипсоид: кортеж с формой (большая полуось, эксцентриситет).
По умолчанию - 'WGS84' из: class: `ellipsoidmodels`.
Возврат:
кортеж: геодезическая высота, широта и долгота
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если эллипсоид None:
ellipsoid = ellipsoidmodels () ['WGS84']
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
lon = np.rad2deg (np.arctan2 (y, x))
B0 = np.arctan2 (z, np.hypot (x, y))
B = np.ones (B0.shape)
e2 = эллипсоид [1] ** 2
если e2 == 0.0:
h, lat, lon = cart2geocentric (x, y, z)
h - = эллипсоид [0]
еще:
while (np.any (np.abs (B - B0)> 1e-10)):
N = эллипсоид [0] / np.sqrt (1 - e2 * np.sin (B0) ** 2)
h = np.hypot (x, y) / np.cos (B0) - N
B = B0.copy ()
B0 = np.arctan (z / np.hypot (x, y) * ((1-e2 * N / (N + h)) ** (- 1)))
широта = np. rad2deg (B)
вернуть ч, лат, долг
[docs] def geodetic2cart (h, lat, lon, ellipsoid = None):
"" "Преобразование из геодезических в геоцентрические декартовы координаты.Геодезические координаты относятся к эталонному эллипсоид
заданный входным эллипсоидом.
См. Раздел документации модуля для определения геоцентрической системы координат.
Параметры:
h: Геодезическая высота (высота над опорным эллипсоидом).
lat: Геодезическая широта.
lon: Геодезическая долгота.
эллипсоид: кортеж с формой (большая полуось, эксцентриситет).
По умолчанию - 'WGS84' из: class: `ellipsoidmodels`.
Возврат:
кортеж: координаты x, y, z... Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если эллипсоид None:
ellipsoid = ellipsoidmodels () ['WGS84']
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
а = эллипсоид [0]
e2 = эллипсоид [1] ** 2
N = a / np.
rad2deg (B)
вернуть ч, лат, долг
[docs] def geodetic2cart (h, lat, lon, ellipsoid = None):
"" "Преобразование из геодезических в геоцентрические декартовы координаты.Геодезические координаты относятся к эталонному эллипсоид
заданный входным эллипсоидом.
См. Раздел документации модуля для определения геоцентрической системы координат.
Параметры:
h: Геодезическая высота (высота над опорным эллипсоидом).
lat: Геодезическая широта.
lon: Геодезическая долгота.
эллипсоид: кортеж с формой (большая полуось, эксцентриситет).
По умолчанию - 'WGS84' из: class: `ellipsoidmodels`.
Возврат:
кортеж: координаты x, y, z... Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если эллипсоид None:
ellipsoid = ellipsoidmodels () ['WGS84']
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
а = эллипсоид [0]
e2 = эллипсоид [1] ** 2
N = a / np. sqrt (1 - e2 * sind (лат) ** 2)
x = (N + h) * (cosd (долг)) * (cosd (долг))
y = (N + h) * (cosd (lat)) * (sind (долг))
# np.ones (np.shape (lon)): Обеспечьте одинаковую форму x, y, z.z = (N * (1 - e2) + h) * (sind (лат)) * np.ones (np.shape (долг))
вернуть x, y, z
[docs] def geodetic2geocentric (h, lat, lon, ellipsoid = None, ** kwargs):
"" "Преобразование геодезических координат в геоцентрические.
Геодезические координаты относятся к эталонному эллипсоид
заданный входным эллипсоидом.
См. Раздел документации модуля для определения геоцентрической системы координат.
Параметры:
h: Геодезическая высота (высота над опорным эллипсоидом).
lat: Геодезическая широта.lon: Геодезическая долгота.
kwargs: Дополнительные аргументы ключевого слова для: func: `cart2geocentric`.
эллипсоид: кортеж с формой (большая полуось, эксцентриситет).
По умолчанию - 'WGS84' из: class: `ellipsoidmodels`.
Возврат:
кортеж: радиус, геоцентрическая широта, геоцентрическая долгота
.
sqrt (1 - e2 * sind (лат) ** 2)
x = (N + h) * (cosd (долг)) * (cosd (долг))
y = (N + h) * (cosd (lat)) * (sind (долг))
# np.ones (np.shape (lon)): Обеспечьте одинаковую форму x, y, z.z = (N * (1 - e2) + h) * (sind (лат)) * np.ones (np.shape (долг))
вернуть x, y, z
[docs] def geodetic2geocentric (h, lat, lon, ellipsoid = None, ** kwargs):
"" "Преобразование геодезических координат в геоцентрические.
Геодезические координаты относятся к эталонному эллипсоид
заданный входным эллипсоидом.
См. Раздел документации модуля для определения геоцентрической системы координат.
Параметры:
h: Геодезическая высота (высота над опорным эллипсоидом).
lat: Геодезическая широта.lon: Геодезическая долгота.
kwargs: Дополнительные аргументы ключевого слова для: func: `cart2geocentric`.
эллипсоид: кортеж с формой (большая полуось, эксцентриситет).
По умолчанию - 'WGS84' из: class: `ellipsoidmodels`.
Возврат:
кортеж: радиус, геоцентрическая широта, геоцентрическая долгота
.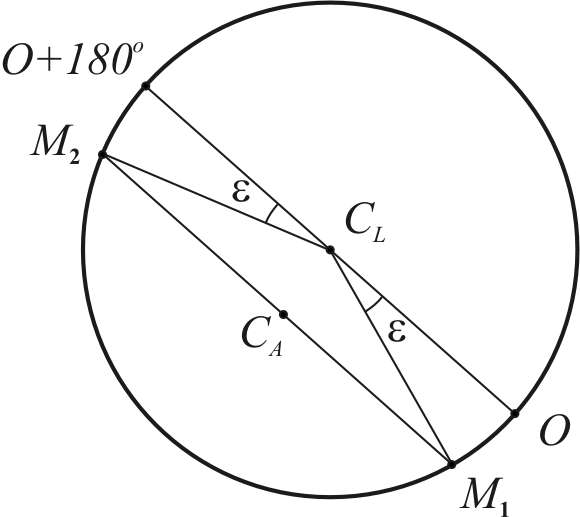 . Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если эллипсоид None:
ellipsoid = ellipsoidmodels () ['WGS84']
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
cart = geodetic2cart (ч, широта, долгота, эллипсоид)
возврат cart2geocentric (* cart, ** kwargs)
[docs] def geocentric2geodetic (r, lat, lon, ellipsoid = None):
"" "Преобразование геоцентрических координат в геодезические.
Геодезические координаты относятся к эталонному эллипсоид
заданный входным эллипсоидом.
См. Раздел документации модуля для определения геоцентрической системы координат.
Возврат:
кортеж: геодезическая высота, широта и долгота
Параметры:
r: Радиус:
lat: геоцентрическая широта.lon: геоцентрическая долгота.
эллипсоид: кортеж с формой (большая полуось, эксцентриситет).
По умолчанию - 'WGS84' из: class: `ellipsoidmodels`.
. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
если эллипсоид None:
ellipsoid = ellipsoidmodels () ['WGS84']
errtext = 'Недопустимое значение эксцентриситета в модели эллипсоида.'
inrange (эллипсоид [1], 0, 1, exclude = 'upper', text = errtext)
cart = geodetic2cart (ч, широта, долгота, эллипсоид)
возврат cart2geocentric (* cart, ** kwargs)
[docs] def geocentric2geodetic (r, lat, lon, ellipsoid = None):
"" "Преобразование геоцентрических координат в геодезические.
Геодезические координаты относятся к эталонному эллипсоид
заданный входным эллипсоидом.
См. Раздел документации модуля для определения геоцентрической системы координат.
Возврат:
кортеж: геодезическая высота, широта и долгота
Параметры:
r: Радиус:
lat: геоцентрическая широта.lon: геоцентрическая долгота.
эллипсоид: кортеж с формой (большая полуось, эксцентриситет).
По умолчанию - 'WGS84' из: class: `ellipsoidmodels`. .. Взято с https://stackoverflow.com/a/29546836/
.. Взято с https://stackoverflow.com/a/29546836/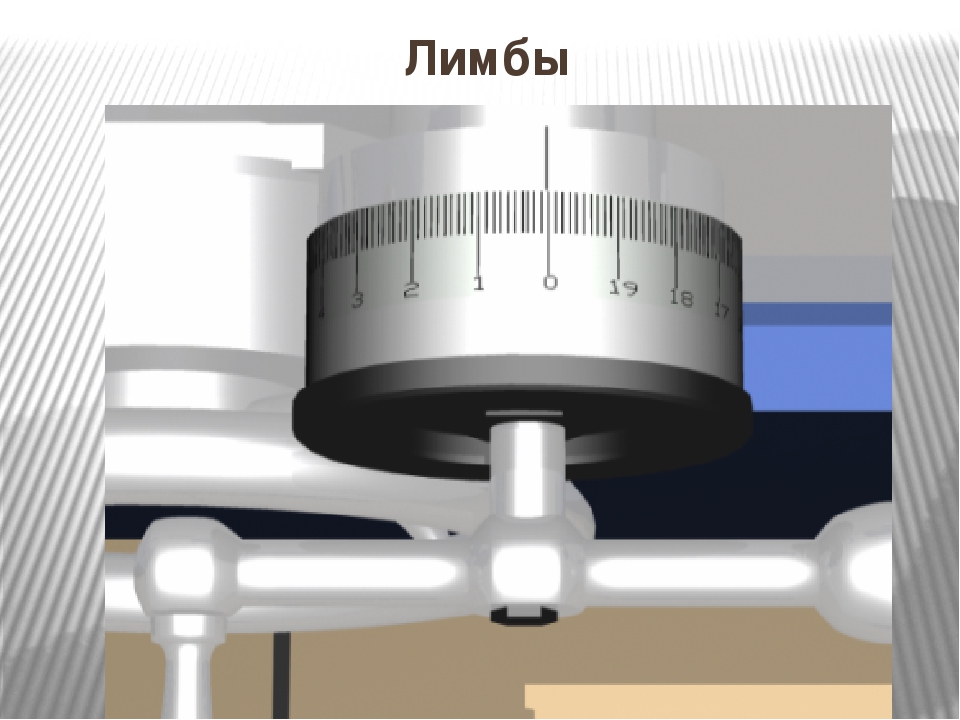 mean (x),
np.mean (y),
np.mean (z),
эллипсоид = эллипсоид)
возврат млат, млон
[docs] def cartposlos2geocentric (x, y, z, dx, dy, dz, ppc = None,
lat0 = Нет, lon0 = Нет, za0 = Нет, aa0 = Нет):
"" "Преобразование декартовых координат POS / LOS в сферические координаты.Положение задается как (x, y, z), а линия прямой видимости задается как (dx, dy, dz).
Соответствующие величины в полярных координатах: (r, lat, lon)
и (za, aa) соответственно.
См. * Содержание * для определения систем координат.
Если указаны необязательные аргументы, гарантируется, что широта и
долгота остается постоянной для случаев зенита или надира, а долгота
и азимутальный угол для случаев с севера на юг. Необязательный ввод должен интерпретироваться
поскольку [x, y, z] получается перемещением из [r0, lat0, lon0] в направлении
из [za0, aa0].Эта версия отличается от версии atmlab тем, что нормализует потери.
vector и требует все или ничего для работы необязательных аргументов.
mean (x),
np.mean (y),
np.mean (z),
эллипсоид = эллипсоид)
возврат млат, млон
[docs] def cartposlos2geocentric (x, y, z, dx, dy, dz, ppc = None,
lat0 = Нет, lon0 = Нет, za0 = Нет, aa0 = Нет):
"" "Преобразование декартовых координат POS / LOS в сферические координаты.Положение задается как (x, y, z), а линия прямой видимости задается как (dx, dy, dz).
Соответствующие величины в полярных координатах: (r, lat, lon)
и (za, aa) соответственно.
См. * Содержание * для определения систем координат.
Если указаны необязательные аргументы, гарантируется, что широта и
долгота остается постоянной для случаев зенита или надира, а долгота
и азимутальный угол для случаев с севера на юг. Необязательный ввод должен интерпретироваться
поскольку [x, y, z] получается перемещением из [r0, lat0, lon0] в направлении
из [za0, aa0].Эта версия отличается от версии atmlab тем, что нормализует потери.
vector и требует все или ничего для работы необязательных аргументов.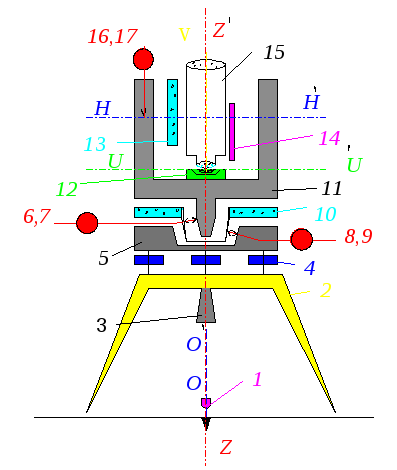 Параметры:
x: координата в измерении x.
y: Координата по оси y.
z: координата по оси z.
dx: компонент LOS в измерении x.
dy: компонент LOS в измерении y.
dz: компонент LOS в измерении z.
ppc: Константа пути распространения = r0 * sin (za0).
lat0: исходная широта.
lon0: Исходная долгота.za0: исходный зенитный угол.
aa0: Исходный азимутальный угол.
Возврат:
кортеж (ndarray): радиус, широта, долгота,
Зенитный угол, Азимутальный угол
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
# Вот драконы!
# Трансляция всех входных переменных в одну и ту же форму. По крайней мере (1)
if (ppc не равно None и za0 не равно None, а lat0 не равно None и
aa0 не равно None, а lon0 не равно None):
x, y, z, dx, dy, dz, ppc, lat0, lon0, za0, aa0 = _broadcast (
x, y, z, dx, dy, dz, ppc, lat0, lon0, za0, aa0)
elif ppc не равно None:
x, y, z, dx, dy, dz, ppc = _broadcast (x, y, z, dx, dy, dz, ppc)
еще:
x, y, z, dx, dy, dz = _broadcast (x, y, z, dx, dy, dz)
r, lat, lon = cart2geocentric (x, y, z, lat0, lon0, za0, aa0)
# Перенормировать длину переменных (не в atmlab)
norm_r = np.
Параметры:
x: координата в измерении x.
y: Координата по оси y.
z: координата по оси z.
dx: компонент LOS в измерении x.
dy: компонент LOS в измерении y.
dz: компонент LOS в измерении z.
ppc: Константа пути распространения = r0 * sin (za0).
lat0: исходная широта.
lon0: Исходная долгота.za0: исходный зенитный угол.
aa0: Исходный азимутальный угол.
Возврат:
кортеж (ndarray): радиус, широта, долгота,
Зенитный угол, Азимутальный угол
.. Портировал из атмлаба. Оригинальный автор: Бенгт Ридберг
"" "
# Вот драконы!
# Трансляция всех входных переменных в одну и ту же форму. По крайней мере (1)
if (ppc не равно None и za0 не равно None, а lat0 не равно None и
aa0 не равно None, а lon0 не равно None):
x, y, z, dx, dy, dz, ppc, lat0, lon0, za0, aa0 = _broadcast (
x, y, z, dx, dy, dz, ppc, lat0, lon0, za0, aa0)
elif ppc не равно None:
x, y, z, dx, dy, dz, ppc = _broadcast (x, y, z, dx, dy, dz, ppc)
еще:
x, y, z, dx, dy, dz = _broadcast (x, y, z, dx, dy, dz)
r, lat, lon = cart2geocentric (x, y, z, lat0, lon0, za0, aa0)
# Перенормировать длину переменных (не в atmlab)
norm_r = np.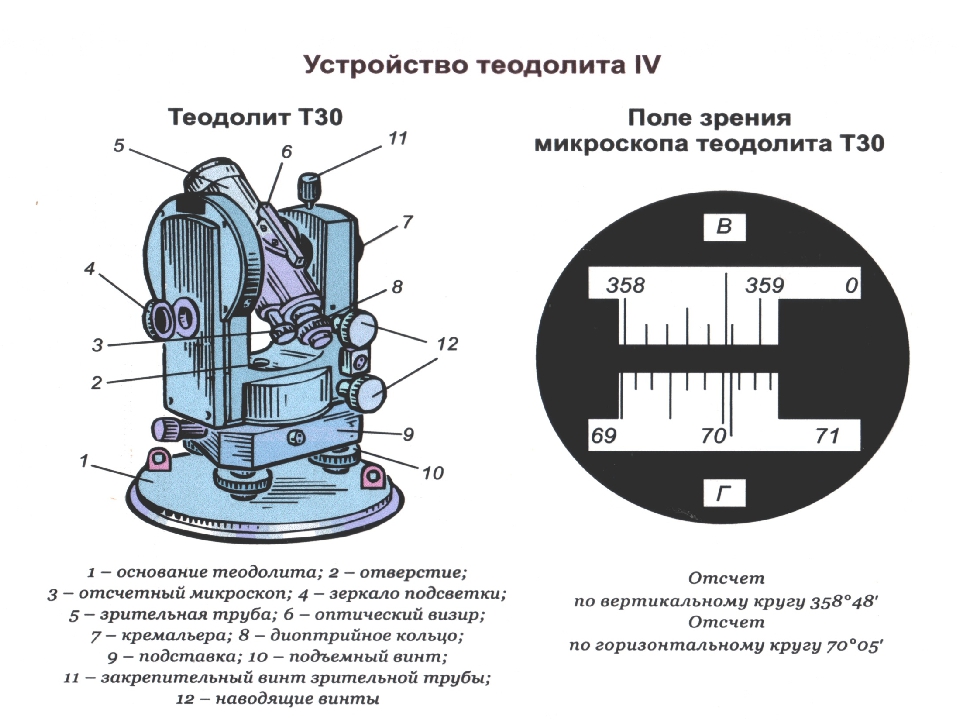 sqrt (dx ** 2 + dy ** 2 + dz ** 2)
dx = dx / norm_r
dy = dy / norm_r
dz = dz / norm_r
coslat = np.cos (np.deg2rad (широта))
sinlat = np.sin (np.deg2rad (лат))
coslon = np.cos (np.deg2rad (долг))
sinlon = np.sin (np.deg2rad (долг))
dr = np.clip (coslat * coslon * dx + sinlat * dz + coslat * sinlon * dy,
-1., 1.)
# Получить угол LOS
если ppc равно None:
za = np.rad2deg (np.arccos (dr))
еще:
za = np.rad2deg (np.arcsin (ppc / r))
aa = np.zeros (za.shape)
# Исправить зенит и азимутальный угол с дополнительным вводом, только когда все существует
если (za0 не равно None и lat0 не равно None и
aa0 не равно None, а lon0 не равно None):
# Определить тип для зенита
noz = np.логическая_ор (za0 <1e-06, za0> 180 - 1e-06)
nan = np.isnan (za)
pre = np.logical_and (~ noz, nan)
# Либо установить, либо нет
za [noz] = za0 [noz]
za [pre] = 90.
# NB: удалена проверка на dr <0, поскольку установка dr == 1 более разумна
# Определить тип по азимуту
cir1 = abs (aa0) <1e-06
cir2 = np.
sqrt (dx ** 2 + dy ** 2 + dz ** 2)
dx = dx / norm_r
dy = dy / norm_r
dz = dz / norm_r
coslat = np.cos (np.deg2rad (широта))
sinlat = np.sin (np.deg2rad (лат))
coslon = np.cos (np.deg2rad (долг))
sinlon = np.sin (np.deg2rad (долг))
dr = np.clip (coslat * coslon * dx + sinlat * dz + coslat * sinlon * dy,
-1., 1.)
# Получить угол LOS
если ppc равно None:
za = np.rad2deg (np.arccos (dr))
еще:
za = np.rad2deg (np.arcsin (ppc / r))
aa = np.zeros (za.shape)
# Исправить зенит и азимутальный угол с дополнительным вводом, только когда все существует
если (za0 не равно None и lat0 не равно None и
aa0 не равно None, а lon0 не равно None):
# Определить тип для зенита
noz = np.логическая_ор (za0 <1e-06, za0> 180 - 1e-06)
nan = np.isnan (za)
pre = np.logical_and (~ noz, nan)
# Либо установить, либо нет
za [noz] = za0 [noz]
za [pre] = 90.
# NB: удалена проверка на dr <0, поскольку установка dr == 1 более разумна
# Определить тип по азимуту
cir1 = abs (aa0) <1e-06
cir2 = np.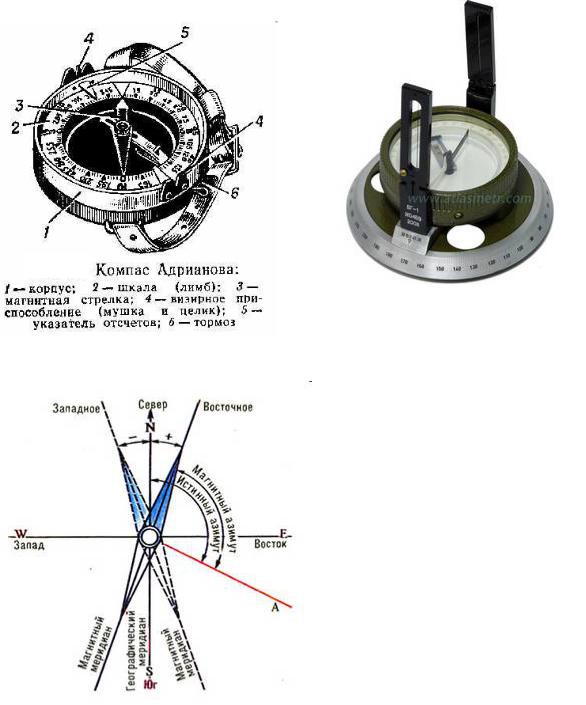 logical_or (cir1, abs (aa0 - 180) <1e-06)
то же = np.equal (lon, lon0)
circ = np.logical_and (cir2, то же самое)
left = np.логическое_и (cir1, ~ то же)
right = np.logical_and (~ cir1, ~ то же)
# Это должно установить все случаи
aa [circ] = aa0 [circ]
аа [слева] = 180.
аа [справа] = 0.
еще:
# Определить тип выполняемых расчетов
noz = np.logical_or (za <1e-06, za> 180 - 1e-06)
pol = abs (широта)> 90 - 1e-08
pre = np.logical_and (~ noz, pol)
non = np.logical_and (~ noz, ~ pol)
аа [noz] = 0.
aa [pre] = np.rad2deg (np.arctan2 (dy [pre], dx [pre]))
dlat = (- sinlat [non] * coslon [non] / r [non] * dx [non] + coslat [non] /
r [non] * dz [non] - sinlat [non] * sinlon [non] / r [non] * dy [non]
)
dlon = (- sinlon [non] / coslat [non] / r [non] * dx [non] + coslon [non] /
coslat [non] / r [non] * dy [non])
aa [non] = (np.
logical_or (cir1, abs (aa0 - 180) <1e-06)
то же = np.equal (lon, lon0)
circ = np.logical_and (cir2, то же самое)
left = np.логическое_и (cir1, ~ то же)
right = np.logical_and (~ cir1, ~ то же)
# Это должно установить все случаи
aa [circ] = aa0 [circ]
аа [слева] = 180.
аа [справа] = 0.
еще:
# Определить тип выполняемых расчетов
noz = np.logical_or (za <1e-06, za> 180 - 1e-06)
pol = abs (широта)> 90 - 1e-08
pre = np.logical_and (~ noz, pol)
non = np.logical_and (~ noz, ~ pol)
аа [noz] = 0.
aa [pre] = np.rad2deg (np.arctan2 (dy [pre], dx [pre]))
dlat = (- sinlat [non] * coslon [non] / r [non] * dx [non] + coslat [non] /
r [non] * dz [non] - sinlat [non] * sinlon [non] / r [non] * dy [non]
)
dlon = (- sinlon [non] / coslat [non] / r [non] * dx [non] + coslon [non] /
coslat [non] / r [non] * dy [non])
aa [non] = (np. rad2deg (np.arccos (r [не] *
dlat / np.sin (np.deg2rad (za [non])))))
fix = np.logical_or (np.isnan (aa), ~ np.isreal (aa))
aa [np.logical_and (fix, dlat> = 0)] = 0
aa [np.logical_and (fix, dlat <0)] = 180
aa [np.logical_and (~ fix, dlon <0)] * = -1
вернуть r, lat, lon, za, aa
[docs] def geocentricposlos2cart (r, lat, lon, za, aa):
"" "
Преобразование из сферической POS / LOS в декартовую POS / LOS
См. Раздел Содержание для определения геоцентрической системы координат.Локальные углы прямой видимости определяются по системе ВОСТОК-СЕВЕР-ВВЕРХ:
за аа
90 0 указывает на север
90 90 очков на восток
0 аа баллов вверх
FORMAT [x, y, z, dx, dy, dz] = geocentricposlos2cart (r, lat, lon, za, az)
ИЗ
Координата x в измерении x
Координата y в измерении y
Координата z по оси z
dx компонент LOS в измерении x
dy Компонент LOS в измерении y
dz LOS
В
r Радиус
широта Широта
долгота
зенитный угол
азимутальный угол
Портировано из атмлаба.
rad2deg (np.arccos (r [не] *
dlat / np.sin (np.deg2rad (za [non])))))
fix = np.logical_or (np.isnan (aa), ~ np.isreal (aa))
aa [np.logical_and (fix, dlat> = 0)] = 0
aa [np.logical_and (fix, dlat <0)] = 180
aa [np.logical_and (~ fix, dlon <0)] * = -1
вернуть r, lat, lon, za, aa
[docs] def geocentricposlos2cart (r, lat, lon, za, aa):
"" "
Преобразование из сферической POS / LOS в декартовую POS / LOS
См. Раздел Содержание для определения геоцентрической системы координат.Локальные углы прямой видимости определяются по системе ВОСТОК-СЕВЕР-ВВЕРХ:
за аа
90 0 указывает на север
90 90 очков на восток
0 аа баллов вверх
FORMAT [x, y, z, dx, dy, dz] = geocentricposlos2cart (r, lat, lon, za, az)
ИЗ
Координата x в измерении x
Координата y в измерении y
Координата z по оси z
dx компонент LOS в измерении x
dy Компонент LOS в измерении y
dz LOS
В
r Радиус
широта Широта
долгота
зенитный угол
азимутальный угол
Портировано из атмлаба.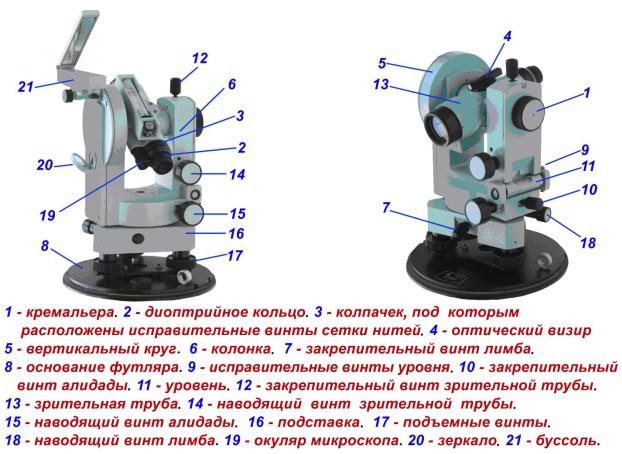 Оригинальный автор: Бенгт Ридберг 2011-10-31
"" "
r, lat, lon, za, aa = _broadcast (r, lat, lon, za, aa)
если есть (r == 0):
Raise Exception ("Эта функция не обрабатывает случай r = 0")
если есть (lat <-90) или любые (lat> 90):
Raise RuntimeError ("Широта вне допустимого диапазона")
если есть (lon <-180) или любое (lon> 180):
Raise RuntimeError («Долгота вне допустимого диапазона»)
если есть (za <0) или любое (za> 180):
Raise RuntimeError («Зенитный угол вне допустимого диапазона»)
deg2rad = np.град2рад (1)
x = np.empty (r.shape)
y = np.empty (r.shape)
z = np. пусто (r.shape)
dx = np.empty (r.shape)
dy = np.empty (r.shape)
dz = np.empty (r.shape)
at_pole = abs (широта)> (90 - 1e-8)
если есть (at_pole):
s = np.sign (широта [at_pole])
х [at_pole] = 0.
y [at_pole] = 0.
z [at_pole] = s * r [at_pole]
dz [at_pole] = s * np.cos (deg2rad * (za [at_pole]))
dx [at_pole] = np.
Оригинальный автор: Бенгт Ридберг 2011-10-31
"" "
r, lat, lon, za, aa = _broadcast (r, lat, lon, za, aa)
если есть (r == 0):
Raise Exception ("Эта функция не обрабатывает случай r = 0")
если есть (lat <-90) или любые (lat> 90):
Raise RuntimeError ("Широта вне допустимого диапазона")
если есть (lon <-180) или любое (lon> 180):
Raise RuntimeError («Долгота вне допустимого диапазона»)
если есть (za <0) или любое (za> 180):
Raise RuntimeError («Зенитный угол вне допустимого диапазона»)
deg2rad = np.град2рад (1)
x = np.empty (r.shape)
y = np.empty (r.shape)
z = np. пусто (r.shape)
dx = np.empty (r.shape)
dy = np.empty (r.shape)
dz = np.empty (r.shape)
at_pole = abs (широта)> (90 - 1e-8)
если есть (at_pole):
s = np.sign (широта [at_pole])
х [at_pole] = 0.
y [at_pole] = 0.
z [at_pole] = s * r [at_pole]
dz [at_pole] = s * np.cos (deg2rad * (za [at_pole]))
dx [at_pole] = np.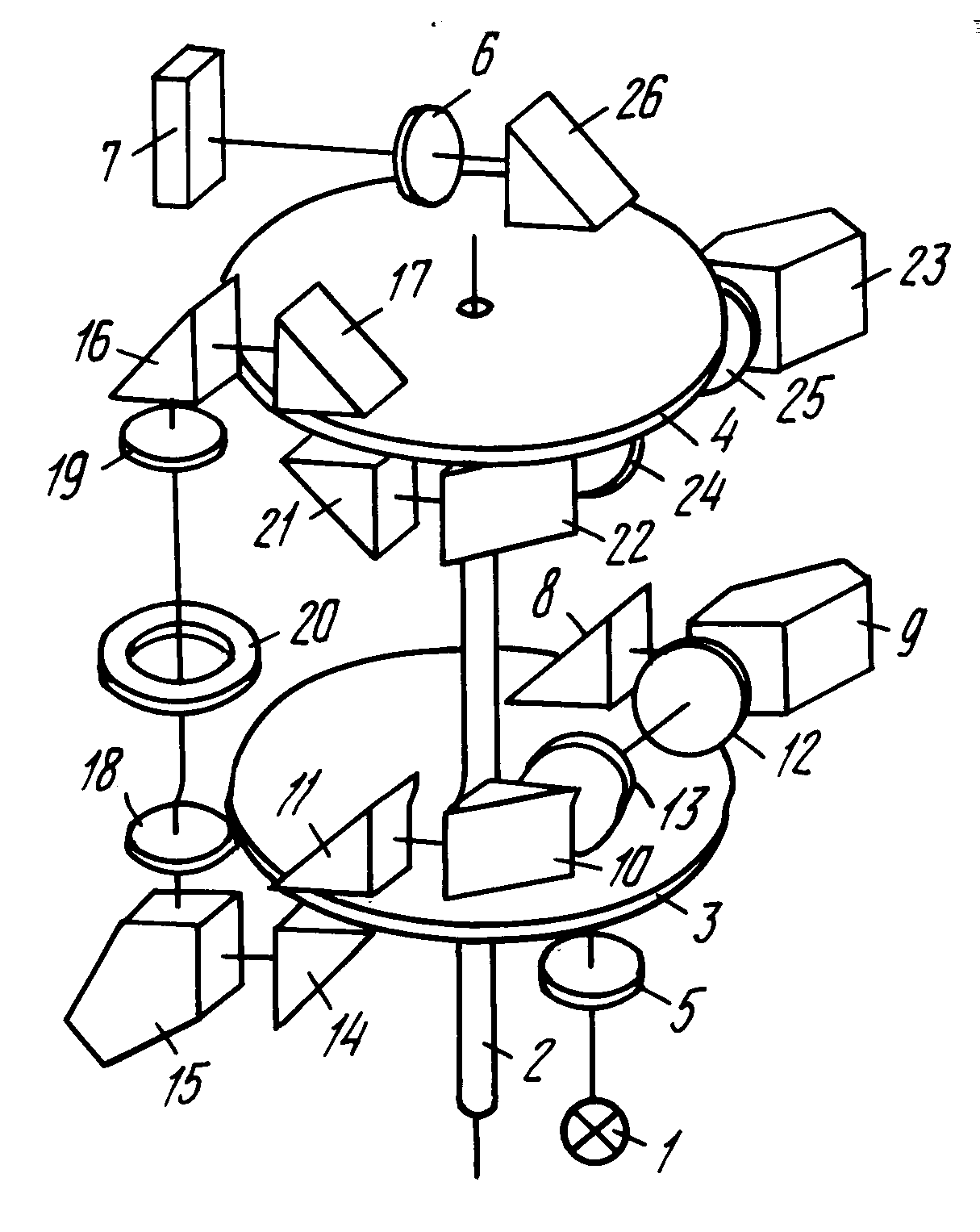 sin (deg2rad * (za))
dy [at_pole] = dx [at_pole] * np.sin (deg2rad * (aa))
dx [at_pole] * = np.cos (deg2rad * (aa))
not_pole = np.logical_not (at_pole)
если есть (not_pole):
latrad = deg2rad * lat [not_pole]
lonrad = deg2rad * lon [not_pole]
zarad = deg2rad * za [not_pole]
aarad = deg2rad * aa [not_pole]
coslat = np.cos (латрад)
sinlat = np.sin (латрад)
coslon = np.cos (лонрад)
sinlon = np.sin (лонрад)
cosza = np.cos (zarad)
sinza = np.sin (зарад)
cosaa = np.cos (aarad)
sinaa = np.sin (аарад)
x [not_pole] = r [not_pole] * coslat
y [not_pole] = x [not_pole] * sinlon
x [not_pole] * = кослон
z [not_pole] = r [not_pole] * sinlat
dr = cosza
dlat = sinza * cosaa
dlon = sinza * sinaa / coslat
dx [not_pole] = (coslat * coslon * dr - sinlat * coslon * dlat -
coslat * sinlon * dlon)
dz [not_pole] = sinlat * dr + coslat * dlat
dy [not_pole] = (coslat * sinlon * dr - sinlat * sinlon * dlat +
coslat * coslon * dlon)
вернуть x, y, z, dx, dy, dz
def get_ellipsoid_semiminor_axis (эллипсоид):
"" "Возвращает малую полуось эллипсоида.
sin (deg2rad * (za))
dy [at_pole] = dx [at_pole] * np.sin (deg2rad * (aa))
dx [at_pole] * = np.cos (deg2rad * (aa))
not_pole = np.logical_not (at_pole)
если есть (not_pole):
latrad = deg2rad * lat [not_pole]
lonrad = deg2rad * lon [not_pole]
zarad = deg2rad * za [not_pole]
aarad = deg2rad * aa [not_pole]
coslat = np.cos (латрад)
sinlat = np.sin (латрад)
coslon = np.cos (лонрад)
sinlon = np.sin (лонрад)
cosza = np.cos (zarad)
sinza = np.sin (зарад)
cosaa = np.cos (aarad)
sinaa = np.sin (аарад)
x [not_pole] = r [not_pole] * coslat
y [not_pole] = x [not_pole] * sinlon
x [not_pole] * = кослон
z [not_pole] = r [not_pole] * sinlat
dr = cosza
dlat = sinza * cosaa
dlon = sinza * sinaa / coslat
dx [not_pole] = (coslat * coslon * dr - sinlat * coslon * dlat -
coslat * sinlon * dlon)
dz [not_pole] = sinlat * dr + coslat * dlat
dy [not_pole] = (coslat * sinlon * dr - sinlat * sinlon * dlat +
coslat * coslon * dlon)
вернуть x, y, z, dx, dy, dz
def get_ellipsoid_semiminor_axis (эллипсоид):
"" "Возвращает малую полуось эллипсоида. "" "
вернуть эллипсоид [0] * np.sqrt (1.0 - эллипсоид [1] ** 2)
def line_ellipsoid_intersect (x, y, z, dx, dy, dz,
эллипсоид, высота = 0,0):
"" "Находит точки пересечения прямой с эллипсоидом
Решает относительно d:
$$ (X / a) ** 2 + (Y / a) ** 2 + (Z / b) ** 2 - 1 = 0 $$
$$ X = x + d * dx $$
$$ Y = y + d * dy $$
$$ Z = z + d * dz $$
где d - множитель sqrt (dx ** 2 + dy ** 2 + dz ** 2), a -
Большая полуось, b - малая полуось. X, Y, Z дает
точка пересечения.Если dx, dy, dz нормализованы, d - расстояние
в единицах размера эллипсоида. Если пересечения нет, код возвращает расстояние np.nan
Для действительного d точка на полпути между точками - это точка касания,
хотя он ниже эллипсоида + высота поверхности
Возврат:
d: массив параметров расстояния, последнее измерение дает 2 решения
Параметры:
x: геоцентрическая декартова координата x
y: геоцентрическая декартова координата y
z: геоцентрическая декартова координата z.
"" "
вернуть эллипсоид [0] * np.sqrt (1.0 - эллипсоид [1] ** 2)
def line_ellipsoid_intersect (x, y, z, dx, dy, dz,
эллипсоид, высота = 0,0):
"" "Находит точки пересечения прямой с эллипсоидом
Решает относительно d:
$$ (X / a) ** 2 + (Y / a) ** 2 + (Z / b) ** 2 - 1 = 0 $$
$$ X = x + d * dx $$
$$ Y = y + d * dy $$
$$ Z = z + d * dz $$
где d - множитель sqrt (dx ** 2 + dy ** 2 + dz ** 2), a -
Большая полуось, b - малая полуось. X, Y, Z дает
точка пересечения.Если dx, dy, dz нормализованы, d - расстояние
в единицах размера эллипсоида. Если пересечения нет, код возвращает расстояние np.nan
Для действительного d точка на полпути между точками - это точка касания,
хотя он ниже эллипсоида + высота поверхности
Возврат:
d: массив параметров расстояния, последнее измерение дает 2 решения
Параметры:
x: геоцентрическая декартова координата x
y: геоцентрическая декартова координата y
z: геоцентрическая декартова координата z. dx: геоцентрическое декартово представление в формате dx
dy: геоцентрическое декартово отображение
dz: геоцентрический декартово вид dz
эллипозид: модель эллипсоида [a, e]
высота: высота над эллипсоидом до точки пересечения [по умолчанию ноль]
Сделать:
Обратитесь к line_sphere_intersect, если эллипсоид является сферой
"" "
# большая полуось
a = эллипсоид [0] + высота
# малая полуось
b = get_ellipsoid_semiminor_axis (эллипсоид) + высота
# Если это скаляры, сделайте их массивами
x, y, z, dx, dy, dz = _broadcast (x, y, z, dx, dy, dz)
# A * d ** 2 + B * d + C = 0, решить относительно d
А = ((dx ** 2 + dy ** 2) / a ** 2 + dz ** 2 / b ** 2).сплющить ()
B = (2 * ((x * dx + y * dy) / a ** 2 + z * dz / b ** 2)). Flatten ()
C = ((y ** 2 + x ** 2) / a ** 2 + z ** 2 / b ** 2 - 1.0) .flatten ()
d = np.zeros ((len (A), 2))
для i в диапазоне (len (A)):
корни = np.roots ([A [i], B [i], C [i]])
если есть (np.
dx: геоцентрическое декартово представление в формате dx
dy: геоцентрическое декартово отображение
dz: геоцентрический декартово вид dz
эллипозид: модель эллипсоида [a, e]
высота: высота над эллипсоидом до точки пересечения [по умолчанию ноль]
Сделать:
Обратитесь к line_sphere_intersect, если эллипсоид является сферой
"" "
# большая полуось
a = эллипсоид [0] + высота
# малая полуось
b = get_ellipsoid_semiminor_axis (эллипсоид) + высота
# Если это скаляры, сделайте их массивами
x, y, z, dx, dy, dz = _broadcast (x, y, z, dx, dy, dz)
# A * d ** 2 + B * d + C = 0, решить относительно d
А = ((dx ** 2 + dy ** 2) / a ** 2 + dz ** 2 / b ** 2).сплющить ()
B = (2 * ((x * dx + y * dy) / a ** 2 + z * dz / b ** 2)). Flatten ()
C = ((y ** 2 + x ** 2) / a ** 2 + z ** 2 / b ** 2 - 1.0) .flatten ()
d = np.zeros ((len (A), 2))
для i в диапазоне (len (A)):
корни = np.roots ([A [i], B [i], C [i]])
если есть (np. isreal (корни)):
d [i, 0] = корни [0]
d [i, 1] = корни [1]
еще:
d [i, 0] = np.nan
d [i, 1] = np.nan
sh = []
для i в x.shape:
sh.append (я)
sh.append (2)
вернуть d.reshape (кортеж (sh))
def geometry_limb_zenith_angle (эллипсоид, r, широта, долгота,
аа = 0.0, alt = 0.0, za_acc = 1e-10):
"" "Численный метод вычисления геометрического зенитного угла лимба, зная
другие параметры спутника
Предполагает, что планета представляет собой эллипсоид, и вычисляет конечность численно
минимизация расстояния между соседними пересечениями эллипсоида.
Скорость сближения с прямым зенитным углом должна составлять 180/30 ** N,
хотя численные ошибки очень точной точности не защищены.
Параметры:
эллипсоид: эллипсоид [a, e]
r: геоцентрический радиус спутника
lat: геоцентрическая широта спутника
lon: геоцентрическая долгота спутника
aa: азимутальный угол спутника
alt: касательная высота
za_acc: точность зенитного угла.
isreal (корни)):
d [i, 0] = корни [0]
d [i, 1] = корни [1]
еще:
d [i, 0] = np.nan
d [i, 1] = np.nan
sh = []
для i в x.shape:
sh.append (я)
sh.append (2)
вернуть d.reshape (кортеж (sh))
def geometry_limb_zenith_angle (эллипсоид, r, широта, долгота,
аа = 0.0, alt = 0.0, za_acc = 1e-10):
"" "Численный метод вычисления геометрического зенитного угла лимба, зная
другие параметры спутника
Предполагает, что планета представляет собой эллипсоид, и вычисляет конечность численно
минимизация расстояния между соседними пересечениями эллипсоида.
Скорость сближения с прямым зенитным углом должна составлять 180/30 ** N,
хотя численные ошибки очень точной точности не защищены.
Параметры:
эллипсоид: эллипсоид [a, e]
r: геоцентрический радиус спутника
lat: геоцентрическая широта спутника
lon: геоцентрическая долгота спутника
aa: азимутальный угол спутника
alt: касательная высота
za_acc: точность зенитного угла. Предупреждение: бесконечный цикл, если он слишком мал
Возврат:
za: зенитный угол спутника для геометрии обзора конечностей. Форма как вход
"" "
если (za_acc == 0):
поднять RuntimeError («Точность зенита не может быть 0»)
r, lat, lon, aa, alt = _broadcast (r, lat, lon, aa, alt)
# Запомните форму, потому что мы сгладим эти массивы для упрощения цикла
sh = r.shape
r = r.flatten ()
lat = lat.flatten ()
lon = lon.flatten ()
aa = aa.flatten ()
alt = alt.flatten ()
za = np.empty_like (r)
для i в диапазоне (len (r)):
za_min = 0.0
za_max = 180,0
while True: # Пока не будет достигнута зенитная точность
# num = 31 означает 180/30 ** N - количество петель для достижения точности
zenith_angles = np.linspace (za_min, za_max, число = 31)
# Получите декартовы представления для зенитной точности зондирования
x, y, z, dx, dy, dz = geocentricposlos2cart (r [i], lat [i], lon [i],
zenith_angles, aa [i])
# Получите пересечения с эллипсоидом на касательной высоте
d = line_ellipsoid_intersect (x, y, z, dx, dy, dz,
эллипсоид, alt [i])
# Если мы каким-то образом разработали сценарий, который невозможен или плох
если нп.
Предупреждение: бесконечный цикл, если он слишком мал
Возврат:
za: зенитный угол спутника для геометрии обзора конечностей. Форма как вход
"" "
если (za_acc == 0):
поднять RuntimeError («Точность зенита не может быть 0»)
r, lat, lon, aa, alt = _broadcast (r, lat, lon, aa, alt)
# Запомните форму, потому что мы сгладим эти массивы для упрощения цикла
sh = r.shape
r = r.flatten ()
lat = lat.flatten ()
lon = lon.flatten ()
aa = aa.flatten ()
alt = alt.flatten ()
za = np.empty_like (r)
для i в диапазоне (len (r)):
za_min = 0.0
za_max = 180,0
while True: # Пока не будет достигнута зенитная точность
# num = 31 означает 180/30 ** N - количество петель для достижения точности
zenith_angles = np.linspace (za_min, za_max, число = 31)
# Получите декартовы представления для зенитной точности зондирования
x, y, z, dx, dy, dz = geocentricposlos2cart (r [i], lat [i], lon [i],
zenith_angles, aa [i])
# Получите пересечения с эллипсоидом на касательной высоте
d = line_ellipsoid_intersect (x, y, z, dx, dy, dz,
эллипсоид, alt [i])
# Если мы каким-то образом разработали сценарий, который невозможен или плох
если нп. isnan (d) .all ():
Raise RuntimeError ("Невозможно получить точку касания." +
«Все попытки упускают из виду эллипсоид».)
Элиф не np.isnan (d) .any ():
Raise RuntimeError ("Невозможно получить точку касания." +
«Внутри эллипсоида или атмосферы»).
# Зенит конечностей от минимизации расстояния между перекрестками
D = d [:, 0] - d [:, 1]
# Вот достопримечательности
эти = np.nan_to_num (D)> 0
# Обновлен первый из зенитных углов, попадающих в атмосферу.
za_max = zenith_angles [эти] [0]
# Обновлен последний зенитный угол без атмосферы
za_min = zenith_angles [np.logical_not (эти)] [- 1]
# Мы уже на месте?
если (za_max-za_min)
isnan (d) .all ():
Raise RuntimeError ("Невозможно получить точку касания." +
«Все попытки упускают из виду эллипсоид».)
Элиф не np.isnan (d) .any ():
Raise RuntimeError ("Невозможно получить точку касания." +
«Внутри эллипсоида или атмосферы»).
# Зенит конечностей от минимизации расстояния между перекрестками
D = d [:, 0] - d [:, 1]
# Вот достопримечательности
эти = np.nan_to_num (D)> 0
# Обновлен первый из зенитных углов, попадающих в атмосферу.
za_max = zenith_angles [эти] [0]
# Обновлен последний зенитный угол без атмосферы
za_min = zenith_angles [np.logical_not (эти)] [- 1]
# Мы уже на месте?
если (za_max-za_min) 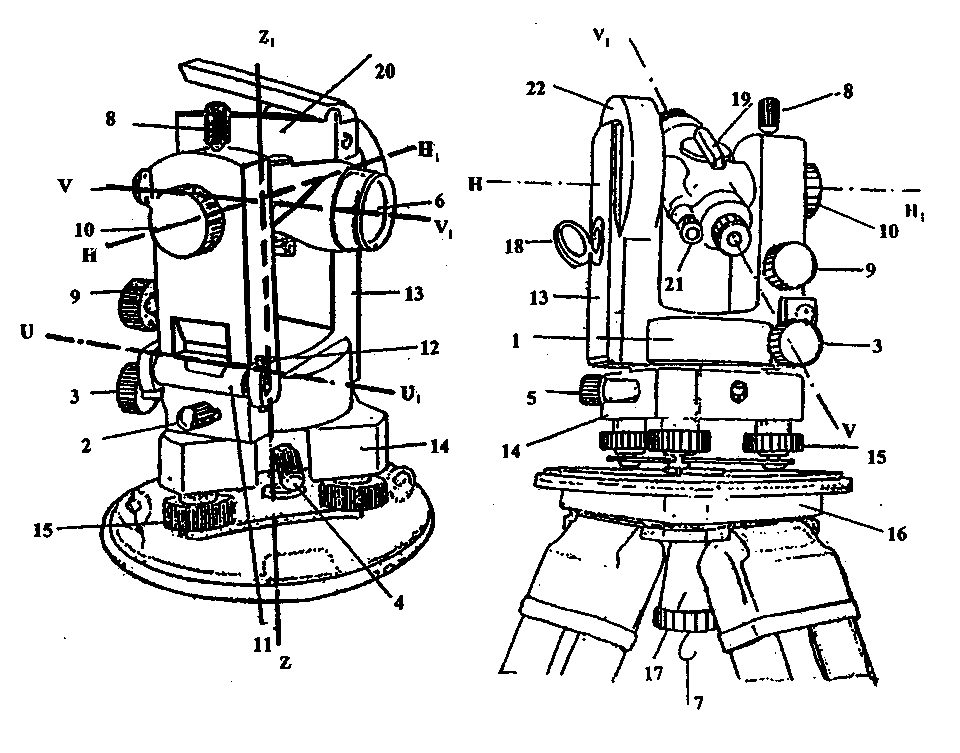 , 30.)
>>> sat = сфера_плоскость_пересечение (np.массив ([x, y, z]), 6978e3)
"" "
assert r> 0.0, "Невозможно работать со сферой нулевого радиуса"
assert len (pos.shape) == 2, "Требуется (N, 3) как pos-shape"
d = np.linalg.norm (pos, axis = 1)
assert all (d> 0.0), «Невозможно работать с 0-вектором для позиции»
число_углов = лен (тета)
number_of_positions = pos.shape [0]
points = np.empty ((число_углов, число_позиций, 3))
если number_of_angles == 0:
точки возврата
# Если сфера находится под плоскостью или по касательной к плоскости
для ii в диапазоне (число_позиций):
если d [ii]> r:
для i в диапазоне (число_углов):
точки [i, ii,:] = np.массив ([np.nan, np.nan, np.nan])
Продолжить
elif d [ii] == r:
для i в диапазоне (число_углов):
точки [i, ii,:] = pos [ii,:]
Продолжить
# Вектор плоскости (нормализованный / единичный)
n = pos [ii] / d [ii]
# Южный вектор
единицы, широта, долгота = cart2geocentric (n [0], n [1], n [2])
если (широта == 90,0):
v1 = np.
, 30.)
>>> sat = сфера_плоскость_пересечение (np.массив ([x, y, z]), 6978e3)
"" "
assert r> 0.0, "Невозможно работать со сферой нулевого радиуса"
assert len (pos.shape) == 2, "Требуется (N, 3) как pos-shape"
d = np.linalg.norm (pos, axis = 1)
assert all (d> 0.0), «Невозможно работать с 0-вектором для позиции»
число_углов = лен (тета)
number_of_positions = pos.shape [0]
points = np.empty ((число_углов, число_позиций, 3))
если number_of_angles == 0:
точки возврата
# Если сфера находится под плоскостью или по касательной к плоскости
для ii в диапазоне (число_позиций):
если d [ii]> r:
для i в диапазоне (число_углов):
точки [i, ii,:] = np.массив ([np.nan, np.nan, np.nan])
Продолжить
elif d [ii] == r:
для i в диапазоне (число_углов):
точки [i, ii,:] = pos [ii,:]
Продолжить
# Вектор плоскости (нормализованный / единичный)
n = pos [ii] / d [ii]
# Южный вектор
единицы, широта, долгота = cart2geocentric (n [0], n [1], n [2])
если (широта == 90,0):
v1 = np. array ([cosd (lon), sind (lon), 0.]) * sind (лат)
еще:
v1 = np.array ([cosd (долг) * синд (лат),
синд (долг) * синд (лат),
cosd (лат-180.0)])
# Восточный вектор
v2 = -np.cross (n, v1) # указывает на восток
# Радиус круга
rc = np.sqrt (r ** 2 - d [ii] ** 2)
для i в диапазоне (число_углов):
точки [i, ii,:] = pos [ii,:] + rc * (cosd (theta [i]) * v1 +
синд (тета [я]) * v2)
точки возврата
def tunnel_distance (lat1, lon1, lat2, lon2):
"" "Рассчитайте туннельное расстояние между двумя точками на поверхности Земли.
Аргументы:
lat1: одно число или массив чисел с широтой в градусах.lon1: одиночное число или массив numpy с долготой в градусах.
lat2: одиночное число или массив numpy с широтой в градусах.
lon2: одиночное число или массив numpy с долготой в градусах.
Возврат:
Расстояние туннеля в метрах
"" "
points1 = np.
array ([cosd (lon), sind (lon), 0.]) * sind (лат)
еще:
v1 = np.array ([cosd (долг) * синд (лат),
синд (долг) * синд (лат),
cosd (лат-180.0)])
# Восточный вектор
v2 = -np.cross (n, v1) # указывает на восток
# Радиус круга
rc = np.sqrt (r ** 2 - d [ii] ** 2)
для i в диапазоне (число_углов):
точки [i, ii,:] = pos [ii,:] + rc * (cosd (theta [i]) * v1 +
синд (тета [я]) * v2)
точки возврата
def tunnel_distance (lat1, lon1, lat2, lon2):
"" "Рассчитайте туннельное расстояние между двумя точками на поверхности Земли.
Аргументы:
lat1: одно число или массив чисел с широтой в градусах.lon1: одиночное число или массив numpy с долготой в градусах.
lat2: одиночное число или массив numpy с широтой в градусах.
lon2: одиночное число или массив numpy с долготой в градусах.
Возврат:
Расстояние туннеля в метрах
"" "
points1 = np. column_stack (
geocentric2cart (constants.earth_radius, lat1, lon1)
)
points2 = np.column_stack (
geocentric2cart (constants.earth_radius, lat2, lon2)
)
вернуть np.sqrt (np.sum ((points2 - points1) ** 2, axis = 1))
def _broadcast (* args):
"" "Аналогично broadcast_arrays в numpy, но с минимальным размером вывода (1,)
"" "
shape = np.трансляция (* args) .shape
если не форма:
shape = (1,)
return [np.broadcast_to (array, shape) for array in args]
column_stack (
geocentric2cart (constants.earth_radius, lat1, lon1)
)
points2 = np.column_stack (
geocentric2cart (constants.earth_radius, lat2, lon2)
)
вернуть np.sqrt (np.sum ((points2 - points1) ** 2, axis = 1))
def _broadcast (* args):
"" "Аналогично broadcast_arrays в numpy, но с минимальным размером вывода (1,)
"" "
shape = np.трансляция (* args) .shape
если не форма:
shape = (1,)
return [np.broadcast_to (array, shape) for array in args]