Выбор дифференциального автоматического выключателя
Дифференциальный автоматический выключатель является устройством, объединяющим функции УЗО и автоматического выключателя (по типу «два в одном»). Устройство предназначено для защиты человека от поражения электрическим током в случае прикосновения к токоведущим частям или поверхности оборудования.
Благодаря высокому быстродействию, дифференциальные автоматы обеспечивают эффективную защиту человека от поражения электрическим током в случае его прикосновения к токоведущим частям или оказавшимся под напряжением в результате повреждения изоляции нетоковедущих частей. Дифференциальный автомат срабатывает в обоих случаях — как при утечке тока на землю, так и при коротких замыканиях и перегрузке. Подобно устройствам защитного отключения, дифференциальные автоматы выпускаются рассчитанными на разный рабочий ток и на разный ток утечки. Выгодным применение такого автомата оказывается в случае, когда на установку двух отдельных устройств в электрошкафу не хватает места Часто стоимость раздельно поставляемых УЗО и автоматического выключателя ниже, чем для заменяющего их дифференциального автомата — все зависит от марки автомата.
Дифференциальный автомат выбирается исходя из расчетного тока и суммарного тока утечки. Необходимо выбирать такие дифференциальные автоматы, которые имеют максимальную коммутационную способность для групповых устройств — на уровне 6000 А, а для оконечных — не менее 3000 А. Из числа электронных дифференциальных автоматов предпочтение следует отдавать тем, которые имеют защиту от обрыва нулевого проводника — обрыв может привести к потере дифференциальными автоматами напряжения питания, что делает их неработоспособными.
Для наилучшей защиты от вышедшего из-под контроля тока целесообразно устанавливать отдельные дифференциальные выключатели на каждую ветвь потребления тока с разными характерами нагрузки. Например, для предотвращения пожара на кухне, на которой находится множество мощных электроприборов, потребуются менее чувствительные выключатели. Зато они не будут отключать электричество от каждого «броска» тока, вызванного включившимся холодильником. А для защиты выделенной линии в ванную комнату и в детскую нужно поставить самые чувствительные устройства, «чувствующие» утечку тока даже в 10 мА.
Модульная защитная аппаратура Hager
Автоматические выключатели, УЗО и дифф. автоматы Hager
автоматы Hager
Линейные защитные автоматы — для защиты кабелей и проводов
Автоматические выключатели Hager HMF на токи 80-125А
Автоматические выключатели SASSIN
Устройства защитного отключения SASSIN
Автоматы дифференциальные SASSIN серии C45L, C45N
Статьи по теме:
Советы для тех, кто строит дом
Выбор автоматического выключателя
Выбор устройства защитного отключения (УЗО)
Выбор дифференциального автомата
Проведение электромонтажных работ
Если у Вас возникли вопросы по материалу статьи или есть что добавить, пишите нам письмо на электронный адрес [email protected], сообщение на странице Обратная связь или в Книге отзывов и предложений
Внимание!
 electromirbel.ru, обязательно наличие активной ссылки, ведущей на главную страницу www.electromirbel.ru или на страницу с копируемым материалом. Гиперссылка не должна быть запрещена к индексации поисковыми системами (например, с помощью тегов noindex, nofollow и т.д.)!!!
electromirbel.ru, обязательно наличие активной ссылки, ведущей на главную страницу www.electromirbel.ru или на страницу с копируемым материалом. Гиперссылка не должна быть запрещена к индексации поисковыми системами (например, с помощью тегов noindex, nofollow и т.д.)!!!По материалам http://energy-etc.ru
Как выбрать дифференциальный автомат — как самостоятельно правильно выбрать дифференциальный автомат
Если вы занимаетесь самостоятельным монтажом электропроводки и находитесь уже на завершающей стадии этого нелегкого процесса, совершенно закономерным для вас будет вопрос: как выбрать дифференциальный автомат правильно, чтобы он выполнял все возложенные на него функции?
Монтаж электропроводки – это сложная процедура, которая требует от исполнителя большого внимания, ответственности и глубокого понимания устройства электросети. Одним из самых важных этапов здесь является правильный выбор устройства, которое будет обеспечивать защитную функцию при утечке тока или при замыкании.
В настоящее время существует два типа таких устройств: УЗО и дифференциальный автомат. Принципы их действия подобны, но первое реагирует только на разность тока.
Говоря простым языком, УЗО срабатывает только в том случае, если будут зафиксированы различные показатели тока на втором обороте. Прибор сравнивает ушедший и пришедший ток. И если эти показатели оказываются разными, то устройство отключает электричество. Недостаток УЗО заключается в ограниченном функционале и отсутствии даже намека на искусственный интеллект.
Этому устройству совершенно безразлично, что конкретно включено в электрическую сеть. Если нет утечки тока, оно будет работать исправно, несмотря на нештатную ситуацию.
Дифференциальный автомат – это более совершенный прибор, который выполняет несколько важных функций:
- защищает человека от удара током
- предотвращает утечку тока
- защищает электросеть от перепадов напряжения
Дифференциальный автомат в своем устройстве уже имеет внутреннее УЗО, поэтому его установка будет более рациональным и логичным решением.
Как правильно выбрать дифференциальный автомат
Самостоятельно выбрать такое сложное устройство, как дифференциальный автомат, не так уж легко. Для этого вы должны как минимум иметь базовое понимание принципов работы электросети, а также точно знать ее параметры.
Также опытные электрики советуют при выборе этого прибора учитывать не только напряжение внутри сети, но и мощность всех электрических приспособлений, которые предположительно будут в нее включены. Это поможет правильно выбрать дифференциальный автомат, который на протяжении долгого времени будет обеспечивать надежную защиту вашей электросети.
На современном рынке производители предлагают широкий выбор дифференциальных автоматов, которые условно делятся на четыре большие категории:
- однополюсные – имеют высокую работоспособность, до десяти тысяч срабатываний. Их особенность заключается в том, что к ним можно подключить кабель с сечением
- двухполюсные – предназначены для защиты двухпроводной сети от превышения уровня рабочего тока и теплового расцепителя.
 Отличаются высокой пропускной способностью и прочностью схемы. Характеризуется длительной работоспособностью – более десяти тысяч срабатываний, их вам хватит на много лет
Отличаются высокой пропускной способностью и прочностью схемы. Характеризуется длительной работоспособностью – более десяти тысяч срабатываний, их вам хватит на много лет - трехполюсные – трансформаторы нулевой последовательности. Срабатывают при появлении разности показаний на вторичной обмотке. Характеризуются высокой пропускной способностью и длительной работоспособностью
- четырехполюсные – предназначены для трехфазной сети. Имеют более четырех модулей и блок дифференциальной защиты
Дифференциальные автоматы различаются также степенью чувствительности к номинальному току, поэтому их условно можно разделить на две основные категории:
- устройства с низкой чувствительностью
- приборы с высокой чувствительностью
Отличаются эти две группы величиной уровня номинального тока. Для первых этот показатель больше 30 миллиампер, для вторых меньше этого уровня.
Виды дифференциальных автоматов
Дифференциальные автоматы – это технически сложные устройства, которые выполняют несколько функций одновременно.
Сегодня существует множество различных моделей дифференциальных автоматов, которые обозначаются латинскими буквами:
- А – специалисты рекомендуют устанавливать их для контроля уровня тока в электросети большой протяженности
- В – чаще всего применяются для общих сетей
- С – характеризуются высокой перезагрузочной способностью
- К – используются для контроля индивидуальных сетей
- Z – рекомендуются к установке для контроля электрической сети с большим количеством подключенных устройств
Несмотря на то, что дифференциальные автоматы имеют различный функционал и рекомендуются для использования в разных электросетях, все устройства имеют примерно одинаковую конструкцию:
- расцепитель
- пластиковый корпус
- рычаги и кнопки управления
- реле
- основной механизм
- трансформатор
По большому счету, устройства такого типа различаются габаритами и дизайнерским исполнением, но при выборе дифференциального автомата данные параметры точно не являются определяющими.![]()
Если вы сомневаетесь в собственной компетентности и не уверены, что сможете самостоятельно выбрать дифавтомат, причем сделать это правильно – обратитесь за помощью к специалистам-электрикам. Они разбираются в устройствах подобного типа и смогут посоветовать вам оптимальную модель прибора.
Как выбрать дифавтомат по мощности и току утечки
Электроприборы и электропроводка являются предметами повышенной опасности, поэтому при проектировании и монтаже этих устройств необходимо устанавливать защитные устройства, отключающие питание в аварийной ситуации. В Правилах Устройства Электроустановок предписывается наличие двух видов защиты — УЗО и автоматические выключатели (автоматы).
В некоторых случаях целесообразно объединить функции этих приборов в одном устройстве — дифференциальном автомате. Параметры этого прибора нельзя выбирать произвольно, для предотвращения ложных срабатываний и надёжной защиты необходимо знать, как выбрать дифавтомат.
От чего защищает дифференциальный автомат
Как видно из названия, это защитное устройство совмещает функции двух аппаратов — дифференциального реле и автоматического выключателя, поэтому он отключает питание сети в следующих ситуациях:
- Появление тока утечки. Это происходит при прикосновении человека к элементам, находящимся под напряжением, или нарушении изоляции между этими деталями и заземлённым корпусом электроприборов. В этом случае срабатывает дифференциальная защита, защищающая людей от поражения электрическим током.
- Перегрузка линии. Происходит при одновременном включении большого количества электроприборов и может привести к перегреву питающих кабелей, разрушению изоляции и короткому замыканию. Отключение питания производится при помощи теплового реле.
- Короткое замыкание. Приводит к сильному перегреву проводов и возгоранию в месте замыкания. Защита осуществляется максимальным расцепителем.

Как выбрать дифавтомат и определить место его установки
Расчёт параметров дифференциального автомата является задачей не менее важной, чем выбор номиналов УЗО и автоматического выключателя по-отдельности. Поэтому перед тем, как выбрать дифавтомат, необходимо определить, какие электроприборы будут подключены к этому защитному устройству, количество фаз и другие факторы.
Выбор места монтажа дифференциального автомата производится аналогично УЗО:
- В небольшой квартире достаточно всего одного защитного устройства этого типа, установленного вместо вводного автомата. Все остальные линии защищаются только обычными автоматическими выключателями.
- В частном доме может быть целесообразным установка нескольких дифавтоматов для разных линий. В первую очередь это гараж, сарай и другие надворные постройки, а так же уличное освещение.
Основным преимуществом этих приборов является меньшие габариты по сравнению с автоматом и УЗО, установленными раздельно, однако такое устройство стоит дороже, чем два отдельных аппарата, поэтому его монтаж производится для экономии места в щитке или для замены обычного модульного устройства защиты при невозможности дополнительной установки УЗО.
В этом случае автоматический выключатель демонтируется, а на его место устанавливается дифавтомат.
По каким параметрам выбирается дифавтомат
Выбор дифавтомата производится по нескольким параметрам. От этого зависит надёжность защиты и безопасность жителей дома.
1. Количество фаз
Число фаз определяется параметрами электроприборов, подключённых к данному защитному устройству. Отличить однофазные приборы от трёхфазных можно по количеству входных или выходных клемм на корпусе:
- Однофазные устройства. К этим приборам подходит и отходит по два провода — L (фаза) и N (нейтраль).
- Трёхфазные дифавтоматы. Имеют по четыре подходящих и отходящих клеммы — L1, L2, L3 и N.
| Информация! При подключении к трёхфазному аппарату электродвигателя клемму N в электромеханических УЗО можно не подключать. |
2. Номинальное напряжение
Этот параметр зависит от количества фаз — 220В в однофазной сети и 380В в трёхфазной. Фактически, все приборы предназначены для напряжения до 1кВ — в низковольтных сетях УЗО не устанавливается, а в высоковольтных цепях используются устройства защиты других типов.
Фактически, все приборы предназначены для напряжения до 1кВ — в низковольтных сетях УЗО не устанавливается, а в высоковольтных цепях используются устройства защиты других типов.
3. Номинальный ток и характеристика расцепителя
Основным параметром при подборе модели дифавтомата является номинальный ток, причём если при выборе УЗО он может быть больше тока автомата, что только увеличивает срок службы устройства, то для дифавтомата слишком большой ток уставки может привести к перегрузке питающей линии и его необходимо выбирать по тем же правилам, что и параметры автоматического выключателя — по сечению отходящих кабелей, но меньше, чем уставка вышестоящего автомата.
Поэтому перед тем, как выбрать дифавтомат по мощности необходимо определить, какие электроприборы будут подключены к этому устройству. В бытовых сетях вместо выполнения расчёта допускается использовать стандартные значения:
- цепи освещения — 10А;
- выделенные линии для стиральной или посудомоечной машины — 16А;
- линия кухонных или комнатных розеток — 25А.

Кроме мощности аппарата имеет значение токовременная характеристика расцепителя. Она обозначается прописной буквой английского алфавита, стоящей перед величиной номинального тока. Для бытовых электроприборов рекомендуется использовать защитные устройства серии «С», для защиты электродвигателей необходимо устанавливать приборы серии «D».
4. Ток утечки
Этот параметр определяет, при какой силе тока, протекающего через защитное заземление или тело человека, дифференциальный автомат отключит питание электроприборов. Смертельной величиной является 100мА, поэтому ток утечки не может быть больше этого значения.
Эта характеристика дифференциального автомата определяется ПУЭ п.7.1.79 и СП31-110-2003 п.А.4.15. Согласно этим документам уставка УЗО не может быть больше 30 мА, а для ванных комнат не более 10 мА.
Таблица выбора дифавтоматов в зависимости от сечения кабеля, тока утечки и места установки:
Информация! Уставка вводных противопожарных УЗО и дифавтоматов, в зависимости от места установки, может достигать 500 мА. Такая величина допускается, так как они защищают не электроприборы, а нижестоящие защитные устройства. Такая величина допускается, так как они защищают не электроприборы, а нижестоящие защитные устройства. |
5. Тип устройства (A или AC)
В бытовых электросетях используются два типа УЗО и дифавтоматов — A и AC, отличающихся типом тока утечки, при котором происходит отключение питания:
- AC. Срабатывает при появлении переменного тока утечки, подходит для большинства электроприборов.
- A. Кроме переменного, аппараты этого типа срабатывают при появлении постоянного пульсирующего тока. Такой ток появляется при замыкании на заземлённый корпус или прикосновении человека к электронным схемам, питающимся выпрямленным напряжением. Это блоки питания большинства электронных приборов.
Максимальную защиту обеспечивают дифференциальные автоматы типа «А», но они намного дороже устройств «АС», защитных свойств которых достаточно для большинства аварийных ситуаций и согласно ПУЭ п.7.1.78 допускается установка аппаратов обоих типов.
6. Электронное или электромеханическое дифреле (УЗО)
Перед тем, как выбрать дифавтомат для установки, необходимо определить необходимую конструкцию УЗО — электронное или электромеханическое. Оба вида имеют свои достоинства и недостатки:
- Электромеханический дифавтомат. Эти приборы не нуждаются в питании для работы, поэтому сохраняют работоспособность при обрыве нейтрали. Дешевле электронных УЗО, но в этих устройствах отсутствует возможность регулировки тока утечки.
- Электронные УЗО. Внутри этих аппаратов находится электронная схема, для питания которой необходимо напряжение и при обрыве нейтрального проводника прикосновение к фазному проводу не приведёт к срабатыванию защиты. Поэтому такие устройства необходимо устанавливать вместе с реле напряжения. Электронные дифавтоматы дороже электромеханических, но наличие регулировки позволяет использовать их в многоуровневой системе защиты.
Информация! Согласно ПУЭ п. 7.1.77 УЗО и дифференциальные автоматы должны сохранять защитные свойства в течение 5с при понижении напряжения на 50%. 7.1.77 УЗО и дифференциальные автоматы должны сохранять защитные свойства в течение 5с при понижении напряжения на 50%. |
Проверка работоспособности (кнопка ТЕСТ)
Дифференциальный автомат и УЗО являются устройствами, непосредственно защищающими жизнь человека, поэтому работоспособность этих приборов необходимо регулярно проверять. Эту операцию рекомендуется производить не реже 1 раза в месяц одним из следующих способов:
- нажатием кнопки «ТЕСТ», расположенной на передней стороне корпуса;
- присоединением батарейки к одноимённым входным и выходным клеммам;
- подключением резистора сопротивлением 6,8 кОм между клеммой L (out) и заземлением;
- специальным прибором, предназначенным для проверки и настройки УЗО.
Самым простым способом из вышеперечисленных является нажатие кнопки. В зависимости от модели она может обозначаться «ТЕСТ», «TEST» или «Т».
Её нажатие имитирует появление тока утечки и должно привести к срабатыванию защиты. Такую проверку может производить любой человек, даже без знаний основ электротехники и опыта практической работы.
Такую проверку может производить любой человек, даже без знаний основ электротехники и опыта практической работы.
| Важно! Для проверки исправности дифавтомата при помощи кнопки аппарат должен быть подключён к сети. |
Вывод
Установка дифавтоматов вместо дифреле рекомендована в ПУЭ п.7.1.76. Этим пунктом ЗАПРЕЩАЕТСЯ так же использование УЗО без автоматического выключателя.
От выбора дифавтомата зависит не только исправность электрооборудования, но и здоровье и жизнь людей, поэтому для правильного составления проекта электропроводки и монтажа защитных необходимо знать, как выбрать дифференциальный автомат.
Для этого нужно учесть различные факторы, но не менее важно установить и подключить защитное устройство с учётом всех правил монтажа и норм ПУЭ и СНиП. Поэтому при необходимости перед началом работ следует получить консультацию профессионалов.
Похожие материалы на сайте:
Понравилась статья — поделись с друзьями!
Выбор дифавтомата для домашних электросетей
Сегодня мы с вами поговорим об устройстве, в котором сосредоточился весь диапазон защиты от электрического тока в домашних условиях. Это дифференциальный автомат, в котором сосредоточены функции обычного автомата и УЗО, обеспечивающие защиту от токов перегрузки, КЗ (короткого замыкания), а также от токов утечки, что особенно важно для предотвращения поражения током человека.
Это дифференциальный автомат, в котором сосредоточены функции обычного автомата и УЗО, обеспечивающие защиту от токов перегрузки, КЗ (короткого замыкания), а также от токов утечки, что особенно важно для предотвращения поражения током человека.
Удобен такой прибор тем, что упрощает монтаж электрических сетей в доме, экономит пространство в распределительном щите.
Что же следует учесть при его выборе?
1. Фазность сети и номинальное напряжение. Трехфазной сети соответствует дифференциальный автомат на четыре полюса, куда подключаются фазы и нулевой проводник. Для однофазной сети следует приобрести дифавтомат на два полюса. В первом случае значение напряжения соответствует 380В, во втором — 220В.
Технические характеристики дифференциальных автоматов, в принципе, ничем не отличаются от характеристик УЗО и обычных автоматов. Чтобы вам было легче разобраться с ними при покупке, рассмотрим сразу их буквенное и цифровое отображение на передней панели прибора.
2. Номинальный ток нагрузки, измеряемый в амперах, который дифференциальный автомат проводит через себя длительное время. Это стандартные значения, установленные на уровне 16, 20, 25 , 32, 40, 50, 63, 80, 100А.
3. Время-токовая динамическая характеристика, которая показывает, насколько быстро срабатывает автомат при токах короткого замыкания, обозначается буквами B, C и D, ее можно увидеть перед цифрой номинального тока нагрузки на передней панели. Именно наличие этой буквы является визуальным отличием дифференциального автомата от УЗО.
Время-токовая характеристика определяет, на сколько зависит время срабатывания автомата от силы протекающего через него тока. Иными словами буквы B, C и D указывают, при каком токе электромагнитный расцепитель автомата мгновенно срабатывает. Значения: B = 3-5, C = 5-10, D = 10-20. Например, рассмотрим автоматы одинаковые по номинальному току нагрузки (16А), но с разными время-токовыми характеристиками — B16 и C16. Это означает, что у В16 диапазон тока, при котором срабатывает автомат, равен 16(3-5) = 48-80А, а у С16: 16(5-10) = 80-160А. То есть, при токе, например, 100А первый диффавтомат отключится мгновенно, второй — не сразу.
Это означает, что у В16 диапазон тока, при котором срабатывает автомат, равен 16(3-5) = 48-80А, а у С16: 16(5-10) = 80-160А. То есть, при токе, например, 100А первый диффавтомат отключится мгновенно, второй — не сразу.
Оба варианта пригодны для использования в квартирах, частных домах и административных зданиях, где особо мощные моторы не используются. Но для бытовых разводок все же чаще используют дифавтомат C, например, для розеточной цепи — С16 или С25, для освещения — C6 или C10. Для вводных квартирных или домовых расцепителей — С50, С63.
Дифавтоматы D применяют в производственных сетях, где к питанию подключены электромоторы и другие мощные механизмы с большими пусковыми токами.
Еще один способ отличить УЗО от дифференциального автомата: посмотреть схему. На схеме УЗО отсутствуют тепловой и электромагнитный расцепители, тогда как на дифавтомате они обозначены.
4. Номинальный отключающий дифференциальный ток — это характеристика принадлежит УЗО, входящего в состав автомата. Она обозначается буквой «дельта» и значением тока утечки в миллиамперах. Например, для розеток и освещения применяют дифавтоматы на 10-30 мА, для ввода — 100-300 мА.
Она обозначается буквой «дельта» и значением тока утечки в миллиамперах. Например, для розеток и освещения применяют дифавтоматы на 10-30 мА, для ввода — 100-300 мА.
5. Типы встроенного УЗО. Как известно, классификация УЗО по типам такова: тип АС — срабатывающие на переменный ток утечки, тип А — на постоянный ток устройств с электронными преобразователями (телевизоры, компьютеры, стиральные машины и так далее). Такая классификация характерна и для УЗО в дифференциальных автоматах. Отсюда следует, что свой выбор автомата для домашних сетей следует остановить на дифавтомате с УЗО типа А.
На передней панели автомата еще указывается напряжение, на которое рассчитан автомат, например, 230В, и напряжение отключения Uоткл. 265В. А также максимальный ток, при котором автомат разомкнет цепь.
Кнопка тест существует для проверки работоспособности дифавтомата, воспользуйтесь ею при установке прибора.
Если в распределительном щите мало места, вы можете воспользоваться обычными автоматами-выключателями для линий освещения и электроплиты. Но на общий вход, на кабель штепсельных розеток, а также в сетях, в составе которых есть защитный нулевой проводник PE, следует установить дифавтомат или УЗО, это является требованием ПУЭ. Защитное заземление предназначено для спасения человеческой жизни. Если оно не предусмотрено, то защита от токов утечки не является эффективной.
Но на общий вход, на кабель штепсельных розеток, а также в сетях, в составе которых есть защитный нулевой проводник PE, следует установить дифавтомат или УЗО, это является требованием ПУЭ. Защитное заземление предназначено для спасения человеческой жизни. Если оно не предусмотрено, то защита от токов утечки не является эффективной.
Как защищен дифференциальный автомат от обрыва «нуля»?
Как мы знаем, дифференциальный автомат совместил в себе простой автоматический выключатель и УЗО. Действия обычного автомата не вызывает вопросов, а вот чтобы срабатывало УЗО, то есть дифференциальная защита, нужна подача электропитания. Это происходит, если все проводники — фазный и нулевой — находятся в порядке. Если пропадает «фаза», то ток утечки не возникнет и проблем не будет, но если оборван «нулевой» провод, то «фаза» становится причиной утечки, при этом, УЗО не сработает, поскольку в сети отсутствует напряжение.
Возникает ситуация, которую желательно исключить. Для этого используется реле напряжения, которое включается в состав дифференциального автомата в виде блока защиты от обрыва «нуля». Наличие реле на схеме, которая есть на шильдике прибора, тоже является отличительной чертой дифавтомата от обычного автомата. Если приобретён дифференциальный автомат без такого блока, советую установить реле напряжения на входе для контроля.
Наличие реле на схеме, которая есть на шильдике прибора, тоже является отличительной чертой дифавтомата от обычного автомата. Если приобретён дифференциальный автомат без такого блока, советую установить реле напряжения на входе для контроля.
Производители. Дифференциальные автоматы можно приобрести, как от европейских, так и от отечественных производителей, но, при этом, придерживаться проверенных брендов, а не вестись на чрезмерно низкую стоимость.
Посудите сами, дифференциальный автомат — это устройство в доме, на котором лежит функция защиты от утечки тока, а значит, защита здоровья и жизни человека, к тому же, эта функция не ничем не дублируется.
Поэтому, такое устройство, вне всякого сомнения, должно быть качественным. В каталоге нашего интернет-магазина вы сможете познакомиться с продукцией немецких, российских и китайских производителей. Это компании AВВ, IEK, о которых я коротко расскажу, чтобы развеять ваши сомнения.
Немецкая электротехническая продукция АBB авторитетна во всём мире. В ассортименте всегда есть устройства защиты от утечки тока — автоматические дифференциальные выключатели, применяемые в быту и на промышленных предприятиях. Изделия изготавливаются из высококачественного материала с применением новых технологий. Технические характеристики всегда высоки и соответствует нормам. Отсюда с уверенностью можно сказать о надежности автоматических выключателей, которые призваны защищать человека.
В ассортименте всегда есть устройства защиты от утечки тока — автоматические дифференциальные выключатели, применяемые в быту и на промышленных предприятиях. Изделия изготавливаются из высококачественного материала с применением новых технологий. Технические характеристики всегда высоки и соответствует нормам. Отсюда с уверенностью можно сказать о надежности автоматических выключателей, которые призваны защищать человека.
Принцип модульности, который используют производители, сделает ваш выбор практичным, поскольку на DIN-рейку вы сможете установить нужное число приборов, которые можно подключить и отдельно, и в группе.
Группа IEK — это ведущие российские производители, электротехническая продукция которых в 2014 году стала лауреатом рейтинга «Марка №1» в России. Продукция долговечна, с оптимальной ценой, ее ассортимент постоянно расширяется, поэтому компании-разработчики используют производственные мощности не только России, но и других стран, в том числе Китая, где в последние десятилетия налажено самое современное производство электротехнических приборов.
Удачных вам покупок!
Ваш Кузьмич
Какой диффавтомат для квартиры выбрать?
Автор Alexey На чтение 6 мин. Просмотров 27 Опубликовано Обновлено
Для специалистов, или пользователей, уже имеющих опыт по выбору автоматов защиты и УЗО (устройств защитного отключения) выбор дифференциального автомата (дифавтомата), совмещающего эти два защитные приборы, не составляет большого труда – они разделяют на два этапа весь процесс.
дифавтомат на 220 ВольтСначала определяются с требованиями защиты электросети по параметрам, свойственным УЗО, а именно: рассчитывают ток утечки IΔn и выясняют тип тока потерь (A, AC, B, S, G). Потом вычисляют показатели предельной нагрузки сети и выясняют характер пусковых токов подключаемых устройств, для определения номинального тока In защитного автомата и его времятоковой характеристики (B, C, D).
По имеющимся параметрам выбирают соответствующий дифавтомат, согласно остальным критериям, имеющим отношение к обоим электротехническим изделиям: количество фаз, номинальное напряжение, температурный режим, предельный ток короткого замыкания (КЗ), степень защиты.
Начинающим электрикам нужно для начала коротко напомнить принцип работы УЗО и защитного автомата, – составляющих дифавтомат (выключатель дифференциального тока автоматический, АВДТ).
Выбрать по параметрам, свойственным УЗО
Принцип действия подробно описан в соответствующих разделах, коротко стоит упомянуть, что во вторичной обмотке дифференциального трансформатора (датчика утечки) создаётся электродвижущая сила, которая инициирует срабатывание электромагнитного реле задвижки отключающего механизма устройства напрямую, или с помощью дополнительного усилителя, питающегося от напряжения сети.
В этом случае нужно осознавать, что при обрыве ноля электронная система усиления не сработает. Также она уязвима при значительных колебаниях напряжения. При выборе дифавтомата нужно учитывать этот нюанс, усилитель на корпусе обозначается треугольником.
При выборе дифавтомата нужно учитывать этот нюанс, усилитель на корпусе обозначается треугольником.
Уставка
Дифференциальные трансформаторы в данных изделиях очень чувствительны и реагируют на ток, который существенно ниже опасного для человека значения в 100 мА, а весь размыкающий механизм срабатывает настолько быстро, что человек ощущает небольшой испуг и лёгкий шок, абсолютно не травматический для организма.
Дифференциальные автоматы, как и УЗО, являющиеся их частью, выпускаются с номинальными дифференциальными токами IΔn различных значений: 10 и 30 мА для защиты от поражения; 100, 300, 500мА для обеспечения пожарной безопасности силовых линий проводки. Данное обозначение IΔn и его эквивалент в миллиамперах электрики называют уставкой.
Согласно ПУЭ 7.1.83 уставку рассчитывают исходя из протяжённости линий и потребляемой нагрузки электроприборов, если IΔn не указан в их паспорте. По длине фазного провода ток утечки IΔL = 0,01мА на каждый метр его длины L. По нагрузке ток потерь IΔP = 0,4А на каждый ампер потребляемого суммарного тока IΣ электроприемников.
Суммарная утечка: IΔΣ =0,4* IΣ +0,01*L. Вышеупомянутый пункт ПУЭ требует также, чтобы IΔn дифавтомата в три раза превышал IΔΣ, то есть IΔn = 3* IΔΣ = 3*(0,4* IΣ +0,01*L). Для облегчения выбора существует таблица:
Таблица выбора тока уставки для дифавтомата и УЗОИсключением из этих правил является электропроводка на кухне, в ванной, сауне, бане – там уставка всегда должна быть 10мА.
Тип срабатывания
На корпусе дифавтомата имеется ещё один символ, унаследованный от УЗО – его тип, определяющий срабатывание при различном характере тока утечек:
- АС – переменный IΔn¬, обозначается – синусоидой, применяем для систем освещения, электронагревательных приборов, электродвигателей;
- А – переменный и постоянный пульсирующий IΔn¬. Символ: Многие производители бытовой техники указывают именно этот тип защитного устройства в паспорте своих изделий.
- В –¬ переменный и постоянный сглаженный IΔn ¬ используемый в промышленных установках;
- S – выборочность (селективность) срабатывания устройства защиты, благодаря задержке во времени 0,1-0,5 с. Применяется для обеспечения многоуровневой селективной защиты;
- G – то же, что и S, но селективность определяется меньшим временем задержки: 0,05-0,09 с.
Выбрать по параметрам автомата
Принцип действия
В случае короткого замыкания в проводке, размыкание цепи в автомате происходит благодаря воздействию тока на электромагнитный расщепитель, в котором обмотка реле притягивает якорь, механически связанный с отключающим механизмом.
При продолжительных перегрузках отключение происходит из-за нагревания превышающим номинальное значение током биметаллической пластины, которая меняя форму под воздействием тепла, давит на защёлку расщепляющего механизма.
Такое конструктивное решение даёт возможность подключения электроприборов (электродвигателей, трансформаторов, блоков питания), имеющих большие стартовые токи запуска, уменьшающиеся до нормального значение при выходе прибора на номинальный режим работы.
Номинальный ток и время-токовая характеристика
Данный параметр, указываемый на корпусах автоматов и дифавтоматов в амперах, означает тот предел нагрузки, при которой устройство не отключится. Существует понятие: «условный ток не отключения», на практике означающий, что выключатель сработает только при превышении данного тока в 1,13 раза от номинального, указанного в паспорте.
Это видно из время-токовой зависимости автоматов (зелёная линия на графике внизу), которая определяет временные рамки для периода срабатывания защиты в зависимости от степени превышения номинального тока.
Данные время-токовые характеристики обозначаются латинскими буквами обозначающими, что мгновенное расщепление произойдёт при такой кратности номинального тока:
- B: 3*In — 5*In;
- C: 5*In — 10*In;
- D: 10*In — 20*In (встречаются до 50*In).
Данные обозначения наносятся перед значением номинального тока на корпусе дифавтоматов.
Для примера ниже приведен график время токовой характеристики для самого распространённого типа С:
Две линии графика означают работу в горячем состоянии (слева) и в холодном (справа). Пунктирная линия обозначает автомат до 32А. Рассмотрим, как он сработает при двукратном превышении номинала. В горячем состоянии на отключение потребуется от десяти секунд, в холодном около 200с.
В реальности это время зависит от температуры уже работающего автомата.
При превышении номинала в три раза отключение произойдёт в течение 2 – 40с, в пять раз: 0,05 – 12с, в десять: 0,01 – 3с. При дальнейшем увеличении видно, что дифавтомат отключится менее 0,05с в любом состоянии. Исходя из данной характеристики, выбирают соответствующий параметрам дифавтомат для защиты электроустановок определённым типом запуска.
Все вышеперечисленные параметры дифавтоматов можно узнать у продавцов–консультантов, или самостоятельно прочитать их на корпусе.
Приобретая изделия авторитетных изготовителей, нужно внимательно проверять наличие паспорта, опасаясь подделок.
УЗО или дифавтомат / Статьи и обзоры / Элек.ру
Обойтись в быту без электричества, а значит и без электроприборов практически невозможно. Но чтобы лишиться благ цивилизации достаточно банального короткого замыкания. Кроме того, электротравма, полученная при утечке тока — не такая уж редкость. Решение проблемы — установка защитного оборудования: УЗО, АВДТ и автоматических выключателей. О тонкостях использования устройств защитного отключения и дифавтоматов — в материале.
Но чтобы лишиться благ цивилизации достаточно банального короткого замыкания. Кроме того, электротравма, полученная при утечке тока — не такая уж редкость. Решение проблемы — установка защитного оборудования: УЗО, АВДТ и автоматических выключателей. О тонкостях использования устройств защитного отключения и дифавтоматов — в материале.
УЗО и АВДТ
Человеку далекому от электрики сложно не только визуально отличить аппараты, но и ответить на вопрос об их назначении. Между тем, непонятные приборы призваны защищать потребителя и его имущество от негативных явлений — коротких замыканий, перегрузок и травм.
Функции и устройство УЗО
Повреждение проводки, особенно если причина этому вы сами — это реальный шанс получить от нее сдачи. Нарушитель целостности изоляции кабеля сам становится проводником для текущего в сети тока. Устройство защитного отключения разработано как раз для предотвращения таких ситуаций. Прибор обнаруживает утечку с помощью трансформатора и размыкает цепь до того, как горе-монтер пострадает.
Токоведущие части электроприборов обычно надежно скрыты от любопытных глаз и рук. Тем не менее, забраться не туда иногда проще, чем кажется. В случае случайного контакта с проводящими ток элементами, УЗО предотвратит трагедию.
Утечка тока может вовсе оставить без крыши над головой. Проводники с поврежденными защитными оболочками — распространенная причина пожаров. Устройство защитного отключения справится и с этой проблемой.
- Устройство защитного отключения (УЗО) ВД1-63 2п 25А 30мА тип A ИЭК
- Устройство защитного отключения (УЗО) Easy9 2п 25А 30мА тип AC Schneider Electric
- Устройство защитного отключения (УЗО) Fh302 2п 40А 30мА тип AC ABB
- Устройство защитного отключения (УЗО) ТX3 2п 25А 30мА тип AС Legrand
- Устройство защитного отключения (УЗО) ВД1-63 2п 25А 30мА тип AС TDM Electric
Конструкция и функции АВДТ
Автоматический выключатель дифференциального тока — прямой потомок автоматов и УЗО. Аппарат унаследовал конструктивные особенности прародителей: комплект расцепителей, дифференциальный трансформатор и дугогасительную систему.
Устройство комплектуется тепловыми и электромагнитными расцепителями. Первые реагируют на нагрев, вызванный токами перегрузок; вторые — на воздействие КЗ на магнитное поле катушки. И те, и другие отвечают за срабатывание защиты. Как и в УЗО, трансформатор дифавтомата находит утечки в сети. Дугогасительная камера предохраняет от повреждений сам АВДТ. Как видно из названия, система гасит электрическую дугу, появляющуюся от разрыва цепи, с помощью металлических пластин.
Таким образом, дифавтомат работает за двоих: выполняет функции устройства защитного отключения и автоматического выключателя. Помимо утечек, аппарат справляется с короткими замыканиями и перегрузками.
- Автоматический выключатель дифференциального тока АВДТ32 2п 16А
- Автоматический выключатель дифференциального тока Easy9 2п 25А 30мА
- Автоматический выключатель дифференциального тока RX3 1П+Н 25А
- Автоматический выключатель дифференциального тока DSH941R 1П+Н
- Автоматический выключатель дифференциального тока АВДТ 34 4п 25А
Различия дифавтомата и УЗО
- Устройство защитного отключения реагирует только на утечки.
 Для борьбы с замыканиями и перегрузками ему нужен напарник — автоматический выключатель.
Для борьбы с замыканиями и перегрузками ему нужен напарник — автоматический выключатель. - АВДТ занимает в щитке меньше места и имеет более простую схему подключения, чем пара УЗО-автоматический выключатель.
- Поскольку устройство защитного отключения лишено излишеств, свойственных АВДТ, его ремонтопригодность выше.
- При срабатывании УЗО совершенно ясно, что причиной была утечка. В аналогичной ситуации дифавтомат дает больше пищи для раздумий.
- Автоматический выключатель дифференциального тока своим существованием опровергает расхожее утверждение о том, что оптом все дешевле: универсальный аппарат обойдется дороже УЗО и выключателя.
Что касается качества исполнения, то оно больше зависит не от разновидности прибора, а от торговой марки. Добросовестные производители одинаково ответственно относятся к выпуску одиночных и комбинированных аппаратов.
Таким образом, если рассматривать УЗО как отдельный продукт, оно однозначно проигрывает АВДТ по части функционала. Однако, устройство защитного отключения с группой поддержки в виде выключателя — достойный противник для дифавтомата. В таком случае выбор будет зависеть исключительно от личных предпочтений потребителя или электрика.
Однако, устройство защитного отключения с группой поддержки в виде выключателя — достойный противник для дифавтомата. В таком случае выбор будет зависеть исключительно от личных предпочтений потребителя или электрика.
Вопрос выбора дифференциального автомата — Электромонтажные работы Минск МО РБ
Почему вопрос дифференциального автомата достиг такой популярности, что о нем стоит говорить более подробно? Прежде всего, автоматические выключатели данного типа обладают одним неоспоримым достоинством – они обеспечивают электрической линии как защиту от сверхтоков короткого замыкания и перегрузок, так и защиту от токов утечки.
Говоря другими словами, одно устройство способно обеспечить весь спектр необходимых защит, что очень удобно, т. к. способствует упрощению монтажа и экономии пространства в распределительном щите.
Итак, о достоинствах дифференциальных автоматов уже известно – осталось лишь разобраться в вопросе выбора данных устройств.
Фазность и номинальное напряжение
Аналогично любому другому аппарату защиты, выбор дифавтомата осуществляется, исходя из фазности сети. Трехфазные дифы снабжены тремя полюсами для подключения фаз и один полюс для нулевого проводника. Конструкция трехфазных устройств способствует их достаточно большим габаритам, в связи с чем, они занимают не менее 6-7 модулей. Для монтажа однофазных дифов требуется от 2-х до 4-х модулей, в зависимости от исполнения. Но, как бы то ни было, для размещения автомата потребуется значительно меньше места, по сравнению с УЗО и обычным автоматом вместе взятыми.
Что касается номинального напряжения, то ошибиться в данном случае весьма трудно: для трех фаз значение составляет 380 вольт, для одной – 220 вольт. Однако без редких неприятных исключений не обходится и номинальное напряжение аппарата лучше принимать во внимание.
Характеристика расцепителей и номинал дифавтомата
Несмотря на особенность своей конструкции, диф все же остается автоматическим выключателем, поэтому обладает собственной характеристикой, которая отображается буквой латинского алфавита, размещенной перед цифровым обозначением номинала по токовой нагрузке. Наиболее популярными автоматами для бытовых сетей считаются автоматы характеристики С.
Наиболее популярными автоматами для бытовых сетей считаются автоматы характеристики С.
Номинал по току утечки
Данное значение характеризует устройство защитного отключения, входящее в конструкцию автомата. Для обозначения номинального тока утечки используется символ Δ “дельта”, а также цифровое обозначение самого тока утечки в миллиамперах. Защиту розеточных и осветительных сетей обеспечивают, как правило, при помощи дифавтоматов с номиналом 10-30 мА.
Тип или класс интегрированного УЗО
Для профессиональных электриков давно не секрет, что существуют УЗО типа АС, способные реагировать исключительно на переменный ток у течки и УЗО типа А, которые реагируют на постоянный ток утечки в устройствах с электронными преобразователями. Речь в данном случае идет об УЗО, встроенных в дифференциальные автоматы. Из этого следует вывод, что использование УЗО типа АС, к примеру, для линий питания компьютерной техники, телевизоров и пр. будет попросту неэффективным, поэтому в данном случае более целесообразно использовать устройство типа А.
будет попросту неэффективным, поэтому в данном случае более целесообразно использовать устройство типа А.
Защита от обрыва нулевого проводника
Этот момент любопытен прежде всего тем, что работа встроенного УЗО требует электропитания блока дифференциальной защиты, которое берется как раз со ввода устройства. Другими словами, для функционирования дифзащиты сеть должна быть под напряжением.
Производитель дифференциального автомата
Несмотря на то, что отечественный рынок предлагает нам дифференциальные устройства защиты самой различной стоимости, экономия в данном случае станет не самым лучшим решением. Нередко случается даже такое, что при более подробном рассмотрении дешевый дифавтомат и автоматом-то не является, т. к. кроме механического ручного не снабжен другими видами расцепителей.
Вполне логично, что можно подобрать дифавтомат аналогичной конструкции. Однако нельзя не учитывать тот факт, что функции дифа никоим образом не дублируются, т. е. безопасность сети зависит от качества его работы.
е. безопасность сети зависит от качества его работы.
Общие указания
Конструкция каждого дифавтомата предполагает наличие кнопки “тест ” для проверки его работы посредством создания намеренной утечки тока. Выполнив установку аппарата, будет не лишним проверить его функционирование при помощи этой кнопки.
Также нельзя забывать, что далеко не каждая электрическая линия нуждается в наличии дифференциальной защиты. Наиболее распространенные случаи установки дифавтоматов – это общий ввод в противопожарных целях и кабельные линии штепсельных розеток. Что касается линий питания электрической плиты и освещения, то они, как правило, данной разновидностью защиты не снабжаются.
Аналогично УЗО, дифференциальные автоматы рекомендуют устанавливать в сетях с защитным нулевым проводником РЕ, что является требованием ПУЭ. Если защитное заземление отсутствует, то эффективность самой защиты от токов утечки значительно снижается и не всегда может обеспечить человеку достаточную защиту от поражения электрическим током.
О йота-дельта-функции: связь между клеточными автоматами и уравнениями в частных производных для моделирования адвекции – дисперсии от постоянного источника
Wolfram S (2002) Новый вид науки. Вольфрам Медиа, Шампейн, Иллинойс
Google ученый
Вольфрам С. (1988) Теория сложных систем. В: Протоколы учредительных семинаров Института Санта-Фе, Аддисон-Уэсли, Emerging Syntheses in Science, стр. 183–189
Вольфрам С (1984) Клеточные автоматы как модели сложности. Nature 311: 419–424
Статья Google ученый
Харди Дж., Помо Й., де Пацци О. (1973) Эволюция во времени двухмерной модельной системы. I. Инвариантные состояния и временные корреляционные функции. J Math Phys 14 (12): 1746–1759
MathSciNet Статья Google ученый
Succi S (2001) Решеточное уравнение Больцмана для гидродинамики и не только.Oxford Science Publications, Oxford
Google ученый
Frisch U, Hasslacher B, Pomeau Y (1986) Автоматы решеточного газа для уравнения Навье – Стокса. Phys Rev Lett 56 (14): 1505–1508
Статья Google ученый
Wolfram S (1986) Жидкости клеточного автомата I: базовая теория. J State Phys 43 (3/4): 471–526
J State Phys 43 (3/4): 471–526
MathSciNet Статья МАТЕМАТИКА Google ученый
Frisch U, d’Humières D, Hasslacher B, Lallemand P, Pomeau Y, Rivet J-P (1987) Гидродинамика решеточного газа в двух и трех измерениях. Комплексная система 1: 649–707
MathSciNet МАТЕМАТИКА Google ученый
Макнамара Г., Занетти Г. (1988) Использование уравнения Больцмана для моделирования автоматов решеточного газа. Phys Rev Lett 61: 2332–2335
Статья Google ученый
de Ozelim LCSM, de Cavalcante ALB, de Borges LPF (2013) Континуум против дискретного: физически интерпретируемое общее правило для клеточных автоматов с помощью модульной арифметики. Комплексный Syst 22 (1): 75–99
Комплексный Syst 22 (1): 75–99
MathSciNet Google ученый
Wuensche A, Lesser MJ (1992) Глобальная динамика клеточных автоматов: Атлас бассейнов полей притяжения одномерных клеточных автоматов. Исследования Института Санта-Фе по наукам о сложности, Аддисон-Уэсли, Рединг, Массачусетс, с.250
Google ученый
Chua L (2006) Перспектива нелинейной динамики нового вида науки Вольфрама, том 1. World Scientific Publishing Company, Сингапур
Google ученый
Chua L (2007) Перспектива нелинейной динамики нового вида науки Вольфрама, том 2. World Scientific Publishing Company, Сингапур
Google ученый
Чуа Л. (2009) Перспектива нелинейной динамики нового типа науки Вольфрама, том 3.World Scientific Publishing Company, Сингапур
Google ученый
Chua L (2011) Перспектива нелинейной динамики нового вида науки Вольфрама, том 4. World Scientific Publishing Company, Сингапур
Google ученый
Chua L (2012) Перспектива нелинейной динамики нового вида науки Вольфрама, том 5. World Scientific Publishing Company, Сингапур
Google ученый
Redeker M, Adamatzky A, Martínez GJ (2013) Выразительность элементарных клеточных автоматов. Int J Mod Phys C 24 (3): 1350010. DOI: 10.1142 / S0129183113500101
DOI: 10.1142 / S0129183113500101
Омохундро С. (1984) Моделирование клеточных автоматов с помощью уравнений в частных производных. Physica D 10: 128–134
MathSciNet Статья МАТЕМАТИКА Google ученый
Chopard B, Droz M (1998) Моделирование физических систем клеточными автоматами.Cambridge University Press, Коллекция Al’ea Saclay
Google ученый
Кунисима В., Нишияма А., Танака Х., Токихиро Т. (2004) Дифференциальные уравнения для создания сложных структур клеточных автоматов. J Phys Soc Jpn 73: 2033–2036
MathSciNet Статья МАТЕМАТИКА Google ученый
de Ozelim LCSM, Cavalcante ALB, de Borges LPF (2013) О функции йота-дельта: универсальность в представлении клеточных автоматов.Комплексный Syst 21 (4): 1–12
MathSciNet МАТЕМАТИКА Google ученый
LeVeque RJ (2007) Конечно-разностные методы для обыкновенных и дифференциальных уравнений в частных производных. Общество промышленной и прикладной математики (SIAM), Филадельфия, PA
Google ученый
Наджафи Х.С., Хаджинежад Х. (2008) Решение одномерной адвекции – дисперсии с реакцией с использованием некоторых конечно-разностных методов.Appl Math Sci 2 (53): 2611–2618
MathSciNet МАТЕМАТИКА Google ученый
Датта Б.Н. (1995) Численная линейная алгебра и приложения. Brooks / Cole Publishing Company, Бельмонт, Калифорния
Google ученый
% PDF-1.2
%
2609 0 объект
>
эндобдж
xref
2609 77
0000000016 00000 н.
0000001895 00000 н.
0000001998 00000 н.
0000003087 00000 н.
0000003382 00000 н.
0000003492 00000 н.
0000003861 00000 н.
0000004156 00000 п.
0000004272 00000 н.
0000005393 00000 п.
0000005517 00000 н.
0000006636 00000 н.
0000006765 00000 н.
0000007057 00000 н.
0000007081 00000 п.
0000008458 00000 п.
0000008482 00000 н.
0000009735 00000 н.
0000009759 00000 п.
0000010938 00000 п.
0000010962 00000 п.
0000012093 00000 п.
0000012117 00000 п.
0000013314 00000 п.
0000013338 00000 п.
0000014560 00000 п.
0000014681 00000 п.
0000014705 00000 п.
0000015935 00000 п.
0000016203 00000 п.
0000016496 00000 п.
0000016520 00000 н.
0000017826 00000 п. 0000017848 00000 н.
0000017870 00000 п.
0000017893 00000 п.
0000018526 00000 п.
0000018550 00000 п.
0000020046 00000 н.
0000020070 00000 н.
0000021490 00000 н.
0000021514 00000 п.
0000023887 00000 п.
0000023910 00000 п.
0000024925 00000 п.
0000024949 00000 п.
0000027201 00000 п.
0000027224 00000 н.
0000028134 00000 п.
0000028157 00000 п.
0000028798 00000 п.
0000028822 00000 п.
0000033864 00000 п.
0000033888 00000 п.
0000038908 00000 п.
0000038932 00000 п.
0000043880 00000 п.
0000043904 00000 п.
0000048731 00000 п.
0000048755 00000 п.
0000050041 00000 п.
0000050064 00000 п.
0000050632 00000 п.
0000050656 00000 п.
0000054249 00000 п.
0000054273 00000 п.
0000058345 00000 п.
0000058369 00000 п.
0000059850 00000 п.
0000059874 00000 п.
0000065021 00000 п.
0000065045 00000 п.
0000068047 00000 п.
0000068071 00000 п.
0000069971 00000 п.
0000002064 00000 н.
0000003064 00000 н.
трейлер
]
>>
startxref
0
%% EOF
2610 0 объект
>
эндобдж
2611 0 объект
>
эндобдж
2684 0 объект
>
транслировать
HT_lEfv6 ޕ + U 5HRzM͕ ۽ B (bV, س i [R ⋆! I1љ]} В ~ из
0000017848 00000 н.
0000017870 00000 п.
0000017893 00000 п.
0000018526 00000 п.
0000018550 00000 п.
0000020046 00000 н.
0000020070 00000 н.
0000021490 00000 н.
0000021514 00000 п.
0000023887 00000 п.
0000023910 00000 п.
0000024925 00000 п.
0000024949 00000 п.
0000027201 00000 п.
0000027224 00000 н.
0000028134 00000 п.
0000028157 00000 п.
0000028798 00000 п.
0000028822 00000 п.
0000033864 00000 п.
0000033888 00000 п.
0000038908 00000 п.
0000038932 00000 п.
0000043880 00000 п.
0000043904 00000 п.
0000048731 00000 п.
0000048755 00000 п.
0000050041 00000 п.
0000050064 00000 п.
0000050632 00000 п.
0000050656 00000 п.
0000054249 00000 п.
0000054273 00000 п.
0000058345 00000 п.
0000058369 00000 п.
0000059850 00000 п.
0000059874 00000 п.
0000065021 00000 п.
0000065045 00000 п.
0000068047 00000 п.
0000068071 00000 п.
0000069971 00000 п.
0000002064 00000 н.
0000003064 00000 н.
трейлер
]
>>
startxref
0
%% EOF
2610 0 объект
>
эндобдж
2611 0 объект
>
эндобдж
2684 0 объект
>
транслировать
HT_lEfv6 ޕ + U 5HRzM͕ ۽ B (bV, س i [R ⋆! I1љ]} В ~ из
Анализ и приложения (Монографии Спрингера по математике): Хаделер, Карл-Петер, Мюллер, Йоханнес: 9783319530420: Amazon.
 com: Книги «Мне понравилось читать эту книгу. Он дает ясное изложение с множеством примеров и хороших доказательств наиболее важных и общих строгих результатов клеточных автоматов в доступной для широкого круга читателей форме. Продвинутые студенты и начинающие аспиранты в нескольких областях … найдут здесь ценный набор инструментов. Книга также полезна для самостоятельного изучения и в качестве справочника, а также помогает устранить разрыв между приложениями / симуляциями и точными математическими результатами.»(Владимир Гарсиа Моралес, Mathematical Reviews, январь, 2018 г.)
com: Книги «Мне понравилось читать эту книгу. Он дает ясное изложение с множеством примеров и хороших доказательств наиболее важных и общих строгих результатов клеточных автоматов в доступной для широкого круга читателей форме. Продвинутые студенты и начинающие аспиранты в нескольких областях … найдут здесь ценный набор инструментов. Книга также полезна для самостоятельного изучения и в качестве справочника, а также помогает устранить разрыв между приложениями / симуляциями и точными математическими результатами.»(Владимир Гарсиа Моралес, Mathematical Reviews, январь, 2018 г.)« Эта книга дает исчерпывающий обзор методов анализа, применимых к этим динамическим системам. … это первая работа, которая дает исчерпывающий обзор методов, которые были предложены для получения клеточного автомата из уравнения в частных производных, и наоборот. … эта книга просто необходима исследователям в этой области ». (Ян Бетенс, zbMATH 1382.37001, 2018)
Эта книга сфокусирована на последовательном представлении основных подходов к анализу динамики клеточных автоматов. Клеточные автоматы — неизбежный инструмент математического моделирования. В отличие от классических подходов к моделированию, таких как уравнения в частных производных, клеточные автоматы легко моделировать, но трудно анализировать. В этой книге мы представляем обзор подходов и теорий, которые позволяют читателю понять поведение клеточных автоматов за пределами моделирования.
Клеточные автоматы — неизбежный инструмент математического моделирования. В отличие от классических подходов к моделированию, таких как уравнения в частных производных, клеточные автоматы легко моделировать, но трудно анализировать. В этой книге мы представляем обзор подходов и теорий, которые позволяют читателю понять поведение клеточных автоматов за пределами моделирования.
Первая часть состоит из введения клеточных автоматов на графах Кэли и их характеризации с помощью фундаментальных теорем Кутиса-Хедлунда-Линдона в контексте различных топологических концепций (топология Кантора, Безиковича и Вейля).Вторая часть посвящена результатам классификации: какая классификация следует из топологических понятий (классификация Херли), устойчивости по Ляпунову (классификация Гилмана) и теории формальных языков и грамматик (классификация Корка). Эти классификации предлагают кластеризацию клеточных автоматов, подобно классификации уравнений в частных производных в гиперболических, параболических и эллиптических уравнениях. Кульминацией этой части книги является вопрос о разрешимости свойств клеточных автоматов.Исследуются сюръективность и инъективность, а также обсуждаются основополагающие теоремы Эдемского сада.
Кульминацией этой части книги является вопрос о разрешимости свойств клеточных автоматов.Исследуются сюръективность и инъективность, а также обсуждаются основополагающие теоремы Эдемского сада.
Третья часть посвящена анализу клеточных автоматов, которые наследуют определенные свойства, часто основанные на математическом моделировании биологических, физических или химических систем. Линейность — это концепция, позволяющая определять самоподобные предельные множества. Модели движения частиц показывают, как преодолеть разрыв между клеточными автоматами и уравнениями в частных производных (модель HPP и ультрадискретный предел).Формирование паттернов связано с линейными клеточными автоматами, с моделью Бар-Яма для паттерна Тьюринга и автоматами Гринберга-Гастингса для возбудимых сред. Обсуждаются также модели песчаных куч, динамика инфекционных заболеваний и эволюция систем хищник-жертва. Математики найдут обзор теории и инструментов для анализа клеточных автоматов. В книге есть приложение, в котором представлены основные математические методы и обозначения, которые также принесут пользу физикам, химикам и биологам, интересующимся клеточными автоматами, выходящими за рамки простого моделирования.
Об авторе
Карл Петер Хаделер, доктор физ. 1965 (Гамбургский университет), диплом 1967 (Гамбургский университет). В 1963/1964 в гостях у МГУ, 1968-1969 в гостях у доцента У. Миннесоты. 1970 г. Адъюнкт-профессор технического факультета Университета Эрлангена. 1971 г. Профессор математики Университета Тюбингена. На пенсии в 2005 г., затем в 2005–2011 гг. Непостоянный профессор Университета штата Аризона. Приглашенный профессор Орхус, Неймеген, Технологический институт Джорджии, Эмори.2009 г. Профессор Джона фон Неймана, Мюнхенский технический университет. Член Центра передового опыта (DFG / German NSF). Область научных интересов: обыкновенные и дифференциальные уравнения в частных производных (уравнения реакции диффузии), уравнения с запаздыванием, теория матриц, математическая биология. С 2011 года около десяти публикаций по математике.
Иоганнес Мюллер учился в Карлсруэ и Тюбингене, где он получил абилитацию в 2001 году. После пребывания в Утрехте и Кельне он стал руководителем исследовательской группы в Институте биоматематики и биометрии в Центре Гельмгольца в Мюнхене. С 2004 года он преподает в Техническом университете Мюнхена в качестве профессора. Научные интересы Йоханнеса Мюллера находятся на стыке математики и наук о жизни. В частности, его исследования связаны с теорией динамических систем, клеточных автоматов и случайных процессов, соответственно, с их применением.
С 2004 года он преподает в Техническом университете Мюнхена в качестве профессора. Научные интересы Йоханнеса Мюллера находятся на стыке математики и наук о жизни. В частности, его исследования связаны с теорией динамических систем, клеточных автоматов и случайных процессов, соответственно, с их применением.Асинхронный адаптивный временной шаг в количественном моделировании клеточных автоматов | BMC Bioinformatics
Quantitative Cellular Automata
Celluar — это система клеточных автоматов с языком программирования Cellang [14].Программа Cellang используется всеми ячейками автомата и описывает вычисления внутри ячеек и между ними. Файл данных, который можно редактировать вручную или создать программой, определяет расположение ячеек в n-мерном массиве ячеек и начальное значение поля (я) ячеек в каждой ячейке. Файл данных используется в качестве входных данных для программы Cellang . Предопределенная переменная и время , которая увеличивается на 1 после каждого шага, обеспечивает синхронизацию для всех ячеек. Хотя предоставляются общие арифметические и логические операторы, в Cellang отсутствуют необходимые средства для числовых вычислений.
Хотя предоставляются общие арифметические и логические операторы, в Cellang отсутствуют необходимые средства для числовых вычислений.
Дискретное значение во многих случаях не является обязательным для моделирования с помощью клеточных автоматов. Используя тот факт, что программа Cellang использует файлы C в качестве промежуточных кодов, мы встроили в нее средства численных вычислений, добавив тип данных с плавающей запятой, вызовы функций (включая математические функции в библиотеке C) и другие средства количественного анализа. С помощью этих расширений численные решения ODE могут быть закодированы, а крупномасштабное параллельное решение ODE (по большому количеству ячеек) может быть реализовано простым и понятным способом.Мы построили несколько моделей с расширенной системой, включая электрофизиологическую модель всего сердца, для которой очень важен предлагаемый метод адаптивного шага по времени.
Модели сердца
Для проверки эффективности асинхронного адаптивного метода временных шагов были разработаны и протестированы две прототипные модели. Первый представляет собой однородный двумерный желудочковый лист размером 128 × 128, с клетками синоатриального узла, расположенными в одном или четырех углах, чтобы инициировать возбуждение. Второй, также с разрешением 128 × 128, представляет собой двухмерный неоднородный кардиальный лист, состоящий из клеток желудочков и предсердий, клеток атриовентрикулярных и синоатриальных узлов, а также проводящих волокон.Электрическая активность в этих клетках описывается соответствующими моделями потенциала действия типа HH [15–19]. Отметим, что двумерная модель 128 × 128 включает 16384 модели потенциала действия, т.е. 16384 системы ОДУ. Численное решение ОДУ проводится с использованием явного метода Эйлера. В обеих моделях принята стандартная окрестность Мура, т.е. каждая ячейка имеет 8 соседей. Принята простая и статическая модель щелевого перехода, которая использует разность потенциалов между двумя ячейками и сопротивление щелевого перехода для определения транс-функционального тока.Сопротивление щелевых контактов не зависит от мембранных потенциалов.
Первый представляет собой однородный двумерный желудочковый лист размером 128 × 128, с клетками синоатриального узла, расположенными в одном или четырех углах, чтобы инициировать возбуждение. Второй, также с разрешением 128 × 128, представляет собой двухмерный неоднородный кардиальный лист, состоящий из клеток желудочков и предсердий, клеток атриовентрикулярных и синоатриальных узлов, а также проводящих волокон.Электрическая активность в этих клетках описывается соответствующими моделями потенциала действия типа HH [15–19]. Отметим, что двумерная модель 128 × 128 включает 16384 модели потенциала действия, т.е. 16384 системы ОДУ. Численное решение ОДУ проводится с использованием явного метода Эйлера. В обеих моделях принята стандартная окрестность Мура, т.е. каждая ячейка имеет 8 соседей. Принята простая и статическая модель щелевого перехода, которая использует разность потенциалов между двумя ячейками и сопротивление щелевого перехода для определения транс-функционального тока.Сопротивление щелевых контактов не зависит от мембранных потенциалов.
Среди различных количественных моделей клеточных автоматов, в которых внутриклеточная активность описывается с помощью ODE, гетерогенная электрофизиологическая модель может быть лучшей для иллюстрации параллельного решения нелинейных уравнений (типа HH) и реализации асинхронных адаптивных временных шагов. В этой модели активность различных видов сердечных клеток, которые, как мы предполагаем, находятся во взаимно однозначном соответствии с клетками автомата, отображается следующим образом: Поле типа определено в программе Cellang с начальным значение, установленное в файле данных.Согласно другому значению типа , программа Cellang разделена на несколько разделов с помощью оператора if-then . Разные ячейки выполняют коды в разных разделах. Объявлен набор полей ячеек для хранения текущего значения мембранного потенциала, трансъункциональных токов и переменных стробирования. Окна создаются для отображения выбранного поля, такого как трансмембранный потенциал всех клеток (рис. 2), а также различных клеточных и канальных электрических активностей любых выбранных клеток (рис. 3).
2), а также различных клеточных и канальных электрических активностей любых выбранных клеток (рис. 3).
Асинхронный шаг адаптивного времени
Хотя существуют разные методы реализации адаптивного временного шага в биологических моделях, построенных с помощью ODE, на самом деле они имеют одну и ту же биологическую основу, т. Е. Колебания активности клетки, такие как активность клеточного цикла и электрическая активность, в которой скорость изменения ключевых переменных разная в разное время. Что мы сделали, так это реализовали метод в количественной и гетерогенной среде клеточных автоматов. Чтобы использовать количественные клеточные автоматы для моделирования системы с ОДУ в большом количестве ячеек, помимо предварительно определенного времени , которое используется для итерации интегрирования в ячейках, определяется пользовательский временной шаг плавающего типа Δ t , который автоматически используется всеми ячейками для численного решения ОДУ.Значение Δ t зависит от природы ODE. В наших двух иллюстративных моделях выбрано 0,01 мс. Δ t может изменяться во время работы. Однако для описания асинхронной клеточной активности, вызванной и связанной нормальной и аномальной связью клеток (такой как распространение возбуждения в этом случае), невозможно динамически изменять Δ t . Для фиксированного Δ t , чтобы смоделировать 1000 мс электрической активности, каждая ячейка в модели должна выполнить 100 000-кратное интегрирование.Тем не менее, есть еще один способ использовать циклическое свойство клеточной активности для сокращения вычислений при моделировании. В случае описанной здесь электрофизиологической модели интегрирование мембранного уравнения можно пропустить, когда клеточная активность не очень активна.
В наших двух иллюстративных моделях выбрано 0,01 мс. Δ t может изменяться во время работы. Однако для описания асинхронной клеточной активности, вызванной и связанной нормальной и аномальной связью клеток (такой как распространение возбуждения в этом случае), невозможно динамически изменять Δ t . Для фиксированного Δ t , чтобы смоделировать 1000 мс электрической активности, каждая ячейка в модели должна выполнить 100 000-кратное интегрирование.Тем не менее, есть еще один способ использовать циклическое свойство клеточной активности для сокращения вычислений при моделировании. В случае описанной здесь электрофизиологической модели интегрирование мембранного уравнения можно пропустить, когда клеточная активность не очень активна.
Как и в других методах [20], для моделирования желудочковых клеток мы можем использовать Ina , ионный ток натрия, чтобы отразить активность каждой желудочковой клетки. Мы используем дополнительное поле ячейки для хранения Ina . На любом этапе вычислений, если значение Ina желудочковой клетки меньше порогового значения, интегрирование всех мембранных уравнений на этом этапе можно пропустить. Основываясь на результатах, полученных при моделировании отдельной ячейки, мы можем указать набор из пороговых значений Ina , чтобы определить, сколько шагов интеграции можно безопасно пропустить в различных ситуациях. В наших примерах установлены четыре порога Ina , чтобы определить, следует ли интегрировать уравнения HH немедленно или пропустить 1, 4 или 6 раз соответственно (задается временной переменной factor , значение которой равно 1, 2, 5, 7).В то же время мы также записываем, сколько шагов было пропущено с момента последней интеграции с полем ячейки skip . Таким образом, шаг реального времени, используемый при каждом интегрировании для каждой ячейки, равен Δ t * skip .
На любом этапе вычислений, если значение Ina желудочковой клетки меньше порогового значения, интегрирование всех мембранных уравнений на этом этапе можно пропустить. Основываясь на результатах, полученных при моделировании отдельной ячейки, мы можем указать набор из пороговых значений Ina , чтобы определить, сколько шагов интеграции можно безопасно пропустить в различных ситуациях. В наших примерах установлены четыре порога Ina , чтобы определить, следует ли интегрировать уравнения HH немедленно или пропустить 1, 4 или 6 раз соответственно (задается временной переменной factor , значение которой равно 1, 2, 5, 7).В то же время мы также записываем, сколько шагов было пропущено с момента последней интеграции с полем ячейки skip . Таким образом, шаг реального времени, используемый при каждом интегрировании для каждой ячейки, равен Δ t * skip .
Отметим, однако, что статический механизм пропуска (конкретное значение Ina определяет конкретное значение фактора ) не может точно справиться с возникающей деполяризацией, которая может быть запущена как нормальными, так и аномальными трансъункциональными токами. Последняя ситуация часто возникает при различных аритмиях. Определение Ina , неизменяемый коэффициент делает окончательное Δ t * пропуск часто слишком большим, что приводит к ошибкам или даже переполнению. Следовательно, мы делаем skip динамически регулируемым следующим образом:
Последняя ситуация часто возникает при различных аритмиях. Определение Ina , неизменяемый коэффициент делает окончательное Δ t * пропуск часто слишком большим, что приводит к ошибкам или даже переполнению. Следовательно, мы делаем skip динамически регулируемым следующим образом:
- 1.
На каждом шаге сначала установите значение по умолчанию , коэффициент равным 1, что означает немедленное интегрирование;
- 2.
Считайте поле Ina , в соответствии с его значением и предустановленными порогами Ina , определите значение , коэффициент ;
- 3.
Если коэффициент <= пропустить , выполнить интегрирование и сбросить пропустить до 1;
- 4.

В противном случае пропустите интегрирование и увеличьте число пропуска на пропустить = пропустить + 1.
Таким образом, для каждой ячейки шаг реального времени, используемый в каждой интеграции, динамически корректируется во время выполнения в соответствии с интенсивностью ее активности.
Для клеток, в которых Ina не является основным направленным внутрь деполяризующим током, dvdt , скорость изменения мембранного потенциала, может быть индикатором клеточной активности.Несмотря на то, что алгоритм может быть помещен перед вычислением транс-функциональных токов, чтобы пропустить даже вычисление транс-функциональных токов, более безопасный выбор — поместить его после вычисления и использовать istim , сумму транс-функциональных токов, которая действует как стимулирующий ток для клетки, для совместно контролировать приостановку интеграции.
Метод нечеткой задержки для динамики ВИЧ с использованием клеточного автомата
Целью данного исследования является изучение эволюции CD4 + Т-лимфоцитов. инфицированы ВИЧ у ВИЧ-серопозитивных лиц, получающих антиретровирусное лечение
используя математическую модель, состоящую из системы дифференциальных уравнений с запаздыванием.Скорость инфицирования CD4 + Т-лимфоцитов является параметром, зависящим от времени.
с опозданием. Такая задержка дается нечетким числом из-за неопределенности
эффекты как фармакологической, так и внутриклеточной задержки. Клеточный автомат — это
используется для оценки параметров системы. Эффекты антиретровирусной терапии в клеточном автомате моделируются с помощью системы на основе нечетких правил с
два входа: эффективность лекарства и приверженность к лечению для трех гипотетических лиц. Для каждого из них мы определяем уровень заражения CD4 + T.
лимфоцитов, которая отличается от нуля, в отличие от других исследований, представленных в
литература.Поскольку уровень заражения считается нечетким параметром, мы определяем
нечеткие и дефаззифицированные растворы для инфицированных CD4 + Т-лимфоцитов. Мы получаем максимальные значения инфицированных клеток для лиц, получающих низкие, средние,
и высокоэффективные лекарства и адгезия лечения.
инфицированы ВИЧ у ВИЧ-серопозитивных лиц, получающих антиретровирусное лечение
используя математическую модель, состоящую из системы дифференциальных уравнений с запаздыванием.Скорость инфицирования CD4 + Т-лимфоцитов является параметром, зависящим от времени.
с опозданием. Такая задержка дается нечетким числом из-за неопределенности
эффекты как фармакологической, так и внутриклеточной задержки. Клеточный автомат — это
используется для оценки параметров системы. Эффекты антиретровирусной терапии в клеточном автомате моделируются с помощью системы на основе нечетких правил с
два входа: эффективность лекарства и приверженность к лечению для трех гипотетических лиц. Для каждого из них мы определяем уровень заражения CD4 + T.
лимфоцитов, которая отличается от нуля, в отличие от других исследований, представленных в
литература.Поскольку уровень заражения считается нечетким параметром, мы определяем
нечеткие и дефаззифицированные растворы для инфицированных CD4 + Т-лимфоцитов. Мы получаем максимальные значения инфицированных клеток для лиц, получающих низкие, средние,
и высокоэффективные лекарства и адгезия лечения. Полученные результаты представлены в
качественно соответствовать тому, что можно было бы ожидать в реальной ситуации.
Полученные результаты представлены в
качественно соответствовать тому, что можно было бы ожидать в реальной ситуации.
1. Введение
СПИД (синдром приобретенного иммунодефицита) — это инфекционное и заразное заболевание, вызываемое ВИЧ (вирусом иммунодефицита человека), которое приводит к прогрессирующей потере иммунитета инфицированных людей.Этот синдром характеризуется сигналами и симптомами, которые связаны с уменьшением количества Т-лимфоцитов в кровотоке, которые являются клетками первостепенной важности для безупречного функционирования иммунной системы человека. С тех пор, как был выявлен ВИЧ, СПИД превратился в мировую эпидемию огромных масштабов. По оценкам экспертов Организации Объединенных Наций, в 2013 году около 35 миллионов человек во всем мире были заражены ВИЧ. В странах Латинской Америки инфицировано 1,6 миллиона человек, что указывает на то, что они сталкиваются с биологической проблемой, имеющей серьезные социальные и экономические последствия [1].Вирус производит три белка, которые имеют первостепенное значение для процесса репликации: обратная транскриптаза, интеграза и протеаза. Когда вирус достигает кровотока, он атакует главным образом Т-лимфоциты. Количество Т-лимфоцитов в периферической крови имеет важное прогностическое значение для развития вирусной инфекции. Антиретровирусное лечение работает за счет ингибирования этих трех белков. Ингибиторы предотвращают заражение свободных вирусных частиц Т-лимфоцитами, задерживая репликацию вируса и позволяя организму реагировать естественным образом.Ингибирование этих трех ферментов привело к значительному улучшению терапии ВИЧ [2].
Когда вирус достигает кровотока, он атакует главным образом Т-лимфоциты. Количество Т-лимфоцитов в периферической крови имеет важное прогностическое значение для развития вирусной инфекции. Антиретровирусное лечение работает за счет ингибирования этих трех белков. Ингибиторы предотвращают заражение свободных вирусных частиц Т-лимфоцитами, задерживая репликацию вируса и позволяя организму реагировать естественным образом.Ингибирование этих трех ферментов привело к значительному улучшению терапии ВИЧ [2].
В последние десятилетия теория нечетких множеств внесла значительный вклад в математическое моделирование неопределенных явлений, например, в случае заражения ВИЧ [3–5]. Зарей и др. [6] предложили нечеткую математическую модель ВИЧ-инфекции, которая состояла из системы линейных нечетких дифференциальных уравнений, описывающих уровень иммунных клеток и вирусную нагрузку из-за присущей им нечеткости силы иммунной системы.Авторы также предложили нечеткую задачу оптимального управления, которая минимизирует как вирусную нагрузку, так и системные издержки для организма.
Детерминированные математические модели, описываемые дифференциальными уравнениями с запаздыванием, иногда более реалистичны, чем модели без запаздывания. Herz et al. [7] разработали детерминированную модель для описания поведения неинфицированных и инфицированных Т-лимфоцитов и нагрузки ВИЧ в плазме с учетом фармакологических и внутриклеточных задержек у лиц, получающих антиретровирусную терапию.Такие задержки определяются, соответственно, как промежуток времени, в течение которого лекарства достигают эффективной концентрации, и промежуток времени между инфицированием клеток и образованием новых вирусных частиц. Они также демонстрируют, что внутриклеточная задержка может влиять на величину диапазона снижения уровня ВИЧ, вызывая вариабельность или неопределенность ответа на терапию ингибиторами протеазы. Во многих случаях параметры уравнения являются неопределенными, и такие уравнения следует интерпретировать заново. Традиционно такая неопределенность обрабатывалась с помощью статистических методологий. Mittler et al. [8] предполагают, что задержка характеризуется распределением вероятностей. Принятие распределенной отсрочки дало хорошие результаты при изучении динамики ВИЧ в процессе лечения. Авторы выше предоставляют моделирование, близкое к биологической информации, предоставленной Herz et al. (1996), в которых различные фазы распада вируса после лечения антиретровирусными препаратами представлены графически.
Mittler et al. [8] предполагают, что задержка характеризуется распределением вероятностей. Принятие распределенной отсрочки дало хорошие результаты при изучении динамики ВИЧ в процессе лечения. Авторы выше предоставляют моделирование, близкое к биологической информации, предоставленной Herz et al. (1996), в которых различные фазы распада вируса после лечения антиретровирусными препаратами представлены графически.
Jafelice et al. [9], используя модель, предложенную Herz et al. [7] моделировали снижение скорости распространения вируса в зависимости от задержки начала лечения.Задержка считалась нечетким параметром; поэтому было определено нечеткое решение для уменьшения распространения вируса.
Клеточные автоматы позволяют моделировать сложные нелинейные динамические системы одновременно во времени и пространстве. Состояние каждой ячейки автомата изменяется в соответствии с ее собственным состоянием и состояниями ячеек в его окрестности. Эти состояния коррелируют между собой посредством простых правил, имитирующих биологические и физические законы, управляющие поведением системы [10]. Jafelice et al. (2009) смоделировали клеточный автомат в форме тора, в котором сосуществуют искусственно неинфицированные и инфицированные Т-лимфоциты, свободные вирусные частицы и вирус-специфические цитотоксические Т-лимфоциты (CTL), которые атакуют инфицированные клетки в организме человека, проходящего антиретровирусную терапию.
Jafelice et al. (2009) смоделировали клеточный автомат в форме тора, в котором сосуществуют искусственно неинфицированные и инфицированные Т-лимфоциты, свободные вирусные частицы и вирус-специфические цитотоксические Т-лимфоциты (CTL), которые атакуют инфицированные клетки в организме человека, проходящего антиретровирусную терапию.
Цель этого исследования — предложить модель эволюции инфицированных Т-лимфоцитов у ВИЧ-серопозитивных людей, получающих антиретровирусное лечение. С помощью клеточного автомата [11] можно получить приблизительную функцию скорости инфицирования, согласованную с динамическим поведением ВИЧ.В этой статье мы изучаем динамику ВИЧ с помощью системы дифференциальных уравнений с неопределенной задержкой у трех гипотетических индивидуумов, подвергшихся трем уровням приверженности к лечению и трем лекарственным потенциям. Параметры и значения скорости заражения для этой системы получены от клеточного автомата. Значения скорости заражения корректируются методом наименьших квадратов. После этого мы определяем численное решение нечеткой модели, рассматривая задержку как треугольное нечеткое число.Наконец, мы получаем дефаззифицированное числовое решение этой модели для каждого из трех человек. Другой аспект нашего исследования заключается в том, что мы считаем уровень заражения отличным от нуля, тогда как в модели Herz et al. (1996), установленный для упрощения, такая ставка была равна нулю. Принятие коэффициента инфицирования равным нулю означает, что антиретровирусные препараты эффективны на 100%, а такой ситуации не существует в действительности, поскольку нет окончательного контроля над СПИДом.
После этого мы определяем численное решение нечеткой модели, рассматривая задержку как треугольное нечеткое число.Наконец, мы получаем дефаззифицированное числовое решение этой модели для каждого из трех человек. Другой аспект нашего исследования заключается в том, что мы считаем уровень заражения отличным от нуля, тогда как в модели Herz et al. (1996), установленный для упрощения, такая ставка была равна нулю. Принятие коэффициента инфицирования равным нулю означает, что антиретровирусные препараты эффективны на 100%, а такой ситуации не существует в действительности, поскольку нет окончательного контроля над СПИДом.
2.Методология
2.1. Основные концепции теории нечетких множеств
Сначала мы определяем нечеткое подмножество , полученное из функции, которая называется функцией принадлежности , которая связана с нечетким множеством, где — непустое множество. Значение представляет степень принадлежности к. Классическое подмножество из представляет собой конкретное нечеткое множество, для которого функция принадлежности является характеристической функцией [12].
-срезы нечеткого множества обозначаются и определяются как,; , где опора.Нечеткое множество называется нечетким числом , когда и все -срезы непусты, все -срезы являются замкнутыми интервалами и носитель ограничен.
Во-вторых, мы напоминаем читателю, что нечеткие системы на основе правил (FRBS) — это концепция, которая играет ключевую роль в теории нечетких множеств. Они широко используются в модельных задачах, управлении и классификации [13] и могут рассматриваться как «экспертные системы» из-за их базового состава, включающего машину логического вывода и базу правил, оба находятся под непосредственным влиянием человеческих экспертных знаний [14 ].Четыре компонента составляют FBRS: процессор ввода, который выполняет фаззификацию входных данных, набор нечетких правил, называемых базами правил, машину логического вывода и процессор вывода, который выдает действительное число. После того, как базы правил типа «Если… то…» установлены, FRBS можно понимать как отображение между входом и выходом формулы, и.
В-третьих, концепция, также использованная в этой статье, — это принцип расширения Заде. Его роль заключается в получении изображений нечетких множеств с помощью классических функций.
Позвольте и быть два непустых универсальных набора и функции. Учитывая нечеткое множество, нечеткое множество с функцией принадлежности, заданной by, называется принципом расширения Заде by. Обратите внимание, что if — это классический набор.
2.2. Классические модели динамики ВИЧ
Herz et al. [7] представляют модель, которая включает антиретровирусное лечение, которое содержит три зависящие от времени переменные: популяция неинфицированных клеток, популяция инфицированных клеток, продуцирующих вирус, и вирусная нагрузка в плазме, причем все три из них умирают с соответствующей скоростью , , и .В этой модели предполагается, что неинфицированные клетки постоянно производятся человеческим организмом с постоянным притоком. Инфицированные клетки производят вирусные частицы со скоростью. Чтобы включить жизненный цикл вируса во внутриклеточную фазу модели, Herz et al. [7] предполагают временную задержку образования вируса после заражения клетки. Это означает, что привлечение вирус-продуцирующих клеток во времени определяется плотностью клеток, которые были недавно инфицированы и все еще живы. Более того, мы предположили постоянный уровень смертности инфицированных, но еще не продуцирующих вирус клеток.Вероятность выживания от времени есть только. В более общем смысле вероятность выживания задается невозрастающей функцией с. Таким образом, модель может быть записана как
Чтобы включить жизненный цикл вируса во внутриклеточную фазу модели, Herz et al. [7] предполагают временную задержку образования вируса после заражения клетки. Это означает, что привлечение вирус-продуцирующих клеток во времени определяется плотностью клеток, которые были недавно инфицированы и все еще живы. Более того, мы предположили постоянный уровень смертности инфицированных, но еще не продуцирующих вирус клеток.Вероятность выживания от времени есть только. В более общем смысле вероятность выживания задается невозрастающей функцией с. Таким образом, модель может быть записана как
. Основываясь на работе [15], мы включаем в систему (2) уравнение для CTL в качестве переменной и уровень смертности от CTL инфицированных клеток во втором уравнении следующим образом: Скорость пролиферации CTL в ответ на антиген составляет. В отсутствие моделирования CTL распадаются со скоростью. Также изучается качественное поведение частоты инфицирования ВИЧ по отношению к лимфоциту T.Переменные и параметры безразмерны, поскольку система дифференциальных уравнений с запаздыванием (3) решается численно в соответствии со значениями параметров и начальными условиями переменных, которые дополнительно описаны в разделе 3. 1.
1.
В следующем подразделе мы описываем клеточный автомат и FRBS, используемые для достижения параметров системы.
2.3. Клеточный автомат и система на основе нечетких правил
В клеточном автомате (CA), описанном Jafelice et al.[11], неинфицированные и инфицированные Т-лимфоциты, свободные вирусные частицы и вирус-специфические CTL (цитотоксические Т-лимфоциты) сосуществуют в кровотоке человека, получающего антиретровирусное лечение. КА двумерна с окрестностью Мура [16] и периодической (тороидальной) границей [17]. Ячейки движутся в восьми направлениях: север, восток, юг, запад, северо-восток, северо-запад, юго-восток и юго-запад. Изменения состояний ячеек осуществляются немедленно; поэтому обновление происходит асинхронно и произвольно.Модель CA использует выходные данные FRBS для моделирования.
Входными переменными FRBS являются приверженность лечению и эффективность (эффективность) лекарства. Следующие лингвистические значения, приписываемые переменным: очень низкое , низкое , среднее , высокое и очень высокое . Для адгезии к лечению определяется интервал, где 0 означает отсутствие, а 1 — полная адгезия. На основании [18] мы определяем интервал активности лекарства как.Выходные переменные — процент инфицированных Т-лимфоцитов и период репликации вируса. Для первого лингвистические термины очень низкий , низкий , средний , высокий и очень высокий , а для последнего очень быстрый , быстрый , средний , медленный , и очень медленный . Для процента инфицированных Т-лимфоцитов интервал равен, а для периода репликации вируса -.Нижние пределы этих двух интервалов соответствуют количеству итераций при наилучшей обработке, а верхние пределы — количеству итераций без обработки [11]. База нечетких правил построена на основе экспертных медицинских знаний (таблицы 1 и 2) с использованием метода вывода Мамдани с дефаззификацией центра тяжести [13].
Для адгезии к лечению определяется интервал, где 0 означает отсутствие, а 1 — полная адгезия. На основании [18] мы определяем интервал активности лекарства как.Выходные переменные — процент инфицированных Т-лимфоцитов и период репликации вируса. Для первого лингвистические термины очень низкий , низкий , средний , высокий и очень высокий , а для последнего очень быстрый , быстрый , средний , медленный , и очень медленный . Для процента инфицированных Т-лимфоцитов интервал равен, а для периода репликации вируса -.Нижние пределы этих двух интервалов соответствуют количеству итераций при наилучшей обработке, а верхние пределы — количеству итераций без обработки [11]. База нечетких правил построена на основе экспертных медицинских знаний (таблицы 1 и 2) с использованием метода вывода Мамдани с дефаззификацией центра тяжести [13].
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
В качестве примера в Таблице 1 первое правило следует читать следующим образом: «Если лекарство очень низкая и адгезия очень низкая, тогда процент инфицированных клеток очень высок. ”
”
На рисунке 1 изображена диаграмма используемой методологии, в которой мы представляем значения входных переменных FRBS (адгезия лечения и эффективность лекарств) и значения выходных переменных FRBS (процент инфицированных Т-лимфоцитов и период репликации вируса). Последние являются входными значениями CA. Из моделирования, выполненного в СА, определены параметры дифференциальной системы с запаздыванием (3).
На каждой итерации подсчитывается количество ВИЧ в окрестностях неинфицированных Т-лимфоцитов.Произведение этого числа на выходную переменную (процент Т-лимфоцитов) и есть количество ВИЧ-инфицированных клеток. Моделирование выполняется с использованием значений адгезии к лечению и эффективности лечения трех ВИЧ-серопозитивных гипотетических индивидуумов (таблица 3). В этой таблице параметры первой, второй и третьей колонок соответствуют серопозитивным индивидуумам, которые представлены на трех уровнях (очень низкий / низкий, средний и очень высокий) эффективности и адгезии лекарств [11].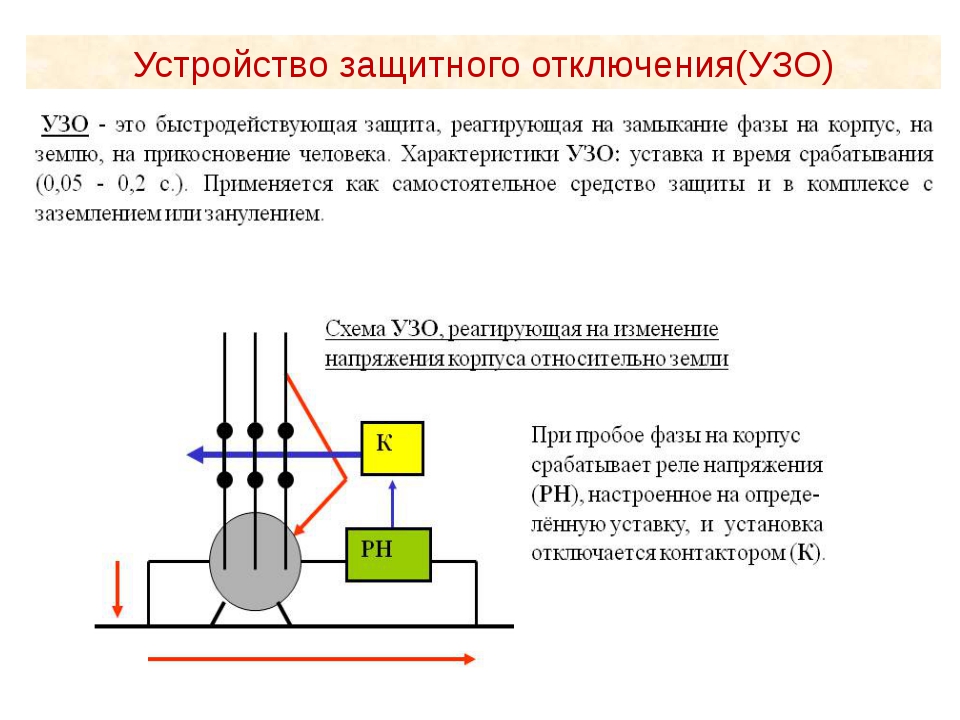 Выходные значения системы на основе нечетких правил показаны в таблице 4.Первая строка показывает процент инфицированных Т-лимфоцитов, а вторая показывает период репликации вируса для входных значений таблицы 3. Моделирование выполняется в прямоугольнике с 38 38 клетками с 101 итерацией. Выбор размера клеточной сетки определяется на основе нескольких экспериментальных прогонов СА, варьирующих количество итераций, а также начальное количество элементов (неинфицированные и инфицированные Т-лимфоциты, свободные вирусные частицы и вирусспецифические CTL) и все другие параметры CA, необходимые для моделирования.Сетка из 38 38 ячеек с 101 итерацией показала наиболее близкое согласие с качественными результатами, найденными в литературе, как в [19–21]. Модель CA выполняется для каждого человека, и результаты, полученные при моделировании в зависимости от времени, представлены на рисунке 2.
Выходные значения системы на основе нечетких правил показаны в таблице 4.Первая строка показывает процент инфицированных Т-лимфоцитов, а вторая показывает период репликации вируса для входных значений таблицы 3. Моделирование выполняется в прямоугольнике с 38 38 клетками с 101 итерацией. Выбор размера клеточной сетки определяется на основе нескольких экспериментальных прогонов СА, варьирующих количество итераций, а также начальное количество элементов (неинфицированные и инфицированные Т-лимфоциты, свободные вирусные частицы и вирусспецифические CTL) и все другие параметры CA, необходимые для моделирования.Сетка из 38 38 ячеек с 101 итерацией показала наиболее близкое согласие с качественными результатами, найденными в литературе, как в [19–21]. Модель CA выполняется для каждого человека, и результаты, полученные при моделировании в зависимости от времени, представлены на рисунке 2.
| |||||||||||||||||||||||||||||||||||||||
3.
 Результаты и обсуждение
Результаты и обсуждение3.1. Оценка и корректировка уровней инфицирования
Уровень инфицирования Т-лимфоцитов ВИЧ является важным параметром для борьбы со СПИДом у ВИЧ-серопозитивных людей; поэтому он определен для трех исследуемых лиц. Этот показатель определяется с использованием отношения количества инфицированных Т-лимфоцитов к произведению неинфицированных Т-лимфоцитов и изменения во времени () [22]; то есть
Поскольку результат достигается для каждой итерации, изменение во времени () численно считается равным 1.На рисунке 3 представлен график зависимости скорости заражения от времени для трех входных значений. Как мы видим, график является потомком, что означает, что скорость заражения Т-лимфоцитов вирусом со временем снижается. Такая нисходящая кривая ожидается, поскольку мы моделируем ситуацию, в которой человек получает лечение антиретровирусными препаратами.
Используя полученные значения (рис. 3), мы определяем три выражения, представляющие скорость заражения в зависимости от времени для трех человек. Значения шести первых итераций не принимаются во внимание, потому что они неадекватно представляют биологический процесс, который необходимо описать. После использования значений 95 итераций для каждого индивидуума корректировка кривой производится с помощью метода наименьших квадратов.
Значения шести первых итераций не принимаются во внимание, потому что они неадекватно представляют биологический процесс, который необходимо описать. После использования значений 95 итераций для каждого индивидуума корректировка кривой производится с помощью метода наименьших квадратов.
На рисунке 4 изображены скорректированные точки и графики выражения в соответствии с таблицами 3 и 4.
Выражения: (i) для первого входа (ii) для второго входа (iii) для третьего input
На рисунках 3 и 4 показано снижение частоты инфицирования Т-лимфоцитами в зависимости от времени.Коэффициенты определения () для корректировок равны, соответственно, и для (5), (6) и (7).
В следующем подразделе мы описываем другие параметры, полученные с помощью СА, чтобы найти решение модели с временной задержкой (3) для трех исследованных лиц.
3.2. Решение для дифференциального уравнения с запаздыванием Модель
Мы рассматриваем параметры системы (3), то есть скорости, где время в клеточном автомате — это количество итераций. Значения скорости: (i) — постоянный приток неинфицированных клеток, продуцируемых в организме человека, которые случайным образом помещаются на каждой итерации в CA; (ii) — уровень смертности неинфицированных клеток в виде количества итераций, установленных для гибели неинфицированных клеток, составляет 4; (iii) — это уровень смертности инфицированных клеток, поскольку количество итераций, установленных для гибели инфицированных клеток, составляет 5; (iv) — это уровень смертности инфицированных клеток из-за со связыванием CTL, поскольку связывание не обязательно является успешным; (v) — это уровень смертности от ВИЧ, поскольку количество итераций для определения смерти от ВИЧ равно 2; (vi), который представляет собой скорость воспроизводства CTL, поскольку число итераций для воспроизводства CTL составляет 14; (vii), который представляет собой уровень смертности CTL, поскольку количество итераций для гибели CTL составляет 15.Мы также получаем процент инфицированных клеток, которые еще не продуцировали вирус.
Значения скорости: (i) — постоянный приток неинфицированных клеток, продуцируемых в организме человека, которые случайным образом помещаются на каждой итерации в CA; (ii) — уровень смертности неинфицированных клеток в виде количества итераций, установленных для гибели неинфицированных клеток, составляет 4; (iii) — это уровень смертности инфицированных клеток, поскольку количество итераций, установленных для гибели инфицированных клеток, составляет 5; (iv) — это уровень смертности инфицированных клеток из-за со связыванием CTL, поскольку связывание не обязательно является успешным; (v) — это уровень смертности от ВИЧ, поскольку количество итераций для определения смерти от ВИЧ равно 2; (vi), который представляет собой скорость воспроизводства CTL, поскольку число итераций для воспроизводства CTL составляет 14; (vii), который представляет собой уровень смертности CTL, поскольку количество итераций для гибели CTL составляет 15.Мы также получаем процент инфицированных клеток, которые еще не продуцировали вирус. В CA мы подсчитали все инфицированные клетки, которые умерли, но не продуцировали вирус на каждой итерации, а затем рассчитали среднее значение (). Зависящий от времени вектор представляет воспроизводство инфицированных клеток, полученное в автомате, оцененное путем прямого подсчета числа вновь воспроизведенных инфицированных клеток на каждой итерации. Этот вектор варьируется от человека к человеку в соответствии с эффективностью лекарства и адгезией к лечению.Параметр представляет уровень заражения за предыдущий раз с задержкой, поэтому необходимо получить корректировку кривой для каждого человека. Для числового решения системы (3), представленного на рисунке 5, мы рассматриваем корректировку (6), которая представляет серопозитивного индивидуума, получающего лечение средней активности и средней адгезии лечения, задержки и скорости, определенных ранее. Начальные условия:,, и. Для получения численного решения системы использовалась программа Matlab.
В CA мы подсчитали все инфицированные клетки, которые умерли, но не продуцировали вирус на каждой итерации, а затем рассчитали среднее значение (). Зависящий от времени вектор представляет воспроизводство инфицированных клеток, полученное в автомате, оцененное путем прямого подсчета числа вновь воспроизведенных инфицированных клеток на каждой итерации. Этот вектор варьируется от человека к человеку в соответствии с эффективностью лекарства и адгезией к лечению.Параметр представляет уровень заражения за предыдущий раз с задержкой, поэтому необходимо получить корректировку кривой для каждого человека. Для числового решения системы (3), представленного на рисунке 5, мы рассматриваем корректировку (6), которая представляет серопозитивного индивидуума, получающего лечение средней активности и средней адгезии лечения, задержки и скорости, определенных ранее. Начальные условия:,, и. Для получения численного решения системы использовалась программа Matlab.
Мы использовали подпрограмму Matlab dde23, которая отслеживает неоднородности и интегрируется с явным методом Рунге-Кутта, где ошибка дается для каждого шага и в целом и интерполянт ode23. Он использует итерацию, чтобы сделать шаги длиннее, чем задержки. ode23 также является реализацией явного метода Рунге-Кутта.
Он использует итерацию, чтобы сделать шаги длиннее, чем задержки. ode23 также является реализацией явного метода Рунге-Кутта.
На рисунке 5 мы наблюдаем, что по прошествии времени неинфицированные клетки и CTL увеличиваются до постоянного числа, а вирусная нагрузка и инфицированные клетки резко снижаются.Это основная цель любой терапии с использованием антиретровирусной терапии, то есть увеличение количества Т-лимфоцитов и снижение вирусной нагрузки.
3.3. Решение для нечетких дифференциальных уравнений с задержкой. Модель
. Мы рассматриваем как фармакологические, так и внутриклеточные задержки как уникальный неопределенный параметр. Mittler et al. (1998) рассматривают распределение задержки как гамма-распределение вероятностей, которое может имитировать множество биологически возможных задержек. В настоящей статье задержка характеризуется распределением возможностей, которое математически моделируется с помощью нечеткого числа.Мы рассматриваем задержку как нечеткое число, как показано на рисунке 6, используя интервал в качестве поддержки. Этот интервал выбран на основании [7], в котором экспериментально неточен и принимает значения 0,08 дня (примерно 2 часа), 0,5 дня (12 часов) и 1 день (24 часа). Мы используем принцип расширения Заде, чтобы получить решение нелинейной системы с нечеткой задержкой (3). В системе (3) задержка появляется только в уравнении инфицированных клеток. В каждый момент этот принцип применяется к численному решению уравнения зараженных клеток с запаздыванием.
Этот интервал выбран на основании [7], в котором экспериментально неточен и принимает значения 0,08 дня (примерно 2 часа), 0,5 дня (12 часов) и 1 день (24 часа). Мы используем принцип расширения Заде, чтобы получить решение нелинейной системы с нечеткой задержкой (3). В системе (3) задержка появляется только в уравнении инфицированных клеток. В каждый момент этот принцип применяется к численному решению уравнения зараженных клеток с запаздыванием.
На рисунке 7 представлено решение уравнения инфицированных клеток. Другие решения уравнений для системы (3) с нечеткой задержкой демонстрируют поведение, подобное решениям с постоянной задержкой, то есть нечеткие, как на рисунке 5. Мы видим, что в центральной области графа зараженных ячеек степень членства близка к 1; то есть чем он темнее, тем меньше градус. Этот регион является лучшим для представления биологических явлений с точки зрения достоверности.
Чтобы представить эволюцию инфицированных клеток в этой модели с помощью детерминированной кривой, график на рисунке 7 должен быть дефаззифицирован. На рисунке 8 представлено дефаззифицированное решение для инфицированных клеток, которое оказывается средним нечетким решением [4].
На рисунке 8 представлено дефаззифицированное решение для инфицированных клеток, которое оказывается средним нечетким решением [4].
Разница между классической детерминированной моделью и нечеткой моделью состоит в том, что в первой неопределенности исключаются вначале, в то время как во второй неопределенности развиваются во времени, а дефаззификация происходит в интересующий момент.Метод центра тяжести используется для дефаззификации в каждый момент, как описано в [9]. На рисунке 9 показаны дефаззифицированные решения для трех ВИЧ-серопозитивных индивидов.
С дефаззифицированным раствором мы получаем максимальные значения инфицированных клеток для гипотетических индивидуумов, которые получали лекарства низкой, средней и высокой активности и адгезию лечения, соответственно, 44,9514, 44,0362 и 0,3523. Эти результаты качественно соответствуют тому, что можно было бы ожидать, поскольку у лиц, получивших самое слабое лечение, наблюдается наибольшее количество инфицированных клеток, даже больше, чем у лиц, получивших лучшее лечение.
Это исследование, хотя и носит вычислительный характер, может сотрудничать для лучшего понимания динамики ВИЧ в качестве дополнения к таким биологическим методам, как распространение ВИЧ, двух- и трехмерные системы культивирования клеток, методы визуализации для визуализации распространения ВИЧ и другие, как указано по Fackler et al. (2014) [23].
4. Заключение
Клеточный автомат имел первостепенное значение для определения скорости инфицирования Т-лимфоцитов () ВИЧ, а также других параметров, необходимых для решения системы дифференциальных уравнений с задержкой.Поведение ВИЧ и неинфицированных Т-лимфоцитов согласуется с соответствующим поведением, описанным в [19–21]. В целом, частота инфицирования Т-лимфоцитами является параметром, который медицинская наука сталкивается с трудностями. Более того, с медицинской точки зрения, может быть важно позволить неопределенности эволюционировать во времени, чтобы можно было найти ответы на эти биологические вопросы. При использовании модели нечеткой задержки мы представляем подход к оценке уровней инфицирования Т-лимфоцитами, который включает возможные неопределенности, присущие такой важной проблеме здоровья.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов в отношении публикации этой статьи.
Благодарность
Первый и третий авторы выражают признательность CNPq, Бразильскому национальному исследовательскому совету, за финансовую поддержку (процесс 477918 / 2010-7 и процесс 305862 / 2013-8, соответственно).
Растущие нейронные клеточные автоматы
Содержание
Эта статья является частью Тема для дифференцируемых самоорганизующихся систем, экспериментальный формат сбора приглашенных коротких статей, углубляющихся в дифференцируемые самоорганизующиеся системы с вкраплениями критических комментарии нескольких экспертов в смежных областях.
Тема для дифференцируемых самоорганизующихся систем Самоклассифицирующиеся цифры MNIST Большинство многоклеточных организмов начинают свою жизнь как отдельная яйцеклетка —
одиночная клетка, потомство которой надежно самоорганизуется в очень сложные
анатомии с множеством органов и тканей в одном и том же расположении
каждый раз. Способность строить собственное тело, наверное, самая
фундаментальный навык, которым обладает каждое живое существо. Морфогенез (
процесс формирования формы организма) является одним из самых ярких
Примеры феномена под названием самоорганизация .Клетки, крошечные
строительные блоки тел, общаются со своими соседями, чтобы решить
форма органов и планы тела, где выращивать каждый орган, как
соединить их, и когда в конце концов остановиться. Понимание взаимодействия
возникновения сложных исходов из простых правил и
гомеостатический
Саморегулирующиеся петли обратной связи, пытающиеся поддерживать тело в стабильном состоянии
или сохранить свою правильную морфологию при внешнем
возмущения
петли обратной связи — активная область исследований
.Что ясно
в том, что эволюция научилась использовать законы физики и вычислений
внедрить высоконадежное морфогенетическое программное обеспечение, работающее на
кодируемое геномом клеточное оборудование.
Способность строить собственное тело, наверное, самая
фундаментальный навык, которым обладает каждое живое существо. Морфогенез (
процесс формирования формы организма) является одним из самых ярких
Примеры феномена под названием самоорганизация .Клетки, крошечные
строительные блоки тел, общаются со своими соседями, чтобы решить
форма органов и планы тела, где выращивать каждый орган, как
соединить их, и когда в конце концов остановиться. Понимание взаимодействия
возникновения сложных исходов из простых правил и
гомеостатический
Саморегулирующиеся петли обратной связи, пытающиеся поддерживать тело в стабильном состоянии
или сохранить свою правильную морфологию при внешнем
возмущения
петли обратной связи — активная область исследований
.Что ясно
в том, что эволюция научилась использовать законы физики и вычислений
внедрить высоконадежное морфогенетическое программное обеспечение, работающее на
кодируемое геномом клеточное оборудование.
Этот процесс чрезвычайно устойчив к возмущениям. Даже когда организм полностью развитые, некоторые виды все еще могут восстанавливать повреждения — процесс, известный как регенерация. Некоторые существа, например саламандры, могут полностью регенерировать жизненно важные органы, конечности, глаза или даже части мозга! Морфогенез — удивительно адаптивный процесс.Иногда даже очень атипичный процесс развития может привести к появлению жизнеспособного организма — например, когда зародыш раннего млекопитающего разрезать пополам, каждая половина сформирует полный особи — однояйцевые близнецы!
Самая большая загадка в этой области — это вопрос о том, как клеточный коллектив
знает, что построить и когда остановиться. Науки о геномике и стволовых клетках
биология — это только часть головоломки, поскольку они объясняют распространение
специфические компоненты в каждой ячейке и создание разных типов
ячеек.Хотя мы знаем о многих генах, которые требуются для
процесса регенерации, мы до сих пор не знаем алгоритм, который достаточно , чтобы клетки знали, как строить или реконструировать сложные органы
к очень конкретной анатомической конечной цели. Таким образом, одна из главных опор будущего
работа в области биомедицины — это открытие процесса, с помощью которого крупномасштабные
анатомия определяется внутри коллективов клеток, и как мы можем это переписать
информация для рационального управления ростом и формой.Это также становится
ясно, что программное обеспечение жизни обладает многочисленными модулями или подпрограммами,
например «Построй глаз здесь», который можно активировать простым сигналом
триггеры. Обнаружение таких подпрограмм и
отображение логики развития — это новая область на пересечении
биология развития и информатика. Следующий важный шаг — попробовать
сформулировать вычислительные модели этого процесса, чтобы обогатить
концептуальный инструментарий биологов и помощь в переводе открытий
биологии в лучшую робототехнику и вычислительные технологии.
Таким образом, одна из главных опор будущего
работа в области биомедицины — это открытие процесса, с помощью которого крупномасштабные
анатомия определяется внутри коллективов клеток, и как мы можем это переписать
информация для рационального управления ростом и формой.Это также становится
ясно, что программное обеспечение жизни обладает многочисленными модулями или подпрограммами,
например «Построй глаз здесь», который можно активировать простым сигналом
триггеры. Обнаружение таких подпрограмм и
отображение логики развития — это новая область на пересечении
биология развития и информатика. Следующий важный шаг — попробовать
сформулировать вычислительные модели этого процесса, чтобы обогатить
концептуальный инструментарий биологов и помощь в переводе открытий
биологии в лучшую робототехнику и вычислительные технологии.
Представьте, если бы мы могли проектировать системы такой же пластичности и надежности, как
биологическая жизнь: структуры и машины, которые могут расти и ремонтироваться
самих себя. Такая технология трансформирует текущие усилия в
регенеративная медицина, где ученые и клиницисты стремятся открыть
входы или стимулы, которые могут заставить клетки тела строить структуры на
спрос по мере необходимости. Чтобы помочь разгадать загадку морфогенетического кода, и
также использовать знания биологии для создания самовосстанавливающихся систем в
реальной жизни, мы пытаемся воспроизвести некоторые из желаемых свойств в in silico эксперимент.
Такая технология трансформирует текущие усилия в
регенеративная медицина, где ученые и клиницисты стремятся открыть
входы или стимулы, которые могут заставить клетки тела строить структуры на
спрос по мере необходимости. Чтобы помочь разгадать загадку морфогенетического кода, и
также использовать знания биологии для создания самовосстанавливающихся систем в
реальной жизни, мы пытаемся воспроизвести некоторые из желаемых свойств в in silico эксперимент.
Модель
Специалисты по инженерным дисциплинам и исследователи часто используют разные виды
моделирование, включающее локальное взаимодействие, в том числе системы частичных
производное уравнение (PDE), системы частиц и различные виды сотовых
Автоматы (СА). Мы сосредоточимся на моделях клеточных автоматов в качестве дорожной карты для
усилия по выявлению правил на уровне ячейки, которые приводят к сложным,
регенеративное поведение коллектива. Центры сертификации обычно состоят из сетки
ячейки обновляются итеративно, с тем же набором правил, применяемых к
каждая ячейка на каждом шагу. Новое состояние ячейки зависит только от состояний
из нескольких ячеек в непосредственной близости. Несмотря на их очевидные
простота, центры сертификации часто демонстрируют богатое, интересное поведение и
долгая история применения для моделирования биологических явлений.
Новое состояние ячейки зависит только от состояний
из нескольких ячеек в непосредственной близости. Несмотря на их очевидные
простота, центры сертификации часто демонстрируют богатое, интересное поведение и
долгая история применения для моделирования биологических явлений.
Давайте попробуем разработать правило обновления клеточного автомата, которое, начиная с
одиночная ячейка, создаст предопределенный многоклеточный узор на 2D-сетке.
Это наша аналогичная игрушечная модель развития организма.Чтобы разработать CA,
мы должны указать возможные состояния ячеек и их функцию обновления. Типичный
Модели CA представляют состояния ячеек с набором дискретных значений, хотя
существуют варианты, использующие векторы непрерывных значений. Использование непрерывного
values имеет то достоинство, что позволяет правилу обновления быть дифференцируемым
функция состояний соседства ячейки. Правила, которыми руководствуются
поведение отдельной клетки, основанное на локальной среде, аналогично
низкоуровневая аппаратная спецификация, кодируемая геномом организма. Запуск нашей модели за заданное количество шагов от начальной конфигурации
покажет поведение паттерна, которое обеспечивается таким оборудованием.
Запуск нашей модели за заданное количество шагов от начальной конфигурации
покажет поведение паттерна, которое обеспечивается таким оборудованием.
Итак — что же такого особенного в дифференцируемых правилах обновления? Они позволят использовать мощный язык функций потерь, чтобы выразить свои пожелания, и обширный существующий механизм вокруг градиентных числовых оптимизация для их выполнения. Искусство складывать отличные друг от друга функции, и оптимизация их параметров для выполнения различных задач имеет долгая история.В последние годы он процветал под разными названиями, такими как (Глубокие) нейронные сети, глубокое обучение или дифференцируемое программирование.
Один шаг обновления модели.Состояние ячейки
Мы представим состояние каждой ячейки как вектор из 16 реальных значений (см.
рисунок выше). Первые три канала представляют цвет ячейки, видимый для
нас (RGB). Целевой шаблон имеет значения цветового канала в диапазоне [0,0,1,0] [0,0, 1,0] [0,0,1,0]
и α \ alphaα равняется 1. 0 для пикселей переднего плана и 0,0 для фона.
0 для пикселей переднего плана и 0,0 для фона.
Альфа-канал (α \ alphaα) имеет особое значение: он разграничивает живое клетки, принадлежащие выращиваемому образцу. В частности, клетки имеющие α> 0,1 \ alpha> 0,1α> 0,1 и их соседи считаются «живыми». Другой ячейки являются «мертвыми» или пустыми, и для них явно заданы значения вектора состояния до 0,0 на каждом временном шаге. Таким образом, клетки с α> 0,1 \ alpha> 0,1α> 0,1 можно рассматривать как как «зрелые», а их соседи с α≤0.1 \ alpha \ leq 0.1α≤0.1 «растут», а могут стать зрелыми, если их альфа превышает порог 0,1.
state⃗ → 0.00 \ vec {state} \ rightarrow 0.00state⃗ → 0.00, когда нет соседа с α> 0.10 \ alpha> 0.10α> 0.10 Скрытые каналы не имеют предопределенного значения, и это зависит от обновления
правило, чтобы решить, для чего их использовать. Их можно интерпретировать как
концентрации некоторых химикатов, электрические потенциалы или другие
сигнальный механизм, который используется клетками для управления ростом. В
с точки зрения нашей биологической аналогии — все наши клетки имеют один и тот же геном
(правило обновления) и различаются только информацией, закодированной
химические сигналы, которые они получают, излучают и хранят внутри (их состояние
векторы).
В
с точки зрения нашей биологической аналогии — все наши клетки имеют один и тот же геном
(правило обновления) и различаются только информацией, закодированной
химические сигналы, которые они получают, излучают и хранят внутри (их состояние
векторы).
Клеточный автомат, правило
Пришло время определить правило обновления. Наш CA работает на обычной 2D-сетке из 16-мерные векторы, по сути, трехмерный массив формы [высота, ширина, 16]. Мы хотим применить одну и ту же операцию к каждой ячейке, и результат этого операция может зависеть только от небольшой (3×3) окрестности ячейки.Этот сильно напоминает операцию свертки, один из краеугольных камней обработки сигналов и дифференциального программирования. Свертка — это линейная операции, но ее можно комбинировать с другими операциями для каждой ячейки для получения сложное правило обновления, способное запомнить желаемое поведение. Наша ячейка Правило обновления можно разделить на следующие этапы, применяемые по порядку:
Восприятие. Этот шаг определяет, что каждая клетка воспринимает.
окружающая среда.Мы реализуем это с помощью свертки 3×3 с
фиксированное ядро. Кто-то может возразить, что определение этого ядра излишне —
в конце концов, мы могли бы просто заставить клетку научиться необходимому восприятию
коэффициенты ядра. Наш выбор фиксированных операций мотивирован
тот факт, что реальные клетки часто полагаются только на химические градиенты, чтобы направлять
развитие организма. Таким образом, мы используем классические фильтры Собеля для оценки
частные производные каналов состояний клеток в x⃗ \ vec {x} x⃗ и
y⃗ \ vec {y} y⃗ направлений, формируя двумерный вектор градиента в каждом направлении, для
каждый государственный канал.Мы объединяем эти градиенты с собственными ячейками.
состояний, образуя 16 * 2 + 16 = 4816 * 2 + 16 = 4816 * 2 + 16 = 48-мерный вектор восприятия , или
скорее воспринимаемых вектора, на каждую ячейку.
Этот шаг определяет, что каждая клетка воспринимает.
окружающая среда.Мы реализуем это с помощью свертки 3×3 с
фиксированное ядро. Кто-то может возразить, что определение этого ядра излишне —
в конце концов, мы могли бы просто заставить клетку научиться необходимому восприятию
коэффициенты ядра. Наш выбор фиксированных операций мотивирован
тот факт, что реальные клетки часто полагаются только на химические градиенты, чтобы направлять
развитие организма. Таким образом, мы используем классические фильтры Собеля для оценки
частные производные каналов состояний клеток в x⃗ \ vec {x} x⃗ и
y⃗ \ vec {y} y⃗ направлений, формируя двумерный вектор градиента в каждом направлении, для
каждый государственный канал.Мы объединяем эти градиенты с собственными ячейками.
состояний, образуя 16 * 2 + 16 = 4816 * 2 + 16 = 4816 * 2 + 16 = 48-мерный вектор восприятия , или
скорее воспринимаемых вектора, на каждую ячейку.
по умолчанию (state_grid):
sobel_x = [[-1, 0, +1],
[-2, 0, +2],
[-1, 0, +1]]
sobel_y = транспонировать (sobel_x)
# Свернутые фильтры Собеля с состояниями
# по x, y и размеру канала.
grad_x = conv2d (sobel_x, state_grid)
grad_y = conv2d (sobel_y, state_grid)
# Объединить каналы состояния ячейки,
# градиенты каналов по x и
# градиент каналов по y.
perception_grid = concat (
state_grid, grad_x, grad_y, axis = 2)
возврат perception_grid
Обновить правило. Каждая ячейка теперь применяет серию операций
к вектору восприятия, состоящему из типичного дифференцируемого программирования
строительные блоки, такие как 1×1-свертки и нелинейности ReLU, которые мы
назовите «правило обновления» ячейки.Напомним, что правило обновления изучено, но
в каждой ячейке выполняется одно и то же правило обновления. Сеть, параметризующая это обновление
Правило состоит примерно из 8000 параметров. Вдохновленный остаточной нервной системой
сетей, правило обновления выводит инкрементное обновление состояния ячейки,
который применяется к ячейке перед следующим временным шагом. Правило обновления
предназначен для демонстрации начального поведения «ничего не делать» — реализовано
инициализация весов последнего сверточного слоя в правиле обновления
с нуля.Мы также отказываемся от применения ReLU к выходу последнего слоя
правило обновления, так как инкрементальные обновления состояния ячейки должны
обязательно уметь как прибавлять, так и убавлять из состояния.
Правило обновления
предназначен для демонстрации начального поведения «ничего не делать» — реализовано
инициализация весов последнего сверточного слоя в правиле обновления
с нуля.Мы также отказываемся от применения ReLU к выходу последнего слоя
правило обновления, так как инкрементальные обновления состояния ячейки должны
обязательно уметь как прибавлять, так и убавлять из состояния.
обновление по умолчанию (perception_vector):
# Следующий псевдокод работает на
# вектор восприятия отдельной клетки.
# В нашей эталонной реализации используется 1D
# сверток по соображениям производительности.
x = плотный (perception_vector, output_len = 128)
x = relu (x)
ds = плотный (x, output_len = 16, weights_init = 0.0)
возврат ds
Обновление стохастической ячейки. Типичное обновление клеточного автомата
все клетки одновременно. Это подразумевает наличие глобальных часов,
синхронизация всех ячеек. Не стоит полагаться на глобальную синхронизацию
можно ожидать от самоорганизующейся системы. Мы ослабляем это требование,
предполагая, что каждая ячейка выполняет обновление независимо, ожидая
случайный интервал времени между обновлениями. Чтобы смоделировать это поведение, мы применяем
случайная маска для каждой ячейки для обновления векторов, установка всех значений обновления на ноль
с некоторой предопределенной вероятностью (мы используем 0.5 во время тренировки). Этот
Операцию можно также рассматривать как приложение отсева для каждой ячейки для обновления
векторов.
Это подразумевает наличие глобальных часов,
синхронизация всех ячеек. Не стоит полагаться на глобальную синхронизацию
можно ожидать от самоорганизующейся системы. Мы ослабляем это требование,
предполагая, что каждая ячейка выполняет обновление независимо, ожидая
случайный интервал времени между обновлениями. Чтобы смоделировать это поведение, мы применяем
случайная маска для каждой ячейки для обновления векторов, установка всех значений обновления на ноль
с некоторой предопределенной вероятностью (мы используем 0.5 во время тренировки). Этот
Операцию можно также рассматривать как приложение отсева для каждой ячейки для обновления
векторов.
def stochastic_update (state_grid, ds_grid):
# Обнулить случайную часть обновлений.
rand_mask = cast (random (64, 64) <0,5, float32)
ds_grid = ds_grid * rand_mask
вернуть state_grid + ds_grid
Маскировка живых клеток. Мы хотим смоделировать процесс роста
который начинается с одной ячейки и не хочет, чтобы пустые ячейки участвовали в
вычислений или несут какое-либо скрытое состояние. Мы обеспечиваем это явным
обнуление всех каналов пустых ячеек. Ячейка считается пустой, если
в его окрестности 3×3 нет «зрелой» (альфа> 0,1) клетки.
Мы обеспечиваем это явным
обнуление всех каналов пустых ячеек. Ячейка считается пустой, если
в его окрестности 3×3 нет «зрелой» (альфа> 0,1) клетки.
def alive_masking (state_grid):
# Возьмем альфа-канал как мерило «жизни».
в живых = max_pool (state_grid [:,:, 3], (3,3))> 0,1
state_grid = state_grid * cast (жив, float32)
вернуть state_grid
Эксперимент 1. Учимся расти
Тренировочный режим для обучения целевому шаблону.В нашем первом эксперименте мы просто обучаем CA для достижения целевого изображения. после случайного количества обновлений. Этот подход довольно наивен и будет работать в вопросы. Но проблемы, с которыми он сталкивается, помогут нам улучшить будущее. попытки.
Мы инициализируем сетку нулями, за исключением одной исходной ячейки в центре,
который будет иметь все каналы кроме RGB
Мы устанавливаем RGB-каналы начального числа на ноль, потому что хотим, чтобы он был виден
на белом фоне. установлен на единицу. После инициализации сетки мы итеративно применяем обновление
правило. Мы выбираем случайное количество шагов CA из [64, 96]
Это должно быть достаточное количество шагов, чтобы вырастить узор
размер, с которым мы работаем (40×40), даже с учетом стохастической природы наших
обновить правило.
диапазон для каждого шага обучения, так как мы хотим, чтобы шаблон был стабильным на протяжении
количество итераций. На последнем шаге мы применяем пиксельную потерю L2 между
Каналы RGBA в сетке и целевом шаблоне.Эта потеря может быть
дифференцированно оптимизированный
Мы наблюдали тренировочную нестабильность, которая проявлялась в виде
резкие скачки величины потерь на более поздних этапах обучения. Мы
удалось смягчить их, применив нормализацию L2 для каждой переменной к
градиенты параметров. Это может иметь эффект, похожий на вес
нормализация. Другое обучение
параметры доступны в сопроводительном исходном коде.
установлен на единицу. После инициализации сетки мы итеративно применяем обновление
правило. Мы выбираем случайное количество шагов CA из [64, 96]
Это должно быть достаточное количество шагов, чтобы вырастить узор
размер, с которым мы работаем (40×40), даже с учетом стохастической природы наших
обновить правило.
диапазон для каждого шага обучения, так как мы хотим, чтобы шаблон был стабильным на протяжении
количество итераций. На последнем шаге мы применяем пиксельную потерю L2 между
Каналы RGBA в сетке и целевом шаблоне.Эта потеря может быть
дифференцированно оптимизированный
Мы наблюдали тренировочную нестабильность, которая проявлялась в виде
резкие скачки величины потерь на более поздних этапах обучения. Мы
удалось смягчить их, применив нормализацию L2 для каждой переменной к
градиенты параметров. Это может иметь эффект, похожий на вес
нормализация. Другое обучение
параметры доступны в сопроводительном исходном коде. в отношении параметров правила обновления путем обратного распространения ошибки во времени,
стандартный метод обучения рекуррентных нейронных сетей.
в отношении параметров правила обновления путем обратного распространения ошибки во времени,
стандартный метод обучения рекуррентных нейронных сетей.
Как только оптимизация сойдется, мы можем запустить моделирование, чтобы увидеть, как наши изученные паттерны роста CA, начиная с семенной клетки. Посмотрим, что происходит, когда мы запускаем его дольше, чем количество шагов, используемых во время обучение персонала. На анимации ниже показано поведение нескольких различных моделей. обучены генерировать различные шаблоны эмодзи.
Ваш браузер не поддерживает видео тег. Многие модели демонстрируют нестабильность в течение более длительных периодов времени.Воспроизвести в записной книжке
Мы видим, что различные обучающие прогоны могут привести к созданию моделей с очень большим различное долгосрочное поведение. Некоторые имеют тенденцию вымирать, некоторые, кажется, не умирают. знаю, как перестать расти, но некоторые из них оказываются почти стабильными! Как мы можем направлять обучение на постоянное создание устойчивых паттернов?
Эксперимент 2: То, что сохраняется, существует
Один из способов понять, почему предыдущий эксперимент был нестабильным, — это нарисовать
параллель динамическим системам. Мы можем рассматривать каждую клетку как
динамическая система, в которой каждая ячейка разделяет одну и ту же динамику, и все ячейки
будучи локально связанными между собой. Когда мы тренируем нашу клетку обновлению
модель мы корректируем эту динамику. Наша цель — найти динамику, которая
удовлетворяют ряду свойств. Изначально мы хотели, чтобы система развивалась
от исходного образца к целевому образцу — траектория, которую мы достигли
в эксперименте 1. Теперь мы хотим избежать наблюдаемой нестабильности, которая
в нашей метафоре динамической системы состоит в том, чтобы сделать целевой шаблон
аттрактор.
Мы можем рассматривать каждую клетку как
динамическая система, в которой каждая ячейка разделяет одну и ту же динамику, и все ячейки
будучи локально связанными между собой. Когда мы тренируем нашу клетку обновлению
модель мы корректируем эту динамику. Наша цель — найти динамику, которая
удовлетворяют ряду свойств. Изначально мы хотели, чтобы система развивалась
от исходного образца к целевому образцу — траектория, которую мы достигли
в эксперименте 1. Теперь мы хотим избежать наблюдаемой нестабильности, которая
в нашей метафоре динамической системы состоит в том, чтобы сделать целевой шаблон
аттрактор.
Одна из стратегий для достижения этого — позволить CA выполнять итерацию в течение гораздо более длительного времени.
и периодически прикладывая урон к цели, тренируя систему
путем обратного распространения через эти более длительные интервалы времени. Интуитивно мы утверждаем
что с более длинными временными интервалами и несколькими приложениями потерь модель
с большей вероятностью создаст аттрактор для целевой формы, поскольку мы
итеративно формировать динамику, чтобы вернуться к целевому паттерну откуда угодно
система решила рискнуть. Однако более длительные периоды времени
существенно увеличить время тренировки и, что более важно, память
требования, учитывая, что промежуточные активации всего эпизода должны
быть сохраненным в памяти для выполнения обратного прохода.
Однако более длительные периоды времени
существенно увеличить время тренировки и, что более важно, память
требования, учитывая, что промежуточные активации всего эпизода должны
быть сохраненным в памяти для выполнения обратного прохода.
Вместо этого мы предлагаем стратегию, основанную на «пуле образцов», для достижения аналогичного эффекта. Мы определить пул начальных состояний для запуска итераций, изначально заполненных с начальным состоянием одиночного черного пикселя. Затем мы пробуем партию из этого бассейн, который мы используем на этапе обучения.Чтобы предотвратить эквивалент «Катастрофическое забывание» заменяем один образец в этой партии на исходное однопиксельное начальное состояние. По завершении этапа обучения мы заменить образцы в пуле, которые были отобраны для партии, выходными состояния из шага обучения над этой партией. На анимации ниже показан случайная выборка записей в пуле каждые 20 шагов обучения.
определение pool_training ():
# Установить альфа и скрытый каналы на (1. 0).
0).
сид = нули (64, 64, 16)
начальное число [64 // 2, 64 // 2, 3:] = 1.0
target = цели [«ящерица»]
пул = [начальное число] * 1024
для i в диапазоне (training_iterations):
idxs, партия = pool.sample (32)
# Сортировать по убыванию, по убыванию.
партия = sort_desc (партия, потеря (партия))
# Замените образец с наибольшими потерями семенем.
партия [0] = начальное число
# Провести обучение.
выходов, потери = поезд (партия, цель)
# Поместите выходы обратно в пул.
пул [idxs] = выводит
Ваш браузер не поддерживает видео тег. Случайная выборка паттернов в пуле во время обучения, отобранная каждые 20 тренировочных шагов.Воспроизвести в записной книжке
На ранних этапах тренировочного процесса случайная динамика в системе позволяет
модель попадет в различные неполные и неправильные состояния. Как эти
состояния выбираются из пула, мы уточняем динамику, чтобы иметь возможность
оправиться от таких состояний. Наконец, по мере того, как модель становится более надежной
из начального состояния в целевое, образцы в пуле отражают это
и с большей вероятностью будут очень близки к целевому паттерну, что позволяет
обучение для дальнейшего совершенствования этих почти завершенных моделей.
Как эти
состояния выбираются из пула, мы уточняем динамику, чтобы иметь возможность
оправиться от таких состояний. Наконец, по мере того, как модель становится более надежной
из начального состояния в целевое, образцы в пуле отражают это
и с большей вероятностью будут очень близки к целевому паттерну, что позволяет
обучение для дальнейшего совершенствования этих почти завершенных моделей.
По сути, мы используем предыдущие конечные состояния как новые отправные точки для
заставить наш центр сертификации научиться сохранять или даже улучшать уже сформированный
шаблон, в дополнение к возможности вырастить его из семени.Это делает это
можно добавлять периодические убытки для значительно более длительных интервалов времени
чем это возможно в противном случае, поощрение генерации аттрактора как
форма цели в нашей связанной системе. Мы также заметили, что пересев
выборка с наибольшими потерями в пакете вместо случайной делает обучение
более стабильна на начальных этапах, так как помогает убирать некачественные
состояния из пула.
Вот как выглядит типичный прогресс обучения правилу CA.Клетка Правило учится стабилизировать паттерн параллельно с уточнением его характеристик.
Ваш браузер не поддерживает видео тег. Поведение CA на шагах обучения 100, 500, 1000, 4000.Воспроизвести в записной книжке
Эксперимент 3. Обучение регенерации
Помимо способности выращивать собственное тело, живые существа отлично их поддерживает. Мало того, что изношенная кожа заменяется новой кожа, но очень тяжелые повреждения сложных жизненно важных органов могут быть восстановлены в некоторые виды.Есть ли шанс, что некоторые из моделей, которые мы обучили выше есть регенеративные способности?
Ваш браузер не поддерживает видео тег. Образцы проявляют некоторые регенерирующие свойства при повреждении, но не полный повторный рост.Воспроизвести в записной книжке
На анимации выше показаны три разные модели, обученные с использованием одного и того же
настройки. Мы позволяем каждой из моделей развить шаблон более 100 шагов, затем
повредить конечное состояние пятью разными способами: удаляя разные половинки
сформированного рисунка, и вырезав из центра квадрат.Один раз
опять же, мы видим, что эти модели показывают совсем другой режим вне тренировки.
поведение. Например, «ящерица» развивает довольно сильную регенеративную
возможности, без явного обучения этому!
Мы позволяем каждой из моделей развить шаблон более 100 шагов, затем
повредить конечное состояние пятью разными способами: удаляя разные половинки
сформированного рисунка, и вырезав из центра квадрат.Один раз
опять же, мы видим, что эти модели показывают совсем другой режим вне тренировки.
поведение. Например, «ящерица» развивает довольно сильную регенеративную
возможности, без явного обучения этому!
Поскольку мы обучили нашу связанную систему ячеек генерировать аттрактор
к целевой форме из одной ячейки, вероятно, что эти системы,
однажды поврежденный, будет обобщен в сторону несаморазрушающих реакций.
Это потому, что системы были обучены расти, стабилизироваться и никогда не
полностью самоуничтожиться.Некоторые из этих систем могут естественным образом притягиваться
к регенеративным способностям, но ничто не мешает им развиваться
различное поведение, такое как взрывные митозы (неконтролируемый рост),
невосприимчивость к повреждению (сверхстабилизация) или даже самоуничтожение,
особенно для наиболее серьезных повреждений.
Если мы хотим, чтобы наша модель показывала более последовательные и точные регенеративные возможности, мы можем попытаться увеличить область притяжения для нашей цели узор — увеличивает пространство конфигураций ячеек, которые естественным образом тяготеют к нашей целевой форме.Мы сделаем это, повредив несколько отобранных из пула состояния перед каждым шагом обучения. Теперь система должна быть способна регенерация из состояний, поврежденных случайно расположенными стирающими кругами. Наш надеюсь, что это будет распространено на регенерационные способности от различные виды повреждений.
Ваш браузер не поддерживает видео тег. Повреждение образцов в бассейне способствует изучению надежных регенеративные качества. Строка 1 — образцы из пула, Строка 2 — их соответствующие состояния после итерации модели.Воспроизвести в записной книжке
На приведенной выше анимации показан прогресс обучения, включая образец повреждений. Мы отбираем 8 состояний из пула. Затем мы заменяем образец с наибольшими потерями
(крайний левый верхний на рисунке выше) с исходным состоянием и повредить три
состояния с наименьшими потерями (верхний правый угол) путем установки случайной круговой области
в шаблоне до нулей. В нижней строке показаны состояния после итерации.
из соответствующего самого верхнего начального состояния. Как и в эксперименте 2,
результирующие состояния возвращаются в пул.
Мы отбираем 8 состояний из пула. Затем мы заменяем образец с наибольшими потерями
(крайний левый верхний на рисунке выше) с исходным состоянием и повредить три
состояния с наименьшими потерями (верхний правый угол) путем установки случайной круговой области
в шаблоне до нулей. В нижней строке показаны состояния после итерации.
из соответствующего самого верхнего начального состояния. Как и в эксперименте 2,
результирующие состояния возвращаются в пул.
Воспроизвести в записной книжке
Как видно из приведенной выше анимации, модели, подвергшиеся повреждениям во время тренировок гораздо более устойчивы, в том числе к видам повреждений не опытных в тренировочном процессе (например, прямоугольные повреждения как над).
Эксперимент 4.
 Вращение поля восприятия
Вращение поля восприятияКак описано ранее, мы моделируем восприятие клеткой соседних ячеек путем оценки градиентов каналов состояний в x⃗ \ vec {x} x⃗ и y⃗ \ vec {y} y⃗ с использованием фильтров Собеля.Удобная аналогия: у каждого агента есть два датчика (например, хемосенсорные рецепторы), указывающие ортогонально направления, которые могут ощущать градиенты в концентрации определенных химикаты по оси датчика. Что произойдет, если мы повернем эти датчики? Мы можем сделать это, вращая ядра Собеля.
[KxKy] = [cosθ − sinθsinθcosθ] ∗ [SobelxSobely] \ begin {bmatrix} K_x \\ K_y \ end {bmatrix} = \ begin {bmatrix} \ cos \ theta & — \ sin \ theta \\ \ sin \ theta & \ cos \ theta \ end {bmatrix} * \ begin {bmatrix} Sobel_x \\ Sobel_y \ end {bmatrix} [Kx Ky] = [cosθsinθ −sinθcosθ] ∗ [Sobelx Sobely]Эта простая модификация поля восприятия дает повернутые версии. шаблона для угла выбора без переобучения, как показано ниже.
Вращение оси, по которой шаг восприятия вычисляет градиенты вызывает повернутые версии узора.
Воспроизвести в записной книжке
В идеальном мире, не квантованном отдельными ячейками в пиксельной решетке, в этом нет ничего удивительного, ведь в конце концов, можно было бы ожидать воспринимаемые градиенты в x⃗ \ vec {x} x⃗ и y⃗ \ vec {y} y⃗ инвариантны к выбранному угол — простая смена системы отсчета. Однако важно обратите внимание, что в модели на основе пикселей все не так просто.Вращающийся пиксель основанная на графике включает в себя вычисление сопоставления, которое не обязательно биективно и обычно включает интерполяцию между пикселями для достижения желаемого результат. Это потому, что один пиксель при повороте теперь, скорее всего, перекрывают несколько пикселей. Успешный рост паттернов, как указано выше, предполагает определенная устойчивость к основным условиям за пределами тех испытал во время обучения.
CA и PDE
Существует обширная литература, описывающая различные
разновидности клеточных автоматов и систем PDE и их приложения для
моделирование физических, биологических или даже социальных систем. Хотя было бы
невозможно дать краткий обзор этой области в нескольких строках, мы будем
опишите несколько ярких примеров, вдохновивших на эту работу. Алан Тьюринг
представил свои знаменитые паттерны Тьюринга еще в 1952 г.
, предлагая, как
системы реакции-диффузии могут быть действительной моделью для химического поведения
во время морфогенеза. Особенно вдохновляющая модель реакции-диффузии, которая
выдержала испытание временем — модель Грея-Скотта
, что показывает крайнее разнообразие
поведение контролируется всего несколькими переменными.
Хотя было бы
невозможно дать краткий обзор этой области в нескольких строках, мы будем
опишите несколько ярких примеров, вдохновивших на эту работу. Алан Тьюринг
представил свои знаменитые паттерны Тьюринга еще в 1952 г.
, предлагая, как
системы реакции-диффузии могут быть действительной моделью для химического поведения
во время морфогенеза. Особенно вдохновляющая модель реакции-диффузии, которая
выдержала испытание временем — модель Грея-Скотта
, что показывает крайнее разнообразие
поведение контролируется всего несколькими переменными.
С тех пор, как фон Нейман представил центры сертификации
как модели для самовоспроизведения они
пленили умы исследователей, которые наблюдали чрезвычайно сложные
поведение, возникающее из очень простых правил. Точно так же более широкая аудитория
за пределами академических кругов были соблазнены жизненным поведением CA благодаря
Игра жизни Конвея. Возможно
частично мотивировано доказательством того, что такая простая вещь, как Правило 110,
Тьюринг завершен, Вольфрам « Новый вид науки» требует сдвига парадигмы
вокруг широкого использования элементарных компьютерных программ, таких как CA как
инструменты для познания мира.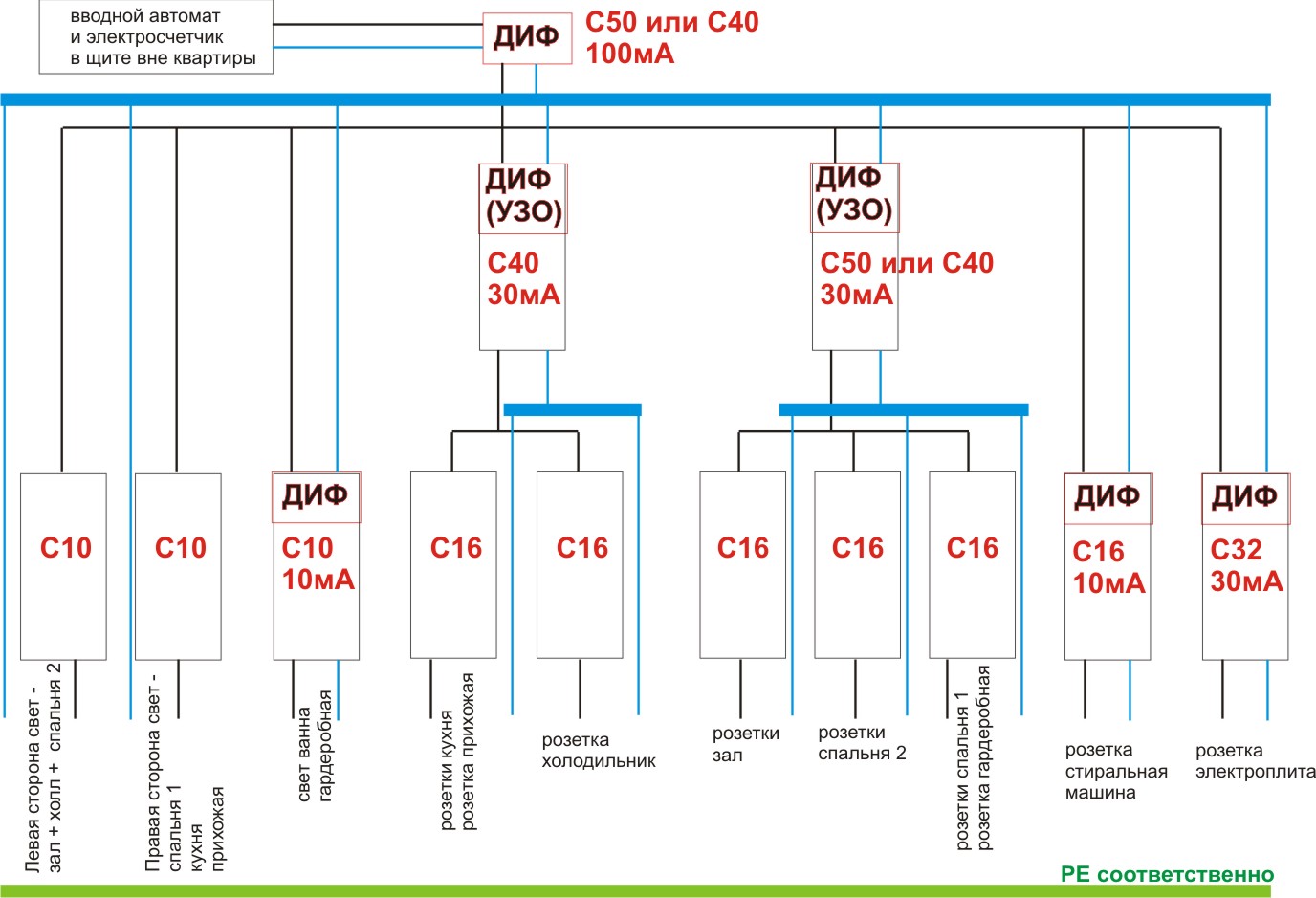
Совсем недавно несколько исследователей обобщили «Игру жизни» Конвея на работу. на более непрерывных доменах. Нас особенно вдохновили работы Рафлера SmoothLife и Ления из Чана , последний из который также обнаруживает и классифицирует целые виды «форм жизни».
Ряд исследователей использовали эволюционные алгоритмы для поиска правил CA. которые воспроизводят предопределенные простые шаблоны . Например, Дж. Миллер предложил эксперимент, аналогичный нашему, с использованием эволюционных алгоритмов для разработки CA Правило, которое могло построить и возродить французский флаг, начиная с семени клетка.
Нейронные сети и самоорганизация
Тесная связь между сверточными нейронными сетями и сотовой
Автоматы уже наблюдались рядом исследователей.
. В
связь настолько сильна, что позволила нам построить нейронные модели CA, используя
компоненты, легко доступные в популярных фреймворках машинного обучения.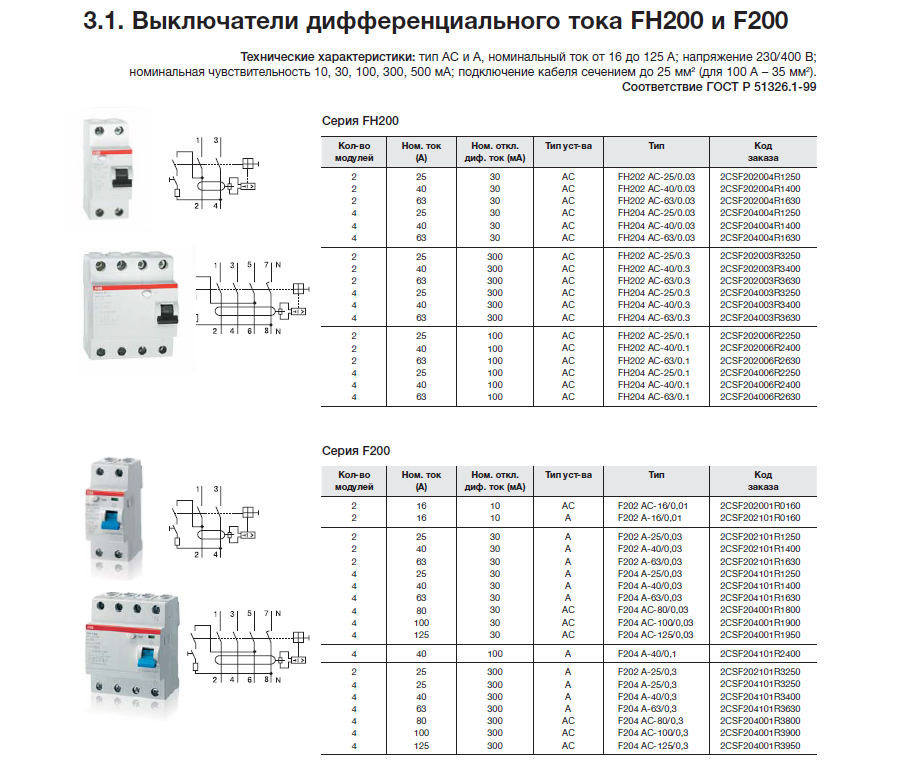 Таким образом, используя
другой жаргон, наш Neural CA потенциально может быть назван «Recurrent
Остаточные сверточные сети с выпадением «на пиксель».
Таким образом, используя
другой жаргон, наш Neural CA потенциально может быть назван «Recurrent
Остаточные сверточные сети с выпадением «на пиксель».
Нейронный графический процессор предложения вычислительная архитектура очень похожа на нашу, но применяется в контекст обучения умножению и алгоритм сортировки.
Если смотреть шире, мы думаем, что концепция самоорганизации
находит свое отражение в массовом машинном обучении с популяризацией
Графические модели нейронных сетей.
Обычно GNN выполняет повторное вычисление по вершинам (возможно,
динамический) график. Вершины сообщаются локально через ребра графа, и
агрегировать глобальную информацию, необходимую для выполнения задачи по нескольким
раундов обмена сообщениями, точно так же, как атомы можно рассматривать как
общаются друг с другом, чтобы создать новые свойства
молекула или даже точки точки
облако разговаривает со своими соседями, чтобы выяснить их глобальную форму
.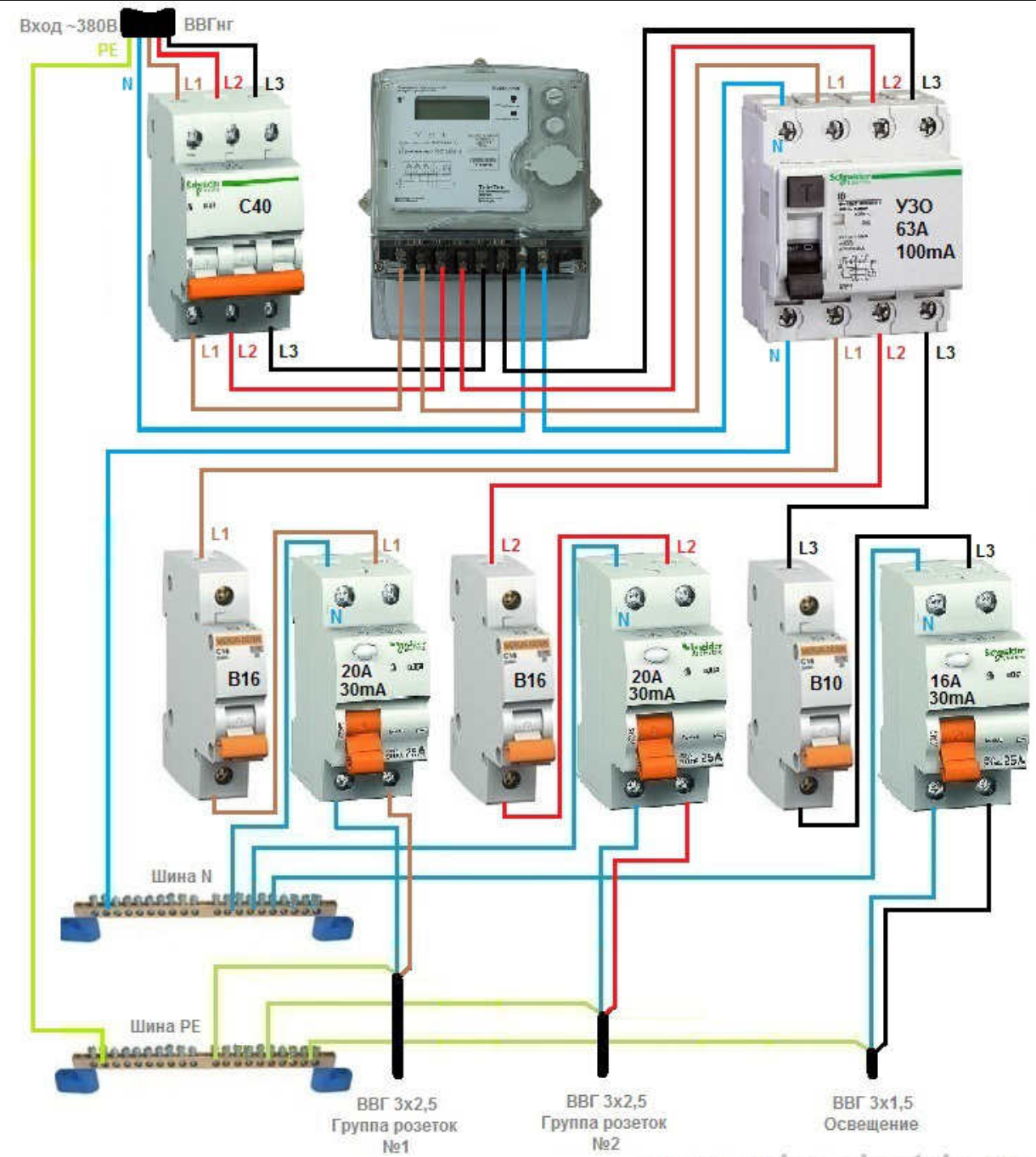
Самоорганизация также проявилась в увлекательной современной работе с использованием большего традиционные сети динамических графов, в которых авторы развили Самостоятельно собирающиеся агенты для решения множества виртуальных задач .
Swarm Robotics
Одна из самых ярких демонстраций силы самоорганизации.
когда это применяется к моделированию роя. Еще в 1987 году Рейнольдс Боидс
смоделировал стайку птиц с
просто крошечный набор правил, созданных вручную.В настоящее время мы можем встраивать крошечных роботов
с программами и проверять их коллективное поведение на физических агентах, как
продемонстрировано такими работами, как Mergeable Nervous Systems
и килоботы
. Насколько нам известно, программы
встроенные в роевые роботы в настоящее время разрабатываются людьми. Мы надеемся, что наш
работа может служить источником вдохновения для данной области и способствовать созданию
коллективное поведение посредством дифференцируемого моделирования.
Обсуждение
Эмбриогенетическое моделирование
Ваш браузер не поддерживает видео тег.Способный к регенерации двухголовый планарий, создание, которое вдохновило этот работуВоспроизвести в записной книжке
В этой статье описывается игрушечная модель эмбриогенеза и регенерации. Это
основное направление для будущей работы со многими приложениями в биологии и
вне. В дополнение к значениям для понимания эволюции и
контроль регенерации и использование этого понимания для биомедицинских
ремонт, есть область биоинженерии.При переходе поля от
синтетическая биология коллективов отдельных клеток до истинной синтетической морфологии
новых живых машин, это
будет иметь важное значение для разработки стратегий программирования на системном уровне.
возможности, такие как анатомический гомеостаз (восстановительное восстановление). Она имеет
давно известно, что регенеративные организмы могут восстанавливать специфические
анатомический узор; однако совсем недавно было обнаружено, что цель
морфология не закодирована жестко ДНК, но поддерживается
физиологический контур, который хранит уставку для этого анатомического гомеостаза
.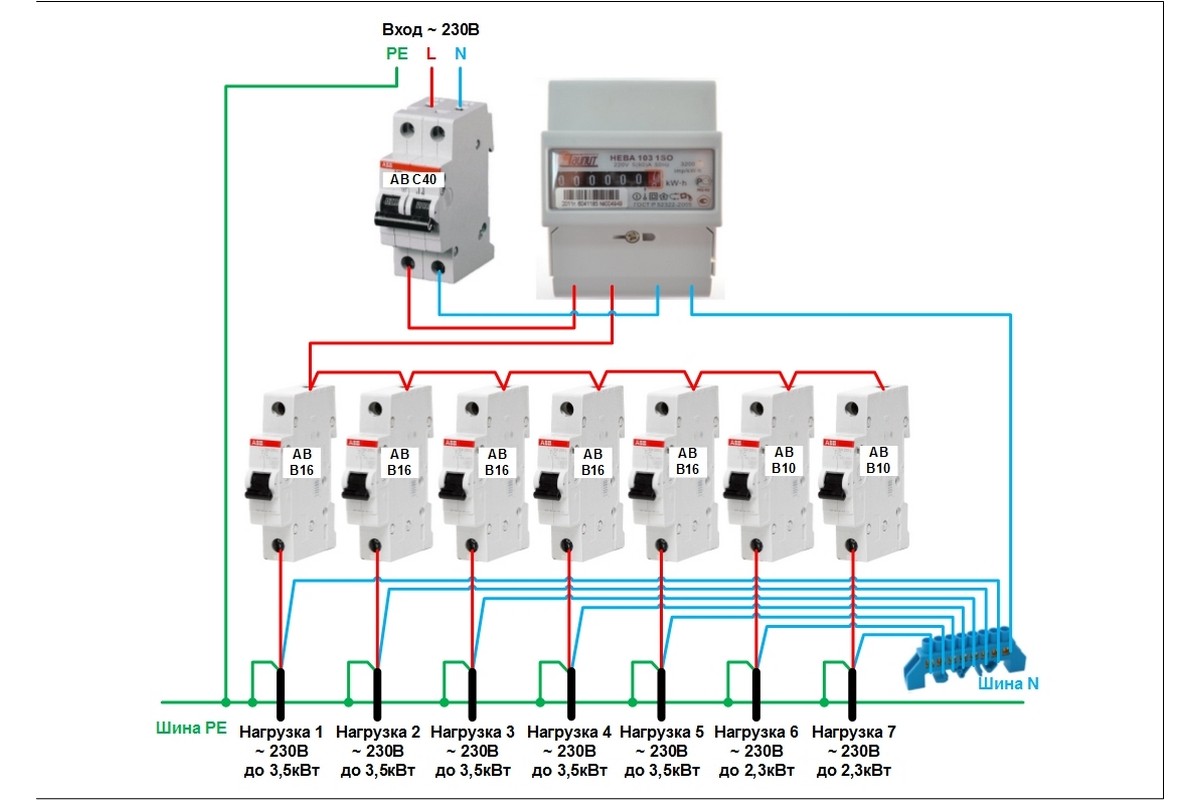 Техники
теперь доступно для перезаписи этой уставки, в результате чего, например,
у двухголовых плоских червей
что при разрезании на части в простой воде (без дополнительных манипуляций)
приводят к появлению последующих поколений регенерированных двухголовых червей (как показано на рисунке).
над). Важно приступить к разработке моделей вычислительной
процессы, которые хранят целевое состояние системного уровня для поведения роя
, чтобы можно было разработать эффективные стратегии для рационального редактирования этого
информационная структура, приводящая к желаемым крупномасштабным результатам (таким образом
победить обратную проблему, которая сдерживает регенеративную медицину и многие
другие достижения).
Техники
теперь доступно для перезаписи этой уставки, в результате чего, например,
у двухголовых плоских червей
что при разрезании на части в простой воде (без дополнительных манипуляций)
приводят к появлению последующих поколений регенерированных двухголовых червей (как показано на рисунке).
над). Важно приступить к разработке моделей вычислительной
процессы, которые хранят целевое состояние системного уровня для поведения роя
, чтобы можно было разработать эффективные стратегии для рационального редактирования этого
информационная структура, приводящая к желаемым крупномасштабным результатам (таким образом
победить обратную проблему, которая сдерживает регенеративную медицину и многие
другие достижения).
Инженерия и машинное обучение
Модели, описанные в этой статье, работают на мощном графическом процессоре современного
компьютер или смартфон. Тем не менее, давайте порассуждаем о том, что «более физическое»
реализация такой системы могла бы выглядеть. Мы можем представить это как сетку
крошечных независимых компьютеров, имитирующих отдельные ячейки. Каждый из этих
компьютерам потребуется примерно 10 КБ ПЗУ для хранения «ячейки
геном »: веса нейронной сети и управляющий код, а также около 256 байт
RAM для состояния ячейки и промежуточных активаций.Клетки должны иметь возможность
для передачи своих 16-значных векторов состояния соседям. Каждая ячейка
также требуется RGB-диод для отображения цвета пикселя, который он представляет. А
обновление одной ячейки потребует около 10 тыс. операций умножения-сложения и выполняет
не нужно синхронизировать по сети. Мы предполагаем, что клетки могут
ждать случайных интервалов времени между обновлениями. Система, описанная выше
единообразно и децентрализовано. Тем не менее, наш метод позволяет его запрограммировать.
для достижения предопределенного глобального состояния и восстановления этого состояния в случае
многоэлементные сбои и перезапуски.Поэтому мы предполагаем такой вид
моделирование может быть использовано для создания надежных самоорганизующихся агентов.
Мы можем представить это как сетку
крошечных независимых компьютеров, имитирующих отдельные ячейки. Каждый из этих
компьютерам потребуется примерно 10 КБ ПЗУ для хранения «ячейки
геном »: веса нейронной сети и управляющий код, а также около 256 байт
RAM для состояния ячейки и промежуточных активаций.Клетки должны иметь возможность
для передачи своих 16-значных векторов состояния соседям. Каждая ячейка
также требуется RGB-диод для отображения цвета пикселя, который он представляет. А
обновление одной ячейки потребует около 10 тыс. операций умножения-сложения и выполняет
не нужно синхронизировать по сети. Мы предполагаем, что клетки могут
ждать случайных интервалов времени между обновлениями. Система, описанная выше
единообразно и децентрализовано. Тем не менее, наш метод позволяет его запрограммировать.
для достижения предопределенного глобального состояния и восстановления этого состояния в случае
многоэлементные сбои и перезапуски.Поэтому мы предполагаем такой вид
моделирование может быть использовано для создания надежных самоорганизующихся агентов.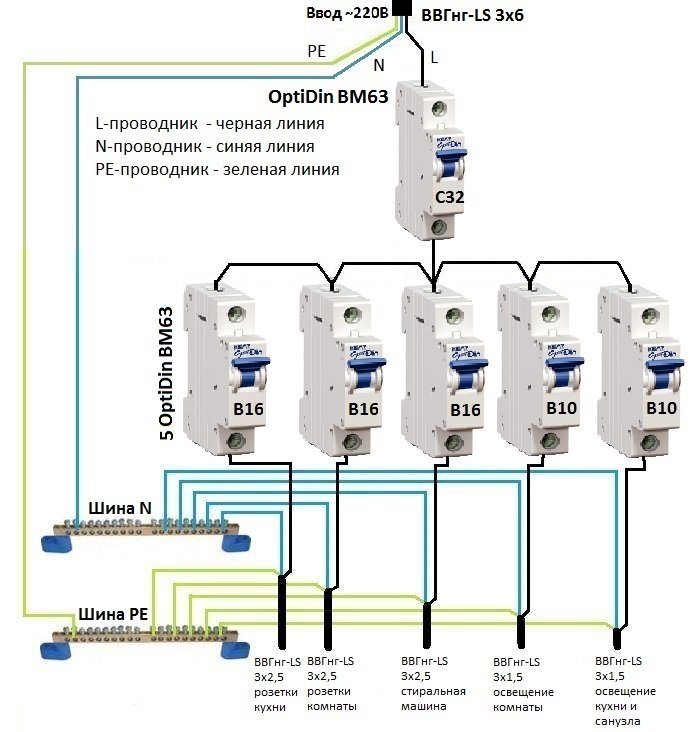 На
более теоретический фронт машинного обучения, мы показываем пример
децентрализованная модель, способная выполнять чрезвычайно сложные задачи. Мы верим
это направление противоположно более традиционному используемому глобальному моделированию.
в большинстве современных работ в области глубокого обучения, и мы надеемся
эта работа послужит источником вдохновения для изучения более децентрализованного обучения
моделирование.
На
более теоретический фронт машинного обучения, мы показываем пример
децентрализованная модель, способная выполнять чрезвычайно сложные задачи. Мы верим
это направление противоположно более традиционному используемому глобальному моделированию.
в большинстве современных работ в области глубокого обучения, и мы надеемся
эта работа послужит источником вдохновения для изучения более децентрализованного обучения
моделирование.
Эта статья является частью Тема для дифференцируемых самоорганизующихся систем, экспериментальный формат сбора приглашенных коротких статей, углубляющихся в дифференцируемые самоорганизующиеся системы с вкраплениями критических комментарии нескольких экспертов в смежных областях.
Тема для дифференцируемых самоорганизующихся систем Самоклассифицирующиеся цифры MNISTдифференциальных уравнений — Как решить (O / P) DE с помощью клеточного автомата?
Вот пример:
dx = 1. / 1000;
сетка = ConstantArray [0, 1000];
сетка [[1]] = 1;
sol = CellularAutomaton [{
{0., x_, _}:> x,
{x_, _, _}:> x + dx x
}, сетка, 1000] [[- 1, 2 ;;]];
sol2 = NDSolveValue [{
y '[x] == y [x],
у [0] == 1
}, y, {x, 0, 1}];
Показать[
ListLinePlot [sol, DataRange -> {0, 1}, PlotStyle -> Толщина [0,02]],
График [sol2 [x], {x, 0, 1}, PlotStyle -> {Dashed, White}]
]
/ 1000;
сетка = ConstantArray [0, 1000];
сетка [[1]] = 1;
sol = CellularAutomaton [{
{0., x_, _}:> x,
{x_, _, _}:> x + dx x
}, сетка, 1000] [[- 1, 2 ;;]];
sol2 = NDSolveValue [{
y '[x] == y [x],
у [0] == 1
}, y, {x, 0, 1}];
Показать[
ListLinePlot [sol, DataRange -> {0, 1}, PlotStyle -> Толщина [0,02]],
График [sol2 [x], {x, 0, 1}, PlotStyle -> {Dashed, White}]
]
Решение дифференциальных уравнений с помощью клеточных автоматов похоже на простое интегрирование Эйлера.Это можно сделать для многих типов дифференциальных уравнений путем их дискретизации с помощью, например, центральные различия. В данном случае я просто применяю простое правило: $$ у (х + \ mathrm dx) = у (х) + у (х) \ mathrm dx $$ В Mathematica это правило выглядит так:
{x_, _, _}:> x + dx x
Левая часть этого правила центрируется на элементе, который будет заменен правой частью.
CellularAutomaton предполагает, что сеть циклична, по крайней мере, я не смог найти способ отключить это. (Конечно, есть и другие способы моделирования клеточных автоматов в системе Mathematica, но я придерживаюсь этого, чтобы подчеркнуть, что я решаю уравнение именно с клеточным автоматом.) Это означает, что первый элемент в списке, установленный равным 1, поскольку это начальное условие, будет заменено нулем, поскольку предыдущий элемент списка равен нулю. Чтобы остановить это, я включил правило
(Конечно, есть и другие способы моделирования клеточных автоматов в системе Mathematica, но я придерживаюсь этого, чтобы подчеркнуть, что я решаю уравнение именно с клеточным автоматом.) Это означает, что первый элемент в списке, установленный равным 1, поскольку это начальное условие, будет заменено нулем, поскольку предыдущий элемент списка равен нулю. Чтобы остановить это, я включил правило
{0., x_, _}:> x
0 в этом правиле — последний элемент в сетке.
Может быть, это спорно, если это действительно клеточный автомат, потому что государства не дискретно, но я также читал о «вещественных клеточных автоматах» и «непрерывных автоматах». Когда говорят о решении УЧП с использованием клеточных автоматов, я почти уверен, что речь идет о более широком классе методов на основе решеток.
Далее я покажу задачу из моего старого домашнего задания, касающуюся системы реакции-диффузии. Это решает связанную систему дифференциальных уравнений на сетке с использованием методов, аналогичных клеточным автоматам (но определенно с использованием непрерывных состояний. 2 в
2 в
Вы можете думать о $ u $ и $ v $ как о количестве частиц двух разных типов. Частицы распространяются (диффундируют) в пространстве, а также вступают в реакцию друг с другом, что может привести к превращению частицы одного типа в частицы другого типа. Можно представить, что это приведет к очень простым решениям; что все частицы в конечном итоге будут одного типа или что все частицы будут равномерно распределены по всему пространству. Однако оказывается, что решения могут быть намного сложнее.2}
$Мы могли бы реализовать это как свертку с таким ядром:
ker = {
{0, 1, 0},
{1, -4, 1},
{0, 1, 0}
};
лапласиан = ListConvolve [кер, сетка];
Но мы могли бы также использовать встроенную функцию лапласиана :
LaplacianFilter [u, 1, Padding-> "Periodic"]
Я указываю, что сетка должна быть периодической, потому что это то, что мы хотим для этого конкретного PDE.
Выполнение (дискретной) свертки и развитие клеточного автомата — это одно и то же. 2 v + d LaplacianFilter [v, 1, Padding -> «Periodic»] шаг [a_, b_, d _] [{uval_, vval_}]: = {
увалы + 0,01 дудт [а, б, увалы, валы],
vval + 0,01 dvdt [b, uval, vval, d]
} смоделировать [d_, nrOfIterations_]: = Модуль [
{u, v, a = 3, b = 8, L = 128},
u = ConstantArray [a, {L, L}] + RandomReal [{- 0,1 a, 0,1 a}, {L, L}];
v = ConstantArray [b / 1, {L, L}] + RandomReal [{- 0,1 b / a, 0,1 b / a}, {L, L}];
Nest [шаг [a, b, d], {u, v}, nrOfIterations]
] res = моделировать [2.3, 20000];
MatrixPlot [#, ImageSize -> 250, PlotTheme -> «Монохромный»] & / @ res // Строка
2 v + d LaplacianFilter [v, 1, Padding -> «Periodic»] шаг [a_, b_, d _] [{uval_, vval_}]: = {
увалы + 0,01 дудт [а, б, увалы, валы],
vval + 0,01 dvdt [b, uval, vval, d]
} смоделировать [d_, nrOfIterations_]: = Модуль [
{u, v, a = 3, b = 8, L = 128},
u = ConstantArray [a, {L, L}] + RandomReal [{- 0,1 a, 0,1 a}, {L, L}];
v = ConstantArray [b / 1, {L, L}] + RandomReal [{- 0,1 b / a, 0,1 b / a}, {L, L}];
Nest [шаг [a, b, d], {u, v}, nrOfIterations]
] res = моделировать [2.3, 20000];
MatrixPlot [#, ImageSize -> 250, PlotTheme -> «Монохромный»] & / @ res // Строка
Левый график показывает решение для и , а правый график — решение для v .Решения дифференциальных уравнений были найдены путем обновления ячеек в решетках по локальным правилам (для обновления используется только значение ячейки и ее четырех прямых соседей). Как я уже сказал, я думаю, что это то, что люди могут называть решением УЧП с клеточными автоматами, потому что у них много общего. Более простой пример с одной переменной отличается еще меньше, главным образом тем, что эти уравнения в частных производных являются непрерывными.
Более простой пример с одной переменной отличается еще меньше, главным образом тем, что эти уравнения в частных производных являются непрерывными.
Растворы u и v могут обозначать концентрацию двух разных типов частиц, и здесь интересно то, что распределения частиц не являются однородными.На самом деле распределения показывают довольно сложные закономерности, и считается, что этот тип формирования узоров объясняет множество сложных закономерностей, которые мы видим повсюду в природе. Свойство, заключающееся в том, что локальные правила могут создавать сложные паттерны, также известно клеточным автоматам с дискретными состояниями, поэтому в этом отношении также существует взаимосвязь.


 Отличаются высокой пропускной способностью и прочностью схемы. Характеризуется длительной работоспособностью – более десяти тысяч срабатываний, их вам хватит на много лет
Отличаются высокой пропускной способностью и прочностью схемы. Характеризуется длительной работоспособностью – более десяти тысяч срабатываний, их вам хватит на много лет


 Для борьбы с замыканиями и перегрузками ему нужен напарник — автоматический выключатель.
Для борьбы с замыканиями и перегрузками ему нужен напарник — автоматический выключатель.
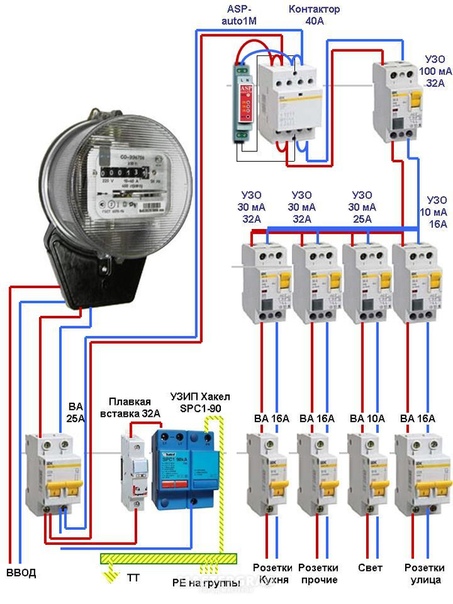 / 1000;
сетка = ConstantArray [0, 1000];
сетка [[1]] = 1;
sol = CellularAutomaton [{
{0., x_, _}:> x,
{x_, _, _}:> x + dx x
}, сетка, 1000] [[- 1, 2 ;;]];
sol2 = NDSolveValue [{
y '[x] == y [x],
у [0] == 1
}, y, {x, 0, 1}];
Показать[
ListLinePlot [sol, DataRange -> {0, 1}, PlotStyle -> Толщина [0,02]],
График [sol2 [x], {x, 0, 1}, PlotStyle -> {Dashed, White}]
]
/ 1000;
сетка = ConstantArray [0, 1000];
сетка [[1]] = 1;
sol = CellularAutomaton [{
{0., x_, _}:> x,
{x_, _, _}:> x + dx x
}, сетка, 1000] [[- 1, 2 ;;]];
sol2 = NDSolveValue [{
y '[x] == y [x],
у [0] == 1
}, y, {x, 0, 1}];
Показать[
ListLinePlot [sol, DataRange -> {0, 1}, PlotStyle -> Толщина [0,02]],
График [sol2 [x], {x, 0, 1}, PlotStyle -> {Dashed, White}]
]